Automated Detection of Cannabis-Induced Alteration in Cardiac Autonomic Regulation of the Indian Paddy-Field Workers Using Empirical Mode Decomposition, Discrete Wavelet Transform and Wavelet Packet Decomposition Techniques with HRV Signals
Abstract
1. Introduction
2. Results
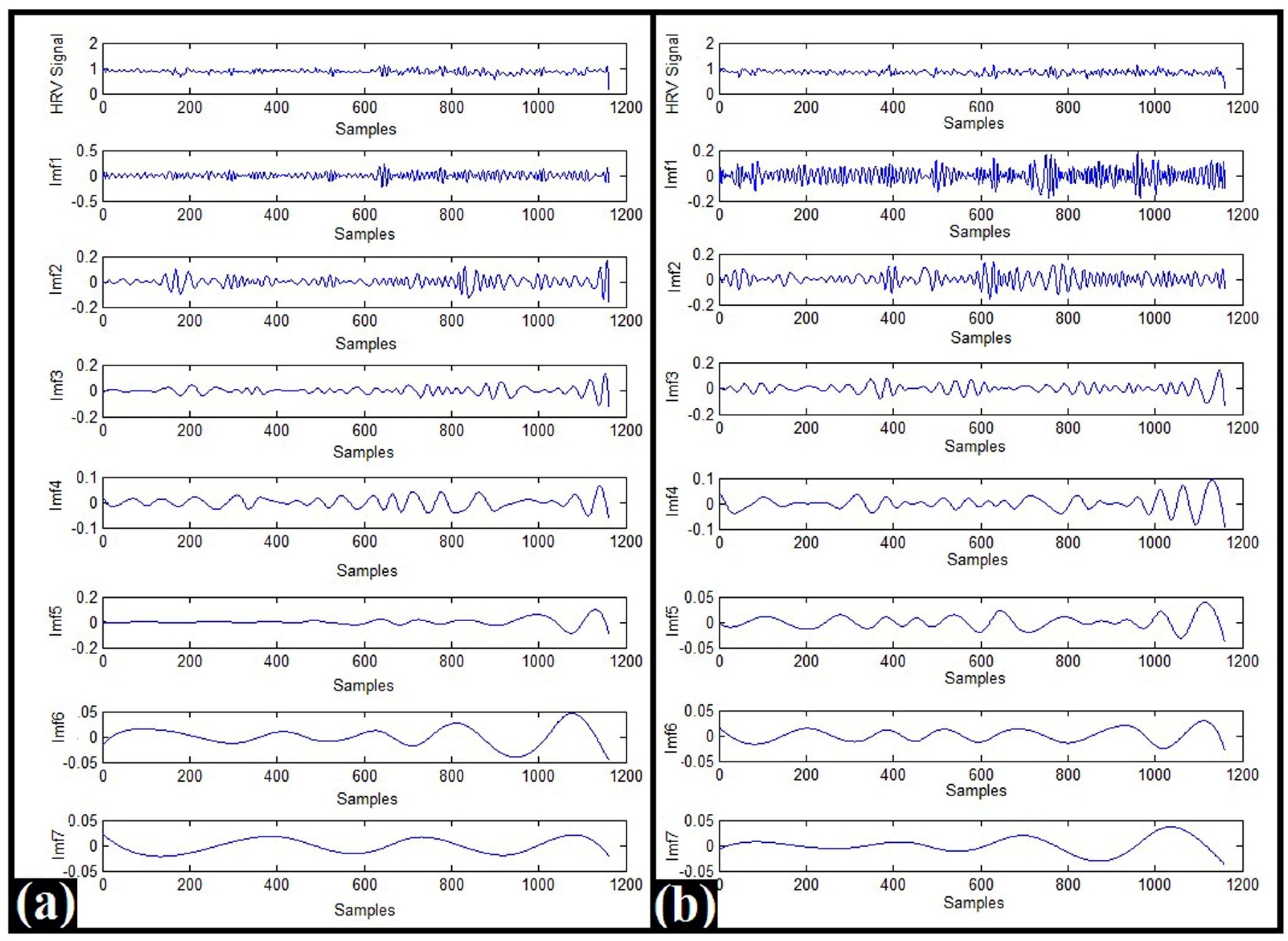
2.1. EMD-Based Analysis of the HRV Signals
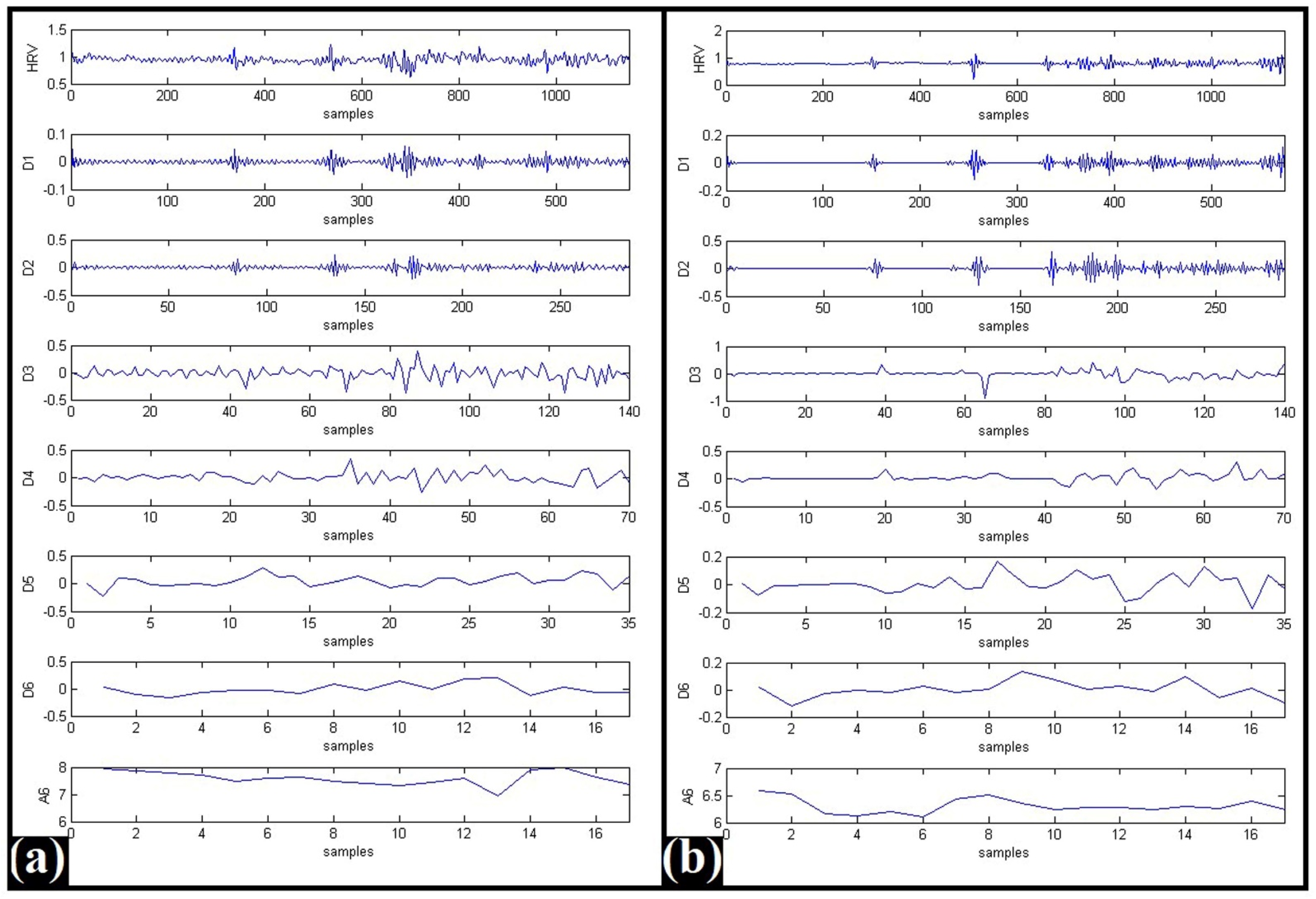
2.2. DWT-Based Analysis of the HRV Signals
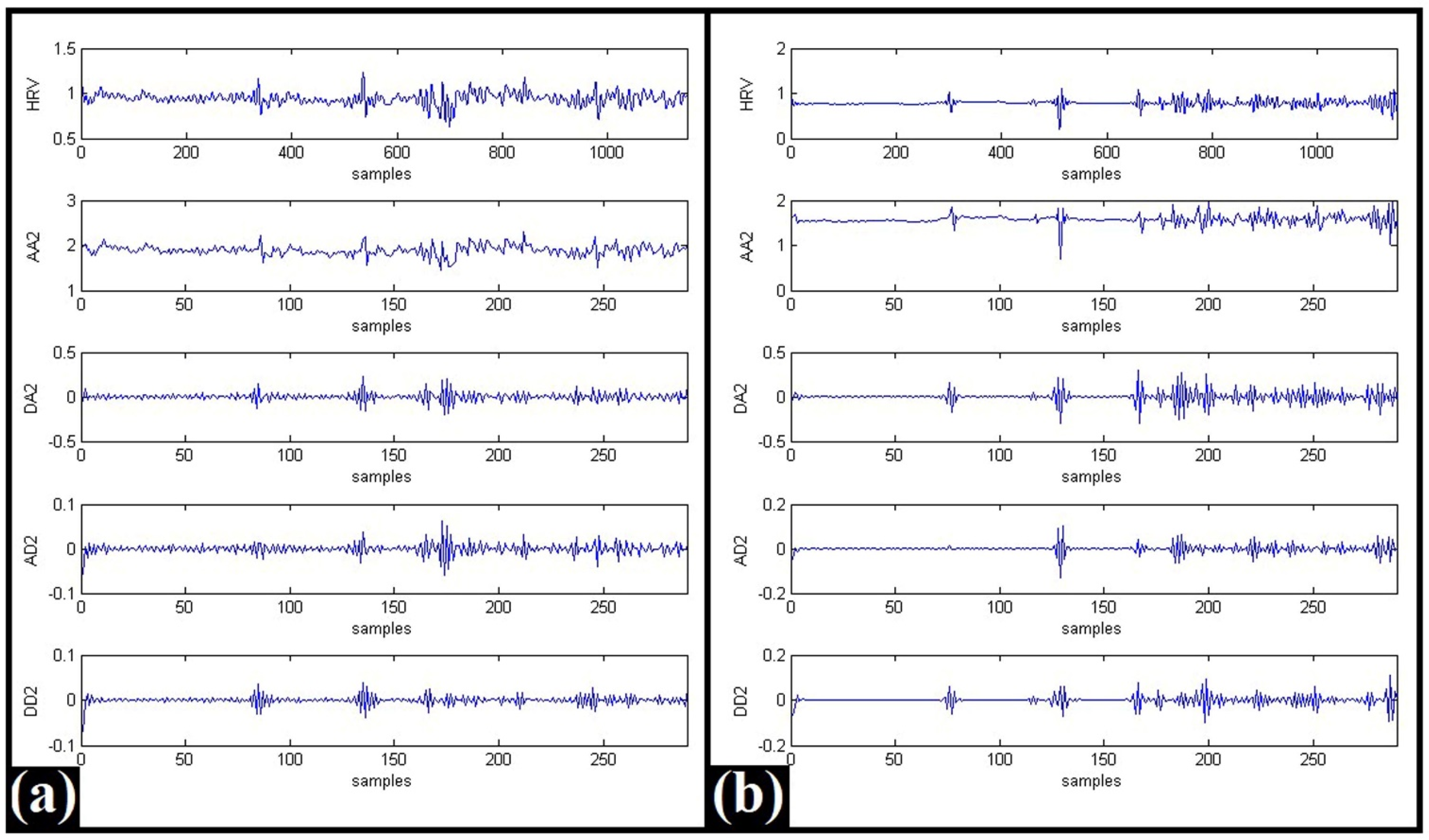
2.3. WPD-Based Analysis of the HRV Signals
3. Discussion
4. Materials and Methods
4.1. Acquisition of the ECG Signals and Extraction of the HRV Signals
4.2. Decomposition of the HRV Signals
4.2.1. EMD
4.2.2. DWT
4.2.3. WPD
4.3. Parameter Extraction
4.3.1. Approximate Entropy (ApE)
4.3.2. Sample Entropy (SaE)
4.3.3. Shannon Entropy (ShE)
4.3.4. Spectral Entropy (SpE)
4.3.5. Singular Value Decomposition Entropy (SVDE)
4.3.6. Permutation Entropy (PeE)
4.3.7. Fisher Information (FI)
4.3.8. Hjorth Descriptors
Signal Activity (SiA)
Hjorth Mobility (HjM)
Hjorth Complexity (HjC)
4.3.9. Petrosian Fractal Dimension (PFD)
4.4. Statistical Analysis
4.5. Development of Machine Learning-Based Models
4.5.1. Selection of Input Parameters
4.5.2. Machine Learning Techniques
4.5.3. Final Model Generation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Jouanjus, E.; Raymond, V.; Lapeyre-Mestre, M.; Wolff, V. What is the current knowledge about the cardiovascular risk for users of cannabis-based products? A systematic review. Curr. Atheroscler. Rep. 2017, 19, 26. [Google Scholar] [CrossRef] [PubMed]
- Arnold, J.C. A primer on medicinal cannabis safety and potential adverse effects. Aust. J. Gen. Pract. 2021, 50, 345–350. [Google Scholar] [CrossRef]
- Kilmer, B. Recreational cannabis—minimizing the health risks from legalization. N. Engl. J. Med. 2017, 376, 705–707. [Google Scholar] [CrossRef] [PubMed]
- Rezkalla, S.; Kloner, R.A. Cardiovascular effects of marijuana. Trends Cardiovasc. Med. 2019, 29, 403–407. [Google Scholar] [CrossRef] [PubMed]
- Nortamo, S.; Ukkola, O.; Kiviniemi, A.; Tulppo, M.; Huikuri, H.; Perkiömäki, J.S. Impaired cardiac autonomic regulation and long-term risk of atrial fibrillation in patients with coronary artery disease. Heart Rhythm. 2018, 15, 334–340. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.E. Guyton and Hall Textbook of Medical Physiology E-Book; Elsevier Health Sciences: Los Angeles, CA, USA, 2015. [Google Scholar]
- Ortiz, A.; Bradler, K.; Moorti, P.; MacLean, S.; Husain, M.I.; Sanches, M.; Goldstein, B.I.; Alda, M.; Mulsant, B.H. Reduced heart rate variability is associated with higher illness burden in bipolar disorder. J. Psychosom. Res. 2021, 145, 110478. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Oh, S.L.; Muhammad, A.; Koh, J.E.W.; Tan, J.H.; Chua, C.K.; Chua, K.P.; Tanet, R.S. Application of empirical mode decomposition (EMD) for automated identification of congestive heart failure using heart rate signals. Neural Comput. Applic. 2017, 28, 3073–3094. [Google Scholar] [CrossRef]
- Geng, D.-Y.; Zhao, J.; Wang, C.-X.; Ning, Q. A decision support system for automatic sleep staging from HRV using wavelet packet decomposition and energy features. Biomed. Signal Process. Control 2020, 56, 101722. [Google Scholar] [CrossRef]
- Acharya, U.R.; Vidya, K.S.; Ghista, D.N.; Lim, W.J.E.; Molinari, F.; Sankaranarayanan, M. Computer-aided diagnosis of diabetic subjects by heart rate variability signals using discrete wavelet transform method. Knowl.-Based Syst. 2015, 81, 56–64. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Pachori, R.B.; Avinash, P.; Shashank, K.; Sharma, R.; Acharya, U.R. Application of empirical mode decomposition for analysis of normal and diabetic RR-interval signals. Expert Syst. Appl. 2015, 42, 4567–4581. [Google Scholar] [CrossRef]
- Djelaila, S.; Berrached, N.-E.; Chalabi, Z.; Taleb-Ahmed, A. The diagnosis of cardie arrhythmias using heart rate variability analysis by the EMD. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 822–825. [Google Scholar]
- Bouziane, A.; Yagoubi, B.; Vergara, L.; Salazar, A. The ANS sympathovagal balance using a hybrid method based on the wavelet packet and the KS-segmentation algorithm. Adv. Circuits Syst. Signal Process. Telecommun. 2015. [Google Scholar]
- Janjarasjitt, S. A Spectral Exponent-Based Feature of RR Interval Data for Congestive Heart Failure Discrimination Using a Wavelet-Based Approach. J. Med. Biol. Eng. 2017, 37, 276–287. [Google Scholar] [CrossRef]
- Nayak, S.K.; Banerjee, I.; Pal, K. Electrocardiogram signal processing-based diagnostics: Applications of wavelet transform. Bioelectron. Med. Devices 2019, 591–614. [Google Scholar] [CrossRef]
- Subasi, A. Electromyogram-controlled assistive devices. In Bioelectronics and Medical Devices; Elsevier: Amsterdam, The Netherlands, 2019; pp. 285–311. [Google Scholar]
- Krauss, C.; Do, X.A.; Huck, N. Deep neural networks, gradient-boosted trees, random forests: Statistical arbitrage on the S&P 500. Eur. J. Oper. Res. 2017, 259, 689–702. [Google Scholar]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Klumpers, L.E.; Thacker, D.L. A brief background on cannabis: From plant to medical indications. J. AOAC Int. 2019, 102, 412–420. [Google Scholar] [CrossRef]
- Hall, W.; Degenhardt, L. Adverse health effects of non-medical cannabis use. Lancet 2009, 374, 1383–1391. [Google Scholar] [CrossRef]
- Cohen, K.; Weizman, A.; Weinstein, A. Positive and negative effects of cannabis and cannabinoids on health. Clin. Pharmacol. Ther. 2019, 105, 1139–1147. [Google Scholar] [CrossRef]
- Hall, W.; Lynskey, M. Assessing the public health impacts of legalizing recreational cannabis use: The US experience. World Psychiatry 2020, 19, 179–186. [Google Scholar] [CrossRef]
- Facts, D. Marijuana. NIoD Abuse 2014. Available online: https://www.ashlanddecisions.org/wp-content/uploads/2018/10/Marijuana-FINAL.pdf (accessed on 21 January 2021).
- Thomas, G.; Kloner, R.A.; Rezkalla, S. Adverse cardiovascular, cerebrovascular, and peripheral vascular effects of marijuana inhalation: What cardiologists need to know. Am. J. Cardiol. 2014, 113, 187–190. [Google Scholar] [CrossRef]
- Kalla, A.; Krishnamoorthy, P.M.; Gopalakrishnan, A.; Figueredo, V.M. Cannabis use predicts risks of heart failure and cerebrovascular accidents: Results from the National Inpatient Sample. J. Cardiovasc. Med. 2018, 19, 480–484. [Google Scholar] [CrossRef]
- Van Keer, J.M. Cannabis-induced third-degree AV block. Case Rep. Emerg. Med. 2019, 2019, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Goyal, H.; Awad, H.H.; Ghali, J.K. Role of cannabis in cardiovascular disorders. J. Thorac. Dis. 2017, 9, 2079. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, M.K.; Kannankeril, P.J.; Goldberger, J.J. Assessment of autonomic function in cardiovascular disease: Physiological basis and prognostic implications. J. Am. Coll. Cardiol. 2008, 51, 1725–1733. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, M.P.; Niskanen, J.-P.; Lipponen, J.A.; Ranta-Aho, P.O.; Karjalainen, P.A. Kubios HRV–heart rate variability analysis software. Comput. Methods Programs Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sudarshan, V.K.; Rong, S.Q.; Tan, Z.; Lim, C.M.; Koh, J.E.; Nayak, S.; Bhandary, S.V. Automated detection of premature delivery using empirical mode and wavelet packet decomposition techniques with uterine electromyogram signals. Comput. Biol. Med. 2017, 85, 33–42. [Google Scholar] [CrossRef]
- Singh, D.; Kumar, V.; Chawla, M. Wavelet filter evaluation for HRV signal processing. In Proceedings of the IET 3rd International Conference MEDSIP 2006. Advances in Medical, Signal and Information Processing, Glasgow, UK, 17–19 July 2006. [Google Scholar]
- Gao, J.; Hu, J.; Tung, W.-W. Complexity measures of brain wave dynamics. Cogn. Neurodynamics 2011, 5, 171–182. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. Based Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Rees, D.G. Essential Statistics; Chapman and Hall/CRC: New York, NY, USA, 2018. [Google Scholar]
- MacFarland, T.W.; Yates, J.M. Mann–whitney u test. In Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer: Berlin/Heidelberg, Germany, 2016; pp. 103–132. [Google Scholar]
- Abhishekh, H.A.; Nisarga, P.; Kisan, R.; Meghana, A.; Chandran, S.; Raju, T.; Sathyaprabha, T.N. Influence of age and gender on autonomic regulation of heart. J. Clin. Monit. Comput. 2013, 27, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Nayak, S.K.; Pradhan, B.K.; Banerjee, I.; Pal, K. Analysis of heart rate variability to understand the effect of cannabis consumption on Indian male paddy-field workers. Biomed. Signal Process. Control. 2020, 62, 102072. [Google Scholar] [CrossRef]
- Rajkomar, A.; Dean, J.; Kohane, I. Machine learning in medicine. N. Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef]
- Nisbet, R.; Elder, J.; Miner, G. Handbook of Statistical Analysis and Data Mining Applications; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- DeAngelis, B.N.; Al’Absi, M. Regular cannabis use is associated with blunted affective, but not cardiovascular, stress responses. Addict. Behav. 2020, 107, 106411. [Google Scholar] [CrossRef]
- Rompala, G.; Nomura, Y.; Hurd, Y.L. Maternal cannabis use is associated with suppression of immune gene networks in placenta and increased anxiety phenotypes in offspring. Proc. Natl. Acad. Sci. USA 2021, 118, e2106115118. [Google Scholar] [CrossRef]
- Lee, K.; Laviolette, S.R.; Hardy, D. Exposure to Δ9-tetrahydrocannabinol during rat pregnancy leads to impaired cardiac dysfunction in postnatal life. Pediatric Res. 2021, 90, 532–539. [Google Scholar] [CrossRef]
- Majhi, M.K.; Pradhan, B.K.; Sarkar, P.; Sivaraman, J.; Pal, K. Can statistical and entropy-based features extracted from ECG signals efficiently differentiate the cannabis-consuming women population from the non-consumer? Med. Hypotheses 2022, 167, 110952. [Google Scholar] [CrossRef]
- Razanouski, Z.; Corcoran, A. The effects of acute cannabidiol on autonomic balance. Physiology 2022, 36. [Google Scholar] [CrossRef]
- LabVIEW for ECG Signal Processing. Available online: http://www.ni.com/tutorial/6349/en/ (accessed on 25 January 2021).
- Zaidi, A.M.A.; Ahmed, M.J.; Bakibillah, A. Feature extraction and characterization of cardiovascular arrhythmia and normal sinus rhythm from ECG signals using LabVIEW. In IEEE International Conference on Imaging, Vision & Pattern Recognition (icIVPR); IEEE: Dhaka, Bangladesh, 2017; pp. 1–6. [Google Scholar]
- Khong, W.; Mariappan, M.; Rao, N.K. National instruments LabVIEW biomedical toolkit for measuring heart beat rate and ECG LEAD II features. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Pulau Pinang, Malaysia, 2019; p. 012020. [Google Scholar]
- Bilgin, S.; Çolak, O.H.; Koklukaya, E.; Arı, N. Efficient solution for frequency band decomposition problem using wavelet packet in HRV. Digit. Signal Process. 2008, 18, 892–899. [Google Scholar] [CrossRef]
- Bajaj, V.; Pachori, R.B. Classification of seizure and nonseizure EEG signals using empirical mode decomposition. IEEE Trans. Inf. Technol. Biomed. 2011, 16, 1135–1142. [Google Scholar] [CrossRef]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hu, Q.; Qin, A.; Zhang, Q.; He, J.; Sun, G. Fault diagnosis based on weighted extreme learning machine with wavelet packet decomposition and KPCA. IEEE Sens. J. 2018, 18, 8472–8483. [Google Scholar] [CrossRef]
- Pincus, S.M.; Huang, W.-M. Approximate entropy: Statistical properties and applications. Commun. Stat. Theory Methods 1992, 21, 3061–3077. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Ghose, U. A Novel Differential Selection Method Based on Singular Value Decomposition Entropy for Solving Real-World Problems. In International Conference on Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2018; pp. 33–47. [Google Scholar]
- Jelinek, H.F.; Donnan, L.; Khandoker, A.H. Singular value decomposition entropy as a measure of ankle dynamics efficacy in a Y-balance test following supportive lower limb taping. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 2439–2442. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Jouny, C.C.; Bergey, G.K. Characterization of early partial seizure onset: Frequency, complexity and entropy. Clin. Neurophysiol. 2012, 123, 658–669. [Google Scholar] [CrossRef]
- Ly, A.; Marsman, M.; Verhagen, J.; Grasman, R.P.; Wagenmakers, E.-J. A tutorial on Fisher information. J. Math. Psychol. 2017, 80, 40–55. [Google Scholar] [CrossRef]
- Frieden, B.R. Science from Fisher Information: A Unification; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Tanveer, M.; Pachori, R.B.; Angami, N. Classification of seizure and seizure-free EEG signals using Hjorth parameters. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 2180–2185. [Google Scholar]
- Hadiyoso, S.; Tati, L.E. Mild Cognitive Impairment Classification using Hjorth Descriptor Based on EEG Signal. In Proceedings of the 2018 International Conference on Control, Electronics, Renewable Energy and Communications (ICCEREC), Bandung, Indonesia, 5–7 December 2018; pp. 231–234. [Google Scholar]
- Chow, J.C.; Ouyang, C.S.; Chiang, C.T.; Yang, R.C.; Wu, R.C.; Wu, H.C.; Lin, L.C. Novel method using Hjorth mobility analysis for diagnosing attention-deficit hyperactivity disorder in girls. Brain Dev. 2019, 41, 334–340. [Google Scholar] [CrossRef]
- Hauben, M. A visual aid for teaching the Mann–Whitney U formula. Teach. Stat. 2018, 40, 60–63. [Google Scholar] [CrossRef]
- McKnight, P.E.; Najab, J. Mann-Whitney U Test. In The Corsini Encyclopedia of Psychology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; p. 1. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Oh, S.L.; Raghavendra, U.; Tan, J.H.; Adam, M.; Gertych, A.; Hagiwara, Y. Automated identification of shockable and non-shockable life-threatening ventricular arrhythmias using convolutional neural network. Future Gener. Comput. Syst. 2018, 79, 952–959. [Google Scholar] [CrossRef]
- Choy, G.; Khalilzadeh, O.; Michalski, M.; Do, S.; Samir, A.E.; Pianykh, O.S.; Geis, R.; Pandharipande, P.V.; Brink, J.A.; Dreyer, K.J. Current applications and future impact of machine learning in radiology. Radiology 2018, 288, 318–328. [Google Scholar] [CrossRef]
- Kotu, V.; Deshpande, B. Predictive Analytics and Data Mining: Concepts and Practice with Rapidminer; Morgan Kaufmann: Waltham, MA, USA, 2015. [Google Scholar]
- Li, T.; Zhou, M. ECG classification using wavelet packet entropy and random forests. Entropy 2016, 18, 285. [Google Scholar] [CrossRef]
- Novaković, J. Toward optimal feature selection using ranking methods and classification algorithms. Yugosl. J. Oper. Res. 2016, 21, 1. [Google Scholar] [CrossRef]
- Hall, M.A.; Smith, L.A. Practical feature subset selection for machine learning. In Proceedings of the Computer Science ’98, 21st Australasian Computer Science Conference ACSC’98, Perth, Australia, 4–6 February 1998; McDonald, C., Ed.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 181–191. [Google Scholar]
- Zhu, W.; Feng, J.; Lin, Y. Using gini-index for feature selection in text categorization. In Proceedings of the 2014 International Conference on Information, Business and Education Technology (ICIBET 2014), Beijing, China, 27–28 February 2014; Atlantis Press: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Liu, H.; Setiono, R. Chi2: Feature selection and discretization of numeric attributes. In Proceedings of the 7th IEEE International Conference on Tools with Artificial Intelligence, Herndon, VA, USA, 5–8 November 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 388–391. [Google Scholar]
- Blessie, E.C.; Karthikeyan, E. Sigmis: A feature selection algorithm using correlation based method. J. Algorithms Comput. Technol. 2012, 6, 385–394. [Google Scholar] [CrossRef]
- RapidMiner 9 Operator Reference Manual. 20 December 2019. Available online: https://docs.rapidminer.com/latest/studio/operators/rapidminer-studio-operator-reference.pdf (accessed on 20 December 2019).
- Kamkar, I.; Gupta, S.K.; Phung, D.; Venkatesh, S. Stable feature selection for clinical prediction: Exploiting ICD tree structure using Tree-Lasso. J. Biomed. Inform. 2015, 53, 277–290. [Google Scholar] [CrossRef] [PubMed]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 1, 213. [Google Scholar] [CrossRef] [PubMed]
- Almansour, N.A.; Syed, H.F.; Khayat, N.R.; Altheeb, R.K.; Juri, R.E.; Alhiyafi, J.; Alrashed, S.; Olatunji, S.O. Neural network and support vector machine for the prediction of chronic kidney disease: A comparative study. Comput. Biol. Med. 2019, 109, 101–111. [Google Scholar] [CrossRef]
- Tan, P.-N. Introduction to Data Mining; Pearson Education: Delhi, India, 2018. [Google Scholar]
- Tripathi, M.; Singal, S.K. Use of Principal Component Analysis for parameter selection for development of a novel Water Quality Index: A case study of river Ganga India. Ecol. Indic. 2019, 96, 430–436. [Google Scholar] [CrossRef]
- Thomas, M.; De Brabanter, K.; De Moor, B. New bandwidth selection criterion for Kernel PCA: Approach to dimensionality reduction and classification problems. BMC Bioinform. 2014, 15, 137. [Google Scholar] [CrossRef]
- Tharwat, A. Principal component analysis-a tutorial. IJAPR 2016, 3, 197–240. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Zaki, M.J.; Meira, W., Jr.; Meira, W. Data Mining and Analysis: Fundamental Concepts and Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Gennari, J.H.; Langley, P.; Fisher, D. Models of incremental concept formation. Artif. Intell. 1989, 40, 11–61. [Google Scholar] [CrossRef]
- Bjaoui, M.; Sakly, H.; Said, M.; Kraiem, N.; Bouhlel, M.S. Depth insight for data scientist with RapidMiner—An innovative tool for AI and big data towards medical applications. In Proceedings of the 2nd International Conference on Digital Tools & Uses Congress; 2020; pp. 1–6. [Google Scholar]
- Subasi, A. Electroencephalogram-controlled assistive devices. In Bioelectronics and Medical Devices; Elsevier: Amsterdam, The Netherlands, 2019; pp. 261–284. [Google Scholar]
- Chang, C.H.; Rampasek, L.; Goldenberg, A. Dropout feature ranking for deep learning models. Bioinformatics 2017, 1–8. [Google Scholar] [CrossRef]
- Wang, G.; Yuan, Y.; Chen, X.; Li, J.; Zhou, X. Learning discriminative features with multiple granularities for person re-identification. In Proceedings of the 26th ACM international conference on Multimedia, Seoul, Korea, 22–26 October 2018; pp. 274–282. [Google Scholar]
- Maguire, T.; Manuel, L.; Smedinga, R.A.; Biehl, M. A review of feature selection and ranking methods. In Proceedings of the 19th SC@RUG 2022 Proceedings 2021–2022; Smedinga, R., Biehl, M., Eds.; Rijksuniversiteit Groningen: Groningen, The Netherlands, 2022; pp. 15–20. Available online: https://pure.rug.nl/ws/portalfiles/portal/214074117/proceedings_2022.pdf (accessed on 9 June 2022).
- Moran, M.D. Arguments for rejecting the sequential Bonferroni in ecological studies. Oikos 2003, 100, 403–405. [Google Scholar] [CrossRef]

| Parameters | Statistical Test Name | Category-C | Category-B | p-Value | ||||
|---|---|---|---|---|---|---|---|---|
| MD ± SD | 25th | 75th | MD ± SD | 25th | 75th | |||
| IMF5SVDE | t-test | 0.329 ± 0.064 | 0.288 | 0.377 | 0.355 ± 0.054 | 0.318 | 0.385 | 0.010 |
| IMF5SpE | t-test | 4.088 ± 0.450 | 3.756 | 4.380 | 4.245 ± 0.523 | 3.825 | 4.555 | 0.049 |
| IMF5FI | t-test | 0.884 ± 0.029 | 0.862 | 0.902 | 0.872 ± 0.025 | 0.858 | 0.889 | 0.011 |
| IMF5HjC | t-test | 0.076 ± 0.021 | 0.063 | 0.092 | 0.085 ± 0.018 | 0.071 | 0.096 | 0.012 |
| IMF7SpE | Mann-Whitney U | 2.420 ± 0.774 | 2.065 | 2.847 | 2.680 ± 0.604 | 2.359 | 3.163 | 0.004 |
| Input Selection Methods | Feature Selection Methods | Classifier | Accuracy (%) | AUC | Precision (%) | F-Measure (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|---|---|---|
| Weight-based (Top 10 important parameters) | CSS | FLM | 61.00 ± 10.49% | 0.641 ± 0.122 | 60.82 ± 9.93% | 62.00 ± 10.81% | 65.00 ± 16.50% | 57.00 ± 17.67% |
| CM PCA | GLM | 61.00 ± 11.01% | 0.618 ± 0.119 | 61.51 ± 12.96% | 61.28 ± 11.86% | 63.00 ± 16.36% | 59.00 ± 15.95% | |
| CM ICA | GBT | 61.00 ± 12.65% | 0.620 ± 0.120 | 62.80 ± 12.95% | 61.03 ± 12.38% | 62.00 ± 15.49% | 60.00 ± 22.11% | |
| CM SVD | GBT | 60.00 ± 10.27% | 0.657 ± 0.104 | 60.34 ± 11.56% | 59.77 ± 11.17% | 60.00 ± 13.33% | 60.00 ± 14.14% | |
| Correlation | RF | 62.50 ± 9.50% | 0.651 ± 0.133 | 67.60 ± 13.48% | 57.26 ± 11.19% | 51.00 ± 12.87% | 74.00 ± 15.06% | |
| Deviation | GBT | 67.00 ± 10.06% | 0.680 ± 0.123 | 70.79 ± 12.86% | 65.57 ± 9.48% | 63.00 ± 11.60% | 71.00 ± 18.53% | |
| GI | LR | 61.00 ± 4.59% | 0.622 ± 0.079 | 62.28 ± 8.07% | 60.49 ± 6.14% | 61.00 ± 12.87% | 61.00 ± 13.70% | |
| IG | GBT | 67.00 ± 9.78% | 0.694 ± 0.104 | 71.45 ± 15.07% | 64.83 ± 12.18% | 64.00 ± 20.66% | 70.00 ± 21.08% | |
| IGR | LR | 58.00 ± 9.78% | 0.628 ± 0.133 | 59.22 ± 10.93% | 57.33 ± 12.12% | 59.00 ± 18.53% | 57.00 ± 19.47% | |
| PCA | FLM | 64.00 ± 9.37% | 0.672 ± 0.132 | 63.42 ± 9.97% | 66.25 ± 8.68% | 71.00 ± 12.87% | 57.00 ± 18.89% | |
| Relief | GBT | 65.00 ± 11.30% | 0.698 ± 0.117 | 68.56 ± 14.11% | 62.92 ± 11.60% | 60.00 ± 14.14% | 70.00 ± 17.64% | |
| Rule | GBT | 62.50 ± 11.61% | 0.661 ± 0.153 | 62.70 ± 11.32% | 61.79 ± 12.92% | 62.00 ± 16.19% | 63.00 ± 14.18% | |
| SVM | FLM | 59.50 ± 13.43% | 0.614 ± 0.154 | 59.25 ± 11.98% | 57.66 ± 15.18% | 57.00 ± 18.89% | 62.00 ± 12.29% | |
| TI | DL | 60.50 ± 12.12% | 0.631 ± 0.144 | 57.90 ± 10.34% | 64.21 ± 14.10% | 74.00 ± 21.19% | 47.00 ± 17.67% | |
| Uncertainty | SVM | 61.00 ± 9.66% | 0.618 ± 0.144 | 59.98 ± 8.02% | 63.09 ± 9.85% | 68.00 ± 15.49% | 54.00 ± 15.06% | |
| Dimension Reduction | PCA | GBT | 58.00 ± 11.11% | 0.609 ± 0.117 | 60.30 ± 17.06% | 58.06 ± 10.35% | 58.00 ± 12.29% | 58.00 ± 18.74% |
| ICA | SVM | 60.50 ± 9.85% | 0.613 ± 0.139 | 60.99 ± 11.44% | 62.08 ± 9.50% | 66.00 ± 17.13% | 55.00 ± 19.58% | |
| Kernel PCA | GBT | 64.00 ± 14.68% | 0.656 ± 0.156 | 66.38 ± 17.96% | 60.12 ± 17.62% | 56.00 ± 19.55% | 72.00 ± 14.76% | |
| SVD | RF | 58.00 ± 9.49% | 0.551 ± 0.142 | 67.58 ± 23.68% | 38.56 ± 18.28% | 28.00 ± 15.49% | 28.00 ± 15.49% | |
| SOM | RF | 62.00 ± 7.89% | 0.647 ± 0.102 | 61.32 ± 9.76% | 60.77 ± 13.44% | 62.00 ± 18.74% | 62.00 ± 12.29% |
| Parameters | Statistical Test Name | Category-C | Category-B | p-Value | ||||
|---|---|---|---|---|---|---|---|---|
| MD ± SD | 25th | 75th | MD ± SD | 25th | 75th | |||
| SVDE1 | t-test | 1.399 ± 0.084 | 1.326 | 1.459 | 1.369 ± 0.070 | 1.317 | 1.412 | 0.016 |
| SpE1 | t-test | 6.808 ± 0.323 | 6.556 | 7.061 | 6.728 ± 0.292 | 6.512 | 6.839 | 0.039 |
| FI1 | t-test | 0.200 ± 0.073 | 0.143 | 0.258 | 0.221 ± 0.060 | 0.185 | 0.266 | 0.013 |
| HjC1 | Mann-Whitney U | 1.843 ± 0.074 | 1.78 | 1.885 | 1.856 ± 0.495 | 1.817 | 1.886 | 0.019 |
| HjM1 | Mann-Whitney U | 1.024 ± 0.017 | 1.015 | 1.035 | 1.019 ± 0.010 | 1.013 | 1.025 | 0.014 |
| PFD1 | t-test | 1.022 ± 0.001 | 1.021 | 1.023 | 1.023 ± 0.001 | 1.022 | 1.023 | 0.003 |
| PFD2 | t-test | 1.018 ± 0.001 | 1.018 | 1.020 | 1.019 ± 0.001 | 1.018 | 1.02 | 0.023 |
| Classification accuracies of the best ML models generated from DWT-based processing of HRV signals at different decomposition levels | ||||||||
| Mother Wavelet | Model Details | Decomposition Level | ||||||
| Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 | Level 8 | ||
| db02 | Parameter selection method | Uncertainty | Relief | Uncertainty | SOM | SVM | IG | SVM |
| ML Model | GBT | GBT | GBT | RF | GLM | NB | SVM | |
| Accuracy | 62.00 ± 9.49% | 64.50 ± 6.85% | 65.00 ± 11.30% | 64.50 ± 6.85% | 61.50 ± 11.07% | 64.50 ± 9.26% | 66.00 ± 12.65% | |
| db04 | Parameter selection method | CSS | Kernel PCA | CSS | CSS | CSS | CSS | CSS |
| ML Model | GBT | RF | GBT | GBT | GBT | GBT | GBT | |
| Accuracy | 62.00 ± 9.49% | 64.50 ± 6.85% | 65.00 ± 11.30% | 64.50 ± 6.85% | 61.50 ± 11.07% | 64.50 ± 9.26% | 66.00 ± 12.65% | |
| db06 | Parameter selection method | TI | GI | CSS | CSS | CSS | Kernel PCA | CSS |
| ML Model | GBT | GBT | GBT | GBT | RF | GBT | GBT | |
| Accuracy | 65.50 ± 13.01% | 67.00 ± 8.88% | 67.00 ± 6.32% | 66.50 ± 5.30% | 68.50 ± 8.51% | 67.00 ± 12.95% | 65.50 ± 8.32% | |
| db08 | Parameter selection method | GI | Rule | CSS | Rule | GI | Uncertainty | GI |
| ML Model | GBT | GBT | NB | GBT | GBT | GBT | GBT | |
| Accuracy | 71.00 ± 8.43% | 65.50 ± 8.64% | 67.00 ± 10.59% | 69.50 ± 14.03% | 68.00 ± 9.19% | 67.50 ± 11.84% | 73.00 ± 5.87% | |
| AUC of the best ML models generated from DWT-based processing of HRV signals at different decomposition levels | ||||||||
| Mother Wavelet | Model Details | Decomposition Level | ||||||
| Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 | Level 8 | ||
| db02 | Parameter selection method | Uncertainty | Relief | Uncertainty | SOM | SVM | IG | SVM |
| ML Model | GBT | GBT | GBT | RF | GLM | NB | SVM | |
| AUC | 0.683 ± 0.141 | 0.661 ± 0.119 | 0.687 ± 0.141 | 0.643 ± 0.104 | 0.661 ± 0.128 | 0.665 ± 0.084 | 0.676 ± 0.064 | |
| db04 | Parameter selection method | CSS | Kernel PCA | CSS | CSS | CSS | CSS | CSS |
| ML Model | GBT | RF | GBT | GBT | GBT | GBT | GBT | |
| AUC | 0.617 ± 0.149 | 0.681 ± 0.097 | 0.651 ± 0.135 | 0.691 ± 0.066 | 0.652 ± 0.095 | 0.708 ± 0.125 | 0.719 ± 0.119 | |
| db06 | Parameter selection method | TI | GI | CSS | CSS | CSS | Kernel PCA | CSS |
| ML Model | GBT | GBT | GBT | GBT | RF | GBT | GBT | |
| AUC | 0.692 ± 0.135 | 0.705± 0.092 | 0.712 ± 0.091 | 0.701 ± 0.106 | 0.742 ± 0.097 | 0.698 ± 0.126 | 0.674 ± 0.107 | |
| db08 | Parameter selection method | GI | Rule | CSS | Rule | GI | Uncertainty | GI |
| ML Model | GBT | GBT | NB | GBT | GBT | GBT | GBT | |
| AUC | 0.726 ± 0.098 | 0.685± 0.141 | 0.657 ± 0.135 | 0.724 ± 0.140 | 0.723 ± 0.096 | 0.710 ± 0.115 | 0.797 ± 0.102 | |
| Parameters | Category-C | Category-B | p-Value | ||||
|---|---|---|---|---|---|---|---|
| MD ± SD | 25th | 75th | MD ± SD | 25th | 75th | ||
| PFD0 | 1.040 ± 0.003 | 1.039 | 1.043 | 1.042 ± 0.003 | 1.04 | 1.044 | 0.015 |
| SVDE1 | 1.344 ± 0.084 | 1.28 | 1.397 | 1.305 ± 0.075 | 0.103 | 0.168 | 0.023 |
| SpE1 | 5.839 ± 0.334 | 5.585 | 6.078 | 5.743 ± 0.306 | 5.543 | 5.869 | 0.023 |
| FI1 | 0.243 ± 0.070 | 0.1988 | 0.2963 | 0.276 ± 0.062 | 0.219 | 0.31 | 0.025 |
| HjC1 | 1.822 ± 0.855 | 1.749 | 1.875 | 1.847 ± 0.057 | 1.803 | 1.873 | 0.021 |
| PFD1 | 1.048 ± 0.002 | 1.046 | 1.049 | 1.050 ± 0.003 | 1.047 | 1.051 | 0.004 |
| SVDE2 | 1.362 ± 0.061 | 1.318 | 1.409 | 1.341 ± 0.068 | 1.292 | 1.388 | 0.002 |
| SpE2 | 6.218 ± 0.388 | 5.936 | 6.541 | 6.060 ± 0.374 | 5.8 | 6.356 | 0.008 |
| FI2 | 0.226 ± 0.050 | 0.188 | 0.266 | 0.246 ± 0.056 | 0.207 | 0.286 | 0.007 |
| HjC2 | 1.720 ± 0.144 | 1.633 | 1.803 | 1.782 ± 0.107 | 1.683 | 1.836 | 0.003 |
| HjM2 | 1.045 ± 0.046 | 1.031 | 1.089 | 1.039 ± 0.041 | 1.027 | 1.078 | 0.024 |
| PFD2 | 1.048 ± 0.002 | 1.046 | 1.05 | 1.050 ± 0.003 | 1.047 | 1.052 | 0.018 |
| HjC3 | 1.756 ± 0.143 | 1.628 | 1.835 | 1.805 ± 0.109 | 1.718 | 1.86 | 0.003 |
| HjM3 | 1.037 ± 0.038 | 1.018 | 1.076 | 1.023 ± 0.028 | 1.017 | 1.042 | 0.008 |
| Classification accuracies of the best ML models generated from WPD-based processing of HRV signals at different decomposition levels | ||||||||
| Mother Wavelet | Model Details | Decomposition Level | ||||||
| Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 | Level 8 | ||
| db02 | Parameter selection method | CSS | Kernel PCA | GI | CSS | IG | SVM | SVM |
| ML Model | RF | SVM | GBT | NB | FLM | SVM | NB | |
| Accuracy | 64.50 ± 7.98% | 66.00 ± 9.37% | 73.00 ± 5.87% | 67.00 ± 10.85% | 71.50 ± 10.01% | 74.00 ± 9.66% | 75.00 ± 13.94% | |
| db04 | Parameter selection method | CM PCA | IG | IG | IG | GI | IG | SVM |
| ML Model | RF | RF | RF | GBT | GBT | GBT | SVM | |
| Accuracy | 67.00 ± 5.87% | 70.00 ± 9.43% | 67.00 ± 12.52% | 70.00 ± 9.43% | 68.50 ± 9.73% | 69.50 ± 9.85% | 72.00 ± 7.15% | |
| db06 | Parameter selection method | CM PCA | CSS | IGR | IG | Correlation | SVM | SOM |
| ML Model | GBT | GBT | GBT | GBT | GBT | NB | RF | |
| Accuracy | 66.00 ± 11.01% | 68.00 ± 13.58% | 64.00 ± 11.01% | 70.50 ± 9.85% | 46.00 ± 8.43% | 67.00 ± 12.95% | 68.00 ± 12.52% | |
| db08 | Parameter selection method | TI | SVM | SVM | GI | IG | CSS | GI |
| ML Model | GBT | GBT | GBT | GBT | LR | GBT | GBT | |
| Accuracy | 66.00 ± 8.43% | 68.00 ± 11.35% | 68.50 ± 12.92% | 64.00 ± 11.25% | 67.50 ± 8.25% | 70.50 ± 8.32% | 73.00 ± 5.87% | |
| AUC accuracies of the best ML models generated from WPD-based processing of HRV signals at different decomposition levels | ||||||||
| Mother Wavelet | Model Details | Decomposition Level | ||||||
| Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 | Level 8 | ||
| db02 | Parameter selection method | CSS | Kernel PCA | GI | CSS | IG | SVM | SVM |
| ML Model | RF | SVM | GBT | NB | FLM | SVM | NB | |
| AUC | 0.690 ± 0.131 | 0.681 ± 0.135 | 0.797 ± 0.102 | 0.669 ± 0.161 | 0.726 ± 0.112 | 0.731 ± 0.064 | 0.797 ± 0.130 | |
| db04 | Parameter selection method | CM PCA | IG | IG | IG | GI | IG | SVM |
| ML Model | RF | RF | RF | GBT | GBT | GBT | SVM | |
| AUC | 0.694 ± 0.091 | 0.708 ± 0.071 | 0.706 ± 0.138 | 68.00 ± 7.89% | 0.711 ± 0.097 | 0.734 ± 0.128 | 0.780 ± 0.087 | |
| db06 | Parameter selection method | CM PCA | CSS | IGR | IG | Correlation | SVM | SOM |
| ML Model | GBT | GBT | GBT | GBT | GBT | NB | RF | |
| AUC | 0.669 ± 0.124 | 0.732 ± 0.123 | 0.687 ± 0.153 | 0.727 ± 0.124 | 0.408 ± 0.102 | 0.693 ± 0.160 | 0.698 ± 0.136 | |
| db08 | Parameter selection method | TI | SVM | SVM | GI | IG | CSS | GI |
| ML Model | GBT | GBT | GBT | GBT | LR | GBT | GBT | |
| AUC | 0.719 ± 0.113 | 0.651 ± 0.124 | 0.722 ± 0.138 | 0.681 ± 0.156 | 0.706 ± 0.069 | 0.711 ± 0.103 | 0.797 ± 0.102 | |
| Author, Year | Signals Used | Processing Methods or Parameters Extracted | Statistical Methods Used | Classifiers Used | Inference |
|---|---|---|---|---|---|
| DeAngelis et al. (2020) [41] | Blood pressure, heart rate, mean arterial pressure | Systolic blood pressure; diastolic blood pressure, heart rate and mean arterial pressure | Independent-sample t-test and chi-square test | - | Reduced positive (euphoria) and negative (stress, anxiety) affective reactions to acute stress have been linked to chronic cannabis use, suggesting dysregulation of emotions. |
| Rompala et al. (2021) [42] | HRV signal at rest and during auditory startle, hair hormone levels and neurobehavioral traits | HF power components of HRV and gene expressions | Generalized linear model | - | Cannabis intake causes increased cortisol, anxiety, aggression, and hyperactivity in young children. |
| Lee et al. (2021) [43] | Echocardiogram, Heart rate and body temperature | Estimation of stroke volume, ejection fraction, fractional shortening, and cardiac output. | Student’s t-test | - | Maternal intake of cannabis during pregnancy harms fetal growth, causing cardiac dysfunction in the offspring |
| Majhi et al. (2022) [44] | ECG Signals | Statistical and Entropy features | Mann–Whitney U test | ML Models (NB, GLM, LR, FLM, DL, DT, RF, GBT, and SVM) | Statistical and entropy features extracted from ECG segments effectively separate women who use cannabis from those who don’t. |
| Razanouski et al. (2022) [45] | Heart rate, blood pressure and HRV signal | Time-domain parameters | - | - | Increase in parasympatheitic activity due to increased dosage of cannabis |
| Our Study | HRV Signals | Signal Decomposition methods (EMD, DWT and WPD) and Entropy computation | Shapiro–Wilk test, Mann–Whitney U test and t-test | ML Models (NB, GLM, LR, FLM, DL, DT, RF, GBT, and SVM) | Detected significant variation in the HRV signals among the regular cannabis users and non-users. Further, ML models for automatic classification of the cannabis-induced changes in HRV signals have been proposed. |
| Method | Description | Rapidminer Implementation | Ref. | |
|---|---|---|---|---|
| IG | IG is a weight-based parameter selection method that describes the dependency between a parameter X with a class variable Y by divulging information about the reduction in entropy. IG is defined by Equation (14) [70]. | The IG method is implemented using the “Weight by Information Gain” operator. It finds out the relevance of the parameters through information gain and allocates weights to them. It has three critical attributes, namely, normalize weights, sort weights, and sort direction. In our study, the following values of the attributes were chosen:
| [70] | |
| (14) | ||||
| where H(Y) represents the entropy of Y and H(Y|X) corresponds to the entropy of Y given X. | ||||
| IGR | IGR is a parameter selection method that is derived from IG by dividing it with the entropy of the parameter (Equation (15)). IGR helps to expiate the bias introduced by the IG method. | The IGR method is implemented using the “Weight by Information Gain Ratio” operator. It detects the relevance of the parameters through the information gain ratio and allocates weights to them. It has three critical attributes, namely, normalize weights, sort weights, and sort direction. In our study, the following values of the attributes were chosen:
| [71] | |
| (15) | ||||
| where H(X) represents the entropy of parameter X. | ||||
| Uncertainty | Uncertainty is another parameter selection method that focuses on eliminating the inherent bias introduced by the IG method. It is computed as the ratio of twice the IG to the sum of the entropies of the parameter X and the class variable Y (Equation (16)). | The uncertainty method is implemented using the “Weight by Uncertainty” operator. The uncertainty method measures the symmetrical uncertainty to identify the importance of the parameters. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and number of bins. In our study, the following values of the attributes were chosen:
| [71] | |
| (16) | ||||
| where U indicates the uncertainty of Y. | ||||
| GI | GI is an impurity-based parameter selection method. It describes the likelihood of the wrong classification of a randomly selected variable. For a given data set S (i.e., s1, s2, s3…sn) and a class variable Ci (1 ≤ i ≤ k), GI is computed using Equation (17). The value of GI lies between 0 and 1, where 0 means the variable is most useful for classification and vice-versa. | The GI method is implemented using the “Weight by Gini Index” operator. It computes the relevance of the parameters through the impurity index. It has three critical attributes, namely, normalize weights, sort weights, and sort direction. In our study, the following values of the attributes were chosen:
| [72] | |
| (17) | ||||
| where Pi refers to the probability of any sample of Ci | ||||
| CSS | CSS is a popular nonparametric method of parameter selection. It determines the importance of a parameter using the value of the chi-squared statistic (χ2) that is calculated using a class as the reference (Equation (18)). A higher value of χ2 refers to the higher importance of the parameter. | The CSS method is implemented using the “Weight by Chi-Squared Statistic” operator. It quantifies the relevance of the parameters through the computation of CSS. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and the number of bins. In our study, the following values of the attributes were chosen:
| [73] | |
| (18) | ||||
| where Oij refers to the perceived frequency, and Eij refers to the expected frequency. | ||||
| Correlation | Correlation can be regarded as a parameter selection method that is based on the extent of similarity among the parameters. The degree of similarity between any two parameters X and Y is represented with the help of correlation coefficient r (Equation (19)). The value of the correlation coefficient ranges from −1 to 1, where the sign represents the kind of association, i.e., negative or positive, respectively. Its value becomes 0 when the parameters are uncorrelated. | The “Weight by Correlation” operator is used for the implementation of the Correlation method. It quantifies the relevance of the parameters through the computation of the absolute or squared value of correlation. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and squared correlation. In our study, the following values of the attributes were chosen:
| [74,75] | |
| (19) | ||||
| where i indicates the increment variable and n refers to the number of samples of the parameters X and Y. | ||||
| Deviation | Deviation refers to the normalized standard deviation of the parameters. For a parameter X, the standard deviation is calculated using Equation (20) and its normalization can be carried out using the maximum or minimum value of the parameter. | The “Weight by Deviation” operator is used for the implementation of the Deviation method. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and normalize. In our study, the following values of the attributes were chosen:
| [75] | |
| (20) | ||||
| where i indicates the increment variable and n refers to the number of samples of the parameters X and Y. | ||||
| Relief | Relief is a supervised parameter selection method generally used in classification problems. In this method, the samples are chosen arbitrarily from the given data set. Then, their nearest samples belonging to the same class (i.e., near-Hit) and their nearest samples belonging to the other class (i.e., near-Miss) is determined. A score (St) is assigned to the parameter under consideration using Equation (21). The S scores of all the parameters are compared, and the top K parameters are finally considered as the relevant parameters. | The relief method is implemented using the “Weight by Relief” operator. It has six critical attributes, namely, normalize weights, sort weights, sort direction, and the number of bins. In our study, the following values of the attributes were chosen:
| [76] | |
| (21) | ||||
| where xt indicates the arbitrarily chosen sample of the given data set at iteration number t, n represents the total number of samples of the given data set, and d(.) corresponds to Euclidean distance. | ||||
| Rule | The Rule represents a parameter selection method that creates a rule for each of the parameters and calculates the error for them. Each parameter is assigned with a weight based on the error associated with it. The relevance of the parameters is decided based on the value of the weights assigned to them. | The rule method is implemented using the “Weight by Rule” operator. It has three critical attributes, namely, normalize weights, sort weights, and sort direction. In our study, the following values of the attributes were chosen:
| [75] | |
| TI | TI represents the parameter selection method that uses a random forest for determining the importance of the parameters. The random forest is an ensemble learning method containing many decision trees. These decision trees are produced using the parameters extracted from the given dataset. The reduction in impurity caused by each node of all the decision trees is computed. The average value of impurity reduction caused by a parameter over all the trees determines the importance of that parameter. | The TI method is implemented using the “Weight by Tree Importance” operator. It has three critical attributes, namely criterion gain_ratio and normalize weights. In our study, the following values of the attributes were chosen:
| [77] | |
| SVM | SVM is a widely used machine learning method that employs hyperplanes (i.e., normal vectors) for classifying the samples of a signal into several classes. The coefficients associated with the hyperplanes are used to assign weights to the parameters and to rank them. Nevertheless, SVM can act as a parameter selection method only when the parameters have numeric values. | The SVM method is implemented using the “Weight by SVM” operator. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and complexity weighting factor (C). In our study, the following values of the attributes were chosen:
| [78] | |
| CM | The CM method is also a weight-based parameter selection method. However, the peculiarity of this method lies in the fact that it assigns weights to the parameters based on a component generated using the techniques like PCA, ICA, etc. The weights are usually normalized to retain them in the span of 0 to 1. | The CM method is implemented using the “Weight by Component Model” operator. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and component number. In our study, the following values of the attributes were chosen:
| [75] | |
| PCA | PCA is a popular statistical method that uses an orthogonal transformation to convert a number of correlated parameters to a set of uncorrelated parameters known as principal components. The orthogonal transformation is carried out using the eigenvalue analysis of the covariance matrix (S), generated from the parameters of the given signal. The elements of the covariance matrix are defined using Equation (22). The well-defined patterns that are stronger than the noise can be detected in the signal using PCA. Therefore PCA-based dimension reduction also finds application in noise removal. The importance of PCA in parameter selection lies in the fact that it employs the variance of the signal and transforms the signal to new dimensions having fewer parameters, but still preserving maximum variance. | The PCA method is implemented using the “Weight by PCA” operator. It has four critical attributes, namely, normalize weights, sort weights, sort direction, and component number. In our study, the following values of the attributes were chosen:
| [79,80] | |
| (22) | ||||
| where sij indicates the covariance of the ith and jth parameters of the given signal. | ||||
| Kernel PCA | Kernel PCA refers to the generalization of the PCA method using kernels (such as linear, polynomial, or Gaussian) for application to nonlinear data. In this method, the input signal is transformed into a new parameter space using a nonlinear transformation. A kernel matrix K is formed through the dot product of the newly generated parameters in the transformed space, which act as the covariance matrix. In the end, PCA is performed on the kernel matrix K and is called the kernel PCA method. | The Kernel PCA method is implemented using the “Weight by PCA (Kernel)” operator. It has two critical attributes, namely kernel type and kernel gamma. In our study, the following values of the attributes were chosen:
| [81] | |
| ICA | ICA can be regarded as a statistical method that decomposes a complex signal into independent components. ICA is a generalization of the PCA method. Nevertheless, ICA optimizes the higher-order statistics (e.g., kurtosis), unlike PCA, which optimizes the 2nd order statistics of the given signal. Therefore ICA produces independent components, whereas PCA generates uncorrelated components. | The ICA method is implemented using an “Independent Component Analysis” operator. The critical attributes of this operator and their values in our implementation are listed below:
| [82,83] | |
| SVD | SVD is also an extension of the PCA method where the highly correlated parameters are eliminated to reduce redundancy. It results in fewer components as compared to PCA, but retains most of the variance of the extracted signal parameters. | The SVD method is implemented using the “Singular Value Decomposition” operator. It has two critical attributes, namely, dimension reduction and dimensions. In our study, the following values of the attributes were chosen:
| [84] | |
| SOM | SOM corresponds to a neural network that helps in dimension reduction-based parameter selection. It is also called the Kohonen map, where the map denotes the low-dimensional representation of the parameters of the given signal. It is distinct from the other artificial neural networks in terms of the implementation of the neighborhood function. This further facilitates the preservation of the topological characteristics of the input parameters and the low-dimensional representation of the high-dimensional signals. | The SOM method is implemented using “Self-Organizing Map” operator. The critical attributes of this operator and their values in our implementation are listed below:
| [85] | |
| Performance Measures | Description | Ref. | |
|---|---|---|---|
| Accuracy | Accuracy represents one of the most popular performance evaluation tools. It can be obtained by dividing the number of accurately classified observations by the total number of observations done by the classification model. Mathematically, accuracy is given by Equation (23). | [87] | |
| (23) | |||
| where TP, TN, FP, and FN refer to the true positive value, the true negative value, the false positive value, and the false-negative value, respectively. A true positive is an outcome when the model accurately predicts the positive class. A true negative is a result for which the model provides an accurate prediction of the negative class. If the model mistakenly predicts a positive class, this is called a false positive. When the model erroneously forecasts the negative class, this is known as a false negative. | |||
| AUC | AUC refers to the total area under the receiver operating characteristics (ROC) curve. The ROC curve represents a probability curve that indicates the performance of an ML model in differentiating between the classes at all classification thresholds. The value of AUC describes the degree of separability of the classification model. | [38] | |
| Precision | Precision represents the ratio of accurately classified positive observations to the number of observations classified as positive (Equation (24)). It is also regarded as the positive predictive value. | [87] | |
| (24) | |||
| where TP and FP refer to the true positive value and the false positive value, respectively. | |||
| Sensitivity | Sensitivity refers to the ratio of accurately classified positive observations to the total number of positive observations (Equation (25)). It is also called true positive rate (TPR) and recall. | [87] | |
| (25) | |||
| where TP and FN refer to the true positive value and the false negative value, respectively. | |||
| F-measure | F-measure represents the harmonic mean of precision and sensitivity (Equation (26)). Its value can vary from 0 to 1 and is nearly the same as accuracy (in %). | [17] | |
| (26) | |||
| where TP, FP, and FN refer to the true positive value, the false positive value, and the false-negative value, respectively. | |||
| Specificity | Specificity corresponds to the ratio of accurately classified negative observations to the total number of negative observations (Equation (27)). | [17] | |
| (27) | |||
| where TN and FP refer to the true negative value and the false positive value, respectively. | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nayak, S.K.; Jarzębski, M.; Gramza-Michałowska, A.; Pal, K. Automated Detection of Cannabis-Induced Alteration in Cardiac Autonomic Regulation of the Indian Paddy-Field Workers Using Empirical Mode Decomposition, Discrete Wavelet Transform and Wavelet Packet Decomposition Techniques with HRV Signals. Appl. Sci. 2022, 12, 10371. https://doi.org/10.3390/app122010371
Nayak SK, Jarzębski M, Gramza-Michałowska A, Pal K. Automated Detection of Cannabis-Induced Alteration in Cardiac Autonomic Regulation of the Indian Paddy-Field Workers Using Empirical Mode Decomposition, Discrete Wavelet Transform and Wavelet Packet Decomposition Techniques with HRV Signals. Applied Sciences. 2022; 12(20):10371. https://doi.org/10.3390/app122010371
Chicago/Turabian StyleNayak, Suraj Kumar, Maciej Jarzębski, Anna Gramza-Michałowska, and Kunal Pal. 2022. "Automated Detection of Cannabis-Induced Alteration in Cardiac Autonomic Regulation of the Indian Paddy-Field Workers Using Empirical Mode Decomposition, Discrete Wavelet Transform and Wavelet Packet Decomposition Techniques with HRV Signals" Applied Sciences 12, no. 20: 10371. https://doi.org/10.3390/app122010371
APA StyleNayak, S. K., Jarzębski, M., Gramza-Michałowska, A., & Pal, K. (2022). Automated Detection of Cannabis-Induced Alteration in Cardiac Autonomic Regulation of the Indian Paddy-Field Workers Using Empirical Mode Decomposition, Discrete Wavelet Transform and Wavelet Packet Decomposition Techniques with HRV Signals. Applied Sciences, 12(20), 10371. https://doi.org/10.3390/app122010371









