A Two-Stage Structural Damage Detection Method Based on 1D-CNN and SVM
Abstract
:1. Introduction
- We propose a new two-stage structural damage detection method which follows the strategy of "divide-and-conquer" to solve the problem of insufficient training data and enhance the model performance for multi-level structural damage detection.
- Our method fully combines the advantages of 1D-CNN and SVM, reducing computational costs and eliminating the need to rely on expertise to design complex feature extraction methods.
- We verify the proposed model on an eight-level steel frame structure. The experimental results show that the proposed method outperforms the state-of-the-art methods in terms of both damage location detection and damage severity detection.
2. Methods
2.1. 1D-CNN
2.1.1. Convolutional Layer
2.1.2. Pooling Layer
2.1.3. Droput Layer
2.1.4. Full Connected Layer
2.2. SVM
2.3. Wavelet Packet Decomposition
3. Experiments
3.1. Dataset
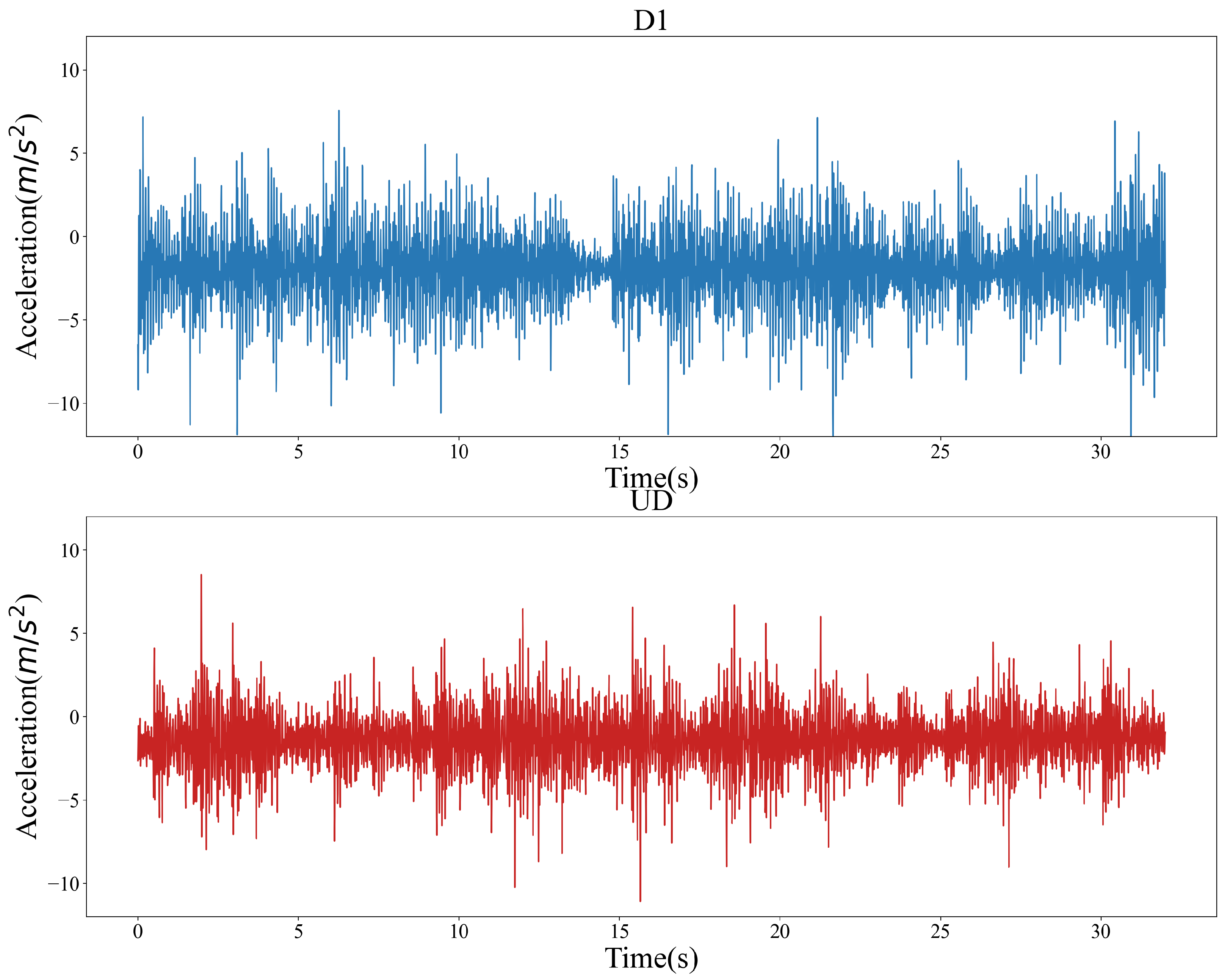
3.2. Data Preprocessing
3.2.1. Offset Elimination
3.2.2. Data Normalization
3.2.3. Data Slicing
3.2.4. Dataset Splitting
3.3. Baselines
- SVM: The feature vector was obtained by four-layer wavelet packet decomposition, and then SVM was used to identify both the damage location and the damage severity.
- 1D-CNN: Using 1D-CNN to identify both damage location and damage severity, the structure of 1D-CNN was the same as the 1D-CNN used in the method proposed in this paper.
- 1D-CNN and1D-CNN: After identifying the damage location using a 1D-CNN, the damage severity was identified using another 1D-CNN. The structure of the two 1D-CNNs were consistent with the 1D-CNN in the method proposed in this paper.
3.4. CNN Configurations
3.5. Experimental Results
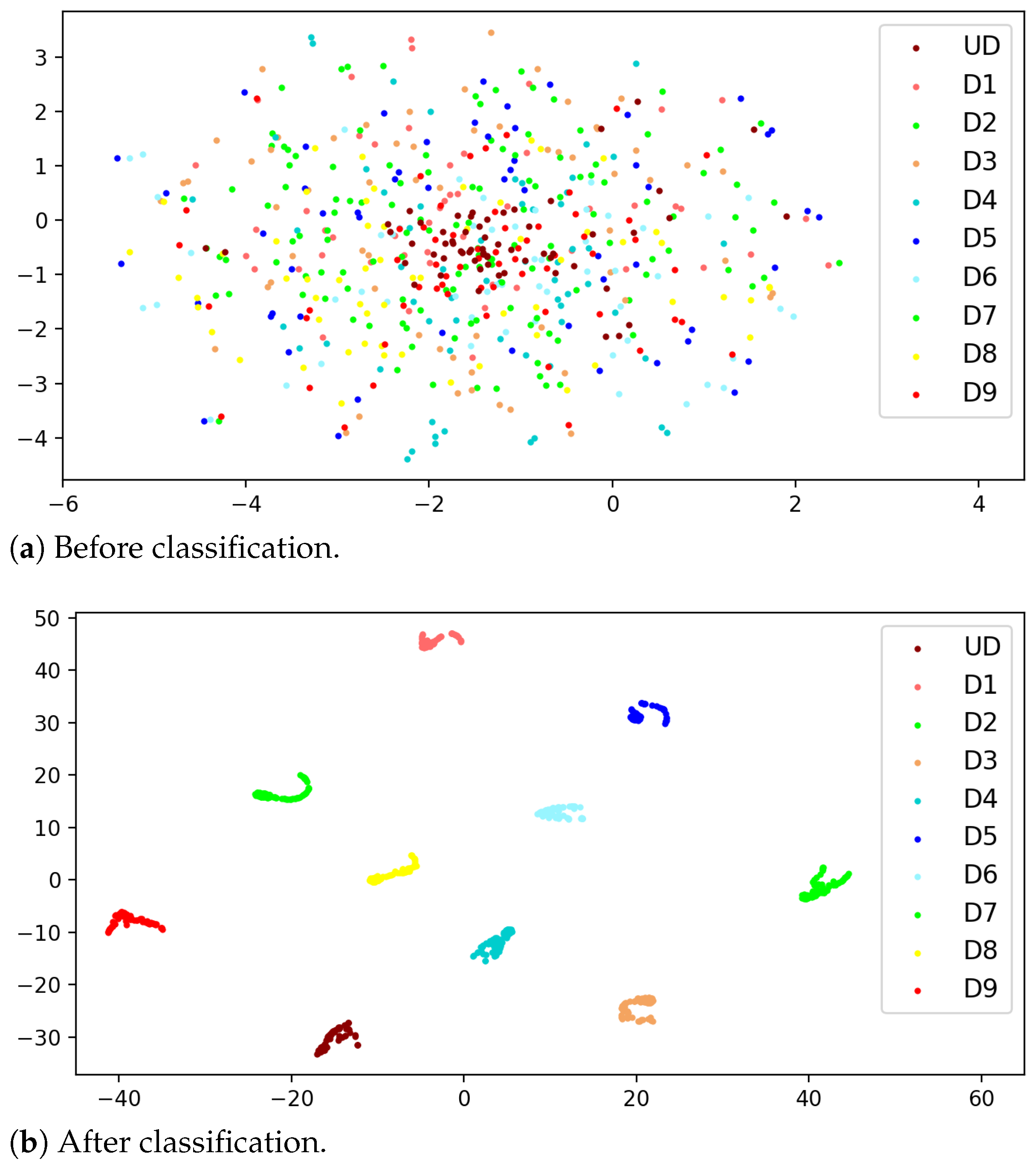
3.6. Further Comparison and Results Visualization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to machine learning and deep learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Wahab, M.M.A.; Roeck, G.D. Damage detection in bridges using modal curvatures: Application to a real damage scenario. J. Sound Vib. 1999, 226, 217–235. [Google Scholar] [CrossRef]
- Park, S.; Yun, C.; Roh, Y. Jong-jae leepzt-based active damage detection techniques for steel bridge component smart mater. Structure 2006, 15, 957–966. [Google Scholar]
- Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibration–based structural damage identification. Philos. Trans. R. Soc. London. Series Math. Phys. Eng. Sci. 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Zhang, Y.; Miyamori, Y.; Mikami, S.; Saito, T. Vibration-based structural state identification by a 1-dimensional convolutional neural network. Comput. -Aided Civ. Infrastruct. Eng. 2019, 34, 822–839. [Google Scholar] [CrossRef]
- Chesne, S.; Deraemaeker, A. Damage localization using transmissibility functions: A critical review. Mech. Syst. Signal Process. 2013, 38, 569–584. [Google Scholar] [CrossRef] [Green Version]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal processing techniques for vibration-based health monitoring of smart structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Meruane, V.; Heylen, W. An hybrid real genetic algorithm to detect structural damage using modal properties. Mech. Syst. Signal Process. 2011, 25, 1559–1573. [Google Scholar] [CrossRef] [Green Version]
- Adeli, H.; Jiang, X. Intelligent Infrastructure: Neural Networks, Wavelets, and Chaos Theory for Intelligent Transportation Systems and Smart Structures; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Wu, R.; Jahanshahi, M.R. Data fusion approaches for structural health monitoring and system identification: Past, present, and future. Struct. Health Monit. 2020, 19, 552–586. [Google Scholar] [CrossRef]
- Lei, J.; Cui, Y.; Shi, W. Structural damage identification method based on vibration statistical indicators and support vector machine. Adv. Struct. Eng. 2022, 25, 1310–1322. [Google Scholar] [CrossRef]
- Diao, Y.; Jia, D.; Liu, G.; Sun, Z.; Xu, J. Structural damage identification using modified hilbert–huang transform and support vector machine. J. Civ. Struct. Health Monit. 2021, 11, 1155–1174. [Google Scholar] [CrossRef]
- Zhang, X.; Han, P.; Xu, L.; Zhang, F.; Wang, Y.; Gao, L. Research on bearing fault diagnosis of wind turbine gearbox based on 1dcnn-pso-svm. IEEE Access 2020, 8, 192248–192258. [Google Scholar] [CrossRef]
- Lin, Y.; Nie, Z.; Ma, H. Structural damage detection with automatic feature-extraction through deep learning. Comput. -Aided Civ. Infrastruct. Eng. 2017, 32, 1025–1046. [Google Scholar] [CrossRef]
- Wang, X.; Shahzad, M.M.; MomanShahzad, M. A novel structural damage identification scheme based on deep learning framework. Structures 2021, 29, 1537–1549. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, W.; Dong, L.; Ogai, H. A novel bridge damage diagnosis algorithm based on deep learning with gray relational analysis for intelligent bridge monitoring system. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 730–742. [Google Scholar] [CrossRef]
- Huang, L.; He, H.X.; Wang, W. Intelligent recognition of bridge damage based on convolutional neural networks and recursive graphs. J. Basic Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector machines for classification. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 39–66. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. Lcml. 2010. Available online: http://www.csri.utoronto.ca/~hinton/absps/reluICML.pdf (accessed on 30 August 2022).
- Tabian, I.; Fu, H.; Khodaei, Z.S. A convolutional neural network for impact detection and characterization of complex composite structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef] [Green Version]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Search; Technical Report, Technical Report SFI-TR-95-02-010; Santa Fe Institute: Santa Fe, NM, USA, 1995. [Google Scholar]
- Chang, C. Libsvm: A Library for Support Vector Machines. 2001. Available online: http://www.csie.ntu.edu.tw/cjlin/libsvm (accessed on 30 August 2022).
- Keerthi, S.S.; Lin, C. Asymptotic behaviors of support vector machines with gaussian kernel. Neural Comput. 2003, 15, 1667–1689. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Melhem, H. Damage detection of structures by wavelet analysis. Eng. Struct. 2004, 26, 347–362. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L. A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Mater. Des. (1980–2015) 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- der Maaten, L.V.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Shao, W.; Sun, H.; Wang, Y.; Qing, X. A multi-level damage classification technique of aircraft plate structures using lamb wave-based deep transfer learning network. Smart Mater. Struct. 2022, 31, 075019. [Google Scholar] [CrossRef]


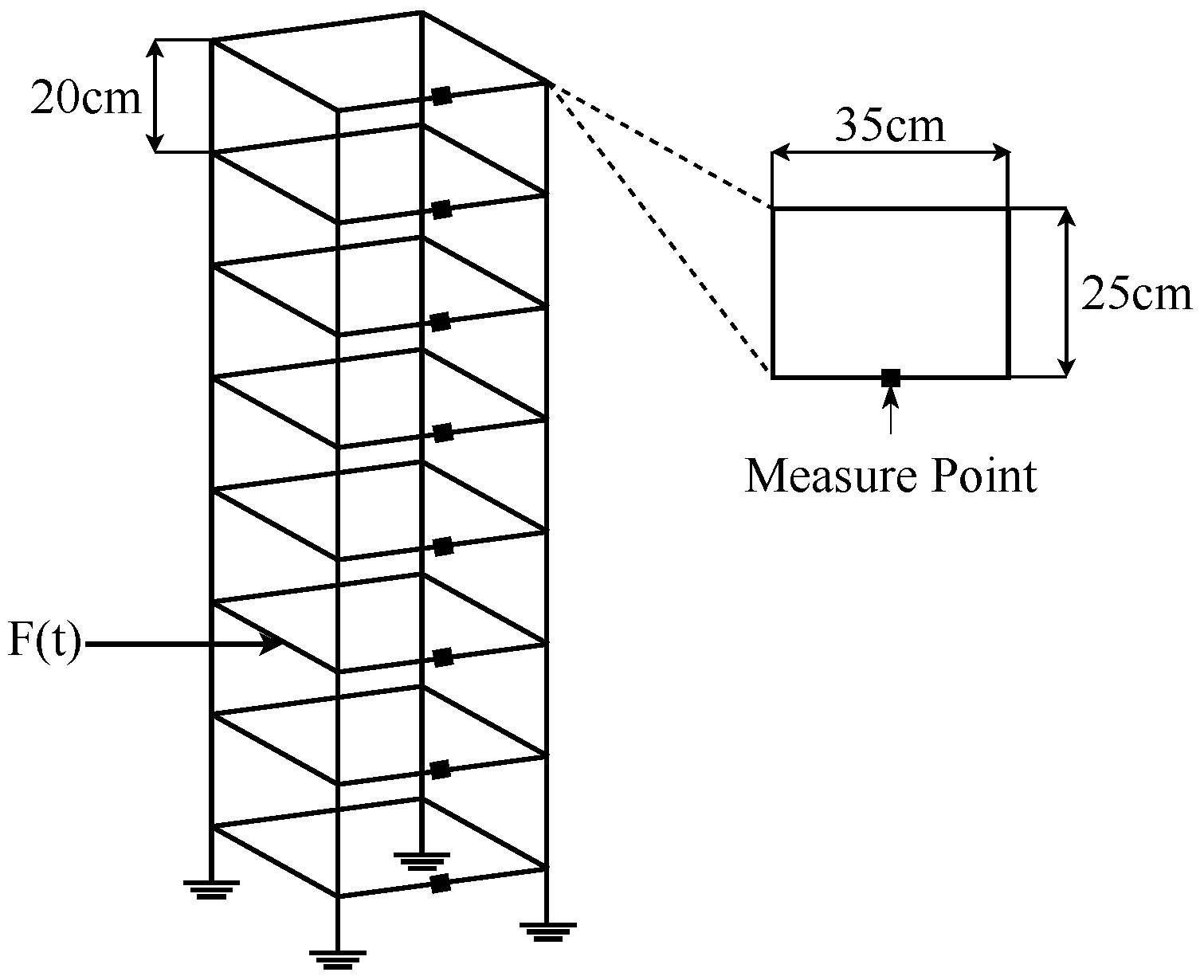


| Case | Location | Decreased Stiffness (%) |
|---|---|---|
| UD | - | 0 |
| D1 | 3 | 8.3 |
| D2 | 3 | 16.7 |
| D3 | 5 | 8.3 |
| D4 | 5 | 16.7 |
| D5 | 7 | 8.3 |
| D6 | 7 | 16.7 |
| D7 | 3 & 5 | 8.3 (both layers) |
| D8 | 3 & 7 | 8.3 (both layers) |
| D9 | 5 & 7 | 8.3 (both layers) |
| Layer | Output Shape | Parameter | Activation | Variables |
|---|---|---|---|---|
| Input | 1024 × 8 | None | None | 0 |
| Convolution 1-D | 1021 × 8 | Kernel number: 4; Kernel size: 8 × 8; | ReLU | 264 |
| Convolution 1-D | 1014 × 16 | Kernel number: 8; Kernel size: 16 × 8; | ReLU | 1040 |
| Max Pooling 1-D | 507 × 16 | Kernel number: 2; | None | 0 |
| Convolution 1-D | 500 × 16 | Kernel number: 8; Kernel size: 16 × 8; | ReLU | 2064 |
| Global Average Pooling 1-D | 16 | None | None | 0 |
| Dropout | 16 | None | None | 0 |
| Dense | 7 | None | Softmax | 119 |
| Total parameters | 3487 |
| SVM | 1D-CNN | 1D-CNN&1D-CNN | 1D-CNN&SVM | |
|---|---|---|---|---|
| Fold 1 | 0.75 | 0.9718 | 0.9833 | 0.9966 |
| Fold 2 | 0.6964 | 0.9364 | 0.9921 | 1.0 |
| Fold 3 | 0.7143 | 0.9833 | 0.9845 | 0.9983 |
| Fold 4 | 0.8036 | 0.9718 | 0.9743 | 1.0 |
| Fold 5 | 0.8214 | 0.9645 | 0.9874 | 0.9989 |
| 1D-CNN&1D-CNN | 1D-CNN&SVM | |||
|---|---|---|---|---|
| Location | Severity | Location | Severity | |
| Fold 1 | 0.9989 | 0.9743 | 0.9984 | 1.0 |
| Fold 2 | 1.0 | 0.9734 | 1.0 | 1.0 |
| Fold 3 | 0.9968 | 0.9876 | 0.9991 | 1.0 |
| Fold 4 | 0.9937 | 0.9804 | 1.0 | 1.0 |
| Fold 5 | 1.0 | 0.9856 | 0.9994 | 1.0 |
| SVM | 1D-CNN | 1D-CNN&1D-CNN | 1D-CNN&SVM | |
|---|---|---|---|---|
| Train | 9.1 s | 31.5 s | 43.2 s | 38.5 s |
| Test | 0.6 s | 0.9 s | 1.5 s | 1.2 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Zhou, Q.; Lei, J.; Wang, X. A Two-Stage Structural Damage Detection Method Based on 1D-CNN and SVM. Appl. Sci. 2022, 12, 10394. https://doi.org/10.3390/app122010394
Jiang C, Zhou Q, Lei J, Wang X. A Two-Stage Structural Damage Detection Method Based on 1D-CNN and SVM. Applied Sciences. 2022; 12(20):10394. https://doi.org/10.3390/app122010394
Chicago/Turabian StyleJiang, Chenhui, Qifeng Zhou, Jiayan Lei, and Xinhong Wang. 2022. "A Two-Stage Structural Damage Detection Method Based on 1D-CNN and SVM" Applied Sciences 12, no. 20: 10394. https://doi.org/10.3390/app122010394
APA StyleJiang, C., Zhou, Q., Lei, J., & Wang, X. (2022). A Two-Stage Structural Damage Detection Method Based on 1D-CNN and SVM. Applied Sciences, 12(20), 10394. https://doi.org/10.3390/app122010394






