The Influence of Flight Direction and Camera Orientation on the Quality Products of UAV-Based SfM-Photogrammetry

Abstract

Unmanned aerial vehicles (UAVs) can provide valuable spatial information products for many projects across a wide range of applications. One of the major challenges in this discipline is the quality of positioning accuracy of the resulting mapping products in professional photogrammetric projects. This is especially true when using low-cost UAV systems equipped with GNSS receivers for navigation. In this study, the influence of UAV flight direction and camera orientation on positioning accuracy in an urban area on the west bank of the Euphrates river in Iraq was investigated. Positioning accuracy was tested in this study with different flight directions and camera orientation settings using a UAV autopilot app (Pix4Dcapture software (Ver. 4.11.0)). The different combinations of these two main parameters (camera orientation and flight direction) resulted in 11 different flight cases for which individual planimetric and vertical accuracies were evaluated. Eleven flight sets of dense point clouds, DEMs, and ortho-imagery were created in this way to compare the achieved positional accuracies. One set was created using the direct georeferencing method (without using GCPs), while the other ten sets were created using the indirect georeferencing approach based on ground truth measurements of five artificially created GCPs. Positional accuracy was found to vary depending on the user-defined flight plan settings, despite an approximately constant flight altitude. However, it was found that the horizontal accuracy achieved was better than the vertical accuracy for all flight sets. This study revealed that combining multiple sets of images with different flight directions and camera orientations can significantly improve the overall positional accuracy to reach several centimeters.

1. Introduction

The positional accuracy of UAV geospatial products is affected by numerous factors, including the nature of the survey area and its morphological characteristics [1]. The other main factors that affect the positional accuracy of UAV products are the model of the UAVs, the type and accuracy of the navigation and orientation instruments on board the UAVs, the camera specification, the ground sensing distance (GSD) [2], the degree of overlap, the UAV flight altitude, and the number and configuration of ground control points (GCPs) [3]. Several previous studies have analyzed and investigated the effects of these factors on the positional accuracy of UAV products [4]. In general, the positional accuracy of UAV products has been tested and analyzed in some studies and research as follows [5]:

In 2015, Whitehead and Hugenholtz used GCPs and Pix4D software to photogrammetrically map a gravelly river channel and achieved a horizontal accuracy of 0.048 m (RMSEH) and vertical accuracy of 0.035 m (RMSEZ), which were compatible with the accuracy standards developed by the American Society for Photogrammetry and Remote Sensing (ASPRS) for digital geospatial data at the 0.1-m RMSE level [6].

Next, Hugenholtz et al. (2016) compared the spatial resolution of three cases of UAV imagery acquired during two missions to a gravel pit. The first case was a surveillance-level GNSS/RTK receiver (direct georeferencing), the second was a lower-level GPS receiver (direct georeferencing), and the third was a lower-level GPS receiver with GCPs (indirect georeferencing). The horizontal and vertical accuracies were RMSEH = 0.032 m and RMSEZ = 0.120 m in the first case, RMSEH = 0.843 m and RMSEZ = 2.144 m in the second case, and RMSEH = 0.034 m and RMSEZ = 0.063 m in the third case, respectively [7].

Later, Lee and Sung (2018) evaluated and analyzed the positional accuracy of UAV mapping with onboard RTK without GCPs compared with UAV mapping without RTK with different numbers and configurations of GCPs. In the case of the non-RTK method with GCPs, the horizontal and vertical accuracies were 4.8 and 8.2 cm with 5 GCPs, 5.4 and 10.3 cm with 4 GCPs, and 6.2 and 12.0 cm with 3 GCPs, respectively, depending on the number of GCPs. The horizontal and vertical accuracies of the non-RTK method without GCPs deteriorated to about 112.9 and 204.6 cm, respectively. The horizontal and vertical accuracies of the RTK-onboard-UAV method without GCPs were 13.1 and 15.7 cm, respectively [8].

In addition, Yang et al. (2020) investigated the influence of the number of GCPs on the vertical positional accuracy of UAV products. This study was conducted on sandy beaches in China. The authors concluded that the number 11 was the optimal number of GCPs in this study area and had a vertical RMSE of about 15 cm [9].

Further, Štroner et al. (2021) investigated georeferencing of UAV imagery aboard GNSS RTK (without GCPs). The researchers evaluated and analyzed the reasons for the high-altitude error, which is a challenge for this technique. They proposed strategies to reduce these types of errors. Several missions were conducted in two study areas with different flight altitudes and image-capturing axes [10]. This study showed that a combination of two flights at the same altitude but with vertical and oblique image acquisition axes could reduce the systematic vertical error to less than 3 cm. In addition, this study demonstrated for the first time the linear relationship between the systematic vertical error and the variation of the focal length. Finally, this study proved that georeferencing without GCPs is a suitable alternative to using GCPs.

All these studies have produced important results and paved the way for further studies. However, few studies have addressed the effects of camera orientation on positional accuracy. Similarly, there have been no studies that have addressed the effects of the direction of the flight lines and their position within the study area on the positional accuracy values.

This paper fills this gap by investigating the effects of camera orientation and flight direction on positioning accuracy. It also investigates and analyzes the positioning accuracy of UAV products to improve this accuracy, especially vertical accuracy.

There were several limitations related to the steps involved in carrying out work for this research, including those related to the possibility of obtaining a drone and those related to the possibility of obtaining security clearances. This was in addition to the social determinants related to the inhabitants’ refusal to be photographed from above, given that there was a kind of intrusion of disturbances, especially at lower elevations. Therefore, we made sure to choose the time of filming when the presence of people was minimal, taking into account the appropriate weather conditions.

2. Importance of This Research

All conventional surveying, whether using a global positioning system (GPS), a total station, or other surveying equipment, requires a great deal of time, effort, and labor. Sometimes the sites where engineering work is performed are harsh and hazardous environments where it is difficult for humans to freely move. To reduce the time, labor, and manpower required for conventional survey work, photogrammetry has been used to survey land areas and locations of engineering projects. The latest findings of researchers and professionals in this field have been related to the use of unmanned aerial vehicles (UAVs) to produce survey maps, digital elevation models (DEMs), orthophotos, and 3D models.

The creation of maps using drones, like other surveying work, differs in its positional accuracy. Therefore, this research was very important because it dealt with the testing, evaluation, and analysis of the positional accuracy of geospatial data products using drones. In this study, positional accuracies without ground control points (direct georeferencing) and with ground control points (indirect georeferencing) were tested using different combinations of image sets acquired with different camera orientations and flight directions.

In reviewing previous studies that have addressed the evaluation and analysis of positional accuracy, it was found that positional accuracy varies from one study to another, as it is influenced by many different factors. It was also noted that the topic of positional accuracy, especially in the vertical, is still in need of renewed study and research, and this was one of the motivations for this study. In this study, UAV photogrammetry products were tested to determine if they are accurate enough to replace current GNSS and total station surveying methods in engineering, cadastral, and topographic surveying [11].

3. Materials and Methods

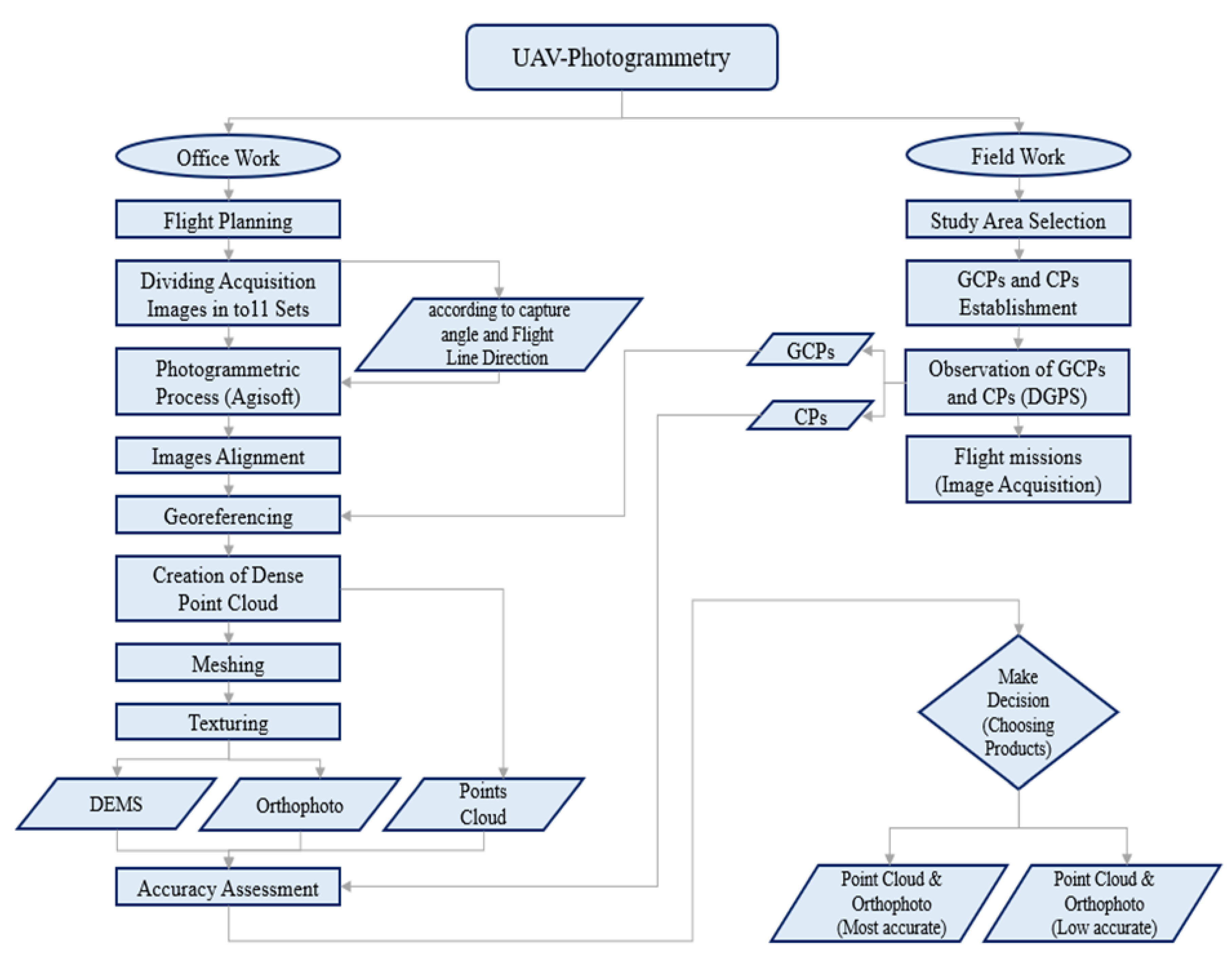
The work methodology in this study included two main phases: the fieldwork phase and the office work phase. The fieldwork included selecting the study area, defining and establishing ground control points and checkpoints, measuring their coordinates with a global positioning system (GPS), and conducting aerial photography with a UAV. The office work included the preparation of the flight plan, data processing, extraction of map products (dense point cloud, DEMs, and orthophotos), and evaluation of positional accuracies.

In this study, the effects of flight direction and camera orientation on UAV photogrammetry geospatial products were studied and analyzed. For this purpose, photogrammetric flight missions were conducted using low-cost UAVs equipped with consumer-level image sensors and low-quality navigation and attitude sensors. Different combinations of image sets were used to evaluate the effects of some parameters such as the use of GCPs, the image acquisition angle, and the flight direction on the positioning accuracy of the UAV products.

Figure 1 shows the methodology proposed in this study, which included the main phases mentioned above and the steps and tasks performed for each phase. The UAV flights in this study were performed using a Mavic 2 manufactured by the Chinese company DJI-Innovation Technology Co. LTD (Figure 2a). This multi-rotation rotary drone has a diameter of only 30 cm and weighs only 2 kg. The Mavic 2 can fly autonomously and is controlled by route-planning software that also takes off and returns automatically. The autonomous flight time of the drone is about 25 min per battery group. The Mavic 2 is equipped with a Hasselblad L1D-20c camera from the manufacturer. This camera provides an image of 12.825 × 8.550 mm, a focal length of 10 mm, and an image size of 5472 × 3648 pixels.

3.1. Study Area

The study area was a rural region which was located on the southern bank of the Euphrates river in Al-Anbar Governorate in the western part of Iraq. It was part of a residential area, as indicated by the yellow line in Figure 2b, with an average built-up area of 150 × 200 m. This area consisted of several internal roads, blocks of buildings, some undeveloped land, and residential buildings, most of which were two-story buildings. The height of the buildings varied from 4 to 12 m. In this area, there were also scattered plantings such as trees and home gardens.

3.2. Flight Planning and Data Acquisition

For any photogrammetric work with UAVs or even with conventional technology, flight planning must first be performed. This step requires some activities, such as obtaining a flight permit, selecting appropriate software, studying the characteristics of the project area, the specifications of the onboard digital camera, and the ground sample distance (GSD) value [12]. Also, the selection of weather conditions suitable for the flight process is one of the most important factors contributing to the success of the study. In this study, the field survey was conducted in a rural region away from vital places between ten to twelve o’clock on 18 November 2022. Shooting in the morning was selected so that the sun’s rays could shine without much misdirection, and the wind speed was very low so as to not affect the drone’s course.

Three flights were conducted over the study area to verify and evaluate the positional accuracy of the UAV photogrammetry products and the influencing factors. Depending on the flights performed, multiple datasets were created, differing in acquisition angle, flight direction, and the georeferencing method. To compare the positional accuracies, eleven groups of dense point clouds, DEMs, and orthoimages with different parameters were created in this study (see

Table 1. The eleven cases of processed images in this study.

No. of Case	Georeferencing Method	Combinations Image Acquisition Angle/Flight Lines Direction	No. of Images
1	Without GCPs	90°/Longitudinal flight lines	113
2	With Five GCPs	90°/Longitudinal flight lines	113
3		90°/Transverse flight lines	120
4		70°/Longitudinal flight lines	126
5		70°/Transverse flight lines	115
6		90°/Longitudinal flight lines + 90°/Transverse flight lines	113 + 120 = 233
7		90°/Longitudinal flight lines + 70°/Longitudinal flight lines	113 + 126 = 239
8		90°/Longitudinal flight lines + 70°/Transverse flight lines	113 + 115 = 228
9		90°/Transverse flight lines + 70°/Longitudinal flight lines	120 + 126 = 246
10		90°/Transverse flight lines + 70°/Transverse flight lines	120 + 115 = 235
11		70°/Longitudinal flight lines + 70°/Transverse flight lines	126 + 115 = 241

).

Pix4Dcapture software (Ver. 4.11.0) was used to create the flight plan in this study, as shown in Figure 3. The flight altitude was set at 60 m with 75% longitudinal overlap and 70% transversal overlap for all UAV photogrammetry tasks. Taking into account the specific imaging time of the UAV used, three tasks were performed in this study.

The first task was to select the GRID MISSION option in the Pix4Dcapture software, set the acquisition angle to 90° (vertical), and align the flight lines along the length of the study area (Figure 3b). These parameters resulted in a GSD value of 1.41 cm/pixel. In this task, 113 images were acquired.

The second task was also selected as a GRID MISSION option in the Pix4Dcapture software, and the acquisition angle was also set to 90° (vertical), but the direction of the flight lines was set in the direction of the width of the study area (Figure 3c). With these parameters, the GSD value was 1.41 cm/pixel, and the number of images in this task was 120 images.

In the third task, the DOUBLE GRID MISSION option of the Pix4Dcapture software was selected and the oblique acquisition angle was set to 70°. With these parameters, the GSD value was 1.50 cm/pixel, and the number of images in this task was 241. The images in this task were divided into two groups: one group with flight lines along the length of the study area, which contained 126 images, and the other group with flight lines along the width of the study area, which contained 115 images. All missions were planned as autonomous flights. Figure 4 shows examples of four consecutive images acquired during this study.

3.3. GCP and CP Distribution

The UAV used in this study was not equipped with precise navigation and orientation instruments, so a sufficient number of GCPs in the study area had to be established and measured before the UAV flight for georeferencing [6]. This step had two main objectives:

1. The identification and measurement of ground control points (GCPs) for indirect georeferencing.

2. The identification and measurement of checkpoints (CPs) to determine and evaluate the positional accuracy of the generated dense point cloud, DEMs, and orthophotos [13].

Field measurements before flights included measuring the coordinates of ground control points and checkpoints using a GNSS/RTK base station and rover [7]. The GCP and CP markers were precisely fabricated from square iron sheets with a side length of 50 cm and divided into four identical parts, which were assigned different colors (black and white) to facilitate their visibility and distinction by drone imagery (Figure 5).

In this study, 18 points were set and measured (numbered from 1 to 18). Point 1 was used as a reference point or base station, 5 points served as ground control points (GCPs) for indirect georeferencing, and 12 points were used as checkpoints (CPs) to calculate the positional accuracy of the work products. All points were placed in appropriate distribution throughout the study area (Figure 6) and were visible in the images. The GNSS survey of the GCPs and CPs was performed in RTK mode. The planimetric coordinate system was the UTM zone 38N with the geodetic reference system WGS84. The altimetric coordinate system was the EGM96 geodetic model for converting ellipsoidal heights to orthometric heights [14].

3.4. Photogrammetric Processing

All images in this study were processed using Agisoft Metashape Professional software, version 1.8.0 [15], and the parameters chosen for the different steps are listed in

Table 2. Setting parameters of Agisoft Metashape used in this study.

Processing Steps	Parameters	Chosen Value
Align Photos	Accuracy	High
	Key point limit	40,000
	Tie point limit	4000
Optimization		Fit all constants (f, cx, cy, k1–k4, p1, p2, b1, and b2)
Build Dense Cloud	Quality	Medium
	Depth filtering	Moderate
Build Mesh	Source data	Dense cloud
	Surface type	Height field
	Face count	High
	Interpolation	Enabled
	Point classes	All
Build Texture	Texture type	Diffuse map
	Source data	Images
	Mapping mode	Adaptive orthophoto
	Blending mode	Mosaic
	Texture size/count:	4096
Build DEM	Projection	Geographic
	Coordinate system	WGS 84/UTM zone 38N
	Source data	Dense cloud
	Interpolation	Enabled
	Point classes	All
	Resolution	0.0532556 m
Build Orthomosaic	Projection	Geographic
	Coordinate system	WGS 84/UTM zone 38N
	Surface	Mesh
	Blending mode	Mosaic
	Pixel size	0.013 m

. Agisoft Metashape is a software tool based on Structure from Motion (SfM) for bundle adjustment and Multiview Stereo (MVS) for dense image matching. This software was the appropriate choice for the reconstruction of DEMs and orthophotos for the scene. The images were automatically processed in this software, except for some interventions in some details, such as the identification and measurement of ground control points (GCPs) and checkpoints (CPs), which were manually performed by the user.

The processing of UAV images in Agisoft Metashape software was performed in the following main steps [2]:

• Import images, GNSS data, and IMU data.
• Align images for interior and exterior orientation and generate a sparse point cloud.
• Import and mark GCPs.
• Optimize the camera.
• Build a dense point cloud using image matching methods.
• Create of a mesh and texture.
• Generate a DEM.
• Create an orthophoto.

In this study, eleven sets of the dense point cloud, DEMs, and orthomosaic were created from the combinations of the acquisition images; one set was processed based on the direct georeferencing method (without GCPs), and the other ten sets were processed by indirect georeferencing using five GCPs. In all cases, the dense point cloud was used to create DEMs, and the last one was used to create the orthophoto for each image. Then, the orthophoto images were aligned to create the orthomosaic for the study area.

3.5. Accuracy Assessment

As mentioned earlier, field measurements were made at eighteen fixed points in the study area using GNSS/RTK before the flight and imaging procedure. One of these points was monitored for approximately 5 h as it served as a reference point. Then, the remaining points were monitored and measured relative to this base point. Five of these points were used as ground control points (GCPs) in indirect georeferencing, and the remaining twelve served as checkpoints (CPs) to verify the accuracy of the digital elevation models and the resulting orthophotos.

The checkpoints were used to calculate the positional accuracy of the DEMs and orthophotos produced. The positional accuracy was determined from the value of the calculated errors between the observed coordinates of the CPs using GNSS/RTK measurements and the predicted coordinates of the CPs from the geospatial data products (DEMs and orthophotos). In addition, the root mean square errors (RMSEs) were calculated for the east (X), north (Y), and vertical (Z) coordinates, as well as the total RMSE.

4. Results and Discussion

This study tested the positional accuracy of geospatial products created from UAV imagery processed with and without GCPs and examined the effects of camera orientation and flight direction. The positional accuracy results for the eleven cases are shown in

Table 3. The positional accuracies of the eleven cases. [red color for maximum error, green color for minimum error].

No. of Case	E. errs. (m)	N. errs. (m)	Z. errs. (m)	Tot. err. (m)
1	1.830	1.203	2.885	3.622
2	0.028	0.019	0.054	0.064
3	0.029	0.029	0.112	0.120
4	0.026	0.036	0.366	0.368
5	0.066	0.080	0.059	0.120
6	0.007	0.017	0.048	0.052
7	0.074	0.125	0.107	0.181
8	0.044	0.028	0.022	0.057
9	0.049	0.039	0.043	0.076
10	0.062	0.082	0.071	0.125
11	0.008	0.009	0.028	0.031

. The results showed that the horizontal and vertical accuracies of the geospatial data mainly depended on the quality of the GNSS and IMU on board the UAV, and whether or not GCPs were used in the photogrammetric processing [16]. Overall, the achieved horizontal accuracy was better than the vertical accuracy in all cases. The RMSEs resulting from direct georeferencing based on the consumer-grade GNSS and IMU showed that the accuracy was severely degraded with an H-RMSE and Z-RMSE of more than 1 and 2 m, respectively.

From the results of the positional accuracy test, reproduced in Table 3, it is clear that the discrepancy was either on the horizontal or vertical planes. From these results, the effect of flight direction and camera orientation on the level of this accuracy was also evident. It can be seen that the best positional accuracy was obtained in the eleventh case (3 cm), in which the DOUBLE GRID MISSION option of the Pix4Dcapture software was selected to create the flight plan [17]. In this case, the images were acquired with an acquisition angle of 70°, regardless of whether the flight direction was longitudinal or transversal.

Figure 7 shows the plots of X, Y, Z, and the total RMSE values for all eleven cases (from the first to eleventh cases). This figure shows the significant difference in RMSEs between the first and other cases, since the first case was based on direct georeferencing, although the onboard GNSS and IMU were of low quality [18]. For further explanation, Figure 8 shows the values of X, Y, Z, and the total RMSEs for the last ten cases (from the second to eleventh cases).

Figure 7 and Figure 8 show that the most influential part of the RMSEs in positional accuracy concerned heights (Z-RMSEs) [19]. From the study of all cases, it can be seen that the Z-RMSEs were strongly influenced by the image acquisition angle and flight direction, especially when the checkpoints (CPs) were at a high elevation while the ground control points (GCPs) were at ground level. In this study, the GCPs used for georeferencing, numbered 2, 7, 12, 15, and 18, were at ground level, and all checkpoints except numbers 4 and 11 were also at ground level. Checkpoints 4 and 11 were located on the roof of the second floor (about 8 m above ground level). Therefore, these checkpoints had large Z errors in all cases, especially in cases with longitudinal flight lines and 70° acquisition angles as in case four.

4.1. Positional Accuracy Test Results Depending on Flight Direction

To investigate the effect of flight direction on positional accuracy, all other parameters were set the same, including the orientation of the camera perpendicular to the ground at a 90° angle; the flight direction relative to the study area was the only variable. This resulted in three cases (two, three, and six) where the direction of the flight was longitudinal, transversal, or a combination of both directions. As shown in Figure 9, the results indicated that when the angle of detection was 90°, the accuracy obtained with the longitudinal flight direction (6 cm) was better than that with the transversal flight direction (12 cm). However, the best accuracy was generally obtained with the combined acquisition of the longitudinal and transversal flight directions (5 cm).

On the other hand, if all parameters were set the same and the camera orientation in this test was set to 70°, and the only variable was the direction of flight, then there were three cases (4, 5, and 11). In this case, the accuracy obtained with the longitudinal flight direction (36 cm) was very poor and the accuracy obtained with the transversal flight direction (12 cm) was the best compared with the first case (Figure 10). This was due to the different detection angles (90° and 70°). In addition, the accuracy was still the best when the longitudinal and transversal flight directions were combined (3 cm).

4.2. Positional Accuracy Test Results Depending on Camera Orientation

To analyze the effect of individual camera orientation on positional accuracy, all other parameters were set the same, including the direction of flight longitudinally to the study area. This resulted in three cases (two, four, and seven) where the camera orientation axis was taken perpendicular (90°), oblique (70°), and both together. As shown in Figure 11, the results showed that for the longitudinal flight direction, the positioning accuracy of the vertical acquisition angle (90°), which was 6 cm, was better than that in the other cases. The worst positioning accuracy (36 cm) was obtained with an oblique detection angle (70°). This difference was very reliable because at an oblique acquisition angle (70°), the geometric distortions increased at large distances, as in the case of the longitudinal flight direction.

On the other hand, if all parameters were set equal and the direction of flight was chosen as traversing relative to the study area, and the only variable was the camera orientation, then three cases were obtained (three, five, and ten). The results showed that the overall accuracy of the three cases in this test was almost the same (12 cm). The horizontal accuracy was better with a vertical acquisition angle (90°), while the vertical accuracy was better with an oblique acquisition angle (70°) (Figure 12).

Figure 13 shows the sparse point cloud, dense point cloud, 3D model, DEM, and orthomosaic of the study area for the eleventh case.

5. Conclusions

We investigated the positional accuracy of UAV geospatial products and analyzed the influences of flight direction and camera orientation on this accuracy. For this purpose, many sets of DSMs and orthophoto mosaics were created by processing UAV images without GCPs and then with five GCPs at different combinations of flight directions and image acquisition angles. In this study, 474 images were acquired from a DJI Mavic 2 multi-rotary UAV equipped with a Hasselblad camera during three flight missions. The workflow in this project was conducted using a case study on the west bank of the Euphrates river in Iraq. The flight altitude was set at 60 m and the overlap in the forward and lateral directions was set at 75% and 70%, respectively. For the first two missions, the images were acquired with a vertical (90°) image acquisition angle, and for the third mission, an oblique (70°) image acquisition angle was set.

The calculated root means square errors (RMSEs) in the horizontal and vertical planes showed that the horizontal accuracy was higher than the vertical accuracy in all cases. This result supports previous studies that have looked at the horizontal and vertical accuracies of UAV geospatial data. In this study, it was shown that processing UAV imagery using a direct georeferencing method for low-cost UAVs resulted in low-accuracy geospatial data products even at low altitudes. The RMSEs (X, Y, Z, and total) for geospatial data products in the first case were 1.830, 1.203, 2.885, and 3.622 m, respectively. The indirect georeferencing approach led to high accuracy, where the RMSEs decreased to several centimeters. On the other hand, this study found that a fusion of two sets of images acquired with different acquisition angles and flight directions could significantly improve positional accuracy. This result was evident from the analysis of the RMSEs (X, Y, Z, and total) of the geospatial products for the last ten cases. The highest positional accuracy for these ten cases came from the eleventh case, where the processed imagery, in this case, combined imagery acquired with a 70° acquisition angle with longitudinal flight direction and imagery acquired with a 70° acquisition angle with a transversal flight direction. The X, Y, Z, and total RMSEs for this case were 0.008, 0.009, 0.028, and 0.031 m, respectively.