Application of Laser-Ultrasonics for Evaluating Textures and Anisotropy
Abstract
:1. Introduction
- Perhaps the most obvious approach is to measure the same property in different directions by rotating the material, with respect to the direction of measurement in the instrument, as described in several publications, e.g., [1,4,5,6,8,10,11,13,16,23]. We also demonstrate a method further below by which this can be achieved with high precision.
- Another approach is to determine the velocities for different wave types propagating along the same direction. This has been demonstrated by using combinations of S0 and SH0 waves [5] or S0, SH0 and P-waves [7,9] and has been applied in steelworks for measuring plastic anisotropy ratios (r-values), using EMATs, under production conditions for (cold) annealed sheets.
- A variant based on the previous concept using resonances of P- and S- waves through the thickness of plates has also been tested under steelwork conditions [12].
- Another approach used P-waves arrivals measured after different numbers of reflections through the thickness of the plate [15]. Thus, although the same fixed positions were used for generation and detection, the waves passed along different directions in the material.
- A LUS variant [14] based on the first method, here, was to convert the generating laser spot into a circle and mask off different sectors so that measurements of P- and SAW-waves could be made in different directions, which was reported to give robust measurements.
- Additionally, the group at Nottingham recently developed the Spatially Resolved Acoustic Spectroscopy (SRAS) technique [24] with which the surface texture can be measured by sampling the orientation of individual grains. From the measured surface, the texture can be calculated in a similar manner to how the textures from EBSD measurements are calculated. The team has recently been able to perform the inverse calculation of the single crystal values from the SRAS measurements [25].
2. Materials and Methods
2.1. Cold-Rolled 316
2.2. Quenched Carbon Steel
3. Results and Discussion
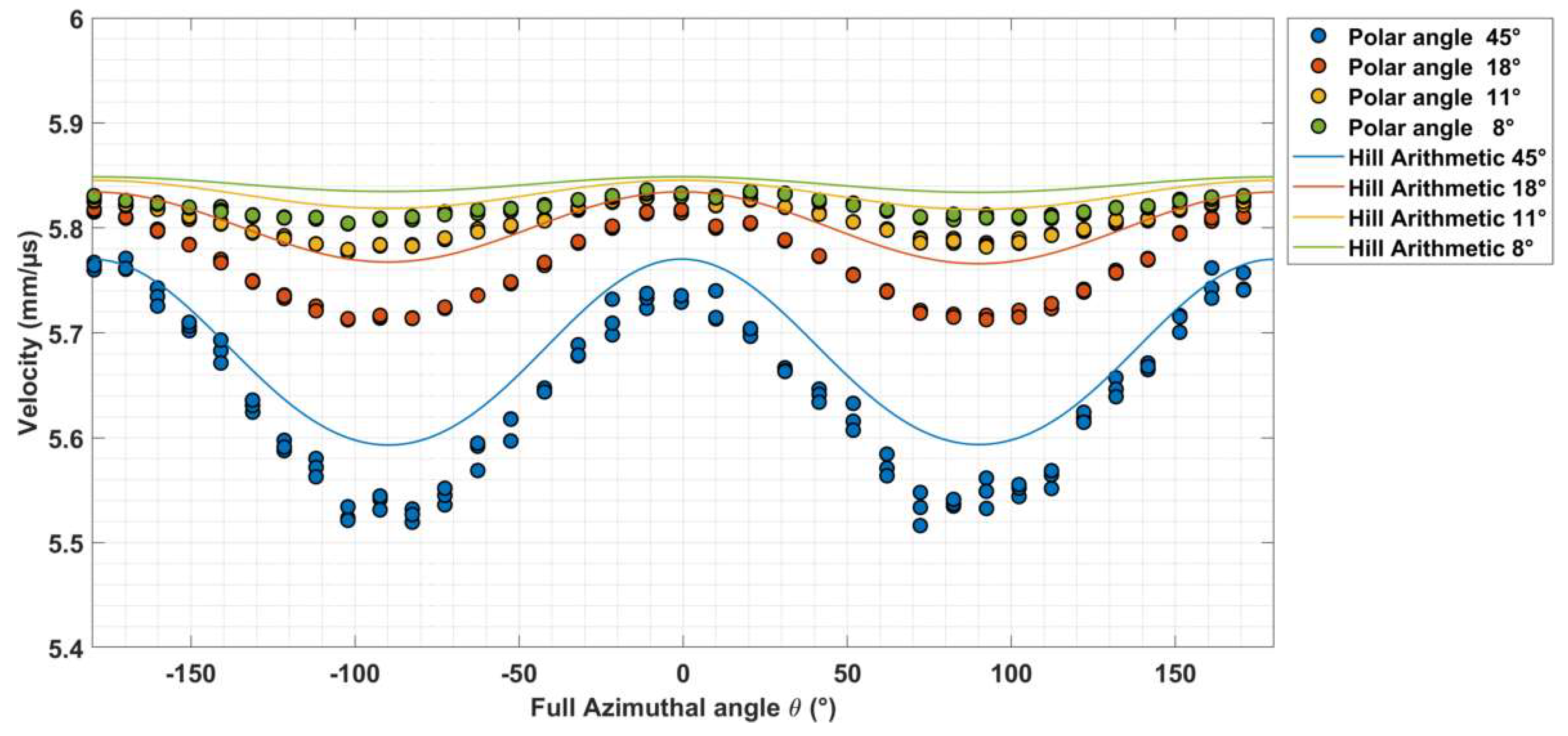
3.1. Stainless Steel–Cylindrical Specimens
3.2. Stainless Steel–Flat Plate Specimens
3.3. Quenched Steel
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Scruby, C.B.; Drain, L.E. Laser Ultrasonics Techniques and Applications; IOP Publishing Ltd. Techno House: Bristol, UK, 1990; ISBN 978-0-7503-0050-6. [Google Scholar]
- Kitagawa, H. Analysis of Elastic Anisotropy in Cold Rolled Steel Sheet. In Proceedings of the Sixth International Conference on Textures of Materials, Tokyo, Japan, 28 September–3 October 1981; Volume 1166, pp. 75–79. [Google Scholar]
- Konishi, T.; Honji, M. Texture Effect of Zircaloy on Ultrasonic Velocity. In Proceedings of the Sixth International Conference on Textures of Materials, Tokyo, Japan, 28 September–3 October 1981; Volume 1166, pp. 983–992. [Google Scholar]
- Thompson, R.B.; Lee, S.S.; Smith, J.F. Angular Dependence of Ultrasonic Wave Propagation in a Stressed, Orthorhombic Continuum: Theory and Application to the Measurement of Stress and Texture. J. Acoust. Soc. Am. 1986, 80, 921–931. [Google Scholar] [CrossRef] [Green Version]
- Ledbetter, H.M. RC Reno Texture and Dislocation Effects on Elastic Constants of Deformed Copper Plate. In Proceedings of the ICOTOM: Eighth International Conference on Textures of Materials, Santa-Fe, NM, USA, 20–25 September 1987. [Google Scholar]
- Spies, M.; Schneider, E. Nondestructive Analysis of Textures in Rolled Sheets by Ultrasonic Techniques. Texture Stress Microstruct. 1990, 13, 219–231. [Google Scholar] [CrossRef] [Green Version]
- Kawashima, K. Nondestructive Characterization of Texture and Plastic Strain Ratio of Metal Sheets with Electromagnetic Acoustic Transducers. J. Acoust. Soc. Am. 1990, 87, 681–690. [Google Scholar] [CrossRef]
- Spalthoff, P.; Wunnike, W.; Nauer-Gerhard, C.; Bunge, H.J.; Schneider, E. Determination of the Elastic Tensor of a Textured Low-Carbon Steel. Textures Microstruct. 1993, 21, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Kawashima, K.; Hyoguchi, T.; Akagi, T. On-Line Measurement of Plastic Strain Ratio of Steel Sheet Using Resonance Mode EMAT. J. Nondestruct. Eval. 1993, 12, 71–77. [Google Scholar] [CrossRef]
- Hiwatashi, S.; Hatakeyama, T.; Ushioda, K.; Usuda, M. Numerical Analysis of Stiffness in Sheet Products Based on Crystal Anisotropy. Mater. Sci. Forum 1994, 157–162, 1585–1592. [Google Scholar] [CrossRef]
- Anderson, A.J.; Thompson, R.B.; Bolingbroke, R.; Root, J.H. Ultrasonic Characterization of Rolling and Recrystallization Textures in Aluminum. Textures Microstruct. 1996, 26, 39–58. [Google Scholar] [CrossRef]
- Moreau, A.; Lévesque, D.; Lord, M.; Dubois, M.; Monchalin, J.-P.; Padioleau, C.; Bussière, J.F. On-Line Measurement of Texture, Thickness and Plastic Strain Ratio Using Laser-Ultrasound Resonance Spectroscopy. Ultrasonics 2002, 40, 1047–1056. [Google Scholar] [CrossRef]
- Artymowicz, D.; Hutchinson, B.; Nogues, M. Effects of Crystallographic Texture on Ultrasonic Wave Velocities in Steels. Mater. Sci. Technol. 2002, 18, 1142–1146. [Google Scholar] [CrossRef]
- Lévesque, D.; Lim, C.S.; Padioleau, C.; Blouin, A. Measurement of Texture in Steel by Laser-Ultrasonic Surface Waves. J. Phys. Conf. Ser. 2011, 278, 012007. [Google Scholar] [CrossRef]
- Bate, P.; Lundin, P.; Lindh-Ulmgren, E.; Hutchinson, B. Application of Laser-Ultrasonics to Texture Measurements in Metal Processing. Acta Mater. 2017, 123, 329–336. [Google Scholar] [CrossRef]
- Duijster, A.; Volker, A.; Stolzenberg, M. Angle Beam Method for Detection of Textural Features in Steel Sheet. In Proceedings of the 12th European Conference of Non-Destructive Testing, Gothenburg, Sweden, 11–15 June 2018; p. 8. [Google Scholar]
- Voigt, W. Theoretische Studien Über Die Elasticitätsverhältnisse Der Krystalle. Der Dieterichschen Buchhandlung: Göttingen, Germany, 1887. [Google Scholar]
- Reuss, A. Computation of the Yield Point of Mixed Crystals Due to Hiring for Single Crystals. JZAMM 1929, 9, 49–58. [Google Scholar]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Park, N.J.; Bunge, H.J.; Kiewel, H.; Fritsche, L. Calculation of Effective Elastic Moduli of Textured Materials. Textures Microstruct. 1970, 23. [Google Scholar] [CrossRef] [Green Version]
- Bunge, H.-J. Texture Analysis in Materials Science: Mathematical Methods; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 1-4832-7839-5. [Google Scholar]
- Roe, R. Description of Crystallite Orientation in Polycrystalline Materials. III. General Solution to Pole Figure Inversion. J. Appl. Phys. 1965, 36, 2024–2031. [Google Scholar] [CrossRef]
- Tägtström, P.; Hutchinson, B. The Influence of Crystallographic Texture and Nitrogen Content on Young’s Modulus of 304 and 316 Stainless Steel Sheet. Appl. Stainl. Steel 1992, 1, 84–93. [Google Scholar]
- Sharples, S.D. All-Optical Scanning Acoustic Microscope. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2003. [Google Scholar]
- Dryburgh, P.; Pieris, D.; Martina, F.; Patel, R.; Sharples, S.; Li, W.; Clare, A.T.; Williams, S.; Smith, R.J. Spatially Resolved Acoustic Spectroscopy for Integrity Assessment in Wire–Arc Additive Manufacturing. Addit. Manuf. 2019, 28, 236–251. [Google Scholar] [CrossRef]
- Ledbetter, H.M. Monocrystal-Polycrystal Elastic Constants of a Stainless Steel. physica status solidi 1984, 85, 89–96. [Google Scholar] [CrossRef]
- Ledbetter, H.M. Sound Velocities and Elastic-Constant Averaging for Polycrystalline Copper. J. Phys. D Appl. Phys. 1980, 13, 1879. [Google Scholar] [CrossRef]
- Falkenström, M.; Engman, M.; Lindh-Ulmgren, E.; Hutchinson, B. Laser Ultrasonics for Process Control in the Metal Industry. Nondestruct. Test. Eval. 2011, 26, 237–252. [Google Scholar] [CrossRef]
- Speich, G.R.; Leslie, W.C. Elastic Constants of Martensite. Met. Mater Trans B 1973, 4, 1873–1875. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Ledbetter, H.; Urbassek, H.M. Experimental and Atomistic Study of the Elastic Properties of A′ Fe–C Martensite. Acta Mater. 2012, 60, 4901–4907. [Google Scholar] [CrossRef]
- Souissi, M.; Numakura, H. Elastic Properties of Fe–C and Fe–N Martensites. ISIJ Int. 2015, 55, 1512–1521. [Google Scholar] [CrossRef]













| Heat Treatment | Rolling Reduction | Start Grain Size | Thickness | Density |
|---|---|---|---|---|
| No treatment | 70% | 20 µm | 12 mm | 7938 kg/m3 |
| 1 h @ 1200 °C | 70% | 60 µm | 12 mm | 7933 kg/m3 |
| No treatment | 50% | 20 µm | 12 mm | 7937 kg/m3 |
| 1 h @ 1200 °C | 50% | 60 µm | 12 mm | 7932 kg/m3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malmström, M.; Jansson, A.; Hutchinson, B. Application of Laser-Ultrasonics for Evaluating Textures and Anisotropy. Appl. Sci. 2022, 12, 10547. https://doi.org/10.3390/app122010547
Malmström M, Jansson A, Hutchinson B. Application of Laser-Ultrasonics for Evaluating Textures and Anisotropy. Applied Sciences. 2022; 12(20):10547. https://doi.org/10.3390/app122010547
Chicago/Turabian StyleMalmström, Mikael, Anton Jansson, and Bevis Hutchinson. 2022. "Application of Laser-Ultrasonics for Evaluating Textures and Anisotropy" Applied Sciences 12, no. 20: 10547. https://doi.org/10.3390/app122010547
APA StyleMalmström, M., Jansson, A., & Hutchinson, B. (2022). Application of Laser-Ultrasonics for Evaluating Textures and Anisotropy. Applied Sciences, 12(20), 10547. https://doi.org/10.3390/app122010547






