Machine Learning Applications for Jet Tagging in the CMS Experiment

Abstract

The fundamental physics research at the frontier accessible by today’s particle accelerators such as the CERN Large Hadron Collider pose unique challenges in terms of complexity and abundance of data to analyse. In this context, it is of paramount importance to develop algorithms capable of dealing with multivariate problems to enhance humans’ ability to interpret data and ultimately increase the discovery potential of the experiments. Machine learning techniques therefore assume an increasingly important role in the experiments at the LHC. In this work, we give an overview of the latest developments in this field, with a particular focus on the algorithms developed and used within the CMS Collaboration. The review follows this structure: (1) Introduction presents the CMS Experiment at LHC and the most common methods used in particle physics; (2) Jet Flavour Tagging briefly describes the main algorithms used to reconstruct heavy-flavour jets; (3) Jet Substructure and Deep Tagging focuses on the identification of heavy-particle decay in boosted jets; (4) Analysis Applications gives examples of applying the algorithm in physics analyses; and (5) Conclusions summarises the state-of-the-art and gives indications for future studies.

1. Introduction

The prime motivation of the Large Hadron Collider (LHC) [1] is to provide an explanation to the open issues of fundamental particle physics, among which one can mention: inclusion of gravity in a unique framework with electromagnetic, weak, and strong interactions; explanation of the dark sector; and discovery of the origin of matter–antimatter asymmetry. LHC activity started in 2008, and the data collected in the first years led to discovery of the Higgs boson in 2012 by the ATLAS and CMS Collaborations [2,3]. The CMS Experiment studies the particles resulting from LHC proton–proton collisions in pursuit of understanding the laws that regulate their interactions. In particular, the CMS Detector [4] is a general purpose apparatus with cylindrical symmetry designed to trigger based on [5,6] and to identify electrons, muons, photons, and hadrons [7,8,9,10]. Particle reconstruction is performed via the “particle-flow” (PF) algorithm [11] that combines the information provided by the many subdetectors comprising the apparatus: the silicon inner tracker, the crystal electromagnet, the brass-scintillator hadron calorimeters, the superconducting solenoid (capable of providing a 3.8 T magnetic field), and the gas-ionisation muon detectors interleaved with the solenoid return yoke. The PF algorithm is able to reconstruct leptons and hadrons as well as more complex objects, such as jets of hadronic particles, and global features of the event such as the missing transverse momentum for the kinematic closure of the event [12,13,14]. In the last years, the performances of the LHC accelerator machine and the complexity of the experiments have grown largely. In the forthcoming Run III, proton beams will collide with a centre-of-mass of 14 $\mathrm{TeV}$ and with a mean number of simultaneous interactions per each bunch crossing around 80 at a frequency of 40 MHz. For each collision, data collected by each subdetector must be stored for the so-called offline reconstruction to be carried out at a later stage and each event provide information on the order of MBs. In order to reduce the event rate, the CMS detector implements a double-tier trigger system that reduces the bandwidth to be written to the disk by up to 100 MHz.

The conditions to face are both the large number of events to analyse and the large size of each event given the number of particles produced. Such issues are tackled by reducing the dimensionality of the problems by grouping the information in step-by-step analysis and reconstruction by applying selection at each step. This task can also be reformulated in terms of a machine learning (ML) problem.

Formally given a certain ensemble of observed data X, we would like to find a function f that returns an ensemble Y of reduced dimensionality by optimising some criteria. This metric $L(y,f(x\left)\right)$ is typically referred to as loss function and can be optimised with machine learning. In this sense, the conditions of the LHC environment are a perfect testing ground for the application of machine learning techniques. A complete discussion of the applicability of ML techniques for the LHC experiments is already provided in [15]. Many algorithms have been developed over the last years, and they are used for many tasks, ranging from physics object reconstruction to signal-to-background discrimination. A very detailed collection of the machine learning algorithms used in particle physics can be found in [16]. One of the most delicate tasks in event reconstruction and interpretation is, in fact, the treatment of signatures originating from outgoing quarks and gluons from the collision. These particles produce jets of hadrons, ultimately losing information on the nature of the originating particle and making it difficult, therefore, to discriminate a potential signature coming from a new physics signal with respect to a process from the Standard Model (SM). We present a review of some of the most interesting and advanced uses of ML algorithms for jet identification developed by the CMS Collaboration. These so-called tagger algorithms have a relevant role in physics studies since they allow researchers to successfully reconstruct and identify the particles that caused the jet and, in some cases, allow analyses that would otherwise be unfeasible.

2. Jet Flavour Tagging

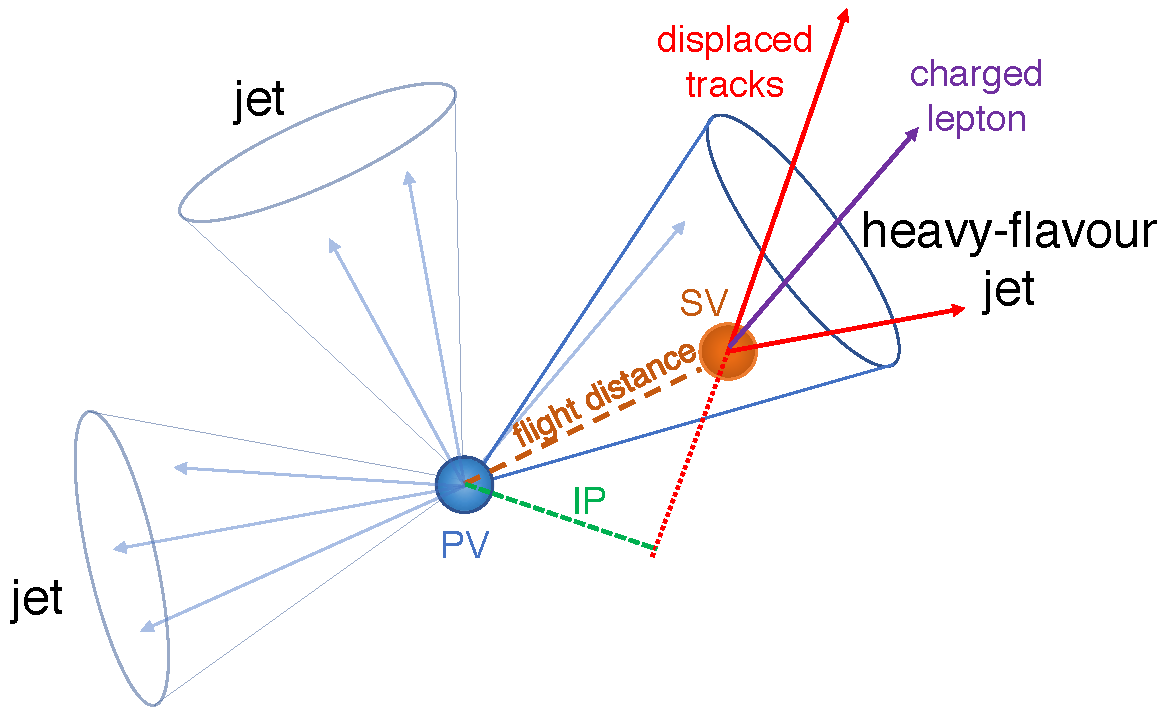
After a proton–proton collision, quarks and gluons hadronise and radiate, producing jets of particles. For the CMS Experiment, the jets are detected and clustered with the anti-$k_t$ algorithm [17] with a radius $R=\sqrt{\Delta {\eta }^2+\Delta {\varphi }^2}=0.4$, where $\eta$ is the pseudorapidity, and $\varphi$ is the azimuthal angle. Of particular interest are the jets coming from radiation and hadronisation of b or c quarks. Heavy-flavour jet tagging is linked to the properties of the heavy-hadrons in the jets. The main feature is the presence of a secondary vertex (SV) due to the long lifetime of heavy-flavour hadrons. The impact vector describes the distance between the primary vertex (PV), defined as the vertex with the greatest amount of transverse momentum (${\mathrm{p}}_{\mathrm{T}}$), and the secondary vertex. Heavy-flavour jets are characterised by high-modulus impact vectors. The impact parameter (IP) is defined from the impact vector in two spatial dimensions (2D), in the transverse plane to the beam line, or in three spatial dimensions (3D). Figure 1 illustrates heavy-flavour jet production and the resulting SV.

Two different algorithms are used to find the secondary vertices: adaptive vertex reconstruction (AVR) and inclusive vertex finding (IVF). After secondary vertex reconstruction is performed, dedicated algorithms have been developed by the CMS Collaboration in order to perform heavy-hadron jet tagging based on the properties of the secondary vertices from which particles in the jets originated. An example is the Combined Secondary Vertex (CSV) algorithm developed in Run-I that combines the variables of secondary vertexes in a likelihood-ratio discriminant [19]. In Run-II, new algorithms were developed for heavy-hadron tagging starting from the CSV and making use of ML techniques: CSVv2 and DeepCSV. Ultimately, a more-sophisticated technique, DeepJet, was developed that makes use of many variables of both high and low level.

2.1. The CSVv2 Tagger

The CSVv2 algorithm is based on the CSV algorithm; however, displaced track information is combined with the relative secondary vertex as input for multivariate analysis. A feed-forward multilayer perceptron with one hidden layer is trained to tag the b-jet. The jet’s ${\mathrm{p}}_{\mathrm{T}}$ and $\eta$ distributions are reweighted in order to have the same spectrum for all the jet flavours in the training, thereby avoiding discrimination based on the spectrum of these variables, which would introduce a dependence on the sample used. Three different jet categories are defined based on the number and type of secondary vertices reconstructed: RecoVertex, PseudoVertex, and NoVertex. The values of the discriminator of the three categories are combined with a likelihood ratio that takes into consideration the fraction of jet flavour derived in a sample composed of top quark–antiquark ($\mathrm{t}\overline{\mathrm{t}}$) events. Moreover, two different trainings are performed with c-jets and light-jets as the background. The final value of the discriminator is the weighted average of the two training outputs, with a relative weight of 1:3 for c-jet to light-jet trainings. The CSVv2 algorithm by default uses vertices reconstructed with the IVF algorithm, but it has also been studied with AVR reconstruction, and this is referred to as CVSv2 (AVR). Figure 2 shows the output of the two versions of the CSVv2 algorithm.

2.2. The DeepCSV Tagger

The DeepCSV algorithm was developed with a Deep Neural Network (DNN) with more hidden layers and more nodes per layer in order to improve the CSVv2 b-tagger. The input is the combination of the IVF secondary vertices and up to the first six track variables, taking into consideration all the jet-flavour and vertex categories. Variable preprocessing is used to speed up training and centres the distributions around zero with a root mean square equal to one. The jet ${\mathrm{p}}_{\mathrm{T}}$ range used in training goes from 20 $\mathrm{GeV}$ up to 1 $\mathrm{TeV}$ and remains within the tracker acceptance by also using the preprocessed jet ${\mathrm{p}}_{\mathrm{T}}$ and $\eta$ as input.

The neural network, developed with KERAS [20], uses four fully connected hidden layers, and each layer has 100 nodes. The activation function of each node is a rectified linear unit that defines the output of the node, with the exception of the last layer, for which the output is a normalised exponential function interpreted as the probability of flavour f of the jet (P(f)). Five jet categories corresponding to the nodes in the output layer are defined: one for b hadron jets, at least two for b hadrons, one for c hadron and no b hadron, at least two for c hadron and no b hadron, and other jets. Figure 3 shows the DeepCSV probability P(f) distributions.

The DeepCSV tagger is used also for c tagging, which combines the probabilities corresponding to the five categories. In particular, the DeepCSVCvsB discriminant is used to discriminate c jets from b jets and is defined as:

$$DeepCSVCvsB=\frac{P\left(c\right)+P\left(\mathrm{c}\overline{\mathrm{c}}\right)}{1-P\left(udsg\right)},$$

(1)

where $1-P\left(usdg\right)$ is the probability of identifying an a, b, or c jet. In the same way, DeepCSVCvsL is defined to discriminate c jets from light jets:

$$DeepCSVCvsL=\frac{P\left(c\right)+P\left(\mathrm{c}\overline{\mathrm{c}}\right)}{1-(P\left(b\right)+P\left(\mathrm{b}\overline{\mathrm{b}}\right))},$$

(2)

and the denominator is the probability of identifying a c jet or a light jet.

2.3. The DeepJet Tagger

Recently, a new network architecture was developed: the DeepJet tagger [21]. Different from CSVv2 and DeepCSV taggers, this architecture examines all jet constituents simultaneously. The DeepJet algorithm uses a large number of input variables that can be categorised into four groups: global variables (jet kinematics, the number of tracks in the jet, etc.), charged and neutral PF candidates, and variables of the SVs related to the jet. For the same reasons seen in Section 2.1, the jets ${\mathrm{p}}_{\mathrm{T}}$ and $\eta$ are reweighted during data preprocessing to avoid discrimination closely related to the kinematic domain used during training.

The basic idea in the DeepJet architecture is to use low-level information from all subjet features. In order to process an input variable space of such dimensions, the architecture needs an appropriate training procedure. Four separate branches are used in the first step: all four of the groups listed above except the global variables are filtered through a $1\times 1$ convolutional layer. Each of the three outputs is then processed into a recurrent layer of the Long Short-Term Memory (LSTM) type [22]. The three LSTM outputs are collected with the global variables and then input in a fully connected layers. In order to discriminate between b-tagging, c-tagging, and quark/gluon tagging, the six output nodes of the previous layers are integrated into a multi-classifier.

Training is performed using the Adam optimiser with a learning rate of $3\times {10}^{-4}$ for 65 epochs and categorical cross entropy loss. The learning rate is halved if the validation sample loss stagnates for more than 10 epochs. In Figure 4, the Receiver–Operative Characteristic (ROC) curves for two different ${\mathrm{p}}_{\mathrm{T}}$ ranges for the same dataset are reported and compared to the performance of the DeepCSV tagger. Such curves display the background misidentification efficiency versus the signal efficiency measured from Monte Carlo simulation.

3. Jet Substructure and Deep Tagging

As seen in the previous section, the properties of heavy-hadrons make it possible to define criteria to discriminate between jets coming from c and b quarks. In this section, we describe algorithms designed to discriminate between hadronically decaying massive SM particles and large Lorentz boosts, namely W, Z, and H bosons and top quarks, by exploiting the jet substructure that develops following the decay chain of such particles. The first methods used by the CMS Collaboration to tag boosted heavy objects (top quarks and W/Z/H bosons) were simple selections based on the mass or jet substructure of the candidate large jet, i.e., those clustered with a radius $R=0.8$. In the following, we refer to these jets as AK8 jets. Examples of these methods are $m_{SD}+{\tau }_{32}$, $m_{SD}+{\tau }_{32}+$ b for the top quark, or $m_{SD}+{\tau }_{21}$ for both the top quark and W boson. The value $m_{SD}$ is the mass of the jet after the grooming procedure is applied. This consists in the removal of the softer and uncorrelated radiation from the total energy of the jet. The grooming algorithm used by the CMS Collaboration is a modified mass-drop tagger [23], which is a particular implementation of the soft-drop method [24]. The values of ${\tau }_{32}$ and ${\tau }_{21}$ are the ratio between two ${\tau }_N$ variables, the so-called N-subjettiness [25] defined as:

$${\tau }_N=\frac{1}{d_0}\sum _i{p}_{\mathrm{T},i}min[\Delta R_{1,i},\Delta R_{2,i},\cdots ,\Delta R_{N,i}],$$

(3)

where the index i refers to the jet constituents, while the $\Delta R$ terms are the distance in the $\eta -\varphi$ plane between a certain jet constituent and the subjets, N is the number of candidate subjet axes obtained by the exclusive $k_{\mathrm{T}}$ clustering algorithm when forced to return exactly N jets, and $d_0$ represents a normalisation constant. One can see that ${\tau }_j$ is the average distance of the jet constituent from j axes. For this reason, this variable gives a measure of the compatibility of an AK8 jet with the presence of a given number of subjets inside of it. Another relevant algorithm is the heavy-object tagger with variable R (HOTVR), which is a clustering method that makes use of a variable R and implements soft radiation removal during clustering. In the last few years, other methods that more efficiently exploit the information coming from the CMS detector have been developed. In particular ML techniques have been used both to combine some of the already-discussed methods and to use particle-level variables. In the following, the three most relevant and better performing algorithms are described in detail.

3.1. ImageTop

The ImageTop [26] tagger is based on a 2D Convolutional Neural Network (CNN) and makes use of image recognition techniques. It is trained to discriminate top quark jets from QCD jets. The image of the jet is obtained by superimposing energy deposits of each PF candidate flavour, namely charged and neutral hadrons, photons, electrons, and muons. The intensity of the obtained images is proportional to the jet energy and is normalised to unity and adjusted in a $37\times 37$ pixel input that corresponds to a space interval of $\Delta \eta =\Delta \varphi =3.2$ coverage.

The so-formatted input is processed by the network, for which the architecture is reported in Figure 5. The full details of the network architecture can be found in [26].

The algorithm also includes the probability of each subjet being a b jet. This is achieved by applying the DeepJet b-tagging algorithm, which returns the probability of the subjet having come from a b quark, $\mathrm{b}\overline{\mathrm{b}}$ pair, leptonic b decay, c quark, light-flavour quark, or gluon. These probabilities along with the soft-drop mass of the subjet are also included in classification of the large jet. Since with the increase of the jet ${\mathrm{p}}_{\mathrm{T}}$, the cone of the jet tends to be more collimated along the jet direction, the image of the jet is adaptively zoomed. This allows for keeping the same granularity of information while maintaining a static pixel-size image. The output of the tagger has a residual correlation to the ${\mathrm{p}}_{\mathrm{T}}$ of the jet, which is removed by applying a correction estimated from Monte Carlo simulation. A soft-drop version of the algorithm, referred to as ImageTop-MD, has also been provided; it has slightly lower performance than the non-mass-decorrelated version. The ROC curves for ImageTop and ImageTop-MD compared to other algorithms on simulated jets are reported in Figure 6a. These algorithms are also validated by data, and corrections for systematic sources of uncertainty are provided by the CMS Collaboration.

3.2. DeepAK8

In order to classify a hadronically decaying particle through a single large jet, the DeepAK8 algorithm defines five main categories: W, Z, H, t, and other. The algorithm’s goal is multi-classification of jets by exploiting particle-level information directly. Due to the different signatures that the same particle can leave in the detector in different decay channels, the five main categories are further subdivided into minor categories based on particle decay modes (e.g., Z →$\mathrm{b}\overline{\mathrm{b}}$, Z →$\mathrm{c}\overline{\mathrm{c}}$, and Z →$\mathrm{q}\overline{\mathrm{q}}$). The DeepAK8 algorithm uses a large number of variables, both low- and high-level, but not all variables are treated in the same way. The architecture of the algorithm consists of two steps: In the first step, the input variables are split in two lists and processed separately with two classifiers. In the second step, the two previous outputs are combined through a third classifier. The first step includes two one-dimensional CNNs (ResNet model-based [27]). A wide number of rough variables is included in the first list; they are made up of the first 100 constituent particles of the jet under investigation. There are 42 variables used for the description of each particle. The limit on the number of constituent particles does not affect efficiency of the algorithm because only a small fraction of jets identified in the detector include more than 100 reconstructed particles. The second list is made up for a different type of discrimination using high-level variables: 7 SVs are used, each with 15 features. Both lists have a specific role in the algorithm: the particle list helps the network obtain features about the presence of heavy-hadrons, while the SV list improves extraction of heavy-flavour content. The first list is processed with a CNN of 14 layers, while the second list is processed with a CNN of 10 layers. A convolution window with a length of three is used, and the number of output channels in each convolutional layer ranges from 32 to 128. In the second step of the architecture, the outputs of the two CNNs are processed by a simple fully connected NN to combine the two different sources of information and then perform jet classification. The NN comprises only one layer with 512 units, followed by a ReLU [28] activation function and a dropout layer with a 20% drop rate. The algorithm is implemented using the MXNET package [29] and trained with the Adam optimiser to minimise the cross-entropy loss. It uses a minibatch size of 1024; the initial learning rate is 0.001, and it is reduced by a factor of 10 at the 10th and 20th epochs to facilitate convergence, for a total of 35 epochs. Classification by the DeepAK8 algorithm is performed ad hoc for jets with ${\mathrm{p}}_{\mathrm{T}}>200$ $\mathrm{GeV}$.

An alternative DeepAK8 algorithm, DeepAK8-MD, has been developed to be largely decorrelated from the mass of jets while providing an efficiency similar to that of the mass-correlated version. The ROC curves in Figure 6b also report the performances of DeepAK8 and DeepAK8-MD on the same simulated dataset used for the other algorithms.

3.3. ParticleNet

The ParticleNet algorithm [30] is a dynamic graph CNN used for jet-tagging problems. A jet is represented as an unordered, permutation-invariant set of particles. A jet is represented as a particle cloud, having, on the one hand, all the advantages and flexibility of a particle-based representation, and on the other hand, the algorithmic strength of the point-cloud representation of 3D shapes used in computer-vision applications. A regular convolution operation is in the form ${\sum }_j{K}_j{x}_j$, where $K_j$ is the kernel, and $x_j$ are the features of each point. However, this convolution is not invariant under point permutation, which is needed in point-cloud representations. The EdgeConv operation [31] connects each point to the k-nearest neighbouring points and, thanks to the edge function and the symmetric aggregation operation, permutationally symmetric operation on point clouds is obtained. Two different versions of the algorithm are used: ParticleNet and ParticleNet-lite. The first one uses three EdgeConv blocks with $k=16$ nearest neighbours, while the second one uses just two EdgeConv blocks and $k=7$. The algorithm is used for top-tagging, i.e., to identify jets from hadronically decaying top quarks, and for quark–gluon tagging, i.e., discriminating between jets initiated by quarks and gluons. For the top-tagging algorithm, only jets with $R=0.8$ and reconstructed with the anti-$k_t$ algorithm are considered; for each jet, up to 100 constituents with high ${\mathrm{p}}_{\mathrm{T}}$ values are taken into account. Only kinematic information is used for each particle, and, compared to various pre-existing algorithms, it shows better performance, with an area under the curve $AUC=0.9858$, as seen in Figure 7a.

ParticleNet quark–gluon tagging is performed on anti-$k_t$ jets with $R=0.4$. Moreover, two different sets of variables for each particle are used: in the first one, only variables related to four-momentum are taken into account, while in the second one, there is also particle identification information (PID). PID information leads to better performance in jet tagging. As shown in Figure 7b, the ParticleNet algorithm with and without PID information leads to the best results with, respectively, $AUC=0.840$ and $AUC=0.828$.

4. Analysis Applications

Many analyses have started to use ML techniques at different stages of the workflow, from physics objects selection, which make use of vertexes and tracks, to the final signal-to-background discrimination based on high-level variables. The first class of these methods has already been described in the previous section. Here the focus is on the second class of use by discussing some of the newest or most original approaches proposed in CMS Collaboration papers. The first of such analyses is reported in [32] and presents the search for a ${\mathrm{W}}^{\prime }$ boson decaying to a top quark, decaying hadronically, and a bottom quark. This analysis aims to study the processes for which the Feynman diagrams are reported in Figure 8.

The DeepJet algorithm is used for the b tagging of the jets related to bottom quark production and hadronisation. The jets are AK4 jets with ${\mathrm{p}}_{\mathrm{T}}>500$ $\mathrm{GeV}$, and the thresholds for the taggers correspond to a misidentification rate of 5% for jets initiated by light quarks or gluons. However, the efficiency is reduced from 75% to 65% for jets with ${\mathrm{p}}_{\mathrm{T}}=500$ $\mathrm{GeV}$ and jets with ${\mathrm{p}}_{\mathrm{T}}=1000$ $\mathrm{GeV}$, respectively, in the barrel region.

For top tagging, the DeepAK8 algorithm is used; it takes into consideration jets with $R=0.8$ and $105<m_{\mathrm{SD}}\left(\mathrm{t}\right)<210$ $\mathrm{GeV}$. The threshold used on the DeepAK8 tagger score corresponds to a misidentification rate of 0.5% for jets initiated by light quarks or gluons, and to an efficiency of approximately 35–45% for jets initiated by top quarks. The use of these ML techniques improves the final state selection compared to previous studies in [33], excluding ${\mathrm{W}}^{\prime }$ boson mass below $3.4$ $\mathrm{TeV}$.

The search for ${\mathrm{W}}^{\prime }$ boson is also characterised by a different final state with a vector-like quark and a top or bottom quark in the all-jets final state. The Feynman diagram of the process is shown in Figure 9.

The final state foresees the presence of a top and bottom quark in association with a Higgs or Z boson. In order to successfully identify events with such topology, two different ML methods are used. The top quark is recognised by means of the newest top tagger developed by the CMS Collaboration: the ImageTop tagger. This study represents the first application of this tagger in a physics analysis. The improvement of ImageTop is quantified by a factor-six gain in tagging efficiency with respect to previous algorithms. This analysis uses the MD version of the algorithm, and since, in this case, the dependence of the tagger response is barely dependent on the top quark mass, a requirement on this variable is also applied. The values for the mass of the top jet are within the window $40<m_{\mathrm{SD}}\left(\mathrm{t}\right)<220$ $\mathrm{GeV}$. The Higgs or the Z jet are instead recognised with the DeepAK8 tagger after imposing a veto on the top jet tagger for the selected jet. Additionally, in this case, a window for the soft-drop mass is applied: precisely $105<m_{\mathrm{SD}}\left(\mathrm{H}\right)<140$ $\mathrm{GeV}$ and $65<m_{\mathrm{SD}}\left(\mathrm{Z}\right)<105$ $\mathrm{GeV}$, respectively, for the Higgs jet and the Z jet candidate.

A third example of analysis in which the final signal-to-background discrimination uses an ML algorithm is reported in [35]. In such analyses, a combined search for the production of a SUSY top quark partner, or top squark, is presented. The new analysis includes a parameter space in which the mass difference ($\Delta m_{cor}$) between the top squark and the neutralino is close to the top quark mass, the so-called top quark corridor region. The final state consists of a dilepton pair with opposite charge and missing ${\mathrm{p}}_{\mathrm{T}}$. A parametric DNN algorithm is used to increase the sensitivity of the signal against the main SM background, represented by $\mathrm{t}\overline{\mathrm{t}}$ events. A total of 11 kinematic variables are used for training, with the addition of two parameters: the top squark and neutralino masses. The choice of network parameters strongly depends on the masses of the new particles, and so a specific model is adopted for each signal point. Training is performed with TensorFlow. All the hyperparameters are optimised with the aim of avoiding overfitting and achieving the highest possible classification accuracy. The final DNN structure is made up of seven hidden layers with a ReLU activation function (300, 200, 100, 100, 100, 100, and 10 neurons). The output consists of two neurons with a softmax normalisation function to allow interpretation of the output numbers as probabilities. The optimiser selected is Adam with a learning rate of 0.0001. Figure 10 shows the DNN output for two different mass parameters for signal and $\mathrm{t}\overline{\mathrm{t}}$ background; it also shows the discrimination power of the DNN. The gain in sensitivity by using the DNN score increases with increasing $\Delta m_{cor}$ and with increasing neutralino mass for a fixed $\Delta m_{cor}$.

Another very important analysis to be discussed is Higgs boson pair production via vector (V) boson fusion in highly Lorentz-boosted topologies. This type of event allows the study of three different types of coupling: trilinear Higgs boson self-couplings (HHH), and trilinear and quartic Higgs boson couplings to Z and W bosons (VVH and VVHH, respectively). A deep comprehension of these couplings could give insight into the properties of the Higgs boson, and precise measurement could shed light on its nature, allowing testing of the SM. At the LHC, HH nonresonant production via vector boson fusion has a small cross-section on the order of 2 fb. The selection can be optimised by choosing the most abundant branching fraction decay of the Higgs boson that turns to H →$\mathrm{b}\overline{\mathrm{b}}$ ($\sim 33\%$). This final state is very challenging in the LHC hadronic environment, especially when looking for highly Lorentz-boosted topologies, for which the standard b-tagging algorithms start to fail. This problem is overcome by the ParticleNet algorithm, which is specifically trained for cases such as this. The analysis reported in [36] represents the first application of this novel technique. The H →$\mathrm{b}\overline{\mathrm{b}}$ discrimination against the QCD processes is achieved by defining the $D_{\mathrm{b}\overline{\mathrm{b}}}$ tagging discriminator as:

$$D_{\mathrm{b}\overline{\mathrm{b}}}=\frac{score(\mathrm{H}\to \mathrm{b}\overline{\mathrm{b}})}{score(\mathrm{H}\to \mathrm{b}\overline{\mathrm{b}})+score\left(QCD\right)},$$

where the $score(\mathrm{H}\to \mathrm{b}\overline{\mathrm{b}})$ and $score\left(QCD\right)$ are the output scores provided by the ParticleNet algorithm. In order to maximise background rejection, a requirement of $D_{\mathrm{b}\overline{\mathrm{b}}}>0.9$ is applied. The analysis makes use of three categories with different signal purity:

• High purity: $D_{\mathrm{b}\overline{\mathrm{b}}}>0.98$ for both the Higgs jets;
• Medium purity: $0.94<D_{\mathrm{b}\overline{\mathrm{b}}}<0.98$ for both the Higgs jets;
• Low purity: $0.9<D_{\mathrm{b}\overline{\mathrm{b}}}<0.94$ for both the Higgs jets.

The signal is then extracted with a binned maximum-likelihood fit performed simultaneously in all the categories.

5. Conclusions

We presented a review of the latest machine learning algorithms developed by the CMS Collaboration to improve jet tagging, i.e., to identify the particle that started the jet—in particular, to discriminate heavy-flavour jets coming from b or c quarks. Moreover, ML is used to tag jets with a more complex internal structure coming from the hadronic decay of Z/H/W bosons or top quarks. The use of these techniques allowed better event selection in different physics analyses, leading to new competitive results.

The development of these technologies is still ongoing both in CMS and in other LHC experiments such as ATLAS [37,38,39]. Among future developments, it is possible to extend deep learning techniques to other decay chains of SM particles, for example, including leptons in the final state, and to particles beyond SM. Further, it is possible to use unsupervised machine learning techniques for anomaly detection in the structure of highly Lorentz-boosted jets, ultimately searching for new physics models that have yet to be accounted for.