A Radiomics Approach Based on Follow-Up CT for Pathological Subtypes Classification of Pulmonary Ground Glass Nodules

Abstract

Preoperative, non-invasive, and accurate identification of the pathological subtypes of pulmonary ground glass nodules (GGNs) play an important role in the precise selection of clinical surgical operations and individualized treatment plans. Efforts have been made for the classification of pathological subtypes of GGNs, but most existing methods focus on benign or malignant diagnosis of GGNs by means of a one-time computed tomography image (CTI), which fails to capture the nodule development based on follow-up CTI. In this paper, a novel method for subtype classification based on follow-up CTIs is presented as a viable option to the existing one-time CTI-based approach. A total of 383 follow-up CTIs with GGNs from 146 patients was collected and retrospectively labeled via posterior surgical pathology. Feature extraction is performed individually to the follow-up CTIs. The extracted feature differences were represented as a vector, which was then used to construct a set of vectors for all the patients. Finally, a subspace K-nearest neighbor classifier was built to predict the pathological subtypes of GGNs. Experimental validation confirmed the efficacy of the new method over the existing method. Results showed that the accuracy of the new method could reach 72.5%, while the existing methods had an upper bound of 67.5% accuracy. Subsequent three-category comparison experiments were also performed to demonstrate that the new method could increase the accuracy up to 21.33% compared to the existing methods that use one-time CTI.

1. Introduction

Lung cancer frequently manifests in the form of a malignant tumor with very high morbidity and mortality worldwide [1]. In 2015, the World Health Organization integrated multidisciplinary research on lung adenocarcinoma, classifying it into four subtypes based on its different pathologies: atypical adenomatous hyperplasia (AAH), adenocarcinoma in situ (AIS), minimally invasive adenocarcinoma (MIA), and invasive adenocarcinoma (IA).

With advancements in imaging technology, and the widespread application of computed tomography image (CTI) for lung cancer scan, the detection rate of early-stage lung adenocarcinoma, manifested as ground glass nodules (GGNs), has increased significantly. GGNs are closely related to lung cancer, especially lung adenocarcinoma [2]. During the pathological progress of lung adenocarcinoma from pre-invasive to invasive lesions, GGNs can be observed in the CTI, but lack specificity [3]. The growth of GGN follows a regular pattern, from benign lesions (e.g., AAH) to malignant lesions (e.g., IA) [4]. Most GGN lesions are benign, but about 30% are malignant including AIS, MIA, and IA [5]. However, GGN is likely to be related to other lung diseases such as viral pneumonia [6], the coronavirus disease 2019 (COVID-19) [7], etc., where COVID-19 has become a global pandemic. To date, how to distinguish their differences remains a key issue.

In the past, traditional computer-aided diagnosis methods utilize various feature extraction protocols to quantify the appearance of nodules on diagnostic CTIs, and machine learning algorithms such as fuzzy clustering [8], threshold segmentation [9], support vector machines [10], etc., have been employed to classify GGNs. Although these works have achieved impressive performance, extracting appropriate nodule features is very time-consuming, unapparent, and unclear. In recent decades, three classes of remarkable progresses on GGN have been made as follows.

(1) Rapid development in digital imaging and artificial intelligence technologies has led to the field of radiomics, a new technique first proposed by Lambin et al. in 2012 for the noninvasive diagnosis of tumors [11]. Radiomics is recognized as an effective quantitative tool for characterizing the phenotypes of lung lesion [12]. It has achieved remarkable results in oncology assessments and diagnosis as well as in post-treatment prognosis [13]. In early pulmonary nodules diagnosis, for example, studies have demonstrated that radiomics performs well when classifying benign or malignant pulmonary nodules, histopathologic lung cancer phenotypes, and invasiveness in lung adenocarcinoma lesions based on quantitative CTIs [14,15].

(2) Deep learning (DL) methods have been demonstrated to greatly reduce the difficulty of feature extraction in CTIs [16]. Unlike the radiomics model, the DL-based model can extract deep imaging features by using an end-to-end deep convolutional neural network [17]. Wang et al. [18] showed that DL combined with the radiomics features could conveniently and automatically obtain the best performance in predicting the invasiveness of lung adenocarcinoma manifesting as GGNs. Moreover, a cascade architecture with both segmentation and classification networks was built. It could perform better and was more stable than the multi-task learning model appearing as GGNs. Ni et al. [19] proposed an automatic GGN invasiveness classification algorithm for the adenocarcinoma. Experiments showed that the algorithm outperformed the traditional machine learning method.

(3) AI techniques have attracted significant attention in the fight against COVID-19. One crucial application to use CTIs is to segment the COVID-19 infections, which can aid doctors in the treatment. A novel evolvable adversarial framework [20] has been developed for COVID-19 infection segmentation that incorporated the gradient penalty into the network, penalizing the discriminator’s gradient norm input. Experiments verified that the proposed model achieved superior effectiveness and stability for COVID-19 infection segmentation. Additionally, a weakly supervised method [21] was proposed for the segmentation of COVID-19 infections in CT slices with scribble supervision. The whole framework was constructed with a mean teacher framework and optimized by a weighted combination of the supervised and unsupervised losses. In the same direction, some other AI methods have been presented for the diagnosis and analysis of COVID-19 [22], and so on.

Although efforts and progress have been made, existing methods are very limited due to the following two issues:

(1) One-time CTI. The existing studies create their diagnosis models or classifiers based on the set of one-time CTIs, while medical professionals compare the change in GGNs in follow-up CTIs by reviewing and comparing visual characteristics rather than performing a quantitative evaluation. Thus, follow-up CTIs at regular intervals are necessary to identify and track the lesion change.

(2) Poor interpretability. As a data driven algorithm, the development of a DL-based model usually needs a large training dataset with thousands of CTIs. However, the diagnosis and therapy results for these models often have poor interpretability and do not respond to the morphological characteristics in CTIs. In the case of a small scale CTI set, their results may be unreliable. Since these characteristics are often atypical, it makes the differential diagnosis of pathological subtypes based on GGNs even more difficult.

In this paper, we propose a follow-up feature difference-based classification method (FFDC) to improve the accuracy of preoperative diagnosis, and overcome the limitation of the existing one-time feature-based (OFDC) method.

2. Materials and Methods

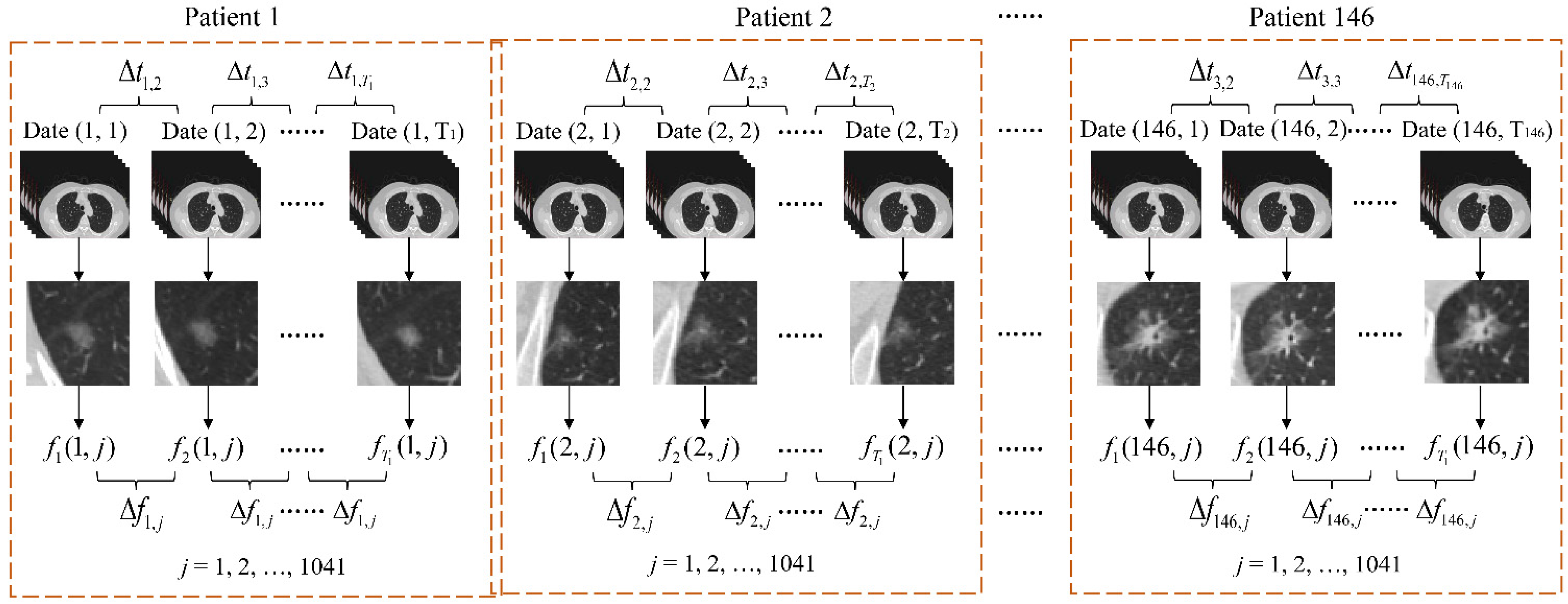
2.1. Sample Acquisition and Labeling

To build a classifier for the pathological subtypes of GGNs, a set of follow-up CTIs with GGNs must be collected.

The CTIs used in this study were retrospectively collected from the department of pulmonary tumor surgery, Tianjin Medical University General Hospital, corresponding to 146 patients with early lung adenocarcinoma from January 2020 to June 2021. All GGNs were retrospectively labeled by their surgical pathology. Figure 1 shows the four pathological subtypes of GGNs. All patients had one-time follow-up CTIs at least in which these lesions manifested as GGNs. These GGNs were pathologically analyzed after surgical resection. Hence, their pathological subtypes were confirmed by histopathology analysis. In this paper, the confirmed subtypes were used to label the GGNs for subsequent classification when constructing a classifier. The study was conducted in accordance with the Declaration of Helsinki, and all experiments were approved by the ethics committee of General Hospital of Tianjin Medical University (IRB2020-YX-145-01). The requirement to obtain informed consent from the participants was waived by the ethics committee.

Table 1. The GGNs subtypes of 146 patients.

	Pathological Subtypes	Number of Patients	Number of Follow-Ups
Malignant	IA	96	249
	MIA	21	50
	AIS	8	37
Benign	AAH	21	47

shows the number subtypes of 146 patients, their number of follow-ups along these subtypes, and the GGNs subtypes in CTIs, respectively.

In this paper, we implemented the segmentation and feature extraction of GGNs using 3D Slicer [23]. 3D Slicer is a free and open-source multi-platform software package that is widely used for medical, biomedical, and related imaging research.

Each GGN corresponded to a group of CTIs with different sizes and shapes, but we fixed the CTI with the largest area for sequential classification purposes. According to the pathological and the CT detection reports, each patient’s GGN location and subtype can be found and labeled. The segmentation and labeling steps of GGN are as follows:

(1)

Import a set of CTIs for each patient into 3D Slicer and locate the GGNs.

(2)

Select CTIs that contain GGNs and then find the CTI with the largest area among these selected CTIs.

(3)

Segment the GGN with the largest area and save it as sequential classification.

(4)

Label the GGNs subtype with pathology reports.

According to 3D Slicer, 1041 features can be extracted from each GGN from the 146 patients’ 386 follow-up CTIs. Algorithmically, let Date (k, i) be the ith follow-up date of kth patient, Δt_k,i be the time interval from ith to (i + 1) paired follow-up dates, f_k (i, j) be the jth extracted feature from GGN in the ith follow-up CTI, and T_k is the total number of follow-up times of k-th patient, k = 1, 2, …, 146, i = 1, 2, …, 383, j = 1, 2, …, 1041.

Consequently, their feature differences along the paired follow-ups is computed as

$$\mathsf{\Delta }{f}_k(i,j)=(f_2(i,j)-f_1(i,j))/\mathsf{\Delta }{t}_{ij}, k=1,2,\dots ,146; i=1,2,\dots ,T_k;\hspace{0.17em}\hspace{0.17em}j=1,2,\dots ,1041$$

(1)

where the denominator of Δt_ij aims to normalize the feature change in two different follow-up time intervals. Hence, the GGN feature changes of different patients at different dates are comparable.

Let S_FFDC be the set of all feature-difference samples from Equation (1) in FFDC, and S_OFDC be the set of samples in OFDC in which the T_kth time CTI for each patient is used to capture the latest features of GGN. Thus, S_FFDC = {Δf_k (i, j)}, S_OFDC = {f_k (T_k, j)}

Figure 2 shows the feature extraction process of our proposed method, where these figures in the third row show CTI samples, and these figures in the fourth row refer to the correspondingly segmented GGNs, respectively.

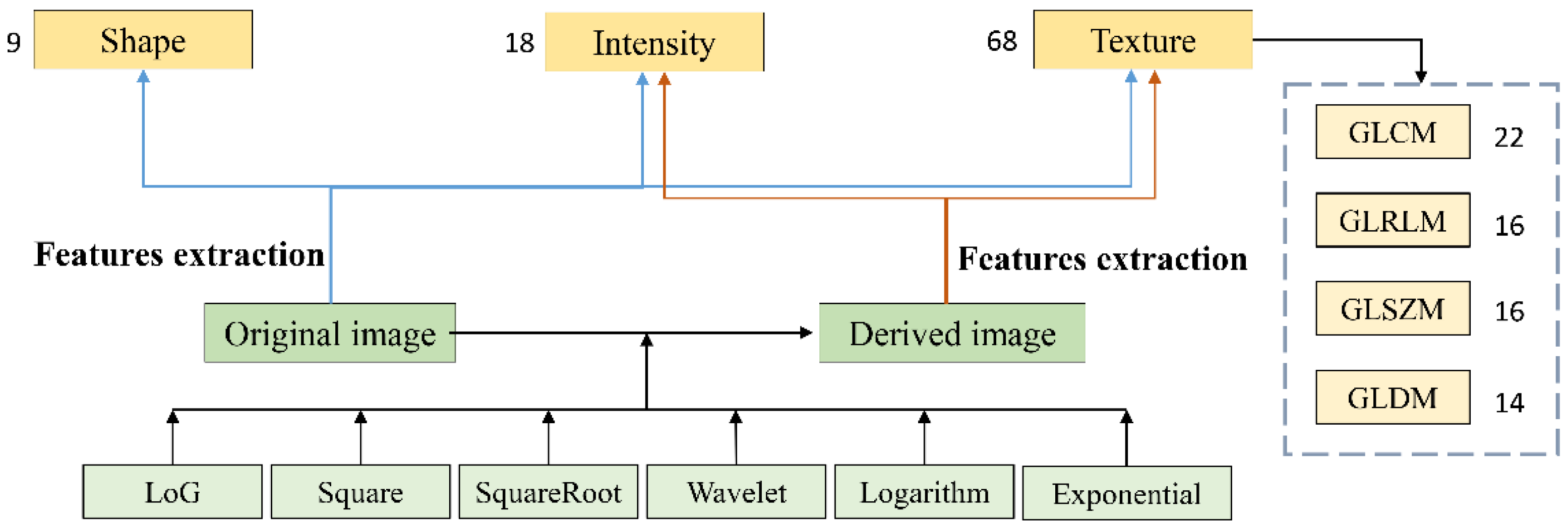
2.2. Radiomics Feature Extraction

The built-in package Pyradiomics in 3D Slicer can extract the main features of GGNs [24]. Through an analysis of the contour, direction, and gray value of GGNs, we can not only obtain the existing morphological characteristics, but also quantify the sufficient radiomics characteristics [25].

These quantitative features from radiomics are then computed on the original CTI and the six transformation images that follow: square, log, square root, exponential, logarithm, and wavelet. The set of initial features consists of 95 original features, 86 square features, 430 log features, 86 square root features, 172 wavelet features, 86 logarithm features, and 86 exponential features. The original features include nine shape features, 18 histogram features, and 68 texture features. These texture features are further divided into four categories: gray level run length matrix (GLRLM), gray level difference matrix (GLDM), gray level co-occurrence matrix (GLCM), and gray level size zone matrix (GLSZM), with their numbers being 16, 14, 22, and 16, respectively. In addition to the features extracted on the original CTI, we could identify the histogram features and texture features in the derived images.

Figure 3 shows the type and number of 1041 extracted features of GGN for the CTI of each patient.

The pair of CTIs from two-time adjacent flow-up records was used for feature extraction in FFDC from the first to the final follow-ups before the patient was operated, since each patient had two-time follow-up CTIs at least. On the other hand, a patient can have multiple GGNs, and thereby the radiomics feature difference between two-time follow-up CTIs of each GGN is regarded as a sample in FFDC. In contrast, only the most recent CTIs before surgery were used in OFDC. These CTIs had a follow-up period of more than three years compared to the most recent preoperative CTI, which were also referenced as samples and empirically compared for diagnosis in OFDC. In all, 383 samples in FFDC were obtained while 146 samples in OFDC were used.

2.3. Feature Selection and Data Augmentation

When all samples are used for the pathological classification of GGNs, two problems remain, as follows:

(1)

The number of samples is much less than that of the features, and some features are unnecessary.

(2)

The sample distribution is imbalanced; Table 1 shows that the number of samples in the majority class is 96, but there are only eight in the minority class.

To overcome these problems, feature selection and sample augmentation are implemented to S_FFDC and S_OFDC in advance. Feature selection removes irrelevant and redundant features [26]. To identify the key features and reduce feature dimensionality, we applied the analysis of variance (ANOVA) method [27]. ANOVA is a single variable analysis method to test whether the effect of any independent feature is obvious for which we computed the three sums of squares in S, SST, SSW, and SSB [28]. According to the four pathological subtypes of GGN and all samples, S consists of four groups of {x_ij} in which each contains n_i samples, i = 1, 2, 3, 4; j = 1, …, n_i.

As a result, SST is computed by

$$SST={\displaystyle {\sum }_{i=1}^4{\displaystyle {\sum }_{j=1}^{n_i}(x_{ij}}}-\overline{X})$$

(2)

where $\overline{X}$ is the mean of all samples in S. SSB is computed as

$$SSB={\displaystyle {\sum }_{i=1}^4{n}_i({\overline{X}}_i-\overline{X})}$$

(3)

Finally, SSW is calculated as

$$SSW=SST-SSB$$

(4)

To calculate the effect of each feature in S, SSB is divided by its freedom degree of 3 to obtain an estimate of MSB. SSW is divided by its freedom degree of 233 to obtain an estimate of MSW. Finally, a statistical value of F-ratio is computed as

$$F=MSB/MSW$$

(5)

We consulted the priori table of critical F values to obtain a significant p value. In this paper, we took a threshold of 0.05. If p > 0.05, the relative feature is rejected; if not, it is accepted for classification. In the following, the feature selection process is implemented in the IBM SPSS Statistics software. The feature number in S based on FFDC and OFDC was reduced to 142 dimensions and 680 dimensions, respectively.

To overcome the problem of the imbalanced sample distribution in S, the synthetic minority oversampling technique (SMOTE) [29,30] is used to increase the balance radio between cases in four classes in S. SMOTE randomly creates synthetic samples by adding a weighted difference between the jth sample and its k nearest neighbors. This enables oversampling of minority samples. These newly synthesized samples will enhance the generality of the classifiers, thereby avoiding overfitting to a certain extent [31]. Before data augmentation, all samples in the set on FFDC and the set on OFDC must be normalized according to the following form:

$$F_{sta}=(F-{\mu }_F)/{\sigma }_F$$

(6)

where F_sta is the standardized feature; μ_F is the mean value of the feature; and σ_F is the standard deviation of the feature.

According to Table 1, SMOTE is configured with five nearest neighbors for oversampling to generate synthetic samples in S_FFDC and S_OFDC. The SMOTE steps are as follows:

(1)

For each sample a in the minority class, five nearest neighbors are found.

(2)

For each randomly selected nearest neighbor b, a new sample c is constructed with the original sample a according to the following equation:

$$c=a+rand(0,1)\left|a-b\right|$$

(7)

(1)

The new sample set is thus obtained by the original and generated samples.

2.4. Performance Assessment

After implementing SMOTE, the number of samples in S_FFDC was extended from 237 to 413, and from 186 to 370 in S_OFDC, as shown in

Table 2. The data distribution of augmentation anterior posterior.

Experiments			IA	MIA	AIS	Benign
FFDC	Before augmentation	Training set	143	19	19	16
		Test set	10	10	10	10
	After augmentation	Training set	143	95	95	80
		Test set	10	10	10	10
OFDC	Before augmentation	Training set	100	14	14	18
		Test set	10	10	10	10
	After augmentation	Training set	100	70	70	90
		Test set	10	10	10	10

. The extended sample set is uniformly denoted as SS. In this study, we chose macro average arithmetic (MavA), macro average geometric (MavG), and mean F-measure (MFM) as the criteria to evaluate the classification performance [32]. These criteria have been widely used in multi-class imbalance datasets [33,34,35]. The confusion matrix for binary classification problems is shown in

Table 3. Confusion matrix for the binary classification problems.

Confusion Matrix		Predicted Class
		Positive	Negative
True class	Positive	True positive (TP)	False negative (FN)
	Negative	False positive (FP)	True negative (TN)

.

The confusion matrix represents the results of correctly and incorrectly categorized samples. Here, the positive rate responds to the minority class and the negative to the majority class. In the binary scenario, several common assessment metrics can be derived from the confusion matrix, as shown in

Table 4. Typical assessment metrics.

Metrics	Equation
True positive rate (TPR) or recall	$\mathrm{TPR}=\mathrm{TP}/(\mathrm{TP}+\mathrm{FN})$
True negative rate (TNR)	$\mathrm{TNR}=\mathrm{TN}/(\mathrm{FP}+\mathrm{FN})$
False positive rate (FPR)	$\mathrm{FPR}=\mathrm{FP}/(\mathrm{FP}+\mathrm{TN})$
False negative rate (FNR)	$\mathrm{FNR}=\mathrm{FN}/(\mathrm{TP}+\mathrm{FN})$
precision	$\mathrm{precision}=\mathrm{TP}/(\mathrm{TP}+\mathrm{FP})$

.

The MavA comprehensively considers the classification results, and each class is assigned the same weight. It calculates the accuracy of each class independently, and then computes their mean to obtain the assessment result. Therefore, the MavA is considered the arithmetic mean of the individual accuracy of each class. MavG is defined as the geometric average of the accuracy for each class. MavA and MavG are formulated as

$$\mathrm{MAvA}=({\displaystyle {\sum }_{i=1}^4{\mathrm{TPR}}_i})/4$$

(8)

$$\mathrm{MAvG}={({\displaystyle {\prod }_{i=1}^4{\mathrm{TPR}}_i})}^{1/4}$$

(9)

where TPR_i represents the accuracy rate for the class i, i = 1, 2, 3, and 4.

F-measure assigns the same importance degree to recall and precision. It is shown as follows:

$$\mathrm{F}-\mathrm{measure}=2\times \mathrm{recall}\times \mathrm{precision}/(\mathrm{recall}+\mathrm{precision})$$

(10)

The F-measure for two-class classification assessment can be extended to deal with multi-class assessment problems. In this paper, MFM was employed to evaluate the four-category task, defined as follows:

$$\mathrm{MFM}=({\displaystyle {\sum }_{i=1}^4{\mathrm{F}-\mathrm{measure}}_i)/4}$$

(11)

where i is the index of the class.

Alternatively, we computed the area under the receiver operating characteristic (ROC) curve, which is also denoted by AUC. In order to extend ROC curve to multi-class classification, the output is binarized. The ROC curve can be drawn by calculating metrics for each label in a one-vs.-all manner and by finding their unweighted mean (macro-averaging). Figure 4 shows the schematic diagram of the FFDC method.

3. Results and Discussion

3.1. Classification Comparison

Contrast experiments were performed for the classification of four pathological subtypes of GGNs using FFDC and OFDC. To avoid large fluctuations in classification accuracy and to ensure that the training process can learn sufficient features, we retained ten cases of four subtypes in the dataset as the test set, and the rest were used to train and develop the classification model after implementing SMOTE. The sample distribution in SS is shown in Table 2.

We input samples in SS into the subspace KNN classifier for pathological subtypes classification, k = 1, 2, …, 20. KNN begins with k nearest labeled neighbors of each sample to determine the label of any unknown sample. In general, with reference to the integer value of k, the prediction output of classifier is determined on the basis of the majority vote cast by the neighbor class [36]. Namely, if any sample X_C is assigned to class C₁, it must be the maximum probability of X_C belonging to class C₁, expressed as

$$KNN(X_C)=\max P(C_1,X_C).$$

(12)

where P(C₁, X_C) denotes the probability of X_C in class C₁. In this paper, the ensemble method was set as the subspace to improve the classification accuracy of each independent classifier. KNN was applied to the pathological subtype classification as the learner. A total of three hyperparameters were included in the training process (i.e., the number of nearest labeled neighbors k, the number of learners, and the subspace dimension). By combining grid search and cross validation, we avoid the situation where the selection of the model and parameter depends greatly on the partition method of the dataset. The selection interval of the nearest labeled neighbors k and the number of learner parameters was 1–10 and 1–100, respectively. The number of predictors to sample for each random subspace learner was specified as a positive integer in the interval 1, … p, where p is the number of predictor variables. For FFDC and OFDC, p is 142 and 680, respectively, corresponding to the maximum feature dimension after feature selection. The five-fold cross validation was applied in the training process. The datasets were divided into five equal parts, using four folds as the training sets and the remaining for validation. The optimal combination of parameter values was selected by grid search with the aid of the five-fold cross validation.

The confusion matrix results and the ROC curve for classification Are shown in Figure 5. Based on the confusion matrix, we calculated the corresponding evaluation indices. The experiments based on FFDC were: MavA was 72.5%, MavG was 72%, MFM was 0.75, and AUC value was 0.83. However, the comparative experiments based on OFDC were as follows: MavA was 67.5%, MavG was 66.2%, MFM was 0.68, and AUC value was 0.78. These quantitative evaluation metrics showed the same conclusion that the FFDC method yielded higher classification performance than the OFDC method in classifying four pathological subtypes of GGNs. This outcome proves that the FFDC method was effective.

Additionally, we found that the classification performance of both methods for MIA was slightly poor. According to the analysis, MIA is the transitional period of pathological changes between pre-invasive and IA. At this stage, most of the cancer cells grow in a wall-attached manner, and the maximum diameter of the infiltration area is less than 0.5 cm. When the infiltration area invades the blood vessels, lymphatic vessels, or adjacent to the pleura, or when the tumor shedding cells spread to the adjacent alveolar cavity or small airway, the tumor enters the invasive stage. Therefore, there is a possibility of overlap between MIA and the two other pathologies, pre-invasive lesions, and IA pathology. As such, the classification performance of MIA was slightly worse than that of other pathological subtypes.

To further test the effectiveness of FFDC, we considered another clinically important three-category classification subtask in distinguishing the IA, MIA, and pre-invasive lesions. This subtask is urgently needed in clinical practice. The lesions corresponding to pre-invasive often require conservative treatment, emphasizing long-term follow-up, while MIA and IA require elective or immediate surgical treatment due to their poorer prognosis when compared to pre-invasive lesions. The experimental steps are the same as the above classification of four pathological subtypes; the results are shown in Figure 6.

We also compared our experiments with other OFDC methods. The results are listed in

Table 5. Comparison of studies using different methods to determine the invasiveness.

Year	Number of Classes			Method	Diagnostic Performance
	Pre-Invasive	MIA	IA		Accuracy	AUC
2018 [37]	205	316	130	OFDC + DenseSharp	64.1%	—
2021 [21]	225	335	180	OFDC + joint deep learning model	58.67%	0.81
2021 [38]	302	349	258	OFDC + 3D multi-task deep learning network	64.9%	0.82
2022 [ours]	52	24	110	OFDC + traditional classifier	70%	0.89
	55	29	153	FFDC + traditional classifier	80%	0.88

. Compared with the previous literature in which a classifier is trained with one-time CTI to determine invasiveness, the FFDC method is seen as more effective. The FFDC classification accuracy was about 15.9% higher than that in [37], 21.33% than that in [21], 15.1% than that in [38], and 10% than that of the OFDC method trained with a traditional classifier. In addition, we found that the FFDC method seldom made misclassifications in discriminating between pre-invasive lesions and MIA in the three-category subtype classification. Only 1/10 MIA was misclassified as pre-invasive lesions, and no pre-invasive lesions were misclassified as MIA. It was shown that FFDC can learn the implicit relationship between the three categories. However, due to the overlap between MIA and two other pathologies, FFDC would misclassify MIA as IA or pre-invasive lesions.

3.2. Different Subtypes Development Based on the Follow-Up Radiomics Features

To further explore the development of different four subtypes of GGNs, we illustrate the statistics of the two-time follow-up features, which were selected from the first three ones with the lowest p value, as shown in

Table 6. The first three follow-up features with the lowest p value.

Features	Pathology				p Value
	IA	MIA	AIS	Benign
wavelet-L_glcm_MaximumProbability	4.15 × 10−5	−1.23 × 10−4	−5.32 × 10−6	2.38 × 10−4	0.00003
log-sigma-5-0-mm-3D_glszm_GrayLevelVariance	−8.84 × 10−3	3.95 × 10−2	−1.55 × 10−3	−5.06 × 10−3	0.00008
exponential_glszm_SmallAreaLowGrayLevelEmphasis	−6.26 × 10−5	−2.03 × 10−4	−1.09 × 10−4	3.21 × 10−4	0.00010

. After the analysis of variance, multiple comparisons were used to determine whether there were significant differences between the follow-up features of each pathological sample.

The variation in the first three features in four pathological stages can be explained as follows:

(1)

‘wavelet-L_glcm_MaximumProbability’ reflects the probability of the highest frequency of adjacent gray pairs in ROI. The smaller the probability, the more complex the texture pattern. The texture complexity of GGNs manifested as IA and benign became uncomplicated over time, and benign changed faster than IA. In contrast, the texture complexity of GGNs gradually increased in MIA and AIS stage.

(2)

‘log-sigma-5-0-mm-3D_glszm_GrayLevelVariance’ reflects the discreteness of each pixel gray, relative to the average gray. The greater the value, the greater the image contrast. Among the four pathological results, only the contrast of GGNs in the MIA stage was gradually increased, and IA changed the fastest in other gradually decreasing stages.

(3)

‘exponential_glszm_SmallAreaLowGrayLevelEmphasis’ measures the distribution of low gray values in small regions of ROI. The larger the value, the more emphasis is placed on the range of low gray values in small regions. In addition to the gradual increase in benign eigenvalues, the values of the other three pathological stages gradually decreased, and the IA stage changed the slowest.

Therefore, we conclude that FFDC has higher accuracy and value for the classification of pathological subtypes of GGNs than OFDC.

4. Conclusions

This paper presents a new method called FFDC for the classification of four pathological subtypes of GGNs. The radiomics tool was used to extract sufficient and quantitative characteristics. The feature difference of two-time follow-up CTIs was used to find the development of GGNs in different pathological subtypes. The classification results demonstrated the following conclusions.

(1) Feature differences between two-time follow-up CTIs are very helpful for building a more effective classifier after the features of GGN are sufficiently extracted. Based on this, FFDC can achieve a better classification performance than the existing OFDC methods.

(2) Classification of all four pathological subtypes can be effectively realized, while most existing research is focused on the limited three-category radiomics classification.

(3) Four pathological subtypes had significant differences along the three extracted texture characteristics, which proves that the development rate of GGNs can reflect the corresponding pathological stages to a certain extent.

Although FFDC showed clear advantages over the existing OFDC methods, there were still limitations as follows.

(1) GGNs were manually segmented and labeled by posterior pathological analysis reports, but the current focus is machine automatic segmentation and labeling to avoid the error of manual segmentation. Moreover, in clinical applications, when the lesion segmentation is performed by human beings, it has been criticized as time-consuming and generally introducing bias.

(2) Radiomics features were extracted based on the two-dimensional CTI, and the three-dimensional information of the entire GGN lesion must be lost. Generally, the diagnosis model based on three-dimensional GGN segmentation and feature extraction is expected to provide more accurate and stable classifications for lung diseases.

(3) The used machine learning methods such as data argument, subspace classification may fail to give an overall comparison with the current DL algorithm due to the lack of sufficient samples.

How to overcome these problems are our future concerns. For example, the automatic segmentation of GGN lesions is not the research content in this paper, but it will be the focus of our future work.