1. Introduction
A thorough analysis of how a system’s parameters influence its response is crucial for optimal and robust product design, which reduces time and costs in the late stages of product development. Running high-fidelity simulations of the physical system, however, requires a large amount of computational resources; thus, extensive exploration over the design space is prohibitive. Because of this, surrogate models have been used in different domains as efficient tools for decision making and risk management [
1,
2,
3]. Surrogates or metamodels are data-driven methods that extract and learn information from input–output pairs obtained from a physics-based simulation to create a proxy with short evaluation time and little loss of accuracy.
Surrogate models have been applied to the vibroacoustic domain as noise, vibration and harshness (NVH) performance arises as a key indicator of customer satisfaction and vibroacoustic simulations are computationally costly due to, for instance, the complex behavior involved in fluid–structure interactions. In many studies, the system response is approximated by a polynomial using the response surface methodology (RSM) [
4,
5,
6]. Second-order polynomials are usually used in RSM for their sample efficiency and interpretability, but they are unable to capture arbitrary nonlinearities in the system response. On the other hand, higher-order polynomials are rarely employed due to the costly training [
7]. Therefore, machine learning (ML)-based surrogates have been used in the vibroacoustic analysis for their capability of learning complex data relations and nonlinear functions and applied in optimization [
8,
9,
10], uncertainty analyses [
11,
12,
13] and knowledge discovery from measured databases [
14].
A surrogate model using Gaussian process regressor (GPR) was implemented in [
9] to optimize the sound transmission loss (STL) of an intake system. Casaburo et al. [
15] trained a GPR-based surrogate model to predict the increase of the STL response at resonance frequencies of porous acoustic metamaterials. The results showed that better accuracy can be achieved when a more feature-rich STL model is used. Bacigalupo et al. [
10] performed the optimization of the band-gap of acoustic metamaterials using a radial basis function (RBF)-based surrogate. Surrogates for crash and NVH response of a body-in-white model using RBF and neural network (NN)-based algorithms were designed in [
8,
16], respectively. Ibrahim et al. [
17] investigated various ML-based surrogate models to predict the noise radiated by electric motors and concluded that global models encompassing structural, electromagnetic, and acoustic physical domains performed better than local surrogates. NN-based surrogate models have also accurately replaced boundary element methods to predict interior vehicle sound-pressure level [
18].
The growing trend in vibroacoustics of relying on surrogates based on high-fidelity simulations not just enables the search for optimal and reliable designs, but also paves the way to the construction of digital twins for real-time vibroacoustic applications, such as online monitoring and control [
19,
20]. However, the reliability of these solutions depends on the accuracy of the surrogate models. In particular, in vibroacoustics, the typical non-smooth functions pose difficulty to the construction of accurate ML-based surrogates as ML methods assume local smoothness of data [
21,
22]. Therefore, to ensure that further surrogate-based developments on vibroacoustics are well-founded, it is imperative to develop scientific-based guidelines to construct physically consistent and accurate ML-based surrogates considering the particulars of the domain.
Thus, the objective of this paper is to identify ML methods capable of modeling non-smooth functions, as well as techniques to incorporate domain knowledge into the surrogate. Furthermore, this work investigates the application of sensitivity analysis methods embedded in the ML to improve surrogate interpretability and enable reasoning about the physical phenomena. The investigations are carried out for the classical acoustic problem of STL formulated with different complexity levels, as the STL problem encompasses important vibroacoustic phenomena well understood by the acoustic community [
23]. The algorithms implemented can be readily applied to other vibroacoustic problems and, thus, enhance the modeling of accurate and interpretable ML-based surrogates in the domain.
The main contributions of the paper can be summarized as:
A set of numerical experiments to evaluate ML-based surrogates’ accuracy in modeling non-smooth vibroacoustic problems.
The implementation of physics-guided features to embed domain knowledge to otherwise black box models.
The sensitivity analysis of trained random forest surrogates to exemplify how this statistical method can improve the interpretability of ML predictors.
Section 2 describes the methodology followed to construct four different physics-based models of STL. The workflow of the surrogate implementation is presented in
Section 3. In
Section 4, the sensitivity analyses results and the effects of adding physics-guided features are shown. Subsequently, in
Section 5, a benchmarking analysis compares the performance of each ML method used to construct the surrogate for different numbers of supporting points and levels of complexity of the STL problem. The pros and cons of each ML method are discussed. The influence of design space size and location is also investigated in
Section 5.
Section 6 presents the paper’s conclusion and a discussion of the transferability of its findings to other vibroacoustic problems.
The data and algorithms used in this work are available at
GitHub (accessed on 19 October 2022).
2. Physics-Driven Models of Sound Transmission Loss
When an acoustic wave hits a plate, it is partially reflected in the incident acoustic field and partially absorbed by the plate itself. Most of the absorbed portion excites the plate, making it vibrate and radiate noise in both the incident and transmitted fields, as illustrated in
Figure 1. The STL is defined by the ratio between the incident sound power
and the sound power transmitted through the plate
, being usually evaluated in decibels as
The transmitted noise is inversely proportional to the system effective impedance, which is the sum of the mechanical impedance of the plate and the fluid-loading impedance [
24]. The effective impedance depends on the fluid properties, the incident
and azimuth
angles of the incident wave and the material, dimensions, and boundary conditions of the plate. This paper considers that the incident field is a random field of incident plane waves in all directions, known as a diffuse field.
At frequencies below the first natural frequency of the plate, the plate dynamics influence on the STL is negligible, and the STL is controlled by the plate bending stiffness,
where
h is the thickness,
E is the elastic modulus,
is the Poisson’s ratio, and
is the damping loss factor of the plate. When the driving frequency is close to the first natural frequencies of the plate, the resonant behavior of the plate governs the STL. As the frequency increases and the resonant behavior attenuates, the plate behavior approaches that of a limp mass, especially for thin plates in frequencies where the bending stiffness is not relevant. At this frequency range, the STL depends solely on the surface mass density
and can be approximated by the mass law, as demonstrated in [
24].
With the increase in frequency, the coincidence phenomenon takes place, and the mass law is no longer valid. The coincidence happens when the trace velocity of the acoustic wave projected in the plate is equal to the velocity of its natural bending wave. These waves superpose and create a scenario of minimal impedance, maximizing the transmission of sound. The coincidence frequency
in which the trace and the bending wavenumbers coincide is evaluated by:
where
is the characteristic sound speed, and
is the plate density. The minimum frequency in which coincidence occurs is for grazing incidence (
) and is called critical frequency
, where the amplitude of the valley in the STL is controlled by the plate damping. Above the critical frequency, the coincidence phenomenon occurs for gradually smaller incidence angles, and the STL is controlled by the plate bending behavior.
Figure 2 illustrates a typical STL curve and its influence regions.
In the literature, different STL models capture the aforementioned curve behaviors with distinct levels of detail [
23]. In this paper, four STL methodologies described in
Section 2.1 are implemented to evaluate the ML-based surrogate capabilities. The first and simplest methodology considered is the analytical STL solution for an infinite plate. As the unbounded infinite plate is not affected by the resonances, the STL in low frequencies relies only on the surface density mass. To account for the plate width
a and length
b, the radiation efficiency of a finite plate may be considered instead of the radiation efficiency of the infinite plate. Spatial windowing and Rayleigh-integral-based techniques can be used for this purpose, resulting in a correction factor applied to the infinite transmission transparency [
23] that modifies mainly the results below the critical frequency, where the plate modal behavior determines the sound radiated. However, detailed STL evaluation of bounded plates must account for its structural response under forced vibrations. The current work implements modal summation (MS) and the finite element method (FEM) to fully model the vibroacoustic phenomena in the STL of a finite plate with simply supported boundary conditions. In these approaches, the STL has a highly rough behavior as the STL is controlled by the plate modes’ natural frequencies and radiation efficiencies control.
In practical scenarios, only the overall STL behavior defines the plate design; thus, the band averaged STL can be considered. Therefore, the results obtained with MS and FEM are also evaluated in one-third octave frequency bands. In summary, six different physics-driven models of STL serve as ground truth for the surrogate models:
- 1.
Analytical solution for infinite plate,
- 2.
Finite plate STL approximated by correction factor,
- 3.
Analytical MS approach,
- 4.
MS approach with band average,
- 5.
Numerical FEM,
- 6.
FEM with band average.
2.1. Methodology of the STL Analyses
The methodologies used to model the STL analyses described here follow the notation in
Figure 1. The isotropic plate is in the plane
, separating the source field
and the transmission field
, both filled with a light fluid with density
and characteristic sound speed
. Considering that a harmonic plane wave with wavenumber vector
impinges the plate with incident angle
and azimuth angle
, the resultant incident acoustic pressure field is
where
is the amplitudes of the incident wave in the incident field
, and
is the amplitude of the wave reflected by the plate, which forms the reflected field
. The plate vibration also radiates a plane wave of magnitude
in the transmission field
, for which acoustic pressure is given by:
The structural–acoustic coupling equation states that there must be continuity of acoustic and mechanics velocities at the interface of the plate with the acoustic fields:
where
is the plate transverse displacement. For the sake of brevity, the factor
will be omitted from the equations hereafter. Therefore, the coupling equations in the source and transmission side are, respectively:
from which the following relationship between the pressure fields amplitudes is obtained:
By definition, the acoustic transparency
is the ratio between transmitted and incident sound intensity, where the sound intensity can be written as:
where the subindice
i indicates the acoustic field, which can be the incident, transmitted or reflected field, and
is the local fluid velocity. Therefore, the acoustic transparency is:
The acoustic transparency for a diffuse field
is the weighted average transmission coefficient of all possible incident and azimuth angles:
The STL is the inverse of the acoustic transparency measured on the dB scale.
To find the relationship between the pressure field amplitudes in Equation (
12), the constitutive equation of motion of the plate should be solved combined with Equation (
10), which for an isotropic plate can be written as:
The solution for each approach addressed in this paper is presented below.
2.1.1. Analytical Model of Infinite Plates
For the case of an infinite an isotropic plate proposed in [
25] and implemented in accordance to [
26], the plate response is independent of
; therefore, one can write:
and Equation (
14) is rewritten as:
Thus, the radiation impedance of the finite-size plate reads as:
Combining Equations (
9), (
16) and (
17), it is possible to find the relation:
which is straightforward applied in Equation (
12) to find the acoustic transparency for a plane wave. As Equation (
13) does not have a close analytical solution, it is numerically evaluated to output STL for a diffuse field.
2.1.2. Correction Factor
Based in the Rayleigh-integral method, Atalla et al. [
27] propose to apply a correction factor to the acoustic transparency of the infinite plate
to account for effects of the plate size, such that the acoustic transparency of a finite plate could be approximated by:
where the radiation efficiency
is given by
The structural impedance
is evaluated as:
where
S designates the surface of the panel, and
G is the half-space Green’s function. Rhazi et al. [
28] proposes analytical simplifications, so that
simplifies into:
where
. This equation can be evaluated using Gaussian numerical integration. The function
and the details of its derivation are found in [
28]. Although the correction factor approach is a simplified approach, the resultant modified STL curve is coherent with experimental curves with band average [
23].
2.1.3. Modal Summation
An analytical solution of the fluid–structure iteration problem of a simple supported plate can also be obtained by modeling the plate displacement
w in terms of a modal summation [
29,
30]:
where
is the short format for
, the subindices
m and
n indicate the mode index,
is the coefficient of contribution of each mode for the displacement field, and
(Equation (
24)) is the modal function that satisfies the simple supported boundary conditions (Equation (
25)).
Using the 2D Fourier Transform, each pressure field
can also be described as a modal summation:
where the signal of the exponential function depends on the propagation direction of the plane wave in the field, and in which the coefficient of contribution of the pressure field
reads as:
Substituting Equations (
23), (
26) and (
27) into Equation (
14) and applying the weighted residuals method:
As the modal functions have orthogonal properties
for
or
, Equation (
28) reads as
if inter-modal coupling is neglected. The integrals on the first term can be analytically evaluated, and the relation from Equation (
8) is used, resulting in:
where
are the natural frequencies of the simply supported plate, and
can be analytically evaluated by solving the integrals from Equation (
27). Finally, the solution of the system of equation in Equation (
30) provides the coefficients of modal participation
and, consequently, the displacement
w (Equation (
23)). The coefficients
are evaluated with Equation (
9), and the acoustic transparency is obtained by:
2.1.4. Finite Element Method
The numerical solution of the STL problem was implemented in COMSOL Multiphysics
® software [
31] using FEM. The plate was modeled by homogeneous shell elements with simply supported boundary conditions, while the receiver acoustic field was modeled by 3D finite elements with perfect matched layer in its external interfaces to simulate the free-field condition. The FEM model does not include the acoustic field on the source side, but an equivalent pressure load is applied to the plate to account for the fluid load. The fluid pressure is modeled as the summation of 200 components in random directions to simulate the diffuse field. The frequency domain formulation is used to solve the coupled plate constitutive equation and acoustic wave equation. The incident and transmitted power are then calculated as the integral of the incident and transmitted intensity on the plate surface, respectively. Details on the theory and numerical implementation can be found in [
32].
3. Development of the Machine-Learning-Driven Surrogate Models
A surrogate model is a computationally inexpensive mathematical approximation of a complex simulation. More formally, let
be the simulated function. The surrogate model can be defined as a function
, where
is the set of interest for the surrogate model, and
is the associated codomain. The relation between the simulated function and the surrogate is given by:
where
is the approximation error. The predictor
is fitted with
N input/output pairs
sampled from the simulated function to minimize the error
for all inputs in the set of interest. Because the number of samples
N must be kept small due to the high computational cost of evaluating
, choosing an efficient sampling method is crucial for designing an accurate surrogate model. In the following, the basic workflow for creating a surrogate model is described, and
Figure 3 shows a block diagram with the main steps.
3.1. Sampling Methods
The first stage in designing a surrogate model is to define informative supporting points using an adequate sampling strategy. In random sampling, all points in the interval of interest have an equal probability of being drawn. Although having low bias and being easy to deploy, random sampling can lead to gaps in the input domain. Thus, another strategy is to segment the input space into
M intervals along each dimension and randomly sample from each interval. This method is the so-called Latin Hypercube Sampling (LHS) and promises to produce a better depiction of the input domain of the target function [
1]. Therefore, this paper uses LHS to define the supporting points for the training of the surrogates.
3.2. Data Preprocessing
The accuracy of data-driven models can improve significantly with the proper operations over the feature set. Here, features refer to the different dimensions of the input data . In feature engineering, domain knowledge is used to select the most informative features of an input set and to add physics-guided features through basic operations over the raw data to improve the predictor’s accuracy and interpretability. Feature scaling is another crucial preprocessing step, especially for ML predictors which are distance-based, for example, GPR, or gradient-based ones, such as NN. The goal of feature scaling is to remove the effect of the different range of values in the input so that equal importance is given to each feature in the fitting of the regressor. In addition, it guarantees that the gradient descent is updated with similar rates for all features, improving convergence. Normalization and standardization are the main methods for feature scaling.
3.3. ML-Driven Surrogate Models
The predictor function can be fitted with different ML models. This paper investigates four popular ML regression algorithms that do not impose assumptions on the form of the modeled function, namely neural networks (NN), Gaussian process regressor (GPR), random forest (RF), and gradient boosting trees (GBT).
Neural Network. The feedforward NN ([
33], Chapter 16.5) is composed of stacked layers of neurons in which the weighted sum of the inputs goes through a nonlinear activation function at each neuron. The outputs of each layer are the inputs of the subsequent layer in a feedforward process. The NN error is usually measured by the Euclidean distance between the predictor output
and the target value
, and the NN parameters, weights and biases are fitted with gradient descent via backpropagation to minimize the prediction error.
Gaussian Process Regressor. GPR [
34] is a probabilistic model that assumes a Gaussian process prior. Therefore, for any finite set of inputs
:
where
is the mean function, and
is the covariance function, also known as kernel. Given the training dataset
and considering that new input–output pairs
belong to the same joint Gaussian distribution:
one can condition the prior distribution on the observations
and infer new output values
, sampling them from the joint posterior distribution. Usually, the mean function is defined as zero, and a Gaussian noise is considered in the observations.The optimization of the kernel hyperparameters is commonly performed to maximize the marginal likelihood of the distribution.
Random Forest. Decision trees perform recursive partitions of the input space using heuristic methods to select the split feature
s and threshold
t that minimize the impurity criterion
. For regression problems, the impurity criterion is commonly based on the mean squared error (MSE) of each subspace created by the partition. RF is an ensemble model made of several decision trees to reduce the variance of single tree predictions, which is achieved by averaging the output of each decision tree in the RF [
35]. Each decision tree of the RF is trained with a different subset of the training dataset using the bagging technique to ensure that each predictor is unique and contributes to generalization improvement.
Gradient Boosting Trees. GBT is an ML model that uses the boosting technique to create an ensemble of decision trees ([
33], Chapter 16.4). In GBT, decision trees are trained sequentially, where each decision tree trains on the mispredicted data of the previous one, thus focusing mainly on reducing the predictor bias. The prediction error is differentiable and is minimized using a gradient descent optimizer.
After the surrogate is trained, it can predict the system response in new points of the design space and be applied to optimization and uncertainty propagation of the system parameters. Furthermore, global and local sensitivity analyses can be used to increase the black-box interpretability and can either be obtained as a by-product of ML methods or be straightforwardly implemented [
36,
37]. The vast literature on sensitivity analyses applied in ML includes methods for NN [
38,
39], GPR [
40], XGB [
41], RF [
35] and model-agnostic approaches [
37].
In this paper, the mean decrease in impurity (MDI) approach [
35] was applied to verify the RF-based surrogate physical consistency. The MDI approach was chosen for exemplary purposes as it is readily available after the training of the RF, and it has a solid mathematical foundation, as it is proved to relate to the normalized total Sobol’s indices [
42], which is a global sensitivity method that takes into account input interactions. The importance of an input feature
in the MDI approach is evaluated as its contribution to the impurity decrease. In other words, the feature importance equals the normalized and weighted summation of the impurity criteria reduction
in all nodes
n from all trees
T in which the split was based on the given feature, that is, in the nodes where
[
35]:
where
is the number of trees in the RF, and the weight
is the fraction of the tree samples at the node.
4. Sensitivity Analysis of Random Forest Surrogate and Influence of Physics-Guided Features
In this section, the consistency of the ML-based surrogates with physics-driven models of STL is investigated. MDI-based sensitivity analysis is used to demonstrate the importance of each parameter in the system response, rendering the surrogate more interpretable. The addition of two physics-guided features to the RF models, namely the mass density m and the real part of the bending stiffness , is also evaluated. According to STL theory, the mass density controls the STL in the mass region, while bending stiffness has a significant influence on both the stiffness and coincidence regions.
The database used has 2000 supporting points sampled with LHS from the design space of
Table 1, which encompasses a wide range of aluminum grades and aluminum matrix composites. The critical frequencies for this design space range between approximately 1000 and 2500 Hz, as shown in
Figure 4. One RF regressor was trained for each frequency of interest to obtain the features’ importance for each output frequency. Each RF was trained with 200 decision trees without a depth limit and with MSE as the impurity criterion. A desktop with a hexa-core 3.1 GHz processor and 32 GB of RAM was used to run the training of the surrogates. The root mean squared error (RMSE) was used to compare the accuracy of surrogates with and without physics-guided features as input.
Figure 5a,b show the MDI-based sensitivity index obtained with the infinite plate models with and without the use of physics-guided features, respectively. The mass-controlled region is distinctly observable at low frequencies in both cases. Approaching the coincidence region, the STL is controlled mainly by the plate density, and the thickness importance is negligible. Despite the damping factor determining the STL amplitude at the critical frequency,
Figure 5b shows that the real part of the bending stiffness is the most significant feature at this frequency range. As noted in [
26], when a set of interest rather than a specific plate design is considered, the location of the critical frequency dip is more relevant for the STL result than its amplitude, which explains this result. At higher frequencies in the coincidence region, the damping importance increases because for each frequency
there will be a component of the diffuse field with an angle
such that
, and the amplitude is again the major aspect of the STL. Finally, it is noted that the inclusion of the physics-guided features improves the surrogate accuracy from an RMSE of
dB to
dB.
The sensitivity indices of STL of finite plates based on the correction factor approach (
Figure 6) differ from the infinite plate indices only in the low-frequency region. This result is coherent with the methodology, which applies a correction factor in the low-frequency range to account for the plate dimensions and comprehend its resonant behavior. Although the plate stiffness would theoretically also impact the resonant modes of the structure, the STL evaluated by the correction factor is insensitive to this feature in the resonant region of
Figure 6. Once more, the RMSE decreases from 0.36 dB to 0.25 dB with the inclusion of physics-guided features.
The MDI-based sensitivity indices change considerably when the model thoroughly considers the structural dynamics of the finite plate and its resonant modes, as for the STL results with MS and FEM approaches in
Figure 7 and
Figure 8, respectively. Overall, the sensitivity indices of the MS and FEM approaches are similar to each other, indicating that they model the vibroacoustic phenomena with analogous considerations. The bending stiffness and the plate dimensions have a considerable high sensitivity index throughout the frequency range. Therefore, the behavior of the finite plates under analysis diverges from the one of a limp mass, an assumption held by the mass law and considered in the mass-controlled region of both the analytical approach for infinite plates and the correction factor approach for finite plates. Indeed, the mass density importance is negligible in the resonant region, and its influence in the middle frequency range is not predominant.
The achieved surrogate accuracy with physics-guided features is
dB for the MS-based results and
dB for the FEM-based results. The errors are higher for the FEM model than for the MS model since the excitation in FEM is modeled by random components, and therefore, the results are non-deterministic. The high complexity and non-smooth behavior of the STL response with ML and FEM approaches lead to poor surrogate accuracy even when the physics-guided features are used, which also compromises the accuracy of the sensitivity analyses. In particular, at high frequencies, the even distribution of the sensitivity indices among the features indicates higher complexity and possibly higher inaccuracies. As the modal behavior of the plate is posing difficulties for the surrogate model, the resonance coefficient term
R in Equation (
36) is included as another physics-guided feature for the surrogates of the FEM and MS models. The resonant term
R is the coefficient of the first term of Equation (
30) and relates with the simply supported plate natural frequencies.
As observed in
Figure 9, the resonance coefficient feature controls the STL in the low-frequency range. Although the accuracy improved to
dB for the MS-based results and to
dB for the FEM-based results, it remains elevated. Extra improvements in the accuracy could be obtained by feature selection, that is, removing unimportant features, a common technique in ML.
Finally, the MDI-based sensitivity index is evaluated with one-third octave band average STL with MS and FEM, as shown in
Figure 10 and
Figure 11, respectively. Once again, the stiffness and dimensions of the plate play a major role for all frequencies. The surrogate models that include the three physics-guided features are the ones with the best accuracy, which is
dB for the MS model and
dB for the FEM model. These surrogates have better accuracy as the band averaging smooths the STL curve while keeping the information valuable for practical purposes.
The results presented in this section show evidence of the physical consistency of the surrogate models as the STL sensitivity indices have a behavior coherent with the literature of each STL physics-driven model. Furthermore, the sensitivity indices of the width and length of the plate are consistently equivalent in all analyses, as expected for isotropic materials. Physical inconsistencies could indicate regions where the ML model is not accurate. The investigation also demonstrates that physics-guided features can be readily included to improve surrogate accuracy and lead to a clearer distinction of STL regions in the sensitivity analysis. However, the interpretation of the resulting feature importance is not straightforward when physics-guided features are included, as the input features are not independent anymore. In summary, the MDI-based sensitivity analyses presented in this section are a cheap-to-evaluate method that improves the surrogate interpretability and reliability and allows for the use of data-based information to deepen physical discussions on variable importance and interactions.
5. Benchmarking of ML Methods and Influence of the Design Space Selected
In this section, surrogate models based on NN, GPR, RF and GBT are evaluated regarding accuracy and training time. The benchmark is conducted for all STL models of
Section 2. The influence of physics-guided features is also considered in the test cases. Supporting points are sampled from the design space of
Table 1 using LHS. Finally, an analysis of the influence of design space size and location in the surrogate accuracy is performed. The training of the ML models was performed using 80% of the dataset, while the remaining 20% was used as a test dataset to evaluate the surrogate performance using the RMSE obtained with five-fold cross-validation as the evaluation metric. The ML models’ hyperparameters were selected based on a trial-and-error search and are as follows:
NN-based surrogate models. The NN were implemented using Keras with tensorflow as backend. One regressor was trained to output all STL predictions at frequencies. Standardization was applied to all input features, while the outputs were scaled in the range [0, 1]. The fully connected NNs had an architecture with nodes in the input layer, 5 hidden layers with 32 nodes each, and nodes in the output layer, where is the number of input features. All hidden layers had the sigmoid as activation function and a L2 regularization penalty of 1 × 10−7. The training was performed with batches of 32 samples and with 1500 epochs, except for the MS and FEM models, in which the NN trained for 2500 epochs. The Adam algorithm was applied to minimize the average mean squared error of the STL curve prediction.
GPR-based surrogate models. The kernel k used to construct the GPR used a constant kernel , a Matern 3/2 kernel , a radial basis function kernel and a white noise kernel combined as . The kernel hyperparameters were optimized to maximize the log-marginal likelihood of the posterior distribution using the L-BFGS-B algorithm with ten restarts. One Gaussian process regressor predicted the STL at frequencies. The preprocessing of the inputs and outputs was the same from the NN-based surrogate models.
RF-based surrogate models. An RF was trained to output the STL for the entire frequency range analyzed. The RF was made up of 200 CARTs without a depth limit. The impurity criterion was the mean of the averaged squared error among the outputs.
GBT-based surrogate models. The GBT predictor was made up of 125 decision trees with a maximum depth of 10 nodes. The learning rate of the training was set to 0.05. A different GBT predictor was trained for each predicted output willing to minimize the mean squared error.
Figure 12 shows the RMSE of each surrogate for all six STL models and different dataset sizes. It can be seen in the results that the surrogates’ performance improves considerably when datasets with a size of up to 1000 samples are used. However, the improvement is reduced for large dataset sizes, and sampling additional points may not justify the increase in accuracy. It is observed that the NN-based surrogates yield better accuracy for all STL models when big datasets are used. This can be justified by the fact that NN can produce a better fit on non-smooth functions than other ML approaches [
43]. The GPR model, widely used to construct surrogates as it is well-suited for regression with small databases, showed good performance for the infinite plate and correction factor models; however its performance for highly non-smooth models is hindered as the GPR relies strongly in spatial correlation of the input features [
34].
Moreover, the addition of physics-guided features consistently produces more accurate models. The improvement obtained due to the physics-guided features in the NN-based surrogate performance is not as significant as for the other ML models, indicating the high capabilities of NN to learn more complex and relevant representations of the data through its depth even without expert guidance. Except for the FEM model, the NN-based surrogates of all STL models achieved RMSE below , which are satisfactory results since measurements errors in STL experiments usually also go up to . The RMSEs for the FEM model are higher due to the overall more complex simulation and stochastic excitation, which renders the data less reliable.
Another important factor in the choice of a surrogate model is the training time, which is presented in
Figure 13. It can be seen that RF and GBT surrogates are significantly faster to train than the other two methods. This is due to the fact that the training of decision-tree-based models scales loglinearly with the dataset size [
44]. It is worth noting that because no efficient multi-output implementation of the GBT model is available, it was required to fit one model for each input frequency, thus increasing the overall training time compared to the RF model. Furthermore, GPR is computationally expensive to train for large datasets as its operations scale as
[
45]. It is also worth noting that GPR, GBT and RF have sensitivity analysis as a by-product and, therefore, are intrinsically more interpretable than NN. On the other hand, NN and GPR extrapolate better than decision-tree-based methods.
Figure 14 shows an example of the predicted STL curve for each STL model using the most accurate surrogate which is the NN model with physics-guided features trained over 2000 supporting points. Visually, the predicted curves are remarkably similar to the simulated ones, indicating that NN-based surrogates can model non-smooth functions from vibroacoustic problems.
Figure 15 provides a deeper look into the NN-based surrogate model errors for each STL model, additionally indicating the mean absolute error (MAE) and the mean maximum error (MME). For instance, the MME indicates that high localized errors occur in MS and FEM models without band average. Therefore, although these surrogates adequately predict the overall STL behavior, they may considerably mispredict local maxima and minima of rough response signal.
An investigation of the NN-based surrogate performance regarding the set of interest
was also performed. For that, four design spaces were considered, namely the standard design space
from
Table 1, the smallest design space
and the biggest design space
and
, which have the same size but are located in different places in the domain
, as illustrated in
Figure 16. The range of damping, Poisson’s ratio, and the width and length of the plates are the same from
Table 1 for all design spaces. The resulting range of critical frequencies is also shown in
Figure 16. For each design space, 500 supporting points were sampled using LHS for the STL models of the infinite plate, correction factor, and MS with and without one-third octave band average.
Figure 17 shows the accuracy obtained with an NN-based surrogate model trained with physics-guided features for each set of interest and the STL method. It is observed that the surrogate error increases with the design space size, especially for the infinite plate and correction factor models. For the MS model without band average, the difference in the surrogates’ accuracy is not relevant. Furthermore, it can be observed that a considerable difference in accuracy is obtained for design spaces
and
, although they have the same size. This is because the samples from
have, on average, a simpler behavior than the samples from
, once many of them present critical frequency higher than 2500 Hz which is above the frequency range modeled by the surrogates.
In conclusion, the developed surrogate models present overall satisfactory performance for most of the studied cases. Even highly discontinuous and rough functions could be properly predicted. Although the ML algorithms’ performance is problem-specific, they usually perform well in related tasks; therefore, the benchmarking conducted provides insights into the suitability of the ML methods to model vibroacoustic problems with non-smooth behavior. Moreover, NN-based surrogates are the most accurate for STL models and thus are useful tools to explore the design space of STL simulations, enabling optimal and robust vibroacoustic designs. It has also been observed that the location of the design space can have more of an effect on surrogate accuracy than its size.
6. Discussion and Conclusions
The present study investigates the use of machine-learning (ML)-based surrogate models for vibroacoustic analyses. We show how to tackle the lack of interpretability of black-box simulators and how to determine the surrogates’ capacities to fit the non-smooth functions which are recurrent in the vibroacoustic domain. As a study case, surrogate models were constructed for sound transmission loss (STL) analyses modeled at different complexities levels, including analytical and numerical approaches.
The physical consistency of the surrogate models was verified through sensitivity analyses intrinsic to the ML methods, without additional computational cost. For each region of the frequency spectrum, the physical behavior identified by the features’ importance results were in accordance with the STL theory. Moreover, aspects such as the differences between the STL models were inferred from the sensitivity study, providing a deeper understanding of the modeled phenomena.
The benchmarking of surrogates based on four ML methods, namely neural networks (NN), Gaussian process regressor (GPR), random forest (RF) and gradient boosted trees (GBT) show that NN consistently performs better. The surrogate presented satisfactory accuracy even for functions with highly non-smooth behavior resulting from resonant and coincidence phenomena. Furthermore, it is shown that including domain knowledge through physics-guided features improves the surrogate performance for all ML methods and STL models. The surrogate errors are also shown to be proportional to the design space size for the surrogate with less complex STL models but do not change significantly with the design space size for the STL with high non-smooth responses. On the other hand, the location of the design space in the input domain has a relevant impact on the accuracy in all cases.
Although the results were generated for the case of STL, some conclusions can be generalized to guide the implementation of accurate surrogates for other vibroacoustic problems with similar behavior. First, sensitivity analysis methods and the inclusion of physics-guided features can be readily applied to other physical domains. Second, the capability of the ML-based surrogate, especially the NN-driven, to predict non-smooth behavior was observed in the case of STL and is an indicator for other vibroacoustic analyses. Therefore, this paper presents good practices and methods to create ML-based surrogate models for vibroacoustic problems with improved interpretability, accurac, and physical guidance, increasing confidence in the model. The vibroacoustic surrogates obtained with those practices can be used as an informed and fast decision-making tool, which is well-suited for real-time applications, the construction of digital twins and robust and optimal product design where extensive domain exploration is required. Furthermore, this work may be extended to include physical constraints in the surrogate to guarantee the model’s physical consistency.











 neural network;
neural network;  Gaussian process regressor;
Gaussian process regressor;  random forest;
random forest;  gradient boosting trees; with
gradient boosting trees; with  and without
and without  physics-guided features: (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
physics-guided features: (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
 neural network;
neural network;  Gaussian process regressor;
Gaussian process regressor;  random forest;
random forest;  gradient boosting trees; with
gradient boosting trees; with  and without
and without  physics-guided features: (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
physics-guided features: (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
 neural network;
neural network;  Gaussian process regressor;
Gaussian process regressor;  random forest;
random forest;  gradient boosting trees; (a) infinite plate; (b) correction factor; (c) MS. (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
gradient boosting trees; (a) infinite plate; (b) correction factor; (c) MS. (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
 neural network;
neural network;  Gaussian process regressor;
Gaussian process regressor;  random forest;
random forest;  gradient boosting trees; (a) infinite plate; (b) correction factor; (c) MS. (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
gradient boosting trees; (a) infinite plate; (b) correction factor; (c) MS. (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).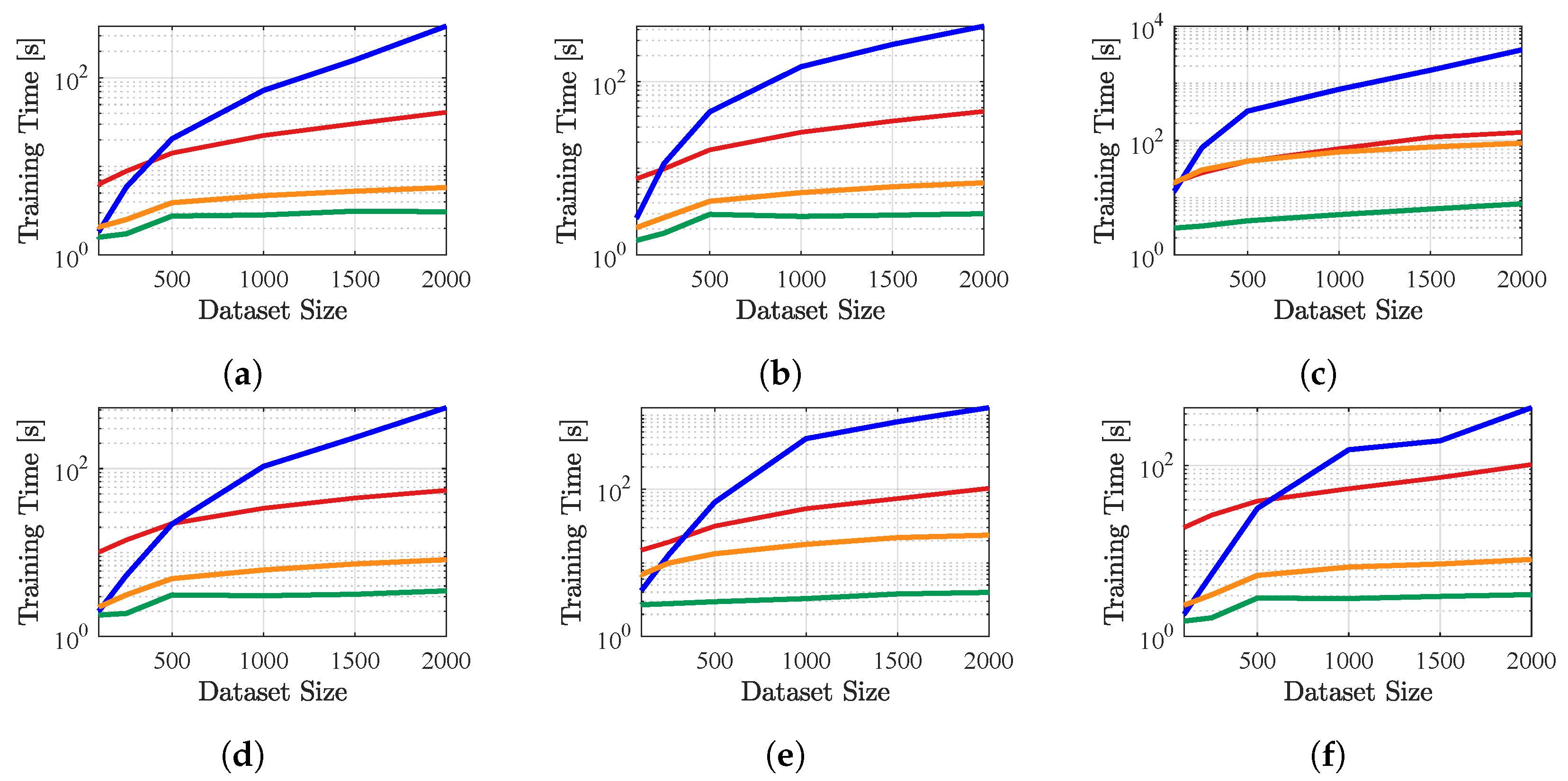
 simulated;
simulated;  predicted; (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
predicted; (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
 simulated;
simulated;  predicted; (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).
predicted; (a) infinite plate; (b) correction factor; (c) MS; (d) MS (band averaged); (e) FEM; (f) FEM (band averaged).












