Application of the Reciprocity Theorem to Scattering of Surface Waves by a Surface Crack in Viscoelastic Material
Abstract
:1. Introduction
2. Incident Surface Wave and the Scattering Problem
2.1. Incident Surface Wave
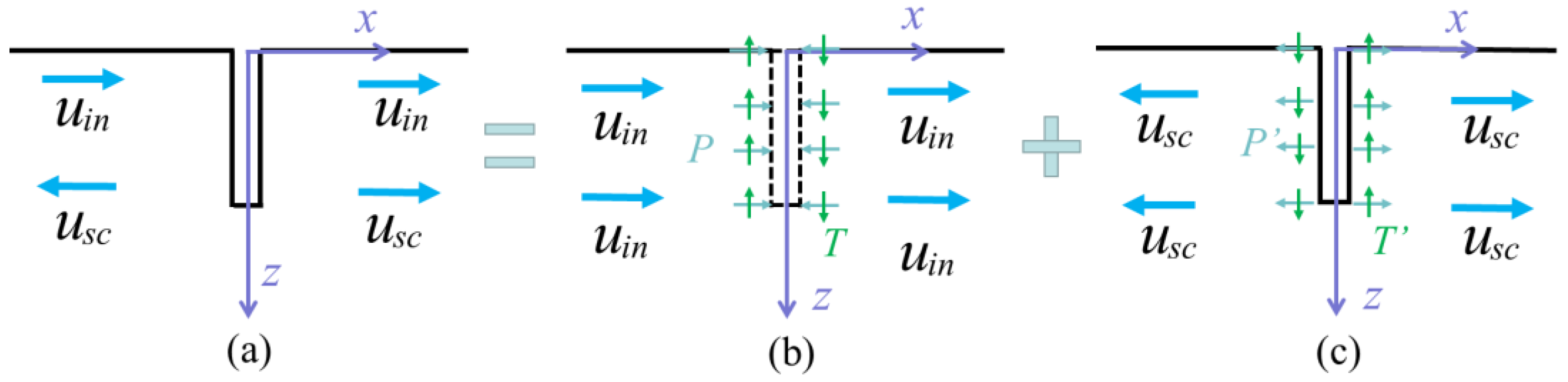
2.2. Scattering Problem
3. Study on Scattered Surface Wave from Surface Crack Based on Reciprocity Theorem
3.1. Form of Scattered Surface Wave
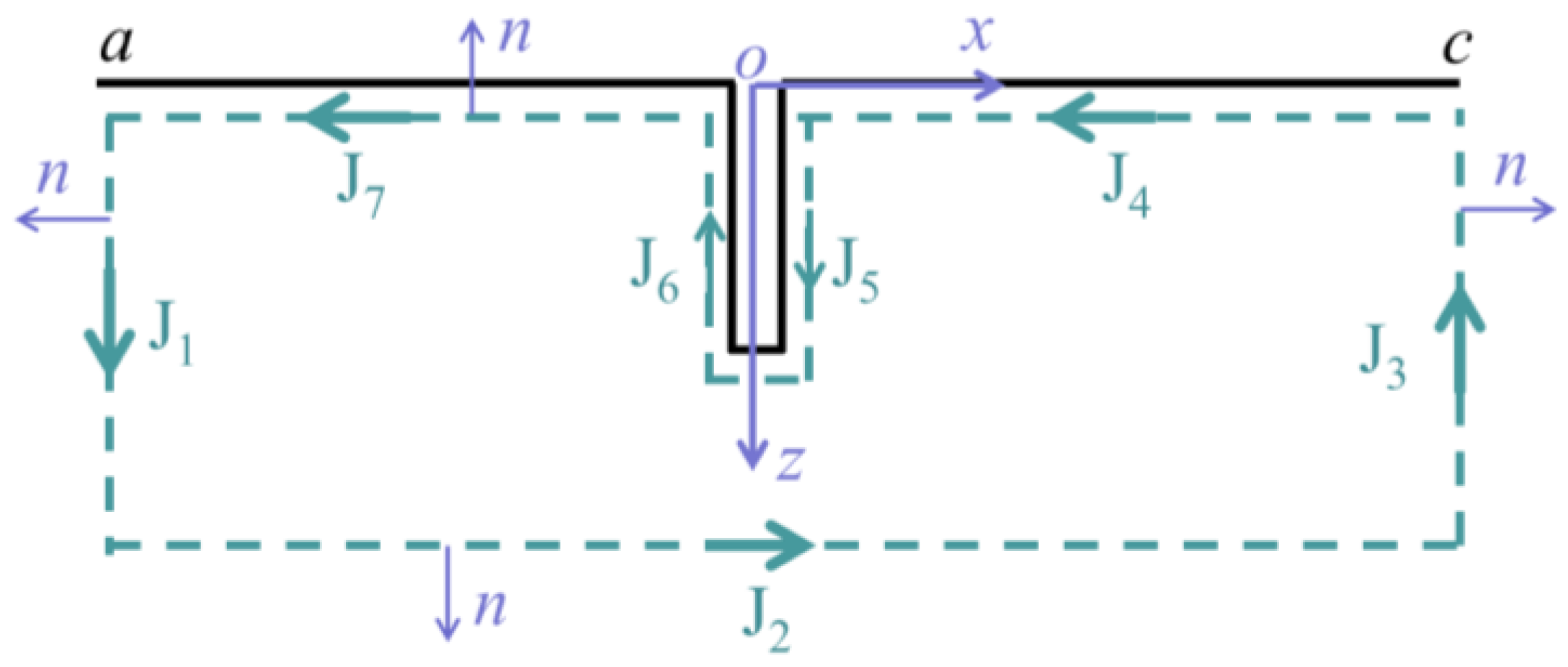
3.2. Reciprocity Theorem for Solving the Amplitude of Scattered Surface Waves
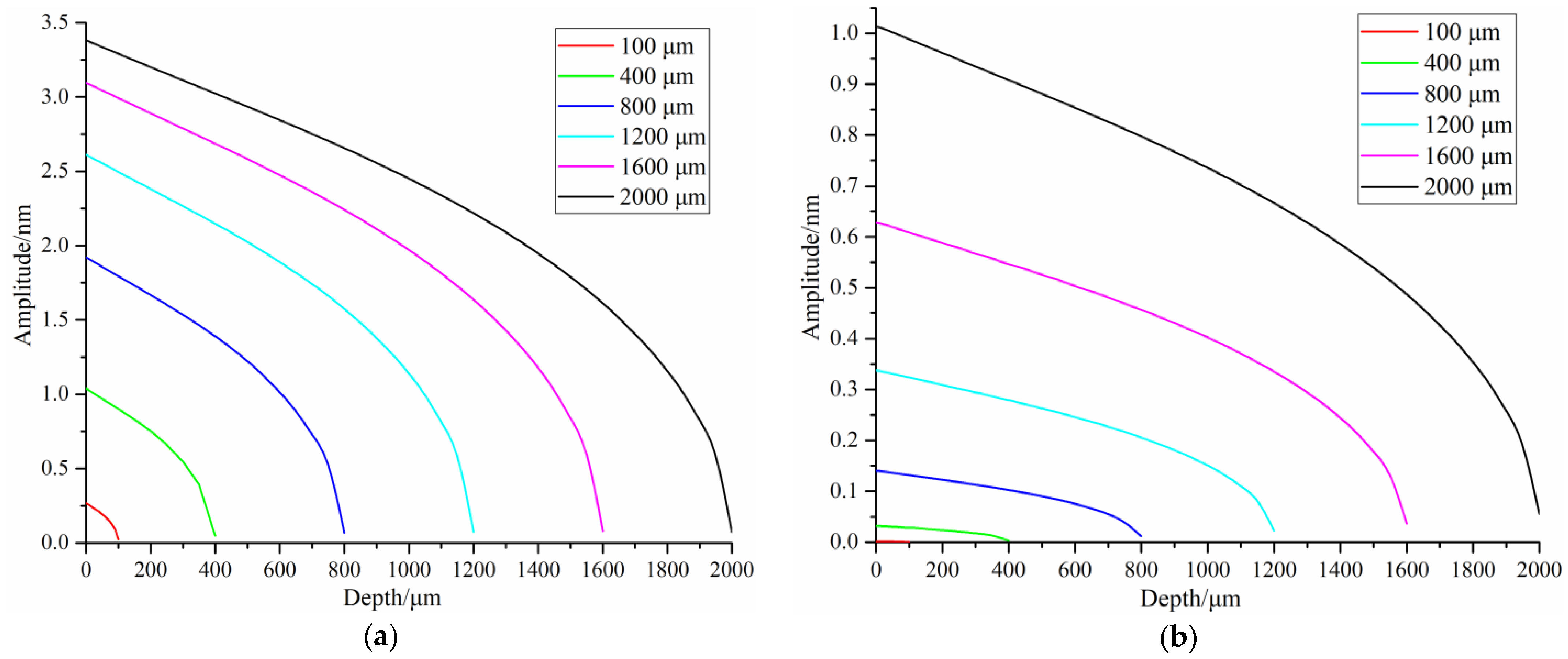
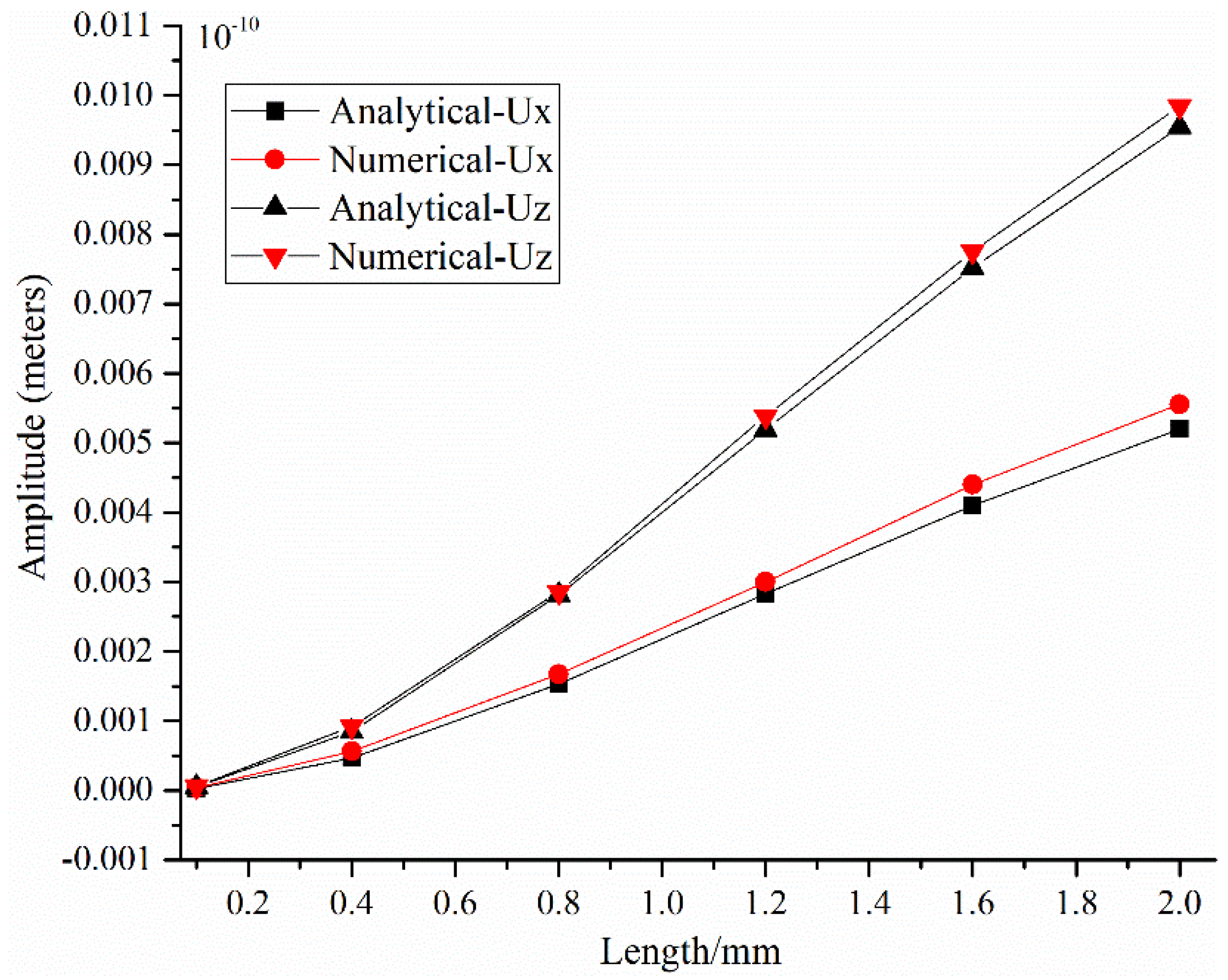
4. Special Case of Low Frequency and Low Viscosity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Samaržija-Jovanović, S.; Jovanović, V.; Marković, G.; Konstantinović, S.; Marinović-Cincović, M. Nanocomposites based on silica-reinforced ethylene–propylene–diene–monomer/acrylonitrile–butadiene rubber blends. Compos. B. Eng. 2011, 42, 1244–1250. [Google Scholar] [CrossRef]
- Noethen, M.; Jia, Y.; Meyendorf, N. Simulation of the surface crack detection using inductive heated thermography. Nondestruct. Test. Eval. 2012, 27, 139–149. [Google Scholar] [CrossRef]
- Hu, B.; Liu, Y.; Yu, R. Magnetic anomaly characteristics of surface crack defects in a titanium alloy plate. Nondestruct. Test. Eval. 2020, 36, 209–224. [Google Scholar] [CrossRef]
- Hirao, M.; Fukuoka, H.; Miura, Y. Scattering of Rayleigh surface waves by edge cracks: Numerical simulation and experiment. J. Acoust. Soc. Am. 1982, 72, 602–606. [Google Scholar] [CrossRef]
- Cook, D.A.; Berthelot, Y.H. Detection of small surface-breaking fatigue cracks in steel using scattering of Rayleigh waves. NDT E Int. 2001, 34, 483–492. [Google Scholar] [CrossRef]
- Kim, J.Y.; Rokhlin, S.I. Surface acoustic wave measurements of small fatigue cracks initiated from a surface cavity. Int. J. Solids Struct. 2002, 39, 1487–1504. [Google Scholar] [CrossRef]
- Hassan, W.; Veronesi, W. Finite element analysis of Rayleigh wave interaction with finite-size, surface-breaking cracks. Ultrasonics 2003, 41, 41–52. [Google Scholar] [CrossRef]
- Arias, I.; Achenbach, J.D. Rayleigh wave correction for the BEM analysis of two-dimensional elastodynamic problems in a half-space. Int. J. Numer. Methods Eng. 2004, 60, 2131–2146. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Cho, Y.; Phan, H.; Achenbach, J.D. Study on the scattering of 2-D Rayleigh waves by a cavity based on BEM simulation. J. Mech. Sci. Technol. 2011, 25, 797–802. [Google Scholar] [CrossRef]
- Golub, M.V.; Fomenko, S.I.; Bui, T.Q.; Zhang, C.; Wang, Y.S. Transmission and band gaps of elastic SH waves in functionally graded periodic laminates. Int. J. Solids Struct. 2012, 49, 344–354. [Google Scholar] [CrossRef]
- Hedayatrasa, S.; Bui, T.Q.; Zhang, C.; Lim, C.W. Numerical modeling of wave propagation in functionally graded materials using time-domain spectral Chebyshev elements. J. Comput. Phys. 2014, 258, 381–404. [Google Scholar] [CrossRef]
- Bövik, P.; Boström, A. A model of ultrasonic nondestructive testing for internal and subsurface cracks. J. Acoust. Soc. Am. 1997, 102, 2723–2733. [Google Scholar] [CrossRef]
- Kang, S.; Wu, Y.C.; Ham, S. Singular Integral Solutions of Analytical Surface Wave Model with Internal Crack. Appl. Sci. 2020, 10, 3129. [Google Scholar] [CrossRef]
- Pecorari, C.; Poznić, M. Nonlinear acoustic scattering by a partially closed surface-breaking crack. J. Acoust. Soc. Am. 2005, 117, 592–600. [Google Scholar] [CrossRef] [PubMed]
- Betti, E. Teoria della elasticita. Il Nuovo Cim. 1872, 7, 158–180. [Google Scholar] [CrossRef]
- Rayleigh, L. Some General Theorems Relating to Vibrations. Proc. London Math. Soc. 1873, 4, 357–368. [Google Scholar]
- Achenbach, J.D. Reciprocity in Elastodynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kino, G.S. The application of reciprocity theory to scattering of acoustic waves by flaws. J. Appl. Phys. 1978, 49, 3190–3199. [Google Scholar] [CrossRef]
- Phan, H.; Cho, Y.; Achenbach, J.D. Verification of surface wave solutions obtained by the reciprocity theorem. Ultrasonics 2014, 54, 1891–1894. [Google Scholar] [CrossRef]
- Phan, H.; Cho, Y.; Achenbach, J.D. Application of the reciprocity theorem to scattering of surface waves by a cavity. Int. J. Solids Struct. 2013, 50, 4080–4088. [Google Scholar] [CrossRef] [Green Version]
- Phan, H.; Cho, Y.; Li, W. A theoretical approach to multiple scattering of surface waves by shallow cavities in a half-space. Ultrasonics 2018, 88, 16–25. [Google Scholar] [CrossRef]
- Achenbach, J.D. Acoustic emission from a surface-breaking crack under cyclic loading. Acta Mech. 2008, 195, 61–68. [Google Scholar] [CrossRef]
- Chao, Y.; Achenbach, J.D. Radiation from Equivalent Body Forces for Scattering of Surface Waves by a Near-Surface Cylindrical Cavity. In Generalized Models and Non-classical Approaches in Complex Materials 2; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Pecorari, C. Scattering of a Rayleigh wave by a surface-breaking crack with faces in partial contact. Wave Motion 2001, 33, 259–270. [Google Scholar] [CrossRef]
- Mardanshahi, A.; Shokrieh, M.M.; Kazemirad, S. Identification of matrix cracking in cross-ply laminated composites using Lamb wave propagation. Compos. Struct. 2020, 235, 111790. [Google Scholar] [CrossRef]
- Zakharov, D.; Castaings, M.; Singh, D. Numerical and asymptotic approach for evaluating complex wavenumbers of guided modes in viscoelastic plates. J. Acoust. Soc. Am. 2011, 130, 764–771. [Google Scholar] [CrossRef] [PubMed]
- Dineva, P.S.; Wuttke, F.; Manolis, G.D. Elastic wave scattering and stress concentration effects in non-homogeneous poroelastic geological media with discontinuities. Soil Dyn. Earthq. Eng. 2012, 41, 102–118. [Google Scholar] [CrossRef]
- Achenbach, J.D. A new use of the elastodynamic reciprocity theorem. Math Mech. Solids 2014, 19, 5–18. [Google Scholar] [CrossRef]


| 50 | 200 | 400 | 600 | 800 | 1000 | |
|---|---|---|---|---|---|---|
| 21.099 | 20.703 | 20.128 | 19.505 | 18.843 | 18.150 | |
| 0.068 | 0.286 | 0.607 | 0.958 | 1.334 | 1.729 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Wang, C.; Lu, J.; Sun, A. Application of the Reciprocity Theorem to Scattering of Surface Waves by a Surface Crack in Viscoelastic Material. Appl. Sci. 2022, 12, 10785. https://doi.org/10.3390/app122110785
Zheng L, Wang C, Lu J, Sun A. Application of the Reciprocity Theorem to Scattering of Surface Waves by a Surface Crack in Viscoelastic Material. Applied Sciences. 2022; 12(21):10785. https://doi.org/10.3390/app122110785
Chicago/Turabian StyleZheng, Li, Chuanyong Wang, Jiangang Lu, and Anyu Sun. 2022. "Application of the Reciprocity Theorem to Scattering of Surface Waves by a Surface Crack in Viscoelastic Material" Applied Sciences 12, no. 21: 10785. https://doi.org/10.3390/app122110785






