Abstract
This paper presents a robust proportional derivative adaptive nonsingular finite-time synergetic tracking control (PDAFS) for a parallel Delta robot system. First, a finite-time synergetic controller combined with a proportional derivative (PD) control is constructed based on an object-oriented model to fulfill the robust tracking control of the robot. Then, an adaptive radial basis function approximation neural network (RBF) is designed to compensate for the effects of uncertainty parameters and external disturbances. Second, a second-order sliding mode (SOSM) differentiator is implemented to reduce the chattering noises due to the low-resolution encoders. Third, the stability theorems of the proposed control scheme are provided, where the Lyapunov stability theory is used to prove the theorems. Then, simulations of the helix trajectory tracking and the pick-and-place task are demonstrated on the Delta robot to validate the advantages of the proposed control scheme. Based on the advances, an implementing control system of the proposed controller is performed to improve the Delta robot’s performance in the experiments.
1. Introduction
Delta parallel robot is the most successful commercial parallel robot to date. The parallel robot has been employed for high-precision tracking and high-speed motions to boost output [1,2]. The robot has three kinematics branches consisting of two arms, and the branches connect a base and a moving plate. Due to the complexity of the closed-loop structure and kinematic constraints of the robot, the robot model is a multi-variable, multi-parameter, coupling, and multi-degree-of-freedom nonlinear system. Many studies have shown the significance of kinematic [3,4,5] and dynamic models [6,7,8,9] on path planning and tracking precision. Accordingly, numerous model-based control techniques are employed to improve the performance of parallel robots. For instance, Codourey proposed a proportional derivative feedforward (PDFF) controller based on a dynamic model of the Delta robot in [10,11] to give more precise trajectory tracking than a kinematic controller. In a recent work [12], a dynamic feedforward decoupling control scheme was proposed for a compensated feedforward gravity and an independently adjustable three PID control loop corresponding to the position, velocity, and current controls of a four-degrees-of-freedom parallel robot. Although the simulation results reveal that the system can reduce tracking errors, it is difficult to be applied due to the decoupling factors in serial control loops, which depend not only on the correctness of the dynamic modal transformations but also on the noises of the feedback signal. In addition, the two model-based methods require not only the accuracy of parameters but also lack influences of uncertainty parameters and unknown disturbances in the systems.
To solve robust tracking problems and reduce the influence of external disturbance, a sliding mode control (SM) technique based on the Delta robot dynamics with uncertain parameters was proposed in [13]. This approach guarantees stability by keeping system states on a sliding plane. Another SM improvement by a terminal attractor technique is the so-called terminal sliding mode (TSM) control, proposed in [14] for finite-time stabilization of robotic manipulators. However, both SM and TSM techniques have a drawback, which produces high-frequency oscillations of the controller outputs, known as chattering noises. The noises can impose vibration on the mechanical actuators. To eliminate the chattering phenomenon, another control methodology for modern and complex systems led to the introduction of the synergetic control (SC) theory [15] by Kolesnikov. Similar to SM properties, the advantages of synergetic control are well-suited for order reductions of the controlled system, robustness to external disturbance, and better control of the off-manifold dynamics. In synergetic control papers [16,17,18], synergetic-based controllers generate chattering-free dynamics of nonlinear systems. Inspired by the TSM, finite-time synergetic control (FS) schemes to control serial robot manipulators were proposed in [19,20]. The finite-time synergetic control (FS) scheme employed the synergetic theory and a terminal attractor technique to control serial robot manipulators. The new synergetic approach is allowed to perform well in multiple connected nonlinear systems with continuous, discontinuous, discrete-time, terminal, and adaptive control, such as robots [20,21], electric drives [22], and flying apparatus [23]. Based on those studies, the benefits of a synergetic approach, such as robustness, quick dynamic reactions, and chattering-free phenomena, are well suited for the Delta robot.
In addition, the Delta parallel robot is a highly nonlinear complexity system. Therefore, developing a suitable control scheme for the robot with parametric and non-parametric uncertainties and external disturbance represents a significant challenge. Boudjedir and co-workers proposed a nonlinear controller to solve robust and precise trajectory problems using SM or a nonlinear PD controller based on iterative learning [24,25,26]. However, the schemes must require a long time to follow continuous repetitive or non-repetitive trajectories before improving the tracking errors. To online estimate uncertain plant parameters, different kinds of adaptive control strategies have been performed to deal with the uncertain parameter or disturbance. The work in [27] proposed an adaptation law for dynamics and friction compensation of the dynamic model of the 2-DOF parallel mechanism based on a Lyapunov method. In ref. [28], an online estimation was proposed for simulating trajectory tracking control with nonlinear joint friction models, which were compensated to the nominal Delta model. Another adaptive control inside an active disturbance rejection framework used the least mean square technique in [29] to produce a reliable tracking control for the low-speed Delta platform, where the researchers did not consider the joint velocity data of the system. As can be seen, uncertainty parameters in the adaptive controllers must be analyzed explicitly in a specific model, which represents the effects of the system tracking errors.
In recent years, there have been numerous adaptive intelligent control techniques. On the one hand, a systematic analysis with sensory noise and uncertainty robustness for a type 2 fuzzy logic was used to position the control of the end-effector of the parallel Delta robot [30]. Or a utilization of fuzzy logic systems can estimate the unknown nonlinear behavior of simple examples and adapt successfully via synergetic control theory [31]. However, the linguistic rules and optimal dataset for stability guarantee remain challenging issues. On the other hand, uncertainty parameters in a model are estimated by approximations using neural networks (NNs). The study in [32] is an example of using NNs to create compensators for the dynamic model. In particular, the robust integral of the sign error (RISE) controller with a B-spline NN feedforward compensation was applied to a Delta robot to regulate the trajectory tracking for a pick-place application. An intelligent compensation term added to the system control can reduce the tracking error considerably and cancel the steady-state error. However, only simulating validations of these NNs are taken into account. Based on a linear motor model with unknown frictions [33], a processing structure of two-layer NNs was proposed successfully to compensate for the effects of the friction model in both simulations and experiments. Ref. [34] gave an output feedback controller with a feedforward term based on a radial basis function (RBF) neural network that dealt with uncertainty compensation in a robotic exoskeleton. It is shown that an RBF network may approximate a continuously nonlinear function with benefits such as low-cost computation and quick convergence. In this work, RBF networks are utilized in addition to a robust synergetic controller to estimate unknown parameters for control quality enhancement.
Based on the benefits and limitations of the above literature review, a novel combination of the advantages of a proportional derivative, a robust synergetic, and an RBF network controller based on the object-oriented technique [7] in a Delta robot system with the generalized disturbance is proposed. Therefore, the main contributions of this paper lie in the following aspects:
- A systematic controller using a PD controller with a finite-time synergetic technique is developed based on the Delta robot dynamics for robust trajectory tracking control. In the proposed controller structure, unknown parameters and external disturbance of the DC motors and the robot manipulator are analyzed in a generalized disturbance model, then compensated torques are estimated online through RBF 2-layer neural networks.
- The stability of the proposed control framework is analyzed and proven through the Lyapunov stability theory.
- The features of the proposed controller are successfully applied to the parallel Delta robot in simulation and practical experiments with different trajectory examples. A comparative study between PD, feedforward, SM, and the proposed approach is provided to reveal the advantages and improvements of the latter.
The rest of this paper is organized as follows. A nonlinear model of the Delta robot with DC motors is analyzed in Section 2. Then, the robust adaptive synergetic control based on RBF neural networks is proposed in Section 3. Finally, the simulation results in Section 4 and the experimental results in Section 5 present the advantages of the proposed method in comparison with the results obtained by the other controllers.
2. Nonlinear Dynamics of Delta Robot Model
2.1. DC Motor Servo Model
The DC motor model for the robot system is described by electrical and mechanical differential equations [35,36]:
where is voltage input applied to the motor’s armature, is armature resistance, is armature inductance, is armature current, and are angular displacement and velocity of the motor shaft, the product is torque generated by armature current with torque constant , represents the coefficient of velocity-dependent friction in the motor, and is torque of load, back electromotive force (EMF) coefficient is denoted by . The dynamic parameters of the DC motor servo in Table 1 are required by performing a system identification experiment [36] and using the MATLAB toolbox [37].

Table 1.
Parameters of the DC motor.
2.2. Delta Robot Manipulator
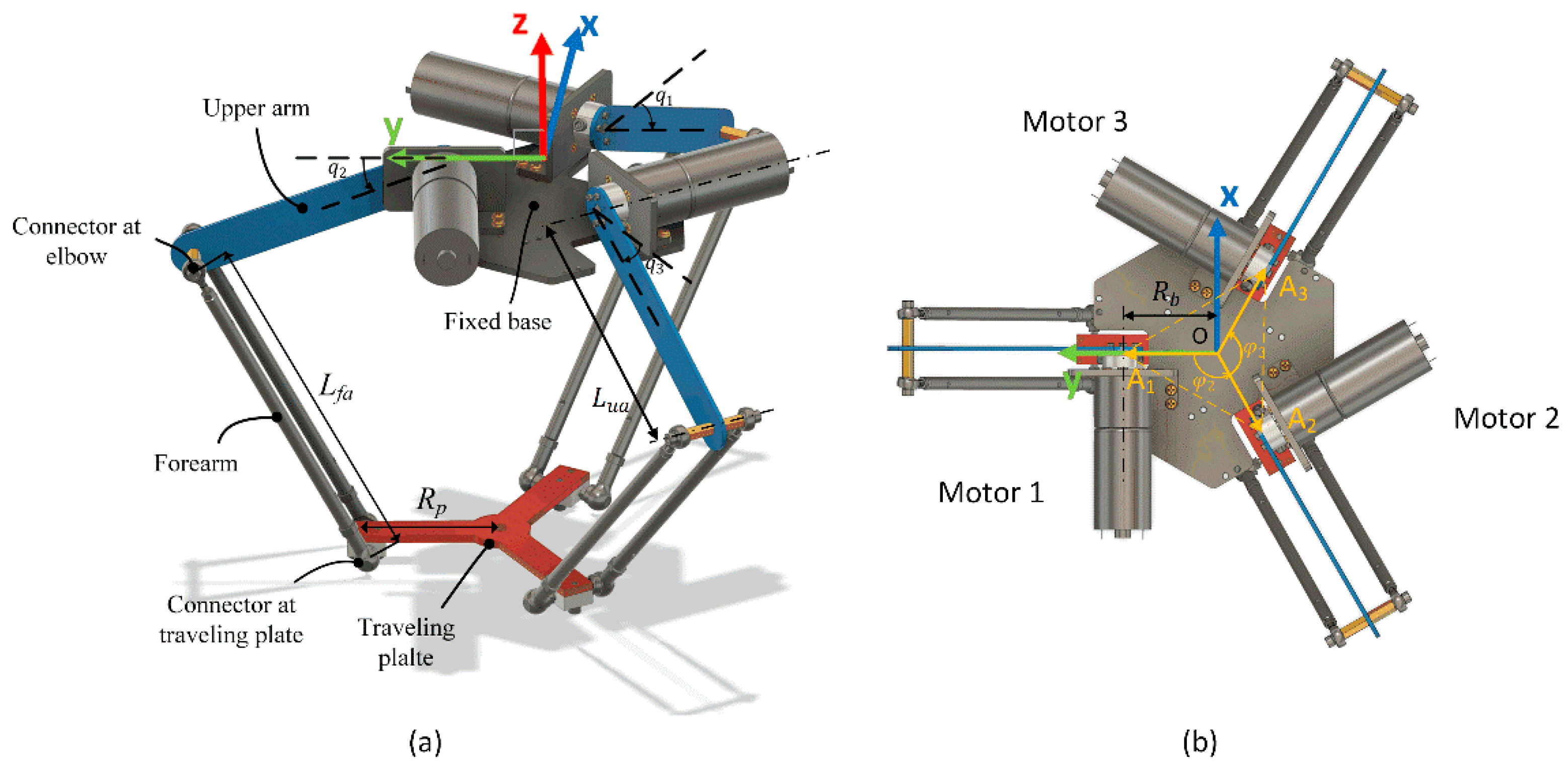
Consider the experimental Delta robot and its parameters illustrated in Figure 1 and Table 2, which consists of three symmetric branches constrained in a kinematic manner by the universal or spherical joint at the traveling plate. The complexity of the model arises mainly due to the movement of the forearms in branches. The forearm is constructed of two lightweight aluminum rods and attached rod end bearings at their extremities. The rod end bearings of the forearms transfer the motion of the upper arms to the traveling plate, giving it three degrees of freedom. By eliminating the forearms’ rotational inertia, we may reduce the intricacy of their motion. This assumption is not very restricting due to the weight distribution of the forearm to the extremities. Moreover, a generalized disturbance of the Delta robot is analyzed in Section 3, so we can neglect the effects of joint friction and elasticity in this section to simplify the dynamic model of the Delta manipulator.
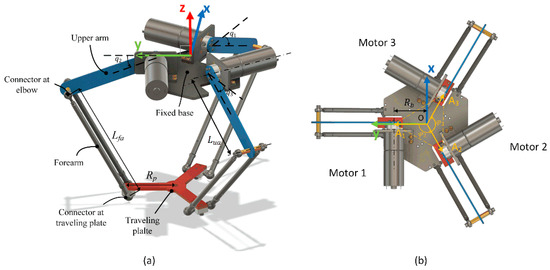
Figure 1.
The Delta robot in 3D view (a) and top-view (b).

Table 2.
Kinematic and dynamic parameters of Delta manipulator.
The inverse dynamic model of the Delta robot is developed as [10,11] based on the Newton–Euler method with the following simplifying hypotheses:
- The rotational inertia of forearms is neglected.
- For analytical purposes, the masses of forearms are optimally separated into portions and at their extremities: a two-thirds majority part at its upper extremity and the other part at its lower extremity, which contributes to the traveling plate mass.
- Friction effects and elasticity are neglected.
With the above-mentioned simplifying hypotheses, the robot can be reduced to only four bodies: the traveling plate and the three upper arms. We choose as the optimal distribution of the three forearm masses, the total virtual mass of the traveling plate based on the hypotheses is calculated as:
At the upper arm level, let denote the mass of each virtual arm. We can define the position of the center of mass in the arm based on the hypothesis as:
where is the length of upper arm, is the mass of the traveling plate and connectors at this plate, , , , are the mass of external load, a forearm, and connectors at an elbow and an upper arm, respectively.
The inertia matrix of the arms in joint space is a diagonal matrix, and the inertia of each arm , , can be defined as:
There are two kinds of forces that act on the traveling plate: the gravity force and the inertia force . They are respectively given by:
where is the gravitational acceleration, is the Cartesian acceleration vector of the traveling plate, with .
We can transform the forces in Equations (6) and (7) into torques to each motor by Jacobian matrix .
Let be an angle between and the y-axis, as shown in Figure 1b, represents the position of the traveling plate in the Cartesian coordinate system. Descriptions of the Jacobian matrix are discussed in more detail in [2] and [3], which is:
where:
The relationships between velocities and accelerations in Cartesian space and joint space are described as:
According to the virtual work principle [8,10], we can calculate the torque contribution of the Delta manipulator applied to the motors from the equilibrium between the contributions of inertia forces and non-inertia forces as:
where is the applied joint torque vector of the nominal Delta manipulator, as the torque vector produced by the gravitational force vector of the arms, is the derivative of the Jacobian matrix, are the angular position, velocity, and acceleration vector of the actuated joint, and is the velocity vector of the traveling plate.
In Equation (14), we state the inverse dynamic model produced by the nominal mass matrix , the nominal Coriolis and centrifugal matrix , and the gravity contribution as the equation below:
where:
3. The Proposed Controller
3.1. The Finite-Time Synergetic Controller (FS) for Delta Manipulator
According to the state variable theory, the nominal nonlinear dynamics of the Delta manipulator (15) can be rewritten as follows:
where is the control input vector, is the state matrix of the robotic system, and , .
The synergetic control design procedure can be stated as follows:
Step 1: We choose a macro-variable associated with the number of joints of the robot as , which is generally a linear combination of the state variables for constructing a surface as follows:
where represents the tracking error states, and are the desired angular position vector, and are the tracking error and its derivative vector. The control law can force the trajectories to operate on the synergetic manifold, we define as a linear combination function of the system states as:
We can find the derivative of the synergetic macro-variable as:
where is a positive-definite, diagonal matrix.
Step 2: The proposed controller is designed here such that it can force the states to approach the manifold smoothly at a finite time by using an evolution constraint of the synergetic manifold according to the following equation:
where is a positive definite number, which affects the quality of convergence, , and are positive odd numbers that satisfy the condition , This constraint can drive the macro-variable and its derivative to zero at a finite time.
Step 3: Substituting into the constraint of Equation (25) into the nonlinear dynamic model (19), we can obtain the resulting finite-time synergetic control law associated with the nominal Delta manipulator as:
Lemma 1.
[14,38] Suppose that a continuous, positive-definite function satisfies the following inequality:
where,are constants. Then, for any given,satisfies the following inequality:
whereand,withis the reaching time, given by:
Theorem 1.
Consider a nonlinear system as (21) with the control law in (26), the tracking errors converge to zero in a finite time with a convergence rate depending on the selected parameter .
Proof of Theorem 1.
To demonstrate the asymptotic stability of the system, we define a Lyapunov candidate function and we have its derivative as:
Substituting the constraint in (25) into (30), and assuming then:
where , if and satisfies Lemma 1. The synergetic manifold can converge to zero in the finite time , given by:
3.2. The PD Adaptive Finite-Time Nonsingular Synergetic Controller (PDAFS) Based on Radial Basis Function Neural Networks
Based on the Delta manipulator (21) and motor dynamics (2), the general equation describing the robot system incorporating the external disturbance is presented as:
where , are the actual mass matrix and actual centrifugal and Coriolis matrix. , , and are the actual gravitational, actual motor dynamic, and actual disturbance torque, respectively.
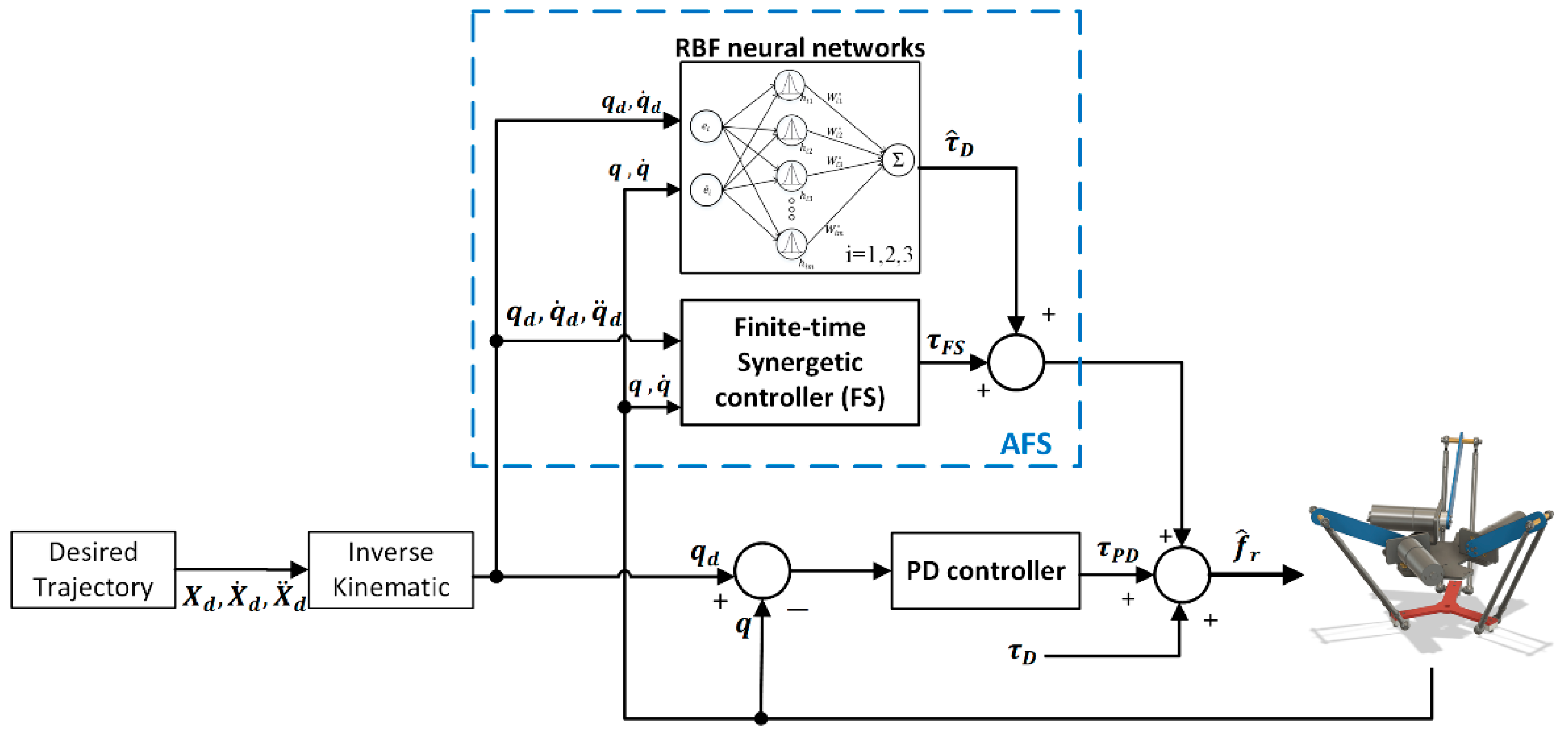
From the dynamic model in (34), we can see that if the dynamic motions of the robot satisfy the desired trajectory, the torque control signal must be calculated precisely. In discrete-time control, the signal controls in (2) and (34) are discrete, quantized, and extremely difficult to achieve accurate torque values. Based on three object-model controls for the motor model, the manipulator model, and a generalized disturbance model in the Delta robot, this paper proposes the PDAFS controller as a combination of PD, finite-time synergetic, and RBF neural network controller.
Throughout this paper, the controller structure is designed with the following propositions, used directly in the convergence analysis.
Proposition 1.
A proportional derivative control (PD) estimates the torques, matching the nominal dynamics of DC motors. To guarantee the stability of angular motor positions without load, we can choose as:
where , , and are positive-definite diagonal matrices, respectively. is the torque vector to control the three motor without torques of load.
Proposition 2.
To overcome the nominal dynamics of the Delta manipulator, the finite time synergetic control scheme is proposed.
where,, andare calculated as in Section 2.2.
Proposition 3.
The unknown parameters and external disturbance of the practical Delta robot system consist of disturbances in the motors, the Delta manipulator from the hypothesis in Section 2.2, and an external load. They all affect the tracking errors of joint positions and velocities by applying an unknown torque value to each motor. For simplifying disturbance models, a generalized disturbance model
with is proposed to estimate online three RBF neural networks [39,40] as:
The adaptive law is designed as:
From descriptions of RBF networks in [39,40], we choose the tracking error and its derivative value as the input vector in this paper.
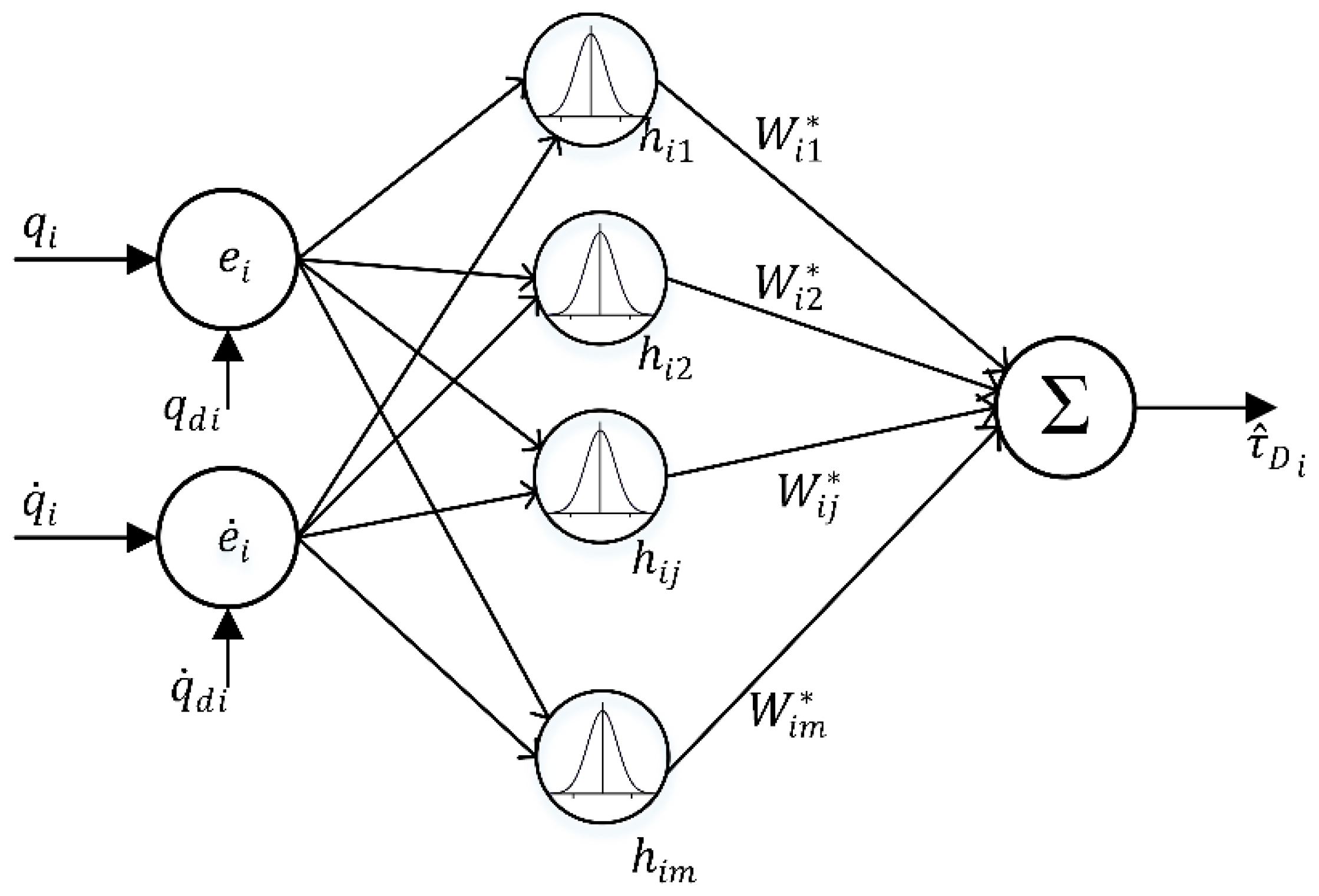
where is the Gaussian function of the j-th neural network of the i-th joint, is the input vector of the i-th joint, represents the center point matrix, are the weight vector and updated weight vector of joint i. j = 1, 2, …, m is hidden neural net number in the hidden layer. is the output vector of hidden layer, with i = 1, 2, 3 as the number order of joint, the learning rate is denoted by . The structure of RBF network is presented in Figure 2.
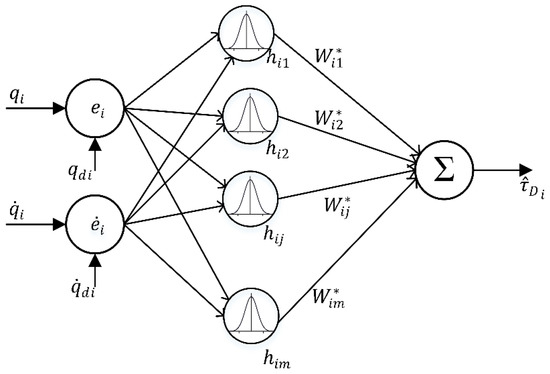
Figure 2.
The RFB neural network in this paper.
The optimal weights are found by using the Gradient descent algorithm and the adaptive law (39)-; the weight vector of the i-th joint is:
In total, the proposal controller of the nonlinear Delta robot is proposed as:
The system errors and error rates converge to zero in the finite time with the rate convergence depending on the parameters , , and if the control law is selected as Theorem 1 and Section 3.1. The disturbance estimation in (38) is used to approximate the external disturbance and model error compensation in order to minimize the tracking errors. In the following, we prove the stability of the Delta robot model controlled by the PDAFS controller.
Assumption 1.
The uncertainty parameters and external disturbance are unknown but bounded. The characteristics of the rigid robotic manipulator associated with the nominal matrices (16)–(18) are used in the stability analysis and are described in [41,42] as follows:
- The inertia matrix is a positive definite symmetric matrix.
- The matrix is a skew symmetric matrix.
Theorem 2.
Assume that the desired trajectories are bounded. Let the control input be given by (40) with the estimated torques calculated as (38). Then, we ensure that is uniformly ultimately bounded.
Proof:
If a Lyapunov candidate function is defined as:
Then we can have its derivative as:
If we consider structural property 2 in Assumption 1, then one can have and:
Substituting the manifold surface in (23) and the robot system model in (34) into (24), we have the equation below.
The reference states and torque to control the generalized Delta robot system are described by Equations (47)–(49):
Therefore, Formula (46) can be simplified.
Substituting (50) into the Lyapunov function derivative in (45), we can get the following formula:
We can rewrite the computed torque vector for the Delta robot from the PDAFS controller (42) as:
where:
With the ideal torque to control the Delta robot as , the computed torque , is the torque vector matching the nominal models with the computed torque vector for controlling the robot system. For any , we have the difference between and caused by the model errors and external disturbances [13,43], denoted as , which is set as follows:
Since the disturbances are always bounded with the desired trajectory, assume that the ideal disturbance at joint i is with calculated as:
To compare with the estimated values in (38), we state that the error uncertainty parameters have an upper bound , which can be written as:
where and .
From (51)–(55), we rewrite Equation (45) as below:
Substituting the adaptive law (37) into (54), yields:
According to the Lyapunov theory and the proof in (32), the proposed PDAFS is stable in the finite time for the tracking control of the Delta robot. The equality is satisfied if and only if . Since the Lyapunov function is positive definite, and is negative definite, which leads to the conclusion that the proposed controller is globally asymptotically stable from the Lyapunov stability criterion.
Remark 1.
Using the PD controller is realistic, where the PD controller is implemented directly on a microcontroller, and it can stabilize the robot system in the short-term control and guarantee the error boundary of the system and the adaptive finite-time synergetic control (AFS) is calculated on the computer. The torque signals of the AFS can compensate for PD control signals on the microcontroller to ensure the accuracy and stability of the robot in long-term control.
Remark 2.
There are two main differences between the finite-time synergetic approach in (42) and sliding mode controllers [13,14]. Firstly, the manifold surface of the synergetic controller is constructed by a system errors function and combined with a finite-time constraint function. In contrast, the sliding surface is a function of system errors with an attached finite-time feature from the tracking errors. The other difference is a switching sign function attached to sliding mode control, whereas the asymptotic stability is caused by an exponential convergence function in the proposed controller. In this way, the synergetic approach can reduce the chattering phenomenon and keep the features of robust controllers.
Remark 3.
In the developed FS in (42), the proposed PDAFS controller can adapt to the existence of external disturbance. The generalized disturbance model based on RBF approximation in the control system can compensate for unknown parameters and significant disturbance influence that assures the error convergence is zero.
From the remarks, the controller contributions in the PDAFS and their advantages are shown in Table 3.

Table 3.
The contribution and advantages of object-oriented model control in PDAFS.
3.3. Control Design Procedure
The tuning method of the PDAFS can be summarized by following the steps below:
Step 1: Based on the motor model (1) and the parameters in Table 1, the parameters of the PD controller for the motor model can be selected by the PID tuning tool in MATLAB. In a practical experiment, the and matrix can be selected by the Zeigler–Nichols tuning method to validate the parameters from the simulation.
Step 2: According to the finite-time synergetic controller, the combined error coefficient matrix represents the ratio contribution between angular position error and angular velocity error, the matrix can be set as the ratio of and . The quality of convergence can be degraded as small as possible in theory if the system is considered in a continuous domain. However, because of the interval time, the parameter should be tuned by degradation until the chattering error appears in the practical experiment.
Step 3: Values of angular position error and angular velocity error are evaluated and prepared as the dataset input of the RBF neural networks after implementing the PDFS controller. The synergetic controller can limit the range of the errors, so the remaining errors are associated with unknown disturbances. Based on the boundary of and , we can optimize the parameters of RBF NNs for compensated disturbance torques to control the errors into a smaller region without a chattering signal.
3.4. The Velocity Second Order Sliding Mode Observer
The proposed controller defined in (42) requires the knowledge of angular positions and velocities. However, we only use the low-resolution encoders to measure the position and velocity of joints for the experimental Delta robot system (34). Hence, a velocity estimator is essential for the practical controller. Popularly, the velocity values can be calculated by the backward differentiator (BD) technique from the position values.
where and are the present and previous angular positions of the ith joint and is the time-delay system.
However, this scheme does not suffer only from the quantization noise due to the low-resolution encoder but also the time-varying delay system in different iterations. To effectively estimate the velocity for this kind of system, a combination of low pass filter (LPF) and second-order exact differentiation via the sliding mode (SOSM) [44,45] is introduced in the experiment results of this paper. The velocity estimator algorithm for the i-th joint is presented as Equations (59)–(61) below.
where is the SOSM velocity, is the recursive angular position estimation from , is the estimated velocity, is the cut-off frequency of the low pass filter, and , are the parameters of the SOSM estimator.
Remark 4.
It can be noticed from equation (59) that the velocity estimator using SOSM can achieve finite time error convergence. Boundedness conditions and stable tracking errors with the desired trajectory satisfy the finite-time stability of the sliding mode differentiator [44,46]. Thus, the proposed controller and observer can be designed separately. In the practical assembly system, the angular velocity signal is always quantized by encoder values and contaminated by time-varying delays during estimation, so the control effort leads to chattering. A combination of SOSM and LPF can reduce the chattering phenomenon from the standard (first-order) sliding mode observer [47,48] and preserve the advantage features of the robust exact differentiator.
4. The Simulation Results
In this section, helix and pick-place characteristics of the nonlinear dynamics of the Delta robot are calculated as the desired trajectory to validate the PDAFS control performance. The planning trajectories followed by a quintic function of time as [6] can generate smoothing velocities and accelerations, which are applied to reduce vibration in the system. The fifth polynomial function describes the quintic function, as below.
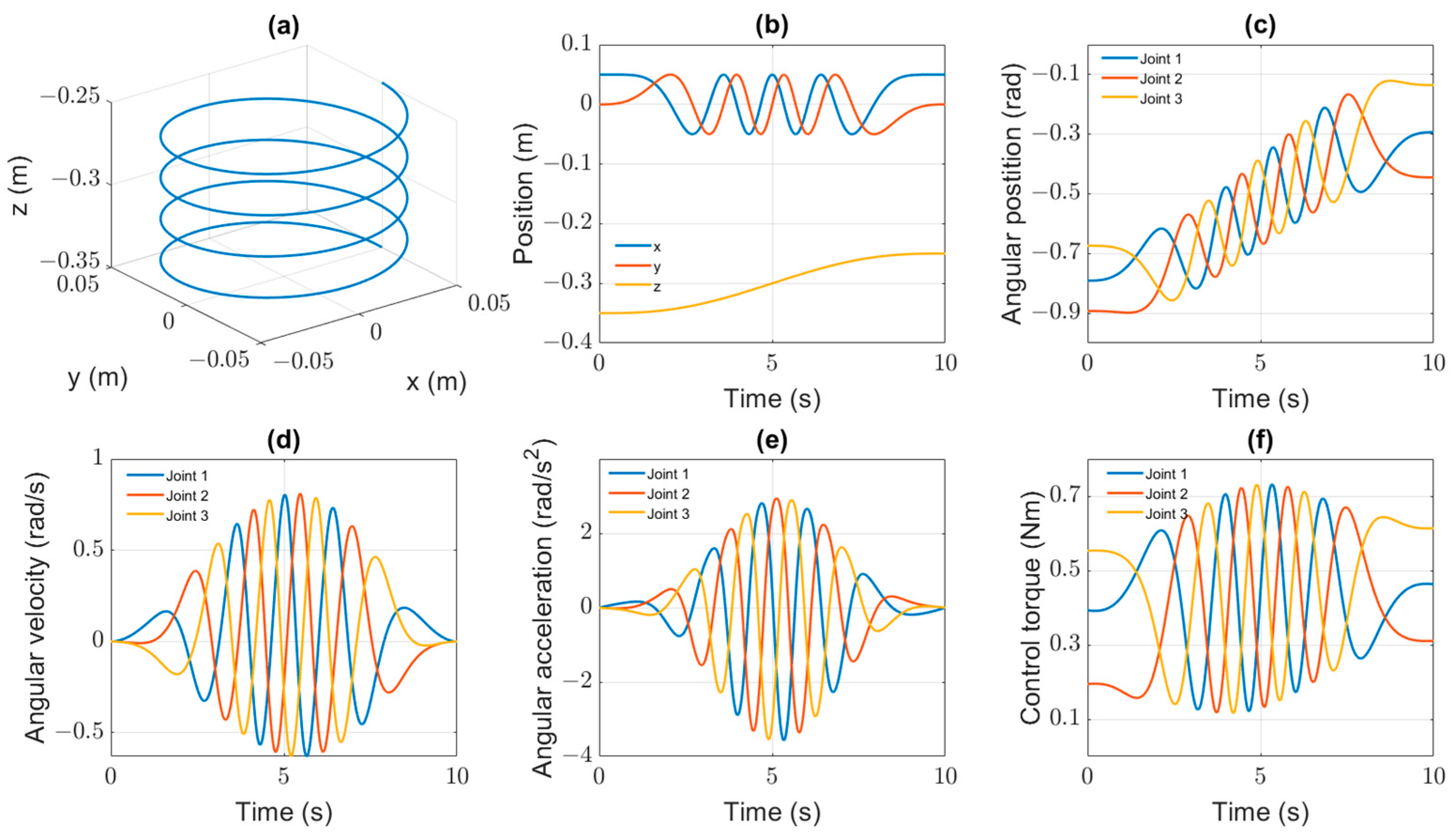
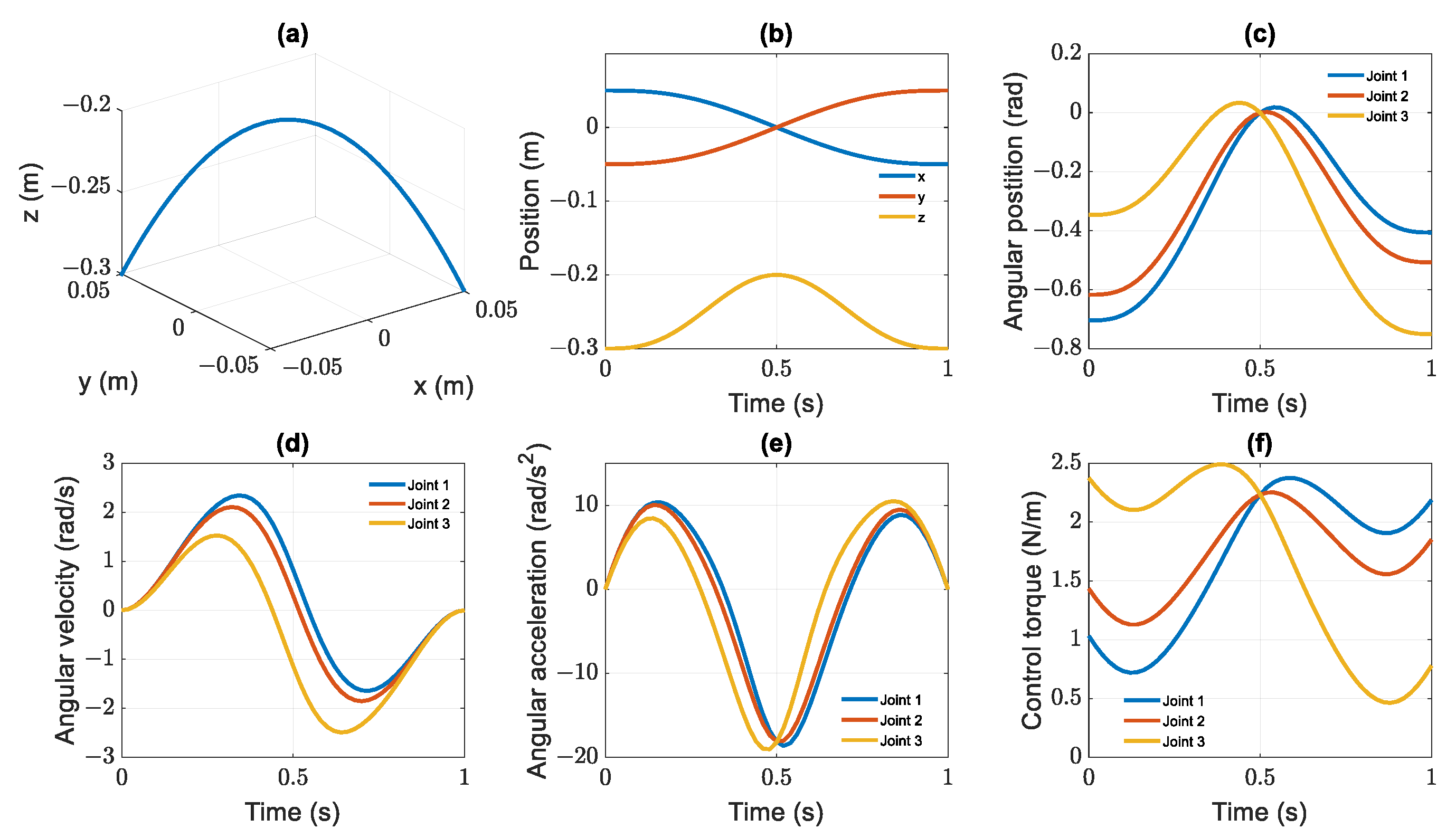
where and are the desired positions in the Cartesian coordinate system of the helix and parabolic curves at the determined time. The coordinates and are initial and final positions. R is the radius, k is the number circle of the helix, whereas h is the height of parabolic on the z-axis, u(t) is the quintic function of time , and is the duration of the movement. The characteristic curves of the nominal robot model in Figure 3 and Figure 4 provide the positions in the Cartesian and angular coordinate systems, velocities, accelerations, and desired joint torques for the Delta manipulator. The parameters are calculated via inverse kinematics [2,3] and Equations (12)–(15), respectively.
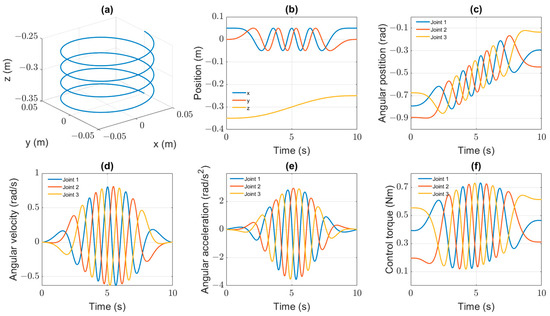
Figure 3.
Helix trajectory characteristics: position transitions in workspace (a), versus time (b); in joint space (c), angular velocities (d); angular accelerations (e); torques of delta manipulator (f).
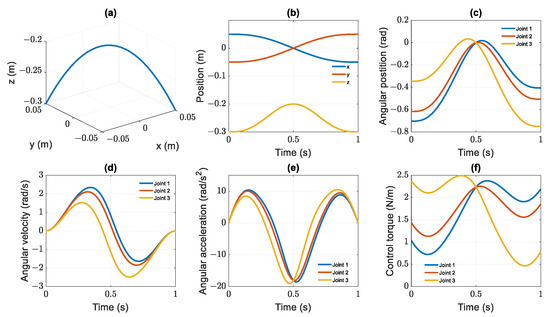
Figure 4.
Parabolic characteristics: position transition in workspace (a), versus time (b); in joint space (c), angular velocities (d); angular accelerations (e); torques of delta manipulator (f).
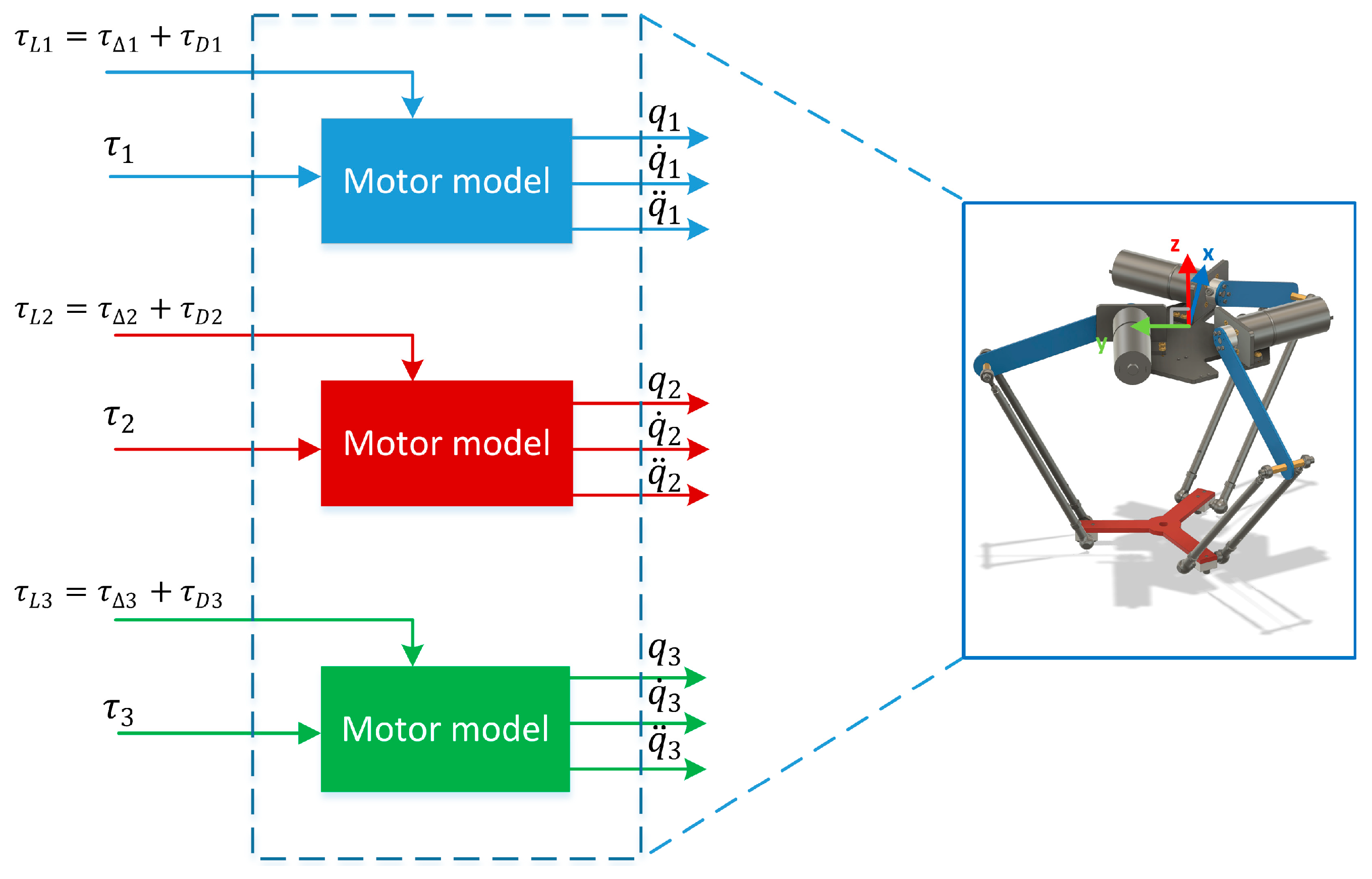
For simulating the dynamic Delta robot model, we use the robot model in Figure 5, which includes the three dynamic DC motors (2) and the Delta manipulator (15). We denote with as the load torque applied to the motor in (2). The proposed control scheme of the Delta robot is shown in Figure 6. For demonstrating the effectiveness and advantages of the proposed PDAFS scheme, the simulation results are instructive to compare with that of proportional derivative (PD), PD feedforward (PDFF) [11], PD sliding mode (PDSM) [13], and PDFS regulators. In particular, the performance quantity of the robot trajectory calculated by the i-th joint root mean square error (RMSE) formula, is expressed as:
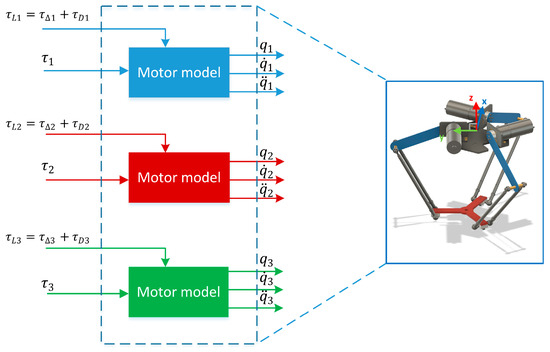
Figure 5.
The Delta robot model in this paper.
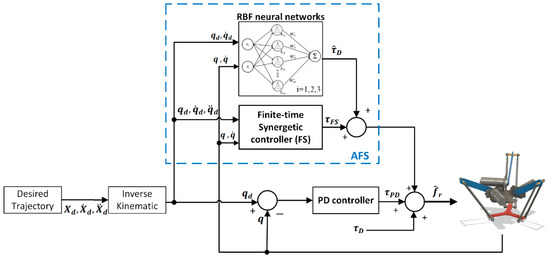
Figure 6.
The proposed control scheme.
The controller parameters are chosen constantly in the two cases. Moreover, the adaptability of RBF neural networks is evaluated by the assumption of external disturbance as (66) in the Delta robot model.
With the initial angular error vector such that in degrees. The desired trajectories for simulation use the information of helix and parabolic trajectory, as shown in Figure 3 and Figure 4, which is generalized by Table 4. The objective of these cases is to validate the effect of the initial condition position and different types of movements on the controllers’ ability.

Table 4.
The parameters of helix and parabolic trajectory for Delta robot.
The values in Table 1 and Table 2 are used as the nominal parameters of the Delta robot. The PDAFS parameters (42) in detail as (36)–(38) are selected as and ; the constraint in (25) takes the parameters as . Otherwise, the manifold in (23) takes . The RBF network has 7 nodes with the center vectors chosen as , . The initial neural network weights are selected as zeros. The updated weight law is given by (39) and (41) with the adaptation rate . These simulations are implemented with the interval time s. The parameters of the proposed controller and the compared controllers are generalized in Table 5.

Table 5.
The parameters of the proposed controller and compared controllers in simulation.
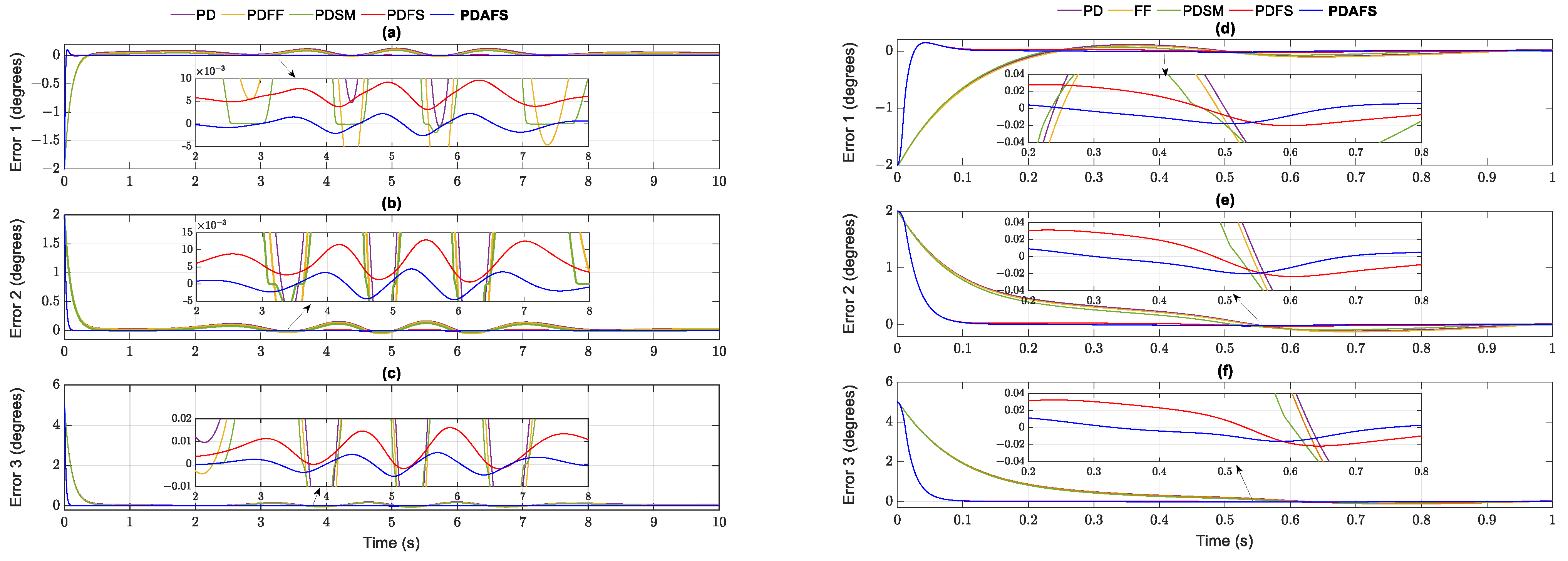
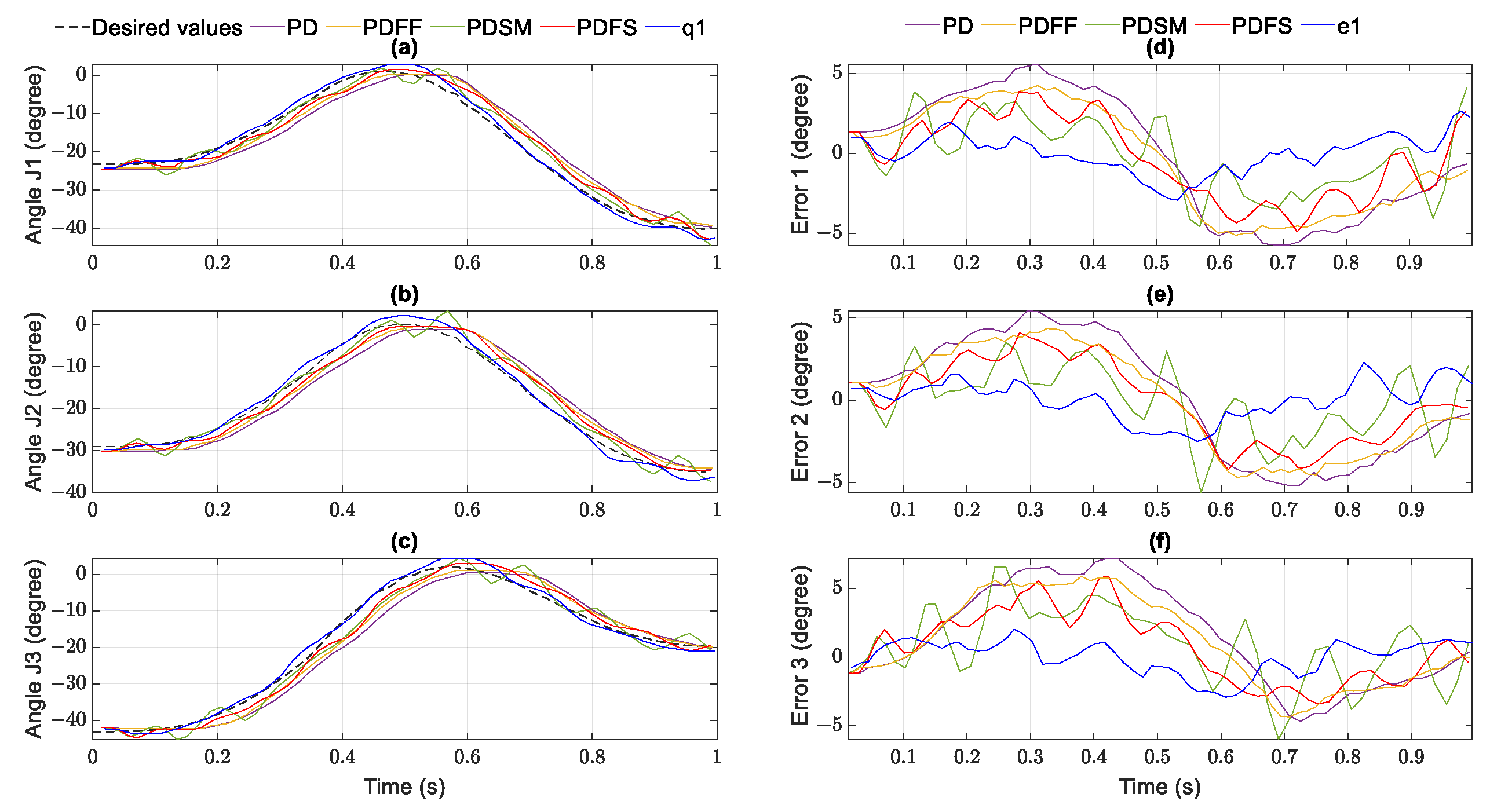
For validating the effectiveness of the PDAFS, the tracking errors in the joint space of the five controllers are illustrated and compared in Figure 7a–c for the helix case and Figure 7d–f for the pick and place object assumption. From the tracking error figures, all controllers provided stable trajectory tracking control. Whereas the PD has a large offset error stability, the dynamic model included in PDFF and PDSM provides a minor improvement in the tracking errors. Thanks to the switching function hidden in SM control, the tracking errors of PDSM are better than PDFF. However, PDFS and PDAFS give more accurate trajectory tracking control with finite time convergence . In particular, the error convergence of PDFS can achieve a small stable value but approximates the mean one as greater than zero. The proposed controller with the disturbance estimator provides remarkable error convergence to zero. The RMSE calculations are processed when the system becomes stable for all controllers. The RMSE of the PDFS and PDAFS controller in Table 6 and Table 7 is lower than the values of the others.
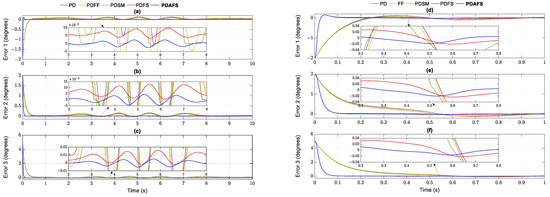
Figure 7.
Tracking error comparison among the controllers and PDAFS in the helix and parabolic simulation: (a) error of joint 1; (b) error of joint 2; (c) error of joint 3 in the helix case; (d) error of joint 1; (e) error of joint 2; (f) error of joint 3 in the parabolic case.

Table 6.
RMSE Comparison among the controllers and PDAFS in the Helix simulation.

Table 7.
RMSE Comparison among the controllers and PDAFS in the Parabolic simulation.
As can be seen, the increasing speed of joints causes the amplitude of the tracking errors to the peaks. This effort is a reason for the error increase caused by the higher maximum speed and acceleration in the parabolic trajectory compared to the helix trajectory. Furthermore, the corresponding maximum errors of the proposed controller are only and in degrees. Indeed, the PDAFS can achieve robust motion characteristics for the Delta robot in the simulation conditions.
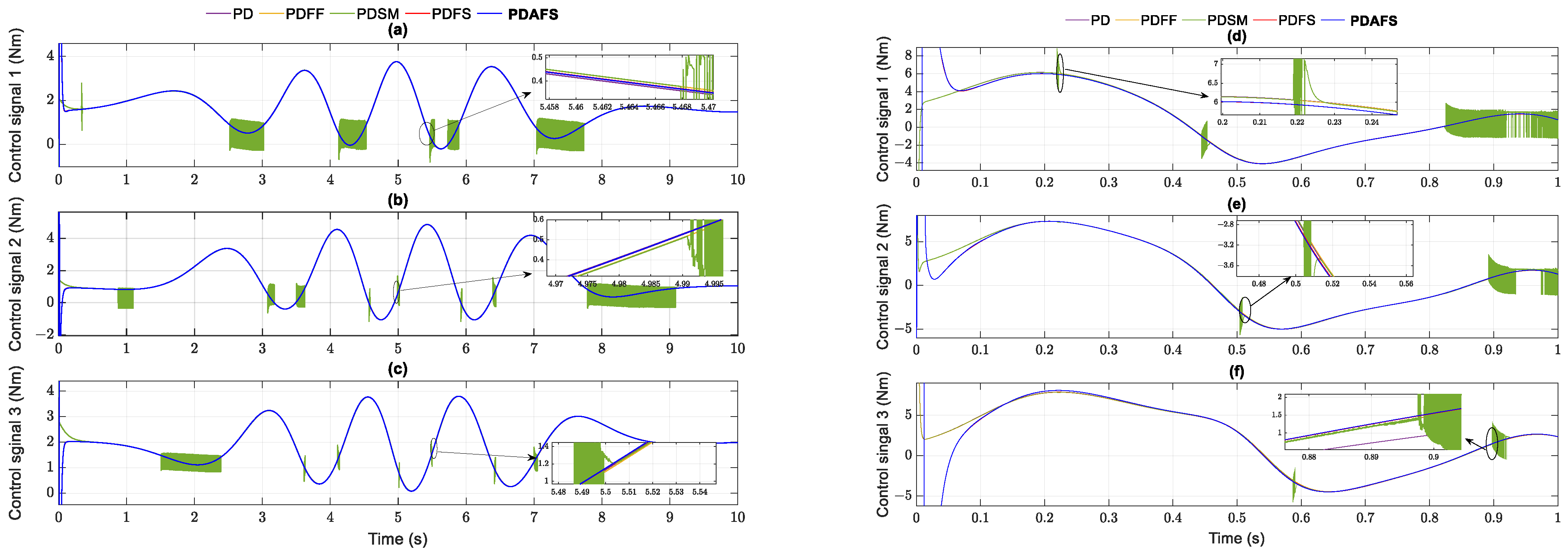
The control signal of the controllers is presented in Figure 8. In general, the control signals provided by the five controllers have the approximated transitions, whereas the controllers based on the synergetic method demonstrated the better strength signal of the control outline. The control signals of PDSM show the drawback with the chattering noises when they transit the errors on the manifold surface.
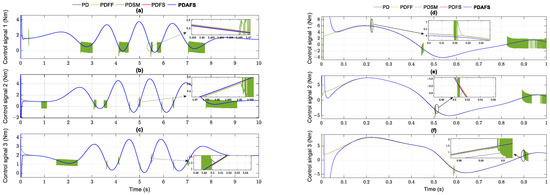
Figure 8.
Control signals generated by the controllers in the helix simulation and parabolic simulation: (a) control signal of joint 1; (b) control signal of joint 2; (c) control signal of joint 3 in the helix case; (d) error of joint 1; (e) error of joint 2; (f) error of joint 3 of the parabolic case.
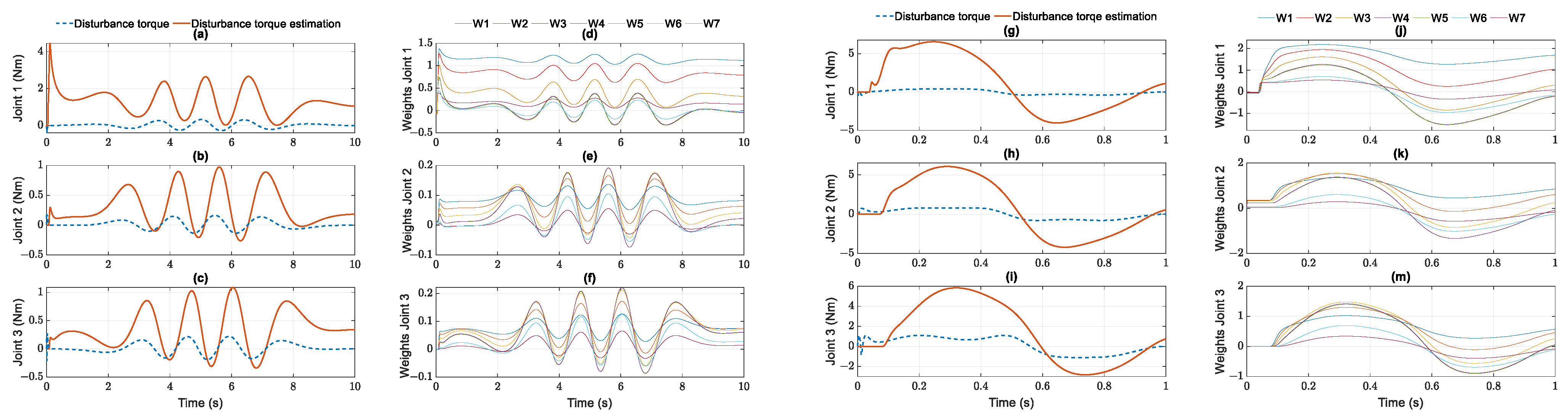
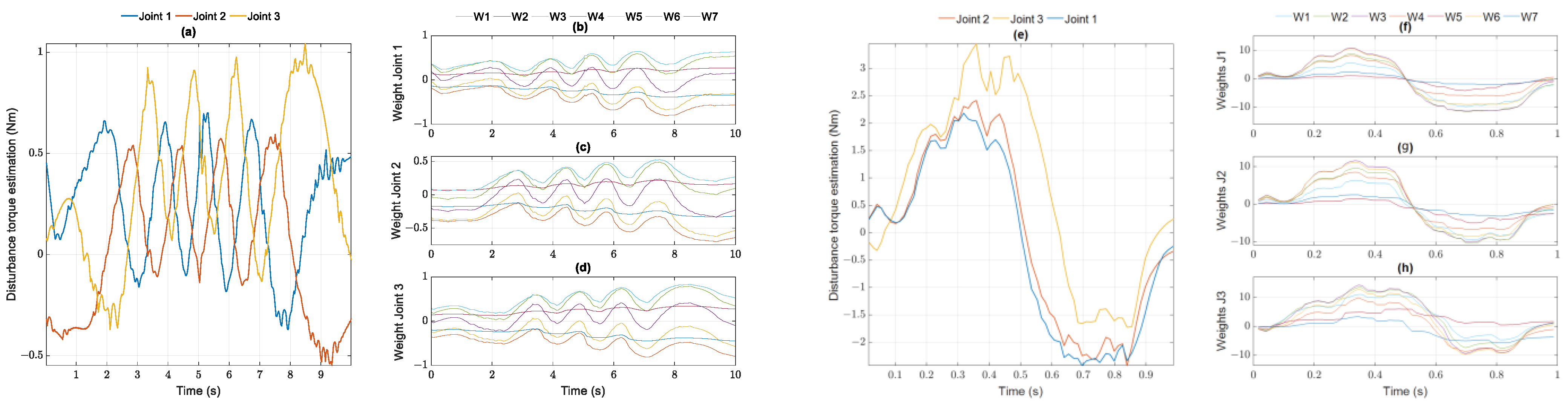
In Figure 9, it is noteworthy that the behavior of external torque estimation is affected by the added external disturbance torques. The effective action of RBF approximation leads the torque compensation to converge to the curves generated by the disturbance assumptions and the remaining torques of the unknown DC motor parameters. The uncertainty disturbance estimation in the control signals leads to the highest performance among the compared controllers in both study cases.
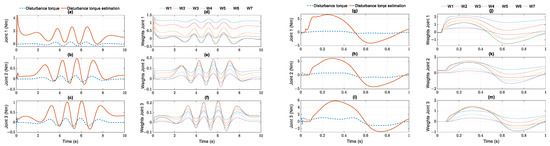
Figure 9.
Disturbance torques estimation and weight update of joints from RBF NNs in the helix and in parabolic simulation: disturbance torque and disturbance torque estimation of (a) joint 1; (b) joint 2; (c) joint 3; weights update of (d) joint 1; (e) joint 2; (f) joint 3 in helix case; disturbance torque and disturbance torque estimation of (g) joint 1; (h) joint 2; (i) joint 3; weights update of (j) joint 1; (k) joint 2; (m) joint 3 in parabolic case.
5. Experimental Results
5.1. Sytem Description
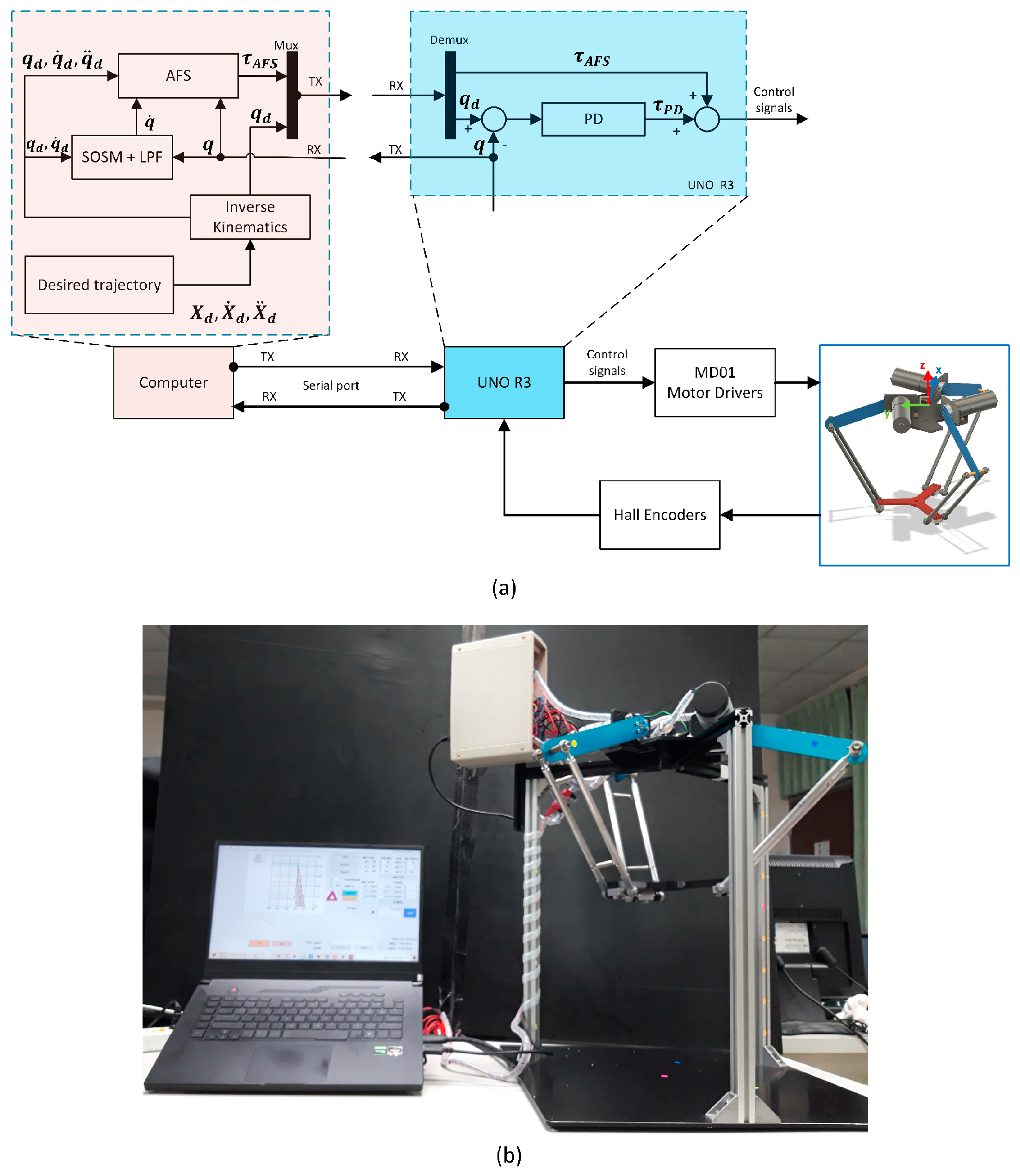
In this section, the proposed control scheme is performed and evaluated based on the hardware system in Figure 10a and the experimental setup in Figure 10b.
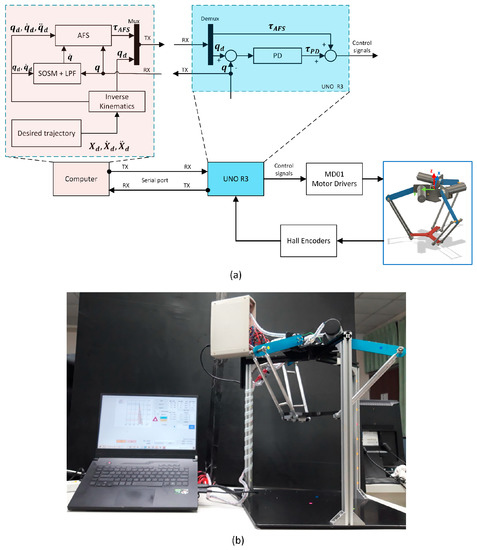
Figure 10.
The measuring system diagram (a) and experiment setup (b).
The robot system with the three motors is driven by the three MD01 high-power motor driver boards. The UNO R3 ATmage328 provides control signals to the motor drivers. For the stability assurance of the Delta robot, the PD controller is programmed directly on the UNO R3 and combines the AFS control signal from a computer to generate the control signal. On the DC motor, the active joint angles are acquired by the mounted three Hall magnetic encoders. The resolution of encoders is 0.367 degrees per pulse based on the specifications. Then, the UNO R3 sends the feedback position signal to the computer for torque calculation in the next iteration. The desired positions of the Delta robot and compensated torques for the tracking control are verified on the computer. After that, the data signals are transferred via the serial port to the microcontroller board. We programmed the AFS controller and GUI control with C# Visual Studio, and the algorithm runs on a Ryzen 7 4800 HS CPU, 16 GB Ram, and GeForce GTX 1660Ti graphic card. The estimated sampling rate in the real-time system is 0.5 ms on the UNO program. The interval time changes from 14 ms to 20 ms on the computer.
5.2. Velocity Estimation Results
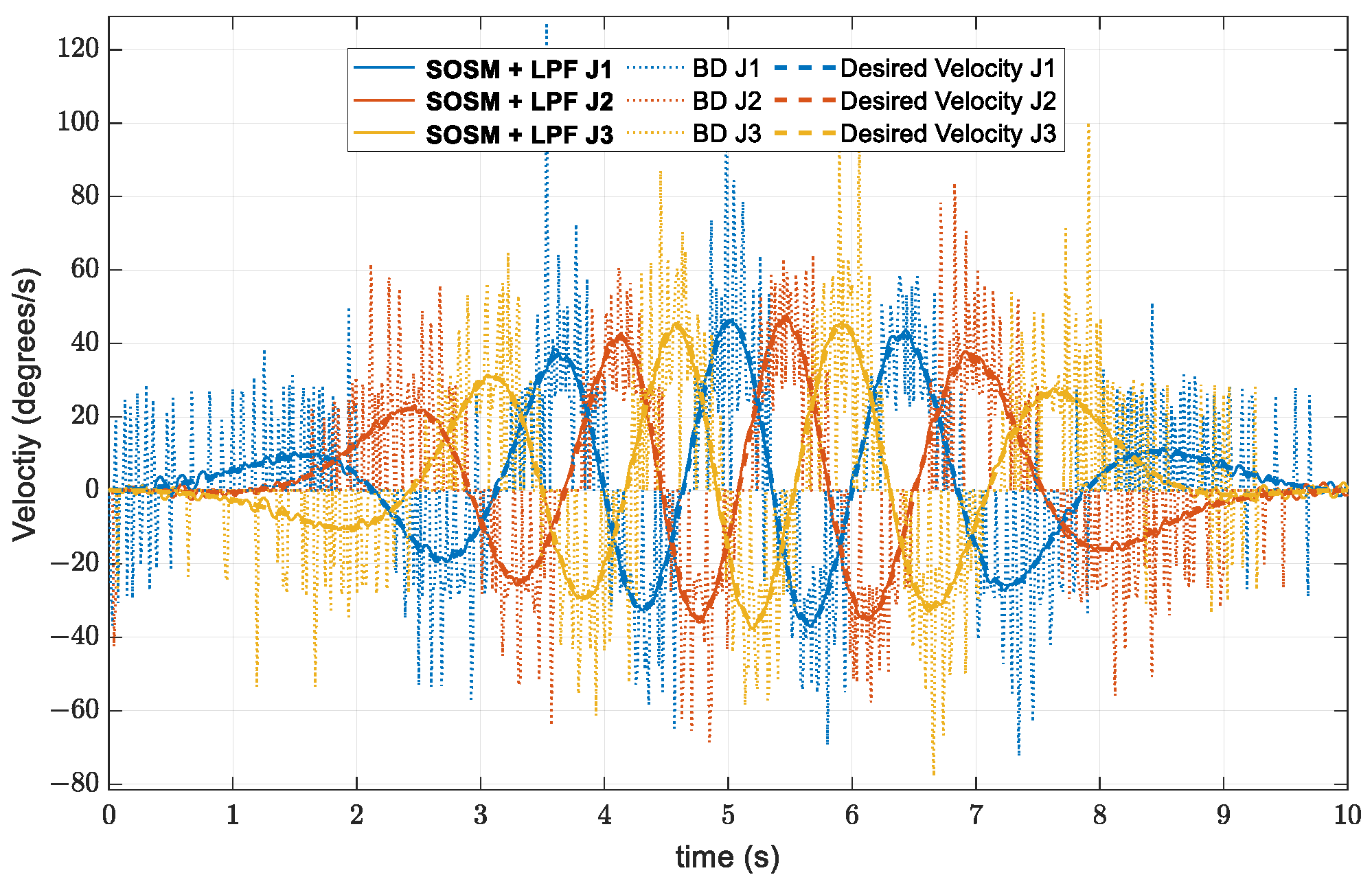
For validating the proposed velocity estimator, the desired helix trajectory function in Equations (62) and (64) is implemented in the system program. Based on the desired trajectory and convergence criterion information in [44,49], we can choose the suitable parameters of the estimator to ensure the error convergence condition and stability of the differentiator. Figure 11 presents the angular velocities estimation using BD and the proposed observer. In particular, the angular velocity estimation obtained by the BD technique shows the large spikes and discontinuous values around the desired velocity. In contrast, the SOSM with LPF estimator does not only give stable fitting values but also reacts with the spike velocities of the BD technique.
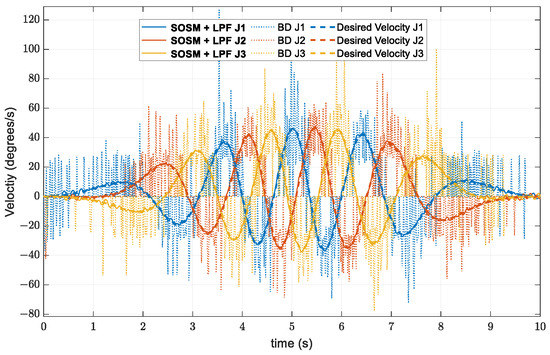
Figure 11.
Desired and estimated velocities using BD and SOSM + LPF techniques.
5.3. Case Study Results
From the system description above, it can be seen that the delay time on the computer is much more than the interval time in the simulation. The long time delay combined with the influence of the low-resolution encoders discretizes the control signal values. Thanks to the novel combination in PDAFS, the control signals are generated effectively for improving the Delta robot control performance. In this section, the two case experiments are conducted based on the desired trajectories in (62)–(64). These conditions can reduce unwanted vibration for the Delta robot in the practical environment. In the first case without external load, the performance of the proposed controller is validated based on the features of a robust adaptive controller to an unknown disturbance in the real robot. In the remaining case, an external load is attached to the traveling plate. The purpose of the experiment is to validate the adaptability of the PDAFS with an external disturbance. In our experiments, the PDAFS and the compared controller parameters are turned and presented in Table 8.

Table 8.
The parameters of the proposed controller and compared controllers in the experiment.
Case 1: Helix and parabolic trajectory without external load
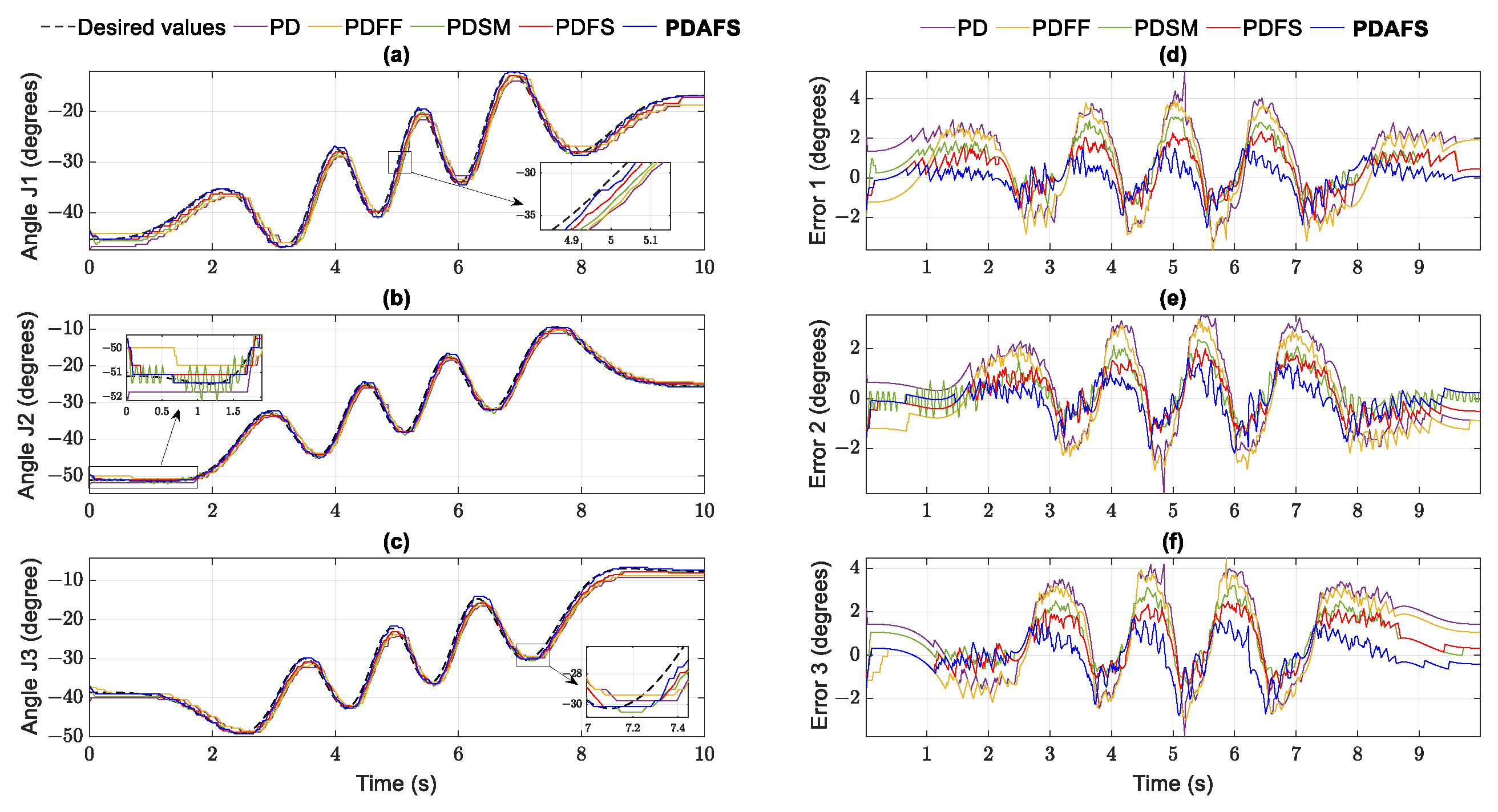
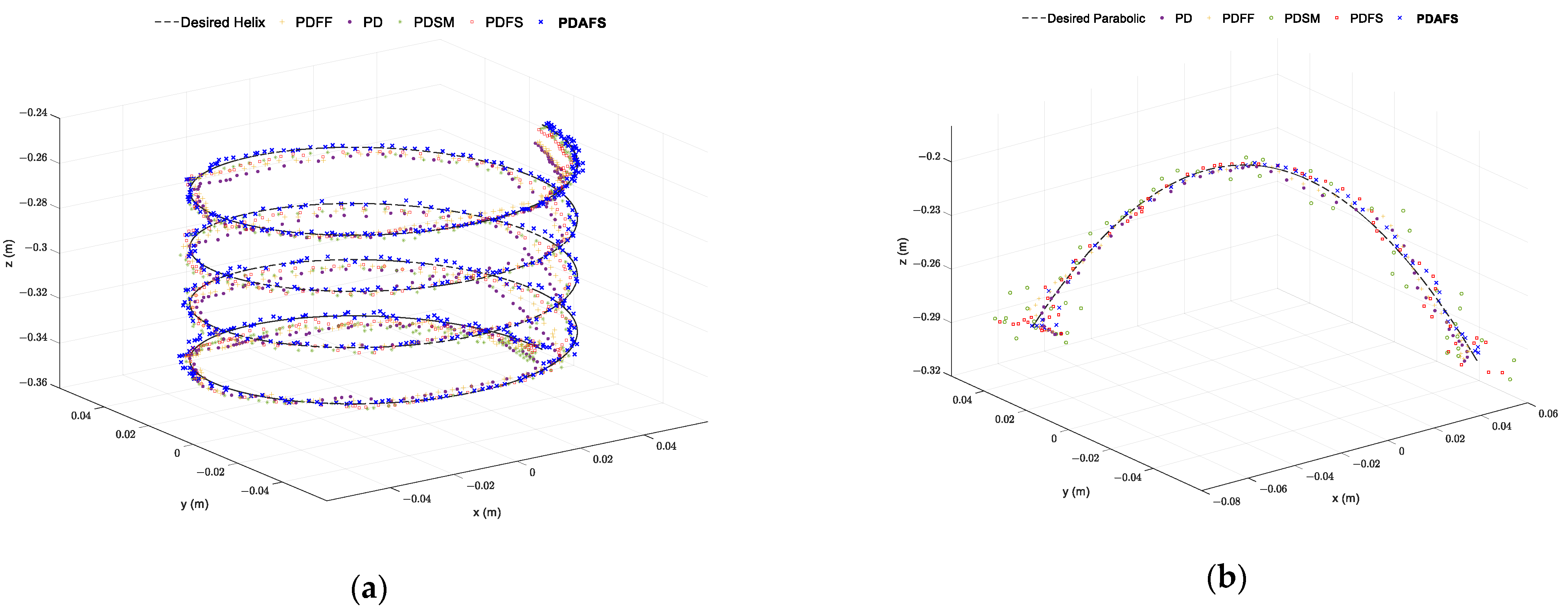
The experiment results of the position and errors in the helix and parabolic path are illustrated in Figure 12 and Figure 13. Figure 14 shows tracking performances in the workspace. The angular errors of PD are stable in the boundedness but non-zero convergent. While the PDFF errors are found with a minor improvement of values, the PDSM errors have some fluctuations in Figure 12b,e and Figure 13, but the SM is more stable than PDFF in RMSE comparison. Significantly, the tracking errors of the proposed controllers are under two ticks of the encoder resolution (0.367 degrees/tick) of the RMSE in the helix path and about 1.2 degrees in the second path, the smallest one among those of the other approaches. Moreover, the finite-time convergence property of both synergetic-based controllers is clearly present at the initial times in Figure 12b,d–f and Figure 13d–f. In addition, it can be shown that the effects of the interval time and quadrature encoders in the experiments lead the tracking errors to performance reductions in Table 9 and Table 10. The tracking signals from these figures show slight fluctuations compared to those in simulations.
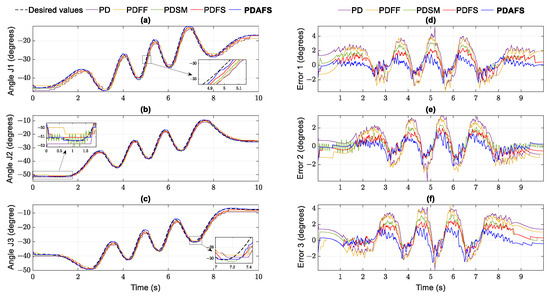
Figure 12.
Helix trajectory performance in joint space: (a) joint 1; (b) joint 2; (c) joint 3 and tracking error of joints: (d) joint 1; (e) joint 2; (f) joint 3 in experiment case 1.
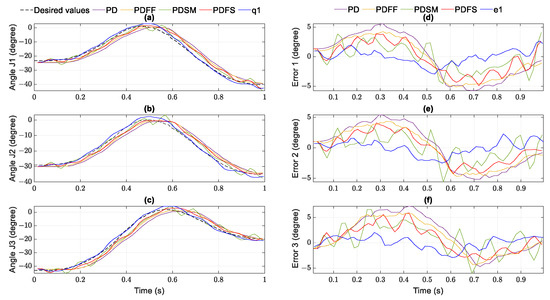
Figure 13.
Parabolic trajectory performance in joint space: (a) joint 1; (b) joint 2; (c) joint 3 and tracking error: (d) joint 1; (e) joint 2; (f) joint 3 in the experiment case 1.
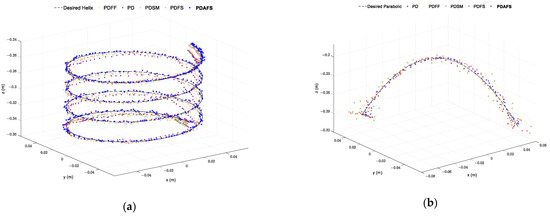
Figure 14.
Tracking performance in workspace of case 1: (a) Helix trajectory; (b) parabolic trajectory.

Table 9.
RMSE Comparison among the controllers and PDAFS in Helix Case 1.

Table 10.
RMSE Comparison among the controllers and PDAFS in Parabolic Case 1.
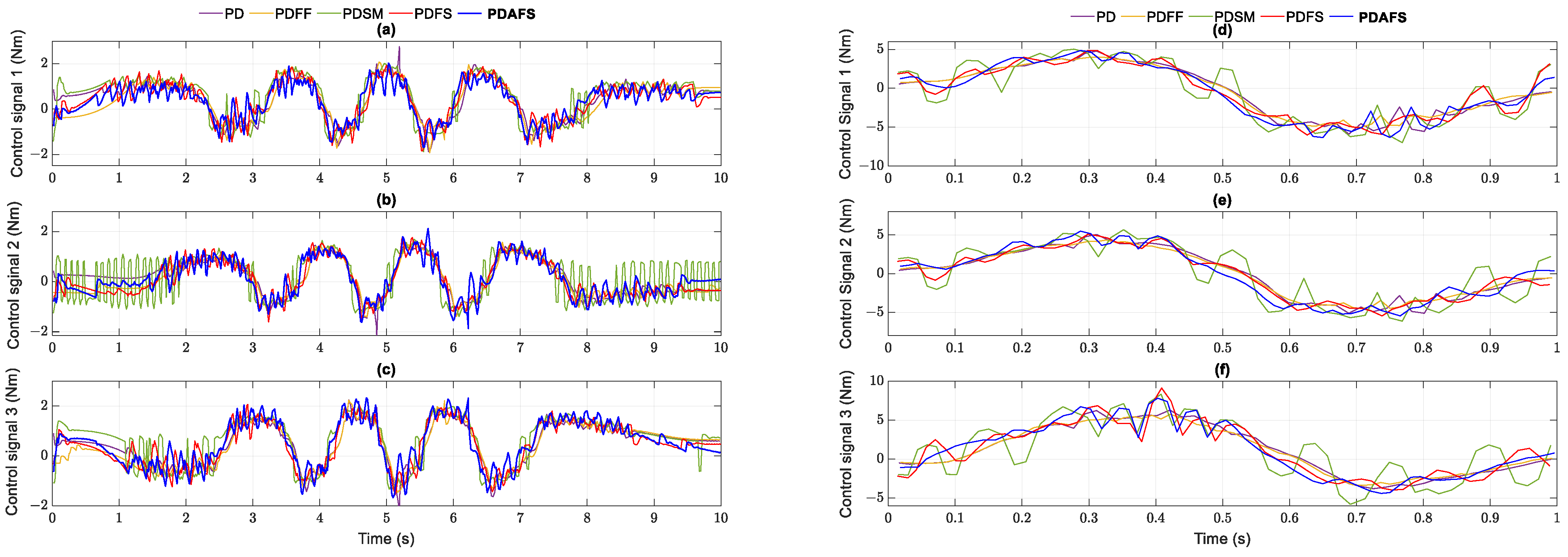
It is noteworthy that the behavior of the proposed controller in Figure 15 is very similar to the control torque signals produced by the remaining schemes. The transitions of velocity efforts to the tracking performance and control signals thus consolidating the analyses in the simulation section. Although the PDSM can guarantee stability, some mechanical stresses caused by the on-off signals are witnessed at nearly 1.5 degrees and over 5 degrees, significantly higher than the values of the PDAFS in Figure 12b and Figure 13, respectively. The vibrations are obtained clearly at the SM control signals in Figure 15. Meanwhile, the smoothing of control output from the synergetic algorithm demonstrates the advantages of chattering noise reduction in maintaining the attractiveness of the finite-time manifold constraint.
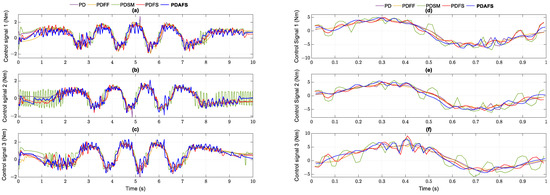
Figure 15.
Control signals generated by the controllers in the helix and parabolic of case 1: (a) joint 1; (b) joint 2; (c) joint 3 in the helix trajectory; (d) joint 1; (e) joint 2; (f) joint 3 in the parabolic trajectory.
Although the controller-based dynamic model can provide performance improvement in tracking control, PDFF improves the least values because of the lack of convergent functions in contrast to the robust PDSM or PDFS. The adaptive unknown torque approximation in the proposed approach reduces the effects of the disturbance, resulting in better dynamic performances than the other four methods. The updated weights in Figure 16 reflect the reaction with the dynamic disturbance changes and convergence to the constant values as soon as the system is in the stationary state. The power of torque estimations in the parabolic case witnesses a higher value than that of the helix case, so it is possible to adapt to the fast transitions of external disturbances and ensure the dynamic motions of the Delta parallel the robot.
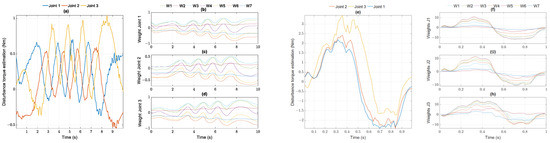
Figure 16.
Disturbance torque estimation (a) and weight update of (b) joint 1; (c) joint 2; (d) joint 3 from RBFNNs in helix case 1; disturbance torque estimation (e) and weight update of (f) joint 1; (g) joint 2; (h) joint 3 from RBFNNs in parabolic case 1.
Case 2: Helix trajectory with the external load
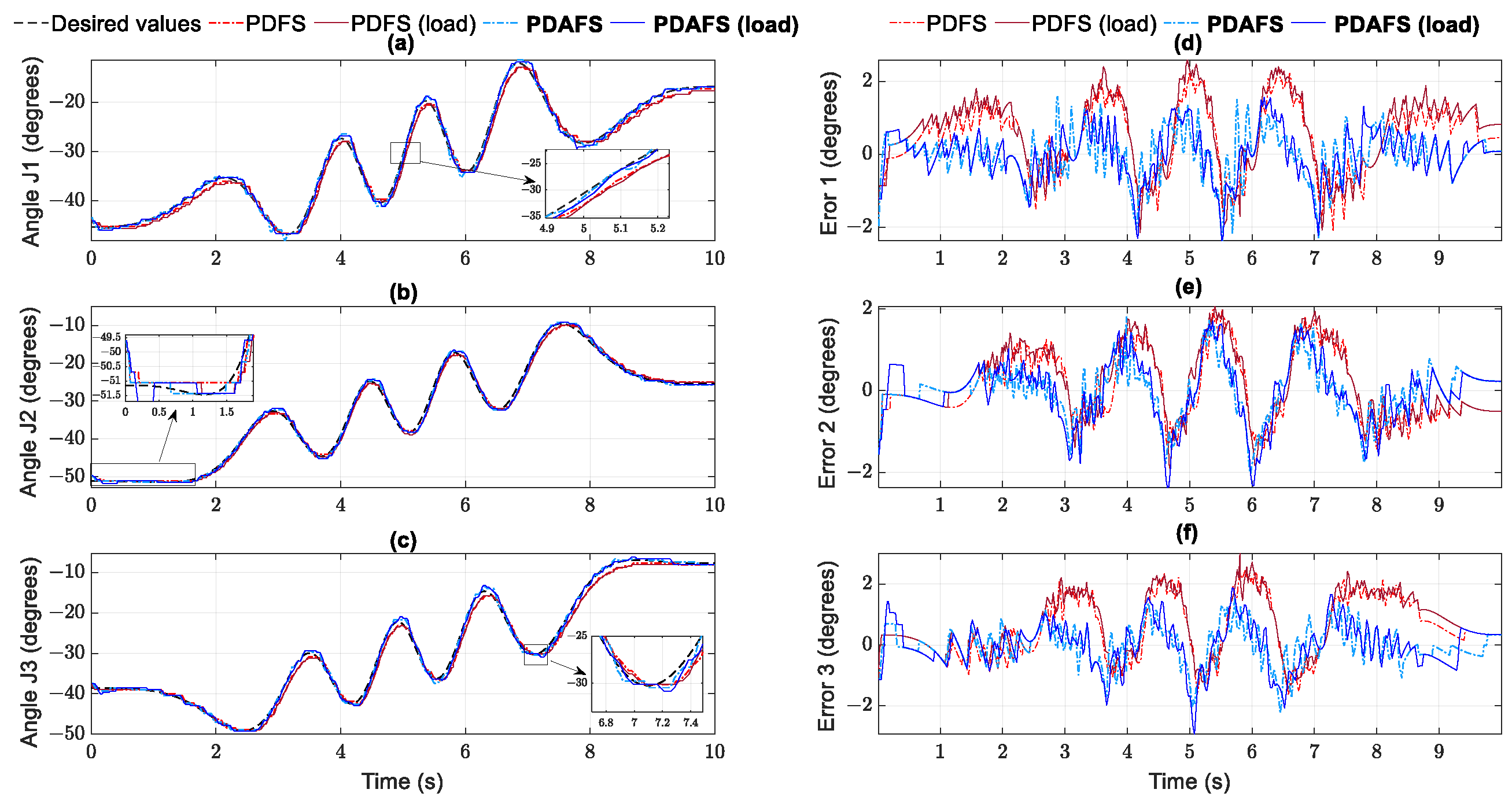
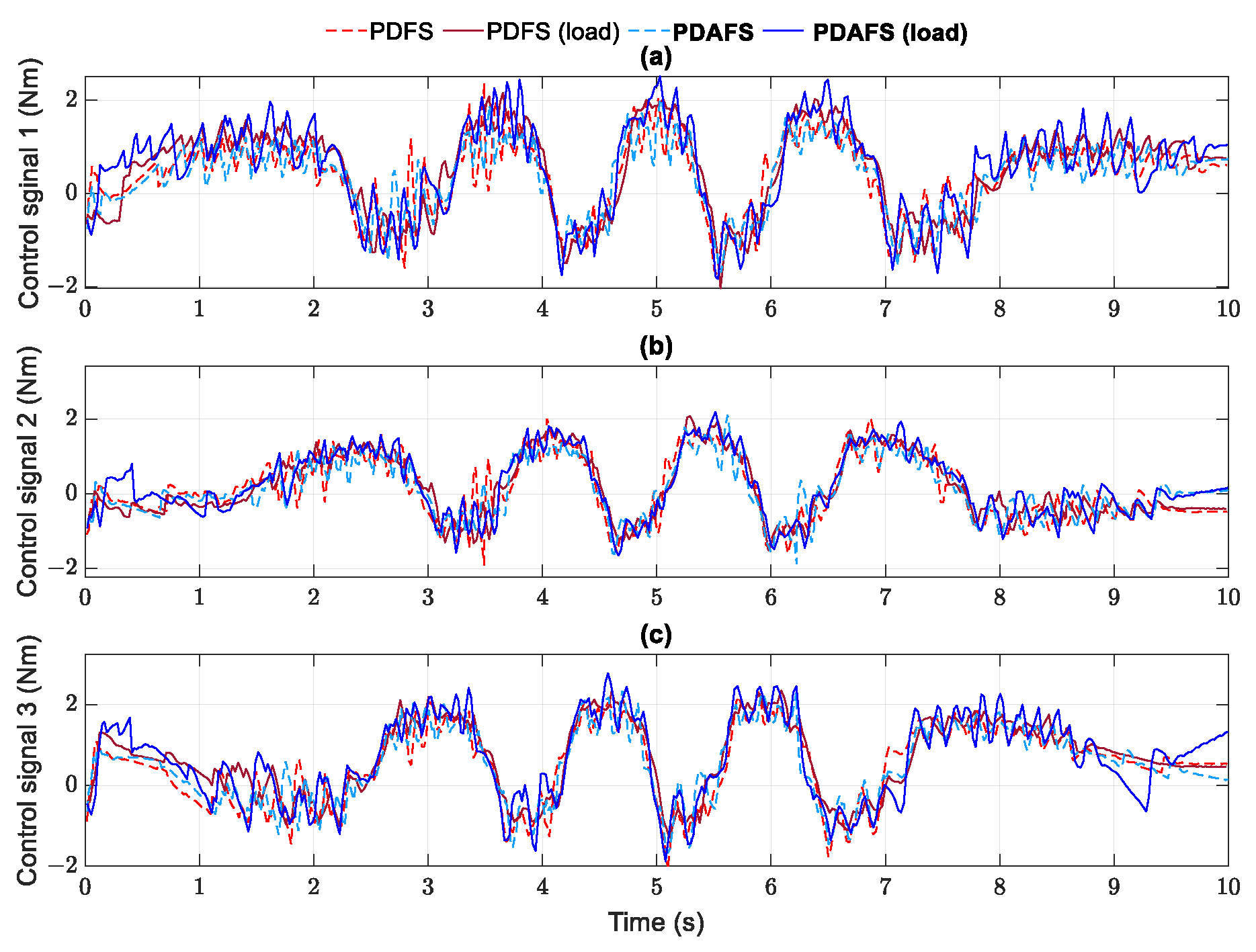
The productiveness of RBF networks in the proposed controller is further performed by an external load attached to the traveling plate of the Delta robot in helix operation. The objective is to evaluate the adaptation and robustness of the proposed approach against model parameter variation. In this case, the traveling plate has added an external object with 0.2 kg. Despite an increasingly small number of errors, the PDAFS algorithm successfully overwhelms the external disturbance to achieve a similar performance compared to others in the no-load case in Figure 17 and Figure 18 and Table 11. The control signal in Figure 18 tends to widen the boundary when the joint velocities increase the speed.
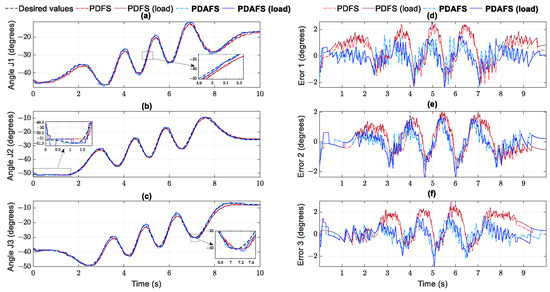
Figure 17.
Helix trajectory performance in joint space: (a) joint 1; (b) joint 2; (c) joint 3 and tracking error: (d) joint 1; (e) joint 2; (f) joint 3 in case 2.
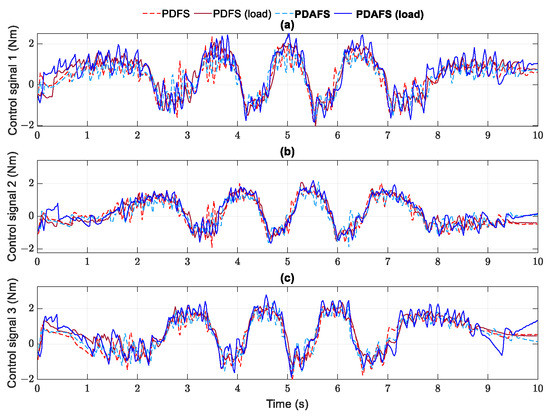
Figure 18.
Control signals generated by the PDFS and PDAFS in case 2: joint 1 (a), joint 2 (b), joint 3 (c).

Table 11.
RMSE Comparison among the controllers and PDAFS in Parabolic Case 1.
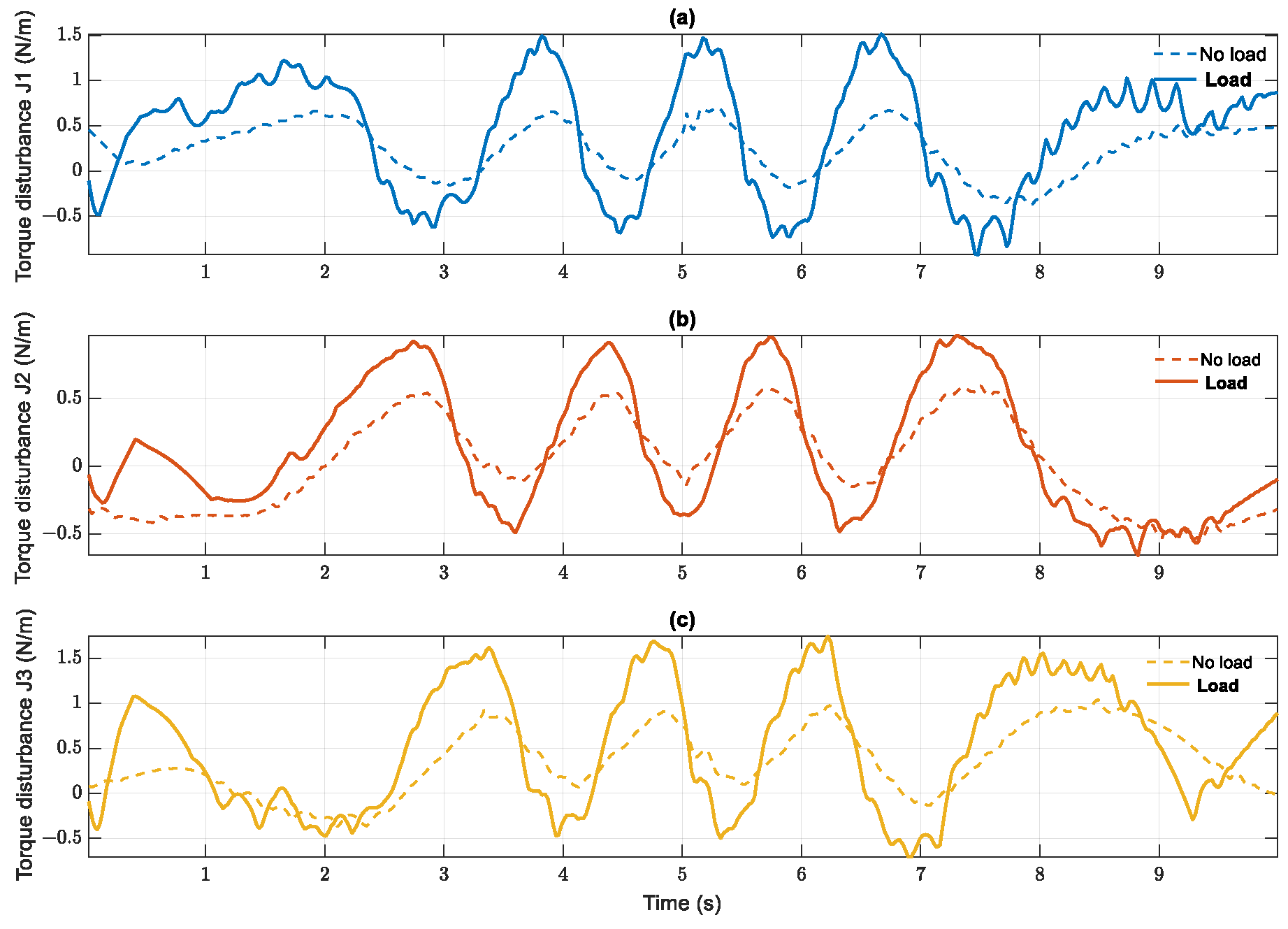
In addition, Figure 19 demonstrates a similar curve of disturbance torques from the RBF estimators. This action creates the reaction to the new disturbance of the control signal to catch up with the speed of tracking errors and guarantee a robust adaptive system. As a result, the adaptation of the proposed controller is validated based on disturbance torque estimation and compared to no-load cases. Despite the influence of the external disturbances generated by the joint frictions or uncertainty parameters, the PDAFS with RBF NNs attachment has presented more stability than the remaining synergetic control.
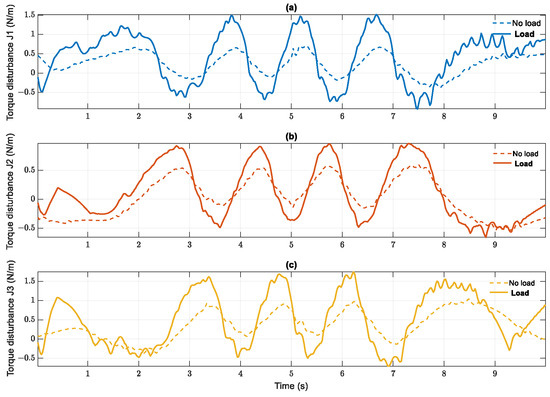
Figure 19.
Disturbance torque estimations comparison in case 2: joint 1 (a), joint 2 (b), joint 3 (c).
6. Conclusions
This paper addresses the issue of the robust adaptive control design using the synergetic theorem for the parallel Delta robot. The control structure has been developed by decoupling the objects’ control in the system, generated by the DC motors model, robot manipulator model, and generalized uncertain parameters. The stability of the robot system is proven through the Lyapunov stability method. As a result, the proposed controller performs better than the other controllers in the trajectory tracking tasks. The combination structure of the proposed controller can not only achieve the advantages of each algorithm but also overcome the limitations of the compared controller. The differences in the PDAFS control compared with the remaining algorithms in Table 12 shows the effectiveness and adaptive properties of the PDAFS in the presence of disturbance and reduction of the chattering phenomenon. Both simulation and experiment results for the Delta robot confirm all the mentioned benefits of the proposed controller.

Table 12.
The property comparison among the controllers and PDAFS.
Author Contributions
Conceptualization, P.-C.P. and Y.-L.K.; methodology, P.-C.P.; software, P.-C.P.; validation, Y.-L.K.; formal analysis, P.-C.P.; investigation, P.-C.P.; resources, Y.-L.K.; data curation, P.-C.P.; writing—original draft preparation, P.-C.P.; writing—review and editing, Y.-L.K.; supervision, Y.-L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology, Taiwan, grant number MOST 109-2221-E-011-068.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported in part by the Ministry of Science and Technology, Taiwan, under MOST 109-2221-E-011-068.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taghirad, H.D. Parallel Robots, 1st ed.; CRC Press: Cham, Switzerland, 2013; ISBN 9780429097454. [Google Scholar]
- Tsai, L.-W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; John Wiley & Sons, Inc.: New York, NY, USA, 1999; ISBN 978-0-471-32593-2. [Google Scholar]
- López, M.; Castillo, E.; García, G.; Bashir, A. Delta Robot: Inverse, Direct, and Intermediate Jacobians. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 103–109. [Google Scholar] [CrossRef]
- Gritsenko, I.; Seidakhmet, A.; Abduraimov, A.; Gritsenko, P.; Bekbaganbetov, A. Delta Robot Forward Kinematics Method with One Root. In Proceedings of the 2017 International Conference on Robotics and Automation Sciences (ICRAS), Hong Kong, China, 26–29 August 2017; pp. 39–42. [Google Scholar]
- Rosquist, K. Modelling and Control of a Parallel Kinematic Robot; Lund University: Lund, Sweden, 2013. [Google Scholar]
- Kuo, Y.L.; Huang, P.Y. Experimental and Simulation Studies of Motion Control of a Delta Robot Using a Model-Based Approach. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417738738. [Google Scholar] [CrossRef]
- Bortoff, S.A. Object-Oriented Modeling and Control of Delta Robots. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications, CCTA 2018, Copenhagen, Denmark, 21–24 August 2018; pp. 251–258. [Google Scholar] [CrossRef]
- Carabin, G.; Scalera, L.; Wongratanaphisan, T.; Vidoni, R. An Energy-Efficient Approach for 3D Printing with a Linear Delta Robot Equipped with Optimal Springs. Robot. Comput.-Integr. Manuf. 2021, 67, 102045. [Google Scholar] [CrossRef]
- Scalera, L.; Carabin, G.; Vidoni, R.; Wongratanaphisan, T. Energy Efficiency in a 4-Dof Parallel Robot Featuring Compliant Elements. Int. J. Mech. Control 2019, 20, 49–57. [Google Scholar]
- Codourey, A. Dynamic Modelling and Mass Matrix Evaluation of the DELTA Parallel Robot for Axes Decoupling Control. IEEE Int. Conf. Intell. Robot. Syst. 1996, 3, 1211–1218. [Google Scholar] [CrossRef]
- Codourey, A. Dynamic Modeling of Parallel Robots for Computed-Torque Control Implementation. Int. J. Robot. Res. 1998, 17, 1325–1336. [Google Scholar] [CrossRef]
- Song, X.; Zhao, Y.; Jin, L.; Zhang, P.; Chen, C. Dynamic Feedforward Control in Decoupling Space for a Four-Degree-of-Freedom Parallel Robot. Int. J. Adv. Robot. Syst. 2019, 16, 1729881418820451. [Google Scholar] [CrossRef]
- Su, T.; Liang, X.; He, G.; Zhao, Q.; Zhao, L. Robust Trajectory Tracking of Delta Parallel Robot Using Sliding Mode Control. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 508–512. [Google Scholar]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Kolesnikov, A.A. Introduction of Synergetic Control. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3013–3016. [Google Scholar]
- Fareh, R.; Khadraoui, S.; Baziyad, M.; Bettayeb, M. Synergetic Workspace Tracking Control for 4-DOF Robot Manipulator. In Proceedings of the 12th International Conference on Computer and Automation Engineering (ICCAE), Sydney, NSW, Australia, 14–16 February 2020; pp. 189–193. [Google Scholar] [CrossRef]
- Nusawardhana; Zak, S.H.; Crossley, W.A. Nonlinear Synergetic Optimal Controllers. J. Guid. Control Dyn. 2007, 30, 1134–1147. [Google Scholar] [CrossRef][Green Version]
- Kuz’menko, A.A. Synchronous Generator Nonlinear Excitation System: Synergetic Sliding Mode Control. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–5. [Google Scholar]
- Liu, C.-H.; Hsiao, M.-Y. A Finite Time Synergetic Control Scheme for Robot Manipulators. Comput. Math. Appl. 2012, 64, 1163–1169. [Google Scholar] [CrossRef]
- Zhai, S.; Chen, Q.; Tang, X. Finite-Time Synergetic Control of Mechanical System Based on Model-Free Friction Compensation. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2015; Volume 337, pp. 275–284. ISBN 9783662464625. [Google Scholar]
- Kondratiev, I.; Nikiforov, A.; Veselov, G.; Kolesnikov, A. Synergetic Control for Induction Motor Based Wheel-Drive System. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–7. [Google Scholar]
- Kanchanaharuthai, A.; Mujjalinvimut, E. Application of Adaptive Synergetic Control to Power Systems with Superconducting Magnetic Energy Storage System. Int. J. Innov. Comput. Inf. Control 2017, 13, 1873–1885. [Google Scholar]
- Veselov, G.E.; Sclyarov, A.A. Synergetic Approach to Unmanned Air Vehicle Control with “Attractor-Repeller” Strategy of Nondeterministic Obstacles Avoidance. In Proceedings of the CHAOS 2013—6th Chaotic Modeling and Simulation International Conference, Istanbul, Turkey, 11–14 June 2013; pp. 713–726. [Google Scholar]
- Boudjedir, C.E.; Boukhetala, D. Adaptive Robust Iterative Learning Control with Application to a Delta Robot. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 207–221. [Google Scholar] [CrossRef]
- Boudjedir, C.E.; Boukhetala, D.; Bouri, M. Nonlinear PD plus Sliding Mode Control with Application to a Parallel Delta Robot. J. Electr. Eng. 2018, 69, 329–336. [Google Scholar] [CrossRef]
- Boudjedir, C.E.; Bouri, M.; Boukhetala, D. Model-Free Iterative Learning Control with Nonrepetitive Trajectories for Second-Order MIMO Nonlinear Systems—Application to a Delta Robot. IEEE Trans. Ind. Electron. 2021, 68, 7433–7443. [Google Scholar] [CrossRef]
- Shang, W.W.; Cong, S.; Ge, Y. Adaptive Computed Torque Control for a Parallel Manipulator with Redundant Actuation. Robotica 2012, 30, 457–466. [Google Scholar] [CrossRef]
- Zhao, R.; Wu, L.; Chen, Y.H. Robust Control for Nonlinear Delta Parallel Robot with Uncertainty: An Online Estimation Approach. IEEE Access 2020, 8, 97604–97617. [Google Scholar] [CrossRef]
- Castaneda, L.A.; Luviano-Juarez, A.; Chairez, I. Robust Trajectory Tracking of a Delta Robot Through Adaptive Active Disturbance Rejection Control. IEEE Trans. Control Syst. Technol. 2015, 23, 1387–1398. [Google Scholar] [CrossRef]
- Linda, O.; Manic, M. Uncertainty-Robust Design of Interval Type-2 Fuzzy Logic Controller for Delta Parallel Robot. IEEE Trans. Ind. Inform. 2011, 7, 661–670. [Google Scholar] [CrossRef]
- Rebai, A.; Guesmi, K.; Hemici, B. Adaptive Fuzzy Synergetic Control for Nonlinear Hysteretic Systems. Nonlinear Dyn. 2016, 86, 1445–1454. [Google Scholar] [CrossRef]
- Escorcia-Hernández, J.M.; Aguilar-Sierra, H.; Aguilar-Mejia, O.; Chemori, A.; Arroyo-Núñez, J.H. A New Adaptive RISE Feedforward Approach Based on Associative Memory Neural Networks for the Control of PKMs. J. Intell. Robot. Syst. 2020, 100, 827–847. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K. Intelligent Friction Modeling and Compensation Using Neural Network Approximations. IEEE Trans. Ind. Electron. 2012, 59, 3342–3349. [Google Scholar] [CrossRef]
- Jabbari Asl, H.; Narikiyo, T.; Kawanishi, M. Neural Network-Based Bounded Control of Robotic Exoskeletons without Velocity Measurements. Control Eng. Pract. 2018, 80, 94–104. [Google Scholar] [CrossRef]
- Reg, L. DC-Motor Modelling and Parameter Identification; Automation Control, Linkoping University: Linkoping, Sweden, 2017. [Google Scholar]
- Urrea Onate, C.; Kern Molina, J. Characterization, Simulation and Implementation of a New Dynamic Model for a DC Servomotor. IEEE Lat. Am. Trans. 2014, 12, 997–1004. [Google Scholar] [CrossRef]
- Turevskiy, A. Estimating DC Motor Parameters. Available online: http://www.mathworks.com/videos/estimating-dc-motor-parameters-97057.html (accessed on 15 March 2020).
- Moulay, E.; Dambrine, M.; Yeganefar, N.; Perruquetti, W. Finite-Time Stability and Stabilization of Time-Delay Systems. Syst. Control Lett. 2008, 57, 561–566. [Google Scholar] [CrossRef]
- Lee, C.-C.; Chung, P.-C.; Tsai, J.-R.; Chang, C.-I. Robust Radial Basis Function Neural Networks. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1999, 29, 674–685. [Google Scholar] [CrossRef]
- Segal, R.; Kothari, M.L.; Madnani, S. Radial Basis Function (RBF) Network Adaptive Power System Stabilizer. IEEE Trans. Power Syst. 2000, 15, 722–727. [Google Scholar] [CrossRef]
- Slotine, J.; Weiping, L. Applied Nonlinear Control; Prentice Hall, Pearson: Hoboken, NJ, USA, 1991; ISBN 0130408905. [Google Scholar]
- Shang, W.W.; Cong, S.; Li, Z.X.; Jiang, S.L. Augmented Nonlinear PD Controller for a Redundantly Actuated Parallel Manipulator. Adv. Robot. 2009, 23, 1725–1742. [Google Scholar] [CrossRef]
- Safaric, R.; Jezernik, K. Trajectory Tracking Neural Network Controller for a Robot Mechanism and Lyapunov Theory of Stability. In Proceedings of the Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994; Volume 1, pp. 626–633. [Google Scholar]
- Levant, A. Robust Exact Differentiation via Sliding Mode Technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite Time Fault Tolerant Control for Robot Manipulators Using Time Delay Estimation and Continuous Nonsingular Fast Terminal Sliding Mode Control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef]
- Ghanes, M.; Barbot, J.P.; Fridman, L.; Levant, A. A Second Order Sliding Mode Differentiator with a Variable Exponent. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 3300–3305. [Google Scholar]
- Slotine, J.J.E.; Hedrick, J.K.; Misawa, E.A. On Sliding Observers for Nonlinear Systems. J. Dyn. Syst. Meas. Control Trans. ASME 1987, 109, 245–252. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Lee, T.H. Sliding Mode Observer-Based Fault-Tolerant Secondary Control of Microgrids. Electronics 2020, 9, 1417. [Google Scholar] [CrossRef]
- Levant, A. Sliding Order and Sliding Accuracy in Sliding Mode Control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).