Decision-Tree-Based Horizontal Fragmentation Method for Data Warehouses

Abstract

Data warehousing gives frameworks and means for enterprise administrators to methodically prepare, comprehend, and utilize the data to improve strategic decision-making skills. One of the principal challenges to data warehouse designers is fragmentation. Currently, several fragmentation approaches for data warehouses have been developed since this technique can decrease the OLAP (online analytical processing) query response time and it provides considerable benefits in table loading and maintenance tasks. In this paper, a horizontal fragmentation method, called FTree, that uses decision trees to fragment data warehouses is presented to take advantage of the effectiveness that this technique provides in classification. FTree determines the OLAP queries with major relevance, evaluates the predicates found in the workload, and according to this, builds the decision tree to select the horizontal fragmentation scheme. To verify that the design is correct, the SSB (star schema benchmark) was used in the first instance; later, a tourist data warehouse was built, and the fragmentation method was tested on it. The results of the experiments proved the efficacy of the method.

1. Introduction

Fragmentation is a design technique in distributed databases that divides database tables into fragments and deals with them like separate database objects; three alternatives exist for this purpose: horizontal, vertical, and hybrid fragmentation. The foundation of the first type of partitioning is the select operator because the selection predicates define the horizontal partitioning; in contrast, the vertical one is carried out by applying the project operator. Hybrid fragmentation involves combining horizontal and vertical fragmentation [1].

A data warehouse (DW) is an integrated, nonvolatile, time-changeable, and subject-oriented data repository that aids in the decision-making activity of the administration. Data warehousing gives frameworks and means for enterprise administrators to methodically prepare, comprehend, and utilize the data to make strategic decisions. DW systems are beneficial assets in the current dynamic and competitive world. Therefore, recently, several corporations (e.g., the Assistance Publique-Hôpitaux de Paris (AP-HP) [2], the National Aeronautics and Space Administration (NASA) Ames Aviation Systems Division [3], John Deere, and DowDuPont [4]) have invested a lot of money in building company-wide data warehouses. The most accepted data model for the development of data warehouses is the multidimensional model, commonly presented as a star, a fact constellation, or a snowflake schema. The star schema is the most conventional modeling paradigm, where the DW is principally composed of a considerably central table (fact table) that contains the volume of the data with no redundancy, and a group of smaller auxiliary tables (dimension tables), one for every single dimension [5]. The main features of data warehouses are (1) their data complexity because of the presence of hierarchy attributes, (2) a high amount of data, and (3) the query complexity due to the presence of joins and aggregations [6].

For a few decades, various fragmentation methods for DW have been presented since this technique has the advantage of minimizing OLAP (online analytical processing) query response time as well as having important benefits in the operations of table loading and maintenance [7]. DW fragmentation is more complex and challenging compared to object-oriented and relational database partitioning due to the variety of options for fragmenting a star schema. In a DW, either the dimension tables, the fact table, or both can be fragmented. Most of the proposed work focuses on horizontal fragmentation because fact tables typically have a high data volume, i.e., they are about millions of tuples [8], and queries usually only require a subset of them. Horizontal fragmentation typically divides DW tables into partitions of tuples according to the workload.

The main advantages of decision trees are that their construction does not require domain expertise or configuration, they deal with multidimensional data, the steps of learning and classification involved in decision tree induction are uncomplicated and quick, and they achieve adequate performance. Furthermore, decision trees are important in classification because they permit obtaining pure partitions (tuple subsets) in a data set utilizing measures including the Gini index, information gain, and gain ratio. Most decision tree induction algorithms have a top-down approach; the decision tree is recursively built by dividing the training data into smaller subsets. The representation of knowledge learned in the shape of a tree is intuitive and usually easy for humans to assimilate; in addition, decision tree classifiers have good precision [9].

Until the time of analyzing the state of the art for this paper, the development of a horizontal fragmentation algorithm for data warehouses that uses decision trees has not been published. The use of a decision tree to horizontally fragment a relational database considering OLTP (online transaction processing) workloads has been reported in [10]; however, [10] does not take into account the characteristics of a DW such as the multidimensional model and OLAP queries. This article describes a horizontal fragmentation method, called FTree, which is focused on obtaining fragmentation schemes that decrease the OLAP query execution cost. To achieve this, first, a comprehensive analysis of the literature about existing horizontal fragmentation methods for DW was realized, and later, FTree was introduced. FTree begins selecting the relevant decision support queries by examining the predicates employed by the workload, and then according to these, it builds the decision tree to choose the horizontal fragmentation scheme. To verify the effectiveness of FTree, the SSB (star schema benchmark) was used in the first instance; later, a tourist data warehouse was developed, and the fragmentation method was tested on this, achieving results that prove the benefit obtained by FTree. Subsequently, some experiments were carried out to compare the horizontal fragmentation scheme (HFS) obtained by FTree with J48 versus the scheme selected by other classifiers; for this comparison, a cost model was used considering that the cost of a decision support query q_i consists of the amount of irrelevant data accessed (ITC) as well as the volume of relevant data located in other fragments (RTC).

Therefore, the contributions of this paper are two-fold: first, a new horizontal fragmentation method for DW is proposed, and second, a cost model to evaluate horizontal fragmentation schemes is introduced.

This paper is made up of the following parts: Section 2 provides the analysis of different works about horizontal fragmentation techniques. Section 3 introduces FTree. Section 4 relates the findings obtained in the development of the fragmentation method and discussion. Finally, Section 5 addresses future work and gives the conclusion.

2. State of the Art of Horizontal Fragmentation Methods

In the literature, some algorithms have been developed to address the challenge of choosing a horizontal fragmentation scheme from a given DW. They are classified as minterm generation algorithms [1], affinity-based algorithms, cost-model-driven algorithms, and data-mining-based algorithms, to mention a few [11]. This section presents some related horizontal fragmentation (HF) techniques and their main characteristics.

The approach proposed in [12] presented a method that uses linear programming to resolve the NP-hard problem of finding an HF scheme in a relational DW. The problem was determined in two concurrent objectives, named: the I/O amount required to answer the queries, and the number of partitions produced to recognize the optimal solutions matched to the Pareto dominance concept.

According to [13], although many techniques have been proposed to speed up data access in the DW, they cannot be applied directly to the object-relational DW (ORDW), since it involves abstract data types for complex data stored in an object format. Therefore, the authors proposed a partition-based approach to efficiently access data in an ORDW. The approach has three steps: (1) obtaining minterm predicates, (2) partitioning the object-relational scheme by derived horizontal partitioning, and (3) fragment selection based on DW properties and query trends.

In contrast, in [14], to obtain fewer fragments and improve the performance of OLAP queries, Kechar and Nait-Bahloul fragmented horizontally just the fact table considering the selectivity of the predicates, their occurrence amount, and their access frequencies. They proposed to split only the fact relation without using the primary HF of the dimension relations. Later, in [15], the authors introduced an improved version of their approach presented in [14].

A technique established on frequent itemset mining was proposed in [16] towards partition, bucket, and sort tables (PBSTs) into a big DW with the more common predicate attributes in the workload. This method considered the quantity of the relation attributes, data skew, and the physical features of the cluster nodes. The authors employed a hash-partitioning approach, which horizontally splits all the tables of a big relational DW, utilizing workload-based PBST methods.

Parchas et al. [17] focused on the “Dist-Key” which is a horizontal partitioning type widely used in DW systems on the market. This kind of horizontal partitioning divides the tuples of a table by using a hash function on the values of a particular attribute identified as the distribution key. Consequently, the proposed strategy tries to reduce the query network cost by choosing the optimal attribute to hash-distribute every DW relation. They suggested BaW (best of all worlds), a mixed method that merges heuristic and exact techniques to select the best distribution key in favor of some tables.

Nevertheless, Barkhoradari and Niamanesh [18] developed a technique called Chabok that involves a two-phase Map–Reduce to resolve DW issues incorporating big data. Chabok is utilized in repositories with the star schema and allows the calculation of distributive measures. This approach deals efficiently with big dimensions; in these dimensions, data size is larger than the bulk of a node. Chabok partitions horizontally the fact table. The Fact Mapper nodes store an identical quantity of tuples in the case of similar nodes. Hadoop and the TPC-DS benchmark were utilized to implement Chabok. The query response time on Chabok overcame significant big data tools for data warehousing, such as Hive and Spark-SQL.

Another approach based on affinity is [19], where the authors considered the horizontal fragmentation of the DW through a simplified decision problem that takes into account the fragmentation derived from the fact table according to the partitioning scheme of a dimension table making use of solely one attribute. The corresponding optimization problem involves calculating a fact table partitioning by limiting the number of fragments by a constant B (quantity of fragments established by the DW administrator) and minimizing the number of I/O operations. A hill-climbing method was developed to choose a near-optimal solution for selecting an optimal fragmentation scheme in a relational DW. The hill-climbing algorithm has two steps: (1) it finds an initial HFS using an affinity algorithm, and (2) it iteratively improves the initial solution to minimize query execution cost and satisfy B.

Likewise, the problem of selecting an HFS that is supported by the ant-colony-based approach was modeled in [20]; the variables were: the non-fragmented DW scheme, the workload commonly executed, and the largest quantity of partitions necessary for the DW administrator. The HFS that minimizes the total cost of request loading is the resulting output. The approach taken was based on cost.

In [9,21], all the DW tables were fragmented into several buckets (NB) using a hash-partitioning approach and then they were distributed evenly among the cluster nodes to optimize star join queries. The buckets were built in three stages: (1) finding out the near-best NB and the partitioning key by employing the balanced k-means algorithm; (2) obtaining the fact table buckets; and (3) building dimension buckets.

Ettaoufik and Ouzzif [22] implemented an assisted incremental horizontal fragmentation technique with temporary materialized views by a web service. This approach has its basis in managing temporary materialized views for optimizing frequent new queries before proceeding with the fragmentation implementation. The authors used a web service to automatically monitor and improve DW performance and reduce both manual efforts and implementation costs. The web service selects and implements the HFS, and then monitors the performance of the DW to avoid any degradation.

However, to adjust decision-making systems with big data management, in [23], the authors proposed the merger of NoSQL graph-oriented data into the DW; the work details a new method named Big Parallel-ETL which has the aim of adjusting the traditional ETL process (extract–transform–load) through big data tools to speed up data manipulation with the basis of the well-known MapReduce concept distinguished by its suitable parallel-processing feature. The system architecture is comprised of two main layers; one of them has the data sources of the system (Neo4j) and the other layer is comprised of the ETL process that works with the MapReduce paradigm. The main idea of the work consists of operating on a JSON file containing Neo4j data mixed with DW metadata to arrange the multidimensional schema utilizing the MapReduce paradigm beginning with the horizontal partitioning operation and then transforming the sub-JSON files into column-oriented tables to obtain the corresponding multidimensional layout to be unified into the target DW.

Likewise, Munerman et al. [24] proposed an allocation approach of “objects” to “storages” where the nature of the former is defined by the subject area. Later, they considered the speed up of the join operation while processing big data in a specific area. To decrease the execution time of this activity, it is required to optimally distribute the operand tables. Therefore, parallel implementation of the join execution needs an equal data distribution among the DW processors in the cluster. To efficiently resolve the optimal big data distribution, the authors formalized a heuristic method with polynomial computational complexity presenting the objective function and the system of restrictions. The study of the established technique considering different data bulks and diverse data warehouses was realized. A report of the experiments to validate the heuristic greedy optimal distribution proposal was given. The executing time of the approach, even considering massive data, is brief; thus, it can be efficiently applied to distribute data for parallel resolving issues with enormous computational complexity.

On the other hand, [25] established that improving OLAP query efficiency in a distributed system of the kind of Hadoop and Spark is a challenge since the star join operation is the most costly operation involved in these queries and the one requiring significant communication cost. A popular technique that reduces the network flow of the star join operation is to co-partition several DW relations on their join key. Nevertheless, this operation still needs multiple MapReduce cycles in established DW partitioning schemes. For that, the authors proposed two approaches called “FKey” and “NewKey” which have their basis in a data-mining technique to lead their physical design. The partitioning and distribution scheme assists the query optimizer to obtain a significant query-processing plan, to perform the star join execution in one Spark phase minus the shuffle stage. The authors performed experiments on a computer cluster to evaluate their approach using the TPC-DS benchmark.

Finally, Ramdane et al. [26] proposed a dynamic method to optimize group-by operation. This proposal applies partitioning and bucketing approaches to distribute a big DW among the nodes of a Hadoop cluster. This new schema aids the system omit accessing irrelevant data blocks, executes a star join operation in a single Spark phase excluding a shuffle stage, and accelerates group-by aggregation. Experimental findings demonstrated that the technique overcomes related methods considering OLAP query response time.

Table 1 establishes the main characteristics of each horizontal fragmentation method described before. Although several DW fragmentation methods are based on data mining, they use clustering or association techniques. This paper introduces a horizontal fragmentation technique, called FTree, which uses decision trees to select the horizontal fragmentation scheme of data warehouses.

Table 1. Main characteristics of horizontal fragmentation methods.

Work	Classification	Validation
[9]	Data mining (clustering)	TPC-DS benchmark employing Scala language applied in a cluster of similar nodes, a Hadoop-YARN platform, a Spark engine, and Hive.
[12]	Metaheuristic	APB-1 benchmark.
[13]	Minterm predicates	TPC-H benchmark.
[14]	Cost	APB-1 benchmark.
[15]	Cost	SSB (star schema benchmark).
[16]	Data mining (association)	TPC-DS benchmark.
[17]	Graph	Real1 and Real2 join graphs randomly extracted from real-life guests of Redshift with different volumes and frequencies as well as the TPC-DS benchmark.
[18]	Other (Map–Reduce)	TPC-DS benchmark.
[19]	Affinity	APB-1 benchmark.
[20]	Cost	APB-1 benchmark.
[21]	Data mining (clustering)	TPC-DS benchmark.
[22]	Cost	APB-1 benchmark.
[23]	Other (Map–Reduce)	JSON file which contains Neo4j vast data combined with DW metadata.
[24]	Metaheuristic	Experiments in a workstation to identify dependencies such as the execution time of the method compared to the number of data warehouses and the distribution quality.
[25]	Data mining (clustering)	Experiments on a computer cluster utilizing the TPC-DS benchmark.
[26]	Partitioning (hash)	Experiments with the TPC-DS benchmark through a cluster of homogeneous nodes, a Spark engine, a Hadoop-YARN platform, a Hive system, a Ray system, and a Redis database.

3. Materials and Methods

This section introduces the FTree method. First, its four steps are explained. Then, the web application to apply FTree in a DW and the elements of its schema are detailed.

3.1. FTree Method

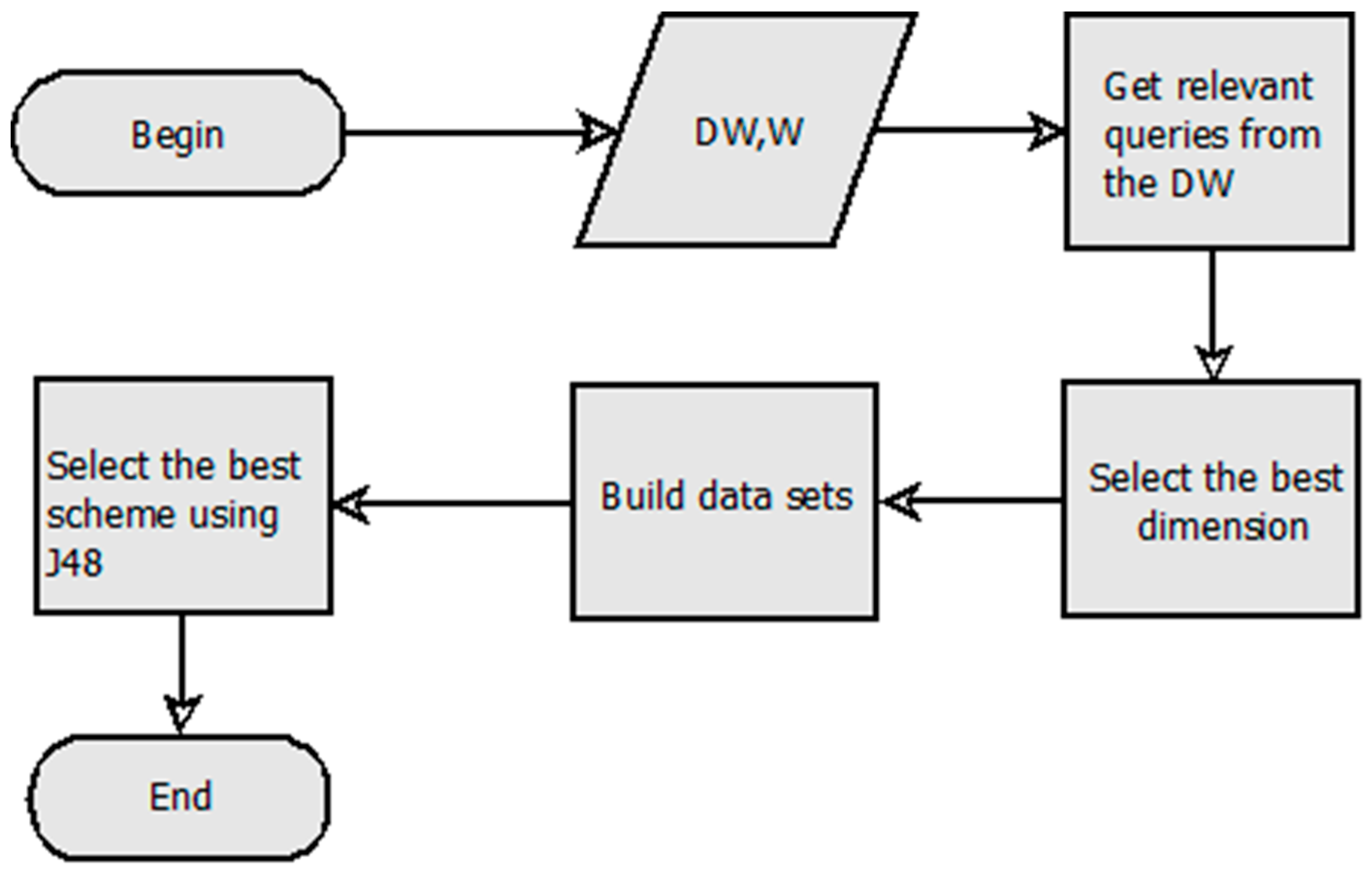
FTree has four steps, as depicted in Figure 1. It takes as the input the DW to be horizontally fragmented and W, i.e., the upper limit of partitions required by the DW administrator (DWA).

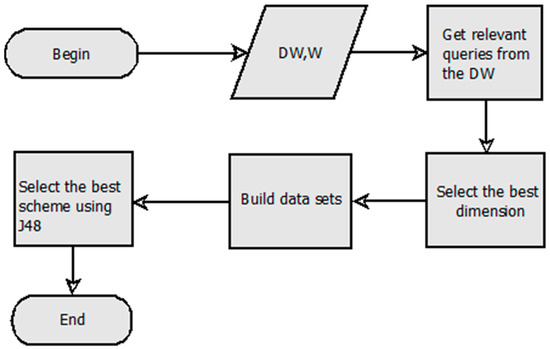
Figure 1. Horizontal fragmentation method for data warehouses based on decision trees.

To explain FTree, we use the SSB (star schema benchmark) [27]; this is demonstrated in Table 2. The SSB consists of a data warehouse with the lineorder fact table as well as the customer, supplier, part, and date dimension tables.

Table 2. Queries executed in SSB.

Query	Frequency
q1: SELECT d_month, sum(lo_quantity) from date, lineorder WHERE d_datekey=lo_orderdate AND d_year=1992 GROUP BY d_month;	3
q2: SELECT d_month, sum(lo_quantity) FROM date, lineorder WHERE d_datekey=lo_orderdate AND d_year=1992 AND d_sellingseason=‘Summer’ GROUP BY d_month;	5
q3: SELECT d_month, avg(lo_ordtotalprice) from date, lineorder WHERE d_datekey=lo_orderdate AND d_year=1993 GROUP BY d_month;	4
q4: SELECT d_month, avg(lo_ordtotalprice) FROM date, lineorder WHERE d_datekey=lo_orderdate AND d_year=1993 AND d_sellingseason=‘Christmas’ GROUP BY d_month;	3
q5: SELECT d_year, sum(lo_quantity) FROM date, lineorder WHERE d_datekey=lo_orderdate AND d_month=‘January’ GROUP BY d_year;	3
q6: SELECT d_month, sum(lo_revenue) FROM lineorder, date WHERE d_datekey=lo_orderdate and d_year=1995 GROUP BY d_month;	2
q7: SELECT d_year, sum(lo_quantity) FROM date, lineorder WHERE d_datekey=lo_orderdate AND d_sellingseason=‘Winter’ GROUP BY d_year;	5
q8: SELECT sum(lo_revenue), d_year, p_brand1 FROM lineorder, date, part, supplier WHERE lo_orderdate=d_datekey AND lo_partkey=p_partkey AND lo_suppkey=s_suppkey AND p_category=‘MFGR#12′ AND s_region=‘AMERICA’ GROUP BY d_year, p_brand1 ORDER BY d_year, p_brand1;	2
q9: SELECT sum(lo_revenue), d_year, p_brand1 FROM lineorder, date, part, supplier WHERE lo_orderdate=d_datekey AND lo_partkey=p_partkey AND lo_suppkey=s_suppkey AND p_brand1=‘MFGR#2221′ AND s_region=‘EUROPE’ GROUP BY d_year, p_brand1 ORDER BY d_year, p_brand1;	2

The data warehouse (DW) is made up of several dimension tables D = {d₁, d₂, …, d_m} and a fact table F. To carry out the fragmentation, the following steps are performed:

1. Obtain relevant queries from DW. For this step, it is necessary to keep only the queries performed in the DW that imply joins of a dimension table d_i with F; every dimension table d_i will have a set of queries Q_i = {q_i1, q_i2, …, q_in}. Additionally, the frequency of queries F_i = {f_i1, f_i2, …, f_in} is obtained, each query q_ij has a set of predicates Pr_ij = {p_ij1, p_ij2, …, p_ijr}, and finally, the selectivity of predicates S_ij = {sel_ij1, sel_ij2, …, sel_ijr} is required. The relevant queries presented in Table 2 are considered. Table 3 depicts the predicates used by the queries and their selectivity.

Table 3. Predicates used by the queries.

Pr	Description	S
p1	d_year = 1992	sel1 = 907,987
p2	d_sellingseason = ’Summer’	sel2 = 2,076,040
p3	d_year = 1993	sel3 = 908,288
p4	d_sellingseason = ’Christmas’	sel4 = 912,008
p5	Dumont = ’January’	sel5 = 541,483
p6	d_year = 1995	sel6 = 909,991
p7	d_sellingseason = ‘Winter ‘	sel7 = 1,577,160
p8	p_category = ‘MFGR#12′	sel8 = 236,816
p9	s_region = ‘AMERICA’’	sel9 = 1,134,371
p10	p_brand1 = ‘MFGR#2221′,	sel10 = 5848
p11	s_region = ‘EUROPE’	sel11 = 1,140,311

2. Select the best dimension. The most important dimension is selected in this step. Equation (1) is used to calculate the importance of each dimension, where n is the number of queries executed against the dimension d_i and r is the number of predicates for the dimension d_i involved in each query. For this, the query frequency is multiplied by the selectivity of its predicates. The selected table is called dim. Table 4 shows the importance of dimensions for the scenario. For example, the importance of dimension part is 485,328 because we multiply f₈ ∗ sel₈ + f₉ ∗ sel₁₀ = 2 ∗ 236,816 + 2 ∗ 5848.

$$I_i={{\displaystyle \sum }}_{j=1}^n{f}_{ij}({{\displaystyle \sum }}_{k=1}^{r}se{l}_{ijk})$$

(1)

Table 4. Dimension importance for the scenario.

Dimension	Importance
date	38,076,239
supplier	4,549,634
part	485,328

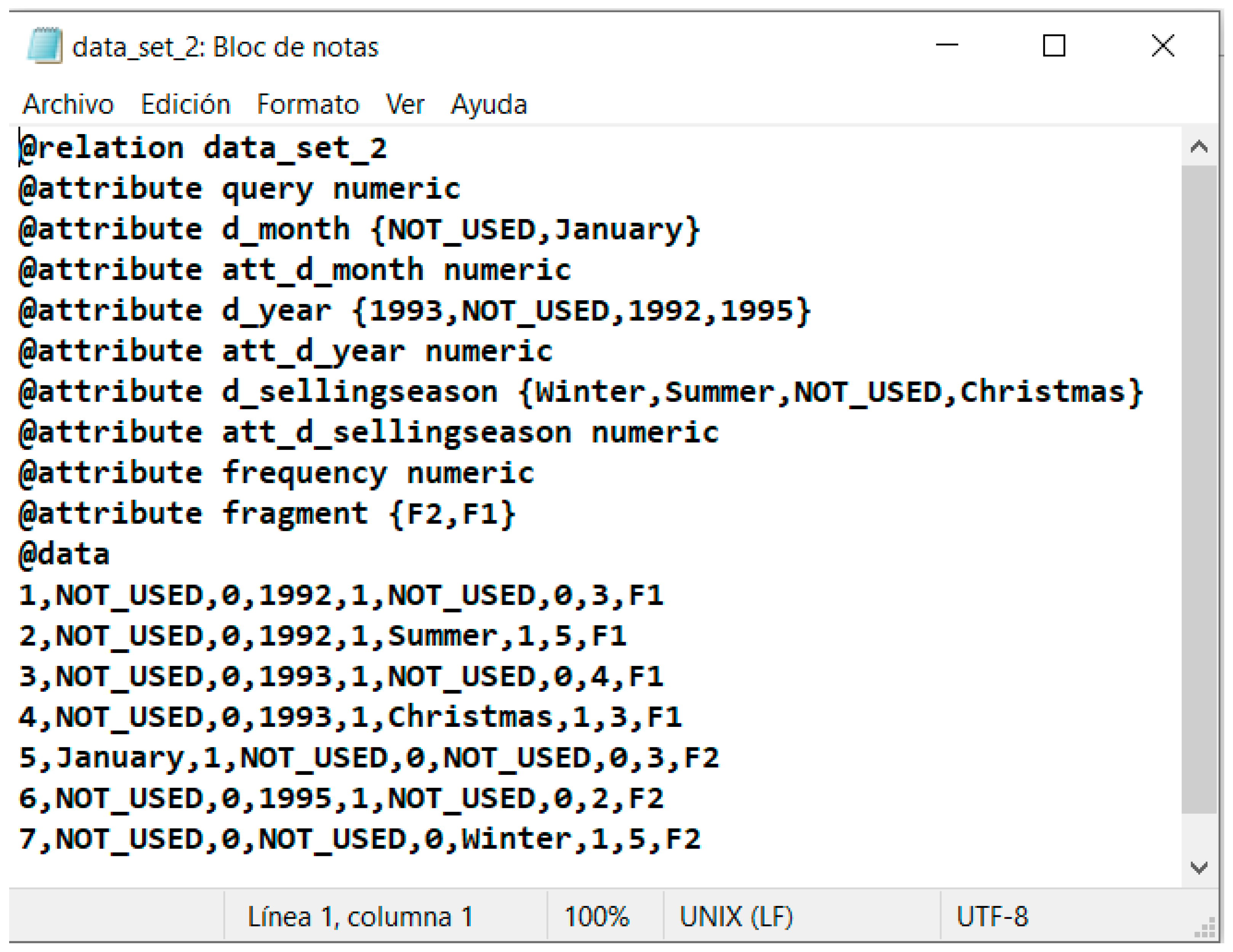
3. Build data sets. This step consists of building W − 1 data sets used to train the J48 algorithm to select the best horizontal fragmentation scheme (HFS). J48 was used because it obtained better performance than other decision tree algorithms according to [28], where it was demonstrated that J48 built decision trees with better results considering four evaluation metrics: precision, recall, F-measure, and ROC area. Algorithm 1 shows the steps to build the data sets. According to lines 1–3, it receives as an input W and a predicate usage matrix (PUM) of the queries executed in both the fact table and dim. Table 5 shows the PUM for the example. The data sets in ARFF (attribute-relation file format) are the output of Algorithm 1 (line 4). In line 5, c is set to two because this is the minimum number of fragments of the scheme. Then, a partition tree (PT) is generated [29], where initially, every predicate is considered to be in a single partition (see Table 6, where each column corresponds to a fragment and the * indicates an empty partition); from step 1 to step r − 1, where r is the number of predicates of dim, a merging profit matrix (MPM) is obtained (lines 6 and 7), which measures the benefit obtained by merging a pair of predicates. When a pair of predicates is merged, the number of remote tuples accessed is reduced, as some queries that previously required tuples from multiple fragments will now only need to access one fragment. For example, the PUM of Table 5 shows that the query q₂ uses the predicates p₁ and p₂; when they are combined in a partition in the second step of the PT depicted in Table 6, q₂ only accesses one fragment, while the number of irrelevant tuples retrieved is increased because some queries will now have to retrieve all tuples from the new fragment even if they only require those from one of the merged fragments. For example, in Table 5, the query q₁ only needs the tuples that satisfy the predicate p₁, but when the two predicates (p₁ and p₂) are merged, it also has to access the tuples from predicate p₂. The MPM is obtained as in [30], which takes the PUM as the input and calculates the decreased volume of remote tuples retrieved (DRT) and the increased number of irrelevant tuples obtained (IIT). The merging benefit of two predicates will be equal to the difference between DRT and IIT. The predicate pair with the highest merging profit will be merged (lines 8–9). When step r-(W-c) is reached (line 10), the first data set (data_set_c) is obtained (line 11). With each merger, a new data set will be generated with one more fragment (line 12), until finding the last data set consisting of W minus one, because the last fragment would be the complement. In the example, W = 4; then, data_set₂ and data_set₃ were obtained for steps 6 and 5, respectively. Figure 2 shows data_set2.arff, which is one of the data sets obtained as a result of Algorithm 1. This data set includes the workload given as input to J48 to build the decision tree.

Table 5. Predicate Usage Matrix for the scenario.

Q/Pr	p1	p2	p3	p4	p5	p6	p7	Fi
q1	1	0	0	0	0	0	0	3
q2	1	1	0	0	0	0	0	5
q3	0	0	1	0	0	0	0	4
q4	0	0	1	1	0	0	0	3
q5	0	0	0	0	1	0	0	3
q6	0	0	0	0	0	1	0	2
q7	0	0	0	0	0	0	1	5
selj	907,987	2,076,040	908,288	912,008	541,483	913,927	1,577,160

Table 6. Partition Tree for the scenario.

Step	Predicates
1	p1	p2	p3	p4	p5	p6	p7
2	p1, p2	*	p3	p4	p5	p6	p7
3	p1, p2	*	p3, p4	*	p5	p6	p7
4	p1, p2	*	p3, p4	*	p5, p6	*	p7
5	p1, p2	*	p3, p4	*	p5, p6, p7	*	*
6	p1, p2, p3, p4	*	*	*	p5, p6, p7	*	*

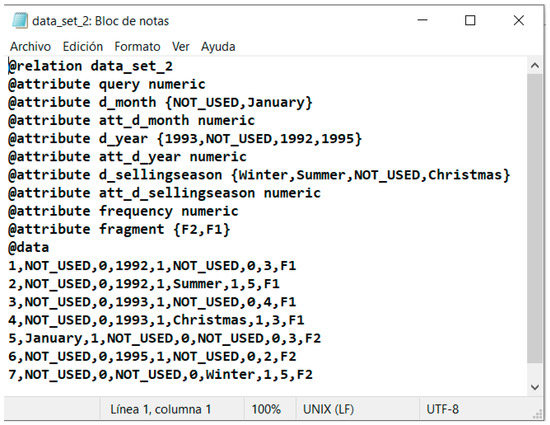
Figure 2. Data set for step 6 of the PT.

Algorithm 1. Generate data sets.
1	Data: PUM of the fact table F and dim (a set of queries Q = {q1, q2, …, qn},
2	the frequency fi of every query qi, a set of predicates Pr = {p1, p2, …, pr}, the
3	selectivity selj of every predicate pj), W
4	Result: data sets D = {data_set2, data_set3, …, data_setw−1}
5	c = 2
6	for each stepi ∈ PT | 1 ≤ i ≤ r − 1 do
7	getMPM(PUM, MPM);
8	choose two fragments with the greatest merging profit;
9	fuse the fragments;
10	if i > r-(W-c)
11	generate data_setc
12	c = c + 1;
13	end;
14	end;

Figure 2 shows that the instances of the data set represent the queries and the attributes correspond to the predicates; a numeric variable is added for each attribute involved in the predicates. Additionally, the query frequency is considered in the data sets. The class label attribute is fragment; the value for this attribute is assigned according to the partition tree and when a query uses predicates located in different fragments, the selectivity is considered. For example, according to Table 5, q₄ uses the predicates p₃ and p₄. The selectivity of these predicates is sel₃ = 908,288 and sel₄ = 912,008. In the second step of the partition tree of Table 6, they are in different fragments; p₃ is in the second fragment (F2) and p₄ is in the third one (F3). Therefore, the label F3 is assigned to q₄, because sel₄ > sel₃.

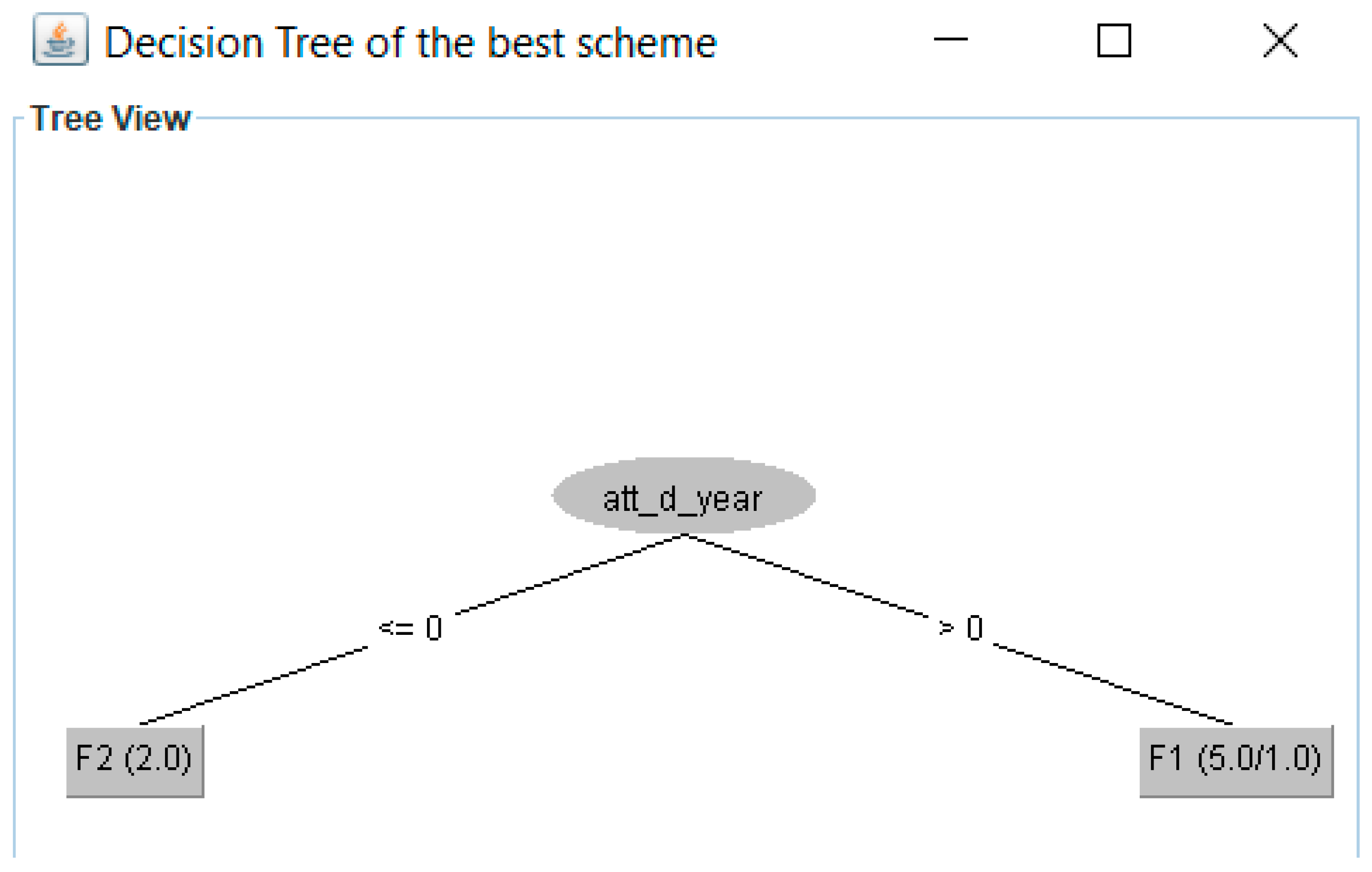
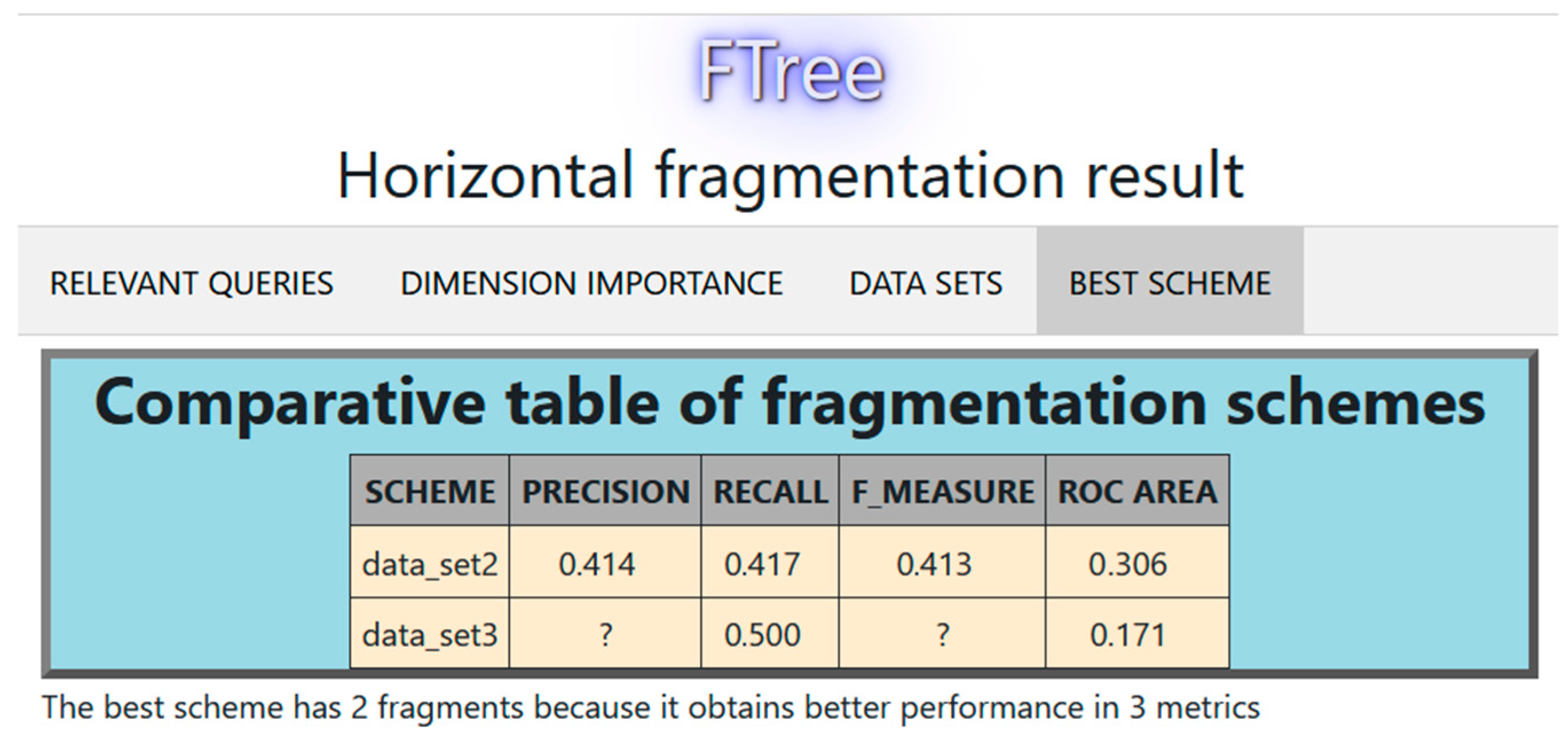
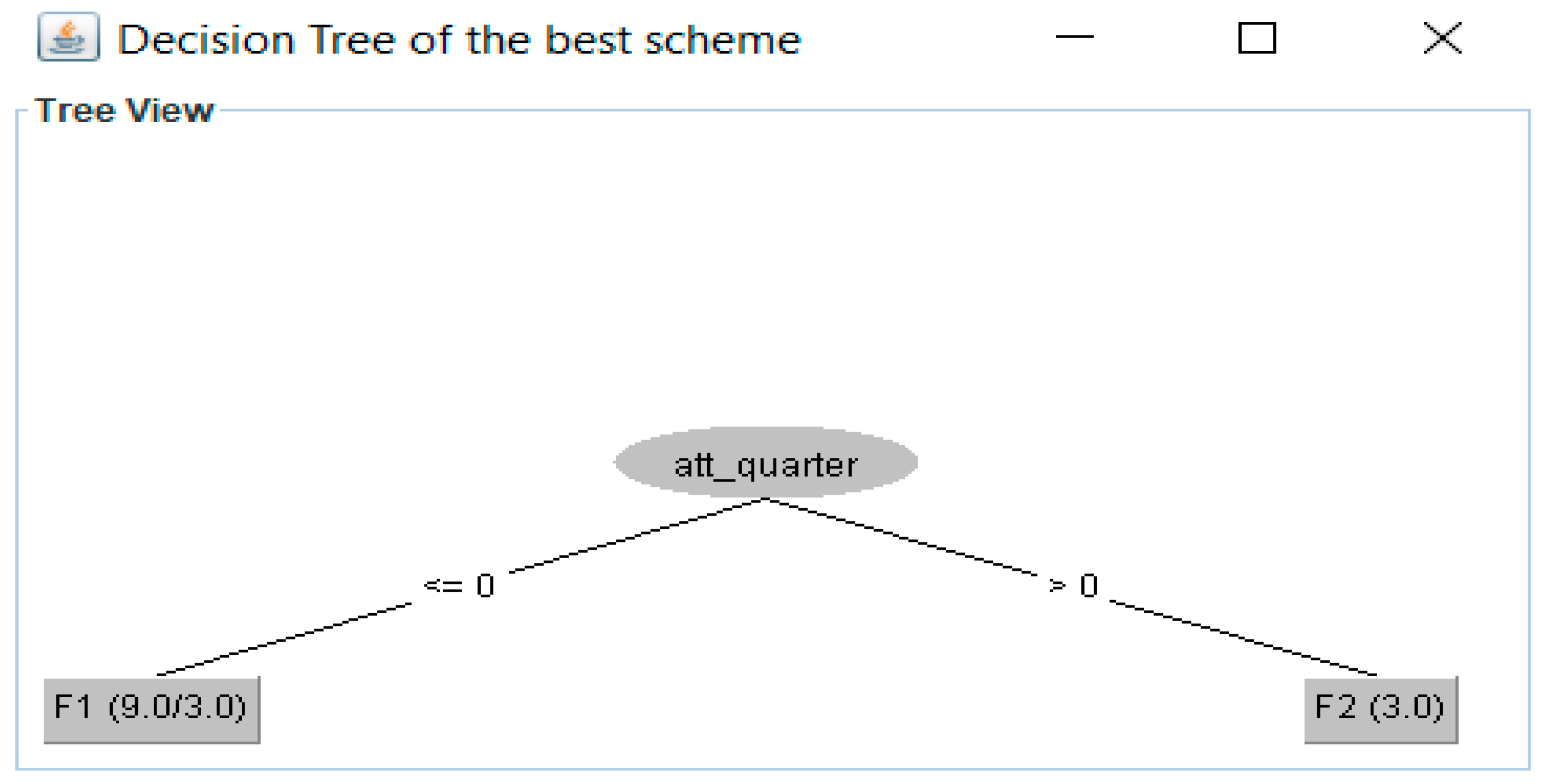
4. Apply J48 to data sets. The Weka API (application program interface) is used to apply the J48 algorithm to the W-1 data sets. The data set with the best results achieved for four performance metrics (precision, recall, F-measure, and ROC area) will be chosen. Table 7 shows the best HFS of the example, i.e., data_set₂. We used 5-fold cross-validation. Figure 3 depicts the decision tree for data_set₂. Therefore, the fragmentation scheme is fr₁ = {p₁, p₂, p₃, p₄}, fr₂ = {p₅, p₆, p₇}, fr₃ = { $\neg$ (p₁, p₂, p₃, p₄), $\neg$ (p₅, p₆, p₇)}.

Table 7. Comparative table of fragmentation schemes.

Scheme	Precision	Recall	F-Measure	ROC Area
data_set2	0.286	0.429	0.343	0.208
data_set3	-	0.429	-	0.244

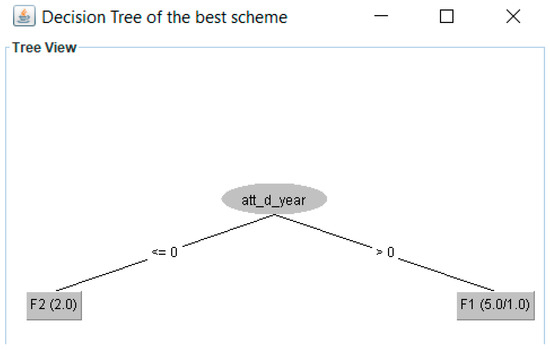
Figure 3. Decision tree of the best scheme (with better results for the evaluation metrics).

3.2. FTree Web Application

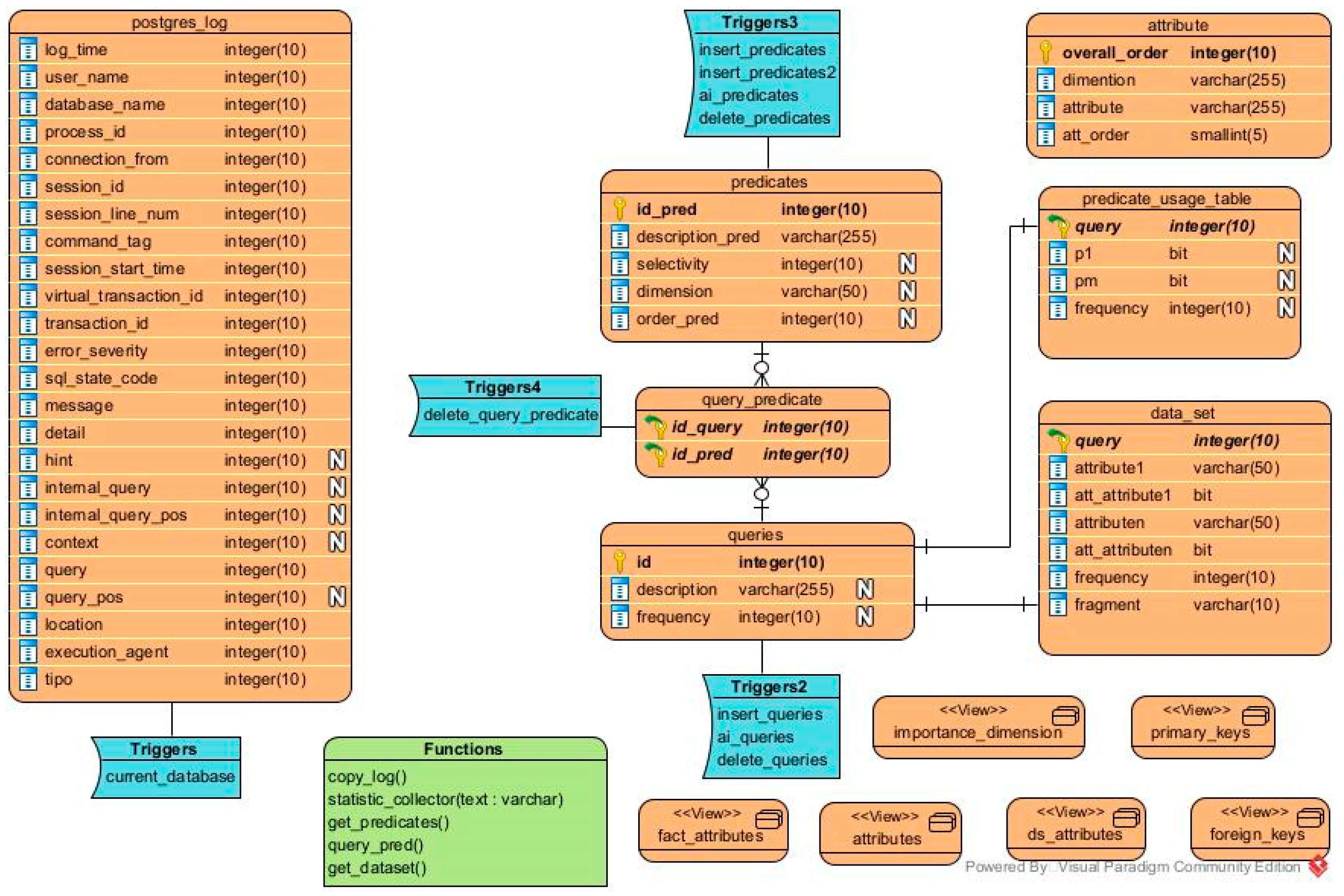
We also developed a web application using the Java programming language, the API of Weka, and the database management system (DBMS) PostgreSQL to apply FTree in a DW. First, the DWA must provide the IP of the server where the data warehouse is located, the port, as well as his/her username and password. Then, the DW to be fragmented and the fact table are selected and the upper limit of partitions is entered (W). When these data are provided and the fragmentation proceeds, the FTree schema of Figure 4 is created in the DW. Table 8 describes every element of this schema. Figure 6 shows a partition tree in the web application, while Figure 8 depicts a PUM, Figure 10 presents the comparative table of two fragmentation schemes, and Figure 3 exhibits a decision tree in the web application.

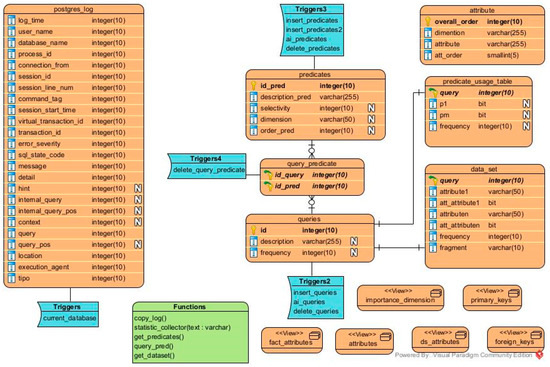
Figure 4. Physical model of the FTree schema.

Table 8. Elements of the FTree schema created in the DW.

Name	Type	Description
postgres_log	Table	It stores all the queries found in the log file.
current_database	Trigger	Before inserting a query into the postgres_log table, it verifies that only the relevant queries were saved.
copy_log()	Function	It copies the contents of the current day’s transaction log to the postgres_log table.
queries	Table	It stores the identifier, the description, and the frequency of the queries.
delete_queries	Trigger	After removing a query on the queries table, it reduces the value of the identifier by 1.
insert_queries	Trigger	Before inserting a query into the queries table, if the query is already stored in this table, then it is not inserted and its frequency is increased by 1.
ai_queries	Trigger	After inserting a query into the queries table, it updates its identifier if it is bigger than the number of tuples.
statistic_collector(text)	Function	It analyzes the queries stored in postgres_log to insert into the table queries only those executed in the table to be fragmented. Its parameter is the fact table.
attributes	View	It stores the names of the dimensions as well as the attributes of each dimension and the order in which they appear in the dimension table.
attribute	Table	It saves the data from the attributes view and adds a global order attribute.
fact_attributes	View	It stores the name of the fact table as well as the names and order of each of its attributes.
predicates	Table	It saves the identifier, description, and selectivity of the predicates, as well as their dimensions and order in that dimension.
insert_predicates	Trigger	Before inserting predicates into the table, it analyzes that only those from queries involving the fact table with the dimension table are taken.
insert_predicates2	Trigger	Before a predicate is inserted into the table, it validates that only different predicates are recorded.
ai_predicates	Trigger	After inserting a predicate into the predicates table, it updates its identifier if it is greater than the maximum number of rows.
delete_predicates	Trigger	After removing a predicate in the predicates table, it reduces the value of the identifier by 1.
get_predicates()	Function	It obtains the predicates of the queries stored in queries and stores them in the predicates table.
query_predicate	Table	It saves the relationship between queries and predicates.
delete_query_predicate	Trigger	After deleting from the query_predicate table, it sets to 1 the sequences for queries and predicates.
predicate_usage_table	Table	It stores the PUM that Algorithm 1 takes as input.
data_set	Table	It contains the data_set obtained by Algorithm 1.
query_pred()	Function	It analyzes which predicates appear in which queries and keeps this relation in query_predicate.
get_dataset()	Function	It creates the data sets that are used to build the decision tree.
importance_dimension	View	It stores the importance of the dimensions.
ds_attributes	View	The attributes of the data set table and their order are in this view.
primary_keys	View	It stores the name and the attributes of primary keys for all the DW tables.
foreign_keys	View	The name of the foreign keys for each dimension and the attribute in the fact table involved in this constraint are in this view.

In the following section, we compare the horizontal fragmentation schemes obtained by FTree with J48 versus FTree with other classification techniques such as naïve Bayes and multilayer perceptron. These algorithms were used in the comparison analysis because they are two classification techniques widely known for their effectiveness [31,32].

Naïve Bayes is a classification algorithm that applies the probability theory to indicate the relationship among variables and class labels; this model is one of the easiest and most known probabilistic classification models. Naïve Bayes realizes a simplifying supposition concerning the class-conditional probabilities, understood as naïve Bayes presumption; using this, it is possible to obtain confident estimates of class-conditional probabilities, still with a large number of attributes [33].

A multilayer perceptron is a kind of artificial neural network (ANN) and is considered a powerful classification approach that can find considerably complex and nonlinear decision boundaries purely coming from the data. In a multilayer perceptron, the basic concept of a perceptron is generalized to more elaborated architectures of nodes that can learn nonlinear decision boundaries [33]. In the next section, the main findings of the evaluation of FTree are presented.

4. Results and Discussion

This section includes the findings obtained with FTree using a real DW and the comparison of FTree with J48 versus other classifiers using a cost model.

4.1. Description of the Second Scenario: Tourist Data Warehouse

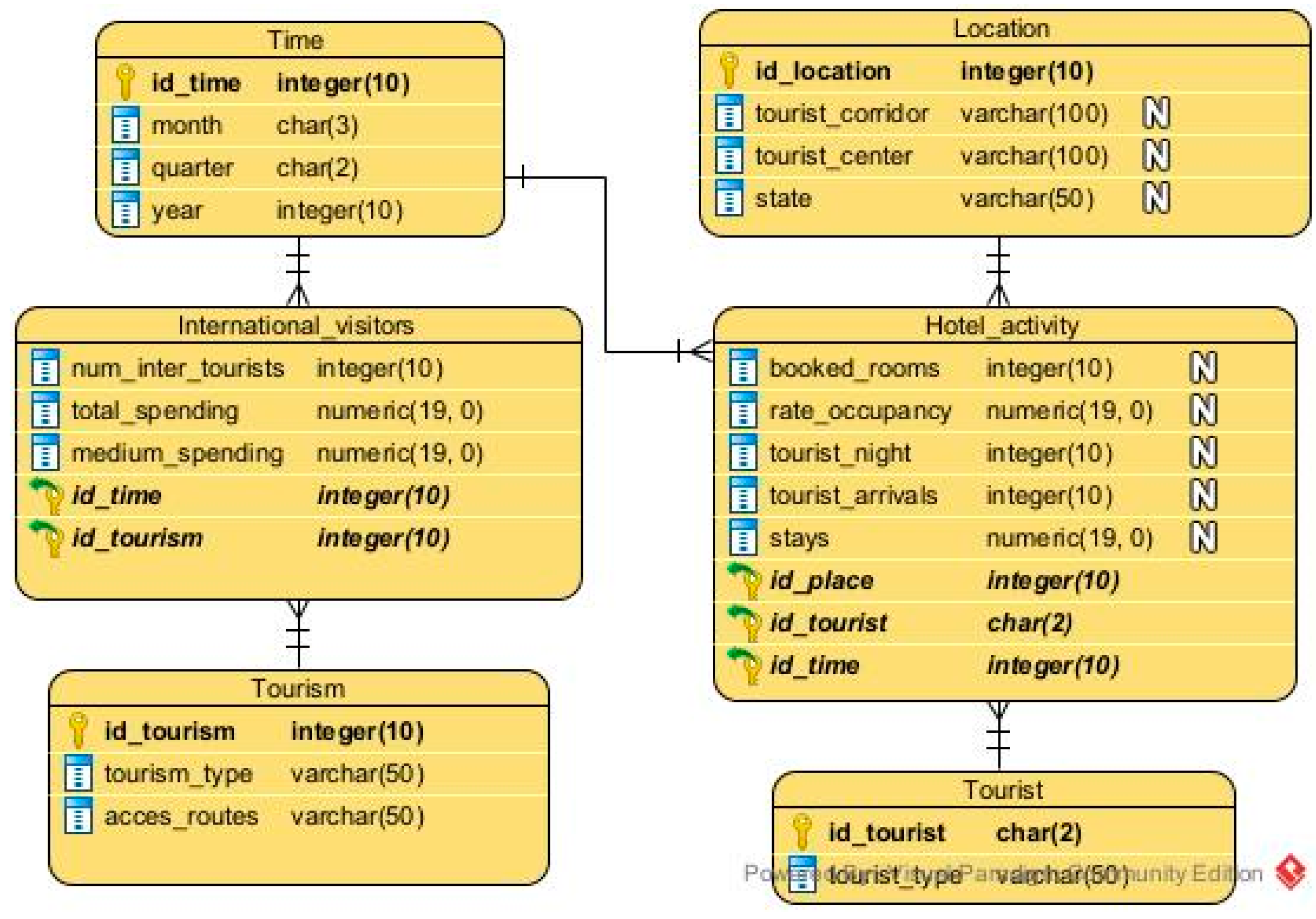
To evaluate FTree with real data, a tourist DW was built following the methodology proposed by [34]. We used information from the main organizations that regulate tourist activity in Mexico: SECTUR (Secretaría de Turismo), SEGOB (Secretaría de Gobernación), UWTO (United Nations World Tourism Organization), and INEGI (Instituto Nacional de Estadística y Geografía). The type of multidimensional scheme to be used in this case corresponds to a constellation of facts. Under PostgreSQL selected as the DBMS and Pentaho as the ETL (extraction/transformation/loading) tool, dimensional modeling of the touristic DW was carried out, which can be seen in Figure 5. Table 9 shows that the DW has two fact tables (Hotel_activity and International_visitors) and four dimensions (Location, Time, Tourism, and Tourist).

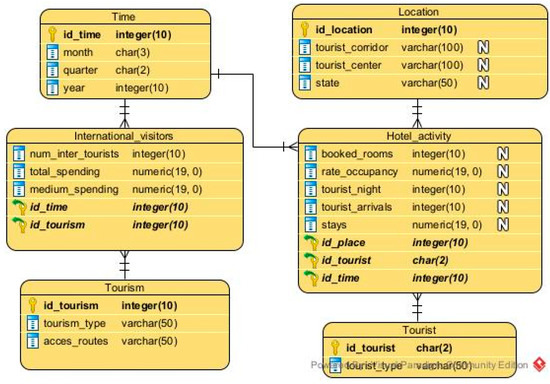
Figure 5. The multidimensional model of the tourist DW.

Table 9. Tables of a tourist DW.

Name	Type	Attributes	Tuples
Hotel_activity	Facts	8	35,424
Internationals_visitors	Facts	5	576
Location	Dimension	4	123
Time	Dimension	4	144
Tourism	Dimension	3	4
Tourist	Dimension	2	2

4.2. Application of FTree in the Tourist Data Warehouse

FTree was applied and tested in the tourist DW. The fact table fragmented was Hotel_activity. We performed the first experiment using the predicate use matrix (PUM) of Table 10.

Table 10. Predicate usage matrix for the first experiment.

Q/Pr	p1	p2	p3	p4	p5	p6	p7	Fi
q1	1	1	1	0	0	0	0	20
q2	1	0	0	1	0	0	0	15
q3	1	0	0	0	1	0	0	15
q4	0	1	0	0	0	1	0	35
q5	0	1	1	0	0	0	0	35
q6	1	0	0	0	0	0	1	30
q7	0	0	0	1	0	0	0	10
q8	0	0	0	0	0	0	1	10
q9	0	0	0	0	1	0	0	10
q10	0	0	1	0	0	0	0	10
selj	2952	8856	2952	2952	2952	2952	2952

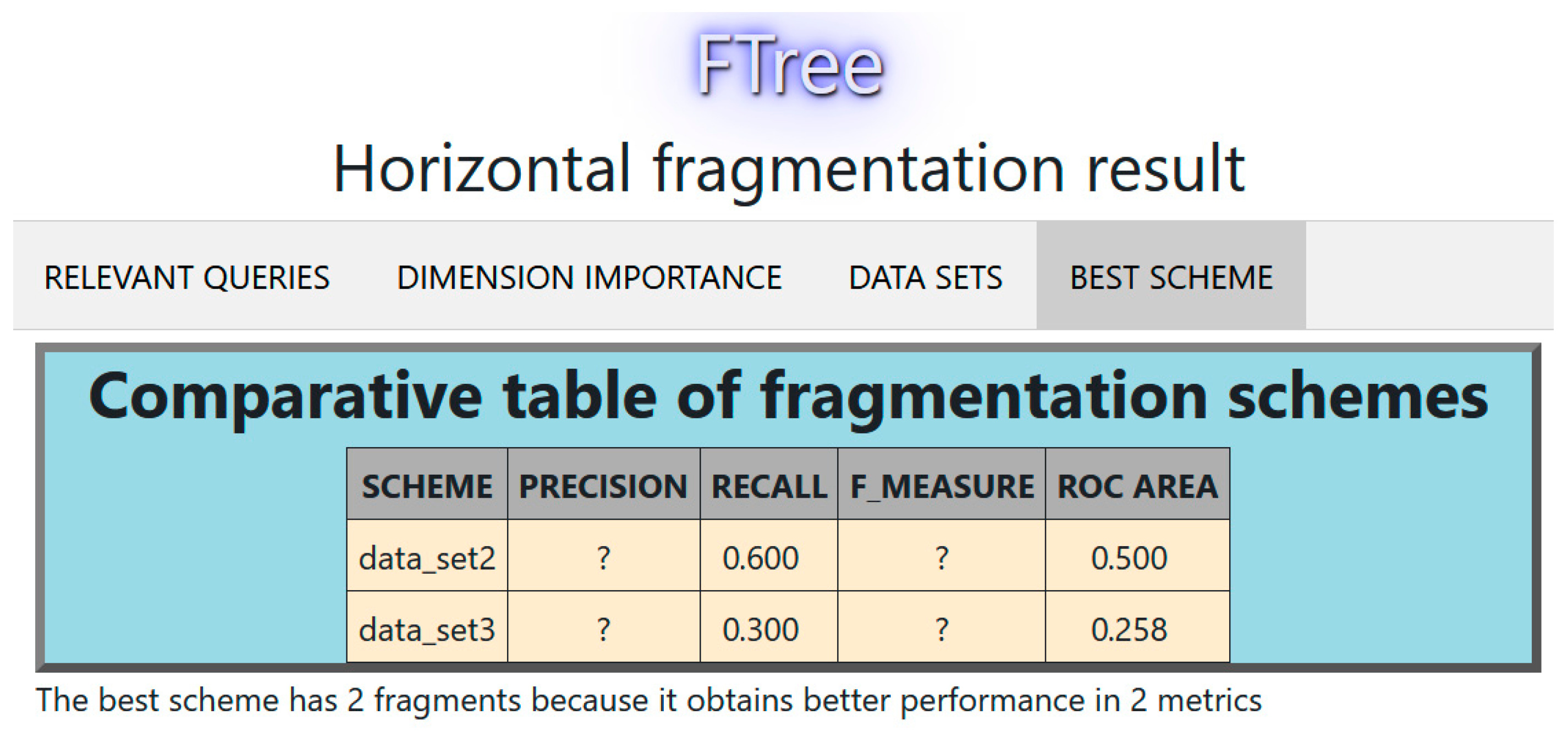
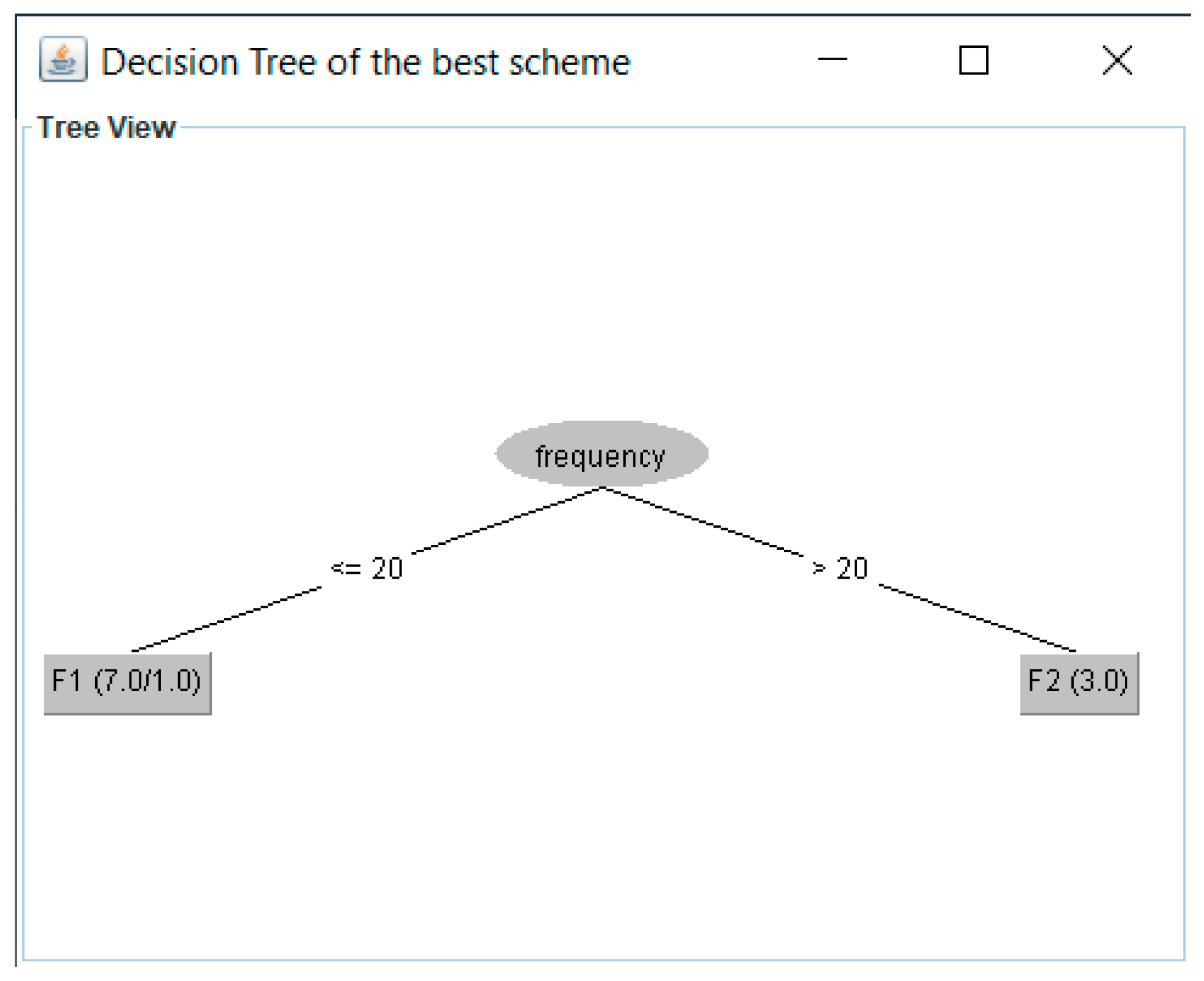
In this case, the upper limit of partitions (W) allowed by the DWA is 4. The predicates considered are presented in Table 11. Using the PUM of Table 10, the partition tree of Figure 6 was obtained by FTree (every column represents a fragment and the * indicates an empty partition). Table 12 depicts the comparison between data_set₂ with fragments fr₁ = {p₁, p₄, p₅, p₇}, fr₂ = {p₂, p₃, p₆} and data_set₃ with fragments fr₁ = {p₁, p₄, p₇}, fr₂ = {p₂, p₃, p₆}, fr₃ = {p₅}. We used 8-fold cross-validation. The best scheme is data_set₂. The decision tree obtained by FTree is visualized in Figure 7.

Table 11. Predicates for the first experiment.

Pr	Pr Text
p1	month = ‘feb’
p2	quarter = ‘T3′
p3	year = 2018
p4	year = 2014
p5	year = 2017
p6	year = 2015
p7	year = 2016

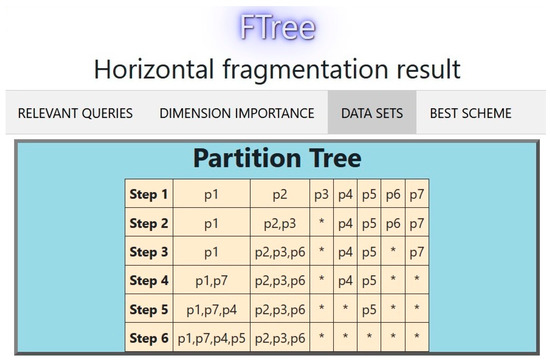
Figure 6. PT for the first experiment.

Table 12. Comparison of the two schemes with J48, Naïve Bayes, and Multi-layer Perceptron.

Scheme	J48				Naïve Bayes				Multi-Layer Perceptron
	P	R	F-M	ROC	P	R	F-M	ROC	P	R	F-M	ROC
data_set2	0.925	0.900	0.903	0.881	0.925	0.900	0.903	0.952	0.880	0.800	0.808	0.857
data_set3	-	0.600	-	0.439	-	0.800	-	0.774	0.750	0.600	0.650	0.694

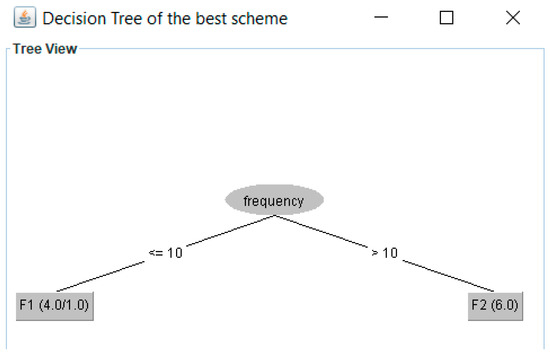
Figure 7. Decision tree for 2 fragments found by FTree for the first experiment.

Other classification algorithms were used to select the fragmentation scheme. Table 12 presents the results of the evaluation metrics precision (P), recall (R), F-measure (F), and ROC area (ROC) with naïve Bayes and multilayer perceptron with one hidden layer with six units, sigmoid activation function, learning rate = 0.3, momentum = 0.2, and number of epochs = 500.

As seen in Table 12, all the algorithms agree that the two-fragment scheme is the most suitable. In addition, the model obtained by FTree (Figure 7) is easier to interpret, which allows the fragmentation of the data warehouse based on the attribute frequency.

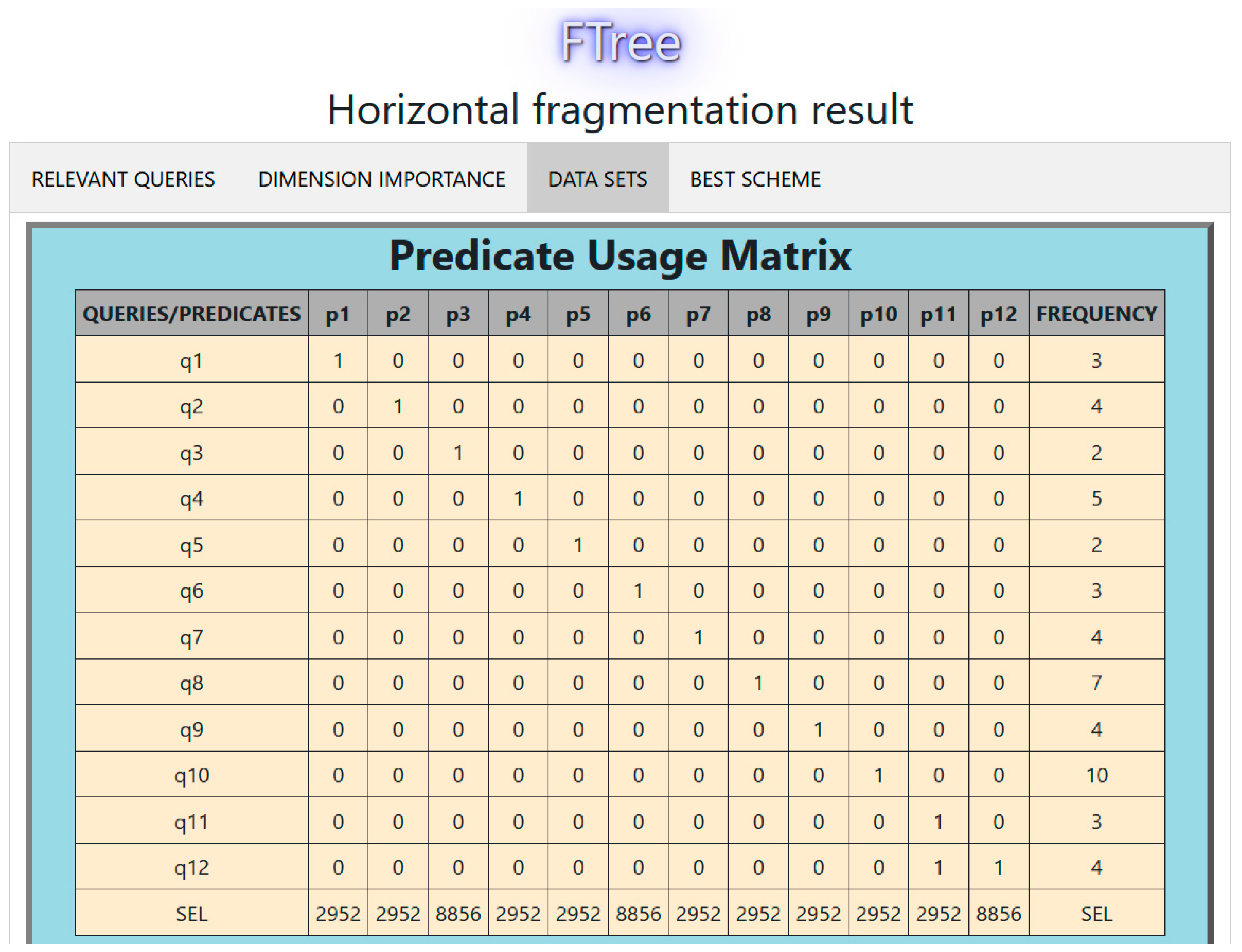
We performed a second experiment. Table 13 presents the OLAP queries executed in the tourist DW. The PUM for this workload is shown in Figure 8.

Table 13. OLAP queries executed in the tourist DW in the second experiment.

Query	Frequency
q1: SELECT month, sum(booked_rooms) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2007 GROUP BY month;	3
q2: SELECT month, sum(booked_rooms) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2008 GROUP BY month;	4
q3: SELECT month, sum(booked_rooms) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.quarter=‘T1′ GROUP BY month;	2
q4: SELECT month, sum(tourist_night) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2009 GROUP BY month;	5
q5: SELECT quarter, sum(tourist_night) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2010 GROUP BY quarter;	2
q6: SELECT year, sum(tourist_night) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.quarter=‘T2′ group by year;	3
q7: SELECT month, sum(tourist_arrivals) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2011 group by month;	4
q8: SELECT year, sum(tourist_arrivals) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.month=‘dic’ group by year;	7
q9: SELECT quarter, sum(tourist_arrivals) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2012 group by quarter;	4
q10: SELECT year, avg(stays) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.month=‘jul’ group by year;	10
q11: SELECT quarter, avg(stays) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2013 group by quarter;	3
q12: SELECT month, avg(stays) FROM time, hotel_activity WHERE time.id_time=hotel_activity.id_time AND time.year=2013 AND time.quarter=‘T4′ group by month;	4

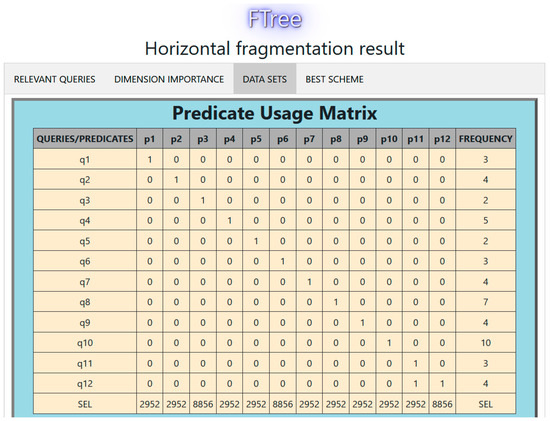
Figure 8. PUM for the second experiment with the tourist DW.

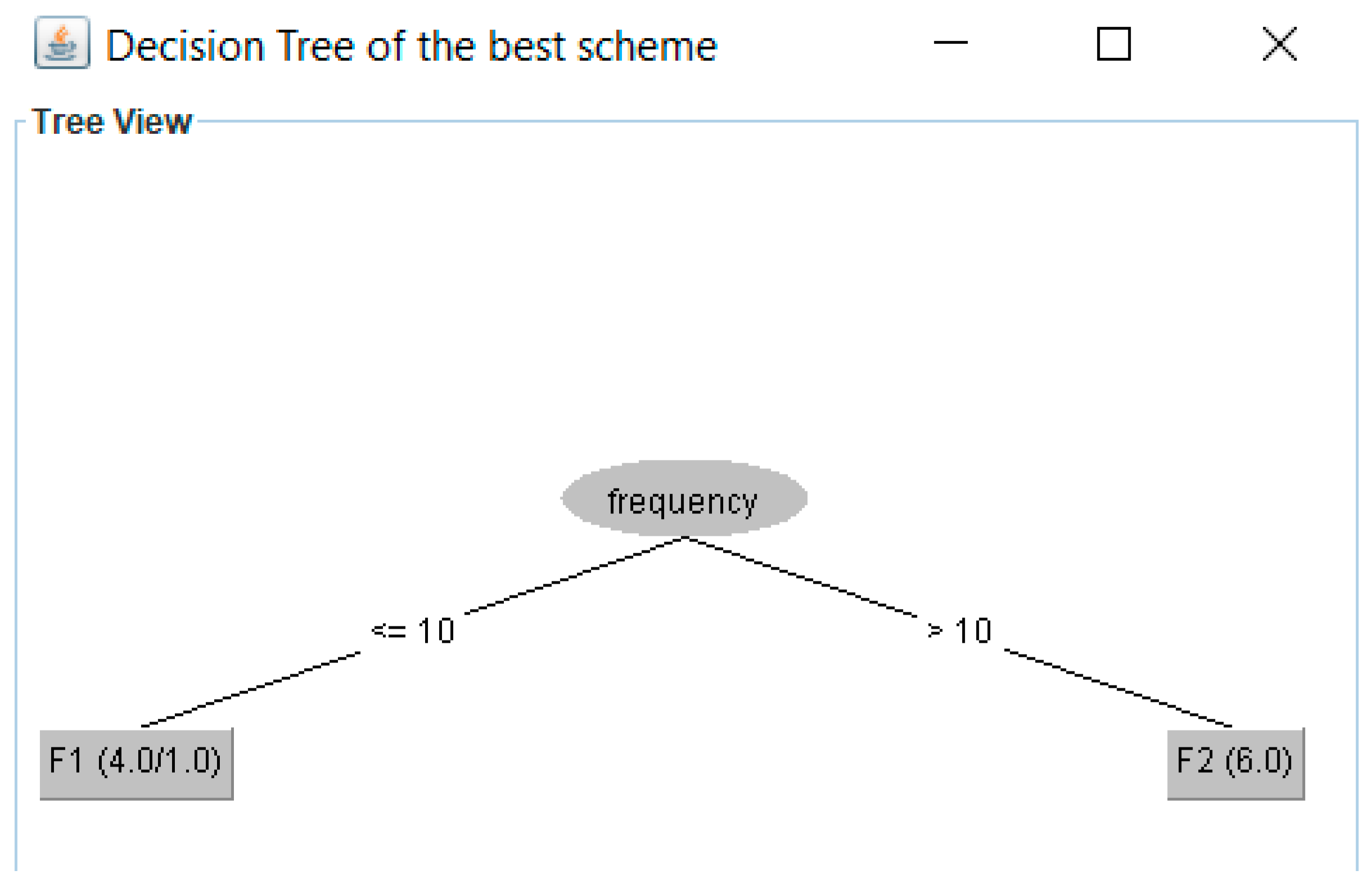
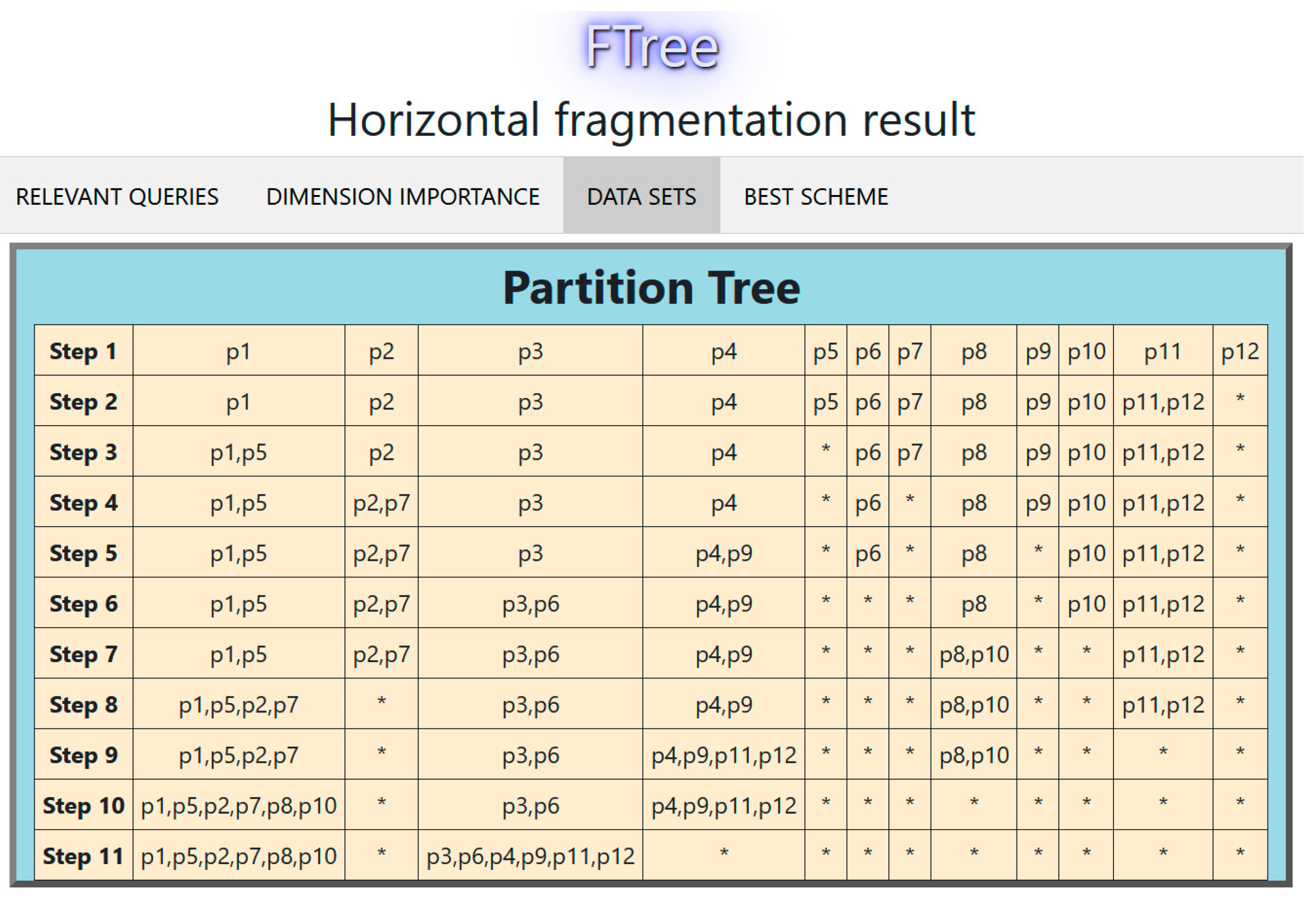
The partition tree for this experiment is shown in Figure 9 (each column represents a fragment, the * indicates an empty partition). In this case, W = 4; therefore, two data sets were obtained. Figure 10 compares the performance of these data sets using 10-fold cross-validation. Figure 11 displays the decision tree for the best fragmentation scheme. It has two fragments fr₁ = {p₁, p₂, p₅, p₇, p₈, p₁₀}, fr₂ = {p₃, p₄, p₆, p₉, p₁₁, p₁₂}.

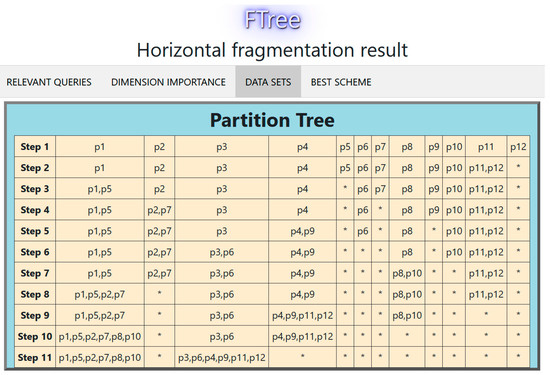
Figure 9. Partition tree for the second experiment with the tourist DW.

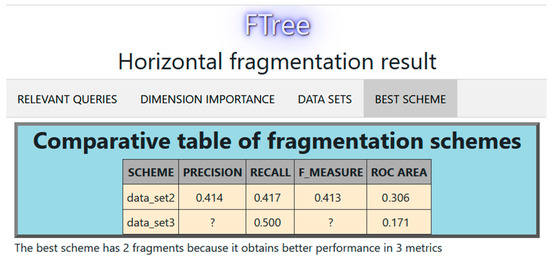
Figure 10. Comparison of fragmentation schemes with 2 and 3 fragments.

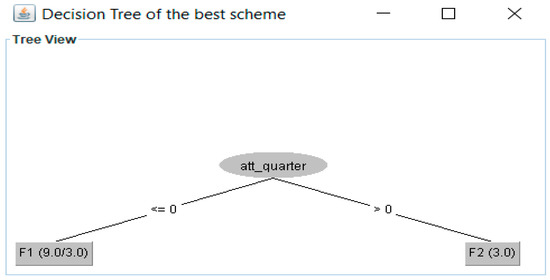
Figure 11. Decision tree for 2 fragments found by FTree for the second experiment.

Other classification techniques were used to select the fragmentation scheme. Table 14 presents the results of the evaluation metrics with naïve Bayes and multilayer perceptron with one hidden layer with six units, sigmoid activation function, learning rate = 0.3, momentum = 0.2, and number of epochs = 500.

Table 14. Comparison of the two schemes with Naïve Bayes and Multi-layer Perceptron.

Scheme	Naïve Bayes				Multi-Layer Perceptron
	Precision	Recall	F-Measure	ROC Area	Precision	Recall	F-Measure	ROC Area
data_set2	0.800	0.667	0.625	0.708	0.688	0.667	0.657	0.694
data_set3	0.857	0.750	0.742	0.750	0.563	0.583	0.570	0.733

The multilayer perceptron selected the same fragmentation scheme as FTree, while naïve Bayes chose the scheme with three fragments. We compared the schemes using a cost model where the cost of a decision support query q_i is given by the irrelevant tuple cost (ITC) and the relevant tuple cost (RTC), as shown in Equation (2).

$$Cost\left(q_i\right)=ITC\left(q_i\right)+RTC\left(q_i\right)$$

(2)

The amount of irrelevant data accessed from a query is calculated by multiplying the number of irrelevant tuples accessed by the query in every fragment fr_k by the query frequency (f_i). Equation (3) is used to obtain ITC where card(fr_k) is the cardinality of the fragment fr_k, sel_j is the selectivity of the predicate p_j, and rt_j is the number of tuples from the predicate p_j located in other fragments required to answer the query.

$$ITC\left(q_i\right)={\displaystyle \sum }_{k=1}^m(card\left(f{r}_k\right)-{\displaystyle \sum }_{p_j|PUM(q_i,p_j)=1\wedge p_j\in f{r}_k}(se{l}_j-r{t}_j))\ast f_i$$

(3)

The amount of relevant data located in other fragments is obtained by Equation (4), where the number of relevant tuples located in other fragments is multiplied by the frequency of the query squared and by the number of fragments (nf_i) required to answer the query.

$$RTC\left(q_i\right)={{\displaystyle \sum }}_{p_j\left|PUM\right(q_i, p_j)=1\wedge r{t}_j>0}^{n}r{t}_j\ast f_i^2\ast n{f}_i$$

(4)

Table 15 shows the cost of the queries in both fragmentation schemes, the one selected by FTree with J48 and the multilayer perceptron, and the scheme chosen by naïve Bayes. In the case of the first scheme, the cardinalities of the fragments are card(fr₁) = 15,744, card(fr₂) = 17,220, and card(fr₃) = 2460. The third fragment is the complement. The ITC of q₃ is calculated as follows:

$$\begin{gathered} ITC\left(q_3\right)=\left(card\left(f{r}_2\right)-(se{l}_3-r{t}_3\right))\ast f_3 \\ =\left(17,220-(8856-2952\right))\ast 2=22,632 \end{gathered}$$

Table 15. Query cost comparison of the fragmentation schemes.

Query	HFS of data_set2			HFS of data_set3
	ITC	RTC	Cost	ITC	RTC	Cost
q1	38,376	0	38,376	38,376	0	38,376
q2	51,168	0	51,168	51,168	0	51,168
q3	22,632	23,616	46,248	11,808	23,616	35,424
q4	73,800	24,600	98,400	22,140	147,600	169,740
q5	25,584	0	25,584	25,584	0	25,584
q6	33,948	53,136	87,084	17,712	53,136	70,848
q7	51,168	0	51,168	51,168	0	51,168
q8	89,544	0	89,544	89,544	0	89,544
q9	59,040	15,744	74,784	17,712	94,464	112,176
q10	127,920	0	127,920	127,920	0	127,920
q11	44,280	8856	53,136	13,284	53,136	66,420
q12	43,296	173,184	216,480	1968	330,624	332,592

The RTC of the same query is obtained as shown below:

$$RTC\left(q_3\right)=r{t}_3\ast f_3^2\ast n{f}_3=2952\ast 2^2\ast 2=23,616.$$

For the scheme chosen by naïve Bayes, the cardinalities of the fragments are card(fr₁) = 15,744, card(fr₂) = 11,808, card(fr₃) = 5412, and card(fr₄) = 2460. The fourth fragment is the complement. Therefore, the costs of the third query in this scheme are:

$$\begin{gathered} ITC\left(q_3\right)=\left(card\left(f{r}_2\right)-\left(se{l}_3-r{t}_3\right)\right)\ast f_3=\left(11,808-(8856-2952\right))\ast 2=11,808. \\ RTC\left(q_3\right)=r{t}_3\ast f_3^2\ast n{f}_3=2952\ast 2^2\ast 2=23,616. \end{gathered}$$

Table 15 shows that the HFS selected by FTree with J48 and the multilayer perceptron is better in most cases. In only two queries, the HFS chosen by naïve Bayes obtained a lower query execution cost. Additionally, the decision tree generated by J48 is easier to interpret than the model of the multilayer perceptron. Therefore, the model obtained by J48 outperformed those of naive Bayes and the multilayer perceptron.

Additionally, to evaluate FTree, it was compared with [14]; for this, the predicate use matrix of Table 16 taken from [14] was used.

Table 16. Predicate use matrix for the third experiment.

Q/P	p1	p2	p3	p4	p5	p6	p7	Fi
q1	0	1	0	0	1	0	1	20
q2	1	1	0	0	0	1	0	15
q3	0	0	1	0	1	0	1	20
q4	0	1	0	1	0	1	0	15
q5	0	0	1	0	1	0	1	15
q6	1	0	0	1	0	1	1	10
q7	0	1	0	1	0	1	0	15
selj	30	50	80	65	20	35	40

The best fragmentation scheme according to [14] is that of the three fragments fr₁ = {p₁, p₂, p₃, p₄, p₅}, fr₂ = {p₆}, and fr₃ = {p₇}. With FTree, in this case, the maximum number of fragments allowed by the data warehouse manager (W) is four. Using the PUM, the partition tree generated by FTree was obtained. Figure 12 shows the comparison between data_set₂ with the fragments fr₁ = {p₁, p₂, p₄, p₆}, fr₂ = {p₃, p₅, p₇}, and data_set₃ with the fragments fr₁ = {p₁, p₂, p₄}, fr₂ = {p₃, p₅, p₇}, fr₃ = {p₆}. We used 8-fold cross-validation. The best scheme is data_set₂. The decision tree obtained with FTree is visualized in Figure 13.

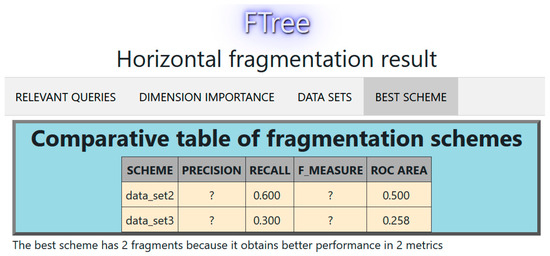
Figure 12. Comparison of fragmentation schemes with 2 and 3 fragments for the third experiment.

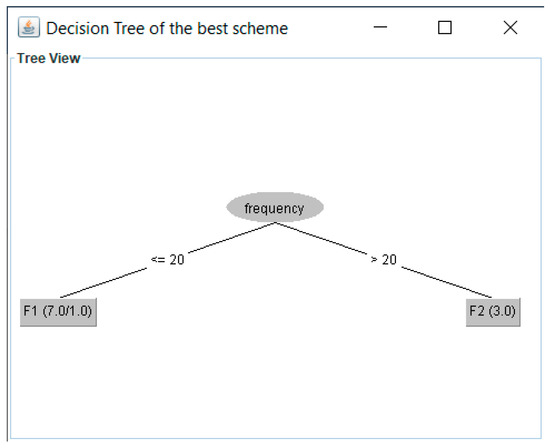
Figure 13. Decision tree for 2 fragments found by FTree in the third experiment.

Table 17 shows the cost of the queries in two fragmentation schemes, that obtained by [14] and that of FTree. In the case of the schema generated by FTree, the cardinalities of the first and second fragments are card(fr₁) = 180 and card(fr₂) = 140. For the scheme produced by [14], the cardinalities of the fragments are card(fr₁) = 245, card(fr₂) = 35, and card(fr₃) = 40.

Table 17. Comparison of query costs for the two fragmentation schemes.

Query		FTree		Kechar & Nait-Bahloul [14]
	ITC	RTC	Cost	ITC	RTC	Cost
q1	4200	0	4200	3500	0	3500
q2	975	0	975	2475	0	2475
q3	0	0	0	2900	0	2900
q4	450	0	450	1950	0	1950
q5	0	0	0	2175	0	2175
q6	1500	0	1500	1500	0	1500
q7	450	0	450	1950	0	1950

As can be seen in Table 17, although both fragmentation methods obtained schemes without RTC, the scheme generated by FTree had lower ITC in most cases. Only the first query was more efficient in the scheme found by [14]. These experiments demonstrated the effectiveness of FTree.

5. Conclusions and Future Work

Technological advances have made it possible to collect large amounts of data in different fields; therefore, there is a constant need to develop tools that help the process of extracting precise information from the enormous volume of data that are converted into knowledge. The DWs have proven to be efficient for the analysis of these massive data; for this reason, they are an excellent option to be implemented in the monitoring of tourist activity, in which, to stay at a competitive level, it is necessary to know the client preferences. As mentioned throughout this article, DW fragmentation achieves optimized response time and execution costs of OLAP queries. Several techniques for both vertical and horizontal fragmentation have been developed; however, to the best of our knowledge, a decision tree has not been used to fragment the DW, which represents an unexplored area within DW research. In this work, the classification capability of decision trees is exploited to use them in DW horizontal fragmentation. A horizontal fragmentation method, called FTree, has been developed that uses decision trees to obtain fragmentation schemes that achieve the optimization of OLAP queries in a DW. FTree was applied in a tourist DW, taking advantage of a large amount of data available in this area. The results will benefit both designers and users of data warehouses as well as researchers from the computational area.

In the future, we will extend FTree to provide dynamic fragmentation of data warehouses, monitoring the access patterns of the DW to detect when to modify the horizontal fragmentation scheme to avoid the reduction in query performance. Additionally, the fragmentation of data lakes will be considered.