Frequency Stability Analysis of a Low Inertia Power System with Interactions among Power Electronics Interfaced Generators with Frequency Response Capabilities
Abstract
:1. Introduction
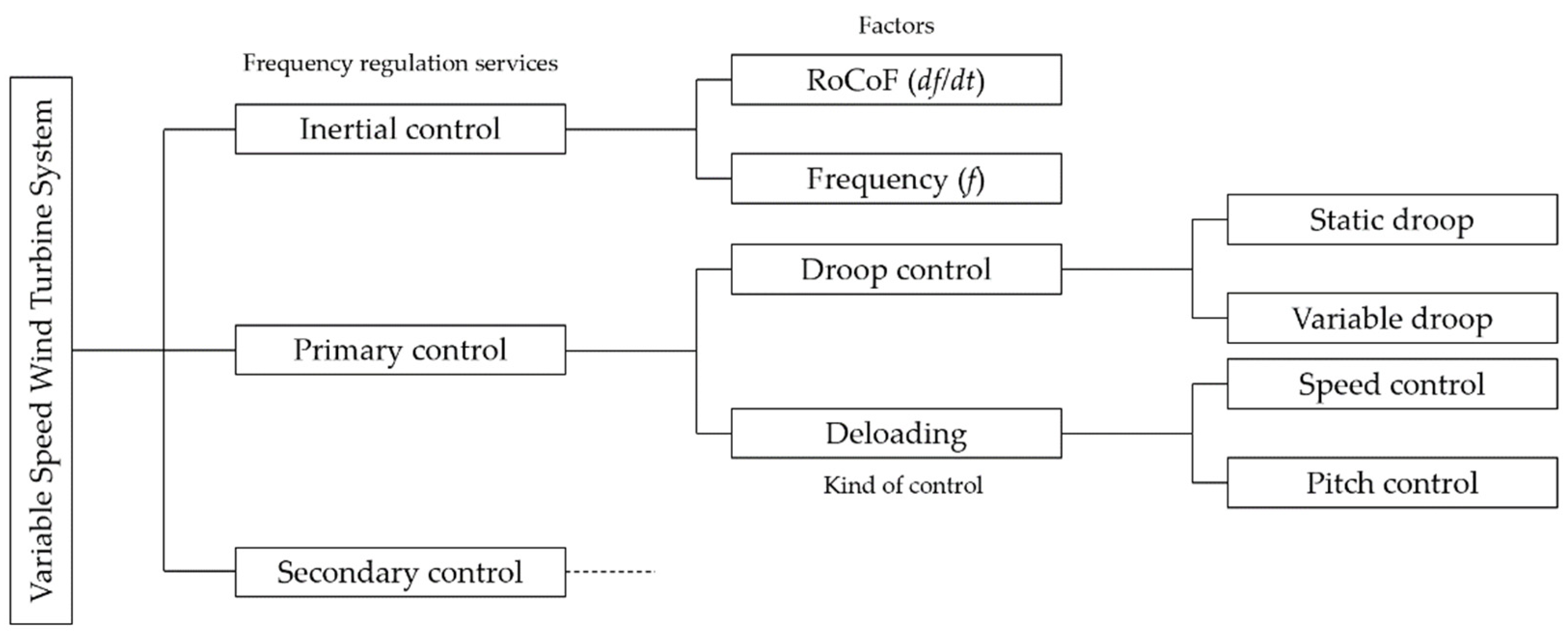
1.1. Power Limiting Control (PLC)
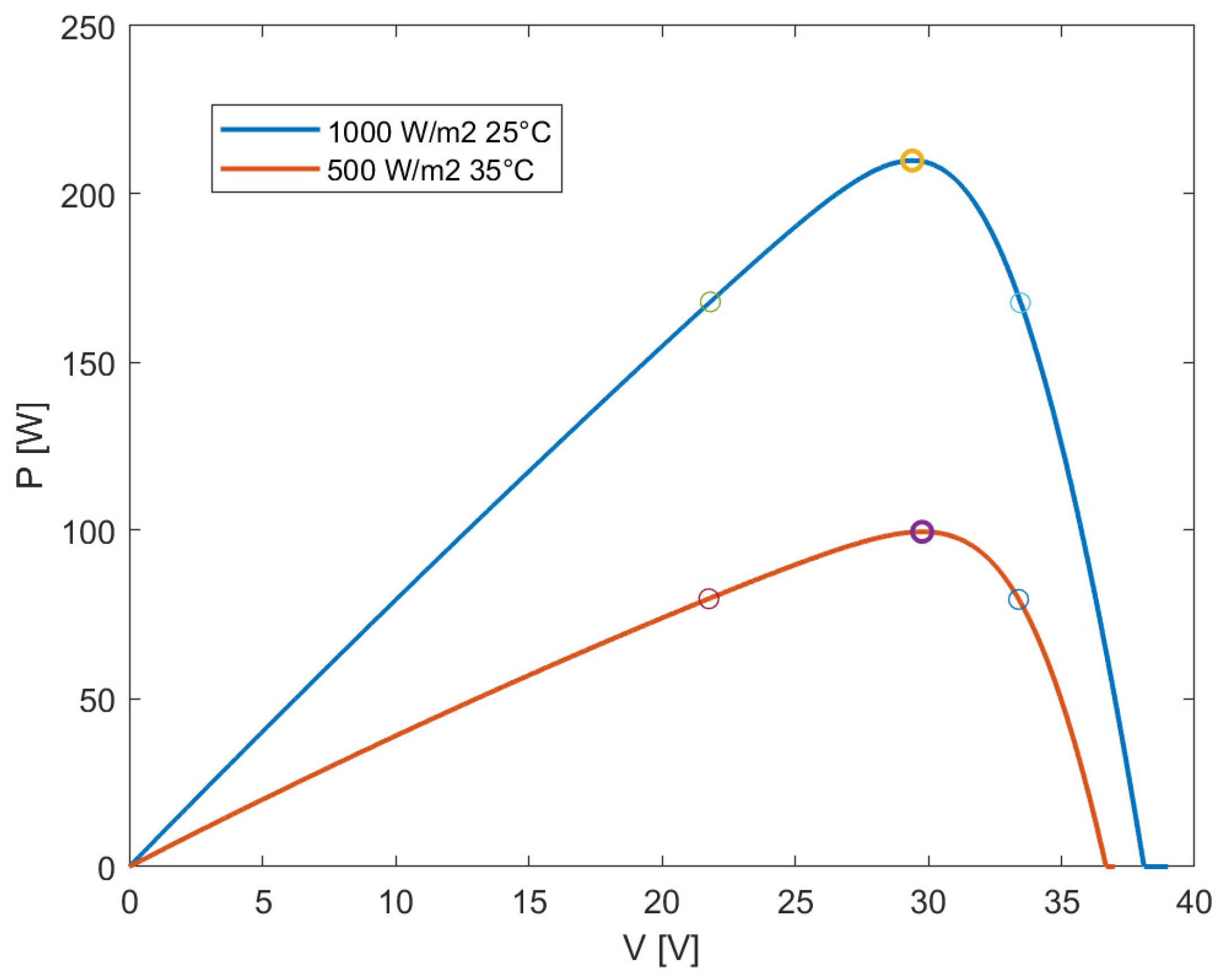
- If Pres ≥ PMPP → MPP operation: the PV system will operate at its maximum power point, so vPV* = vMPP and PPV = PMPP.
- If Pres < PMPP → curtailed operation: the PV system will operate at a voltage vPV* = v and PPV = Pres.
1.2. Power Ramp-Rate Control (PRRC)
1.3. Power Reserve Control (PRC)
2. Model for a Small Island Power System with Renewable Generators Participating in the Primary Frequency Control
2.1. Assumptions of the Model
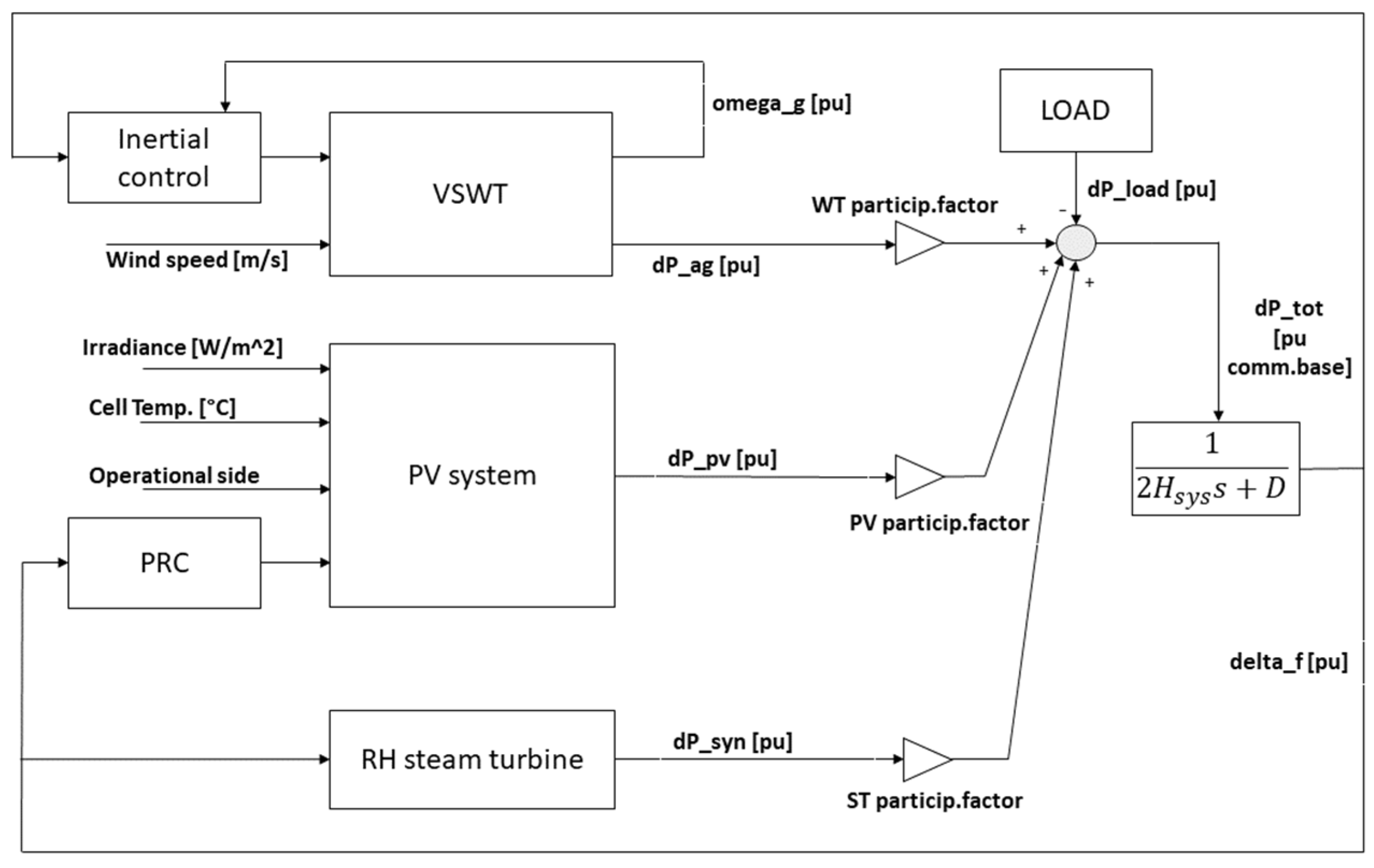
2.2. Overview of the General Model
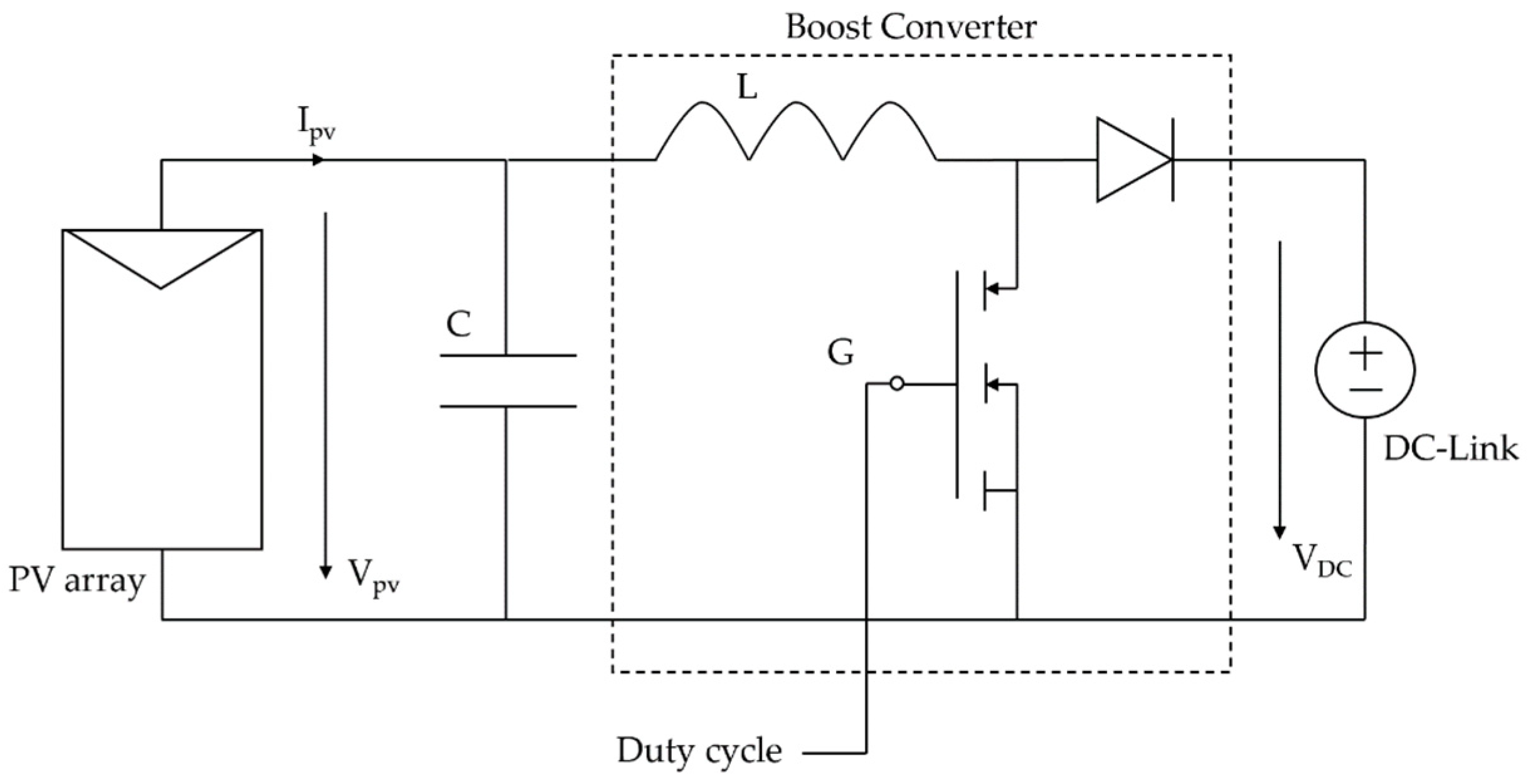
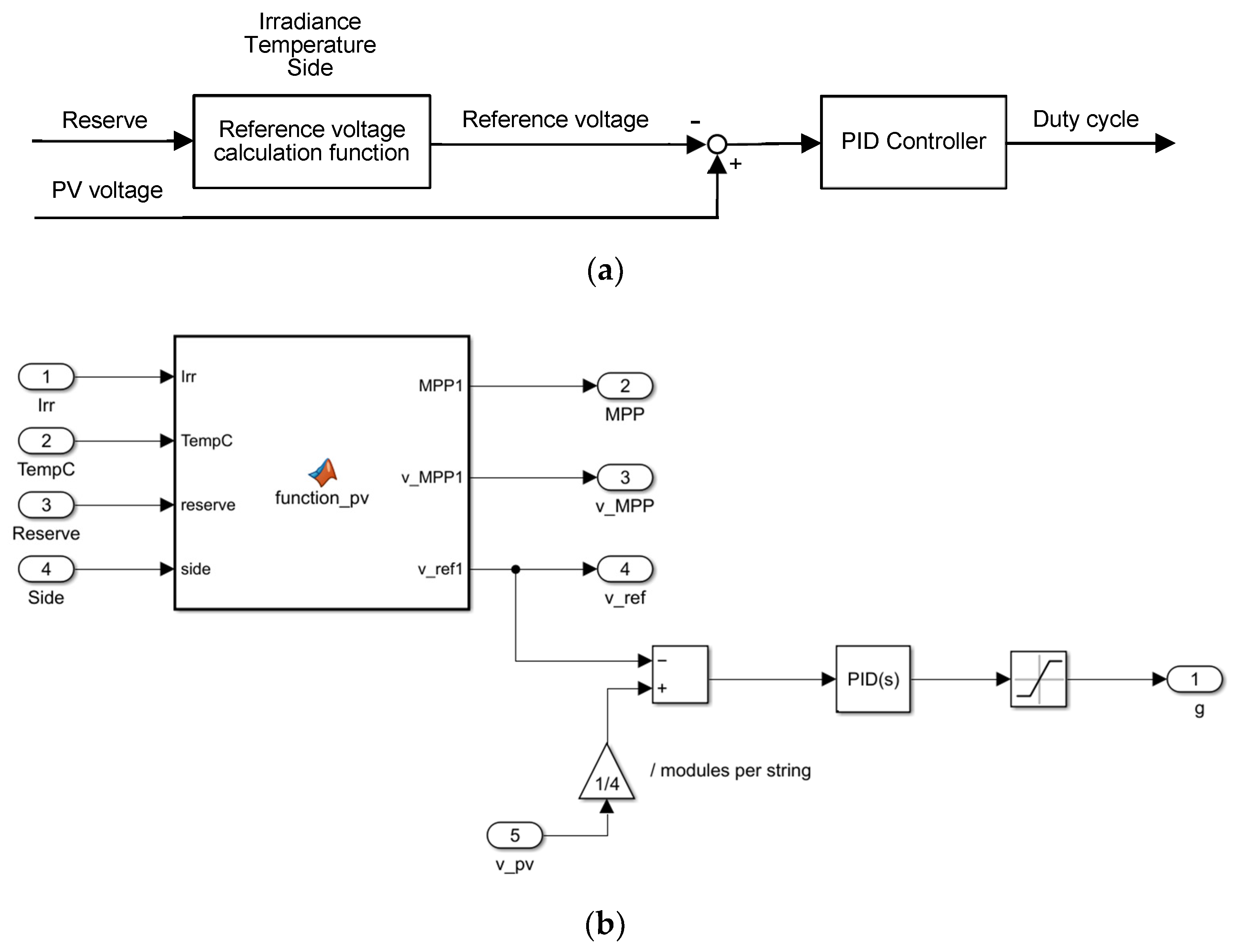
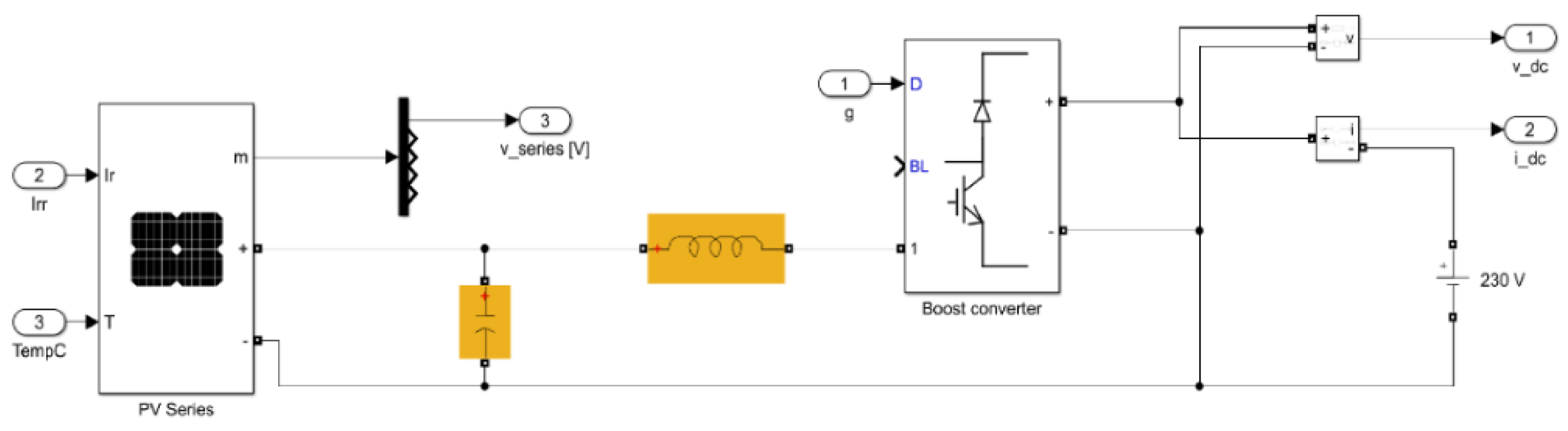
2.3. Photovoltaic Generators Model
- Irradiance and cell temperature are the two ambient conditions that mainly influence the performance of the photovoltaic modules. They are assumed to be measured in real time: this is a strong assumption, which implies higher costs with respect to other solutions such as non-linear least squares fitting methods. This assumption comes from the fact that the aim of this work is centered on the control logic, not on the determination of the irradiance and cell temperature.
- The reserve signal is produced by another subsystem that is presented in the following. It is sensible to frequency variation: if the frequency is at its nominal value, the reserve level is fixed at a certain value imposed by the steady state conditions. When the frequency oscillates, the reserve level is adapted automatically to face this variation. Of course, this signal is required by the control system to calculate the operating PV string voltage corresponding to a curtailed operation.
- The last external input, indicated with Side, represents the desired operating side of the power-voltage curve for implementing the reserve control. In this work, the innovative approach proposed in [17] has been adopted, which allows, depending on the requirements, to operate on both sides of the power curve, by simply switching this input value.
5.973869∙10−3 log(G/Gref)2 + 761.6178∙10−6 log(G/Gref)3
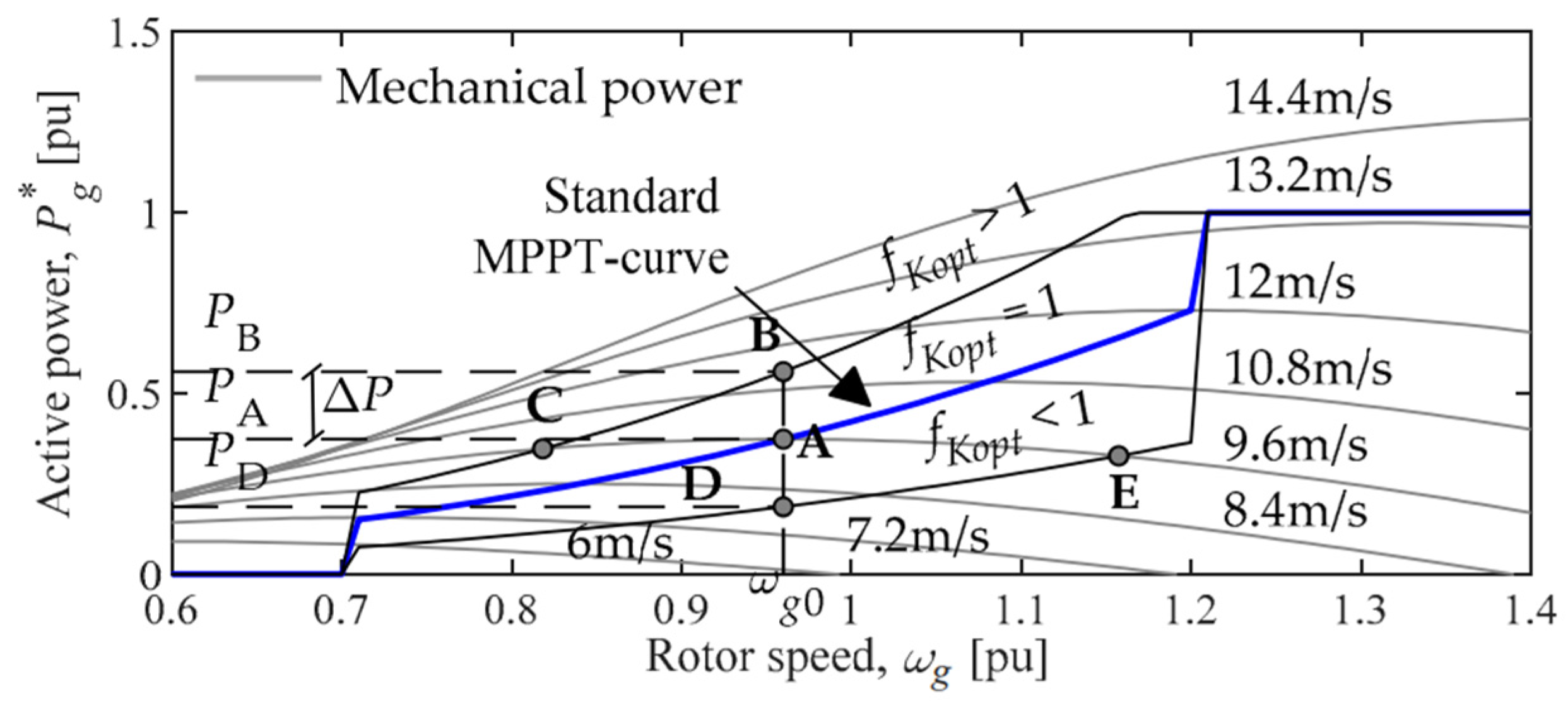
2.4. Variable Speed Wind Turbines Model
3. Simulations Summary and Metrics to Evaluate the Results
- Participation factors of the three equivalent generating units: pwind = 0.2; psynchronous = 0.7; ppv = 0.1 (30% of renewable penetration on nominal power basis).
- Incoming wind speed at t = 0 s: 9.6 m/s for constant wind simulations; 11.457 m/s for real wind profile simulations.
- Irradiance at t = 0 s: 1000 W/m2.
- Cell temperature: 25 °C.
- Constant load power requirement.
- Primary frequency control provided only by the synchronous generators (wind turbines without virtual inertia control, PV without power reserve control).
- Primary frequency control provided by synchronous generators and wind turbines (Extended OPPT Method enabled).
- Primary frequency control provided by synchronous generators and photovoltaic strings (Power Reserve Control enabled).
- All the generators participate in the primary frequency control (from now on it is denoted as complete FC).
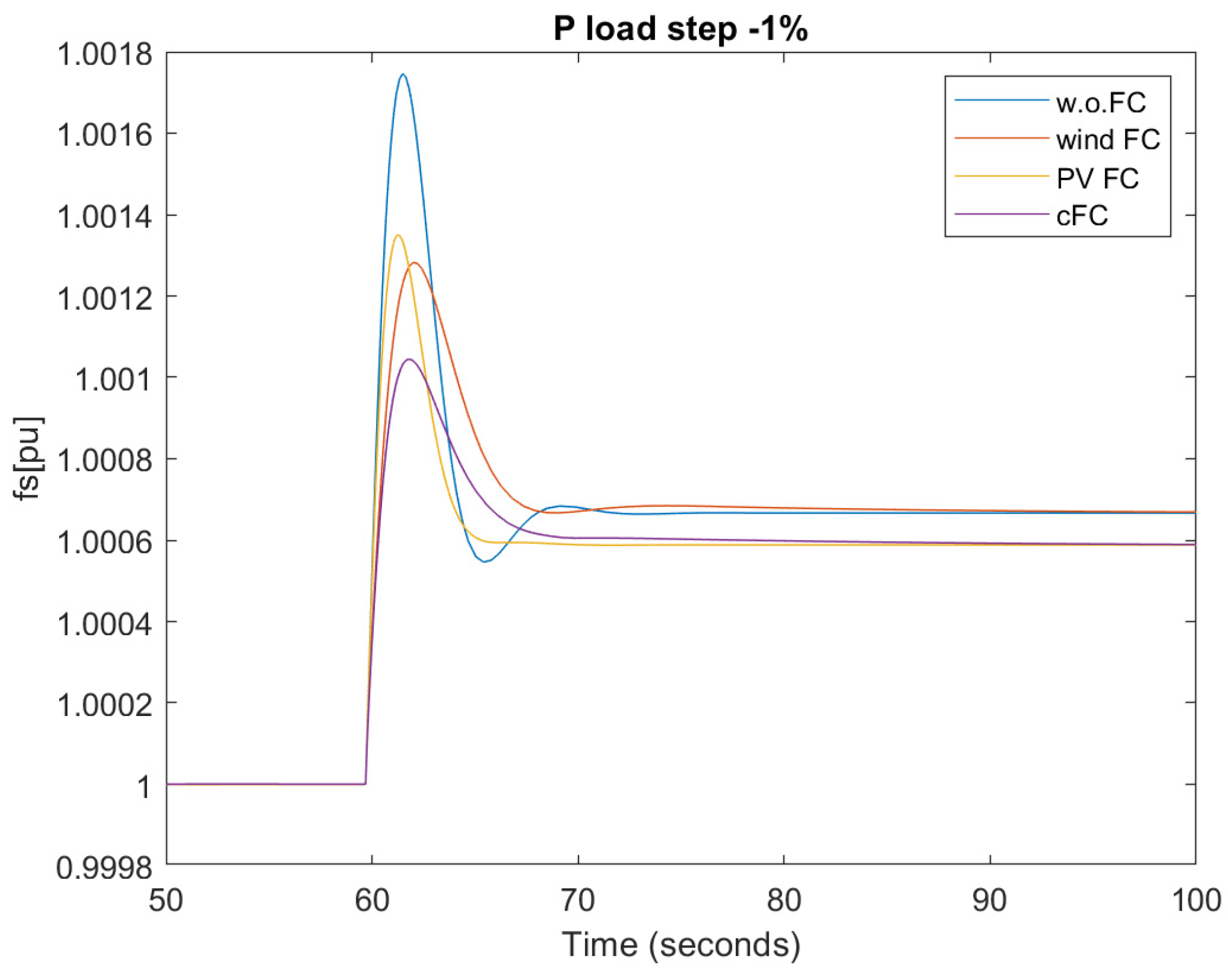
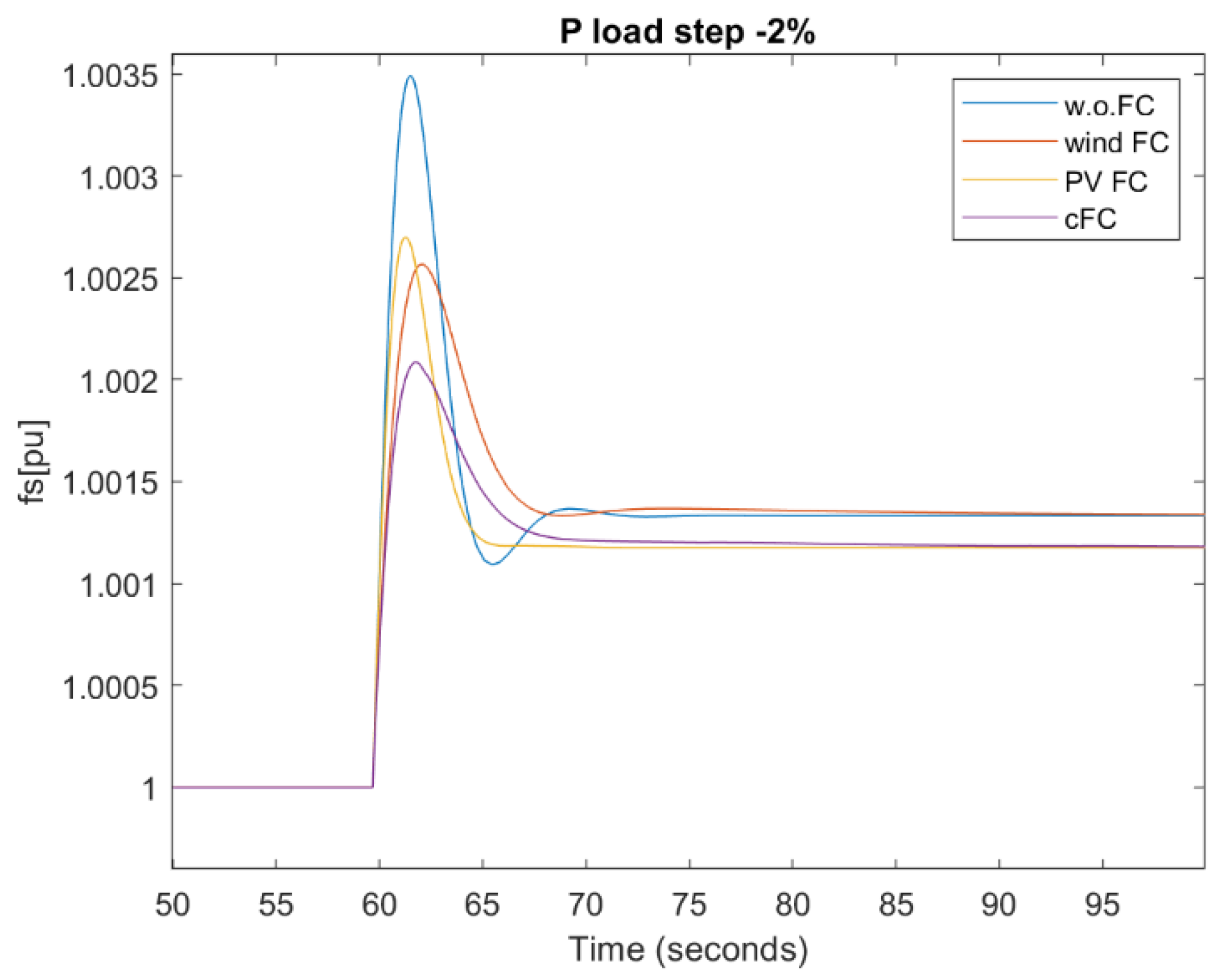
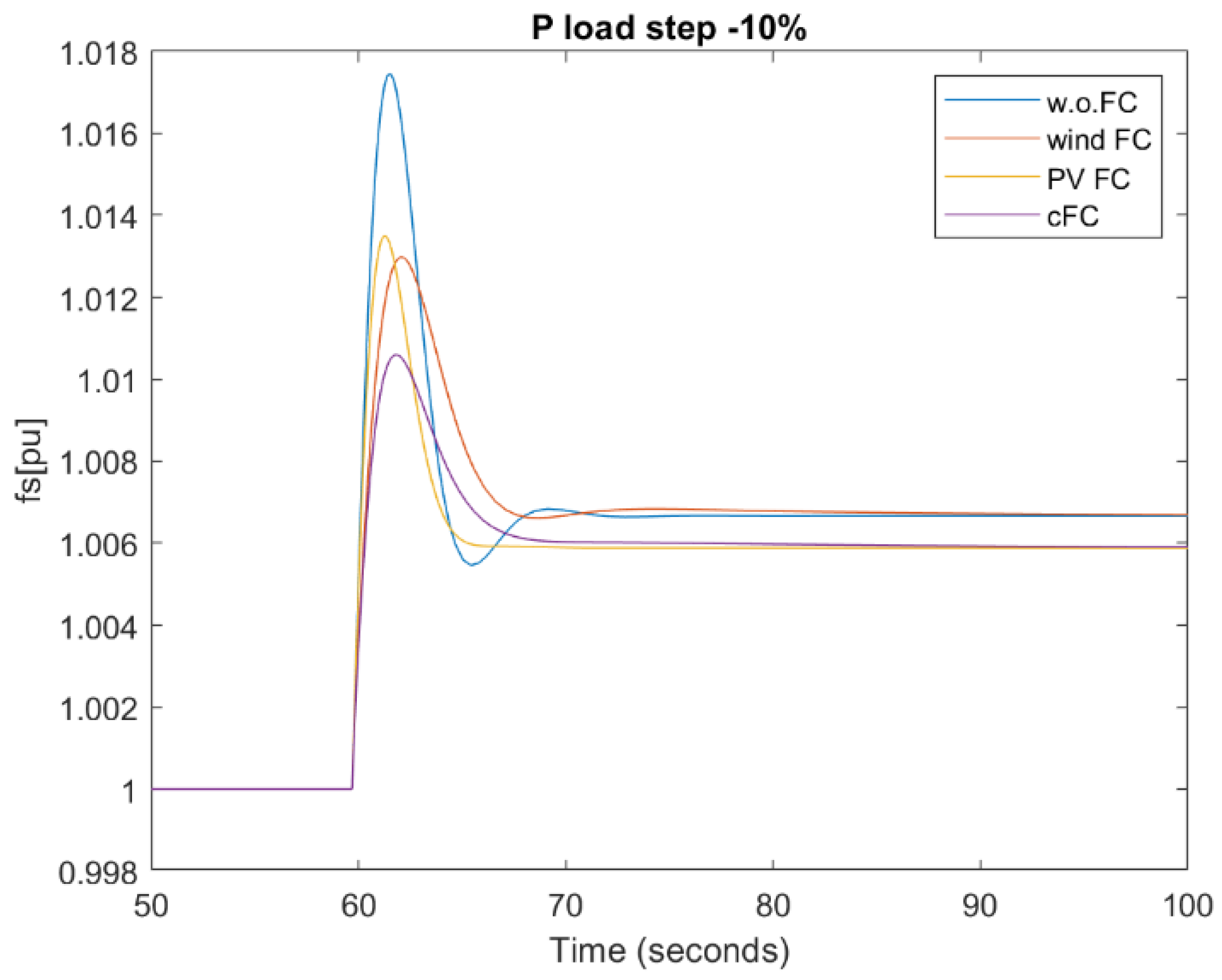
- Frequency nadir [Hz]: it is a direct measure of the primary frequency control adequacy. It is calculated as the maximum/minimum value of frequency deviation occurring after an active power imbalance. The closer it is to the nominal frequency, the better.
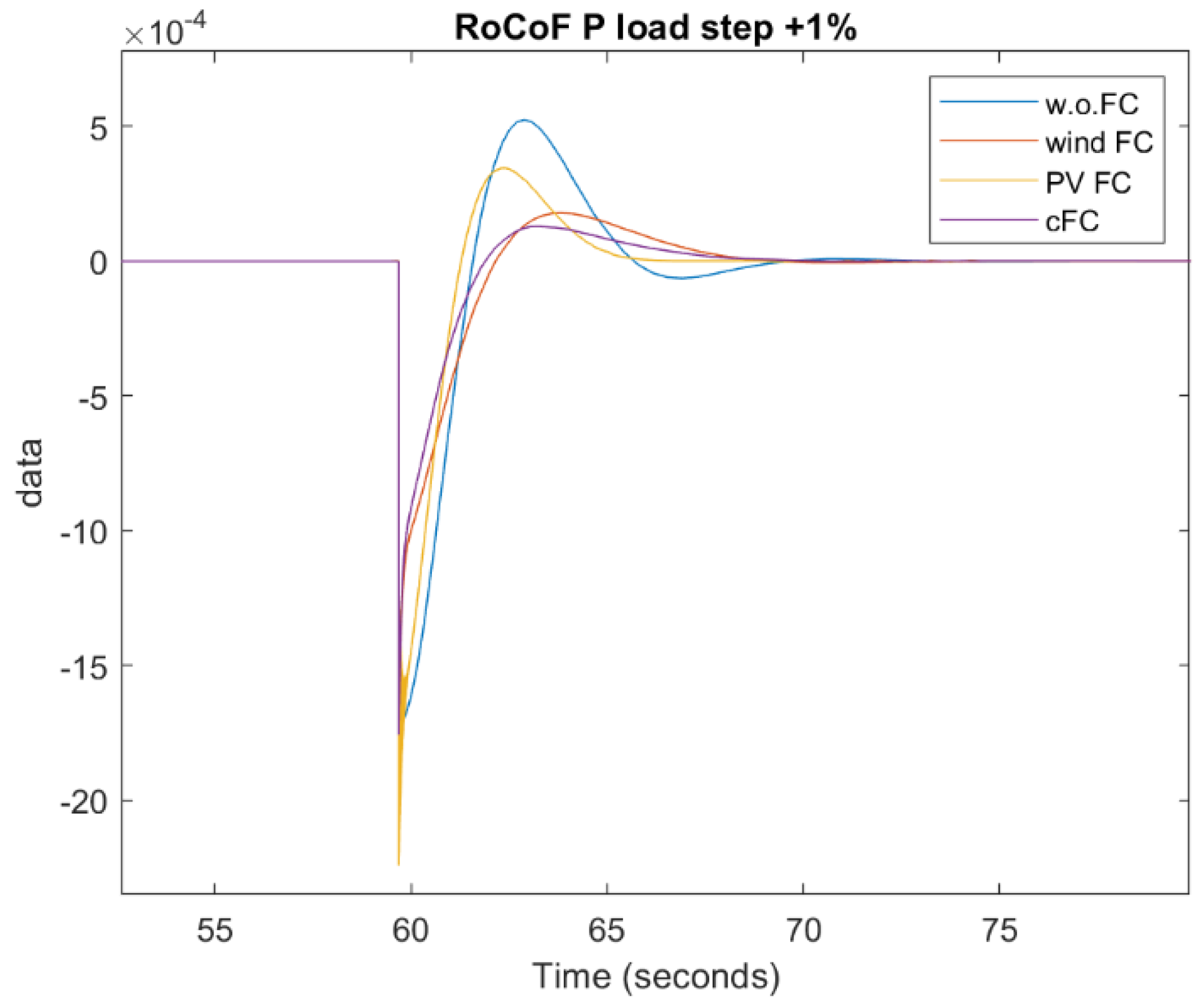
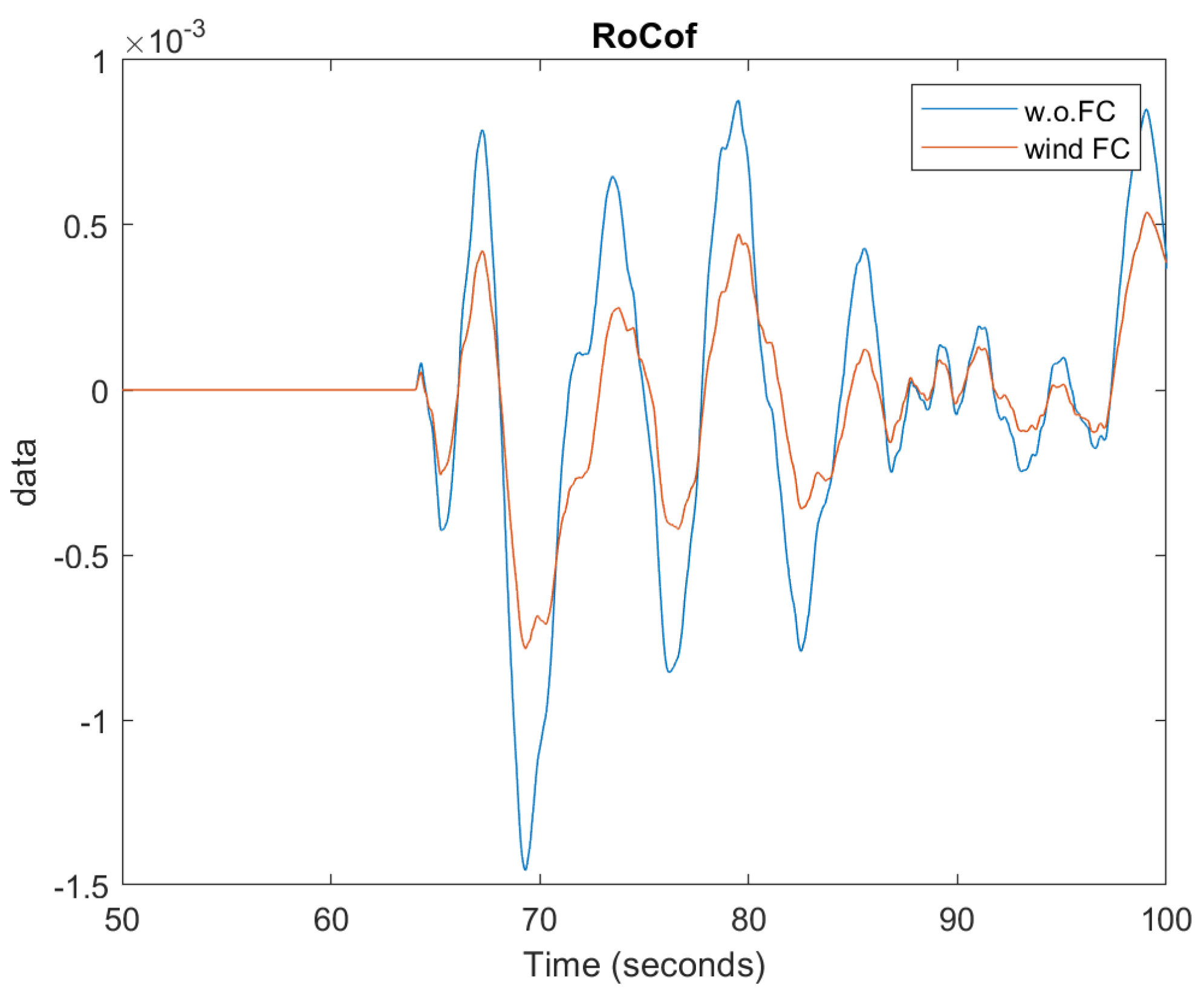
- RoCoF [Hz/s]: it is the time derivative of the system’s frequency. The smaller it is, the better for the system.
- Nadir-based frequency response: it expresses how good the primary frequency control has performed in stabilizing the frequency after a perturbation. It can be calculated as [37]:
4. Simulation Results
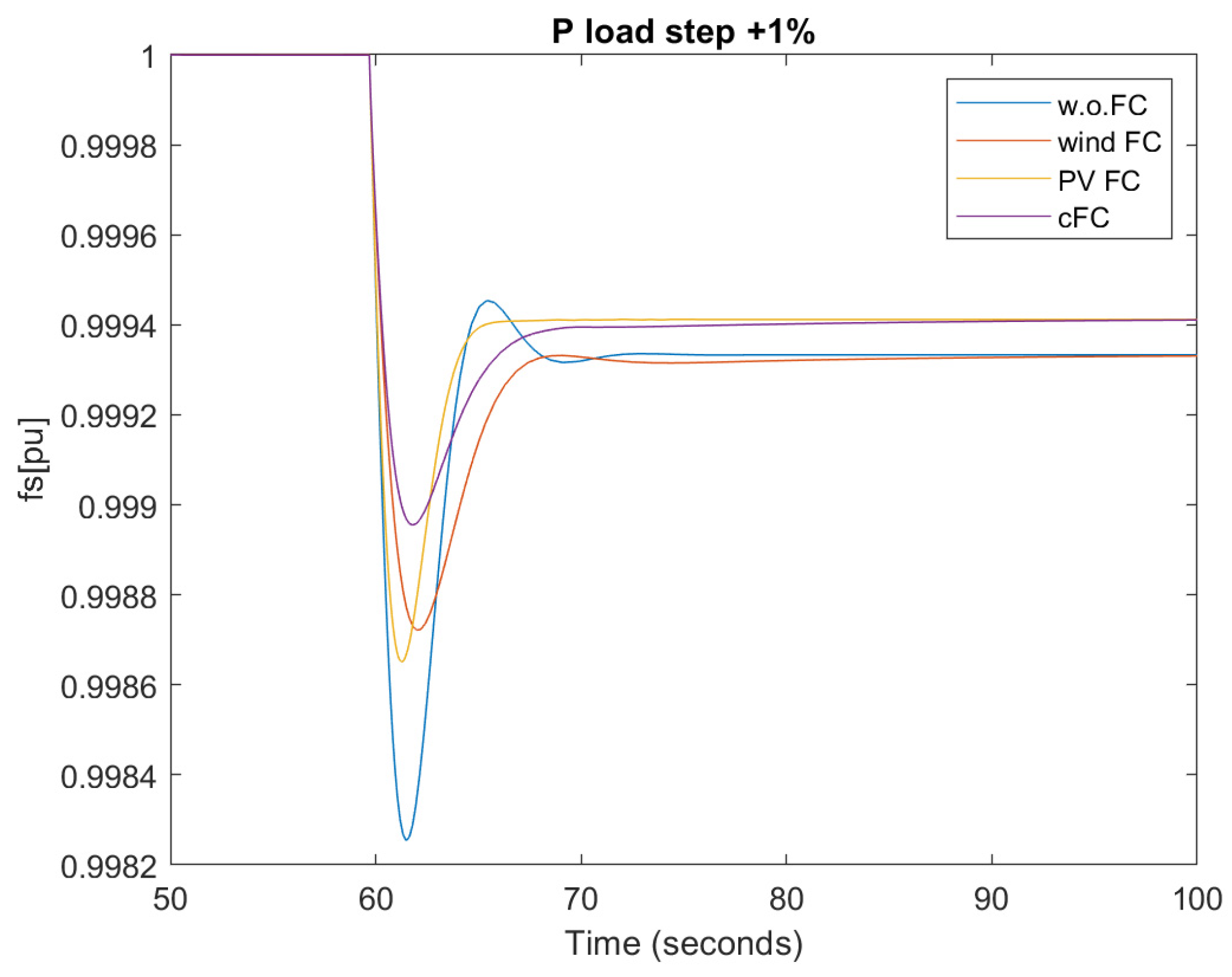
4.1. Load Power Step Up/Down
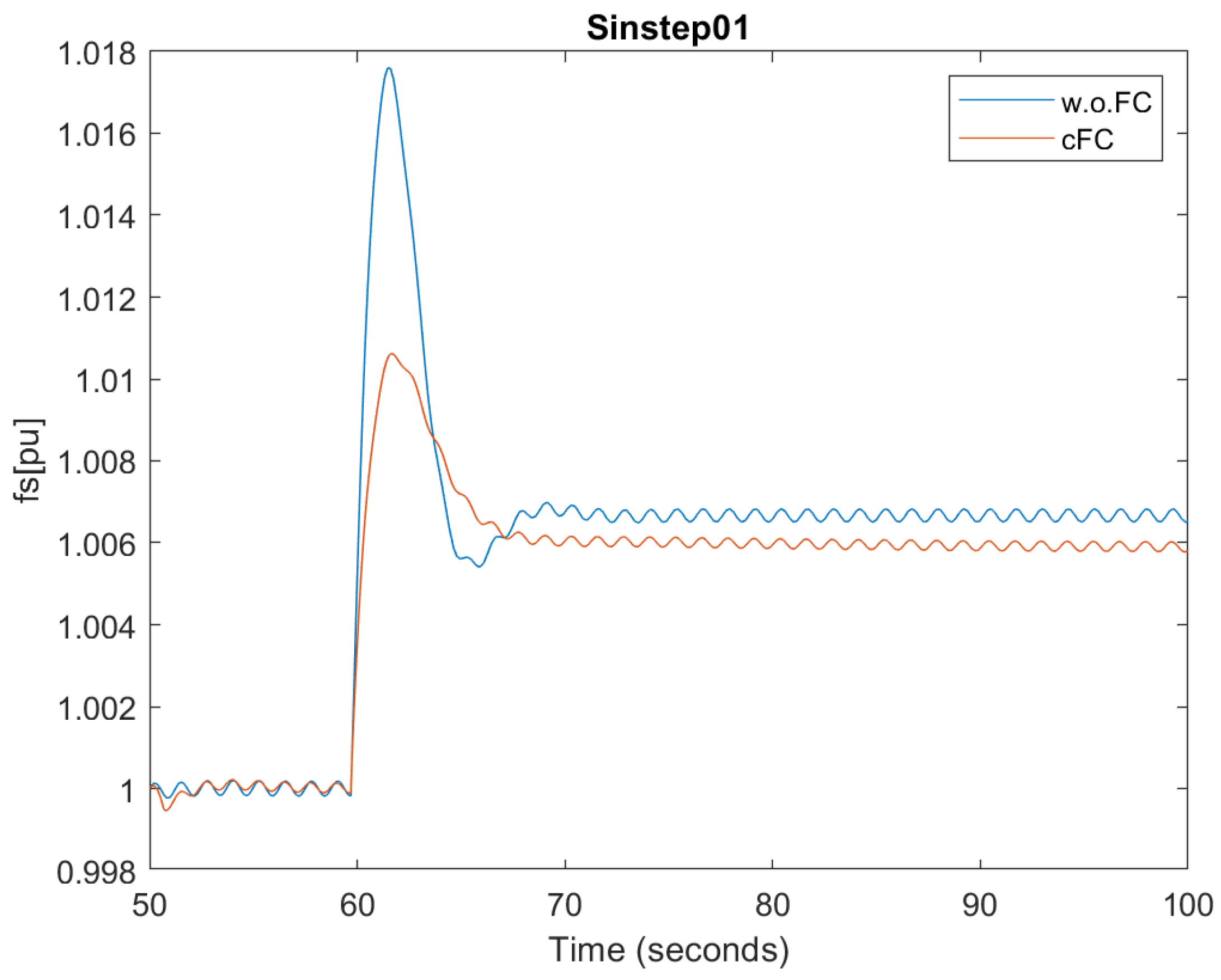
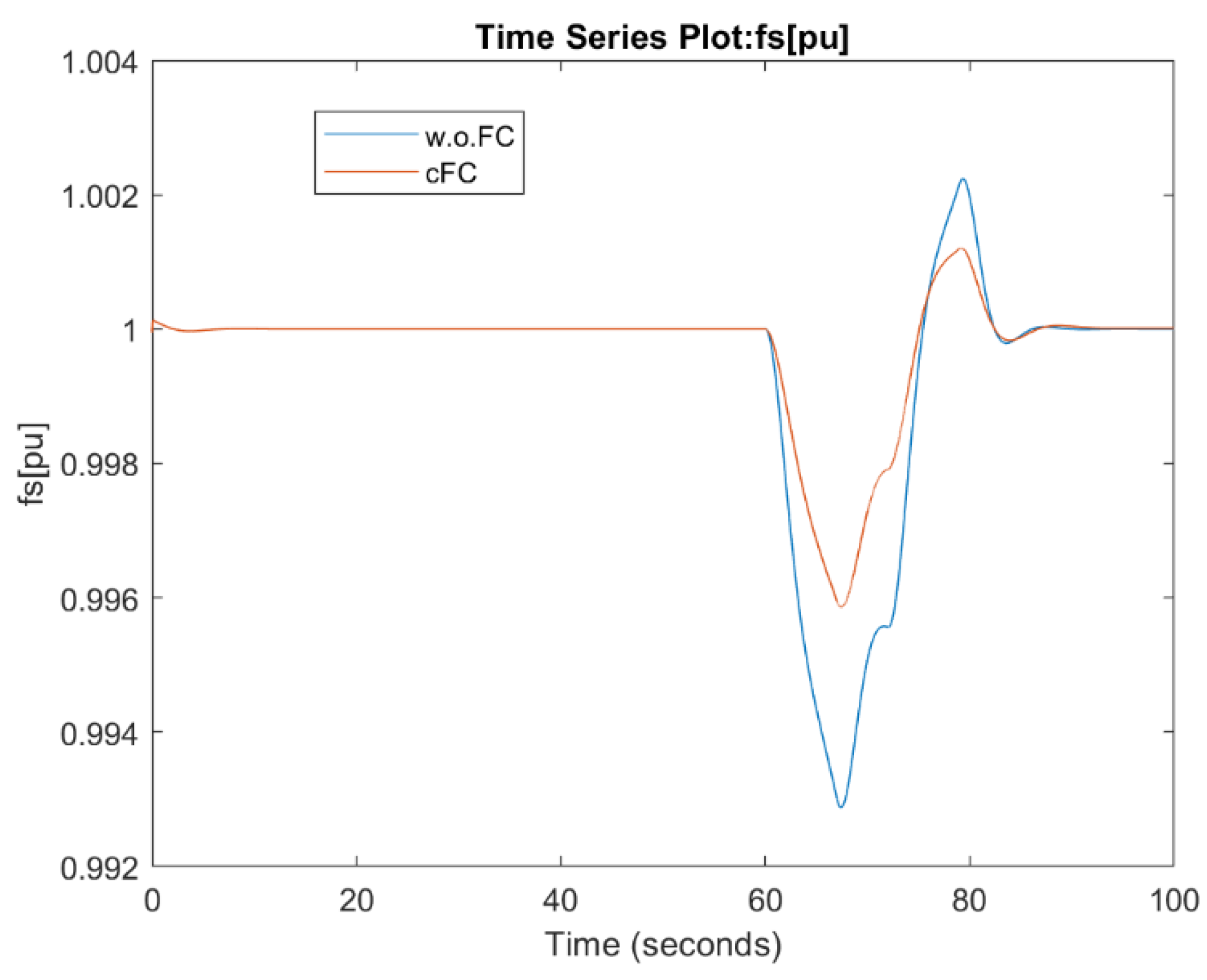
4.2. Small Sinusoidal Oscillations and Step down Load Active Power
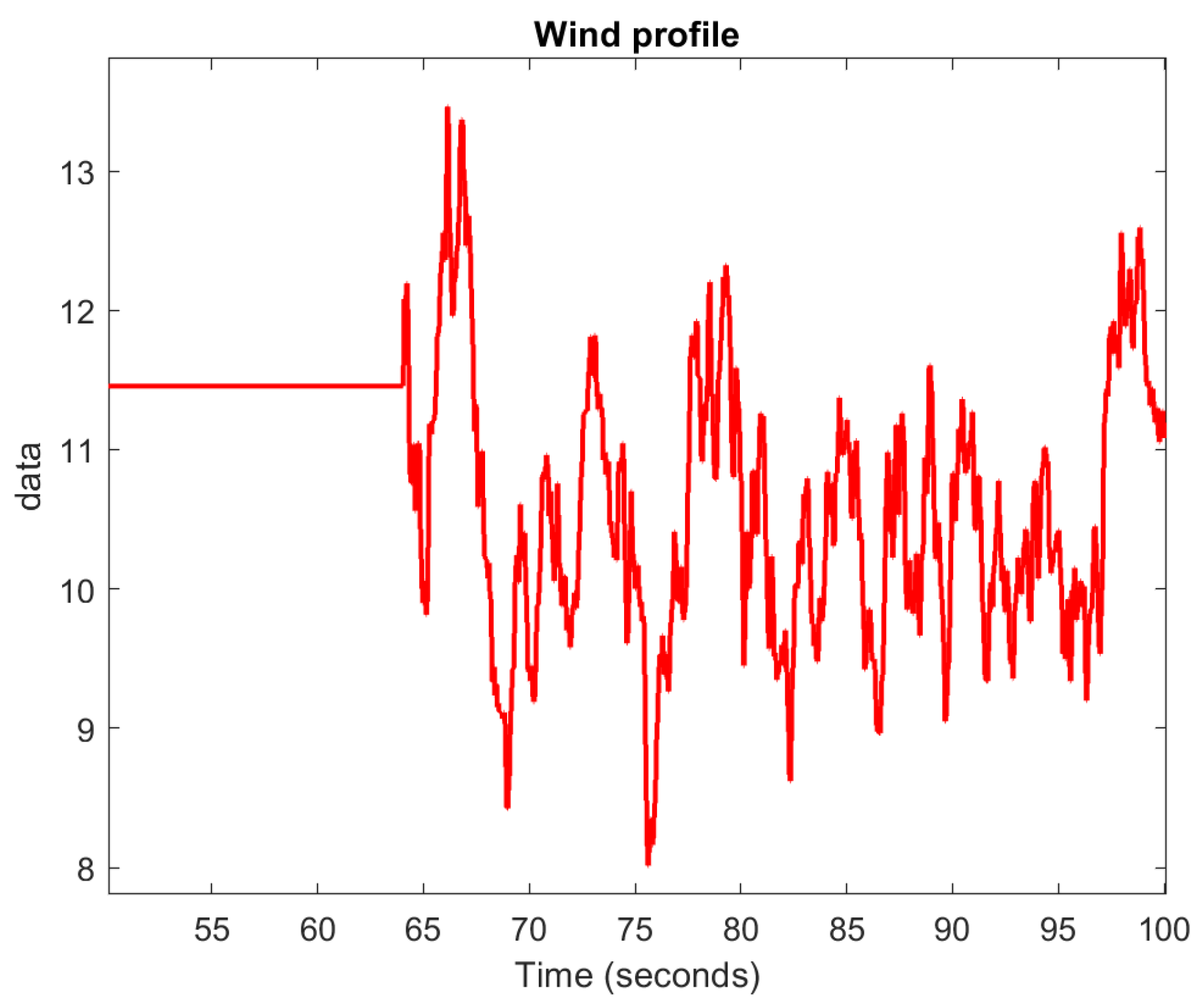
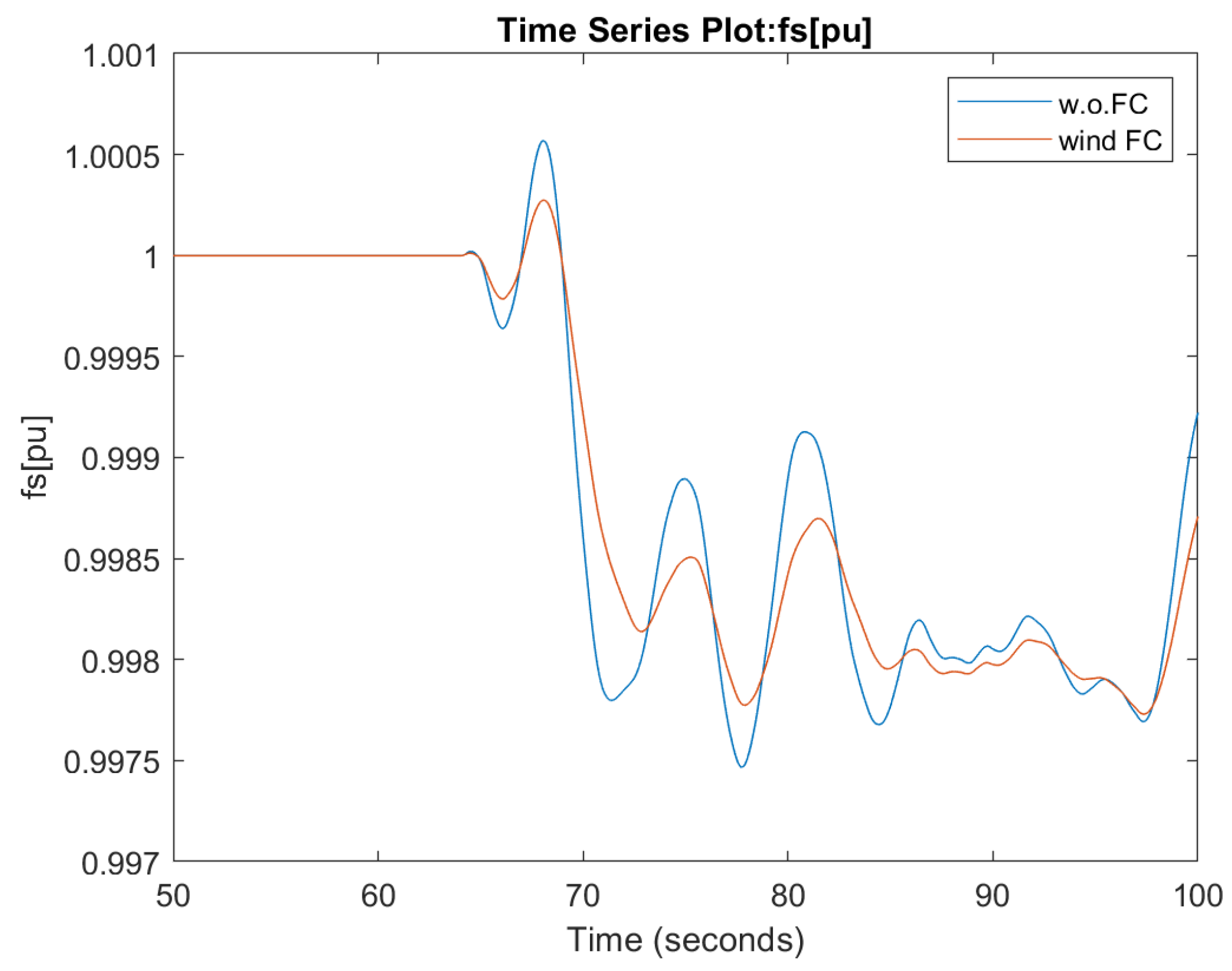
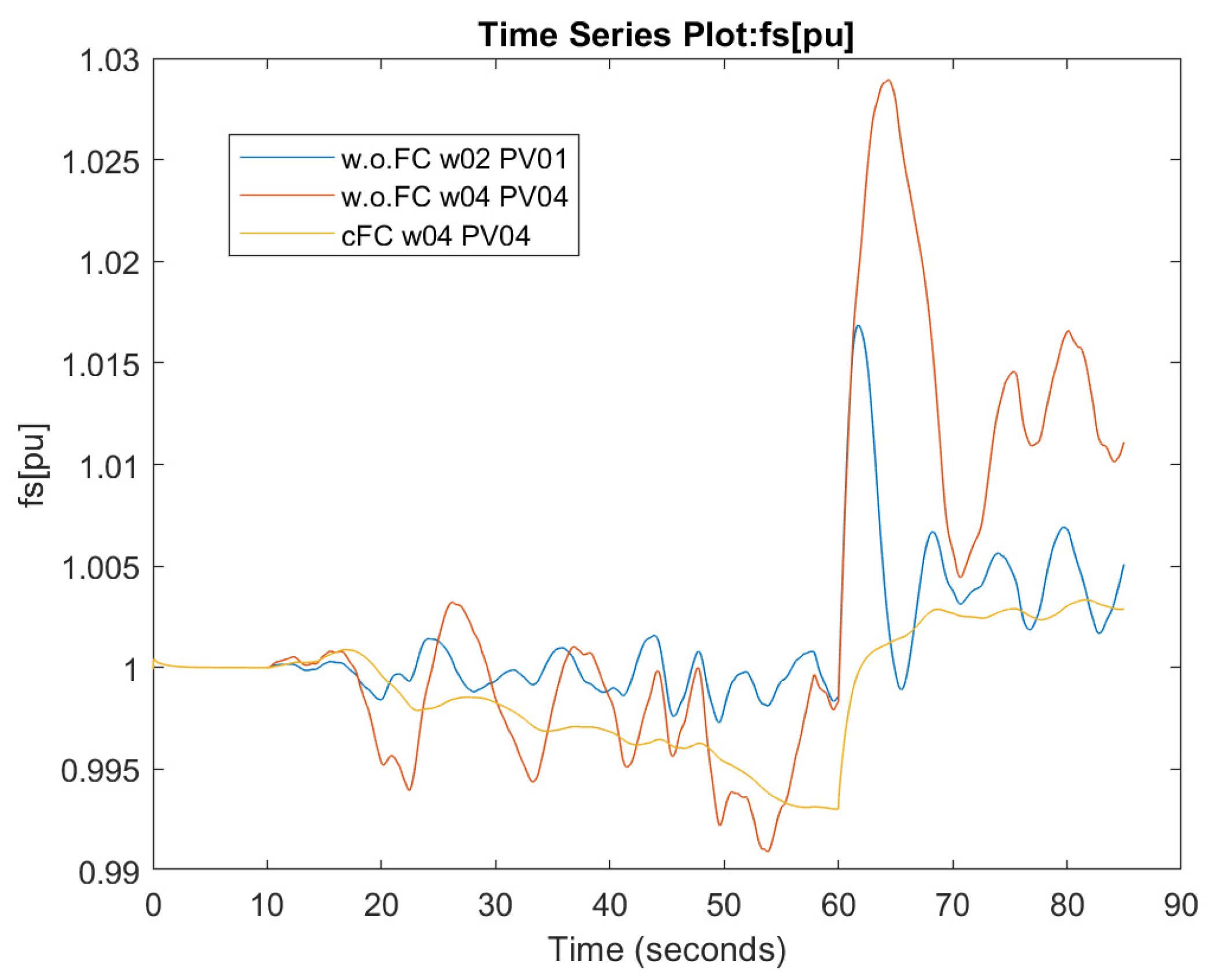
4.3. Variable Environmental Conditions
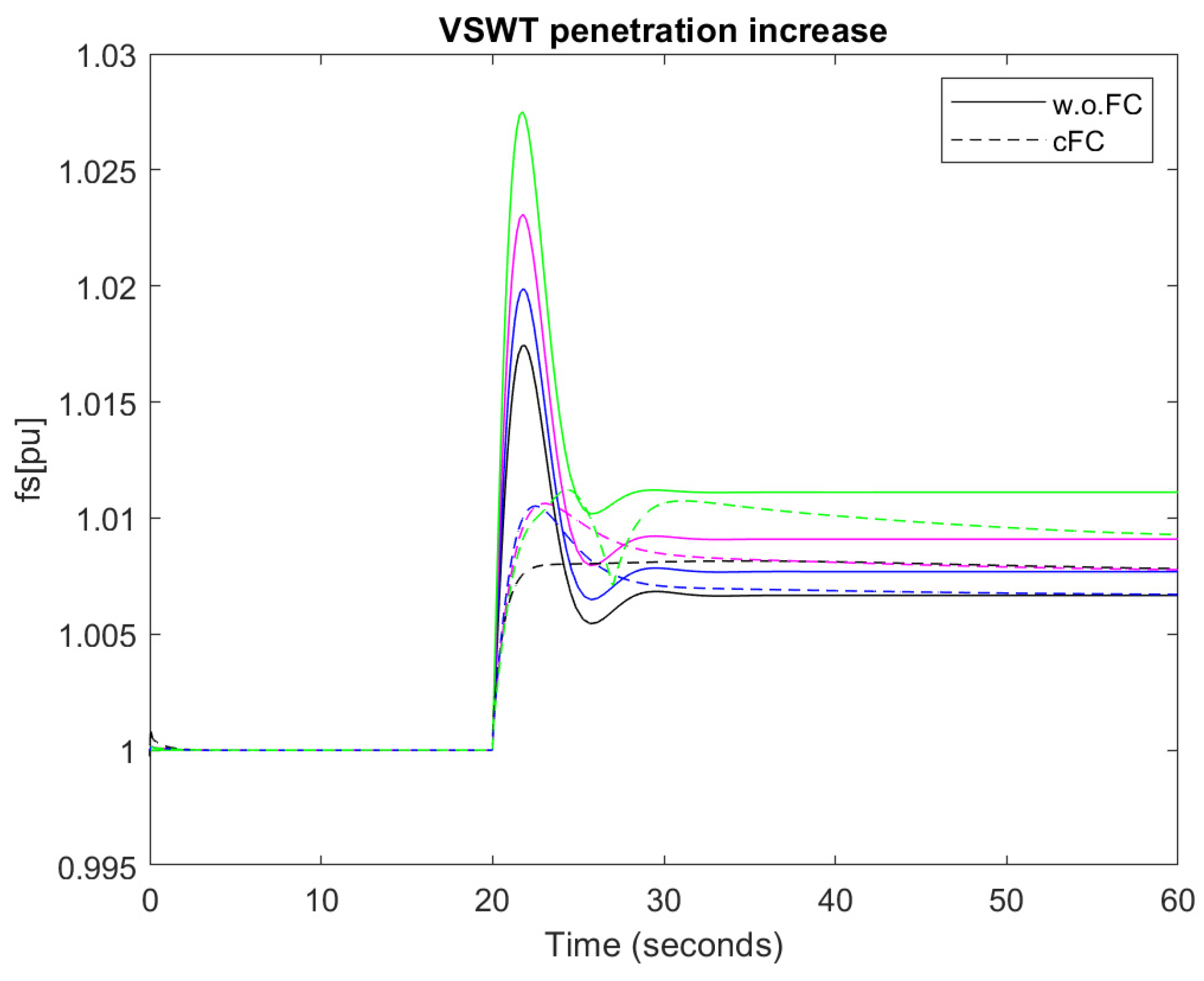
4.4. Increasing Renewables Penetration
5. Conclusions and Future Developments Proposals
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Values of Constants Used in the Model
- PV subsystem
- ▪
- PV module: Solartech Power SPM210P (four modules in series and variable number of arrays as a function of the participation factors)
- ▪
- Ccapacitor = 100 μF
- ▪
- Linductor = 10 mH
- ▪
- D-controlled boost converter with default Simulink settings
- ▪
- PI controller: P = 0.03; I = 1
- ▪
- Droop constant of active power reserve adaptation = 0.05
- ▪
- Initial reserve level = 0.2
- VSWT system
- ▪
- Pbase = Pt,base = Pg,base = 1.5 MW, vnom = 12 m/s, ωt,base = 1.644 rad/s, ωg,base = 157.08 rad/s, f = 50 Hz
- ▪
- Values for the model blocks taken from [36]
- ▪
- Speed governor PI controller: P = 3; I = 80
- ▪
- Pitch governor P controller: P = 500
- ▪
References
- European Council. Available online: https://www.consilium.europa.eu/en/policies/climate-change/paris-agreement/ (accessed on 1 August 2022).
- UNFCCC. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 1 August 2022).
- IEA. Available online: https://www.iea.org/data-and-statistics/data-browser?country=WORLD&fuel=CO2%20emissions&indicator=CO2BySector (accessed on 2 August 2022).
- European Energy Agency. Available online: https://www.eea.europa.eu/ims/share-of-energy-consumption-from (accessed on 2 August 2022).
- IRENA. Global Energy Transformation—A Roadmap to 2050; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- IRENA. Grid Codes for Renewable Powered Systems; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2022. [Google Scholar]
- Hassan, F.; Bollen, M. Integration of the Distributed Generation in the Power System; IEEE Press: New York, NY, USA, 2011. [Google Scholar]
- Riquelme-Dominguez, J.M.; De Paula Garcia-Lopez, F.; Martínez, S. Power Ramp-Rate Control via power regulation for storageless grid-connected photovoltaic systems. Int. J. Electr. Power Energy Syst. 2022, 138, 107848. [Google Scholar] [CrossRef]
- Brivio, C.; Mandelli, S.; Merlo, M. Battery energy storage system for primary control reserve and energy arbitrage. Sustain. Energy Grids Netw. 2016, 6, 152–165. [Google Scholar] [CrossRef]
- NREL. On the Path to Sunshot: The Role of Advancements in Solar Photovoltaic Efficiency, Reliability, and Costs; NREL: Golden, CO, USA, 2016.
- Solomon, A.A.; Bogdanov, D.; Breyer, C. Curtailment-storage-penetration nexus in the energy transition. Appl. Energy 2019, 235, 1351–1368. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. Development of Flexible Active Power Control Strategies for Grid-Connected Photovoltaic Inverters by Modifying MPPT Algorithms. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia, Kaohsiung, Taiwan, 3–7 June 2017. [Google Scholar]
- Batzelis, E.I.; Kampitsis, G.E.; Papathanassiou, S.A. Power Reserves Control for PV Systems With Real-Time MPP Estimation via Curve Fitting. IEEE Trans. Sustain. Energy 2017, 8, 1269–1280. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F.; Sera, D. Delta Power Control Strategy for Multi-String Grid-Connected PV Inverters. IEEE Trans. Ind. Appl. 2017, 53, 3862–3870. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wen, H.; Zhu, Y.; Jiang, L.; Hu, J.; Xiao, W. A Novel Sensorless Photovoltaic Power Reserve Control With Simple Real-Time MPP Estimation. IEEE Trans. Power Electron. 2019, 34, 7521–7531. [Google Scholar] [CrossRef]
- Hoke, A.; Chakraborty, S.; Shirazi, M.; Muljadi, E. Rapid Active Power Control of Photovoltaic Systems for Grid Frequency Support. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1154–1163. [Google Scholar] [CrossRef]
- Riquelme-Dominguez, J.M.; Martinez, S. A Photovoltaic Power Curtailment Method for Operation on Both Sides of the Power-Voltage Curve. Energies 2020, 13, 3906. [Google Scholar] [CrossRef]
- Nanou, S.; Papakonstantinou, A.; Papathanassiou, S. A generic model of two-stage grid-connected PV systems with primary frequency response and inertia emulation. Electr. Power Syst. Res. 2015, 127, 186–196. [Google Scholar] [CrossRef]
- Riquelme-Dominguez, J.M.; Martínez, S. Systematic Evaluation of Photovoltaic MPPT Algorithms Using State-Space Models Under Different Dynamic Test Procedures. IEEE Access 2022, 10, 45772–45783. [Google Scholar] [CrossRef]
- Aziz, A.; Oo, A.T.; Stojcevski, A. Frequency regulation capabilities in wind power plant. Sustain. Energy Technol. Assess. 2018, 26, 47–76. [Google Scholar] [CrossRef]
- Clark, K.; Miller, N.W.; Sanchez-Gasca, J.J. Modelling of GE Wind Turbine-Generators; Tech. Rep.; Version 4.5; General Electric International: Schenectady, NY, USA, 2010. [Google Scholar]
- Engelken, S.; Mendonca, A.; Fischer, M. Inertial response with improved variable recovery behaviour provided by type 4 WTs. IET Renew. Power Gener. Spec. 2017, 11, 195–201. [Google Scholar] [CrossRef]
- Wu, Y.; Shu, W.; Hsieh, T.; Lee, T. Review of inertial control methods for DFIG-based wind turbines. Int. J. Electr. Energy 2015, 3, 174–178. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, D.; Martínez, S. Analytical Approach to Understanding the Effects of Implementing Fast-Frequency Response by Wind Turbines on the Short-Term Operation of Power Systems. Energies 2021, 14, 3660. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Senroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Hwang, M.; Muljadi, E.; Park, J.W.; Sorensen, P.; Kang, T.C. Dynamic droop-based inertial control of a doubly-fed induction generator. IEEE Trans. Sustain. Energy 2016, 7, 924–933. [Google Scholar] [CrossRef]
- Fairley, P. Can Synthetic Inertia from Wind Power Stabilize Grids? IEEE Spectrum 2016, 7. [Google Scholar]
- Fu, Y.; Zhang, X.; Hei, Y.; Wang, H. Active participation of variable speed wind turbine in inertial and primary frequency regulations. Electr. Power Syst. Res. 2017, 147, 174–184. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasua, J.I.; Perez-Diaz, J.I.; Martínez, S.; Ochoa, D. Analysis of the Implementation of the Primary and/or Inertial Frequency Control in Variable Speed Wind Turbines in an Isolated Power System with High Renewable Penetration. Case Study: El Hierro Power System. Electronics 2020, 9, 901. [Google Scholar] [CrossRef]
- Díaz-González, F.; Hau, M.; Sumper, A.; Bellmunt, O. Participation of wind power plants in system frequency control: Review of grid code requirements and control methods. Renew. Sustain. Energy Rev. 2014, 34, 551–564. [Google Scholar] [CrossRef]
- O’Sullivan, J.; Rogers, A.; Flynn, D.; Smith, P.; Mullane, A.; O’Malley, M. Studying the maximum instantaneous non-synchronous generation in an island system—Frequency stability challenges in Ireland. IEEE Trans. Power Syst. 2014, 29, 2943–2951. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; Electric Power Research Institute: Palo Alto, CA, USA, 1993. [Google Scholar]
- Li, S.; Deng, C.; Shu, Z.; Huang, W.; Jun He, J.; You, Z. Equivalent inertial time constant of doubly fed induction generator considering synthetic inertial control. J. Renew. Sustain. Energy 2016, 8, 053304. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variations of PV module parameters with irradiance and temperature. Energy Procedia 2017, 134, 276–285. [Google Scholar] [CrossRef]
- Carrero, C.; Ramírez, D.; Rodríguez, J.; Platero, C.A. Accurate and fast convergence method for parameter estimation of PV generators based on three main points of the I-V curve. Renew. Energy 2011, 36, 2972–2977. [Google Scholar] [CrossRef]
- Ochoa, D.; Martínez, S. A Simplified Electro-Mechanical Model of a DFIG-based Wind Turbine for Primary Frequency Control Studies. IEEE Lat. Am. Trans. 2016, 14, 3614–3620. [Google Scholar] [CrossRef] [Green Version]
- Eto, J.H. Use of Frequency Response Metrics to Assess the Planning and Operating Requirements for Reliable Integration of Variable Renewable Generation; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2011; Available online: https://escholarship.org/uc/item/0kt109pn (accessed on 20 October 2022).
- DTU Data: Database on Wind Characteristics. Available online: https://gitlab.windenergy.dtu.dk/fair-data/winddata-revamp/winddata-documentation/-/blob/master/readme.md/ (accessed on 20 October 2022).
- Ochoa, D.; Martinez, S. Fast-Frequency Response Provided by DFIG-Wind Turbines and Its Impact on the Grid. IEEE Trans. Power Syst. 2017, 32, 4002–4011. [Google Scholar] [CrossRef]







| N° | Authors | Reference |
|---|---|---|
| 1 | Batzelis et al. | [13] |
| 2 | Sangwongwanich et al. | [14] |
| 3 | Li et al. | [15] |
| 4 | Hoke et al. | [16] |
| 5 | Riquelme et al. | [17] |
| Simulation Group | Aim |
|---|---|
| Load active power step up/down | Observing the frequency response of the system after a sudden variation of the load power for different step magnitudes |
| Small sinusoidal oscillations + step of load active power | Observing the frequency response of the system to small and continuous variations of the load, i.e., similar to the real behavior, and to a step if a part of the reserve is already in use to balance the small variations |
| Variable environmental conditions (real wind speed profile, irradiance variations) | Understanding how the system responds to environmental condition changes, as well as to a sudden load power variation in such a situation |
| Variable participation factors | Understanding what is the impact of an increasing penetration of renewable sources on the system’s frequency stability |
| N° Simulation | Features |
|---|---|
| 1 | Step up Pload +1% |
| 2 | Step down Pload −1% |
| 3 | Step down Pload −2% |
| 4 | Step down Pload −10% |
| 5 | Small sinusoidal variation of Pload (amplitude 5‰) + step down Pload −10% |
| 6 | Real wind profile |
| 7 | Real wind profile + step down Pload −10% |
| 8 | Steep irradiance ramp up—ramp down |
| N° Simulation | pwind | psynchronous | ppv |
|---|---|---|---|
| 9 | 0.3 | 0.6 | 0.1 |
| 10 | 0.4 | 0.5 | 0.1 |
| 11 | 0.5 | 0.4 | 0.1 |
| 12 | 0.2 | 0.6 | 0.2 |
| 13 | 0.2 | 0.5 | 0.3 |
| 14 | 0.2 | 0.4 | 0.4 |
| 15 | 0.3 | 0.5 | 0.2 |
| 16 | 0.4 | 0.3 | 0.3 |
| 17 | 0.4 | 0.2 | 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radaelli, L.; Martinez, S. Frequency Stability Analysis of a Low Inertia Power System with Interactions among Power Electronics Interfaced Generators with Frequency Response Capabilities. Appl. Sci. 2022, 12, 11126. https://doi.org/10.3390/app122111126
Radaelli L, Martinez S. Frequency Stability Analysis of a Low Inertia Power System with Interactions among Power Electronics Interfaced Generators with Frequency Response Capabilities. Applied Sciences. 2022; 12(21):11126. https://doi.org/10.3390/app122111126
Chicago/Turabian StyleRadaelli, Lucio, and Sergio Martinez. 2022. "Frequency Stability Analysis of a Low Inertia Power System with Interactions among Power Electronics Interfaced Generators with Frequency Response Capabilities" Applied Sciences 12, no. 21: 11126. https://doi.org/10.3390/app122111126





