1. Introduction
In recent decades, the rapid increase in the world’s population, the social, economic, and industrial growth as well as urbanization, have significantly amplified the energy needs, the utilization of fossil fuels, and greenhouse gas emissions [
1]. These facts have affected negatively not only the natural environment and the atmosphere, but they also can cause health problems for human beings; therefore, the international community has decided to act via international environmental policies such as the Kyoto Protocol (1997), and the Paris agreement (2015). These agreements focus on the avoidance of environmental damage and global warming, as well as the replacement of non-renewable energy sources [
2]. Human needs can be covered through cleaner, more sustainable, and energy-efficient ways [
1], using renewable energy sources such as biomass, wind, or solar [
3].
Solar energy is an environmentally friendly source with very high potential. Many different technologies and devices have been developed to exploit solar irradiation into electricity or thermal energy. Photovoltaic (PV) cells can transform solar energy directly into electricity, while solar thermal collectors produce useful heat. Solar collectors can be utilized for small-scale applications, such as space and water heating, as well as in large-scale installations, to provide industrial heat or drive power plants [
4]. The most developed and utilized solar technology is the parabolic trough collector (PTC). A PTC exploits solar beam irradiation and includes a parabolic mirror, as well as a tubular receiver, in which the heat transfer medium absorbs heat and its temperature increases. In parallel, the collectors track the Sun during the day and are incorporated with thermal energy storage (TES) units, to improve their efficiency. Moreover, PTCs operate at low- and medium-temperature levels, with values up to 400 °C; therefore, these devices can be used for industrial heating applications and can properly feed electricity generation systems [
5], such as organic Rankine cycles (ORC), or Brayton cycles [
6].
First of all, Yu et al. [
7] investigated a solar-powered ORC unit, which consisted of a PTC field, as well as a hot, and cold TES tank. In the case of using toluene as a working medium, the most proper performance was achieved, as the overall efficiency was enhanced by 24.8%, in comparison with another study in the literature. The thermal and exergy efficiencies were also increased by 11.3% and 10.8%, respectively, for the case of using a supercritical ORC, compared with the corresponding subcritical cycle. In addition, Arslan and Kilic [
8] studied an ORC plant fed by PTCs, which was supposed to be installed in a low-solar radiation zone. A hot and cold storage tank was also integrated. Six eco-friendly organic refrigerants, as well as water steam, were investigated. According to the results of dynamic analysis, the optimum and the most economically viable design was the case of the water-steam cycle, when the net present value was calculated at USD 9.012 × 10
6. The maximum rates of energy and exergy performance were determined as 11.05% and 11.86%, respectively. Moreover, configurations based on the combination of a steam Rankine cycle and an ORC were analyzed in publications. For example, Bahari et al. [
9] investigated a PTC-based power generation unit that included a two-stage steam Rankine cycle and an ORC as a bottoming cycle. Molten salt was used as a heat transfer and storage fluid in the incorporated tank. The configuration was optimized via the particle swarm optimization (PSO) algorithm considering the maximum exergy efficiency and the minimum levelized cost of electricity (LCOE). At the optimum scenario, the overall exergy efficiency, and the levelized cost of electricity were found at 63.89% and 0.1529 USD/kWh, respectively. Furthermore, Li et al. [
10] studied a solar-driven electricity plant that contained a PTC field, a storage unit based on a phase change material (PCM), a steam Rankine cycle, and an ORC. The system was modeled and optimized in off-design conditions taking into account different isentropic efficiencies of the Rankine cycle screw expander when the pressure ratio was varied. The maximum achieved values of the solar thermal power efficiency were calculated as 13.74–15.45%, with an expander volume ratio that was equal to five. Finally, Wang et al. [
11] analyzed a recompression supercritical CO
2 Brayton cycle, that was used to generate power and was powered by a PTC. A molten salt TES unit was also included. The system performance was investigated for different design parameters, as well as weather and irradiation conditions. The cycle energy efficiency could be found greater than 40%, in optimal conditions.
However, solar irradiation is not always available and is varied during the day and the year. Production intermittency is the main drawback of solar energy; therefore, it is important to integrate a TES system. This unit can store useful heat during the sunshine, which can be used when solar irradiation is limited or there is no irradiation. The most common and mature technology is sensible TES [
12]. Most of the time, solar-based plants include one or more storage tanks, to store heat during the day and release it to continue their operation after sunset; therefore, insulated tanks are capable of short-term TES for a couple of hours [
13,
14]. In parallel, several other forms of energy storage have been developed to store surplus electricity during off-peak hours. Because of the further integration of renewable sources in the energy mix, it is essential to use methods for long-term or seasonal storage, such as the technologies of pumped hydro energy storage (PHES), compressed air energy storage (CAES), and thermochemical energy storage [
15,
16]. In addition, hydrogen has gained further attention in recent years as a way of seasonal energy storage [
17]. Because of the fact that hydrogen is not directly available in nature, it can be produced from fossil fuels via steam methane reforming or renewable energy sources via water electrolysis. The water electrolyzer is fed with excess renewable electricity, to produce green hydrogen without carbon emissions. When it is reacted with oxygen, the only by-product is water; therefore, hydrogen is a sustainable energy carrier that can be used in transportation, power generation, buildings, and industry [
18]. Hydrogen can be stored as a compressed gas (compressed hydrogen), as a liquid (liquified hydrogen), as well as in solid or liquid storage materials [
19]. Thus, hydrogen energy storage promotes the sustainability and autonomy of the energy systems [
20].
Plenty of studies based on solar-fed power plants or multigeneration units have been published by researchers that contain hydrogen as a product. These kinds of systems are more energy-efficient compared to single-production units [
21]. At first, Atiz et al. [
22] investigated a solar-geothermal-driven configuration that generated electricity and hydrogen. This system was made up of a PTC field, an ORC, a proton exchange membrane (PEM) electrolyzer, and a cooling tower for the ORC condenser. According to the results, the energy and exergy efficiency was found to be 5.85% and 8.27%, respectively, while the average electricity production was determined at 66.02 kW between the hours of 11:00–13:00, and the daily hydrogen production amount was 9807.1 g. Moreover, Mahmood et al. [
23] analyzed a polygeneration system installed in a greenhouse that produced electricity, fresh water, and space cooling. The system contained a PTC, a TES unit, an ORC, an absorption cooling cycle, a desalination unit, and a PEM water electrolyzer. The produced hydrogen and oxygen amounts could feed a hydrogen-oxy combustor if there was no solar irradiation. The plant energy and exergy efficiencies were determined to be 41.0% and 28.4%, respectively, while the hydrogen production rate was determined at 0.01 kg/s. Furthermore, Tukenmez et al. [
24] proposed a multigeneration configuration that provided electricity, heating, cooling, drying, hydrogen, hot water, and freshwater. Consequently, the unit included a PTC field, a distillation plant, a PEM electrolyzer, a hydrogen compression system, a Kalina cycle, an ORC, an ejector cooling cycle, a domestic water heater, a dryer, as well as a hot and a cold storage tank. The overall energy efficiency, the exergy efficiency, and the hydrogen production rate were calculated to be equal to 59.34%, 56.51%, and 0.0043 kg/s, respectively. In parallel, the integration of hydrogen into the energy networks of islands and remote communities has also been investigated. More specifically, Katsaprakakis et al. [
25] proposed the installation of a PHES system and a wind park, which would work together with the existing PV panels and wind turbines, on the Greek island of Sifnos. The fundamental purpose of the whole project was the coverage of the entire electricity demand by the previously mentioned modules, and the energy independence of the island. The surplus electricity was used to produce potable water and hydrogen. Then, the produced hydrogen would power the passenger ships connecting Sifnos with the nearby islands.
According to the previous literature review, the majority of solar-based power plants and polygeneration systems, include storage tanks to store the excess thermal energy that comes from solar irradiation. This method can store energy only for a couple of hours. Hydrogen energy storage is a long-term method, as hydrogen can be stored and used as a fuel with numerous applications. The present study is an innovative one because two storage technologies are incorporated simultaneously, the solar TES tank and chemical energy storage in the form of compressed hydrogen. Moreover, there is a lack of studies that focus on the hydrogen storage capacity of an energy plant powered by solar energy. The surplus electricity produced by the solar ORC unit is fed to a water electrolyzer to produce hydrogen for later use after several days and even months.
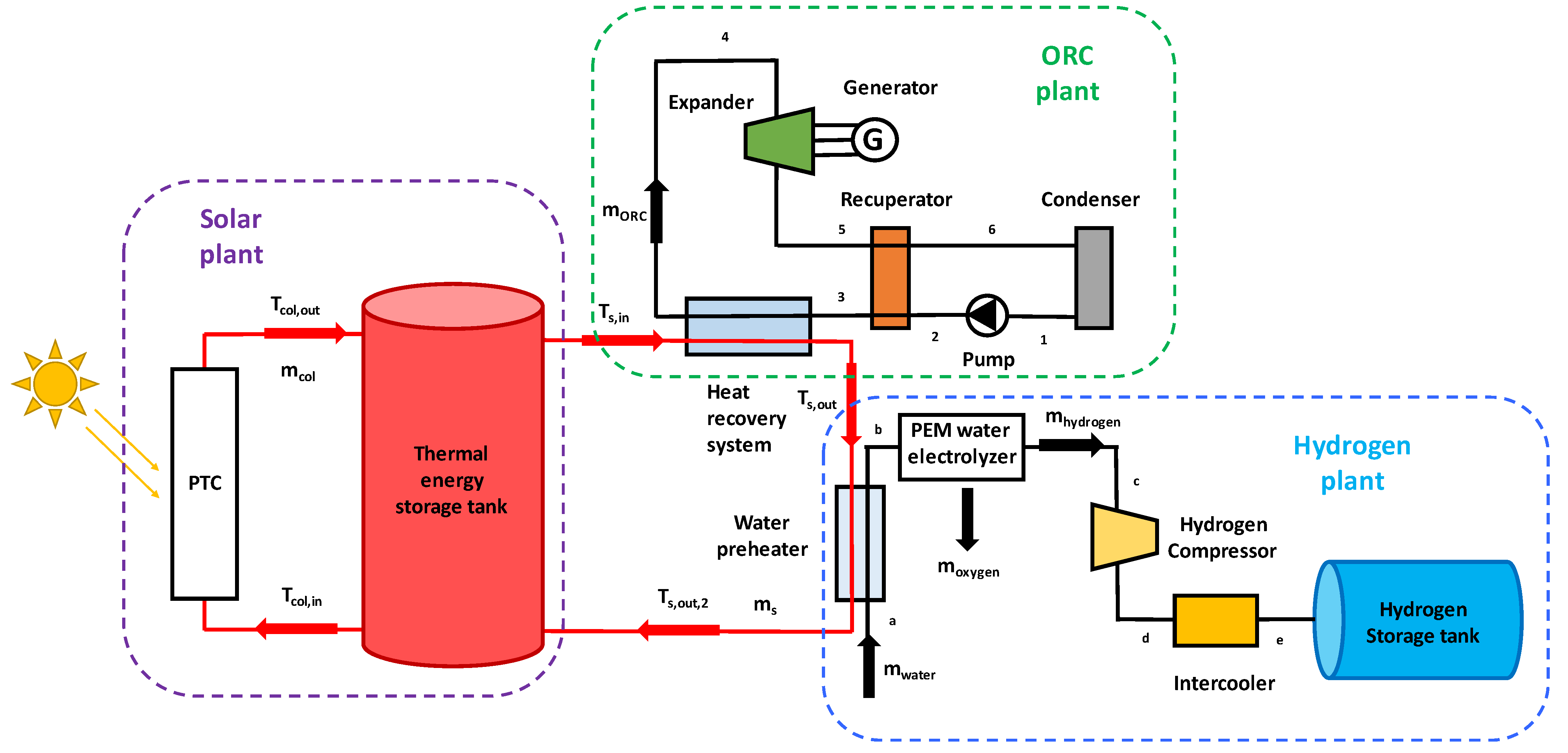
The examined configuration is planned to be installed on the Greek island of Kythnos, close to Athens. This island is not interconnected to the national grid; therefore, it is important to cover the electricity demand with its own sources and to store energy for later use. The proposed plant consists of a few PTC modules that absorb the solar beam irradiation to provide useful heat as an input to the ORC module. Furthermore, the installation contains a TES tank, a PEM water electrolyzer, a hydrogen compressor, and a hydrogen storage tank. A share of the ORC power generation feeds both the electrolyzer and the hydrogen compression system, while the remaining electricity can cover the island’s electricity demand. The other useful output is compressed hydrogen fuel, which can be sold or used on-site to power fuel cell vehicles or vessels. Therefore, this small-scale solar-powered energy unit provides electricity and green hydrogen while the integration of two storage technologies increases the system’s dispatchability.
At first, a preliminary analysis is conducted, and then the system is analyzed and optimized under dynamic conditions. The whole configuration is evaluated by calculating the main energetic, exergetic, and economic indexes. Finally, the preliminary analysis is performed by an Engineering Equation Solver (EES) software code, while the dynamic simulation is carried out using Matlab.