A Method of Predicting Critical Derailment Speed and Analysis of Derailment Process
Abstract
:1. Introduction
2. Vehicle–Track System Dynamic Model
3. Calculation Methods of Critical Speed
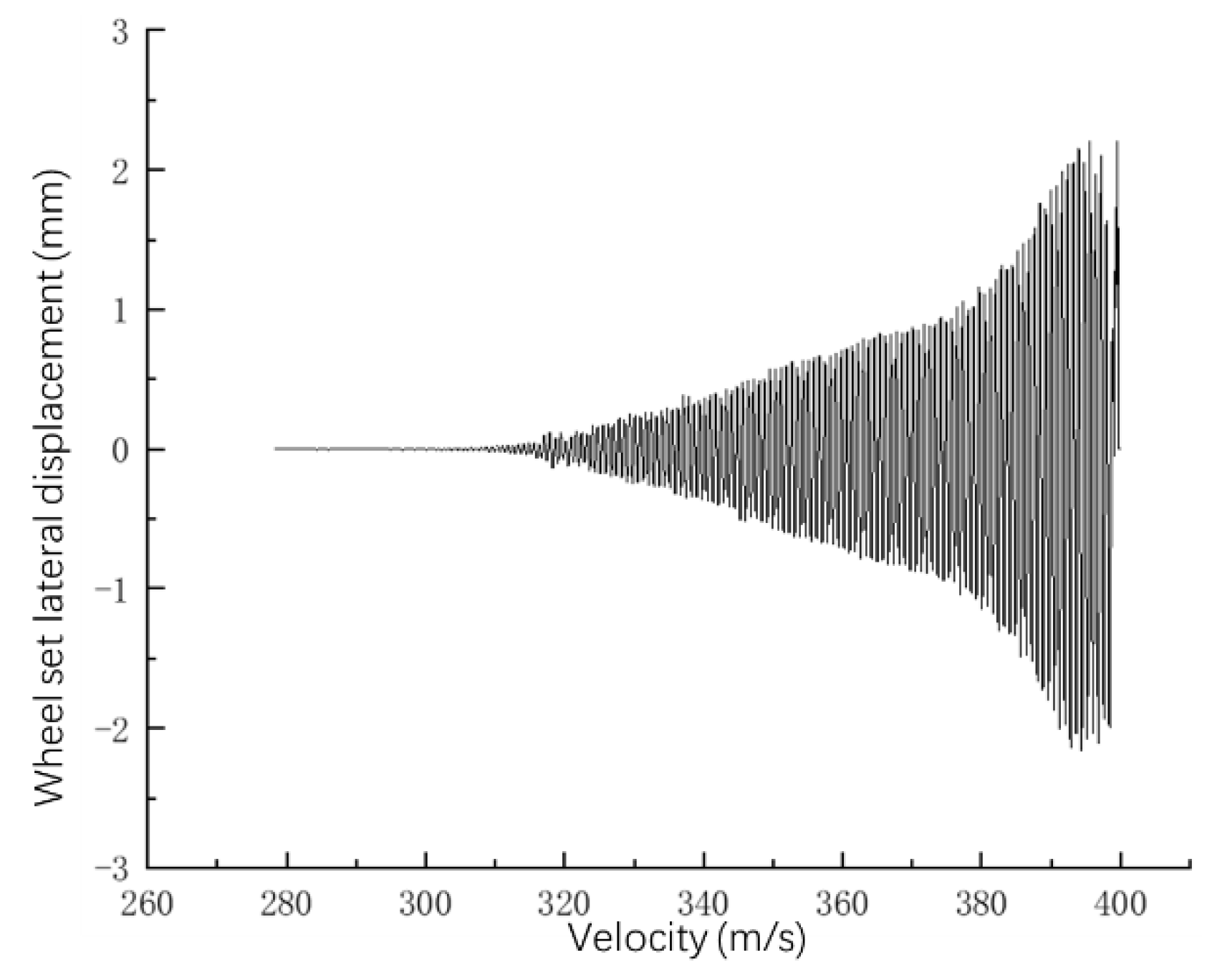
3.1. The Limit Cycle Method and Root Locus Method
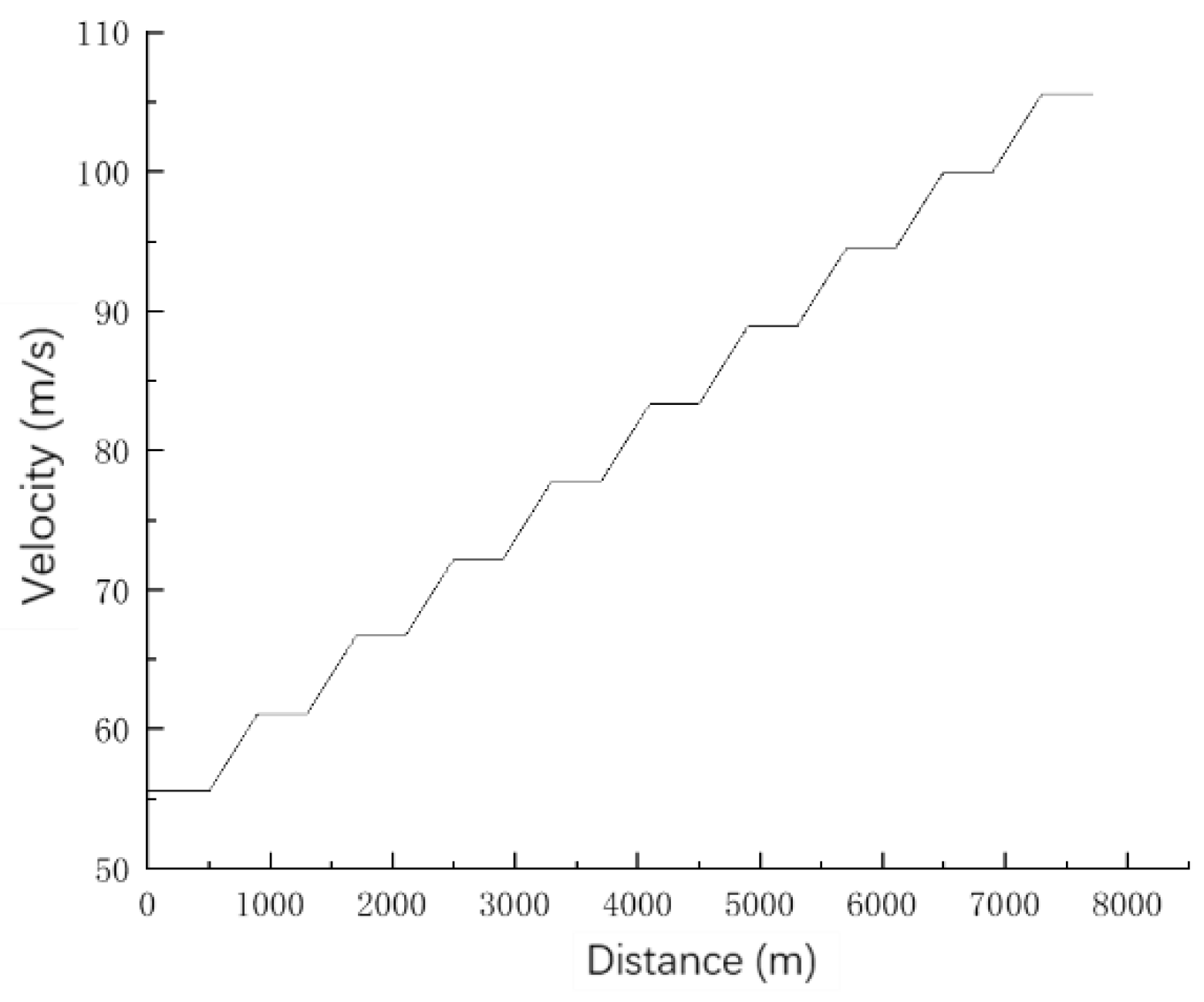
3.2. Progressive Trial Method
3.3. Comparison of Results of Different Calculation Methods
3.3.1. Root Locus Method and Progressive Trial Method
3.3.2. Limit Cycle Method and Progressive Trial Method
4. Wheel–Rail Contact Analysis at Critical Derailment Speed
4.1. Wheel–Rail Contact Analysis Method
4.2. Analysis of Wheel–Rail Contact Spot
5. Derailment Process Analysis
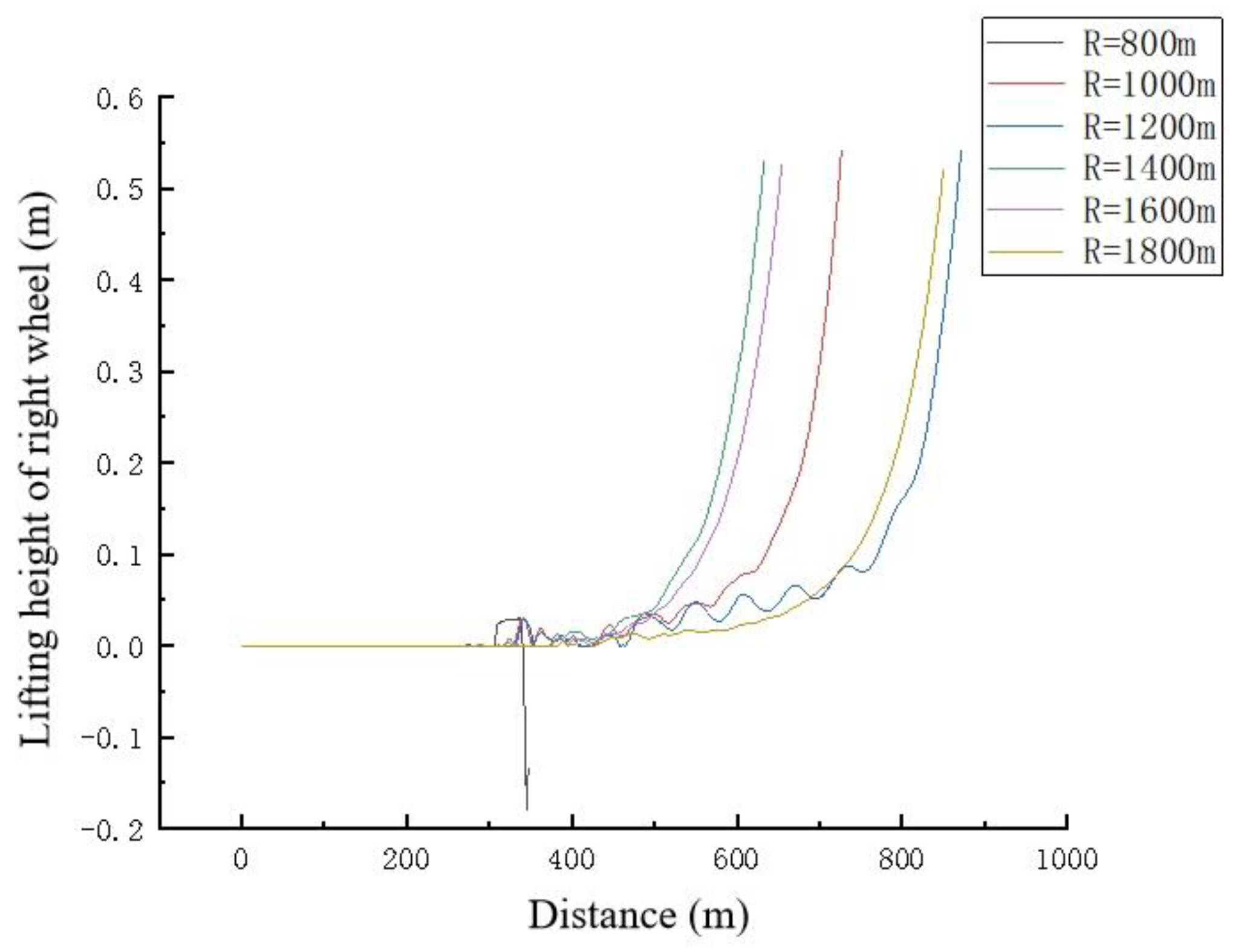
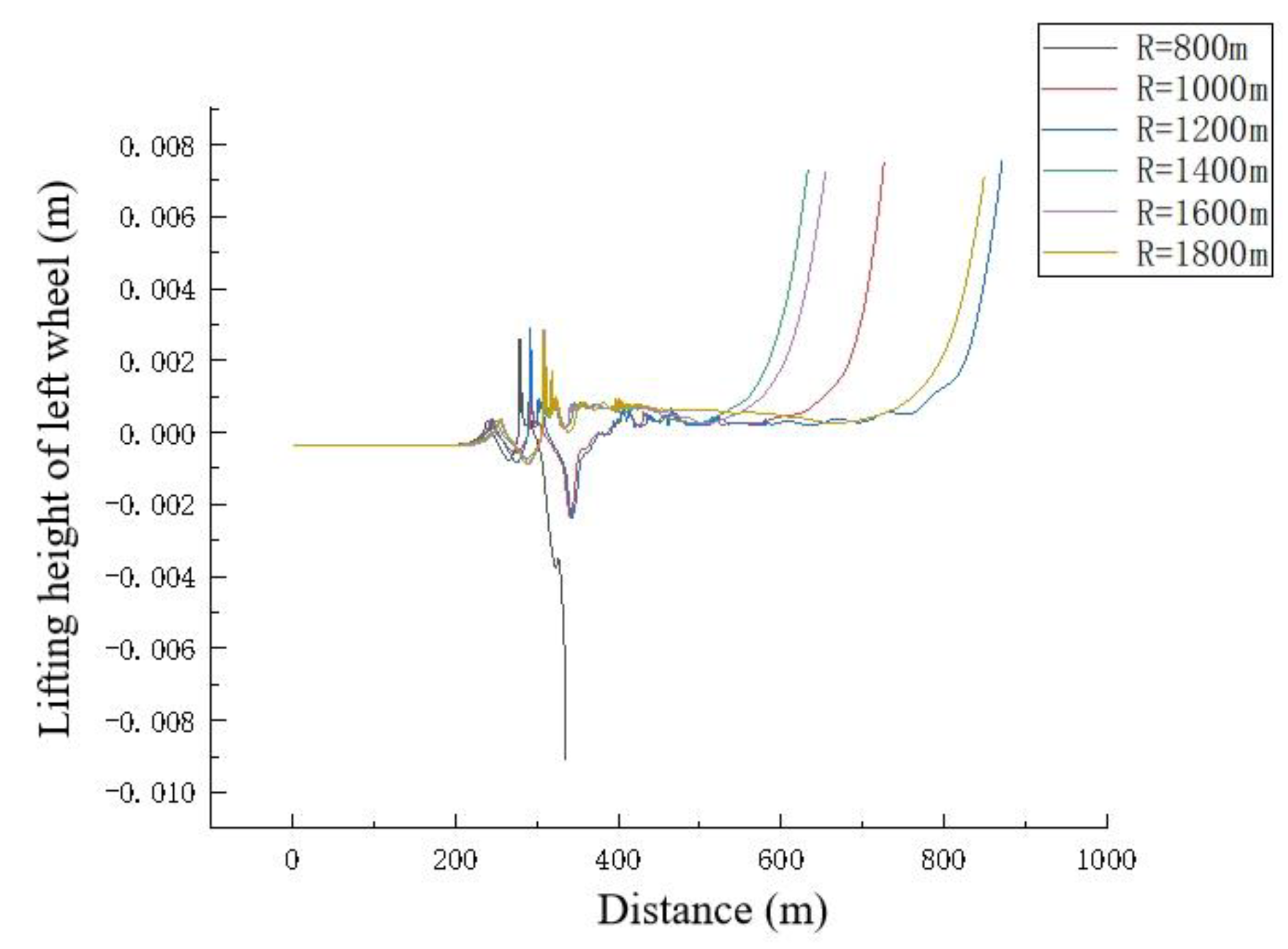
5.1. Wheel Lifting Height
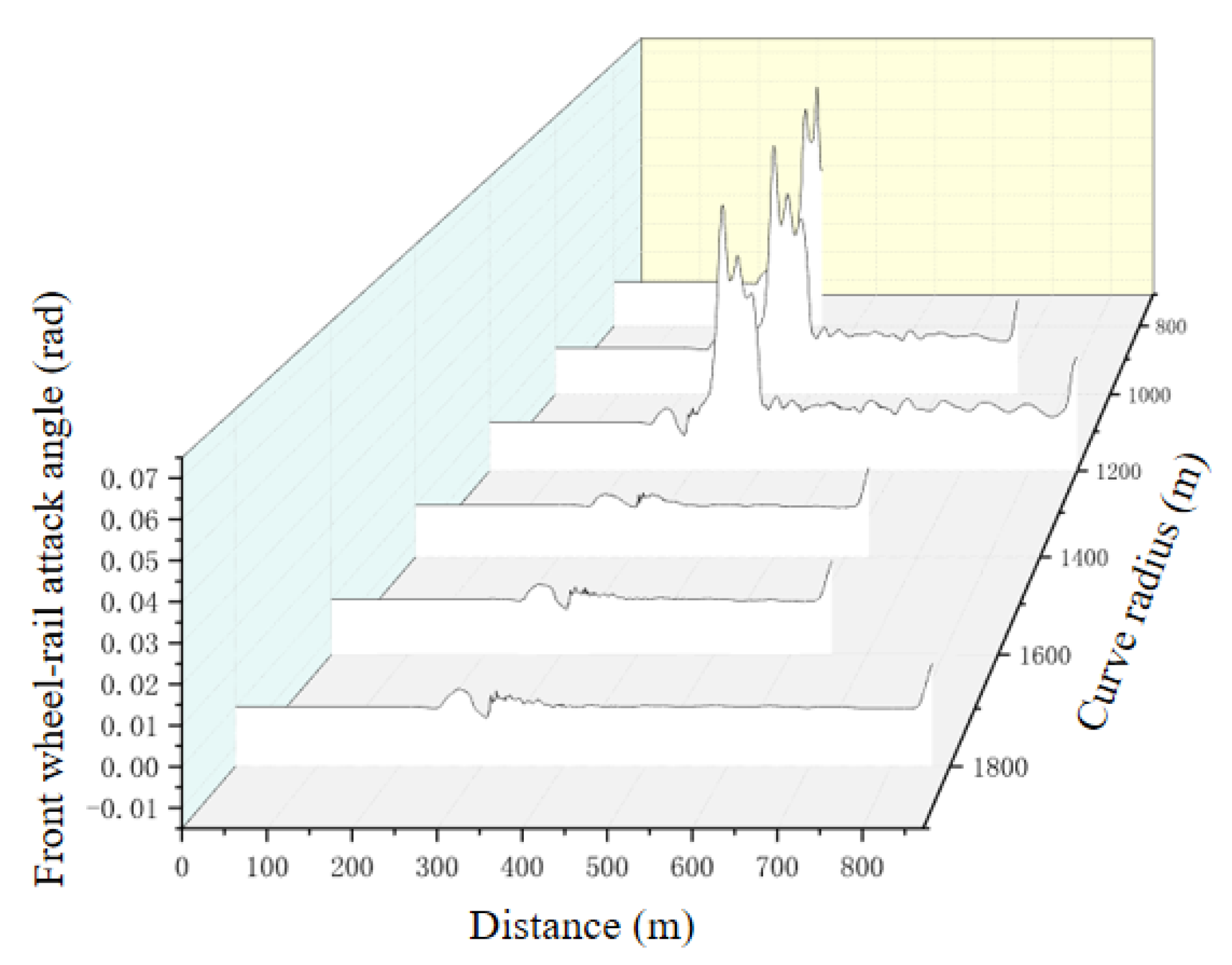
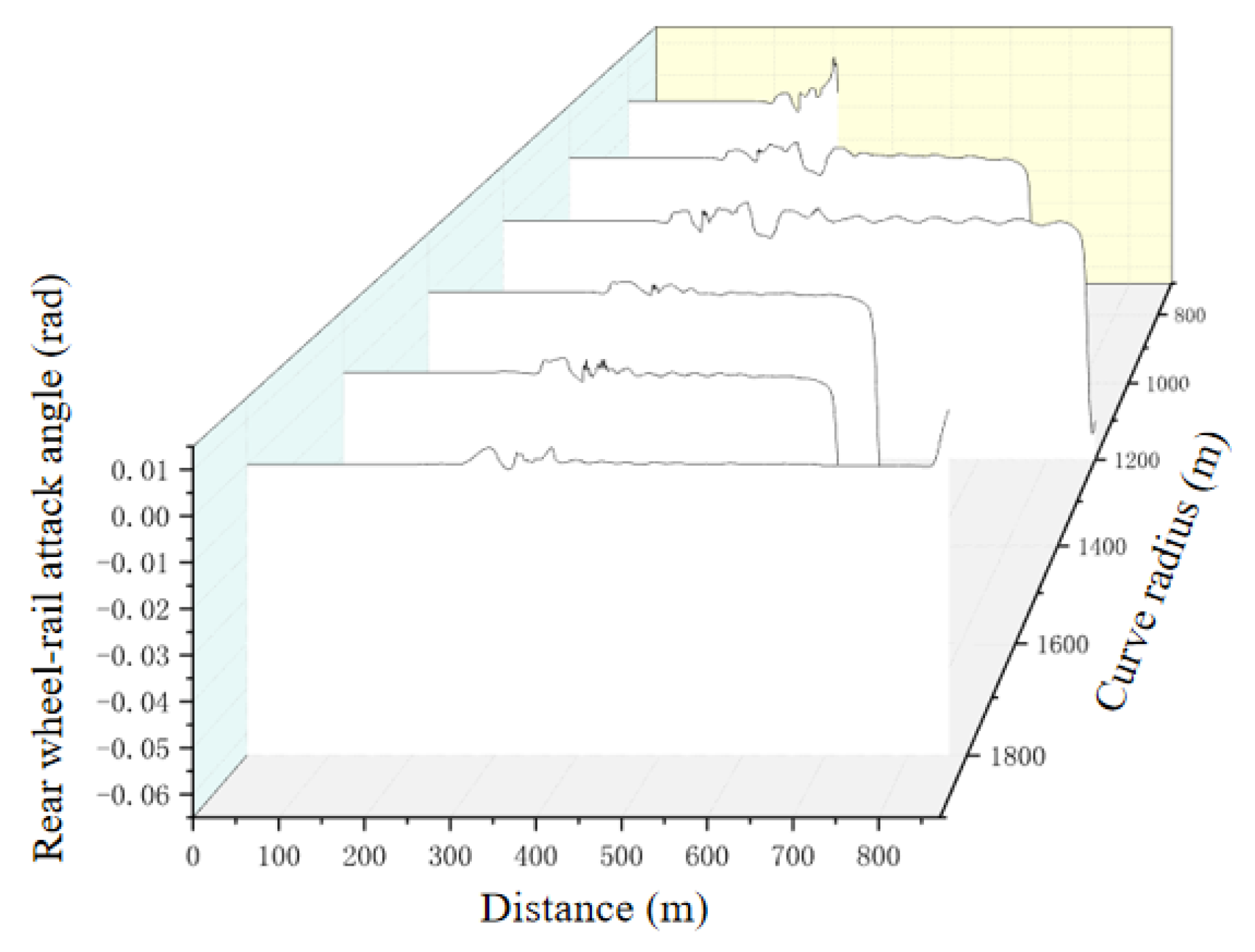
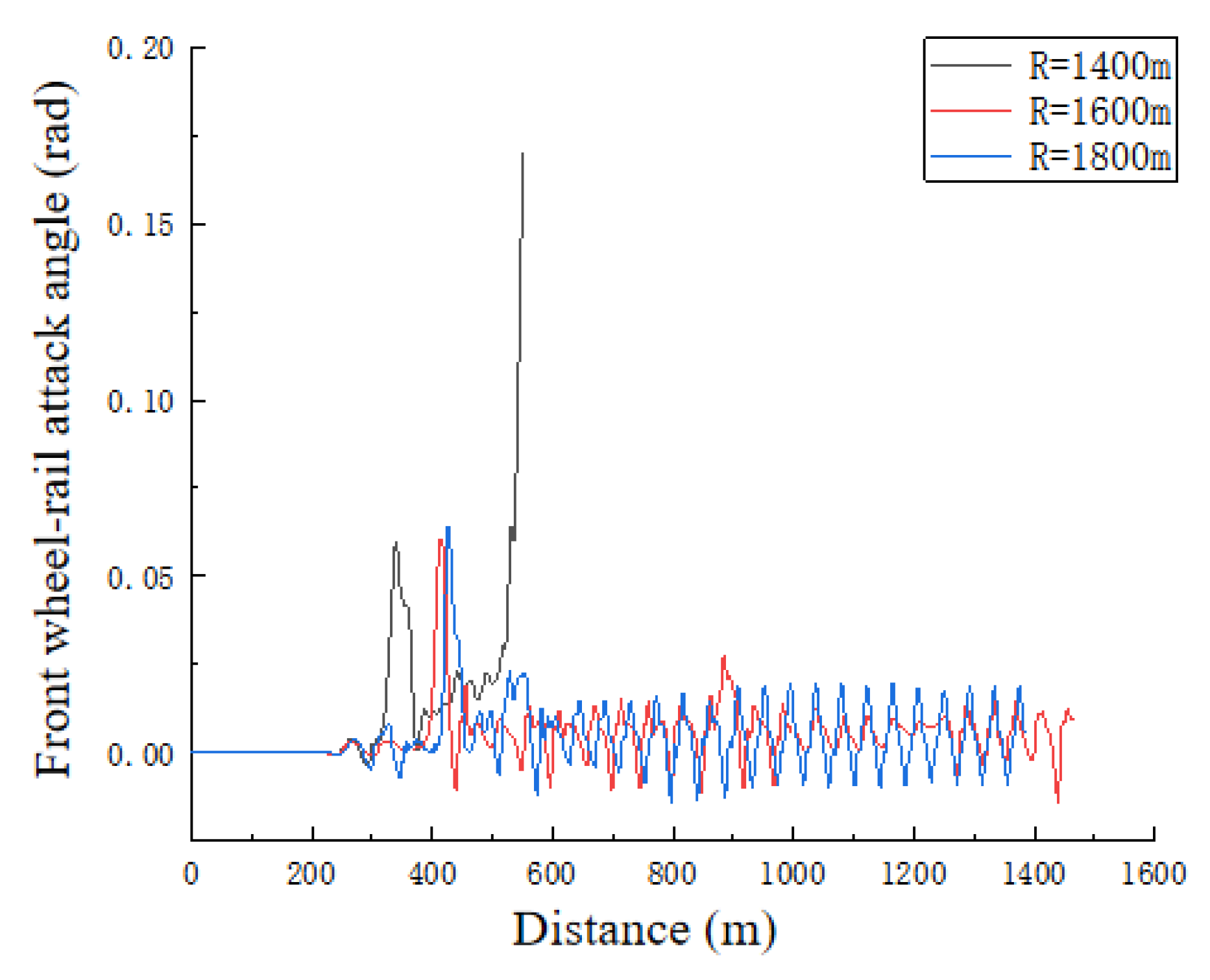
5.2. Wheel–Rail Attack Angle
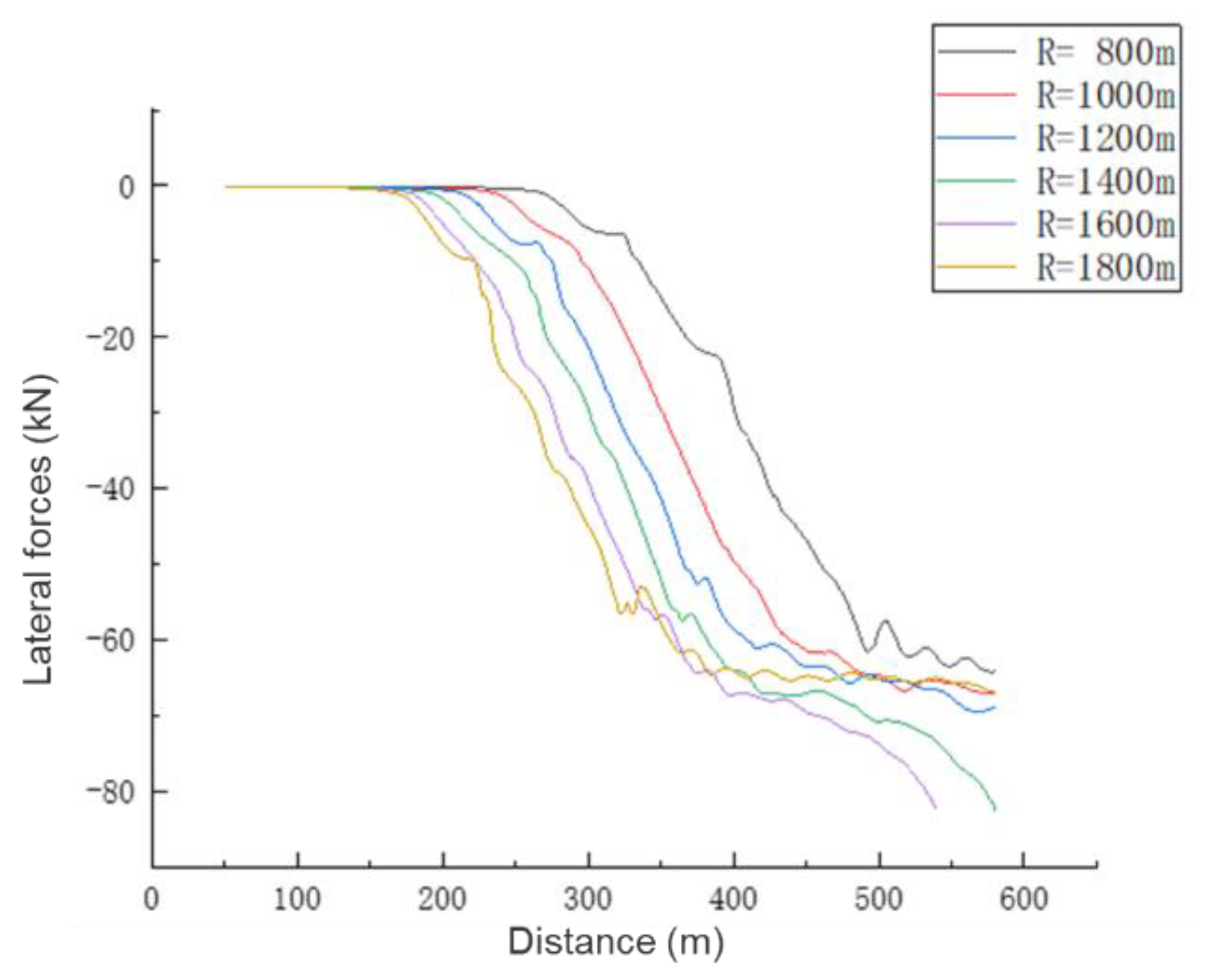
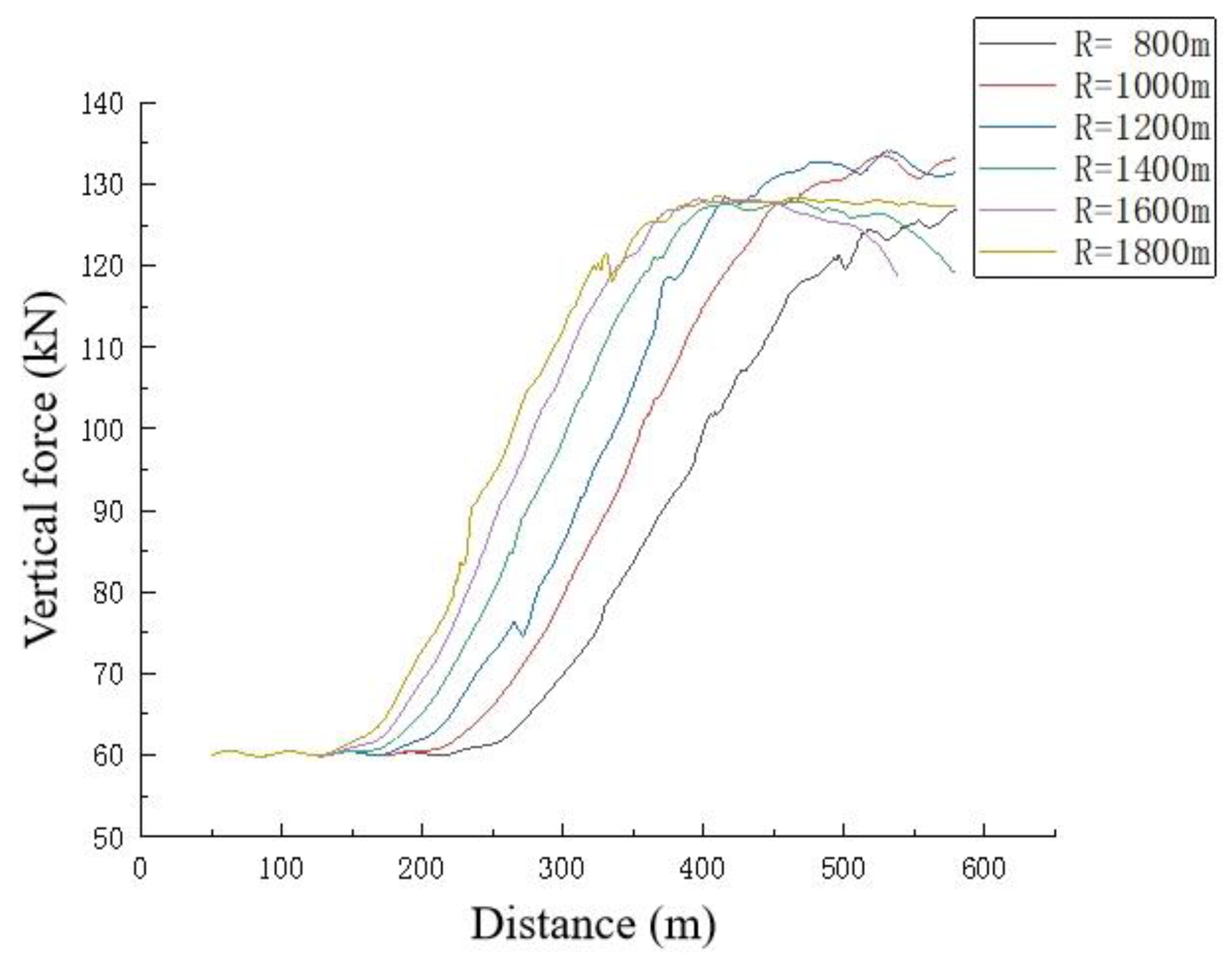
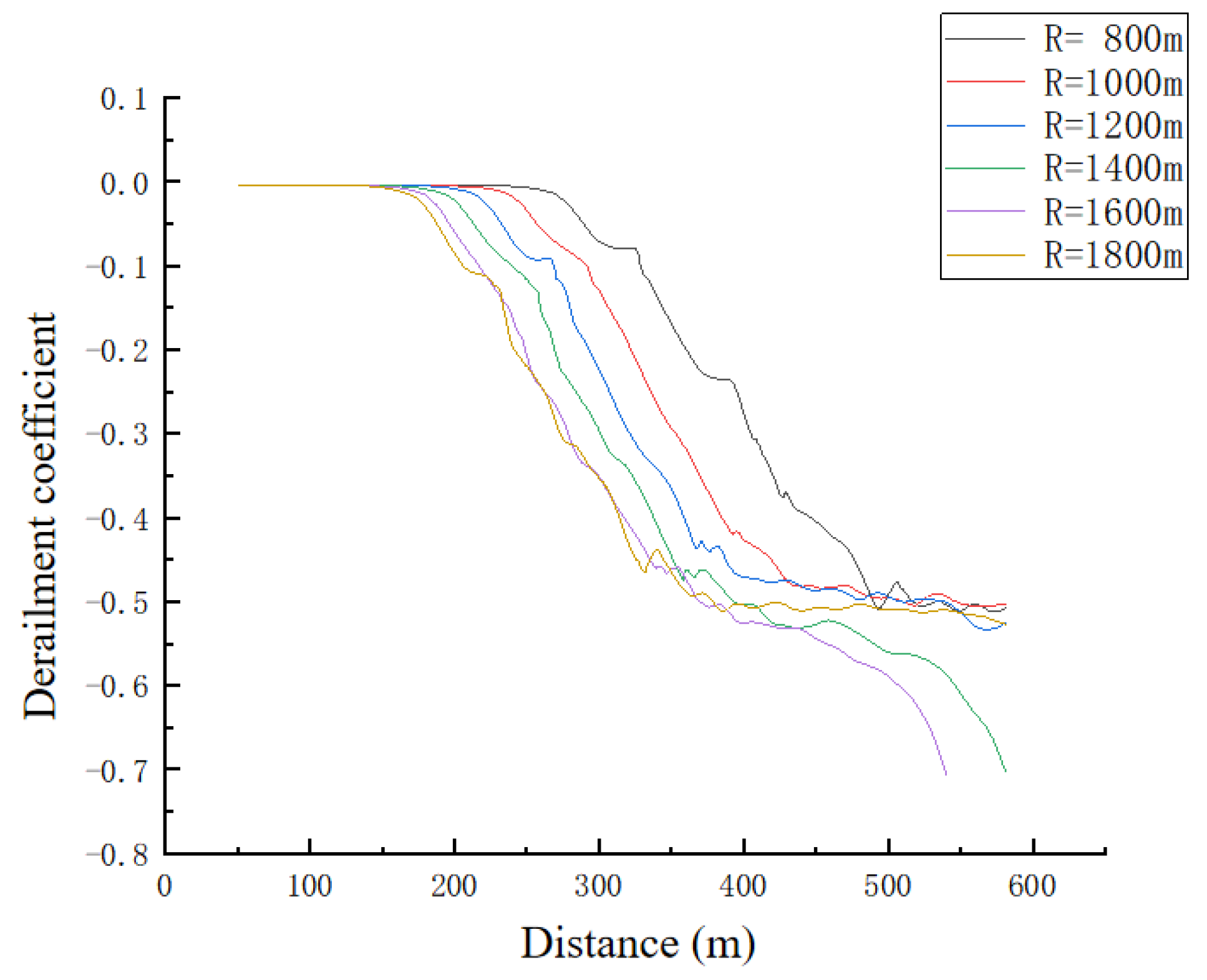
5.3. Lateral and Vertical Forces and Derailment Factor
6. Conclusions
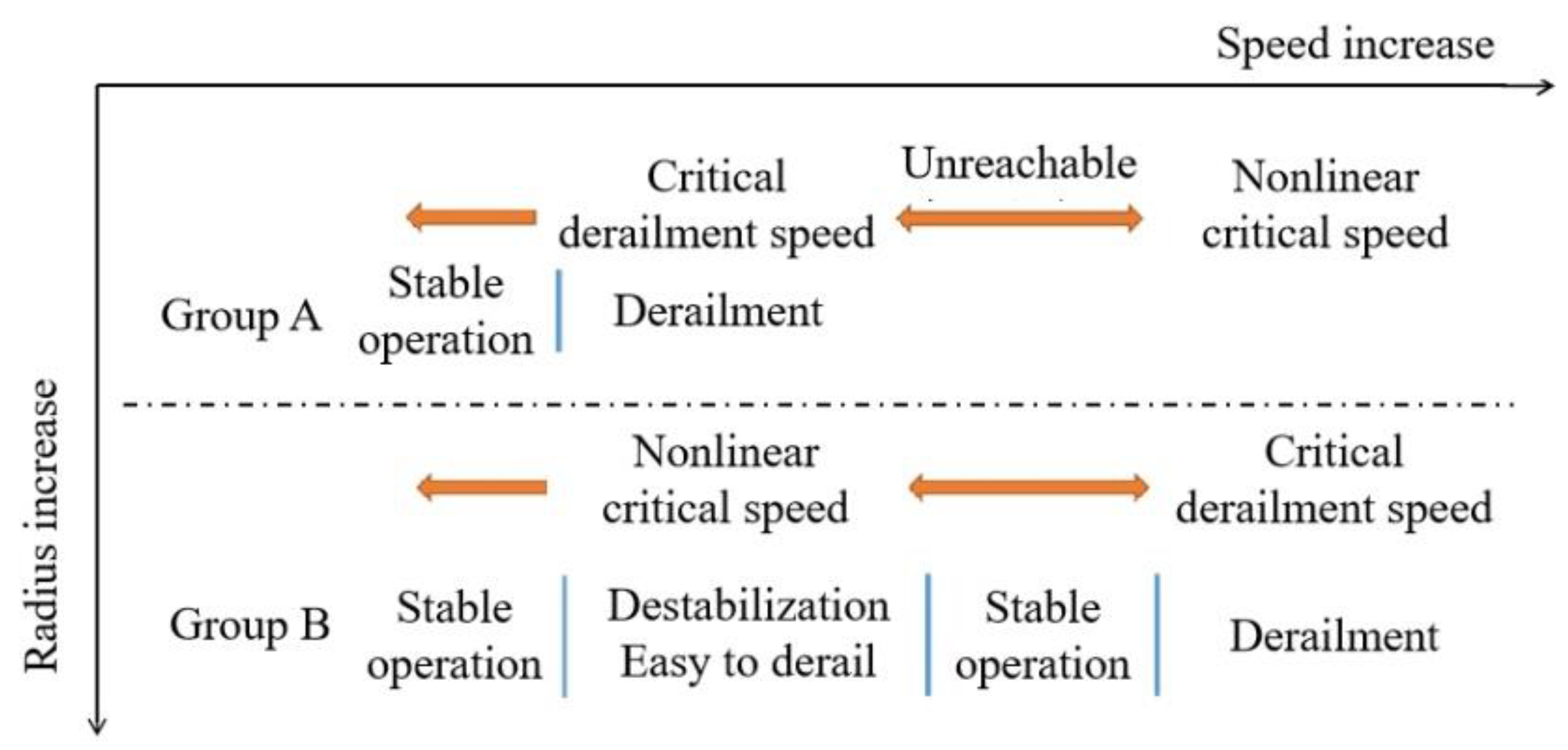
- Compared with the root locus method, both the progressive trial method and the limit cycle method take into account the nonlinear factors in the vehicle system, but the calculated critical speed is lower. Compared with the limit cycle method, the progressive trial method is more suitable for calculating the safe speed of trains running on small radius curves.
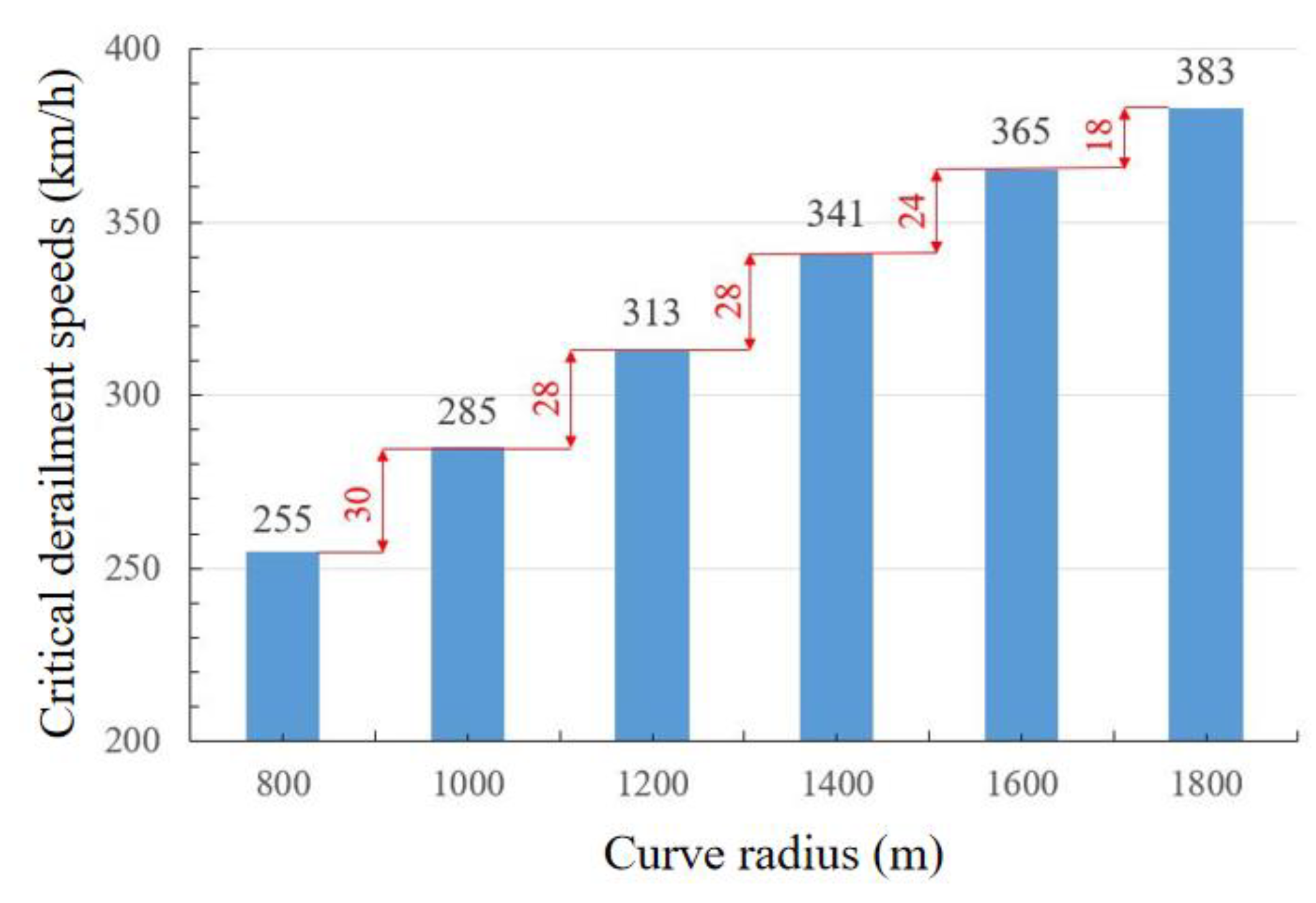
- The critical derailment speed is positively correlated with the curve radius, and its growth trend slows down with the increase in the curve radius. The smaller the radius of the curve, the greater the influence of this factor on the critical speed.
- When that the wheel–rail attack angle exceeds 0.06 rad, the vehicle is in a critical state of instability. Attention should be paid in time to avoid derailment accidents.
- On curved lines of different radii, when the train is derailed at the corresponding critical derailment speed, the maximum derailment coefficient is less than 0.8, but the derailment phenomenon still occurs. It indicates that the single derailment coefficient standard is not enough to measure whether the train derails or not.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, J.; Guan, Q.H. Wheelset climb derailment criteria for evaluation of railway vehicle running safety. J. Transp. Eng. 2007, 6, 1–5. [Google Scholar]
- Wang, P.; Lai, J.; Liao, T.; Xu, J.; Wang, J.; Chen, R. Study on safety limit of wheelset derailment under quasi-static condition. J. Railw. 2019, 41, 123–130. [Google Scholar]
- Li, M.; Wang, C.; Ma, W. Derailment dynamic response analysis at low speed for a metro vehicle. Mech. Des. Manuf. 2019, 5, 121–124. [Google Scholar]
- Karmel, A.; Sweet, L.M. Wheelset mechanics during wheel climb derailment. J. Appl. Mech. 1984, 51, 680–686. [Google Scholar] [CrossRef]
- Braghin, F.; Bruni, S.; Diana, G. Experimental and numerical investigation on the derailmcnt of a railway wheelset with solid axde. Veh. Syst. Dynamnics 2006, 44, 305–325. [Google Scholar] [CrossRef]
- Lirong, G.; Kaiyun, W.; Huijiong, W.; Bing, Z.; Jianhui, L. Dynamic responses of motor vehicle in low-speed derailment. J. Transp. Eng. 2015, 15, 52–60+68. [Google Scholar]
- Kuzuta, M.; Ueki, K.; Miyamoto, T.; Nishiyama, Y.; Maebashi, E. Numerical Dynamic Simulation of a Train Set Running on Ballasted Track after Derailment. Q. Rep. RTRI 2013, 54, 112–117. [Google Scholar] [CrossRef] [Green Version]
- Sun, L. Evaluation Method Study and Theory Analysis of Lateral Running Stability and Dynamic Derailment of High Speed Train; China Academy of Railway Science: Bejing, China, 2014. [Google Scholar]
- Xiao, X. Study on High-Speed Train Derailment Mechanism in Severe Environment; Southwest Jiaotong University: Chengdu, China, 2013. [Google Scholar]
- Hou, S.; Huo, X.; Zhang, X.; Zuo, T.; Guo, G. Study on dynamic characteristics and structural strength of lateral limiting device for high-speed train under collision derailment accident. J. Railw. Sci. Eng. 2021, 18, 588–595. [Google Scholar]
- Wu, X. Research on the Safety of Vehicle Derailment under Seismic Conditions; Southwest Jiaotong University: Chengdu, China, 2016. [Google Scholar]
- Yao, C. Study on Reliability of High-Speed Train Running on Embankment under Crosswind; Dalian Maritime University: Dalian, China, 2020. [Google Scholar]
- Keiichi, G.; Masamichi, S.; Munemasa, T. Seismic Train-Running Safety on Structures. Proceedings 2018, 2, 1143. [Google Scholar]
- Mu, D.; Gwon, S.-G.; Choi, D.-H. Dynamic Responses of a Cable-stayed Bridge under a High Speed Train with Random Track Irregularities and a Vertical Seismic Load. Int. J. Steel Struct. 2016, 16, 1339–1354. [Google Scholar] [CrossRef]
- Gong, K.; Liu, L.; Xiang, J.; Luo, K. Calculation of passenger train derailment course induced by overspeeds in curve. J. Cent. South Univ. 2020, 51, 2673–2680. [Google Scholar]
- The First Survey and Design Institute Group of China Railway Co. Railroad Line Design Specification; China Railway Press: Bejing, China, 2018. [Google Scholar]
- Liu, H.; Gao, C.; Wang, Y.; Hu, H. Method to determine the critical hunting speed of bogies for 160 km/h rapid freight cars. Railr. Veh. 2017, 55, 1–5+18+6. [Google Scholar]
- Shi, H.; Luo, R.; Zeng, J. Review on domestic and foreign dynamics evaluation criteria of high-speed train. J. Transp. Eng. 2021, 21, 36–58. [Google Scholar]
- Xiang, J.; Zeng, Q.Y.; Zhou, Z.F. Mechanical mechanism and random energy analysis theory of train derailment on the bridge and its application. J. Railw. 2004, 2, 97–104. [Google Scholar]
- Xiang, J. Study on Mechanism and Analysis Theory of Train Derailment; Central South University: Changsha, China, 2006. [Google Scholar]
- Shabana, A.A.; Zaazaa, K.E.; Escalona, J.L.; Sany, J.R. Development of elastic force model for wheel/rail contact problems. J. Sound Vib. 2004, 269, 295–325. [Google Scholar] [CrossRef]


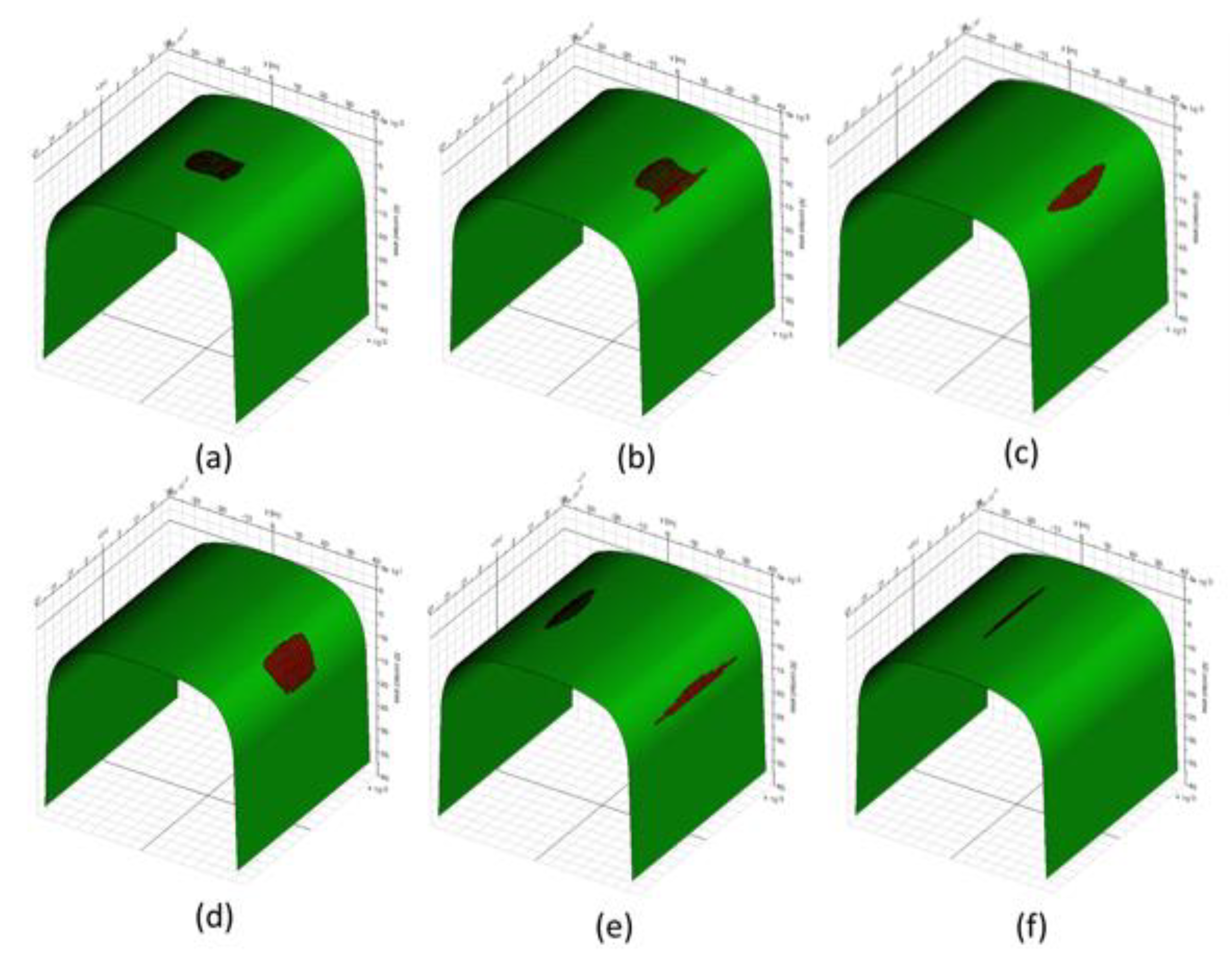
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Body mass/kg | 32,000 | Vehicle distance setting/m | 17.5 |
| Frame mass/kg | 3300 | Wheelbase/m | 2.5 |
| Wheel mass/kg | 1780 | tread rolling circle radius/m | 0.46 |
| Tread surface profile | LM | Rail profile | UIC60 |
| Alignment | Length (m) | Superelevation (mm) | Curve Radius (m) |
|---|---|---|---|
| Straight | 200 | 0 | ∞ |
| Transition curve | 200 | 0~175 | ∞~R |
| Curve | 1000 | 175 | R |
| Transition curve | 200 | 175~0 | R~∞ |
| Straight | 200 | 0 | ∞ |
| Limit Cycle Method | Root Locus Method |
|---|---|
| Consider non-linear factors | Consider linear factors |
| Perform integral operation in time domain | Perform integral operation in frequency domain |
| The vehicle passes through the exciting line at a certain speed, and then runs on the smooth line to observe whether the lateral displacement of the wheelset converges. When the lateral displacement of the wheelset exceeds 0.1 mm, that is, the lateral displacement diverges, the speed at the moment is defined as the instability critical speed. | The instability speed of the vehicle is determined based on the inherent vibration frequency of each rigid body at different vehicle speeds. The minimum damping value less than 0 represents the system destabilization. |
| Resistance work increment > load energy increment | Stable equilibrium state |
| Resistance work increment < load energy increment | Unstable equilibrium |
| Resistance work increment = load energy increment | The equilibrium state is at the critical point of stability and instability, i.e., critical instability |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, R.; Ma, H.; Zhang, J.; Niu, Y. A Method of Predicting Critical Derailment Speed and Analysis of Derailment Process. Appl. Sci. 2022, 12, 11199. https://doi.org/10.3390/app122111199
Yu R, Ma H, Zhang J, Niu Y. A Method of Predicting Critical Derailment Speed and Analysis of Derailment Process. Applied Sciences. 2022; 12(21):11199. https://doi.org/10.3390/app122111199
Chicago/Turabian StyleYu, Ruodan, He Ma, Jun Zhang, and Yan Niu. 2022. "A Method of Predicting Critical Derailment Speed and Analysis of Derailment Process" Applied Sciences 12, no. 21: 11199. https://doi.org/10.3390/app122111199
APA StyleYu, R., Ma, H., Zhang, J., & Niu, Y. (2022). A Method of Predicting Critical Derailment Speed and Analysis of Derailment Process. Applied Sciences, 12(21), 11199. https://doi.org/10.3390/app122111199






