Method to Predict Performances of PCB Silicone Conformal Coating under Thermal Aging
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Conformal Coating Material Selection
2.2. Conformal Coating Sample Preparation
2.3. Tensile and Elongation Test
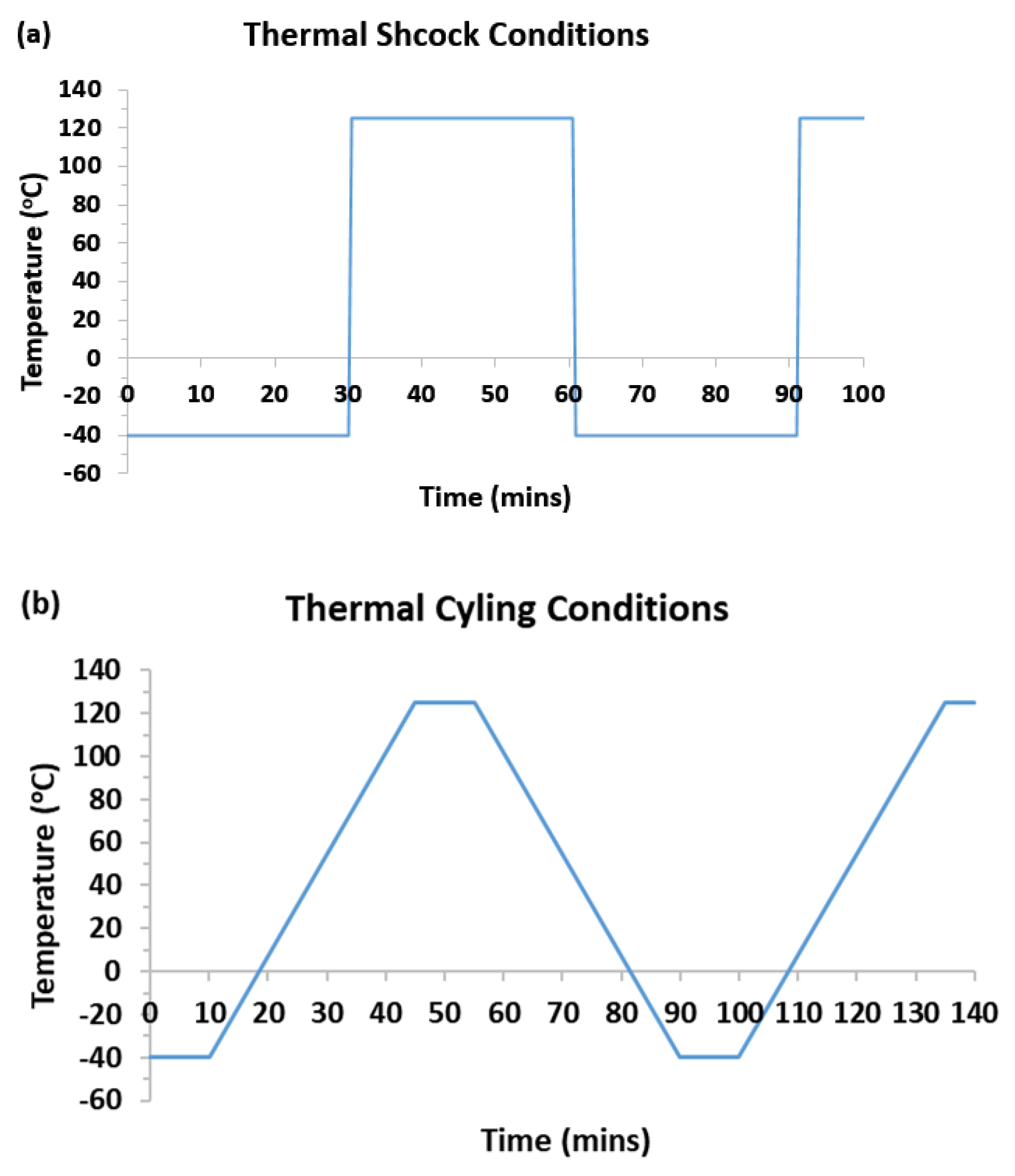
2.4. Thermal Shock and Thermal Cycling
2.5. Microscope
3. Results
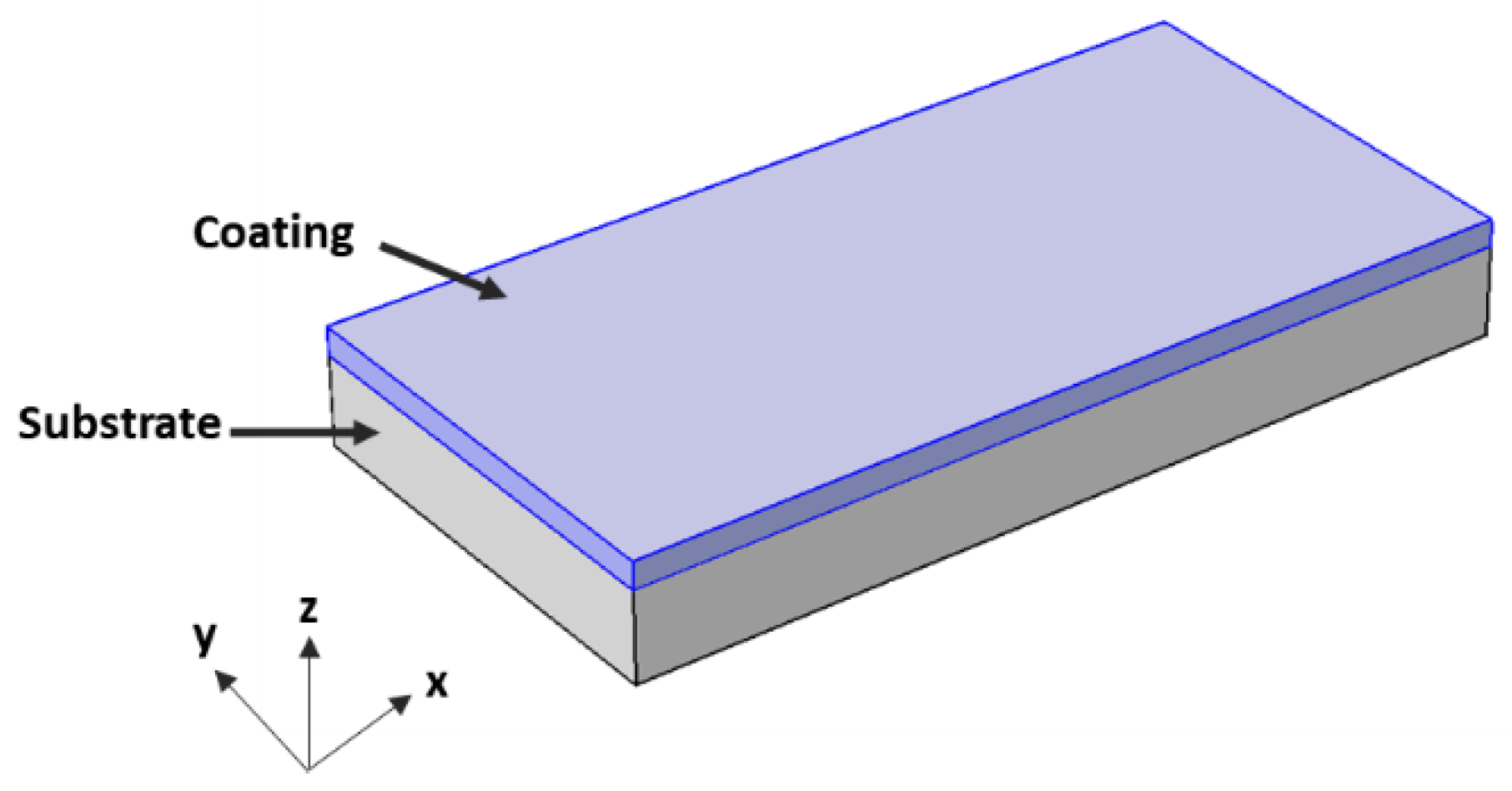
3.1. Bi-Material Strip Bending (BMSB) Characterization and Modeling
3.2. Modelling Stress Build-up Associated with CTE Mismatch during Thermal Cycle Aging
- FEA modeling requires an accurate identification of the material elastic model: most silicone materials show a stress-strain nonlinear dependence, requiring multiple test piece geometries (uniaxial testing, pure shear, bi-axial testing) to accurately describe mechanical behavior, particularly when having stress-strain dependence showing saddle point that requires high order nonlinear models. Those measurements are particularly complex with very rigid material, having low deformation capabilities;
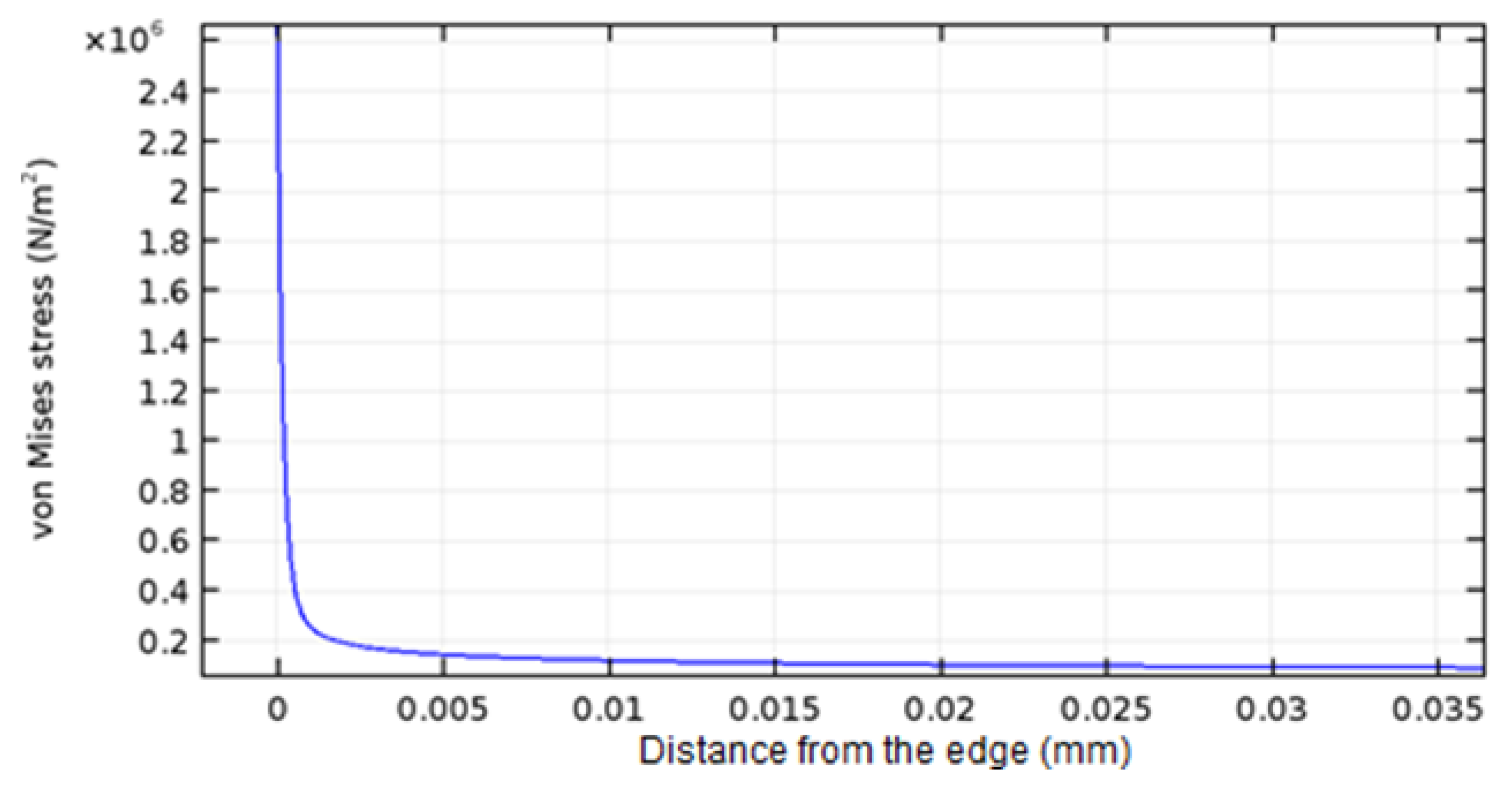
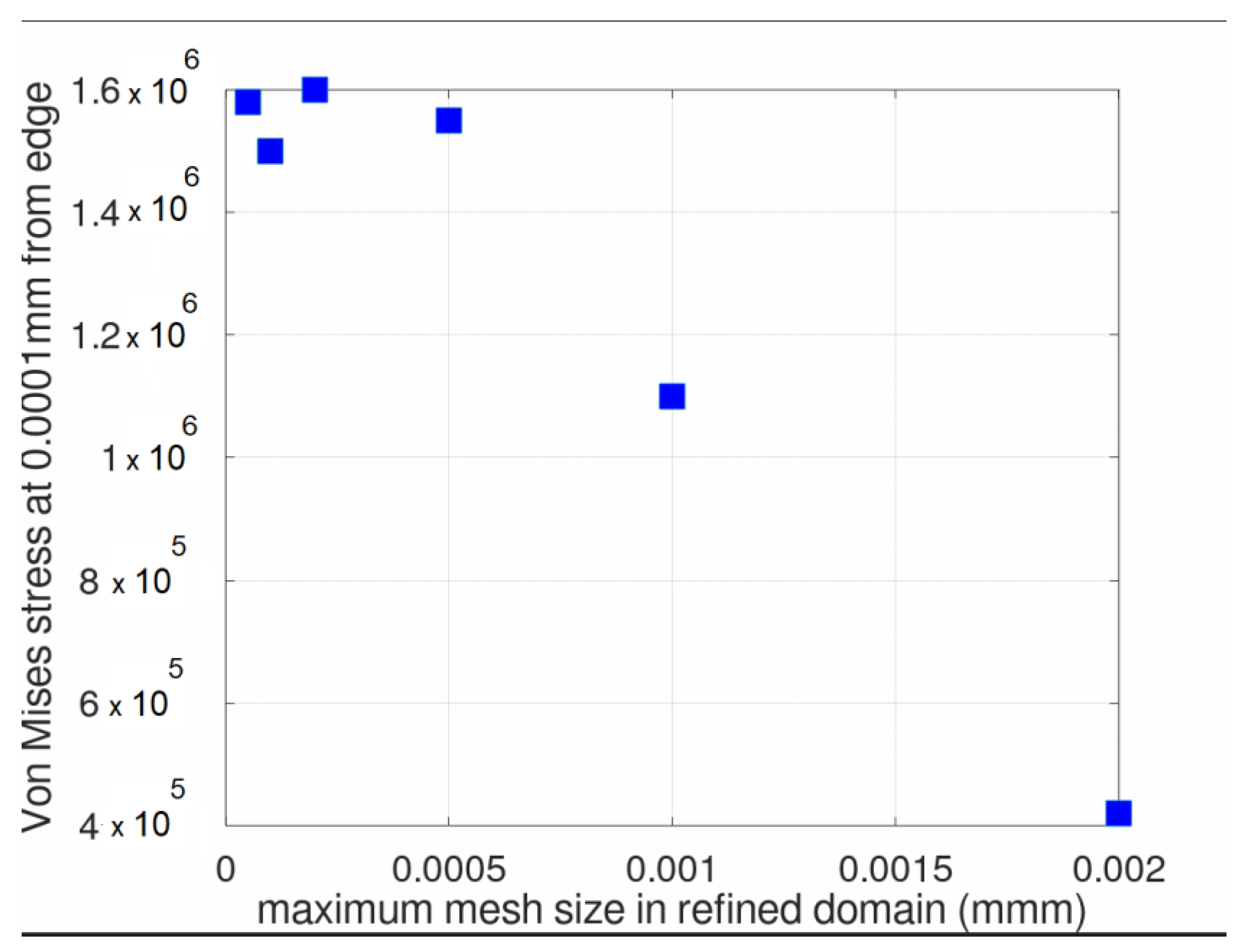
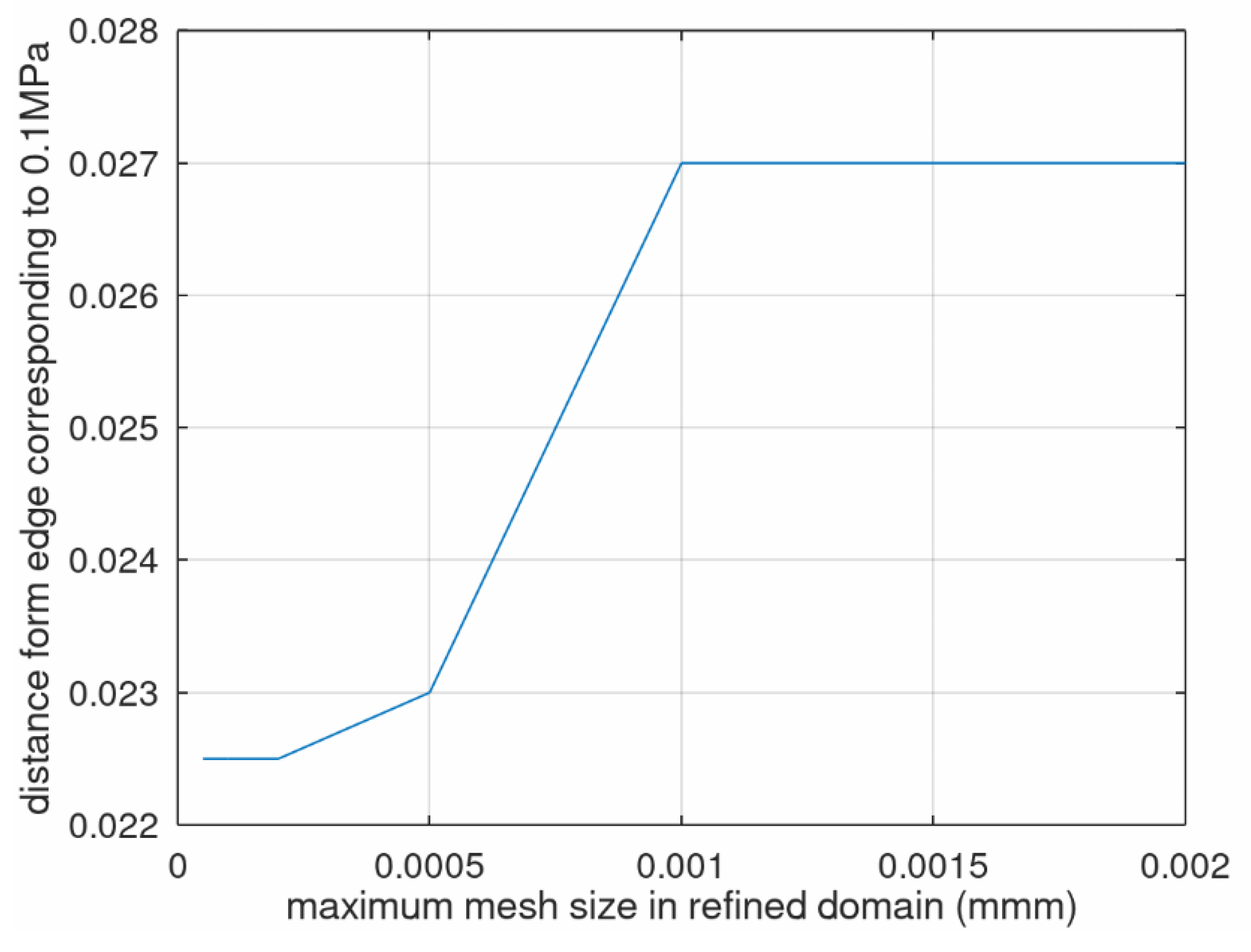
- Silicone compounds are nearly incompressible; therefore, high local stress builds up near the interface between the substrate and the coating and particularly close to composite edges, demanding a high grid density to obtain a mesh-independent solution. This point is discussed later in the paper.
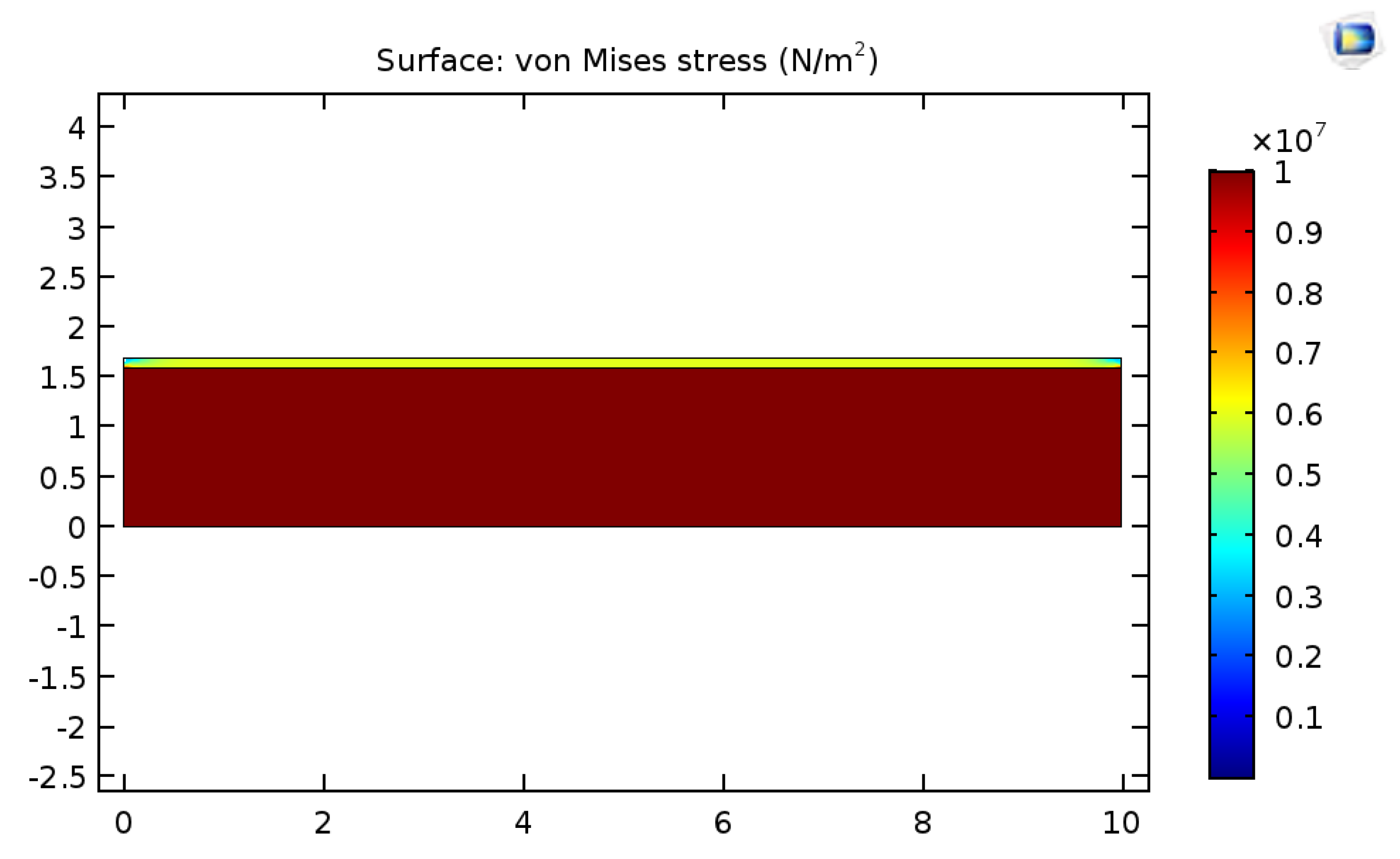
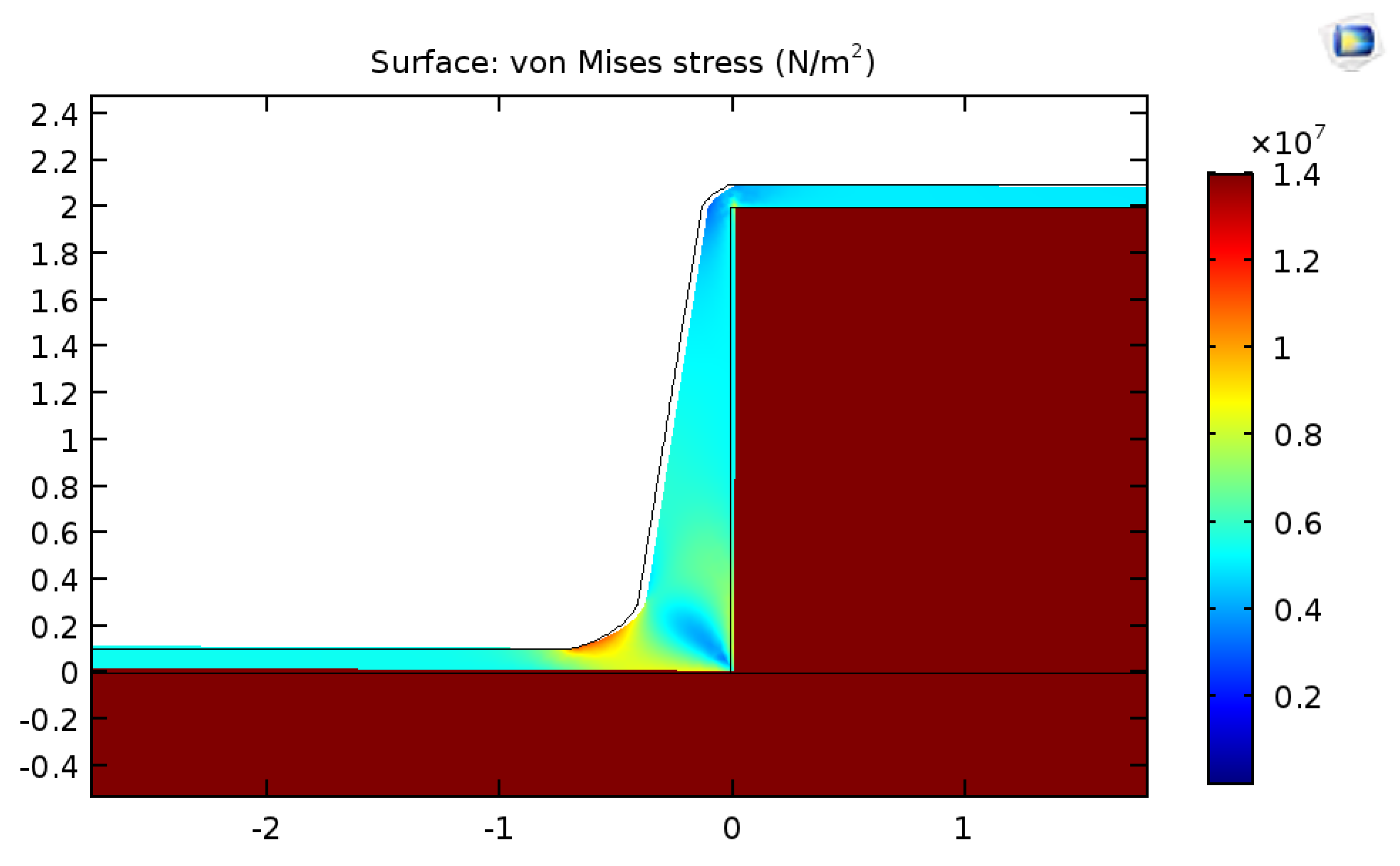
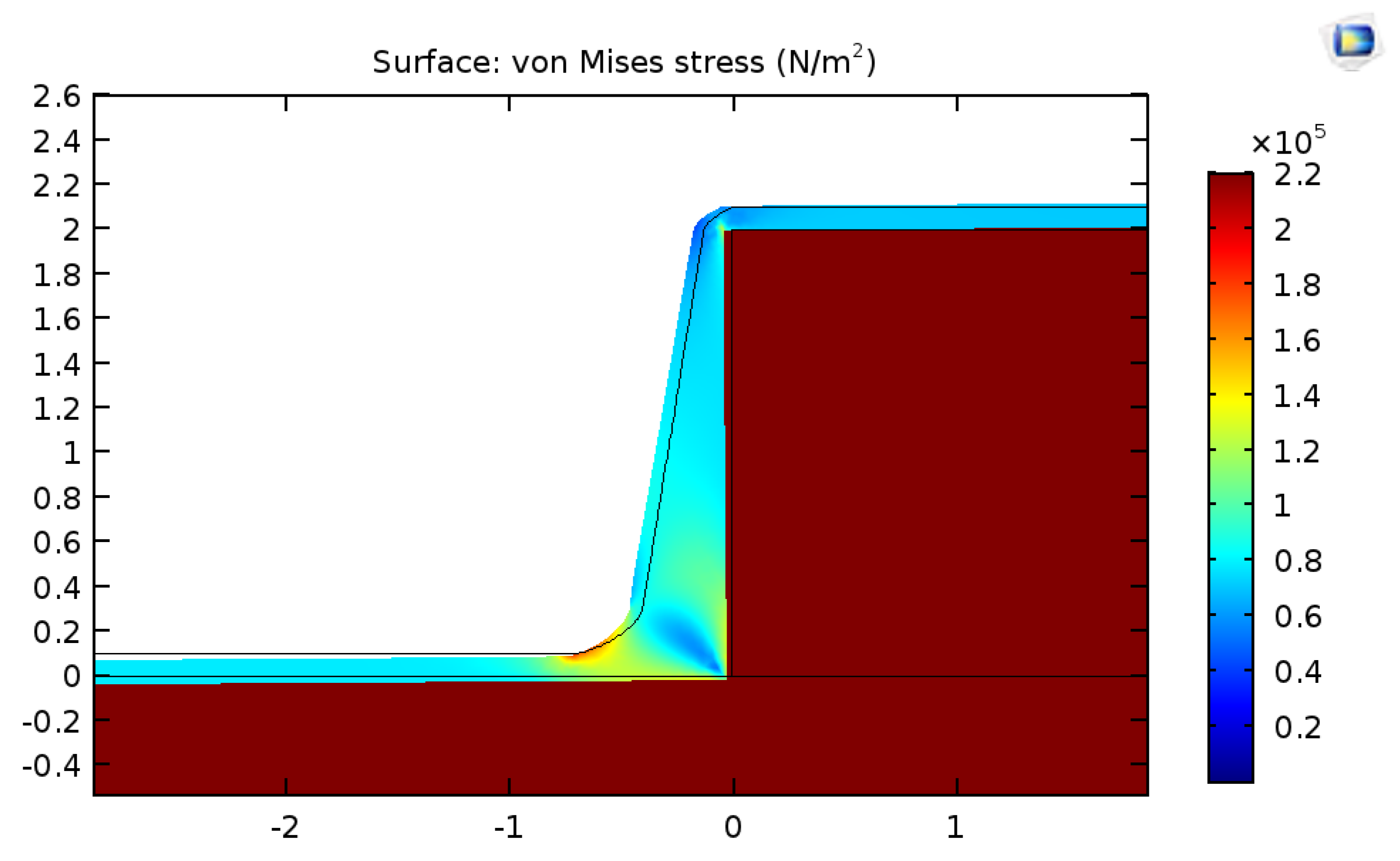
3.3. Testing Stress Predictions of Simplified Model Compared to the Stress Distribution Calculated Using FEA Code for the Case of a Bi-Layer Thin Plate
3.4. Comparing Stresses Calculated Either by Simplified Model or FEA to the Local Stress Threshold Leading to Silicone Failure
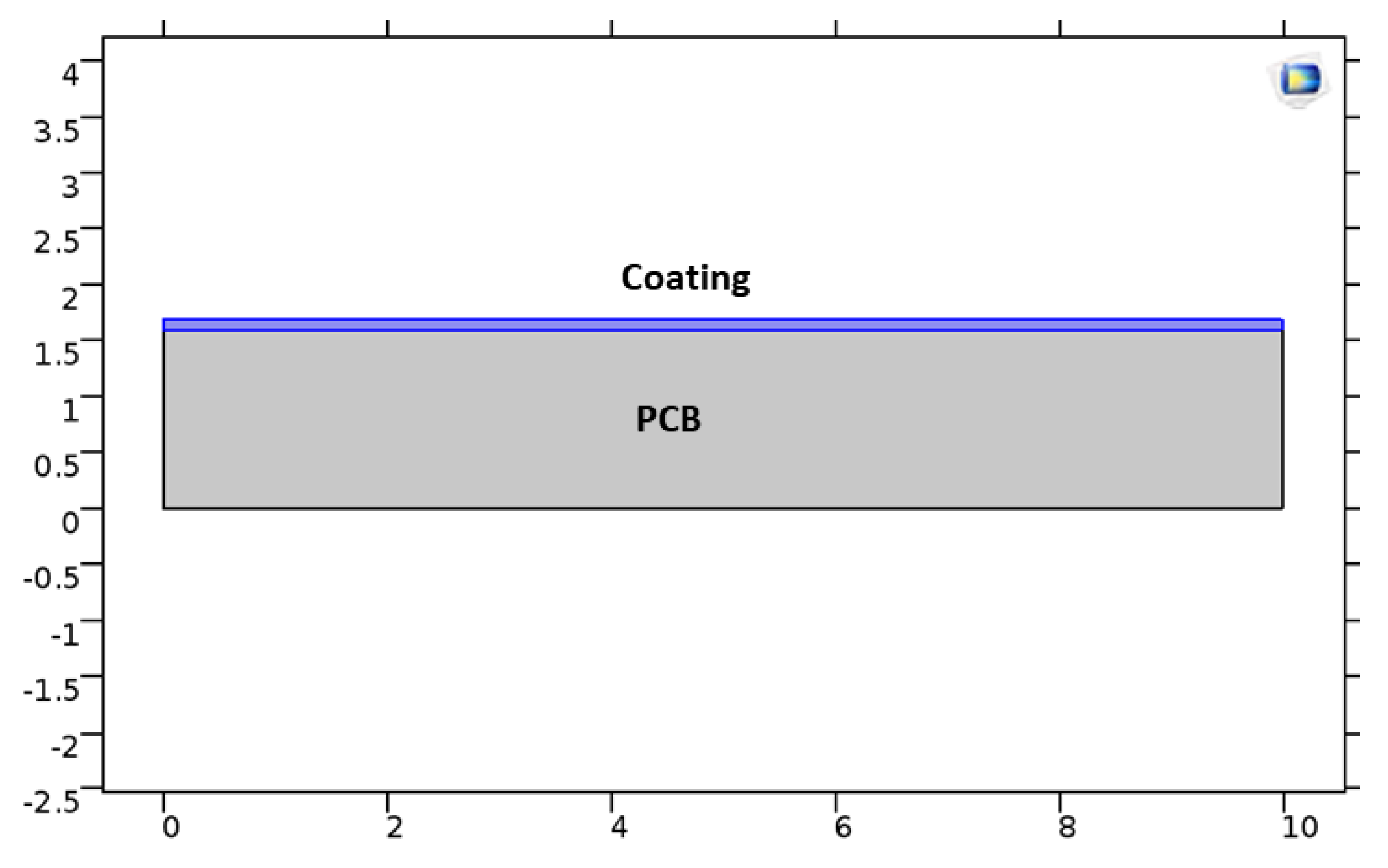
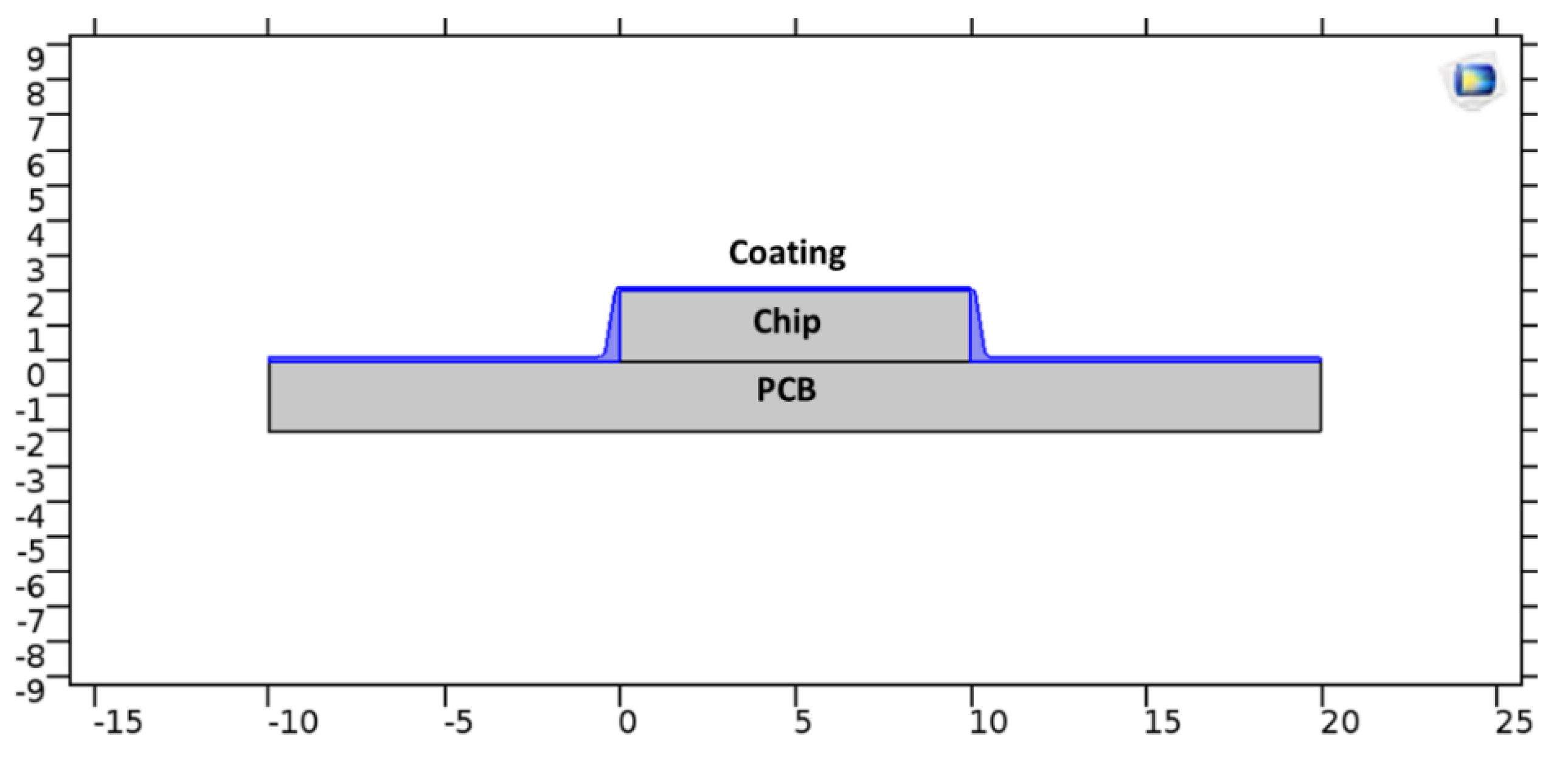
3.5. D FEA Modeling of the Stress Distribution for the Case with Chip Attached to the PCB
3.6. Experimental Observation: Reliability Test
4. Conclusions
- Allows simplified analytical solution of solid mechanics equations to calculate both the high shear stress dominant close to the edges and the lateral tension stress dominant far from the edges where shear stress becomes ~0;
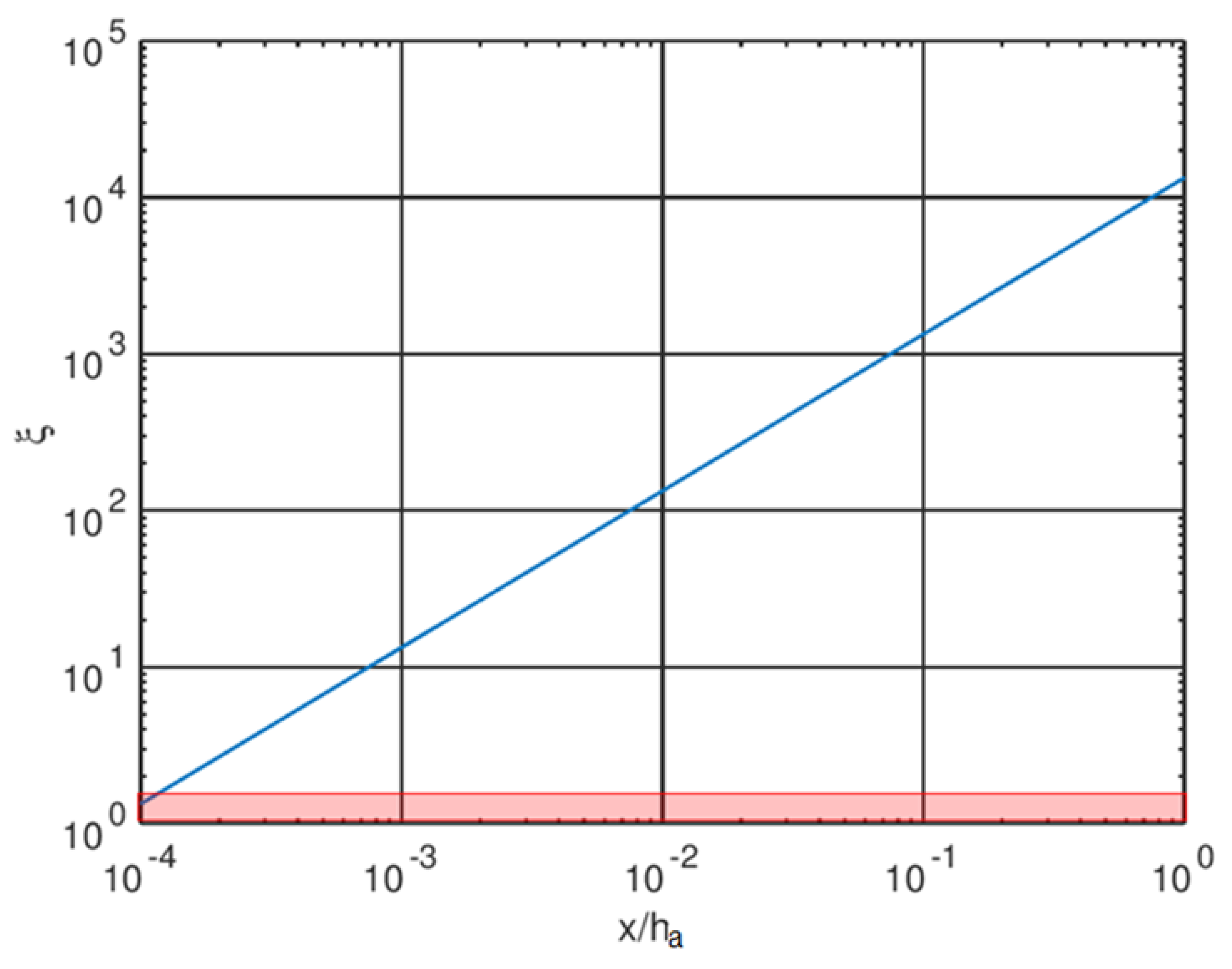
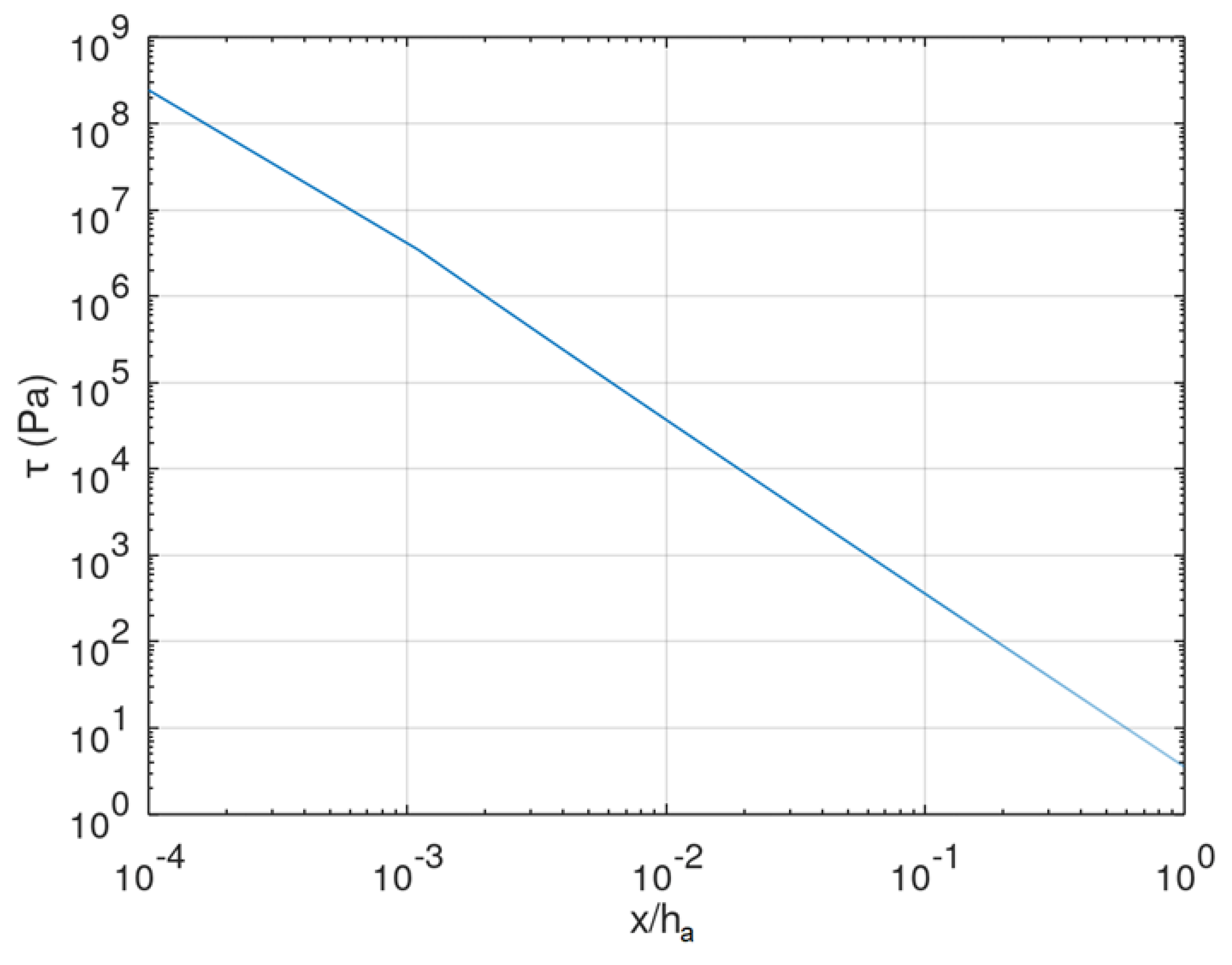
- Creates a very localized high shear stress close to the edges, confirmed by the analysis of the analytical shear stress solution that demonstrates that high shear stress decreases very abruptly over a very short distance when the elastic modulus of the coating is much smaller than the elastic modulus of the substrate;
- Makes FEA models of shear stress near the edge complex, requiring mesh spatial density and cell dimensions differing by order of magnitude, the extent of the nonlinear shear stress decrease being ~10−3 mm. Therefore, a simplified solution offers benefits for checking the outcome of FEA models and guiding the build-up of the meshing scheme;
- The modeling and stress calculation are combined with an experimental part;
- Measurement of the stress threshold that leads to rupture carried out using dog bone test pieces;
- PCB specimens with electronic components are submitted to temperature cycles with extreme low and high temperatures equal to the temperatures used in both simplified and FEA models. Optical microscope observation of potential cracks appearance is carried out, and their correspondence with the regions of modeled high stress is studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weide-Zaage, K. Simulation of packaging under harsh environment conditions (temperature, pressure, corrosion and radiation). Microelectron. Reliab. 2017, 76–77, 6–12. [Google Scholar] [CrossRef]
- Abbas, A.-A.F.; Pandiarajan, G.; Iyer, S.; Greene, C.; Santos, D.; Srihari, K. Impact of conformal coating material on the long-term reliability of ball grid array solder joints. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1861–1867. [Google Scholar] [CrossRef]
- Pippola, J.; Marttila, T.; Frisk, L. Protective coatings of electronics under harsh thermal shock. Microelectron. Reliab. 2014, 54, 2048–2052. [Google Scholar] [CrossRef]
- Sivakumar, P.; Du, S.M.; Selter, M.; Daye, J.; Cho, J. Improved adhesion of polyurethane-based nanocomposite coatings to tin surface through silane coupling agents. Int. J. Adhes. Adhes. 2021, 110, 102948. [Google Scholar] [CrossRef]
- Han, S.; Osterman, M.; Meschter, S.; Pecht, M. Evaluation of Effectiveness of Conformal Coatings as Tin Whisker Mitigation. J. Electron. Mater. 2012, 41, 2508–2518. [Google Scholar] [CrossRef]
- Sivakumar, P.; Du, S.M.; Selter, M.; Ballard, I.; Daye, J.; Cho, J. Long-term thermal aging of parylene conformal coating under high humidity and its effects on tin whisker mitigation. Polym. Degrad. Stab. 2021, 191, 109667. [Google Scholar] [CrossRef]
- Suppa, M. Conformal Coatings for Electronics Applications; Lackwerke Peters: Kempen, Germany, 2012. [Google Scholar]
- Keeping, J. Conformal Coatings. In Lead-Free Soldering Process Development and Reliability; Bath, J., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Pippola, J.; Marttila, T.; Frisk, L. Effect of Protective Casting Materials on Product Level Reliability under Accelerated Test Conditions. In Proceedings of the 2013 European Microelectronics Packaging Conference (EMPC), Grenoble, France, 9–12 September 2013; pp. 1–6. [Google Scholar]
- Lowndes, R.; Cotton, I.; Emersic, C.; Rowland, S.; Freer, R. Thermal Stresses of Conformal Coatings on Printed Circuit Boards. In Proceedings of the 2015 IEEE Electrical Insulation Conference (EIC), Seattle, WA, USA, 7–10 June 2015; pp. 106–109. [Google Scholar]
- Serebreni, M.; Wilcoxon, R.; Hillman, D.; Blattau, N.; Hillman, C. The Effect of Improper Conformal Coating on SnPb and Pb-Free BGA Solder Joints During Thermal Cycling: Experiments and Modeling. In Proceedings of the 2017 33rd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 13–17 March 2017; pp. 40–47. [Google Scholar]
- Emersic, C.; Lowndes, R.; Cotton, I.; Rowland, S.; Freer, R. The Effects of Pressure and Temperature on Partial Discharge Degradation of Silicone Conformal Coatings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2986–2994. [Google Scholar] [CrossRef]
- Reedy, E.D. Tensile cracking of a brittle conformal coating on a rough substrate. Int. J. Fract. 2016, 199, 245–250. [Google Scholar] [CrossRef]
- Francis, L.F.; Mccormick, A.V.; Vaessen, D.M.; Payne, J.A. Development and measurement of stress in polymer coatings. J. Mater. Sci. 2001, 37, 4717–4731. [Google Scholar] [CrossRef]
- Wang, X.S.; Tang, H.P.; Li, X.D.; Hua, X. Investigations on the Mechanical Properties of Conducting Polymer Coating-Substrate Structures and Their Influencing Factors. Int. J. Mol. Sci. 2009, 10, 5257–5284. [Google Scholar] [CrossRef] [PubMed]
- Biernath, R.W.; Soane, D.S. Characterization of Stresses in Polymer Films for Microelectronics Applications. In Polymeric Materials for Electronics Packaging and Interconnection; Lupinski, J.H., Moore, R.S., Eds.; American Chemistry Society: Washington, DC, USA, 1989. [Google Scholar]
- Sham, M.-L.; Kim, J.-K. Evolution of residual stresses in modified epoxy resins for electronic packaging applications. Compos. Part A 2004, 35, 537–546. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.W.; Kim, C.S. FEA Study on the Stress Distributions in the Polymer Coatings of Cardiovascular Drug-Eluting Stent Medical Devices. Ann. Biomed. Eng. 2014, 42, 1952–1965. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, Y.-C.; Hutchens, S.; Lawrence, J.; Emrick, T.; Crosby, A.J. Directly Measuring the Complete Stress–Strain Response of Ultrathin Polymer Films. Macromolecules 2015, 48, 6534–6540. [Google Scholar] [CrossRef]
- Nazir, M.H.; Khan, Z.A. A review of theoretical analysis techniques for cracking and corrosive degradation of film-substrate systems. Eng. Fail. Anal. 2017, 72, 80–113. [Google Scholar] [CrossRef]
- Naebe, M.; Abolhasani, M.M.; Khayyam, H.; Fox, A.B. Crack Damage in Polymers and Composites: A Review. Polym. Rev. 2016, 56, 31–69. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Astapov, A.N.; Nushtaev, D.V.; Rabinskiy, L.N. Calculation of Thermal Stresses in a Substrate−Coating System. Compos. Mech. Comput. Appl. Int. J. 2017, 8, 267–286. [Google Scholar] [CrossRef]
- Freund, L.B.; Hu, Y. Shear Stress at a Film-Substrate Interface Due to Mismatch Strains; Brown University Report; Brown University: Providence, RI, USA, 1988. [Google Scholar]
- Wolf, A.; Descamps, P. Determination of Poisson’s Ratio of Silicone Sealants from Ultrasonic and Tensile Measurements. In Performance of Exterior Building Walls; Johnson, P., Ed.; ASTM International: West Conshohocken, PA, USA, 2003; pp. 132–142. [Google Scholar]






| Material | Unit | Conformal Coating A | Conformal Coating B |
|---|---|---|---|
| Viscosity | mPa·s | 1050 | 350 |
| Tack-free time (25 °C) | Mins | 6 | 8 |
| Density | g/cm3 | 1.12 | 0.98 |
| Hardness | Shore A | 85 | 34 |
| Elastic modulus (25 °C) | MPa | 77.1 | 1.50 |
| CTE | ppm/K | 300 | 490 |
| Dielectric strength | kV/mm | 13 | 17 |
| Volume resistivity | Ohm·cm | 1.9 × 1014 | 5.5 × 1015 |
| Performance | Unit | Coating A (−40 °C) | Coating A (125 °C) | Coating B (−40 °C) | Coating B (125 °C) | PCB |
|---|---|---|---|---|---|---|
| Density | Kg/m3 | 1120 | 1120 | 980 | 980 | 1900 |
| Thermal Conductivity | W/(m·K) | 0.2 | 0.2 | 0.2 | 0.2 | 0.3 |
| Heat Capacity | J (Kg·K) | 1500 | 1500 | 1500 | 1500 | 1369 |
| CTE | 1/K | 3.0 × 10−4 | 3.0 × 10−4 | 4.9 × 10−4 | 4.9 × 10−4 | 1.8 × 10−5 |
| Young’s Modulus E | MPa | 160.1 | 1.28 | 1.33 | 1.92 | 22000 |
| Poisson’s ratio γ | NA | 0.49 | 0.49 | 0.49 | 0.49 | 0.15 |
| Property | Unit | Coating A | Coating B |
|---|---|---|---|
| Tensile stress in x direction (−40 °C, 2D Equation (5)) | MPa | 5.77 | 0.08 |
| Tensile stress in x direction (−40 °C, 2D FEA model) | MPa | 5.98 | 0.08 |
| Tensile stress in x direction (125 °C, 2D Equation (5)) | MPa | 0.07 | 0.18 |
| Tensile stress in x direction (125 °C, 2D FEA model) | MPa | 0.07 | 0.16 |
| Property | Unit | Coating A | Coating B |
|---|---|---|---|
| Tensile strength | MPa | 5.54 | 1.40 |
| Tensile strength standard deviation | MPa | 0.08 | 0.26 |
| Elongation | % | 104.4 | 142.0 |
| Elongation standard deviation | % | 1.3 | 8.2 |
| Property | Unit | Coating A | Coating B |
|---|---|---|---|
| Corresponding local stress in the dog bone during tensile test | MPa | 11.33 | 3.39 |
| Tensile stress in x direction (−40 °C, 2D Equation (5)) | MPa | 5.77 | 0.08 |
| Tensile stress in x direction (−40 °C, 2D FEA model) | MPa | 5.98 | 0.08 |
| Tensile stress in x direction (125 °C, 2D Equation (5)) | MPa | 0.07 | 0.18 |
| Tensile stress in x direction (125 °C, 2D FEA model) | MPa | 0.07 | 0.16 |
| Number of Triangular Elements | Number of Cell’s Vertices | Maximum Von Mises Stress (MPa) |
|---|---|---|
| 914 | 523 | 0.15 |
| 1196 | 670 | 0.19 |
| 1748 | 960 | 0.21 |
| 3024 | 1627 | 0.21 |
| Performance | Unit | Coating A (−40 °C) | Coating A (125 °C) | Coating B (−40 °C) | Coating B (125 °C) |
|---|---|---|---|---|---|
| Lamé parameters λ | MPa | 2642.38 | 21.38 | 21.87 | 31.57 |
| Lamé parameters μ | MPa | 53.93 | 0.44 | 0.45 | 0.64 |
| Performance | Unit | Chip | PCB |
|---|---|---|---|
| Density | Kg/m3 | 1200 | 1900 |
| Thermal Conductivity | W/(m·K) | 0.2 | 0.3 |
| Heat Capacity | J (Kg·K) | 1100 | 1369 |
| CTE | 1/K | 5.0 × 10−5 | 1.8 × 10−5 |
| Young’s Modulus E | MPa | 10,000 | 22,000 |
| Poisson’s ratio γ | NA | 0.30 | 0.15 |
| Property | Unit | Coating A | Coating B |
|---|---|---|---|
| Max. local stress (−40 °C, 2D FEA model) | MPa | 10.65 | 0.15 |
| Max. local stress (125 °C, 2D FEA model) | MPa | 0.16 | 0.44 |
| Conformal Coating | Coating Crack Observation |
|---|---|
| A | No Crack after TS 517 shocks. Crack after TS 517 shocks + TC 350 cycles |
| B | No crack even after 3 rounds of (TS 517 shocks + TC 517 cycles) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, L.; Descamps, P. Method to Predict Performances of PCB Silicone Conformal Coating under Thermal Aging. Appl. Sci. 2022, 12, 11268. https://doi.org/10.3390/app122111268
Zou L, Descamps P. Method to Predict Performances of PCB Silicone Conformal Coating under Thermal Aging. Applied Sciences. 2022; 12(21):11268. https://doi.org/10.3390/app122111268
Chicago/Turabian StyleZou, Lu, and Pierre Descamps. 2022. "Method to Predict Performances of PCB Silicone Conformal Coating under Thermal Aging" Applied Sciences 12, no. 21: 11268. https://doi.org/10.3390/app122111268
APA StyleZou, L., & Descamps, P. (2022). Method to Predict Performances of PCB Silicone Conformal Coating under Thermal Aging. Applied Sciences, 12(21), 11268. https://doi.org/10.3390/app122111268


_Yang.png)


