Common-Mode Driven Synchronous Filtering of the Powerline Interference in ECG
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. ECG Databases
2.1.1. CTS-ECG Database
2.1.2. PTB Diagnostic ECG Database
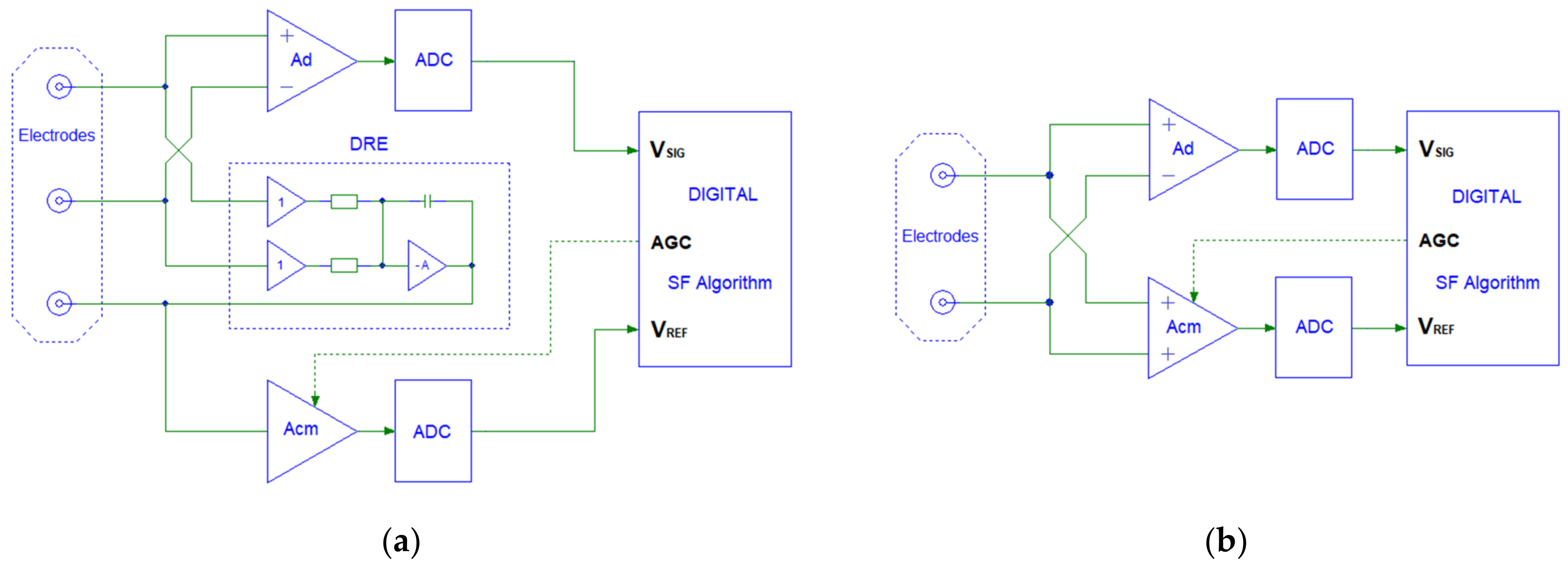
2.2. Biopotential Readout Circuits with Synchronous PLI Filtering
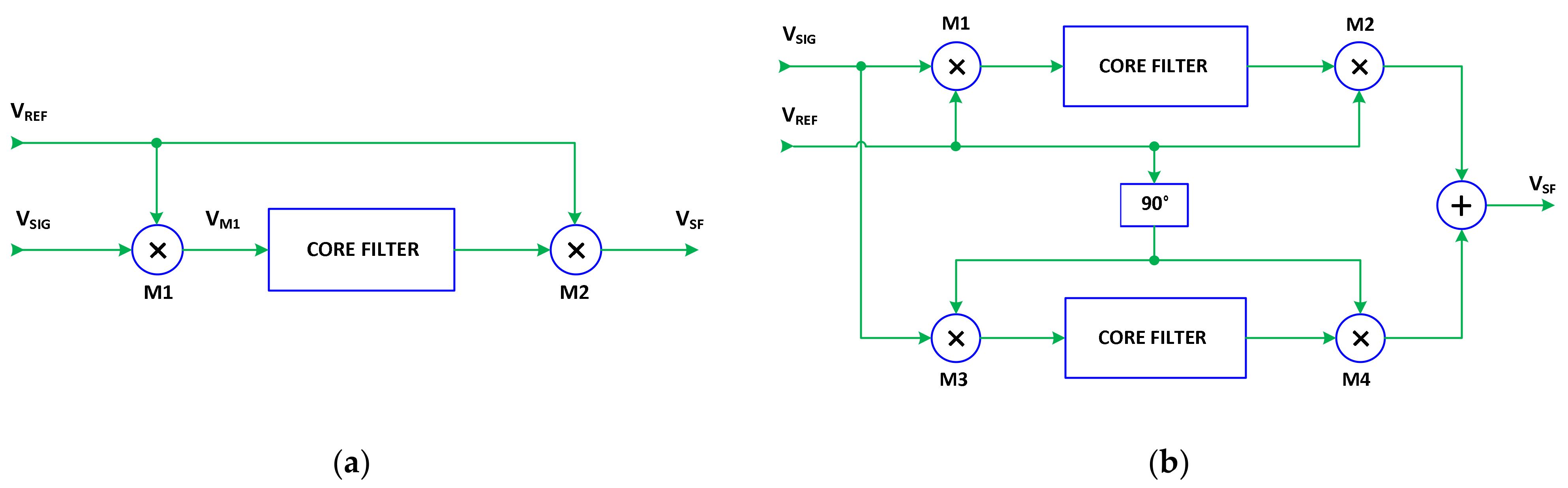
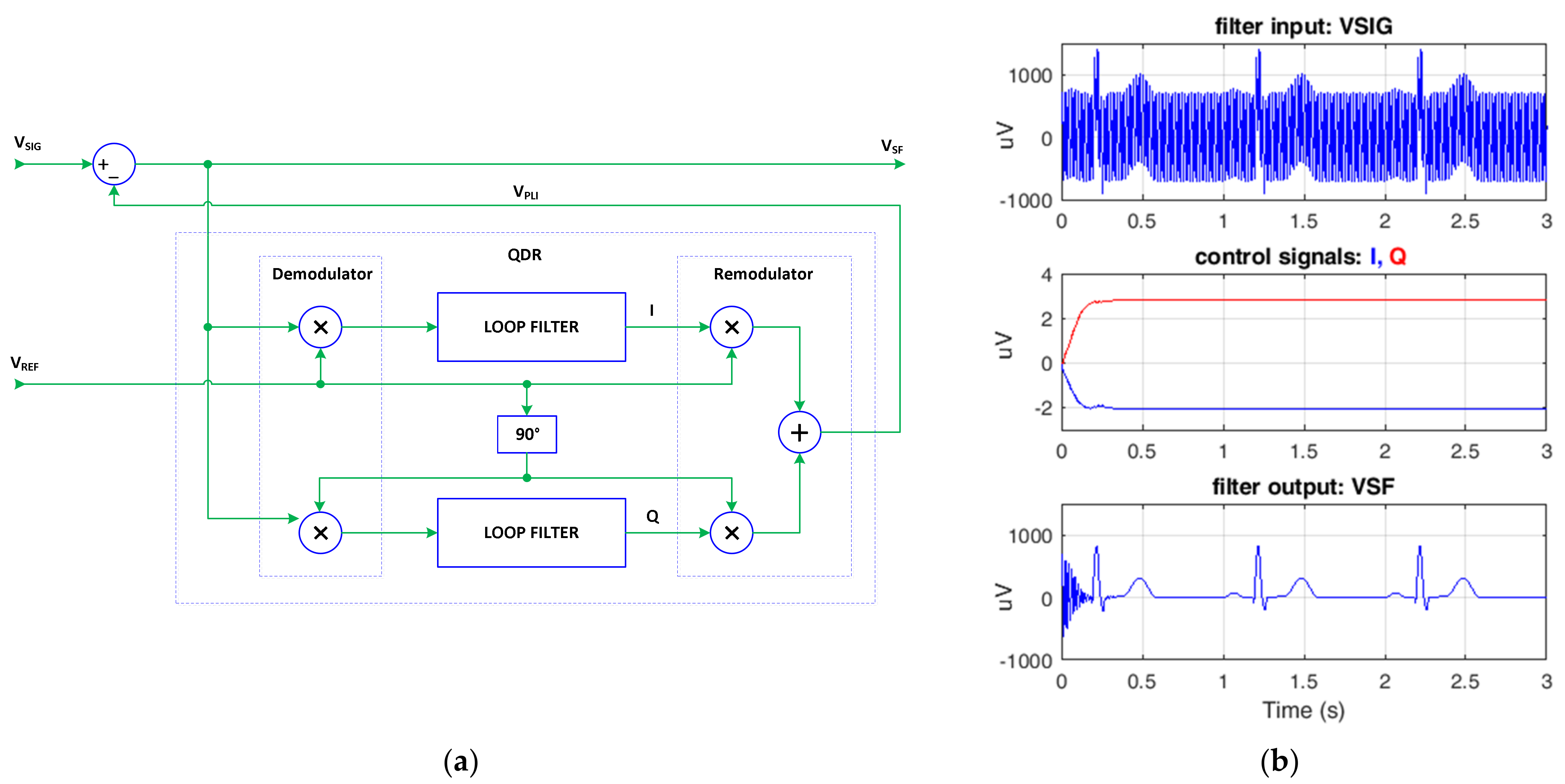
2.3. Synchronous Filtering Concept
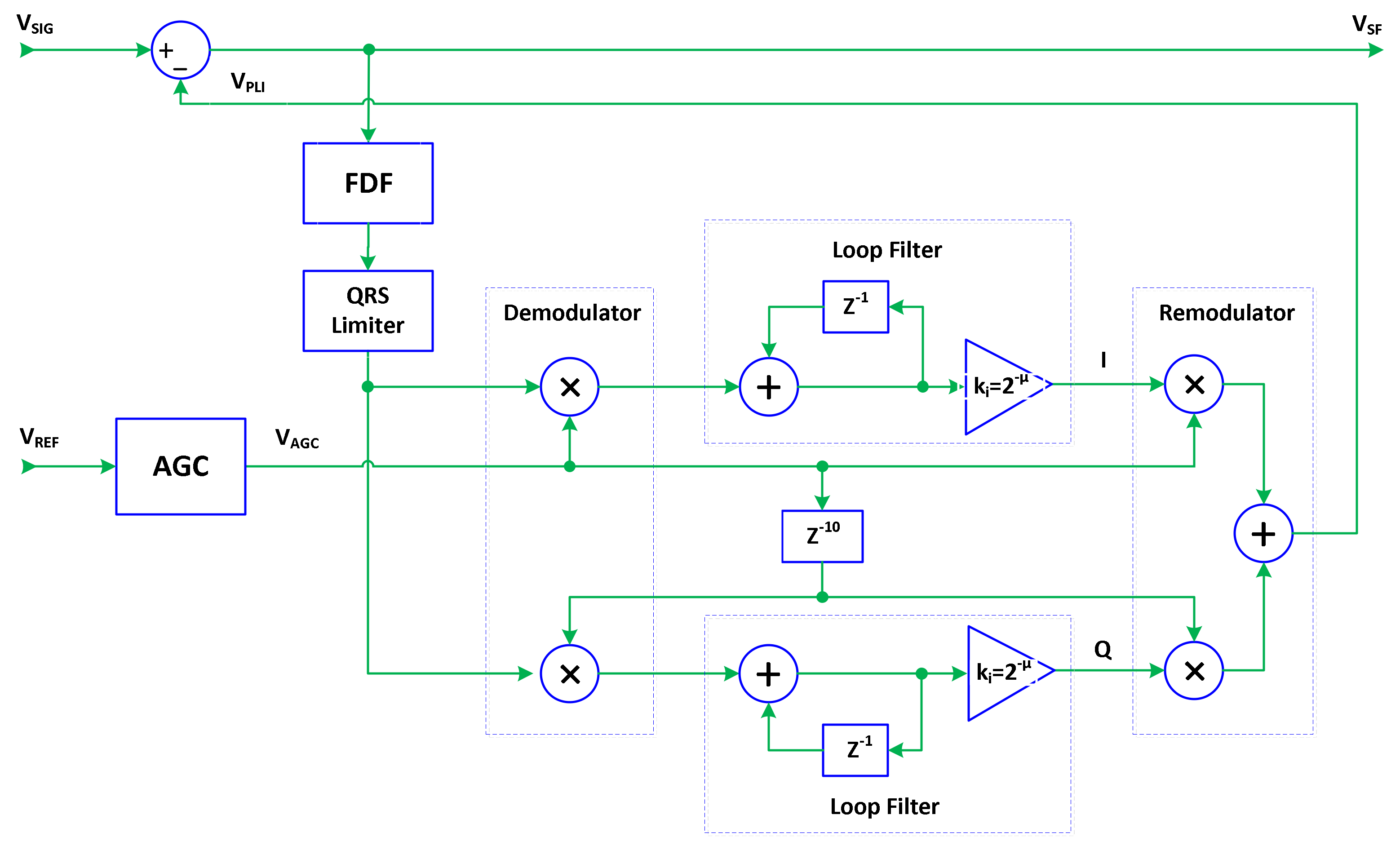
2.4. Automatic Common-Mode Gain Control
2.5. Optimization of SF Architecture for PLI Suppression in ECG Signals
2.6. Estimation of the SF Performance
- PLI with constant amplitude: APLI0 = 50–1000 μV r.m.s. computed over 10 s. The maximal setting was chosen to represent a severe realistic scenario with peak-to-peak PLI amplitude reaching 2800 μV.
- PLI with constant frequency: fPLI = 48–52 Hz, exceeding the standards for maximal mains frequency deviation in the synchronous European grid of 49.8 Hz to 50.2 Hz.
- PLI with linear amplitude change: ΔAPLI = ±(10–200) μV/s. The maximal slew rate was chosen to represent the worst realistic scenario with peak-to-peak PLI amplitude span from 0 to 4000 μV within 10 s.
- PLI with linear frequency change: fPLI = 50 Hz, ΔfPLI = ±(0.01–0.1) Hz/s. The maximal slew rate was chosen to represent the worst realistic scenario for a change in the frequency of 1 Hz over 10 s, e.g., covering a span of 49–50 Hz and 50–51 Hz.
- PLI with phase shift of the reference input VREF: φPLI = 0–360° in Equation (18).
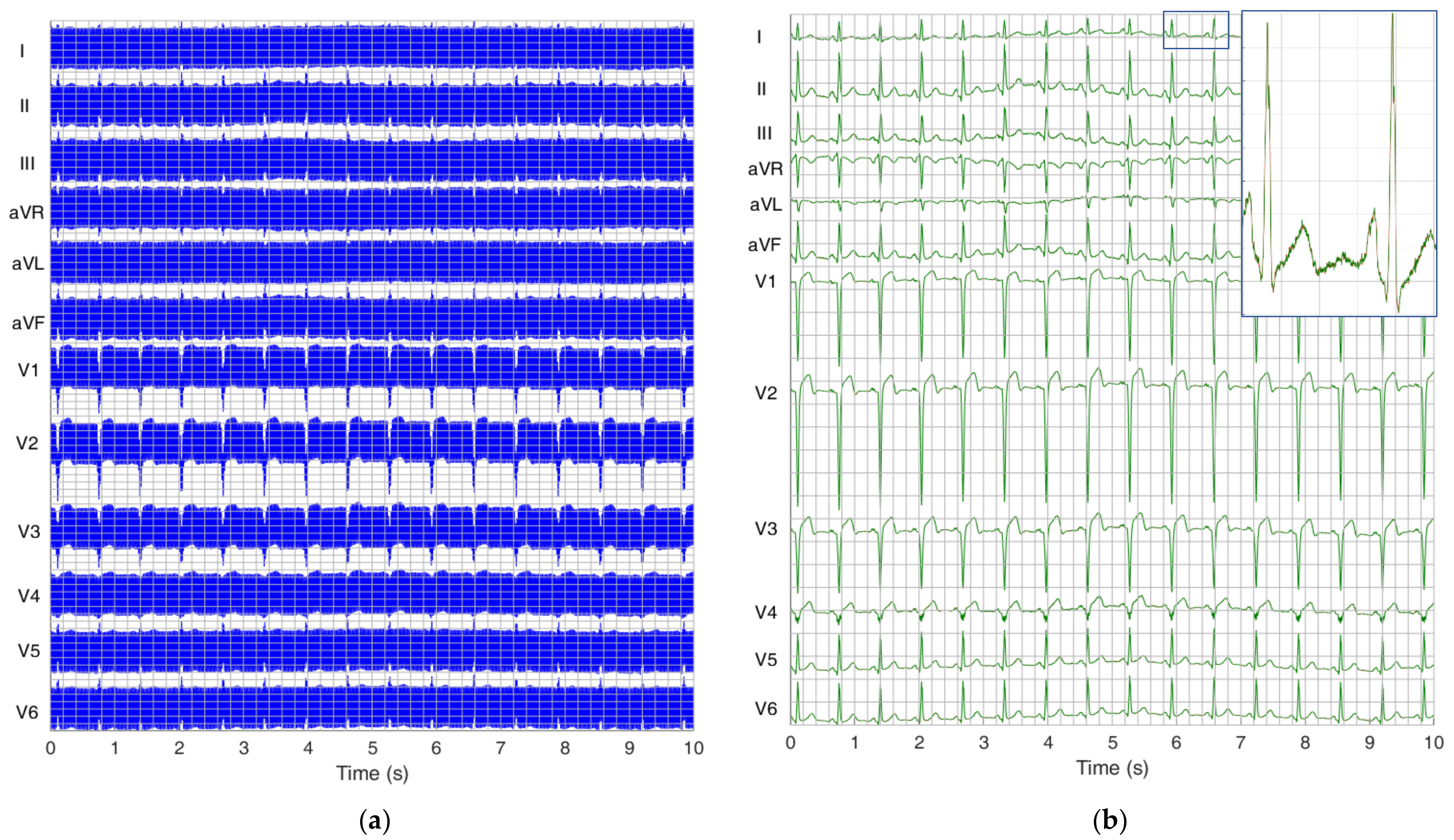
3. Results
3.1. Optimization of SF Algorithm
3.2. Test of SF Algorithm with PTB Diagnostic ECG Database
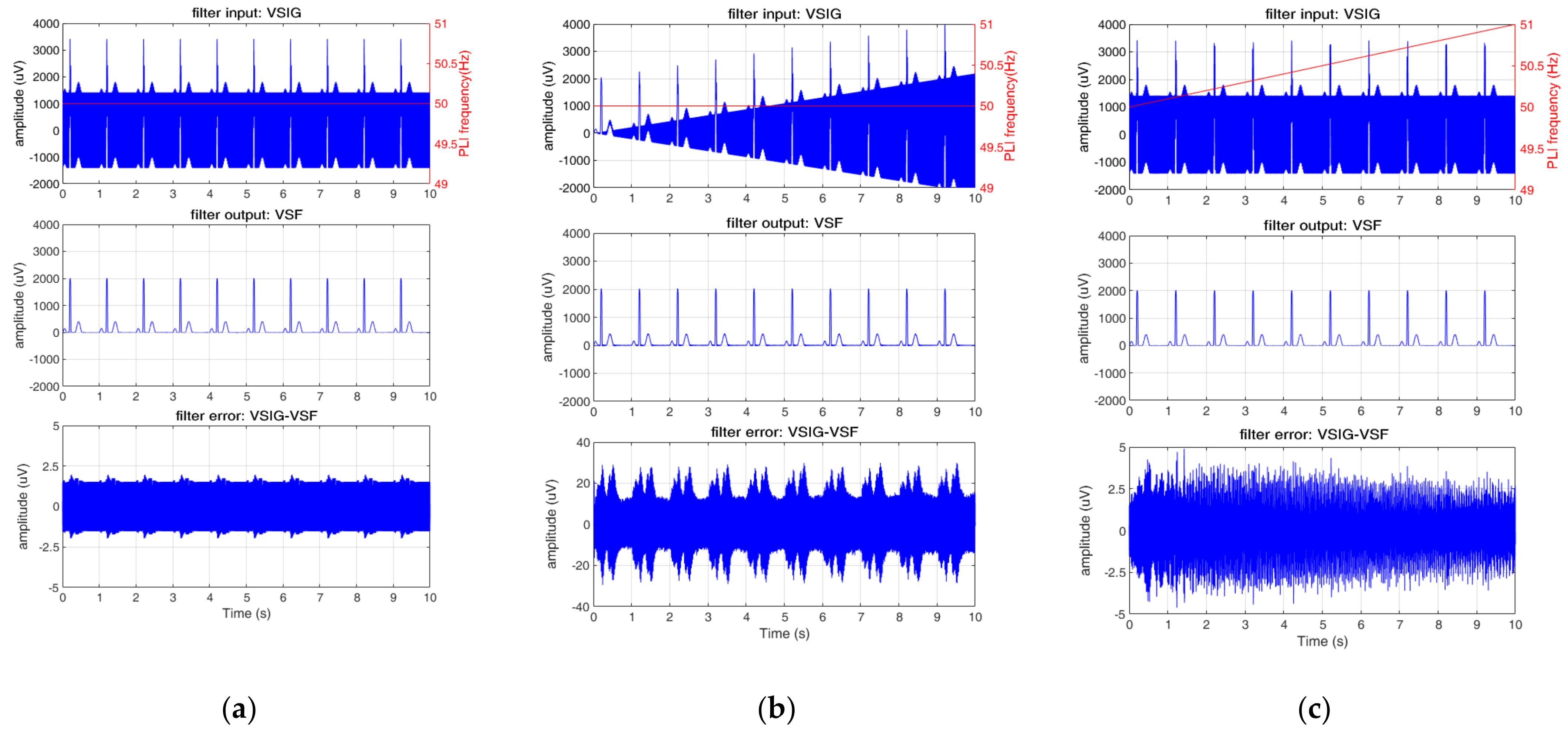
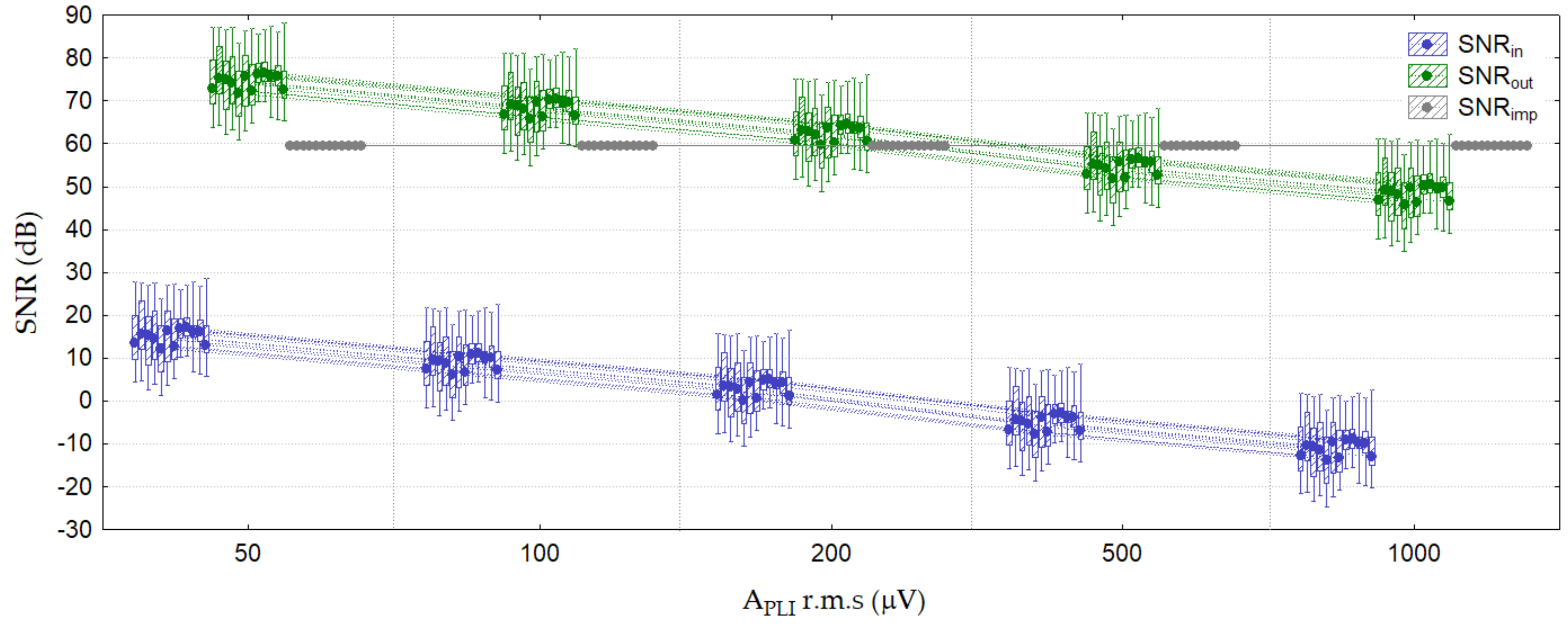
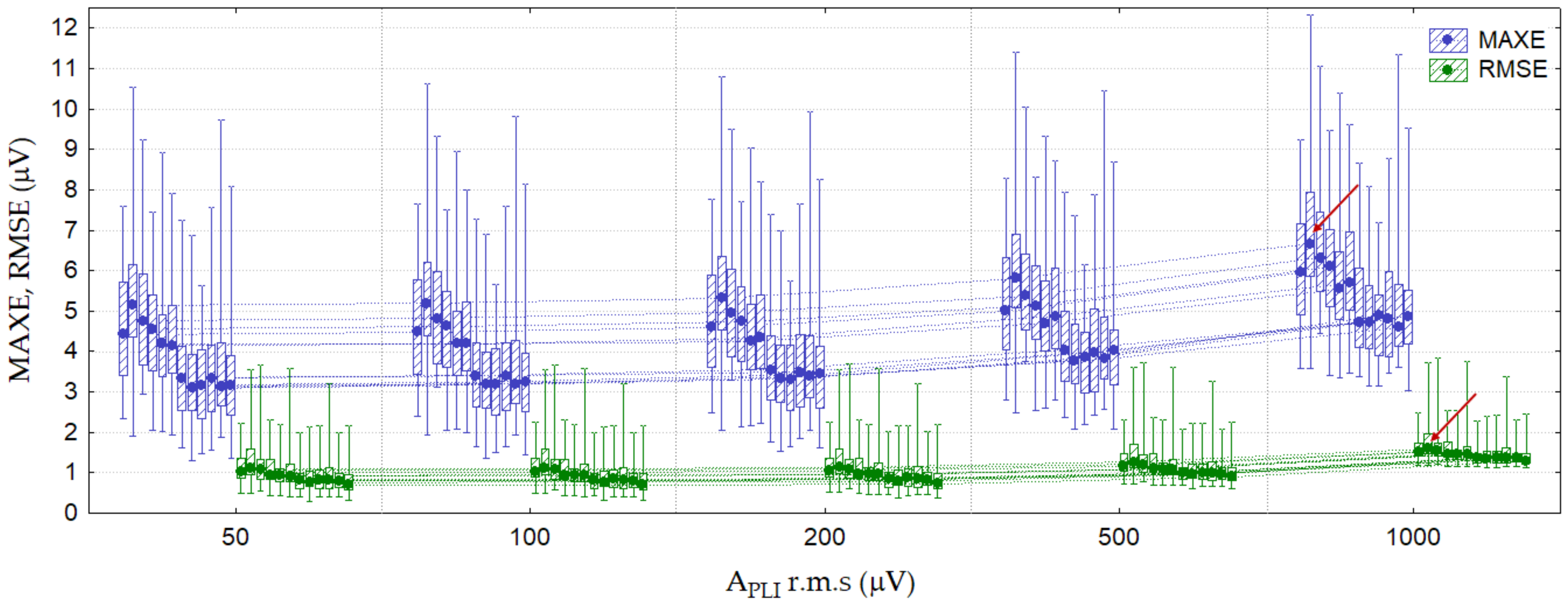
3.2.1. Test 1: PLI Constant (Amplitude Test)
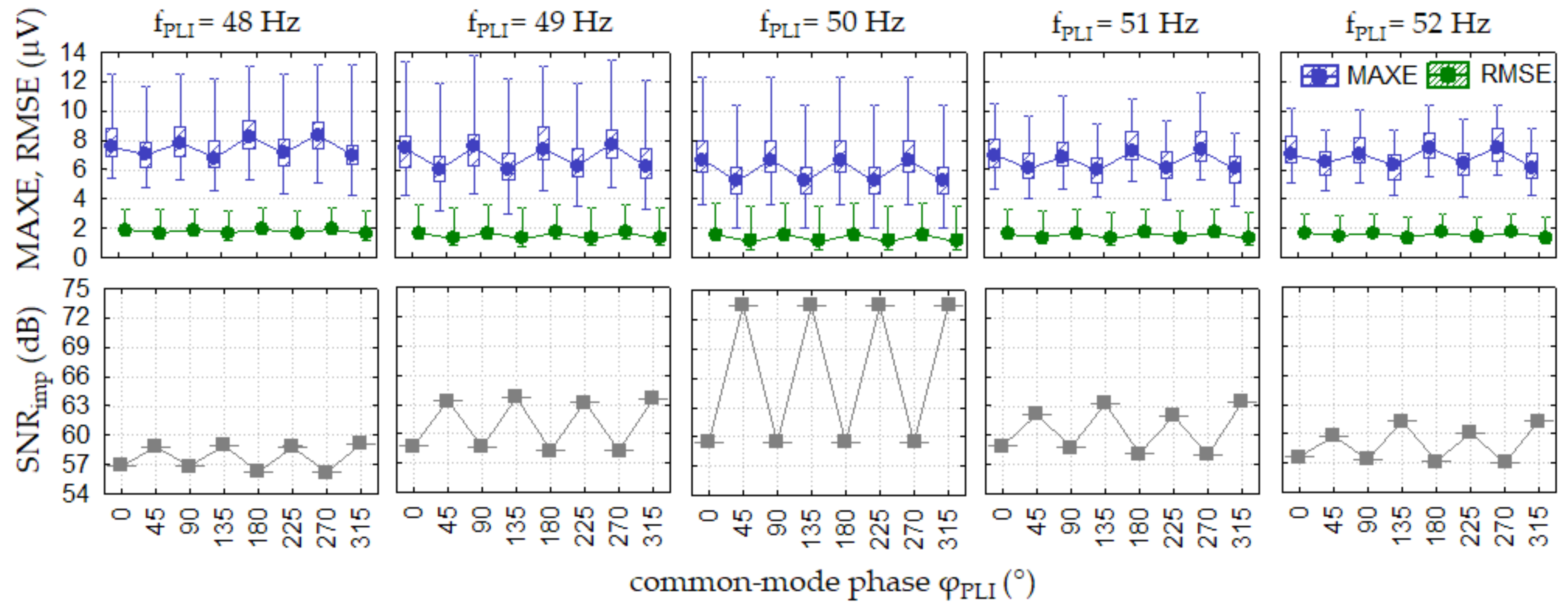
3.2.2. Test 2: PLI Constant (Frequency Test)
3.2.3. Test 3: PLI Constant (Common-Mode Phase Test)
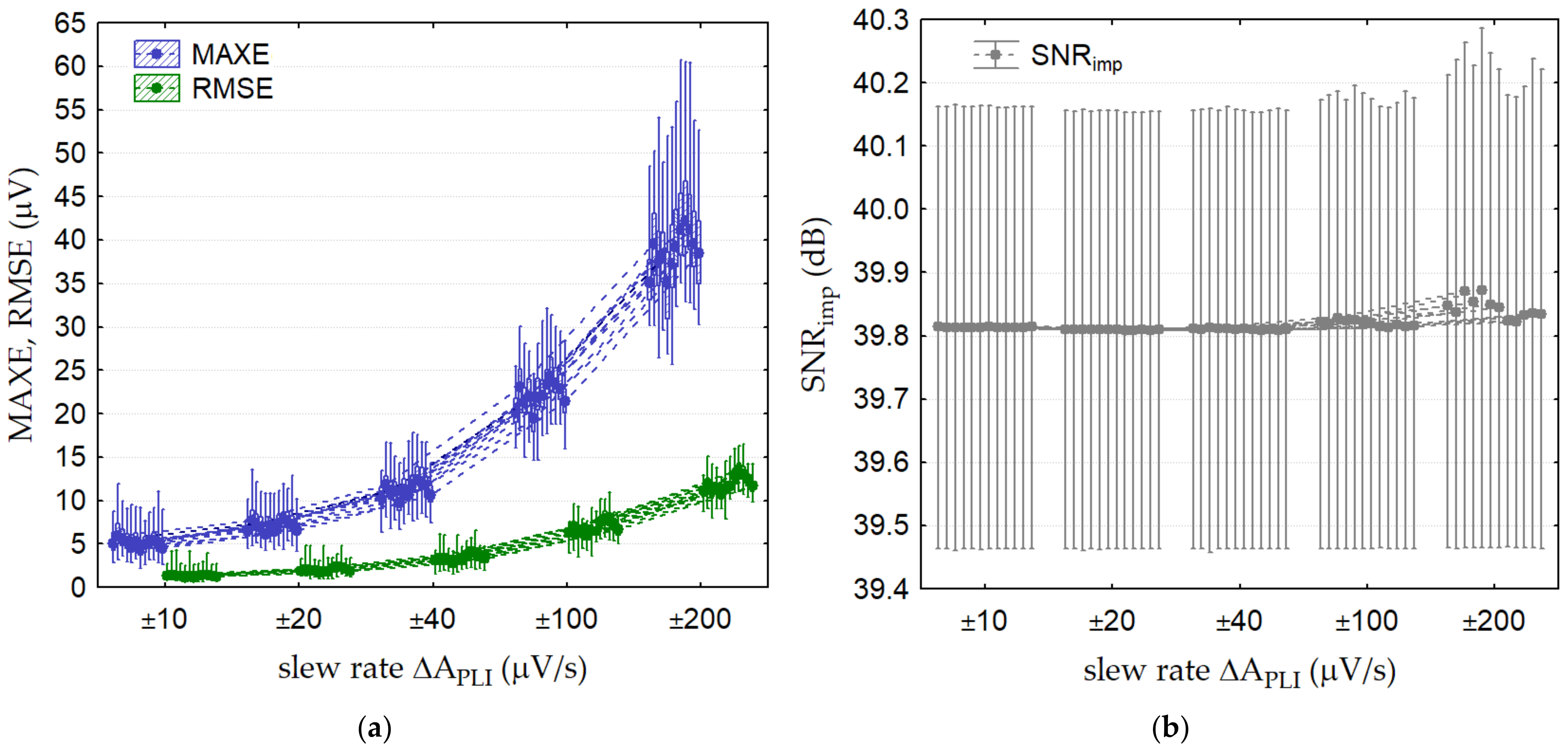
3.2.4. Test 4: PLI Linear Amplitude Change
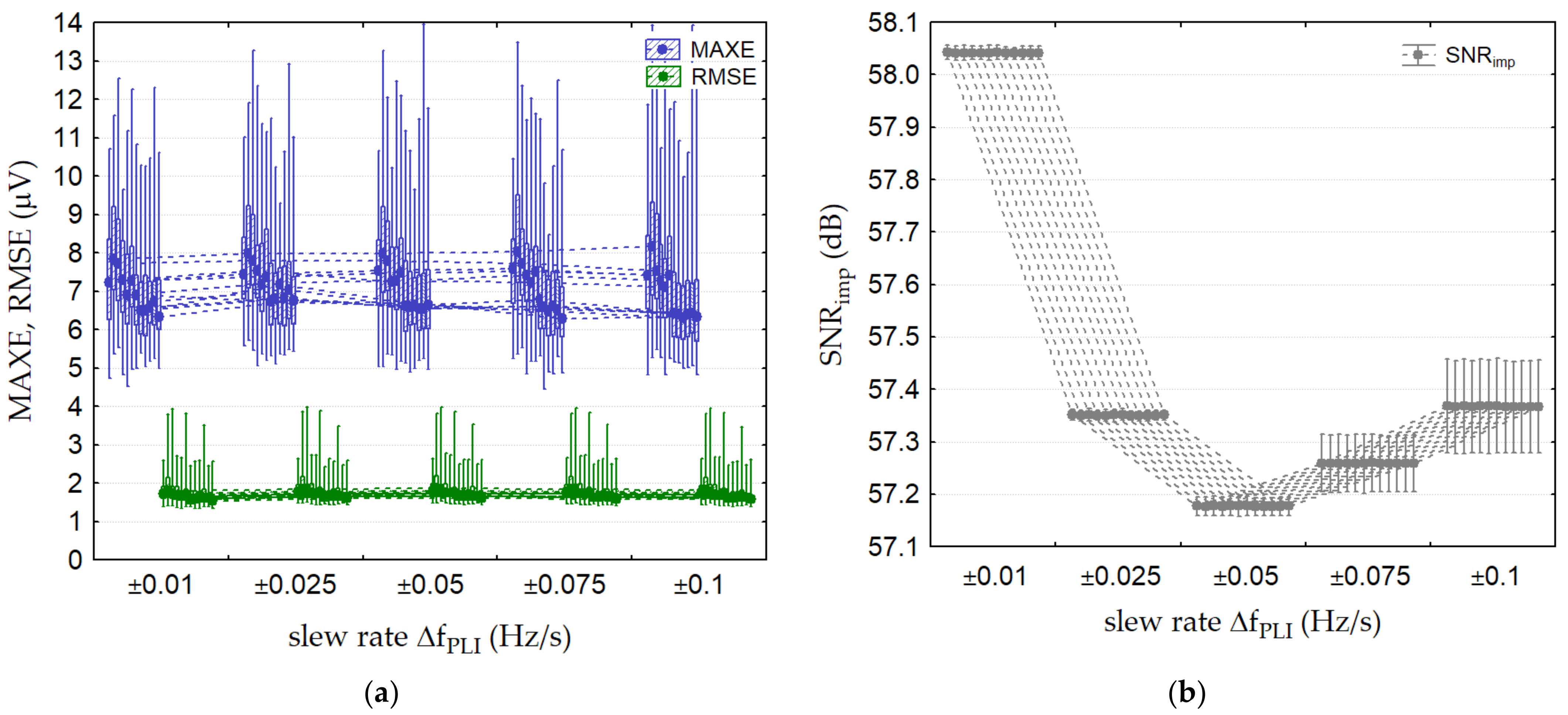
3.2.5. Test 5: PLI linear Frequency Change
3.3. Extremity Test of SF Algorithm against Standards
4. Discussion
5. Conclusions
- A novel biopotential readout circuit processing both differential-mode and common-mode signals in systems with and without DRE.
- An innovative closed-loop SF algorithm, robust against amplitude and frequency variations in PLI.
- An optimized loop filter for operation with ECG signals.
- A novel QRS limiter with an adaptive threshold, effectively eliminating the QRS influence.
- A tricky all-digital open-loop AGC with a fast response and making possible the SF operation without SPLL.
- A novel, extensively tested, and validated concept using real and synthesized ECG signals and PLI with variable amplitude and frequency.
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reilly, R.; Lee, T. Electrograms (ECG, EEG, EMG, EOG). Technol. Health Care 2010, 18, 443–458. [Google Scholar] [CrossRef] [PubMed]
- Kaniusas, E. Biomedical Signals and Sensors III, Linking Electric Biosignals and Biomedical Sensors; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Neuman, M. Biopotential amplifiers. In Medical Instrumentation: Applications and Design, 5th ed.; Webster, J., Nimunkar, A., Eds.; John Wiley & Sons: New York, NY, USA, 2020; pp. 333–395. [Google Scholar]
- Pallás-Areny, R.; Colominas, J. Simple, fast method for patient body capacitance and power-line electric interference measurement. Med. Biol. Eng. Comput. 1991, 29, 561–563. [Google Scholar] [CrossRef] [PubMed]
- Haberman, M.; Cassino, A.; Spinelli, E. Estimation of stray coupling capacitances in biopotential measurements. Med. Biol. Eng. Comput. 2011, 49, 1067–1071. [Google Scholar] [CrossRef] [PubMed]
- Pallas-Areny, R.; Colominas, J. Differential mode interferences in biopotential amplifiers. In Proceedings of the Images of the Twenty-First Century. Proceedings of the Annual International Engineering in Medicine and Biology Society, Seattle, WA, USA, 9–12 November 1989; pp. 1721–1722. [Google Scholar] [CrossRef]
- De Cheveigné, A.; Nelken, I. Filters: When, Why, and How (Not) to Use Them. Neuron 2019, 102, 280–293. [Google Scholar] [CrossRef] [PubMed]
- Hejjel, L. Suppression of power-line interference by analog notch filtering in the ECG signal for heart rate variability analysis: To do or not to do? Med. Sci. Monit. 2004, 10, MT6-13. [Google Scholar]
- Zhou, X.; Zhang, Y. A hybrid approach to the simultaneous eliminating of power-line interference and associated ringing artifacts in electrocardiograms. BioMed. Eng. OnLine 2013, 12, 42. [Google Scholar] [CrossRef]
- Smith, S. Digital Signal Processing. A Practical Guide for Engineers and Scientists; Elsevier: Newnes, NSW, Australia, 2003; pp. 277–284. [Google Scholar]
- Levkov, C. Fast integer coefficient FIR filters to remove the ac interference and the high-frequency noise. Med. Biol. Eng. Comput. 1989, 27, 330–332. [Google Scholar] [CrossRef]
- Tanji, A.K., Jr.; de Brito, M.; Alves, M.; Garcia, R.; Chen, L.; Ama, N. Improved noise cancelling algorithm for electrocardiogram based on moving average adaptive filter. Electronics 2021, 10, 2366. [Google Scholar] [CrossRef]
- Dobrev, D.; Neycheva, T.; Mudrov, N. High-Q comb filter for mains interference suppression. Annu. J. Electron. 2009, 3, 47–49. [Google Scholar]
- Piskorowski, J. Suppressing harmonic powerline interference using multiple-notch filtering methods with improved transient behavior. Measurement 2012, 45, 1350–1361. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, B. Power line interference reduction in ECG using combination of MA method and IIR notch filter. Int. J. Recent Trends Eng. 2009, 2, 125–129. [Google Scholar]
- Tabakov, S.; Iliev, I.; Krasteva, V. Online digital filter and QRS detector applicable in low resource ECG monitoring systems. Ann. Biomed. Eng. 2008, 36, 1805–1815. [Google Scholar] [CrossRef]
- Verma, A.; Singh, Y. Adaptive tunable notch filter for ECG signal enhancement. Procedia Comput. Sci. 2015, 57, 332–337. [Google Scholar] [CrossRef]
- Daskalov, I.; Dotsinsky, I.; Christov, I. Developments in ECG Acquisition, Preprocessing, Parameter Measurement and Recording. IEEE Eng. Med. Biol. 1998, 17, 50–58. [Google Scholar] [CrossRef]
- Levkov, C.; Mihov, G.; Ivanov, R.; Daskalov, I.; Christov, I.; Dotsinsky, I. Removal of power-line interference from the ECG: A review of the subtraction procedure. Biomed. Eng. Online 2005, 4, 50. [Google Scholar] [CrossRef]
- Mihov, G.; Dotsinsky, I. Power-line interference elimination from ECG in case of non-multiplicity between the sampling rate and the power-line frequency. Biomed. Signal Process. Control 2008, 3, 334–340. [Google Scholar] [CrossRef]
- Dotsinsky, I.; Stoyanov, T.; Mihov, G. Power-line interference removal from high sampled ECG signals using modified version of the subtraction procedure. Int. J. Bioautom. 2020, 24, 381–392. [Google Scholar] [CrossRef]
- Tompkins, W. Biomedical Signal Processing. C-Language Examples and Laboratory Experiments for the IBM PC; Prentice-Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- Haykin, S. Adaptive Filter Theory; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Maniruzzaman, M.; Billah, K.; Biswas, U.; Gain, B. Least-mean-square algorithm based adaptive filters for removing power line interference from ECG signal. In Proceedings of the International Conference on Informatics Electronics & Vision, Dhaka, Bangladesh, 18–19 May 2012; pp. 737–740. [Google Scholar] [CrossRef]
- Makwana, G.; Gupta, L. De-noising of Electrocardiogram (ECG) with Adaptive Filter Using MATLAB. In Proceedings of the Fifth International Conference on Communication Systems and Network Technologies, Gwalior, India, 4–6 April 2015; pp. 511–514. [Google Scholar] [CrossRef]
- Ren, A.; Du, Z.; Li, J.; Hu, F.; Yang, X.; Abbas, H. Adaptive interference cancellation of ECG signals. Sensors 2017, 17, 942. [Google Scholar] [CrossRef]
- Chandrakar, C.; Kowar, M.K. Denoising ECG Signals Using Adaptive Filter Algorithm. Int. J. Soft Comput. Eng. 2012, 2, 120–123. [Google Scholar]
- Rahman, M.Z.U.; Karthik, G.V.S.; Fathima, S.Y.; Lay-Ekuakille, A. An efficient cardiac signal enhancement using time–frequency realization of leaky adaptive noise cancelers for remote health monitoring systems. Measurement 2013, 46, 3815–3835. [Google Scholar] [CrossRef]
- Faiz, M.; Kale, I. Removal of multiple artifacts from ECG signal using cascaded multistage adaptive noise cancellers. Array 2022, 14, 100133. [Google Scholar] [CrossRef]
- Dobrev, D.; Neycheva, T.; Mudrov, N. Digital lock-in techniques for adaptive power-line interference extraction. Physiol. Meas. 2008, 29, 803–816. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, Y.; Lin, P.; Lin, Y. A novel PLI suppression method in ECG by notch filtering with a modulation-based detection and frequency estimation scheme. Biomed. Signal Process. Control 2020, 62, 102150. [Google Scholar] [CrossRef]
- Grandmaison, M.; Belzile, J.; Thibeault, C.; Gagnon, F. Frequency domain filter using an accurate reconfigurable FFT/IFFT core. In Proceedings of the IEEE Workshop on Circuits and Systems, Montreal, QC, Canada, 23 June 2004; pp. 165–168. [Google Scholar] [CrossRef]
- Ferdjallah, M.; Barr, R. Frequency-domain digital filtering techniques for the removal of powerline noise with application to the electrocardiogram. Comput. Biomed. Res. 1990, 23, 473–489. [Google Scholar] [CrossRef]
- Slimane, A.; Zaid, A. Real-time FFT-based notch filter for single-frequency noise cancellation: Application to electrocardiogram signal denoising. J. Med. Signals Sens. 2021, 11, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Wang, S.; Li, F.; Wang, J.; Sangaiah, A.; Sheng, V.; Ding, X. An ECG signal de-noising approach based on wavelet energy and sub-band smoothing filter. Appl. Sci. 2019, 9, 4968. [Google Scholar] [CrossRef]
- Oliveira, R.; Duarte, Q.; Abreu, E.; Vieira, J. A wavelet-based method for power-line interference removal in ECG signals. Res. Biomed. Eng. 2018, 34, 73–86. [Google Scholar] [CrossRef]
- Dobrev, D.; Neycheva, T. High-quality biopotential acquisition without a reference electrode: Power-line interference reduction by adaptive impedance balancing in a mixed analog–digital design. Med. Biol. Eng. Comput. 2022, 60, 1801–1814. [Google Scholar] [CrossRef]
- Dobrev, D.; Neycheva, T. Software PLL for power-line interference synchronization: Design, modeling and simulation. Annu. J. Electron. 2014, 8, 58–61. [Google Scholar]
- Dobrev, D.; Neycheva, T. Software PLL for power-line interference synchronization: Implementation and results. Annu. J. Electron. 2015, 9, 18–21. [Google Scholar]
- Zywietz, C. CTS-ECG Test Atlas; Center for Computer Electrocardiography, Biosignal Processing, Medical School: Hannover, Germany, 1999; Available online: https://www.medteq.net/ctscse-database-information (accessed on 8 June 2022).
- IEC 60601-2-25:2011; Medical Electrical Equipment—Part 2-25: Particular Requirements for the Basic Safety and Essential Performance of Electrocardiographs. 2nd ed. International Electrotechnical Commission: Geneva, Switzerland, 2011; pp. 1–196ISBN 978-2-88912-719-1.
- Bousseljot, R.; Kreiseler, D.; Schnabel, A. Nutzung der EKG-signaldatenbank CARDIODAT der PTB über das Internet. Biomed. Tech. 1995, 40, S317. [Google Scholar] [CrossRef]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.; Mark, R.; Stanley, H. PhysioBank PhysioToolkit and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Winter, B.B.; Webster, J.G. Driven-right-leg circuit design. IEEE Trans. Biomed. Eng. 1983, 30, 62–66. [Google Scholar] [CrossRef]
- Dobrev, D.; Neycheva, T. Software automatic gain control. In Proceedings of the XXIX International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 16–18 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Drentea, C. Modern Communications Receiver Design and Technology; Artech House Inc.: Santa Clara, CA, USA, 2010. [Google Scholar]
- Frey, D. Synchronous filtering. IEEE Trans. Circuits Syst. 2006, 53, 1772–1782. [Google Scholar] [CrossRef]
- Weaver, D. A Third Method of Generation and Detection of Single-Sideband Signals. Proc. IRE 1956, 44, 1703–1705. [Google Scholar] [CrossRef]
- Dobrev, D.; Neycheva, T. Open-loop Software Automatic Gain Control: Common-mode Power-line Interference Stabilization During ECG Recording. In Proceedings of the XXXI International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 13–15 September 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Perez, J.; Pueyo, S.; Lopez, B. Automatic Gain Control. Techniques and Architectures for RF Receivers; Springer Nature AG: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jekova, I.; Krasteva, V.; Ménétré, S.; Stoyanov, T.; Christov, I.; Fleischhackl, R.; Schmid, J.-J.; Didon, J.-P. Bench study of the accuracy of a commercial AED arrhythmia analysis algorithm in the presence of electromagnetic interferences. Physiol. Meas. 2009, 30, 695–705. [Google Scholar] [CrossRef]
- Vale-Cardoso, A.; Guimaraes, H. The effect of 50/60 Hz notch filter application on human and rat ECG recordings. Physiol. Meas. 2010, 31, 45–58. [Google Scholar] [CrossRef]
- Chaitanya, M.K.; Sharma, L.D. Electrocardiogram signal filtering using circulant singular spectrum analysis and cascaded Savitzky-Golay filter. Biomed. Signal Process. Control 2022, 75, 103583. [Google Scholar] [CrossRef]
- Martens, S.M.M.; Mischi, M.; Oei, G.; Bergmans, J.W.M. An Improved Adaptive Power Line Interference Canceller for Electrocardiography. IEEE Trans. Biomed. Eng. 2006, 53, 2220–2231. [Google Scholar] [CrossRef] [PubMed]
- Razzaq, N.; Sheikh, S.A.; Salman, M.; Zaidi, T. An Intelligent Adaptive Filter for Elimination of Power Line Interference from High Resolution Electrocardiogram. IEEE Access 2016, 4, 1676–1688. [Google Scholar] [CrossRef]
- Saxena, S.; Jais, R.; Hota, M.K. Removal of Powerline Interference from ECG Signal using FIR, IIR, DWT and NLMS Adaptive Filter. In Proceedings of the 2019 IEEE International Conference on Communication and Signal Processing, Chennai, India, 4–6 April 2019; pp. 12–16. [Google Scholar] [CrossRef]
- Tomasini, M.; Benatti, S.; Milosevic, B.; Farella, E.; Benini, L. Power Line Interference Removal for High-Quality Continuous Biosignal Monitoring With Low-Power Wearable Devices. IEEE Sens. J. 2016, 16, 3887–3895. [Google Scholar] [CrossRef]
- Biswas, U.; Maniruzzaman, M. Removing power line interference from ECG signal using adaptive filter and notch filter. In Proceedings of the IEEE International Conference on Electrical Engineering and Information & Communication Technology, Dhaka, Bangladesh, 10–12 April 2014. [Google Scholar] [CrossRef]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. Noise-aware dictionary-learning-based sparse representation framework for detection and removal of single and combined noises from ECG signal. Healthc. Technol. Lett. 2017, 4, 2–12. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.S.; Krishnamoorthy, G.; Vaithiyanathan, D. An adaptive denoising approach to powerline interference reduction in ECG recording. Indian J. Eng. Mater. Sci. 2020, 27, 939–951. [Google Scholar] [CrossRef]
- Bodile, R.M.; Talari, V.K.H.R. Removal of Power-Line Interference from ECG Using Decomposition Methodologies and Kalman Filter Framework: A Comparative Study. Traitement Du Signal 2021, 38, 875–881. [Google Scholar] [CrossRef]
- Leski, J.M. Robust nonlinear aggregation operator for ECG powerline interference reduction. Biomed. Signal Process. Control 2021, 69, 102675. [Google Scholar] [CrossRef]
- Mateo, J.; Sanchez, C.; Torres, A.; Cervigon, R.; Rieta, J.J. Neural Network Based Canceller for Powerline Interference in ECG signals. Comput. Cardiol. 2008, 35, 1073–1076. [Google Scholar]
- Qiu, Y.; Huang, K.; Xiao, F.; Shen, H. Power-Line Interference Suppression in Electrocardiogram Using Recurrent Neural Networks. In Proceedings of the 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics, Shanghai, China, 14–16 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Poungponsri, S.; Yu, X.H. An adaptive filtering approach for electrocardiogram (ECG) signal noise reduction using neural networks. Neurocomputing 2013, 117, 206–213. [Google Scholar] [CrossRef]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L. Sparsity-based modified wavelet de-noising autoencoder for ECG signals. Signal Process. 2022, 198, 108605. [Google Scholar] [CrossRef]
- Neycheva, T.; Dobrev, D. Design of Fractional Filters for Power-line Interference Suppression in ECG Signals. In Proceedings of the XXXI International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 13–15 September 2022; pp. 1–6. [Google Scholar] [CrossRef]


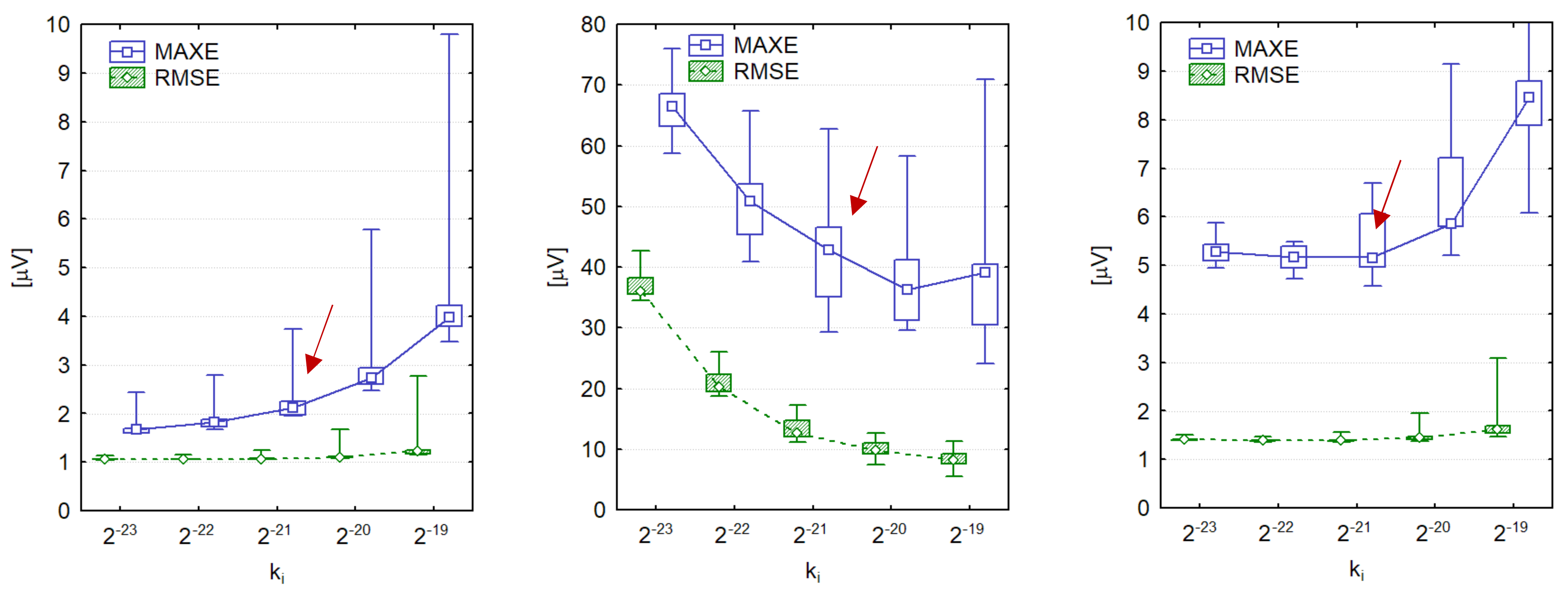
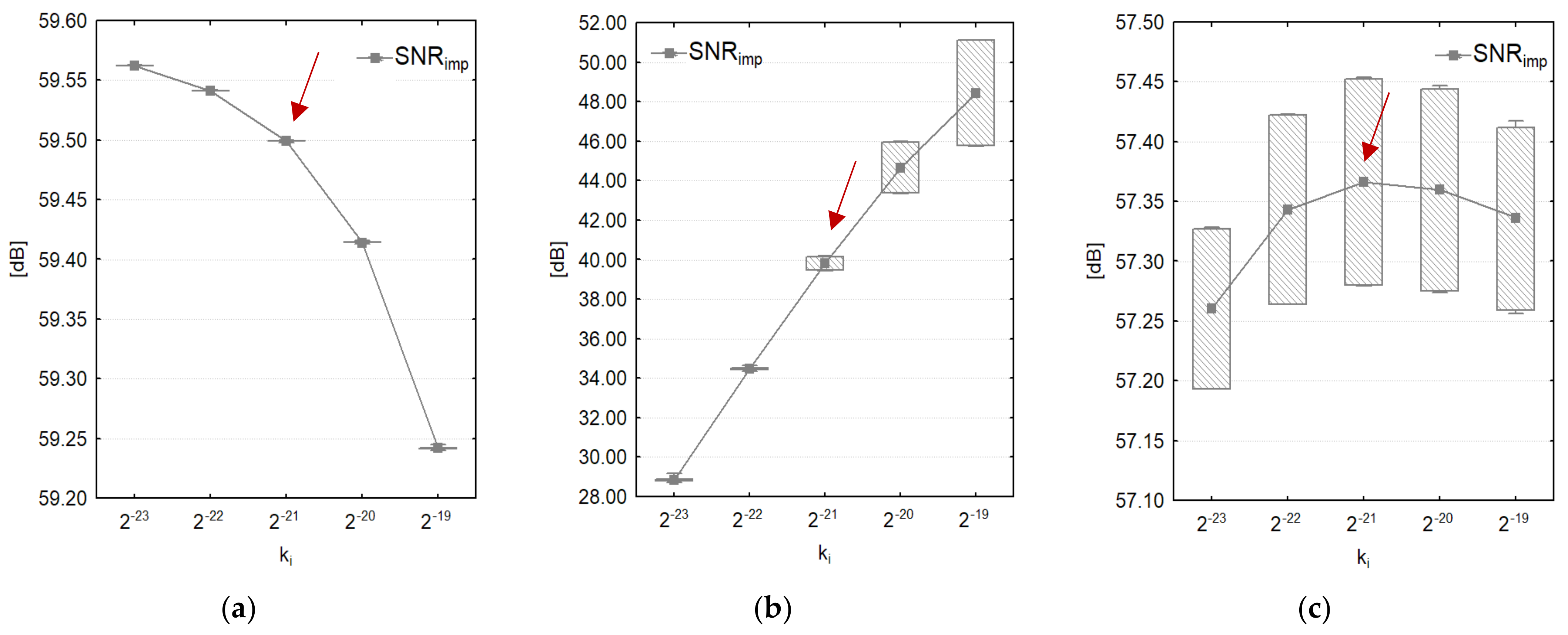


| PLI Amplitude APLI r.m.s (μV) | PLI Amplitude Slew Rate ΔAPLI (μV/s) | PLI Frequency Range fPLI (Hz) | PLI Frequency Slew Rate ΔfPLI (Hz/s) | |
|---|---|---|---|---|
| PLI constant | 1000 | 0 | 50 | 0 |
| PLI linear amplitude change | 1000 | ±200 | 50 | 0 |
| PLI linear frequency change | 1000 | 0 | 49–51 | ±0.1 |
| PLI Ampl. APLI r.m.s (μV) | PLI Ampl. Slew Rate ΔAPLI (μV/s) | PLI Frequency fPLI (Hz) | PLI Frequency Slew Rate ΔfPLI (Hz/s) | VREF Phase φPLI (°) | ECG Leads | |
|---|---|---|---|---|---|---|
| Test 1: PLI constant (amplitude test) | 50, 100, 200, 500, 1000 | 0 | 50 | 0 | 0 | 12 leads |
| Test 2: PLI constant (frequency test) | 1000 | 0 | (48, 48.1, 48.2, …, 51.8, 51.9, 52) | 0 | 0 | worst lead in Test 1 |
| Test 3: PLI constant (common-mode phase test) | 1000 | 0 | (48, 49, 50, 51, 52) | 0 | (0, 45, 90, 135, 180, 225, 270, 315) | worst lead in Test 1 |
| Test 4: PLI linear amplitude change | (50, 100, 200, 500, 1000) | ±(10, 20, 40, 100, 200) | 50 | 0 | 0 | 12 leads |
| Test 5: PLI linear frequency change | 1000 | 0 | 50 | ±(0.01, 0.025, 0.05, 0.075, 0.1) | 0 | 12 leads |
| PTB Diagnostic ECG Database 12 Leads | CTS-ECG Analytical Database 8 Leads | ||||||
|---|---|---|---|---|---|---|---|
| Setting with Maximal Error | MAXE (μV) | RMSE (μV) | SNRimp (dB) | MAXE (μV) | RMSE (μV) | SNRimp (dB) | |
| Test 1: PLI constant (amplitude test) | Lead II, V2 * APLI = 1000 μV r.m.s. fPLI = 50 Hz | 6.7 (3.5–12.5) | 1.5 (1.2–2.8) | (60) | 2.4 (2.3–5.5) | 1.1 (1.1–1.7) | (60) |
| Test 2: PLI constant (frequency test) | Lead II, V2 * APLI = 1000 μV r.m.s. fPLI = 49.3–49.9 Hz | 8.5 (5–15) | 2 (1.2–3.8) | (57–58) | 6.4 (4–8.2) | 1.5 (1.4–2.1) | (57–58) |
| Test 3: PLI constant (common-mode phase test) | Lead II, V2 * APLI = 1000 μV r.m.s. fPLI = 48, 52 Hz | 8 (2.5–14) | 2 (1.8–3.8) | (57–62) | 5 (2.5–8.1) | 1.6 (0.7–2.8) | (57–62) |
| Test 4: PLI linear amplitude change | Lead V2 ΔAPLI = ±40 μV/s fPLI = 50 Hz | 12 (7–17) | 4 (2–7) | (39.8) | 13 (11–14.5) | 5 (2.8–6) | (39.8) |
| Test 5: PLI linear frequency change | Lead II, V2 * APLI = ±1000 μV r.m.s. ΔfPLI = 0.1 Hz/s | 8.2 (5–14) | 1.8 (1.5–4) | (57.3) | 6.5 (4.1–19.8) | 1.5 (1.2–4.2) | (57.3) |
| Study | Database | Methods | PLI Freq [Hz] | SNRin (dB) | SNRout (dB) | SNRimp (dB) | MAXE (μV) | RMSE (μV) |
|---|---|---|---|---|---|---|---|---|
| This study | DB1 | • Common-mode Driven Synchronous Filtering | 50 | −10–15 | 50–75 | 60 | 3–6.7 | 0.8–1.5 |
| 48 | −5 | 52 | 57 | 7.6 | 1.9 | |||
| 52 | −5 | 53 | 58 | 7.0 | 1.8 | |||
| 50 | −10–15 # | 30–55 | 40 | 1–14 | 5–42 | |||
| 49–51 # | −5 | 52 | 57 | 6.8 | 1.8–2 | |||
| Chaitanya and Sharma (2022) [53] | DB2 | • Four-stage cascaded Savitzky–Golay filter | 50 | −5 | 20.3 | 25.3 | NA | 9.6 |
| 50 | −10 | 16.8 | 26.8 | NA | 14.4 | |||
| Tanji et al. (2021) [12] | 1 ECG record | • Moving average PLL | 60 | −11.6 | 38.9 | 50.6 | 300 | NA |
| 66.7 | −11.6 | 46.9 | 58.5 | 300 | NA | |||
| 50.9 | −11.6 | 30.6 | 42.2 | 500 | NA | |||
| Martens et al. (2006) [54] | 1 ECG record | • Improved adaptive filter | 50 | −20–20 | 36 | 16–56 | NA | NA |
| • Simple adaptive filter | 50 | −20–20 | 19–24 | 4–49 | NA | NA | ||
| • Wide notch filter | 50 | −20–20 | 15 | 5–35 | NA | NA | ||
| • Narrow notch filter | 50 | −20–20 | 23 | 3–53 | NA | NA | ||
| • Improved adaptive filter | 48–52 # | 0 | 37 | 37 | NA | NA | ||
| • Simple adaptive filter | 48–52 # | 0 | 20 | 20 | NA | NA | ||
| • Wide notch filter | 48–52 # | 0 | 15 | 15 | NA | NA | ||
| • Narrow notch filter | 48–52 # | 0 | 11 | 11 | NA | NA | ||
| Rahman et al. (2013) [28] | DB2 | • Leaky block adaptive filter | 50 | NA | NA | 11–31 | NA | NA |
| Razzaq et al. (2016) [55] | 1 ECG record | • State space RLS adaptive filter | 50.38 | 1.4–7.5 | 25–32 | 24 | NA | NA |
| 50.38 | 2.5 # | 28 | 26 | NA | NA | |||
| 50.4–51.8 | 7.5 | 22 | 15 | NA | NA | |||
| Saxena et al. (2019) [56] | DB2 | • Normalized LMS adaptive filter | 50 | NA | 51 | NA | NA | 1.5 |
| • Discrete wavelet transform | 50 | NA | 36 | NA | NA | 8.6 | ||
| • IIR filter (order 8) | 50 | NA | 28 | NA | NA | 19.5 | ||
| • FIR filter (order 50) | 50 | NA | 26 | NA | NA | 25.8 | ||
| Tomasini et al. (2016) [57] | DB1 | • RLS adaptive filter | 50–51 | −20–20 | 35 | 15–55 | NA | NA |
| Verma and Singh (2015) [17] | 1 ECG record | • Adaptive notch FIR filter with tunable notch frequency | 50 | 7–15 | 14–25 | 7–10 | NA | NA |
| Biswas and Maniruzzaman (2014) [58] | DB2 | • Normalized LMS adaptive filter | 50 | NA | 6.3 | NA | NA | 5.6 |
| • RLS adaptive filter | 50 | NA | 6.7 | NA | NA | 8.9 | ||
| • Notch filter | 50 | NA | 6.7 | NA | NA | 7.9 | ||
| Satija et al. (2017) [59] | DB2 | • Notch filter | 50 | NA | 30.1 | NA | 100 | NA |
| • LMS adaptive filter | 50 | NA | 25.3 | NA | 130 | NA | ||
| • Algorithm using ECG noise-aware dictionary, sparse signal decomposition, and reconstruction | 50 | NA | 32.9 | NA | 50 | NA | ||
| Kumar et al. (2020) [60] | DB1, DB2, DB3 | • Synchrosqueezing transform with adaptive filter | 50 | −3 | NA | 48–52 | NA | 8.2–13 |
| 48 | −3 | NA | 47–49 | NA | 3.6–15 | |||
| 52 | −3 | NA | 49–50 | NA | 3.4–12 | |||
| Bodile and Talari (2021) [61] | DB2 | • Discrete wavelet transform | 50 | −10–10 | 6–23 | 13–16 | NA | NA |
| • Empirical mode decomposition | 50 | −10–10 | 20–23 | 23–30 | NA | NA | ||
| • Kalman filter | 50 | −10–10 | 22–23 | 13–22 | NA | NA | ||
| • Kalman backward–forward filter | 50 | −10–10 | 22–23 | 13–33 | NA | NA | ||
| Zhou and Zhang (2013) [9] | DB1 | • Hybrid filter with two-sided filtration and multi-iterative approximation techniques | 50 | 10 | 25.4 | 15.4 | NA | NA |
| Leski (2021) [62] | DB1 | • Nonlinear aggregation operator | 50 | (−5; 0) * | NA | NA | 1.3–35.5 | 1–17.4 |
| Mateo et al. (2008) [63] | DB1, DB2, DB3 | • Notch filter | 48.5–51.5 | NA | NA | 14 | NA | 3.5–42 |
| • Notch adaptive filter | 48.5–51.5 | NA | NA | 15 | NA | 2.1–32 | ||
| • Artificial neural network | 48.5–51.5 | NA | NA | 19 | NA | 1.5–16 | ||
| Qui et al. (2017) [64] | DB2 | • Recurrent neural network | 50 ± 0.1 | 0 | 36 | 36 | NA | NA |
| • Kalman smoother | 50 ± 0.1 | 0 | 32 | 32 | NA | NA | ||
| • IIR notch filter | 50 ± 0.1 | 0 | 23 | 23 | NA | NA | ||
| Poungponsri and Yu (2013) [65] | DB2 | • Wavelet transform and artificial neural network | 60 | 11 | 33 | 22 | NA | NA |
| Chatterjee et al. (2022) [66] | DB2 | • Sparsity-based wavelet denoising neural network autoencoder | 50 | 5 | 27.4 | 22.4 | NA | 16.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neycheva, T.; Dobrev, D.; Krasteva, V. Common-Mode Driven Synchronous Filtering of the Powerline Interference in ECG. Appl. Sci. 2022, 12, 11328. https://doi.org/10.3390/app122211328
Neycheva T, Dobrev D, Krasteva V. Common-Mode Driven Synchronous Filtering of the Powerline Interference in ECG. Applied Sciences. 2022; 12(22):11328. https://doi.org/10.3390/app122211328
Chicago/Turabian StyleNeycheva, Tatyana, Dobromir Dobrev, and Vessela Krasteva. 2022. "Common-Mode Driven Synchronous Filtering of the Powerline Interference in ECG" Applied Sciences 12, no. 22: 11328. https://doi.org/10.3390/app122211328
APA StyleNeycheva, T., Dobrev, D., & Krasteva, V. (2022). Common-Mode Driven Synchronous Filtering of the Powerline Interference in ECG. Applied Sciences, 12(22), 11328. https://doi.org/10.3390/app122211328








