Soil Classification by Machine Learning Using a Tunnel Boring Machine’s Operating Parameters
Abstract
1. Introduction
2. Soil Classification
2.1. Soil Classification by Particle Size
2.2. Classification of Soil by Standard Penetration Testing
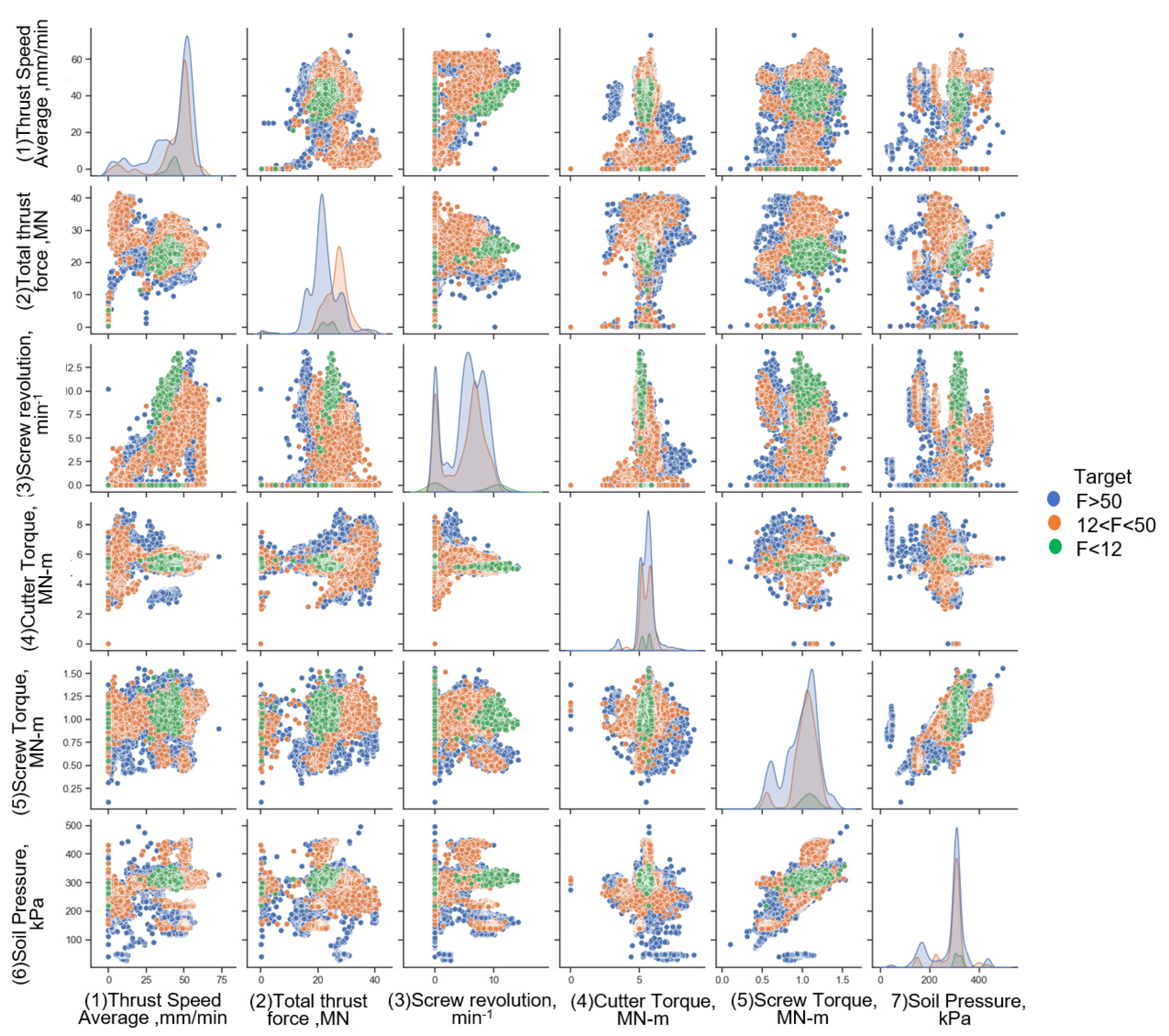
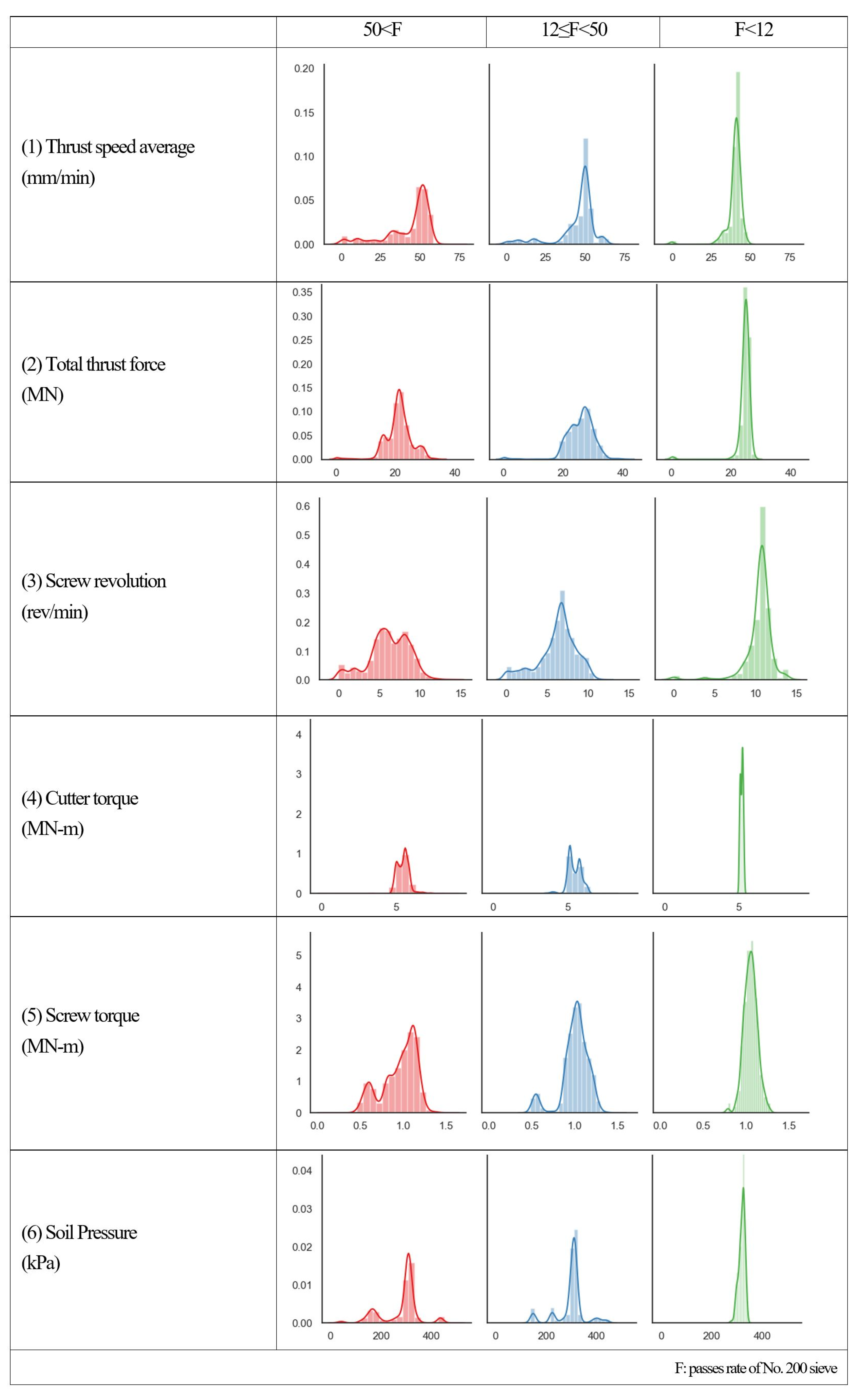
3. Dataset
3.1. Project Description
3.2. Data Preparation
4. Methodology
4.1. ML Models
4.1.1. Decision Tree
4.1.2. Ensemble Learning Method (Boosting)
4.1.3. Support Vector Machine (SVM)
4.2. Modeling Methodology
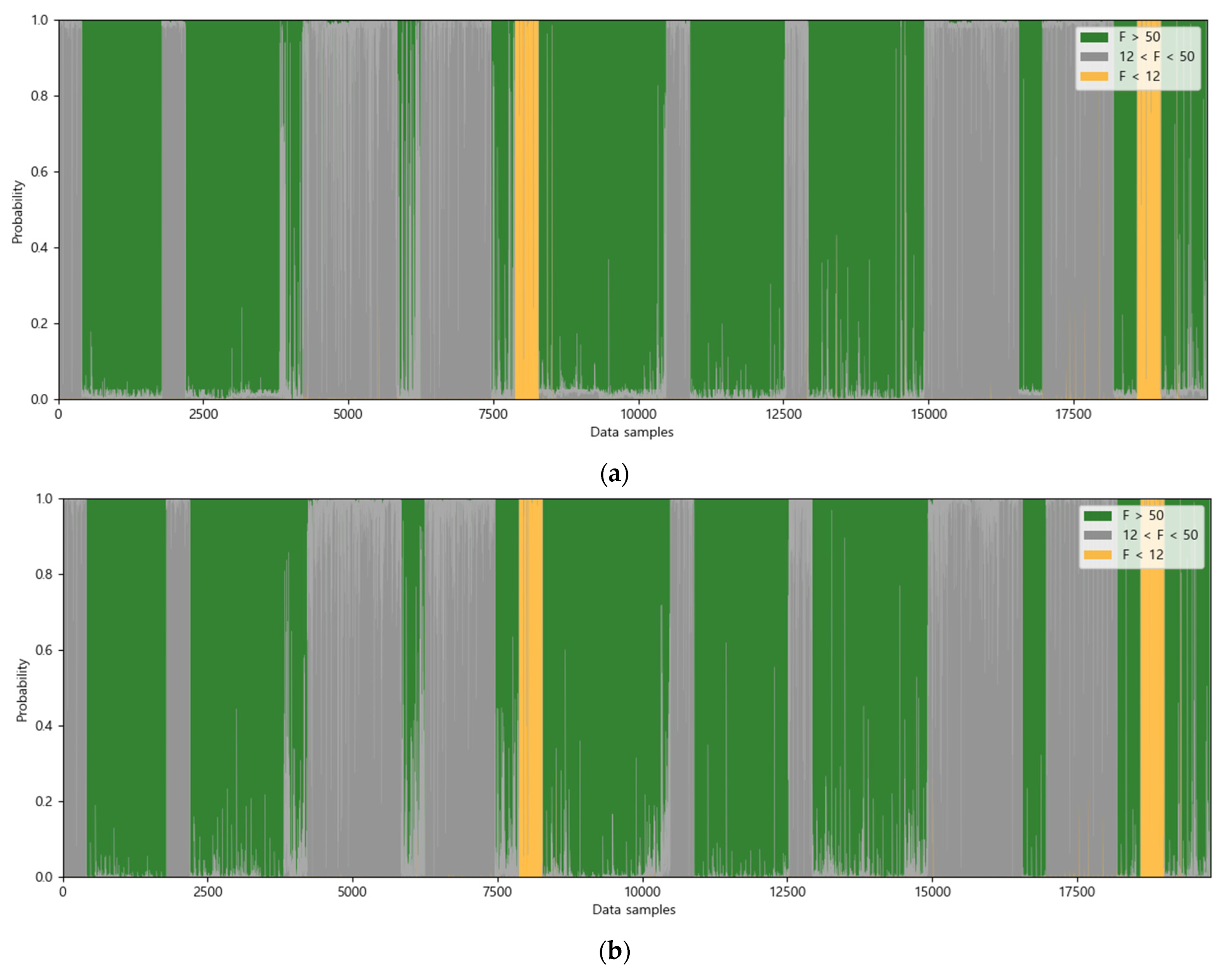
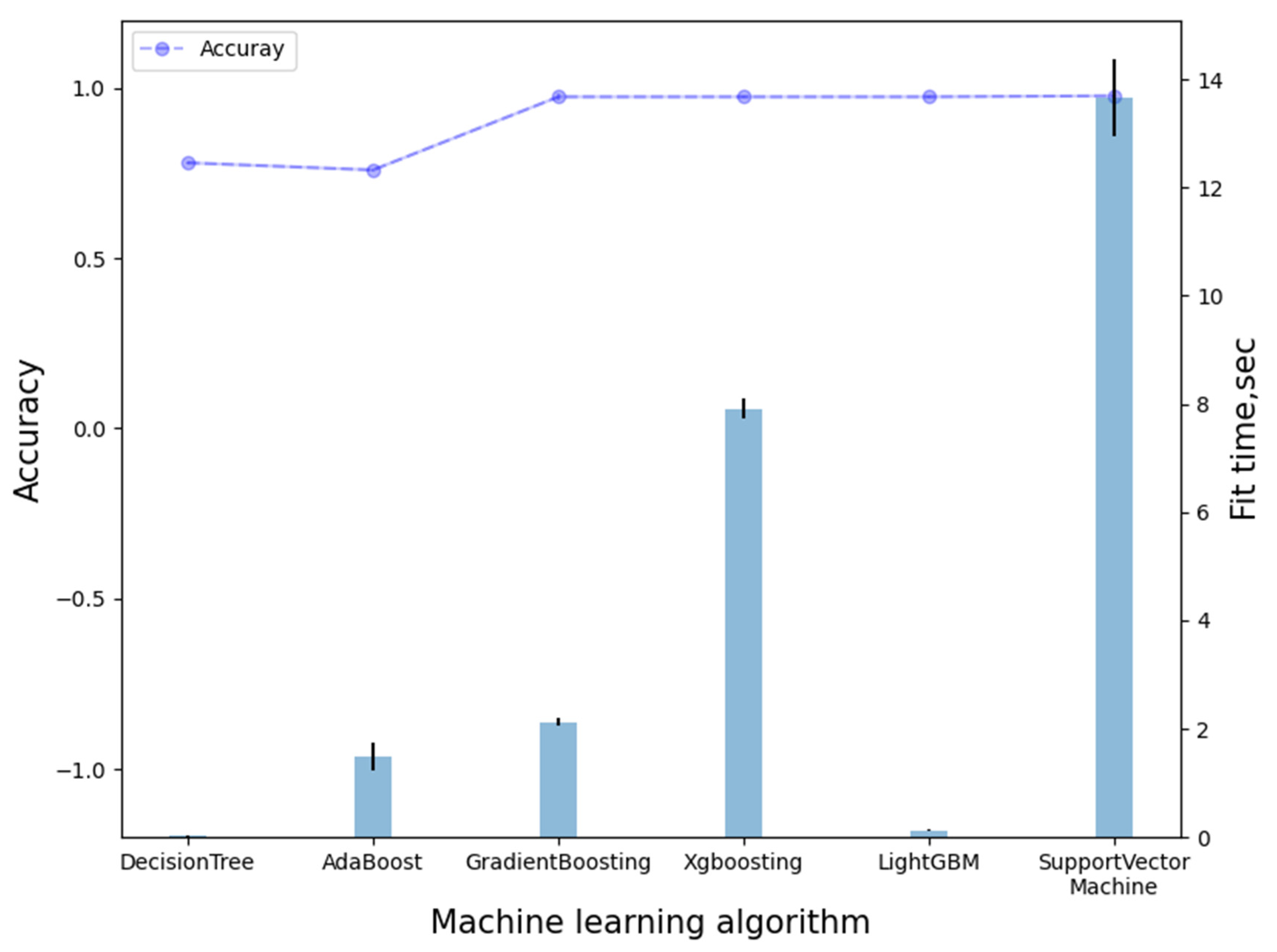
5. Results
5.1. Classification Results by Soil Particle Size (Step 1)
5.2. Classification Results by N-Value (Step 2)
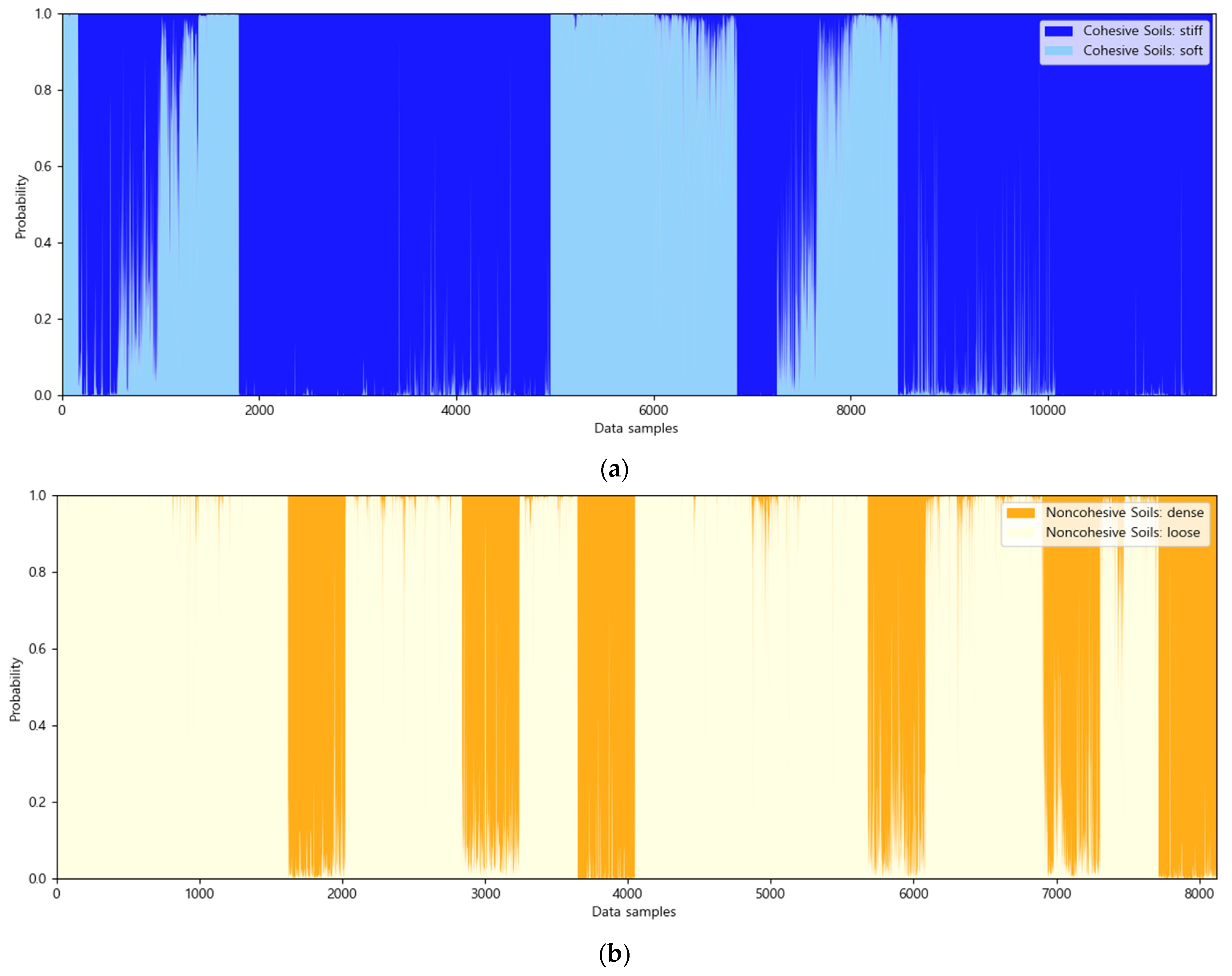
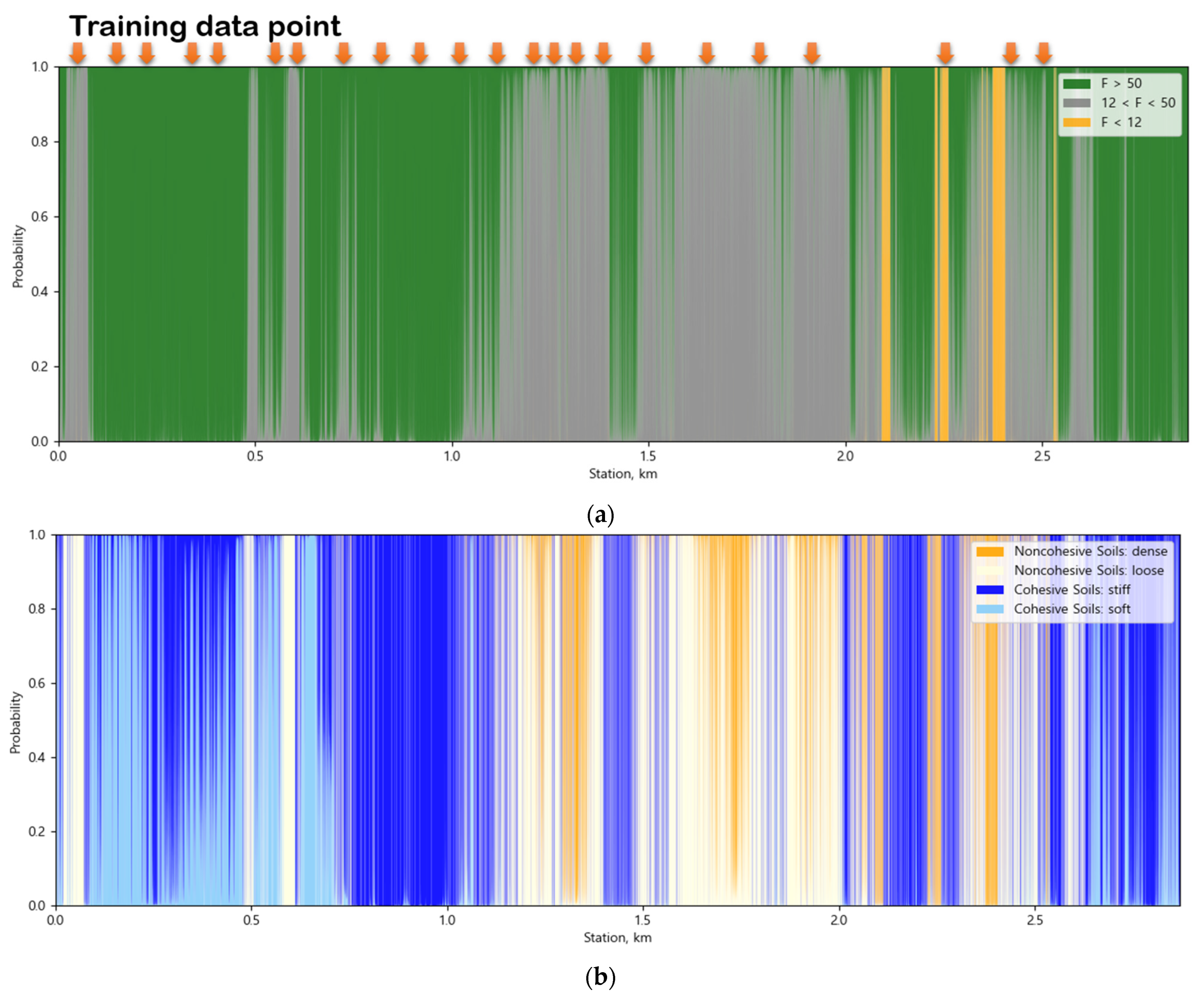
5.3. Classification Results for the Entire Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, H.; Zhou, J.; GAsteris, P.; Jahed Armaghani, D.; Tahir, M.M. Supervised Machine Learning Techniques to the Prediction of Tunnel Boring Machine Penetration Rate. Appl. Sci. 2019, 9, 3715. [Google Scholar]
- Liu, B.; Wang, Y.; Zhao, G.; Yang, B.; Wang, R.; Huang, D.; Xiang, B. Intelligent decision method for main control parameters of tunnel boring machine based on multi-objective optimization of excavation efficiency and cost. Tunn. Undergr. Space Technol. 2021, 116, 104054. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C.; Delisio, A. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunn. Undergr. Space Technol. 2016, 58, 236–246. [Google Scholar] [CrossRef]
- Ahangari, K.; Moeinossadat, S.R.; Behnia, D. Estimation of tunnelling-induced settlement by modern intelligent methods. Soils Found. 2015, 55, 737–748. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, P.; Wu, H.; Wang, Z.; Zhong, Z. Prediction of shield tunneling-induced ground settlement using machine learning techniques. Front. Struct. Civ. Eng. 2019, 13, 1363–1378. [Google Scholar] [CrossRef]
- Mahdevari, S.; Shahriar, K.; Yagiz, S.; Shirazi, M.A. A support vector regression model for predicting tunnel boring machine penetration rates. Int. J. Rock Mech. Min. 2014, 74, 214–229. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Narayanasamy, M.S.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43. [Google Scholar] [CrossRef]
- Gao, X.; Shi, M.; Song, X.; Zhang, C.; Zhang, H. Recurrent neural networks for real-time prediction of TBM operating parameters. Autom. Constr. 2019, 98, 225–235. [Google Scholar] [CrossRef]
- Mokhtari, S.; Mooney, M.A. Predicting EPBM advance rate performance using support vector regression modeling. Tunn. Undergr. Space Technol. 2020, 104, 103520. [Google Scholar] [CrossRef]
- Erharter, G.H.; Marcher, T.; Reinhold, C. Application of artificial neural networks for Underground construction–Chances and challenges–Insights from the BBT exploratory tunnel Ahrental Pfons. Geomech. Tunn. 2019, 12, 472–477. [Google Scholar] [CrossRef]
- Jung, J.-H.-H.; Chung, H.; Kwon, Y.-S.-S.; Lee, I.-M.-M. An ANN to Predict Ground Condition ahead of Tunnel Face using TBM Operational Data. KSCE J. Civ. Eng. 2019, 23, 3200–3206. [Google Scholar] [CrossRef]
- Zhuang, D.Y.; Ma, K.; Tang, C.A.; Liang, Z.Z.; Wang, K.K.; Wang, Z.W. Mechanical parameter inversion in tunnel engineering using support vector regression optimized by multi-strategy artificial fish swarm algorithm. Tunn. Undergr. Space Technol. 2019, 83, 425–436. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Hu, W.F.; Liu, Z.Y.; Tan, J.R. TBM performance prediction with Bayesian optimization and automated machine learning. Tunn. Undergr. Space Technol. 2020, 103, 103493. [Google Scholar] [CrossRef]
- Ayawah, P.E.; Sebbeh-Newton, S.; Azure, J.W.; Kaba, A.G.; Anani, A.; Bansah, S.; Zabidi, H. A review and case study of Artificial intelligence and Machine learning methods used for ground condition prediction ahead of tunnel boring Machines. Tunn. Undergr. Space Technol. 2022, 125, 104497. [Google Scholar] [CrossRef]
- Xue, Y.D.; Zhao, F.; Zhao, H.X.; Li, X.; Diao, Z.X. A new method for selecting hard rock TBM tunnelling parameters using optimum energy: A case study. Tunn. Undergr. Space Technol. 2018, 78, 64–75. [Google Scholar] [CrossRef]
- Yang, H.; Song, K.; Zhou, J. Automated recognition model of geomechanical information based on operational data of tunneling boring machines. Rock Mech. Rock Eng. 2022, 55, 1499–1516. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley and Sons: New York, NY, USA, 1948. [Google Scholar]
- Brown, T.; Hettiarachchi, H. Estimating Shear Strength Properties of Soils Using SPT Blow Counts: An Energy Balance Approach; ASCE Geotechnical Special Publication No. 179; ASCE: Reston, VA, USA, 2008. [Google Scholar] [CrossRef]
- Kulhawy, F.H.; Mayne, P.W. Manual on Estimating Soil Properties for Foundation Design; Electric Power Research Institute: Palo Alto, CA, USA, 1990. [Google Scholar]
- Peck, R.B.; Hanson, W.E.; Thornburn, T.H. Foundation Engineering, 2nd ed.; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice, 2nd ed.; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Peck, R.B.; Hanson, W.E.; Thornburn, T.H. Foundation Engineering; John Wiley & Sons: New York, NY, USA, 1953; p. 410. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Kearns, M.; Valiant, L.G. Cryptographic limitations on learning Boolean formulae and finite automat. J. Assoc. Comput. Mach. 1994, 41, 67–95. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R. A decision theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29(5), 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting; R Package Version 0.4-2 1.4; 2015; pp. 1–4. Available online: https://cran.r-project.org/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 10 October 2022).
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Yagiz, S.; Karahan, H. Application of various optimization techniques and comparison of their performances for predicting TBM penetration rate in rock mass. Int. J. Rock Mech. Min. Sci. 2015, 80, 308–315. [Google Scholar] [CrossRef]




| USCS Classification | Particle Size (mm) |
|---|---|
| Gravel | 76.2~4.75 |
| Sand | 4.75~0.075 |
| Silt | <0.075 |
| Clay | <0.002 |
| Cohesive Soils | Non-Cohesive Soils | ||
|---|---|---|---|
| N | Consistency | N | Density |
| <2 | Very soft | 0~4 | Very loose |
| 2~4 | Soft | ||
| 4~8 | Medium | 4~10 | Loose |
| 8~15 | Stiff | 10~30 | Medium dense |
| 16~32 | Very stiff | ||
| >32 | Hard | 30~50 | Dense |
| 50< | Very dense | ||
| TBM Type | EPB |
|---|---|
| TBM outside diameter (m) | 7.9 |
| Max. shield jack thrust force (MN) | 50 (2 × 25 shield jack) |
| Max. cutterhead torque (MN·m) | 9.6 |
| Max. RPM (rev/min) | 0.89 |
| Max. screw revolution (rev/min) | 14.2 |
| Segment ring length (m) | 1.2 |
| Factors | Min | Q1 (25%) | Q2 (50%) | Q3 (75%) | Max | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|
| (1)Thrust speed average (mm/min) | 0 | 38 | 49 | 52 | 73 | 42.2 | 14.6 |
| (2) Total thrust force (MN) | 0 | 20.7 | 23.3 | 27.4 | 41.4 | 23.7 | 5.4 |
| (3) Screw revolution (rev/min) | 0 | 2.4 | 5.9 | 7.7 | 14.2 | 5.2 | 3.3 |
| (4) Cutter torque (MN-m) | 0 | 5.18 | 5.55 | 5.81 | 9.01 | 5.5 | 0.62 |
| (5) Screw torque (MN-m) | 0 | 0.92 | 1.04 | 1.13 | 1.56 | 1.0 | 0.19 |
| (6) Soil pressure (kPa) | 27 | 289 | 306 | 314 | 496 | 287.7 | 62.4 |
| Class | Positive (1) | Negative (0) |
|---|---|---|
| Positive (1) | True Positive (TP) | False Positive (FP) |
| Negative (0) | False Negative (FN) | True Negative (TN) |
| Formulas for Measuring Performance | Definition of the Terms | |
|---|---|---|
| Accuracy | Accuracy is the proportion of the total number of predictions that are correct | |
| Precision | Precision is the ratio of the total number of correctly classified positive examples and the total number of predicted positive examples | |
| Recall | Recall is also referred to as true positive rate or sensitivity | |
| F1-score | F1-score is a weighted average of the recall (sensitivity) and precision | |
| Algorithm | Hyperparameter | |
|---|---|---|
| Tree-Based Methods | Decision Tree | max depth: 5 |
| Ensemble Learning Method, Boosting | AdaBoost | learning rate: 0.1, n estimators: 300 |
| Gradient Boosting | learning rate: 0.5, max depth: 4, max features: 3, n estimators: 500 | |
| XG boosting | learning rate: 0.2, max depth: 4, n estimators: 400 | |
| Light GBM | learning rate: 0.1, max depth: 5, n estimators: 300 | |
| Support Vector Machine | SVM | C: 2.0, gamma: 2.8 |
| Class Range | Description | |
|---|---|---|
| 0 | * F ≥ 50 | Fine-Grained Soil |
| 1 | 12 < F < 50 | Coarse-Grained Soil |
| 2 | F ≤ 12% | |
| Model | Test Dataset | ||||
|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | ||
| Decision Tree | class 0 | 0.781 | 0.77 | 0.89 | 0.83 |
| class 1 | 0.77 | 0.6 | 0.68 | ||
| class 2 | 0.95 | 0.83 | 0.89 | ||
| AdaBoost | class 0 | 0.759 | 0.76 | 0.87 | 0.81 |
| class 1 | 0.73 | 0.57 | 0.64 | ||
| class 2 | 0.91 | 0.91 | 0.91 | ||
| Gradient Boosting | class 0 | 0.974 | 0.98 | 0.98 | 0.98 |
| class 1 | 0.97 | 0.97 | 0.97 | ||
| class 2 | 0.96 | 0.96 | 0.96 | ||
| XG boosting | class 0 | 0.974 | 0.98 | 0.98 | 0.98 |
| class 1 | 0.97 | 0.96 | 0.97 | ||
| class 2 | 0.97 | 0.97 | 0.97 | ||
| Light GBM | class 0 | 0.974 | 0.98 | 0.98 | 0.98 |
| class 1 | 0.97 | 0.96 | 0.97 | ||
| class 2 | 0.96 | 0.95 | 0.96 | ||
| Support Vector Machine | class 0 | 0.977 | 0.98 | 0.98 | 0.98 |
| class 1 | 0.98 | 0.97 | 0.97 | ||
| class 2 | 0.96 | 0.96 | 0.96 | ||
| Class Range | Description | |||
|---|---|---|---|---|
| Cohesive Soils | Non-Cohesive Soils | |||
| 0 | N ≥ 5 | stiff | N > 10 | dense |
| 1 | N < 5 | soft | N ≤ 10 | loose |
| Model | Test Dataset | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Cohesive Soils | Non-Cohesive Soils | ||||||||
| Accuracy | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score | ||
| Decision Tree | class 0 | 0.835 | 0.84 | 0.94 | 0.89 | 0.794 | 0.80 | 0.43 | 0.56 |
| class 1 | 0.82 | 0.61 | 0.70 | 0.80 | 0.96 | 0.87 | |||
| AdaBoost | class 0 | 0.879 | 0.87 | 0.97 | 0.92 | 0.855 | 0.86 | 0.65 | 0.74 |
| class 1 | 0.91 | 0.69 | 0.78 | 0.87 | 0.95 | 0.91 | |||
| Gradient Boosting | class 0 | 0.955 | 0.96 | 0.97 | 0.97 | 0.963 | 0.94 | 0.94 | 0.94 |
| class 1 | 0.93 | 0.92 | 0.93 | 0.97 | 0.97 | 0.97 | |||
| XG Boosting | class 0 | 0.956 | 0.96 | 0.97 | 0.97 | 0.964 | 0.94 | 0.94 | 0.94 |
| class 1 | 0.94 | 0.92 | 0.93 | 0.98 | 0.98 | 0.97 | |||
| Light GBM | class 0 | 0.956 | 0.97 | 0.97 | 0.97 | 0.962 | 0.94 | 0.94 | 0.94 |
| class 1 | 0.93 | 0.93 | 0.93 | 0.97 | 0.97 | 0.97 | |||
| Support Vector Machine | class 0 | 0.943 | 0.95 | 0.93 | 0.93 | 0.963 | 0.94 | 0.93 | 0.94 |
| class 1 | 0.92 | 0.90 | 0.91 | 0.97 | 0.98 | 0.97 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, T.-H.; Choi, S.-W.; Lee, C.; Chang, S.-H. Soil Classification by Machine Learning Using a Tunnel Boring Machine’s Operating Parameters. Appl. Sci. 2022, 12, 11480. https://doi.org/10.3390/app122211480
Kang T-H, Choi S-W, Lee C, Chang S-H. Soil Classification by Machine Learning Using a Tunnel Boring Machine’s Operating Parameters. Applied Sciences. 2022; 12(22):11480. https://doi.org/10.3390/app122211480
Chicago/Turabian StyleKang, Tae-Ho, Soon-Wook Choi, Chulho Lee, and Soo-Ho Chang. 2022. "Soil Classification by Machine Learning Using a Tunnel Boring Machine’s Operating Parameters" Applied Sciences 12, no. 22: 11480. https://doi.org/10.3390/app122211480
APA StyleKang, T.-H., Choi, S.-W., Lee, C., & Chang, S.-H. (2022). Soil Classification by Machine Learning Using a Tunnel Boring Machine’s Operating Parameters. Applied Sciences, 12(22), 11480. https://doi.org/10.3390/app122211480








