Torsional Stress Analysis of Improved Composite Box Girder with Corrugated Steel Webs
Abstract
:1. Introduction
2. Research Methods
2.1. Mechanical Properties of a Corrugated Steel Web
2.1.1. Longitudinal Modulus of Elasticity
2.1.2. Effective Shear Modulus
2.1.3. Section Conversion
2.2. Torsional Stress Analysis
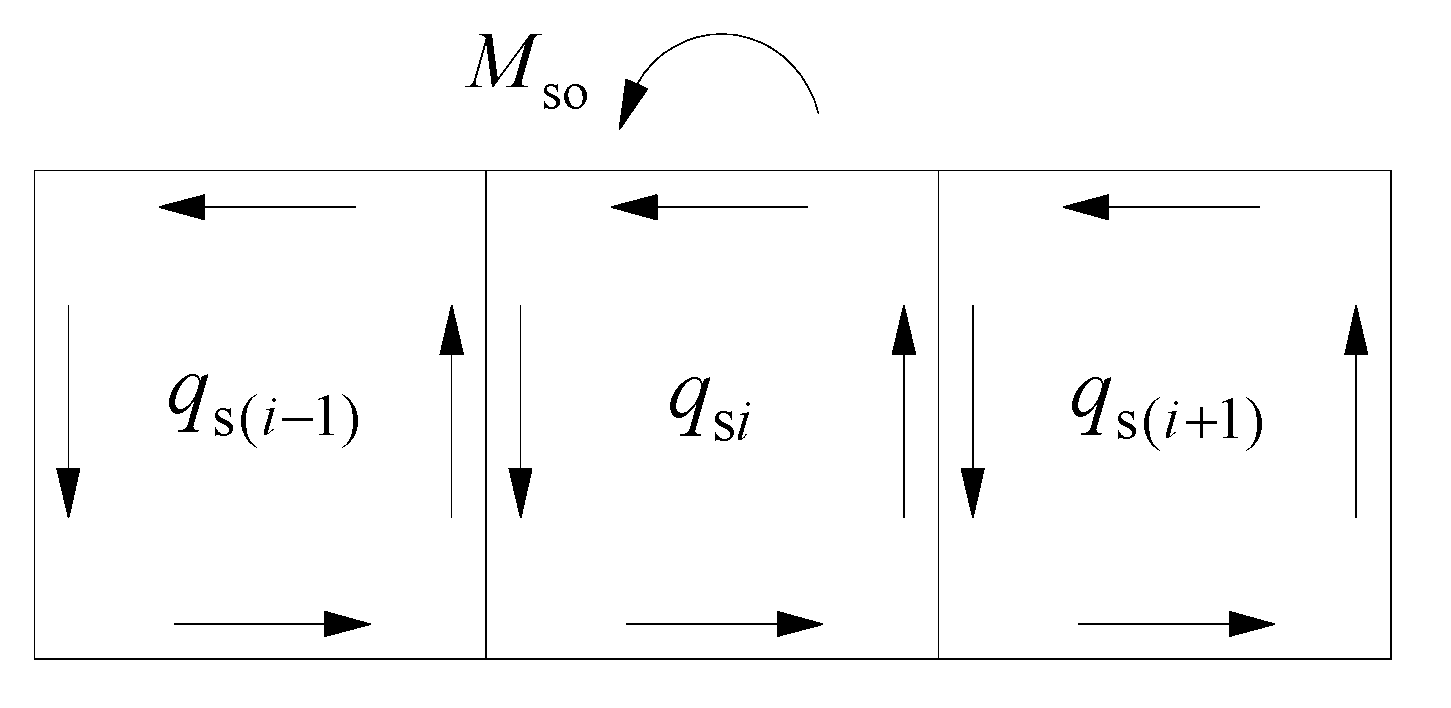
2.2.1. Free Torsional Shear Stress
2.2.2. Restrained Torsional Normal Stress
2.2.3. Restrained Torsional Shear Stress
2.2.4. Solving the Torsional Differential Equations
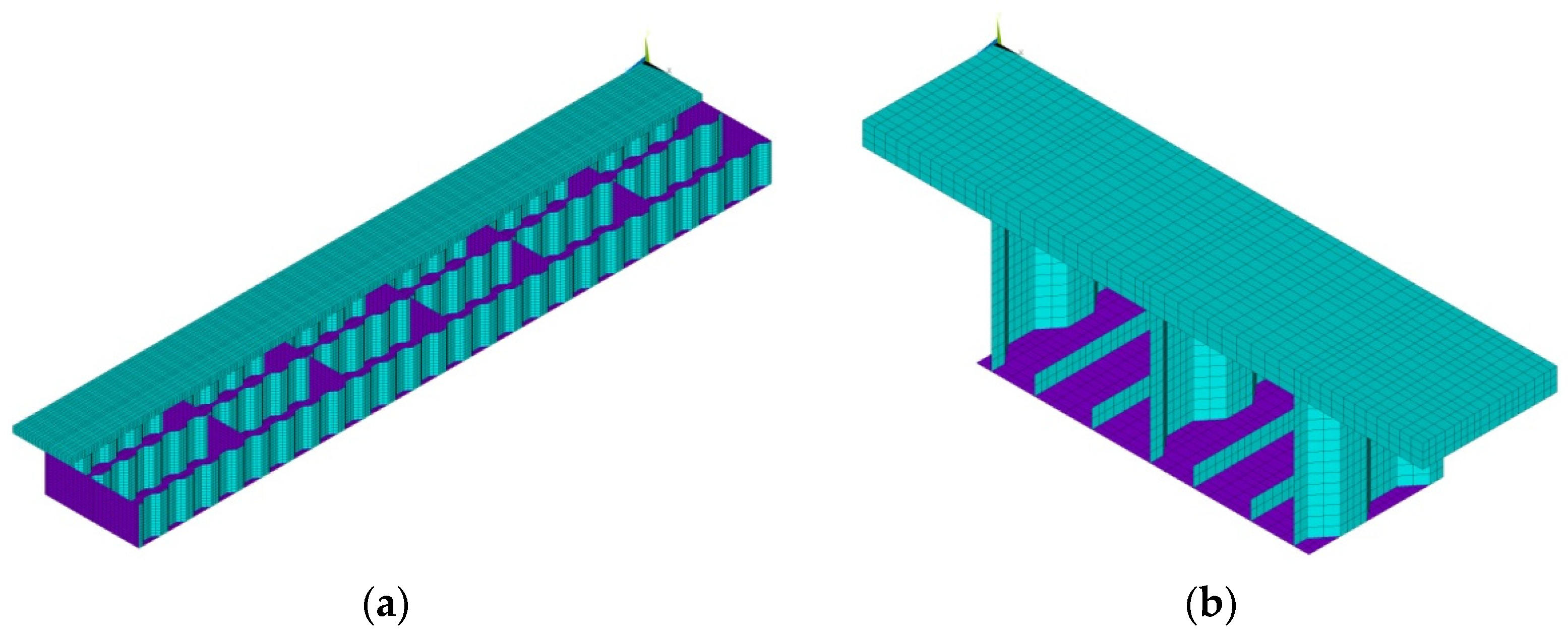
2.3. Physical Testing
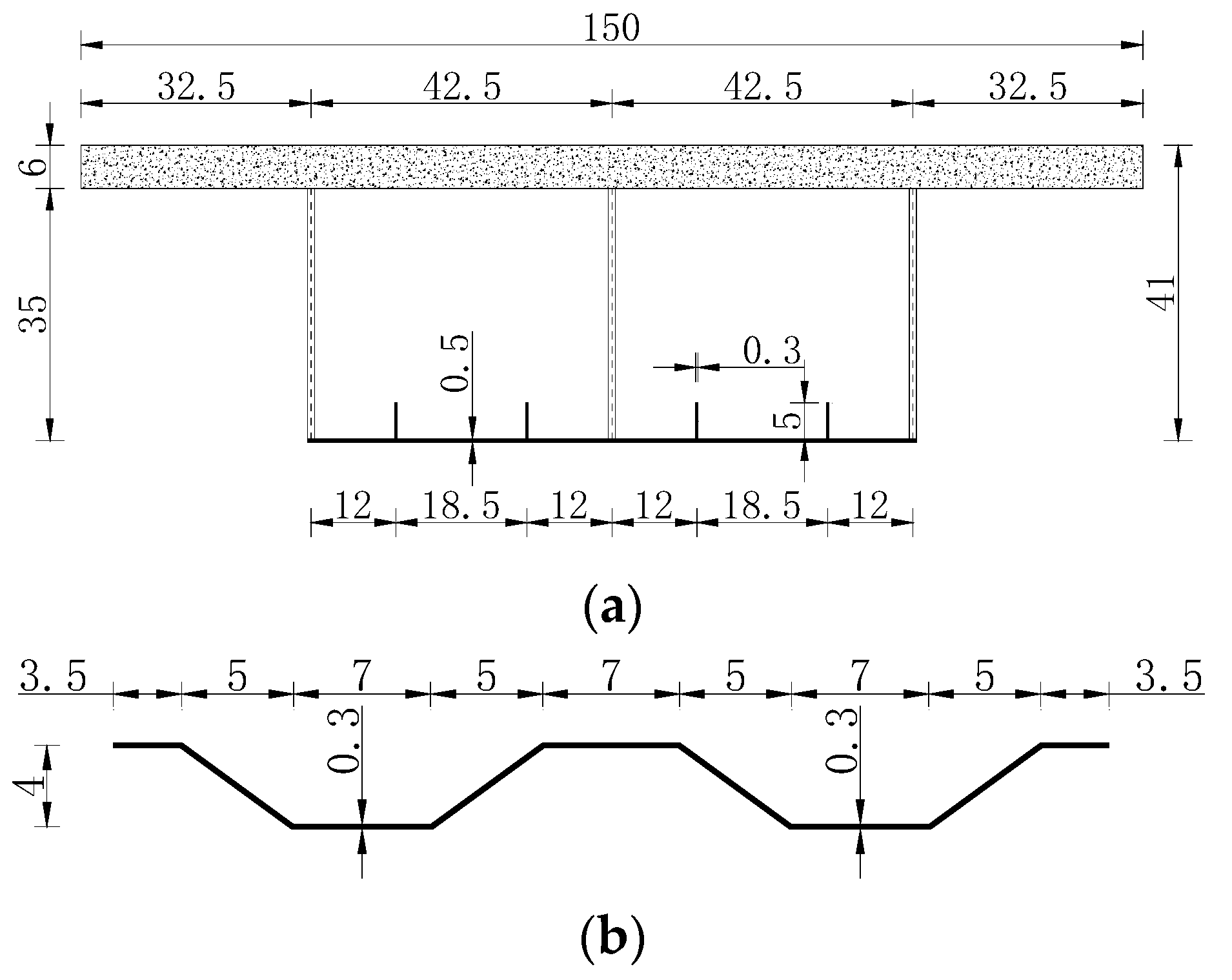
2.3.1. Model Beam Size
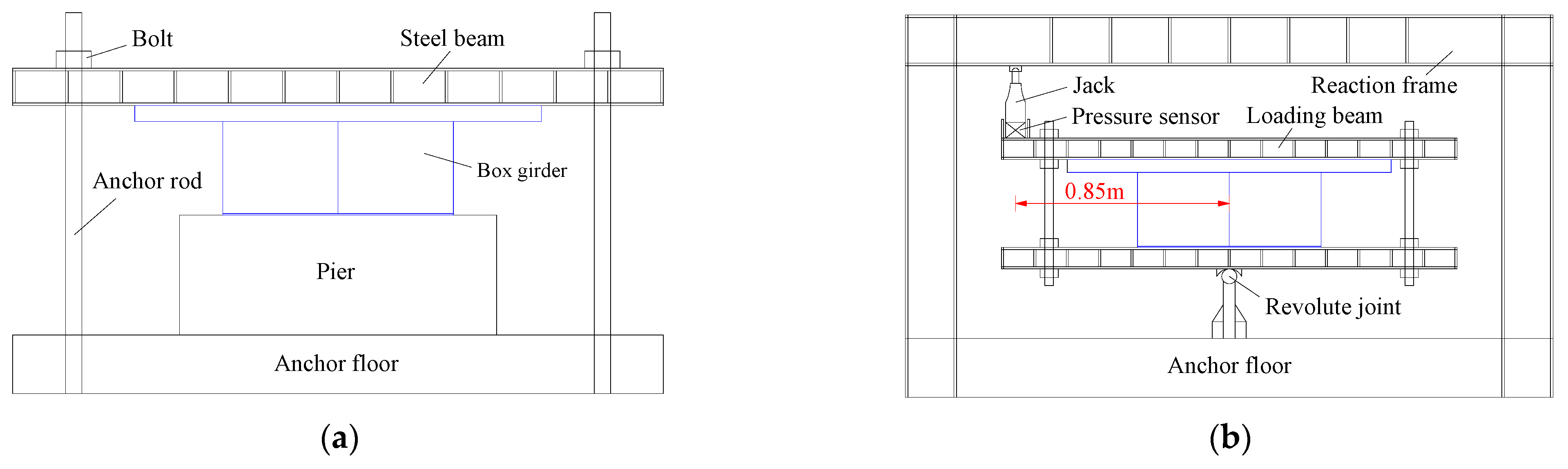
2.3.2. Loading Device
2.3.3. Test Arrangement
3. Results & Discussion
3.1. Results Analysis
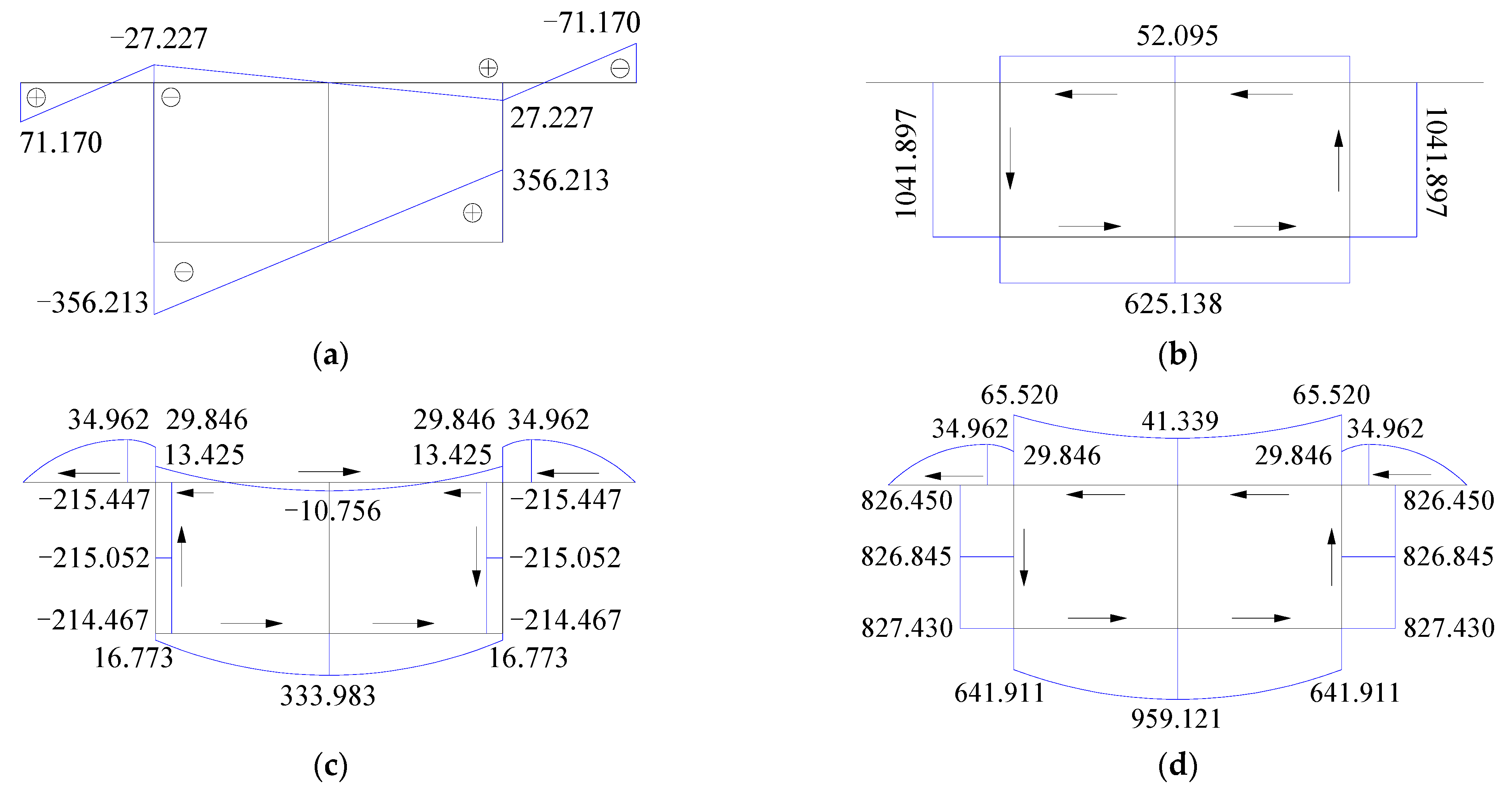
3.1.1. Torsional Stress Comparison
3.1.2. Distribution of Torsional Stress
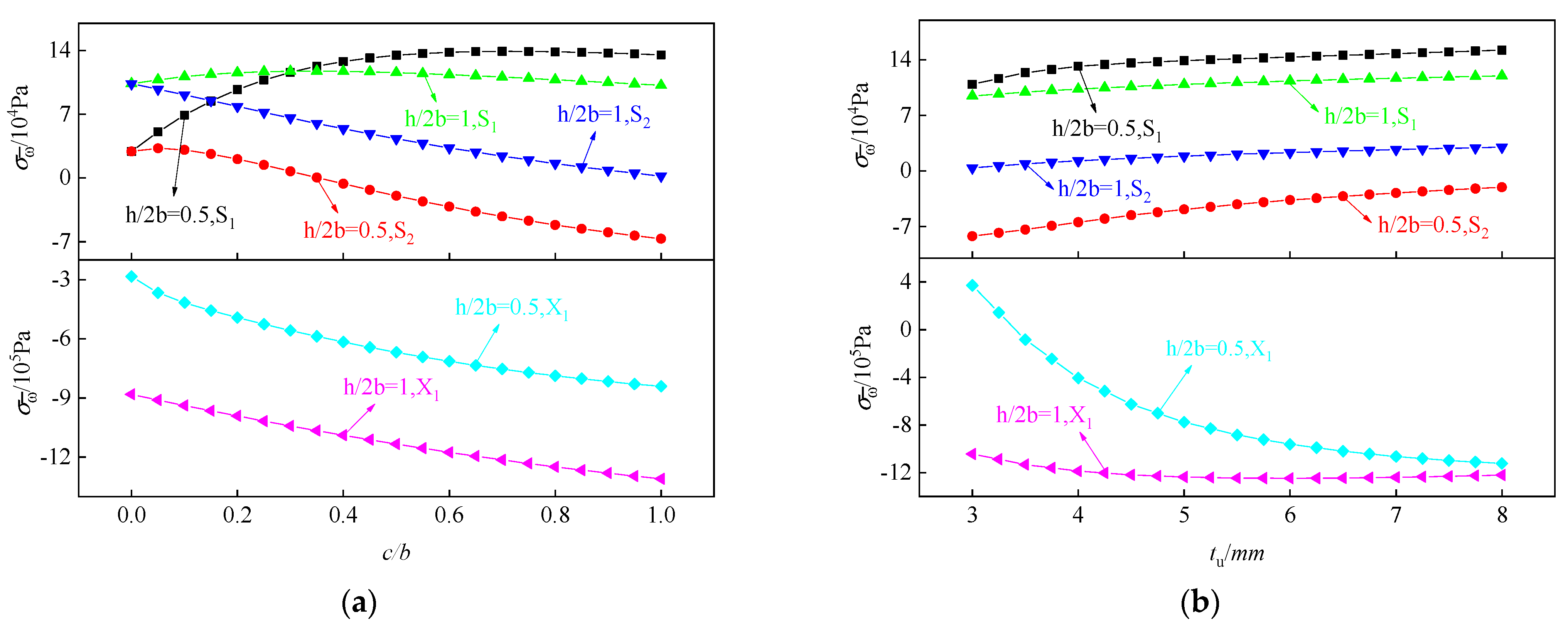
3.2. Parameter Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, K.J.; Wan, S.; Jiang, Z.W.; Mo, Y.L. Whole process analysis on pure torsional behavior of concrete composite box girders with corrugated steel webs. J. Southeast Univ. (Nat. Sci. Ed.) 2017, 47, 112–117. [Google Scholar]
- Yang, B.W.; Li, Y.L.; Wan, S.; Zhang, J.D. Stress analysis of box girder with corrugate steel webs under torsion. J. South China Univ. Technol. (Nat. Sci. Ed.) 2012, 40, 19–22+34. [Google Scholar]
- Li, H.J. Experimental Study and Analysis on Torsion and Distortion of Box-Girder with Corrugated Steel Webs. Ph.D. Thesis, Southeast University, Nanjing, China, 2003. [Google Scholar]
- Kato, H.; Nishimura, N. Practical analysis methods for continuous girder and cable stayed bridges composed of beams with corrugated steel webs. Earthq. Eng. Struct. Dyn. 2004, 21, 207–222. [Google Scholar] [CrossRef] [Green Version]
- Sayed-Ahmed, E.Y. Behaviour of steel and (or) composite girders with corrugated steel webs. Can. J. Civ. Eng. 2001, 28, 656–672. [Google Scholar] [CrossRef]
- Ma, L.; Wan, S.; Jiang, Z.W. Research on torsion and distortion performance of single box double-cell girder with corrugated steel webs. China J. Highw. Transp. 2016, 29, 77–85. [Google Scholar]
- Deng, W.Q.; Mao, Z.L.; Liu, D.; Zhang, J.D. Analysis and experimental study of torsion and distortion of single box three-cell cantilever girder with corrugated steel webs. J. Build. Struct. 2020, 41, 173–181. [Google Scholar]
- Mo, Y.L.; Jeng, C.H.; Chang, Y.S. Torsional behavior of prestressed concrete box-girder bridges with corrugated steel webs. ACI Struct. J. 2000, 97, 849–859. [Google Scholar]
- Mo, Y.L.; Fan, Y.L. Torsional design of hybrid concrete box girders. J. Bridge Eng. 2006, 11, 329–339. [Google Scholar] [CrossRef]
- Ko, H.J.; Moon, J.; Shin, Y.W.; Lee, H.E. Non-linear analyses model for composite box-girders with corrugated steel webs under torsion. Steel Compos. Struct. 2013, 14, 409–429. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Jiang, K.B.; Liu, Y.W. Nonlinear analysis for PC box-girder with corrugated steel webs under pure torsion. Thin Wall. Struct. 2012, 51, 167–173. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, K.B.; Zhou, Y.Z.; Yang, J.K. Analytical model for torsional strength of prestressed concrete box-girder with corrugated steel webs. Chin. J. Comput. Mech. 2013, 30, 137–142. [Google Scholar]
- Jiang, K.B.; Ding, Y.; Yang, J.K.; Zhou, Y.Z. Experimental study on ultimate torsional strength of PC composite box-girder with corrugated steel webs under pure torsion. Eng. Mech. 2013, 30, 175–182. [Google Scholar]
- Jeng, C.H.; Hsu, T. A softened membrane model for torsion in reinforced concrete members. Eng. Struct. 2009, 31, 1944–1954. [Google Scholar] [CrossRef]
- Jeng, C.H. Simple rational formulas for cracking torque and twist of reinforced concrete members. ACI Struct. J. 2010, 107, 189–198. [Google Scholar]
- Zhou, C.; Li, L.F.; Wang, L.H.; Shi, X.W. Full-range analysis of prestressed composite box girders with corrugated steel webs subject to pure torsion based on softened membrane theory. China Civ. Eng. J. 2018, 51, 97–106. [Google Scholar]
- Wei, N.; Zhang, Y.H.; Yao, X.D. Analysis on restrained torsional shear stresses of box girders with corrugated steel webs. Appl. Math. Mech. 2020, 41, 386–395. [Google Scholar]
- Qin, A.A.; Liu, S.Z.; Ji, W.; Li, A.J.; Cheng, Z. Analysis on torsion performance of single-box twin-cell composite box girder with corrugated steel webs and steel bottom plates. J. Southeast Univ. (Nat. Sci. Ed.) 2021, 51, 740–746. [Google Scholar]
- Ji, W.; Shao, T.Y. Finite element model updating for improved box girder bridges with corrugated steel webs using the response surface method and fmincon algorithm. KSCE J. Civ. Eng. 2021, 25, 586–602. [Google Scholar] [CrossRef]
- Gong, B.J.; Liu, S.Z.; Mao, Y.N.; Qin, A.A.; Cai, M.H. Correction of shear lag warping function of steel bottom–Corrugated steel web box girder. Structures 2022, 37, 227–241. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, Y.; Li, J.; Hai, L. Torsional behavior of box-girder with corrugated web and steel bottom flange. J. Constr. Steel Res. 2020, 167, 105855. [Google Scholar] [CrossRef]
- Li, H.J.; Ye, J.S.; Wan, S.; Wu, W.Q. Analysis and experimental study of torsion and distortion of box girder with corrugated steel webs. Bridge Constr. 2003, 6, 1–4. [Google Scholar]
- Xiang, H.F. Advanced Theory Bridge Structures, 2nd ed.; China Communications Press: Beijing, China, 2013; pp. 24–35. [Google Scholar]
- Huang, H.M.; Zhang, Y.H. Restrained torsion analysis of box girders with corrugated steel webs based on Reissner’s principle. J. Southwest Jiaotong Univ. 2022, 57, 1137–1145. [Google Scholar]
- Zhang, Y.H.; Sun, C.C. Analysis on the torsion considering effect of box girders with corrugated steel webs local longitudinal stiffness of webs. J. Southeast Univ. (Nat. Sci. Ed.) 2021, 51, 195–201. [Google Scholar]
- Zhang, Y.H.; Huang, H.M.; Liang, Y.Y. Calculation of shear stress of thin-walled box girders under restrained torsion. J. Southeast Univ. (Nat. Sci. Ed.) 2021, 51, 942–948. [Google Scholar]
- Yang, X.L.; Yu, X.Q.; Zhang, Y.H. Analysis on torsion effect of concrete composite box girder with steel truss webs. Chin. J. Comput. Mech. 2021, 38, 230–238. [Google Scholar]
- Shen, K.J. Study on Torsional Behavior of Single Box Multi-Cell Composite Box Girders with Corrugated Steel Webs. Ph.D. Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]

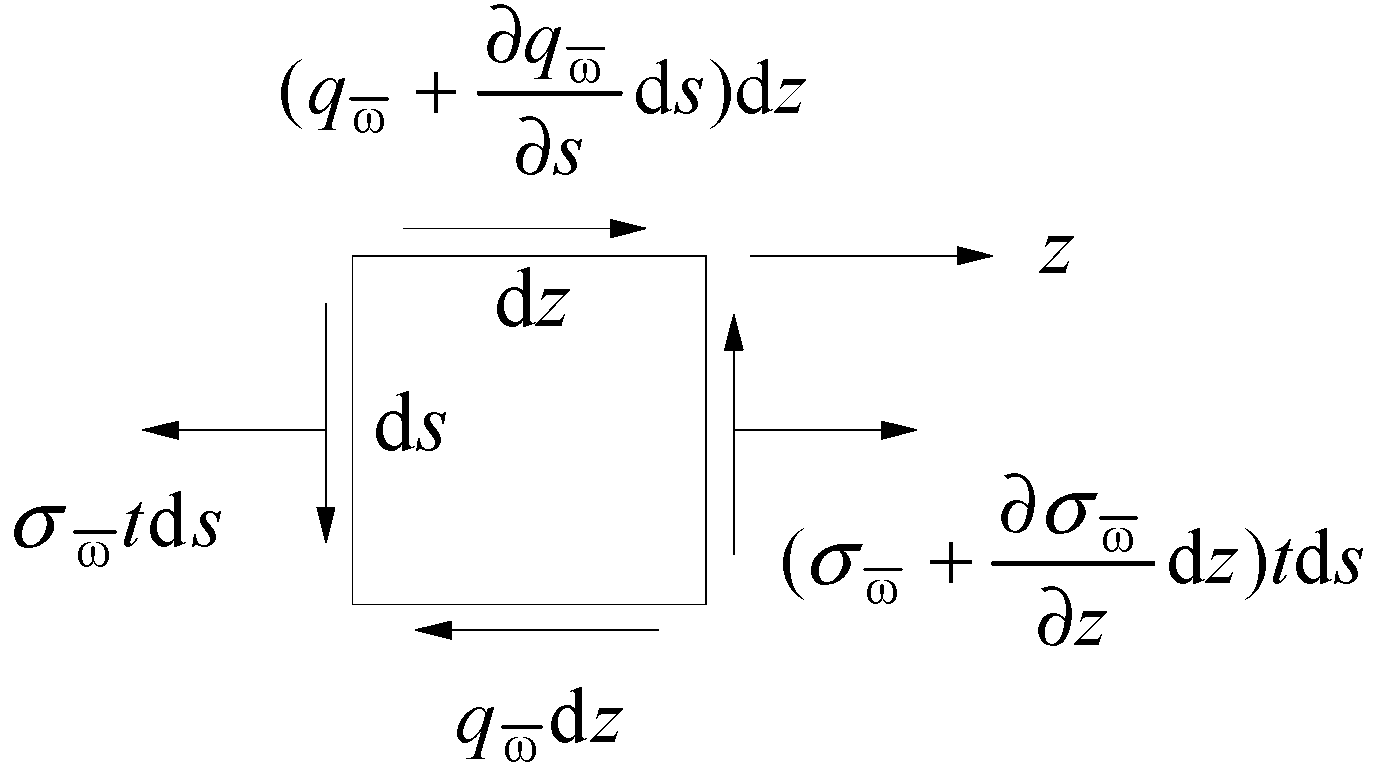
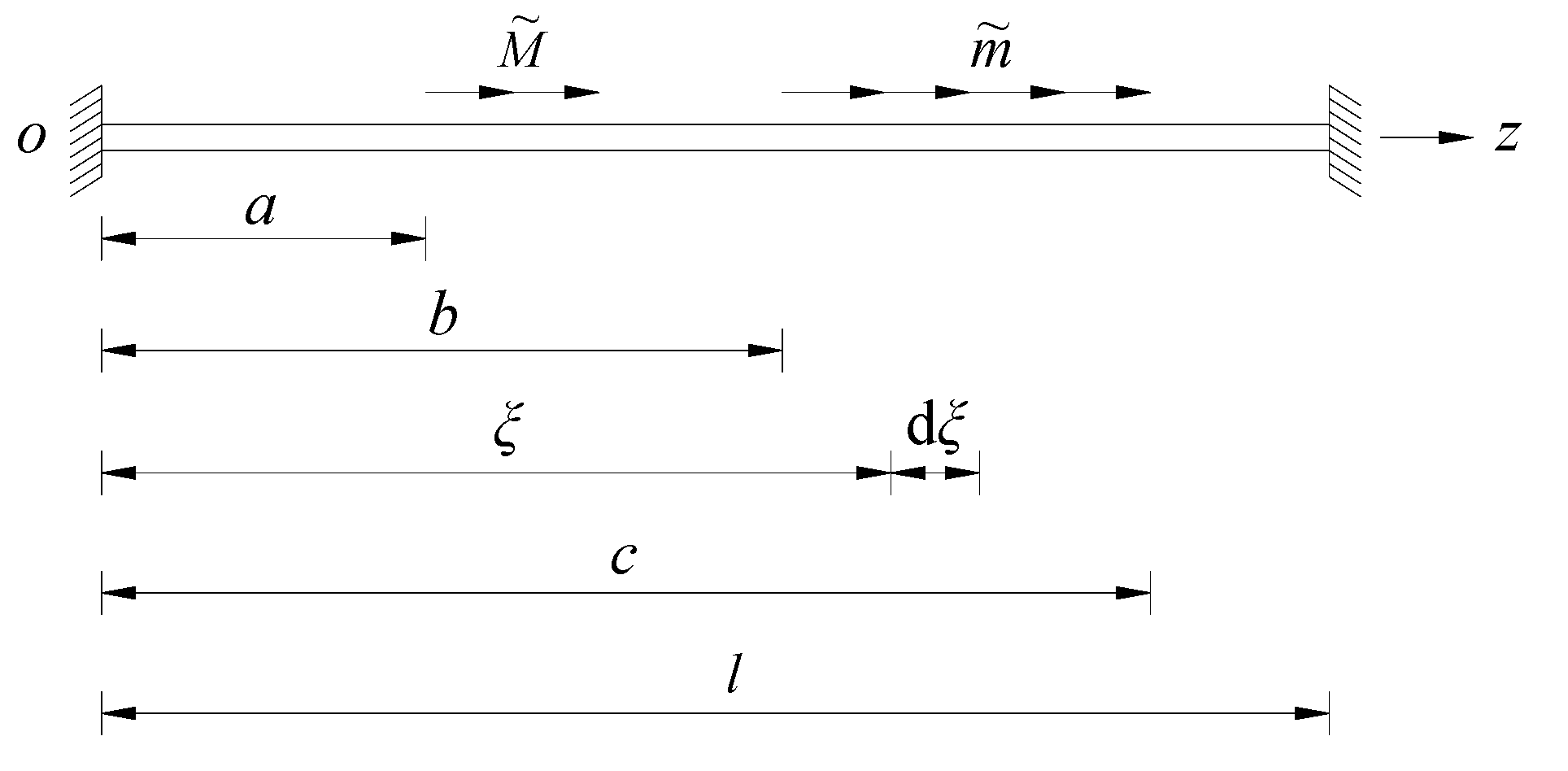


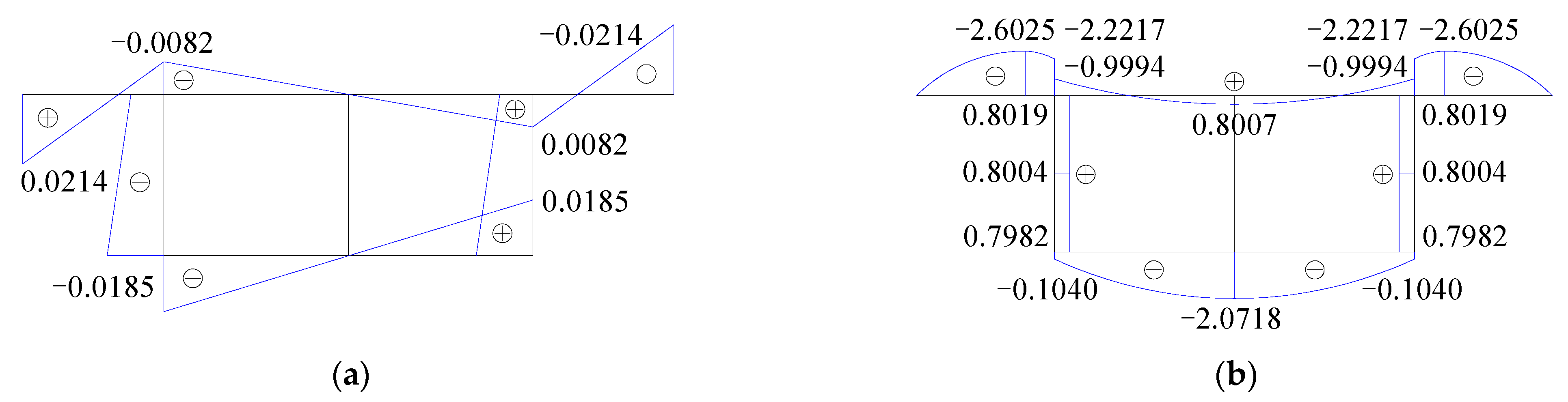

| Section | Torsional Stress | Measuring Point | Tt (MPa) | Th (MPa) | Te (MPa) | (Th − Tt)/Th (%) | (Te − Tt)/Te (%) |
|---|---|---|---|---|---|---|---|
| A | S1 | 0.1351 | 0.1423 | 0.1396 | 5.06 | 3.22 | |
| S2 | −0.0514 | −0.0545 | −0.0562 | 5.69 | 8.54 | ||
| X1 | −0.6736 | −0.7124 | −0.7042 | 5.45 | 4.35 | ||
| S4 | 0.0787 | 0.0827 | 0.0812 | 4.84 | 3.08 | ||
| W2 | 1.6113 | 1.6537 | 1.7164 | 2.56 | 6.12 | ||
| X3 | 1.8242 | 1.9182 | 1.8858 | 4.90 | 3.27 | ||
| B | S1 | −0.0096 | −0.0103 | −0.0098 | 6.80 | 2.04 | |
| S2 | 0.0038 | 0.0040 | 0.0041 | 5.00 | 7.32 | ||
| X1 | 0.0502 | 0.0518 | 0.0513 | 3.09 | 2.14 | ||
| S4 | 0.1032 | 0.1083 | 0.1061 | 4.71 | 2.73 | ||
| W2 | 2.0874 | 2.1663 | 2.1979 | 3.64 | 5.03 | ||
| X3 | 1.2832 | 1.3674 | 1.3017 | 6.16 | 1.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, A.; Liu, S.; Gong, B.; Cai, M.; Wang, F. Torsional Stress Analysis of Improved Composite Box Girder with Corrugated Steel Webs. Appl. Sci. 2022, 12, 11571. https://doi.org/10.3390/app122211571
Qin A, Liu S, Gong B, Cai M, Wang F. Torsional Stress Analysis of Improved Composite Box Girder with Corrugated Steel Webs. Applied Sciences. 2022; 12(22):11571. https://doi.org/10.3390/app122211571
Chicago/Turabian StyleQin, Aoao, Shizhong Liu, Baojia Gong, Minghao Cai, and Fangxu Wang. 2022. "Torsional Stress Analysis of Improved Composite Box Girder with Corrugated Steel Webs" Applied Sciences 12, no. 22: 11571. https://doi.org/10.3390/app122211571




