Condition Assessment and Adaptation of Bailey Bridges as a Permanent Structures
Abstract
:1. Introduction
1.1. Background
1.2. Bailey Bridge Structural Characteristics
1.2.1. First Generation
1.2.2. Second Generation
1.2.3. Third Generation
2. Field Experiment
2.1. Target Bailey Bridge
2.2. Load Test
2.2.1. Static Loading Condition
2.2.2. Dynamic Loading Condition
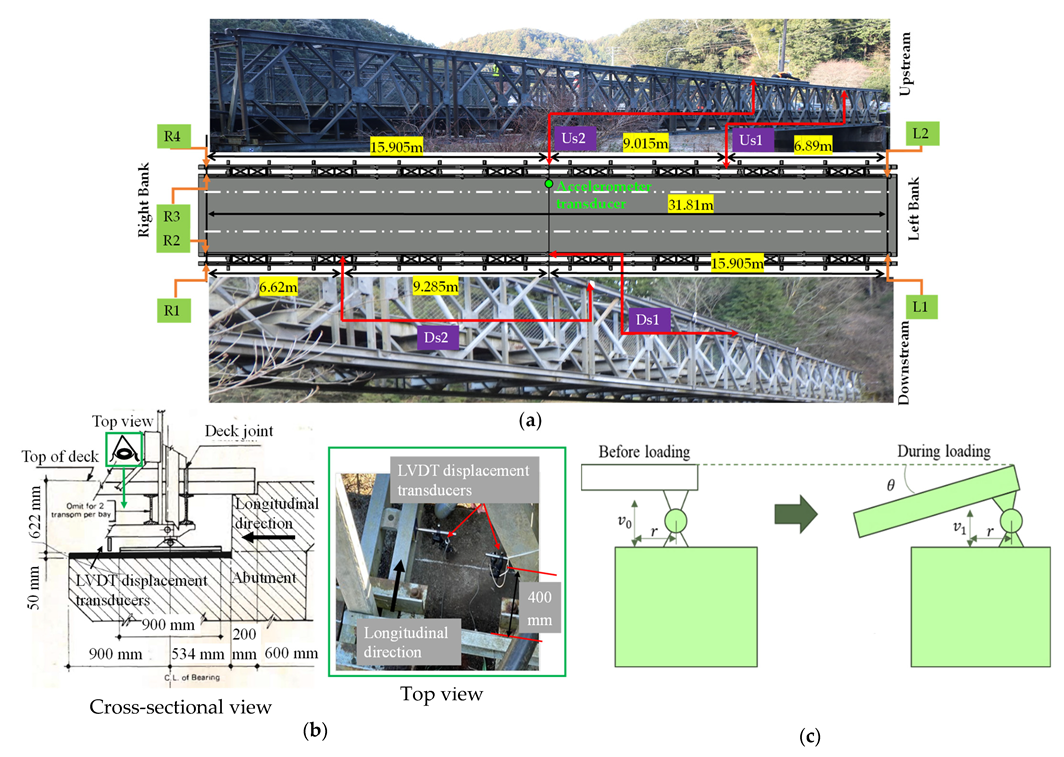
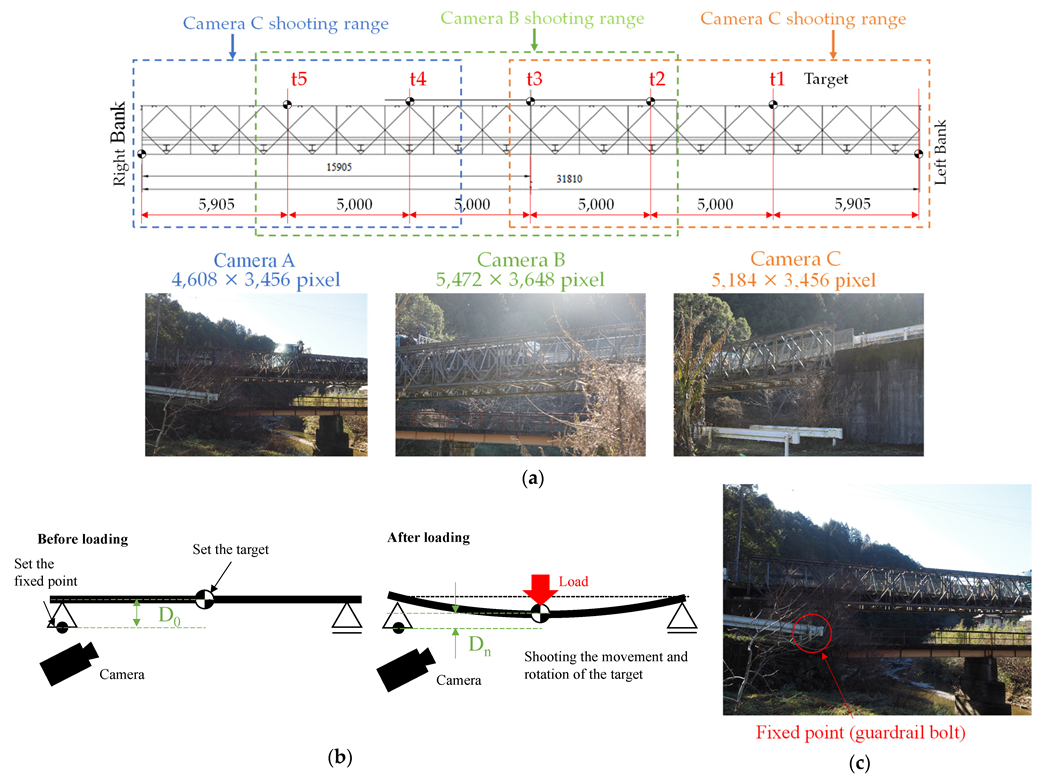
2.3. Measurement Plan
2.3.1. LVDT Displacement Transducer Setting
2.3.2. Frictional Strain Gauge Setting
2.3.3. Target Setting for Image Processing Approach
2.3.4. Accelerometer Transducer Setting
3. Results of the Field Experiment
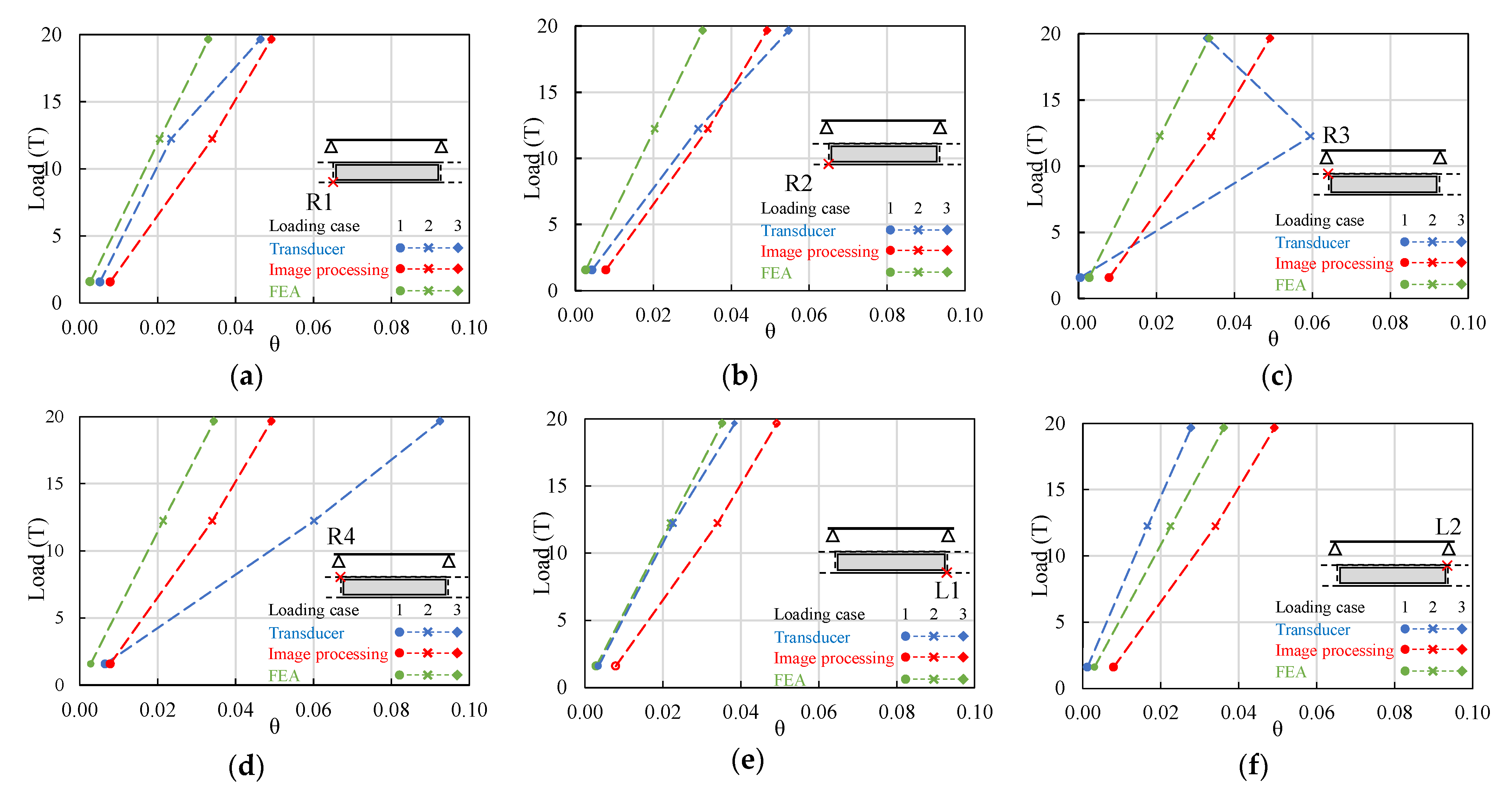
3.1. Static Behavior
3.2. Dynamic Behaviour
4. Structural Analysis
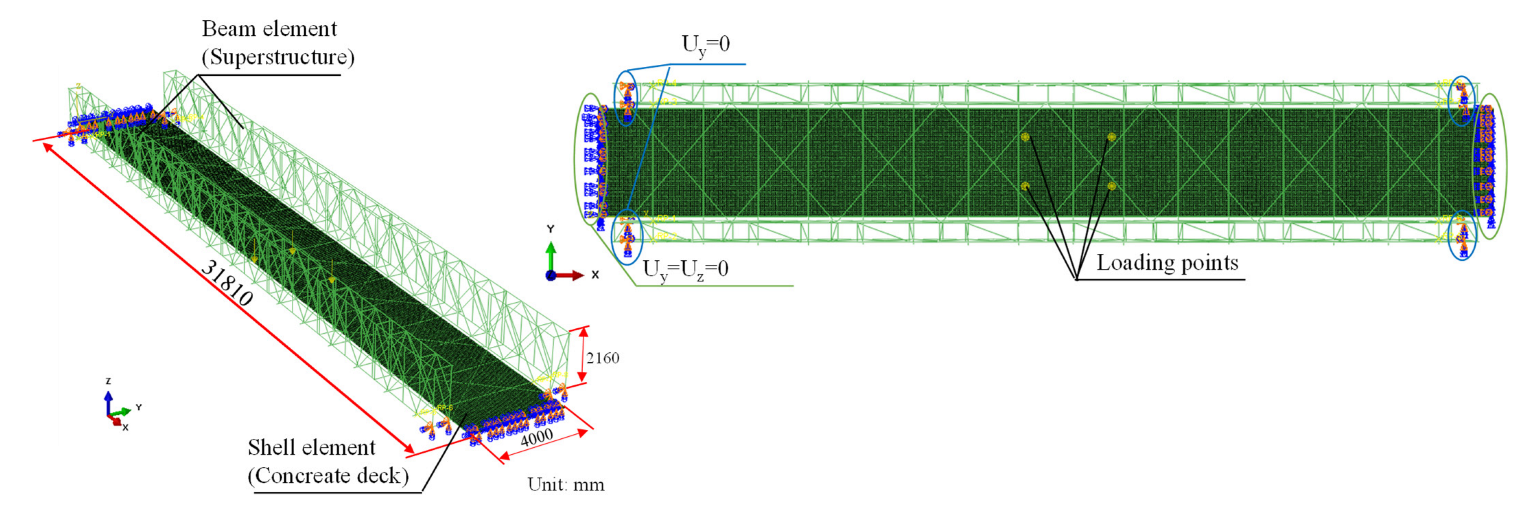
4.1. Structural Modelling
4.2. Material Modelling
4.3. Linear Elastic and Nonlinear Elastic-Plastic Analysis
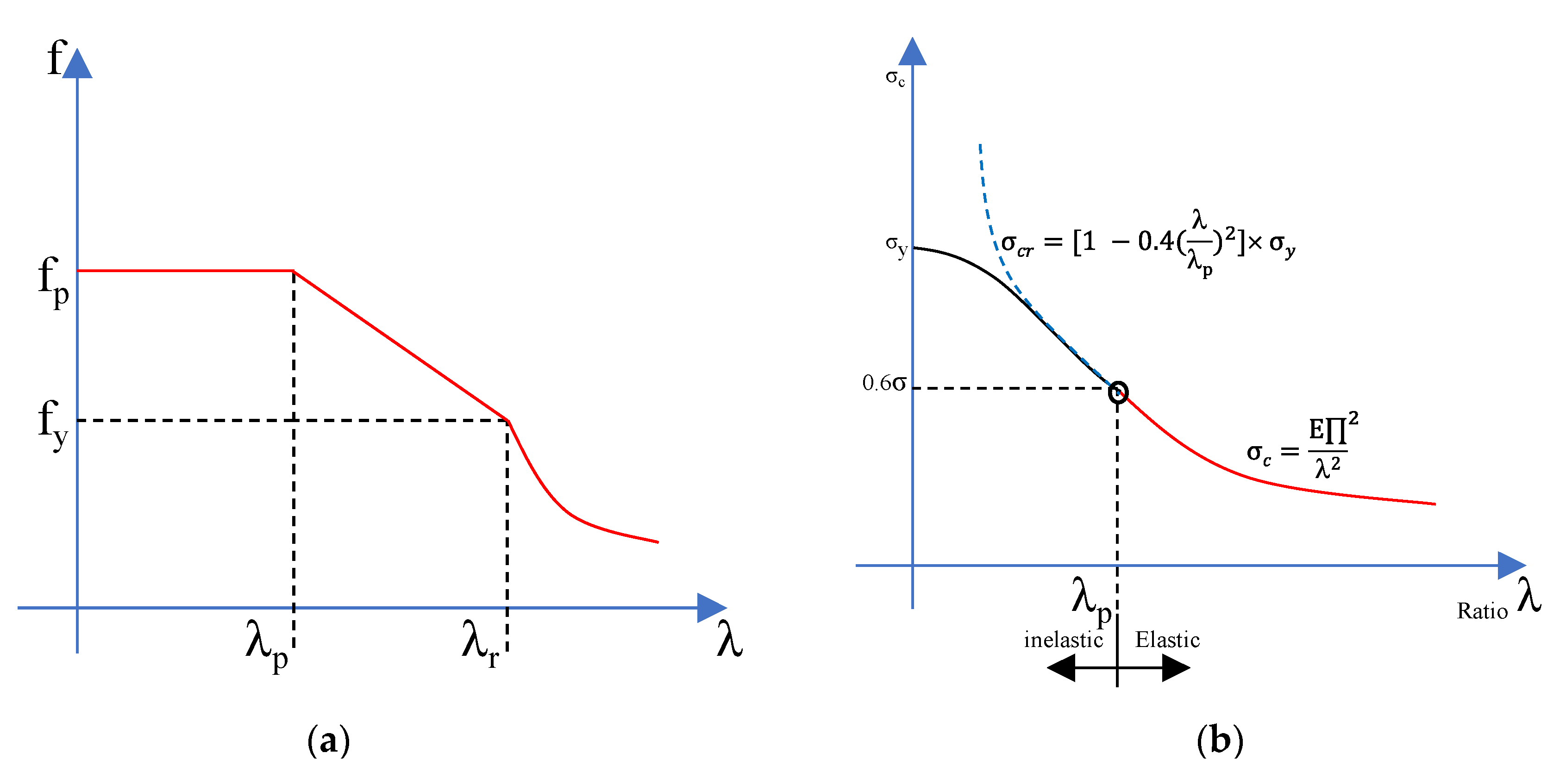
4.3.1. Condition of Linear Elastic Analysis
4.3.2. Condition of Nonlinear Elastic-Plastic Analysis
Linear Buckling Analysis—Linear Perturbation
Non-Linear Buckling Analysis—Static Riks
4.4. Validation of the Model’s Accuracy by Linear Elastic Analysis
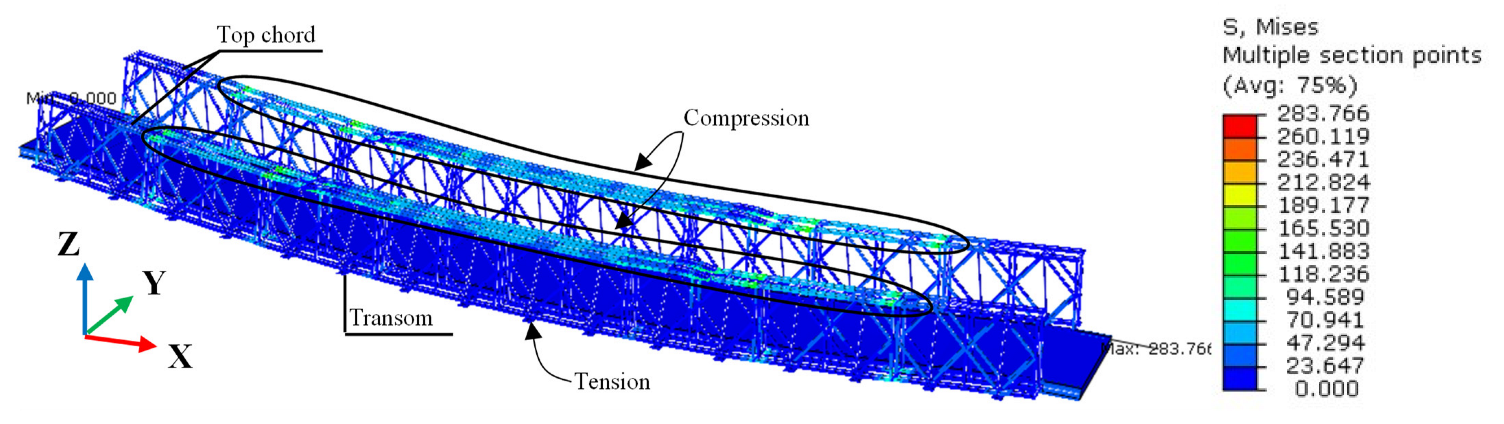
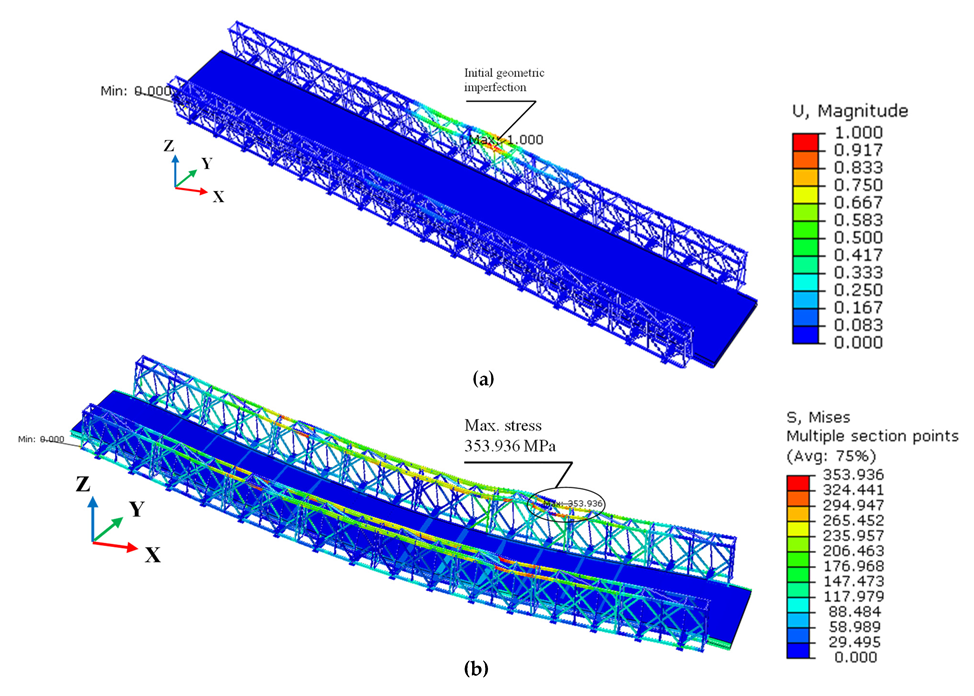
4.5. Identification of Critical Members before Determination of the Bearing Capacity
4.5.1. Identification Methods of Critical Members
4.5.2. Results of Identification of Critical Members
4.6. Determination of the Bearing Capacity by Nonlinear Elastic-Plastic Analysis
5. Conclusions
- Loading case 1-3 gave deflection (θ) ranging from 0.0004–0.0066, 0.0166–0.0596, and 0.0278–0.0925, correspondingly, with a validation coefficient of less than 2 on both measurement approaches that were considered within the required threshold. The maximum deformation at midspan was 14.43 mm on loading case 3.
- In that order, the image processing approach recorded deflections (θ) of 0.0079, 0.0340, and 0.0492 from Loading case 1.
- The transducer to image processing variance (Δθ) varied significantly, especially on Load case 1, by 0.0007 to 0.0050, indicating a good accuracy of the LVDT transducer on small deflections.
- Stresses were derived from an SM490 steel material with Young’s modulus of 2.0 × 105 MPa from experimental field strains that increased from Loading cases 1–3 (ε ≈ 0–104.85) within the linear elastic region.
- Static loading, under all loading conditions/cases, showed the structure operated within reasonable deflection (span/800-[39.3 mm]) and stress limits (below 325 MPa). The strain performance was also observed in typical symmetry at the center span, a trait common in Bailey Bridges.
- The results of the structural dynamic response of 3–20 km/h were 0–15.55 mm from Loading case 1, recording higher deflection than static loading by 1.4 mm at midspan, on account of the maximum recorded deflection.
- DAF (1 + μ) derived from Rdyn and Rstat resulted in 1.09. The DAF corresponded with the design criteria provided by Euro-code 1. The pavement condition was deemed ambient, with a limited deterioration range between 1.0–1.4.
- DSL’s results within the linear elastic domain validated the analytical model showing good agreement with a mean validation coefficient ranging from 1.4–2.0 and similar residual characteristics across all measurement approaches.
- The response of the model compared to similar research showed a good agreement.
- The results from the literature indicated that bridge structural elements operate in sync; therefore, their examination, espoused in Eurocode 3, gives conservative results.
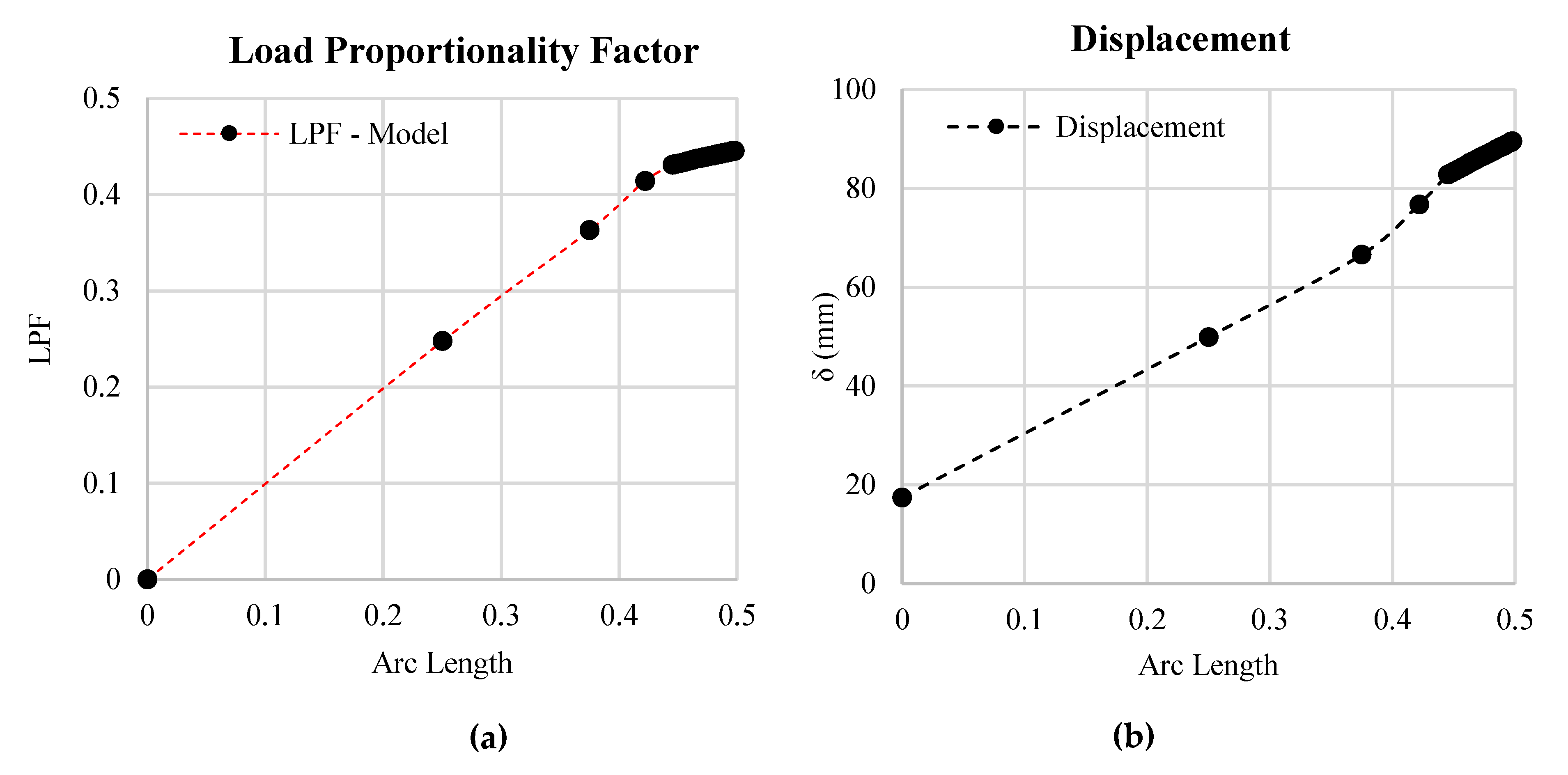
- The out-of-plane eigenvalue mode one vector was established to have a first eigenmode value of 1.06 × 106 from an incrementing load of an initial magnitude of 1.
- The result of the nonlinear analysis indicated 26 Tons and 47 Tons as SLS and ULS, respectively, as the bridge’s bearing capacity with a redundancy ratio of 1.8.
- Checking for resistance of members as individuals gives conservative results. However, checking for the resistance of the whole superstructure using linear and nonlinear buckling gives non-conservative results of their interaction. These results can be deployed for evaluating structural capacity in situ without necessarily analyzing individual members, as enshrined in Eurocode 3.
- The lack of historical data can be supplemented by in situ measurement for ex situ FEM modeling. Consequently, create a digital twin of the bridge for monitoring by updating it with onsite structural data to examine its bearing capacity (digital twin models).
- A bridge operates as a monolithic structure. Thus, the 3-dimensional structural analysis of the members’ interactions is prudent for typical results. As a result, determine the ultimate resistance.
- For long-span and high bridges, wind, earthquake, and temperature loads should be considered using a case-based approach with reference to local codes and the structure’s condition, specifically abutment clearance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parivallal, S.; Narayanan, T.; Ravisankar, K.; Kesavan, K.; Maji, S. Instrumentation and Response Measurement of a Double-Lane Bailey Bridge during Load Test. Strain 2005, 41, 25–30. [Google Scholar] [CrossRef]
- Khounsida, T.; Takafumi, N.; Shozo, N.; Toshihiro, O.; Khampaseuth, T. Study on Static and Dynamic Behavior of Bailey Bridge. Adv. Struct. Eng. Mech. 2019, 46, 9425–9428. [Google Scholar] [CrossRef]
- Sindorf Trading Holland Ltd. Bailey Panel Bridge System—Triple Truss Single Storey Class 100. Available online: https://www.sindorf.nl/Portals/0/BAILEYBRIDGES.pdf (accessed on 16 November 2022).
- Yi, P.; Vaghela, G.; Andrew, B. Condition Assessment And Load Rating of Arched Bailey Bridge. In Proceedings of the Austroads Bridge Conference, Sydney, NSW, Australia, 22–24 October 2014; pp. 1–11. [Google Scholar]
- King, W.S.; Wu, S.M.; Duan, L. Laboratory Load Tests and Analysis of Bailey Bridge Segments. J. Bridg. Eng. 2013, 18, 957–968. [Google Scholar] [CrossRef]
- Khounsida, T.; Nishikawa, T.; Nakamura, S.; Okumatsu, T.; Thepvongsa, K. Experimental and Analytical Study on Dynamic Behavior of Bailey Bridge. Proc. Constr. Steel 2020, 28, 771–777. [Google Scholar]
- Motion Analysis Software MOVIAS Neo|Video Measurement|Knack. Available online: https://www.nacinc.jp/analysis/software/movias-neo/?add_list=MOVIAS+Neo (accessed on 4 November 2022).
- Jatmiko, J.; Psimoulis, P. Deformation Monitoring of a Steel Structure Using 3D Terrestrial Laser Scanner (TLS). In Proceedings of the 24th International Workshop on Intelligent Computing in Engineering, Nottingham, UK, 12 July 2017; Volume 2017, pp. 168–177. [Google Scholar]
- Tokyo Measuring Instruments Ltd. Precise and Flexible Strain Gauges; Tokyo Measuring Instruments Ltd.: Tokyo, Japan, 2020; p. 96. [Google Scholar]
- Japan Road Association. Fatigue of Steel Bridge; Japan Road Association: Tokyo, Japan, 1997; pp. 47–309. [Google Scholar]
- Godoi, F.C.; Prakash, S.; Bhandari, B.R. Prefabricated Steel Bridge Systems; FHWA SOLICITATION NO. DTFH61-03-R-00113; Structure Design and Rehabilitation, Inc.: Gaithersburg, MD, USA, 2005; Volume 1, pp. 1–261. [Google Scholar]
- Masatoshi, N.; Yuki, C.; Ichiro, A. Topological Optimum Shape of a Fundamental Module of the Periodic Structure and Cantilever Bridge. J. Struct. Eng. 2021, 67A, 90–98. [Google Scholar]
- Joiner, C.J.H. The Story of the Bailey Bridge. Proc. Inst. Civ. Eng.-Eng. Hist. Herit. 2011, 164, 65–72. [Google Scholar] [CrossRef]
- Department of the Army. Bailey Bridge; Field Manual—TM 5-277; Department of the Army: Washington, DC, USA, 1986; pp. 3–349. [Google Scholar]
- Gómez-Martínez, R.; Sánchez-García, R.; Escobar-Sánchez, J.A.; Arenas-García, L.M.; Mendoza-Salas, M.A.; Rosales-González, O.N. Monitoring Two Cable-Stayed Bridges during Load Tests with Fiber Optics. Structures 2021, 33, 4344–4358. [Google Scholar] [CrossRef]
- Umekawa, Y.; Suganuma, H. Bridge Displacement Monitoring Using Acceleration Measurement and Development of Efficient Bridge Management System. In Proceedings of the IABSE Symp. Nantes 2018 Tomorrow’s Megastructures, Nantes, France, 19–21 September 2018; pp. S6-11–S6-18. [Google Scholar] [CrossRef]
- Lichti, D.D.; Gordon, S.J.; Stewart, M.P.; Franke, J.; Tsakiri, M. Comparison of Digital Photogrammetry and Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2002, 39–44. [Google Scholar]
- Tokyo Measuring Instruments Laboratory Co High Sensitive Displacement Transducer. Available online: https://tml.jp/e/product/transducers/displacement_high.html (accessed on 1 November 2022).
- Bridge Deflection Measurement Service INTEGRAL PLUS® |TTES Co., Ltd. Available online: https://ttes.co.jp/service/integral/ (accessed on 1 September 2022).
- Umekawa, Y.; Hisatada, S.; Kinoshita, K.; Ono, T. A Study on Displacement Monitoring of Bridges Using Acceleration Data Associated with Vehicle Traffic. In Proceedings of the 72nd Annual Conference of Japan Society of Civil Engineers JSCE, Kyushu, Japan, 11 September 2017; Volume 8, pp. 699–700. [Google Scholar]
- Shimosato, T.; Tai, M.; Hisatada, S.; Umekawa, Y.; Hiyama, Y. Deflection Measurement of Bridge Using TWM System. In Proceedings of the Japan Society of Civil Engineers Western Branch Okinawa Meeting, 7th Technical Research Conference, JSCE, Okinawa, Japan, 7–11 May 2018; pp. 146–147. [Google Scholar]
- Ma, M.J. Dynamic Load Test Analysis for Continuous Steel Bridge. Appl. Mech. Mater. 2013, 275–277, 1078–1081. [Google Scholar] [CrossRef]
- Paeglite, I.; Paeglitis, A.; Smirnovs, J. Dynamic Amplification Factor for Bridges With Span Length From 10 To 35 Meters. Eng. Struct. Technol. 2015, 6, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Bruls, A.; Calgaro, J.A.; Mathieu, H.; Prat, M. ENV1991–Part 3: The Main Models of Traffic Loads on Bridges: Background Studies; IABSE Colloquim: Delft, The Netherlands, 1996; pp. 215–228. [Google Scholar]
- Ghavami, P. Mechanics of Materials: An Introduction to Engineering Technology; Springer: New York, NY, USA, 1956; Volume 78, ISBN 9783319075716. [Google Scholar]
- Gross, D.; Ehlers, W.; Wriggers, P.; Schröder, J.; Müller, R. Mechanics of Materials-Formulas and Problems: Engineering Mechanics 2; Springer: Berlin/Heidelberg, Germany, 2016; Volume 2, pp. 1–212. [Google Scholar]
- Maros, H.; Juniar, S. Inspection and Maintenance of Steel Girders, 3rd ed.; Indian Railways Institute of Civil Engg: Pune, India, 2016; ISBN 2013206534. [Google Scholar]
- Aashto. AASHTO LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010; ISBN 9781560514510. [Google Scholar]
- Yuji, I.; Nakamura, S.; Kusaba, T.; Nishikawa, T. Field Measurement and Structural Analysis of Bailey Bridge for Understanding Fundamental Load-Bearing Configuration. In Proceedings of the Japan Society of Civil Engineering-West; I-023. JSCE: Tokyo, Japan, 2022; pp. 45–46. [Google Scholar]
- Benčat, J.; Kohár, R. Bridges Subjected to Dynamic Loading. In Bridge Engineering; Intech: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef] [Green Version]
- Kalin, J.; Žnidarič, A.; Anžlin, A.; Kreslin, M. Measurements of Bridge Dynamic Amplification Factor Using Bridge Weigh-in-Motion Data. Struct. Infrastruct. Eng. 2021, 18, 1164–1176. [Google Scholar] [CrossRef]
- Umekawa, Y.; Hisatada, S.; Kinoshita, K.; Ono, T. A Study on Displacement Response Monitoring Using Acceleration Response. In Proceedings of the JSCE Western Branch Okinawa Meeting, 6th Technical Research Presentation, Okinawa, Japan, 11–13 September 2017; JSCE: Okinawa, Japan, 2017; Volume 8, pp. 88–89. [Google Scholar]
- Association of Structural Engineers of the Philippines. National Structural Code of the Philippines; Nscp C101-15; Association of Structural Engineers of the Philippines: Quezon City, Philippines, 2015; pp. 1–1008. [Google Scholar]
- GRSE. Garden Reach Shipbuilders and Engineers Limited Kolkata—India; GRSE—Teschnical Manual; GRSE: Kolkata, India, 2016; Volume 4, pp. 1–93. [Google Scholar]
- CEN. Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2011. [Google Scholar]
- CEN. Eurocode 1: Actions on Structures—Part 2: Traffic Loads on Bridges on Bridges; CEN: Brussels, Belgium, 2003. [Google Scholar]
- Tian, Q.; Hang, C.; Wan, Z.; Zou, Y. Local Optimization Analysis of Bailey Beam Bracket Based on Multiscale Model. Key Eng. Mater. 2019, 815, 229–234. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind Loading of Structures, 2nd ed.; Spon Press: New York, NY, USA, 2018; ISBN 041924610X. [Google Scholar]
- Çiftçioğlu, A.Ö.; Yildizel, S.A.; Yildirim, M.S.; Doğan, E. Wind Load Design of Hangar-Type Closed Steel Structures with Different Roof Pitches Using Abaqus CAE Software. TEM J. 2017, 6, 336–341. [Google Scholar] [CrossRef]
- LRFD Steel Girder SuperStructure Design Example-LRFD-Structures-Bridges & Structures-Federal Highway Administration. Available online: https://www.fhwa.dot.gov/bridge/lrfd/us_ds8.cfm#designstep86_5 (accessed on 19 October 2022).
- Poddaeva, O.; Fedosova, A.; Gribach, J. The Study of Wind Effects on the Bridge Constructions. E3S Web Conf. 2019, 97, 03030. [Google Scholar] [CrossRef]
- Gorenc, B.E.; Tinyou, R.; Syam, A.A. Steel Designers’ Handbook, 7th ed.; UNSW Press: Sydney, Australia, 2005. [Google Scholar]
- Ochshorn, J. Structural Elements for Architects and Builders: Design of Columns, Beams, and Tension Elements in Wood, Steel, and Reinforced Concrete; Elsevier: New York, NY, USA, 2009; ISBN 9781856177719. [Google Scholar]
- American Society of Civil Engineers. American Society of Civil Engineers Design Loads on Structures During Construction American Society of Civil Engineers Design Loads on Structures During Construction; Amer Society of Civil Engineers: Reston, VA, USA, 2003; ISBN 0784406189. [Google Scholar]
- Kumamoto, T. Seismic Hazard Maps of Japan and Computational Differences in Models and Parameters. Geogr. Rev. Jpn. Ser. B 1999, 72, 135–161. [Google Scholar] [CrossRef] [Green Version]
- Dassault Systèmes. In Abaqus CAE User’s Manual; Simulia: Johnston, RI, USA, 2012; pp. 1–1174.
- Chakrabarty, J. Theory of Plasticity, 3rd ed.; Elsevier Butterworth-Heinemann: Burlington, Singapore, 2006; ISBN 0750666382. [Google Scholar]
- Sun, S.; Lei, G.; Sun, Z. Dynamic and Static Load Tests on a Large-Span Rigid-Frame Bridge. Math. Model. Eng. Probl. 2019, 6, 409–414. [Google Scholar] [CrossRef]
- Miki, C. Civil Engineering: Steel Structures, 10th ed.; Kyoritsu Publishing: Tokyo, Japan, 2000; ISBN 9784320073913. [Google Scholar]
- British Standard 5950-1:2000; Structural Use of Steel Work in Buildings Part 1. BSI: London, UK, 2001; ISBN 0 580 33238 X.


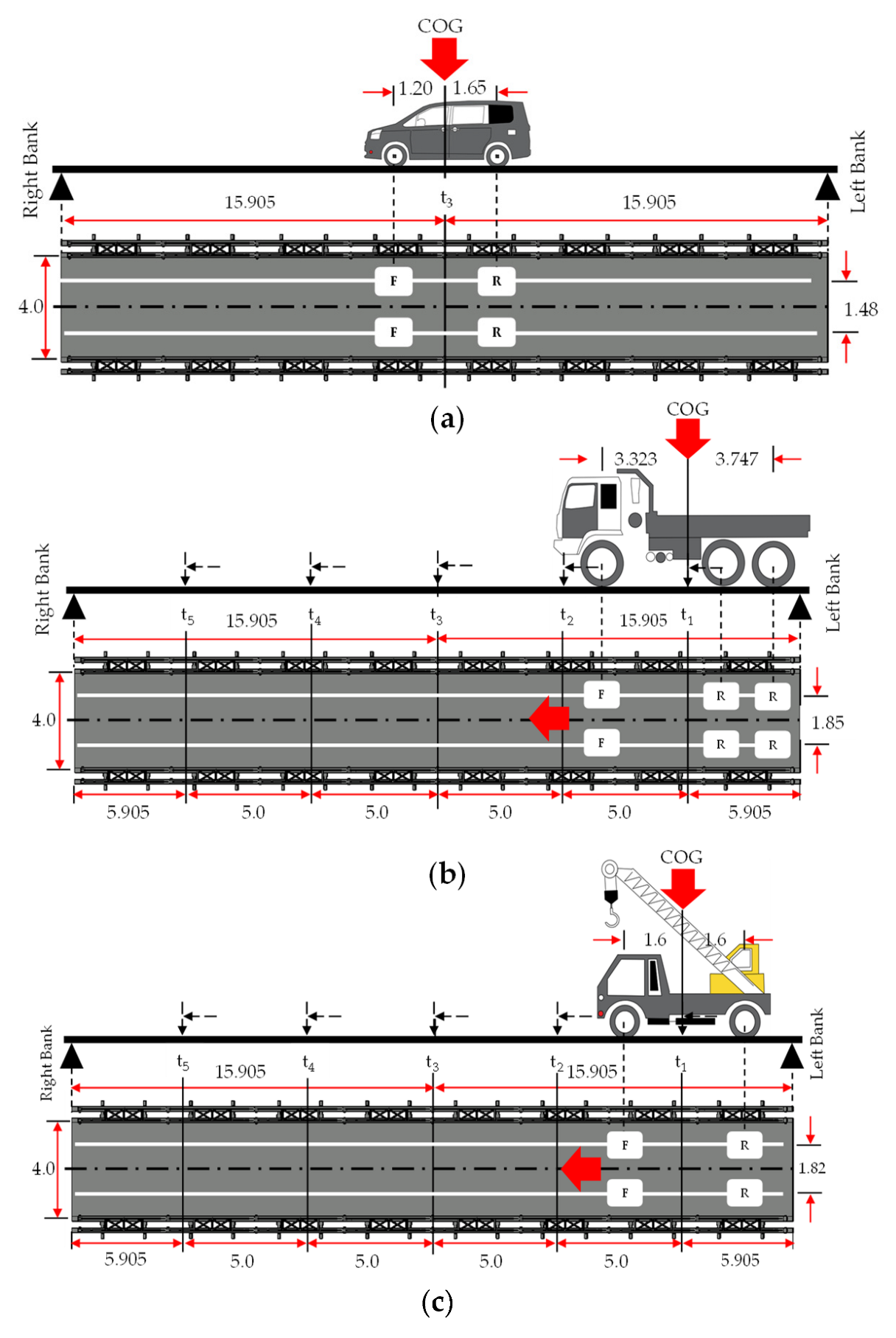


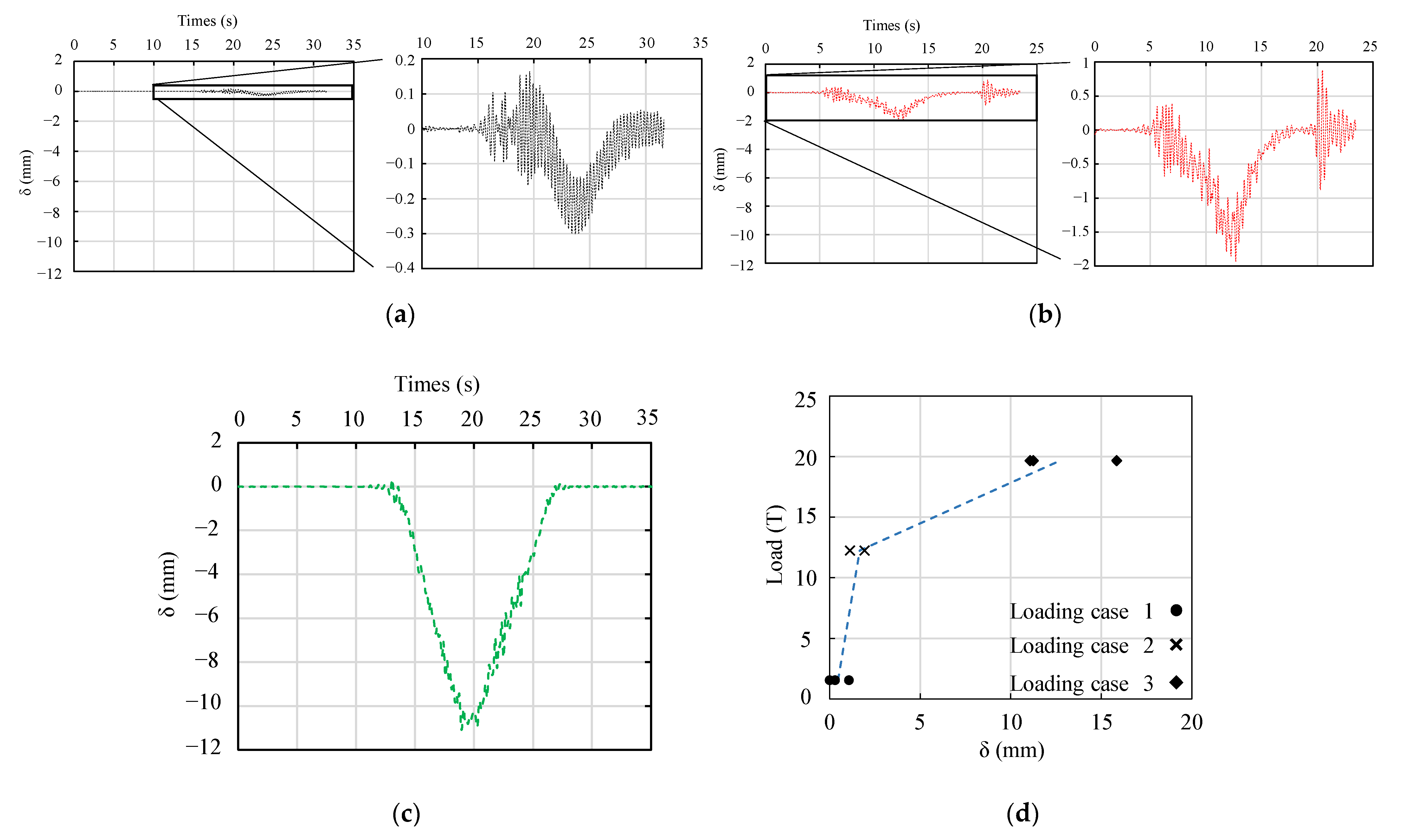


| Load | Model | Weight (Tons) | Loading Case |
|---|---|---|---|
| Car | DBA-ZRR80G | 1.57 | 1 |
| Truck | KLL-CW55E | 12.24 | 2 |
| Crane | Tadano YDS-T014 | 19.66 | 3 |
| The average weight of the driver: 55 kg | |||
| S/No. | Description | Section | Dimensions (mm) | ||||
|---|---|---|---|---|---|---|---|
| H | B | tw | tf | Diameter | |||
| 1 | Top and Bottom Member | Channel | 103 | 65 | 9.2 | 7.5 | - |
| 2 | Transom/Cross Beam | I-Section | 300 | 300 | 10 | 15.6 | - |
| 3 | Vertical & Diagonals | Box | 78 | 78 | 7.2 | 7.2 | - |
| 5 | Chord reinforcement | Channel | 103 | 65 | 9.2 | 7.5 | - |
| 6 | Sway brays | Rect. Plate | - | - | - | - | - |
| 7 | Bracing frame | Channel | 75 | 36 | 8.5 | 5.8 | - |
| 8 | Tubular racker | Tubular | - | - | - | - | d-36; t-8.85 |
| 9 | Tie-plate | Channel | 75.67 | 38 | 5.7 | 7.5 | - |
| 10 | Racker | Channel | 75 | 36 | 8.5 | 5.8 | - |
| Loading Case | F (Tons) | ẋ (θ) | Residuals | ɳ | ||||
|---|---|---|---|---|---|---|---|---|
| FEA | Transducer | Image/P | Transducer | Image/P | Transducer | Image/P | ||
| Case 1 | 1.57 | 0.0028 | 0.0035 | 0.0079 | 0.0007 | 0.0051 | 1.25 | 2.79 |
| Case 2 | 12.24 | 0.0213 | 0.0357 | 0.0340 | 0.0144 | 0.0127 | 1.67 | 1.60 |
| Case 3 | 19.66 | 0.0342 | 0.0488 | 0.0492 | 0.0146 | 0.0150 | 1.43 | 1.44 |
| σ Distribution | Standard | λp | λr | Slenderness Ratio | |
|---|---|---|---|---|---|
| Chord | I-Section | ||||
| FLB | Japanese | 56.76 | - | 7.60 | 2.65 |
| Eurocode | 7.65 | 8.50 | |||
| British | 8.28 | 9.20 | |||
| Philippines | 9.43 | 24.81 | |||
| WLB | Japanese | 56.76 | - | 7.83 | 7.83 |
| Eurocode | 61.22 | 70.58 | |||
| British | 25.76 | 29.44 | |||
| Philippines | 93.27 | 141.40 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusimba, B.A.; Rinzin, T.; Banno, Y.; Kinoshita, K. Condition Assessment and Adaptation of Bailey Bridges as a Permanent Structures. Appl. Sci. 2022, 12, 11673. https://doi.org/10.3390/app122211673
Kusimba BA, Rinzin T, Banno Y, Kinoshita K. Condition Assessment and Adaptation of Bailey Bridges as a Permanent Structures. Applied Sciences. 2022; 12(22):11673. https://doi.org/10.3390/app122211673
Chicago/Turabian StyleKusimba, Barasa Anthony, Tshewang Rinzin, Yuki Banno, and Koji Kinoshita. 2022. "Condition Assessment and Adaptation of Bailey Bridges as a Permanent Structures" Applied Sciences 12, no. 22: 11673. https://doi.org/10.3390/app122211673
APA StyleKusimba, B. A., Rinzin, T., Banno, Y., & Kinoshita, K. (2022). Condition Assessment and Adaptation of Bailey Bridges as a Permanent Structures. Applied Sciences, 12(22), 11673. https://doi.org/10.3390/app122211673





