Study on the Erosion Morphology of Cohesive Soil under the Vertical Impact of a High-Pressure Moving Water Jet
Abstract
:1. Introduction
2. Materials and Methods
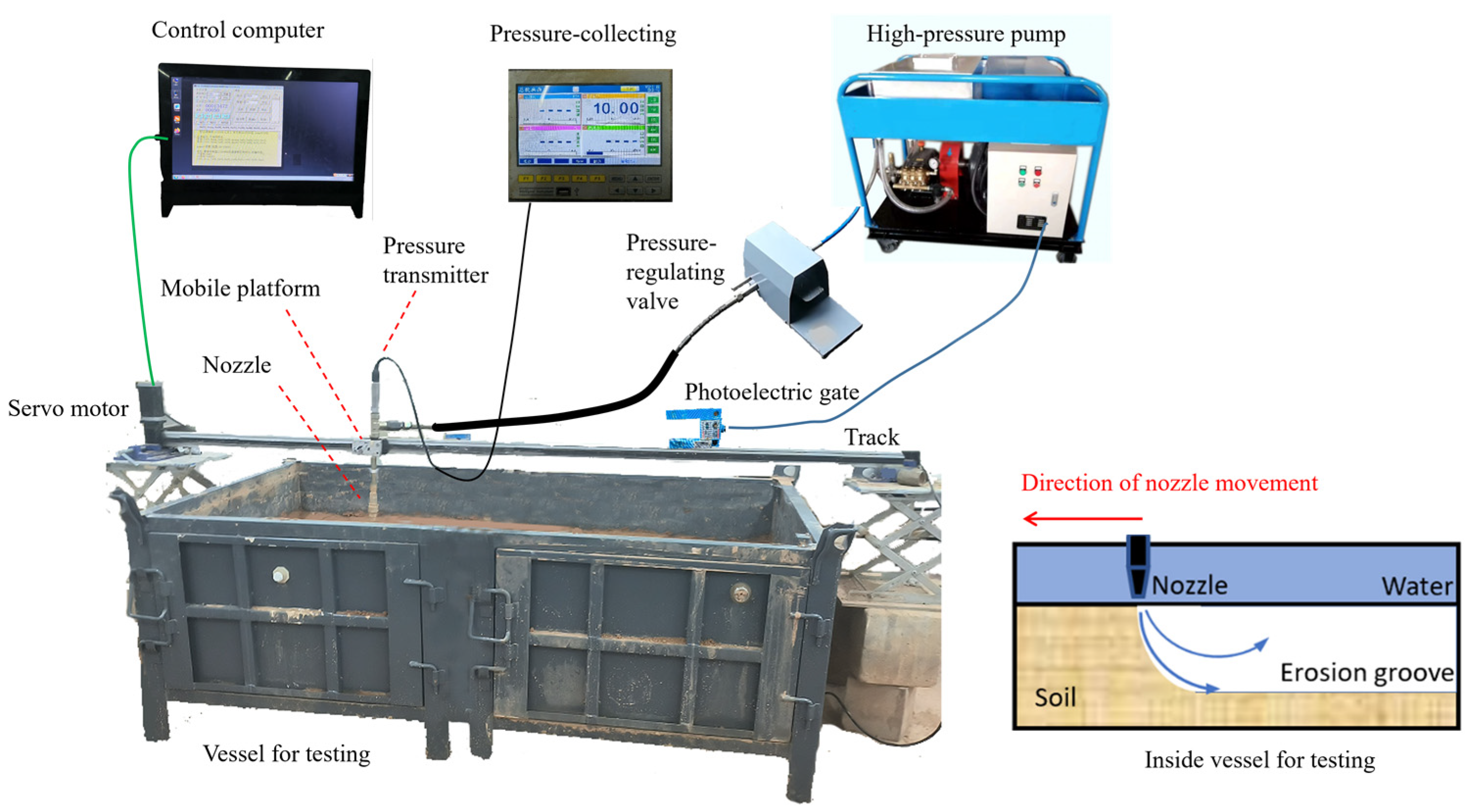
2.1. Test System
- (1)
- Test box
- (2)
- Jet pressure supply module
- (3)
- Control module
2.2. Test Scheme
- (1)
- Selection of test soil samples
- (2)
- Test conditions
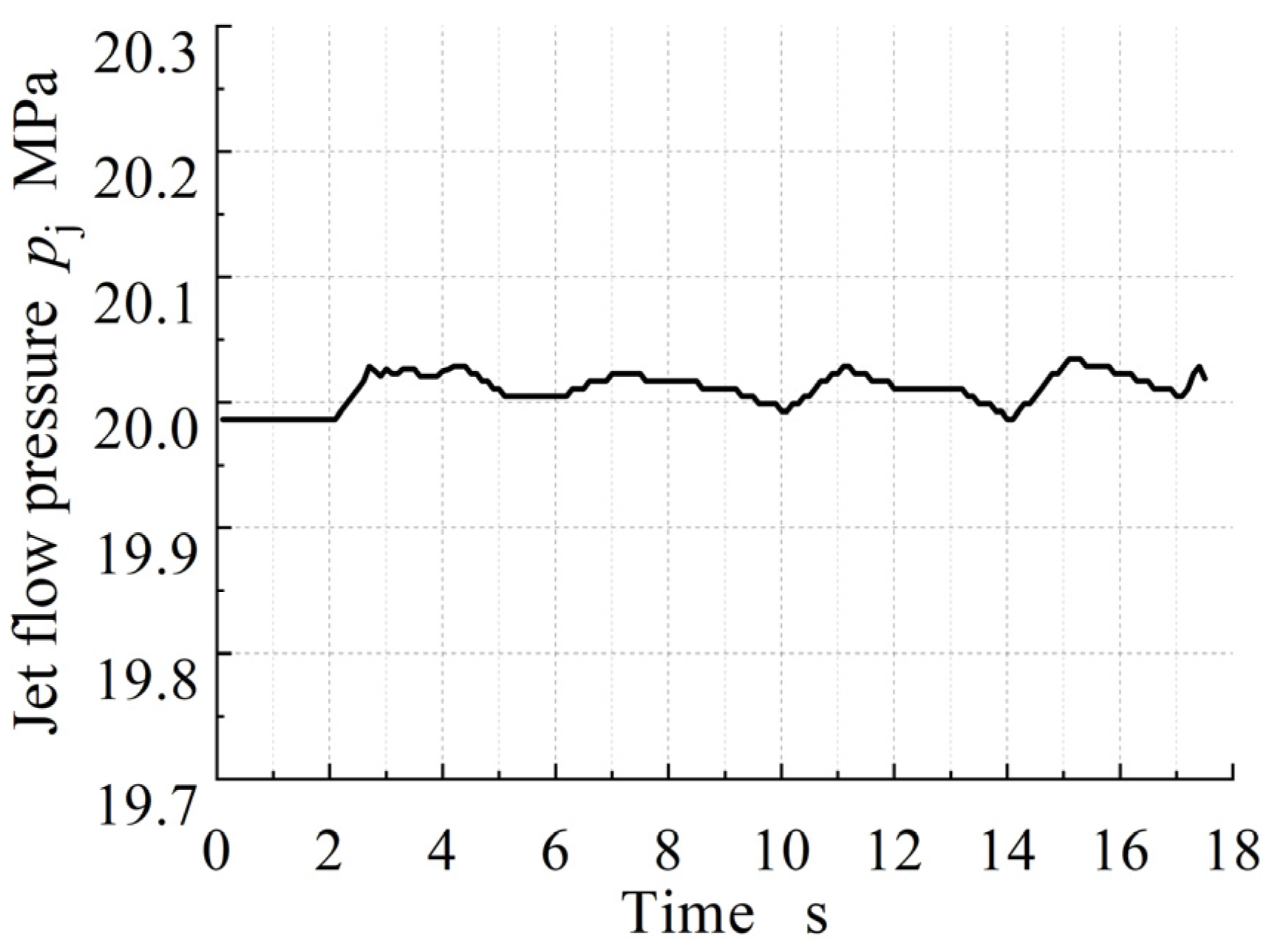
2.3. Test Procedure
3. Results and Discussion
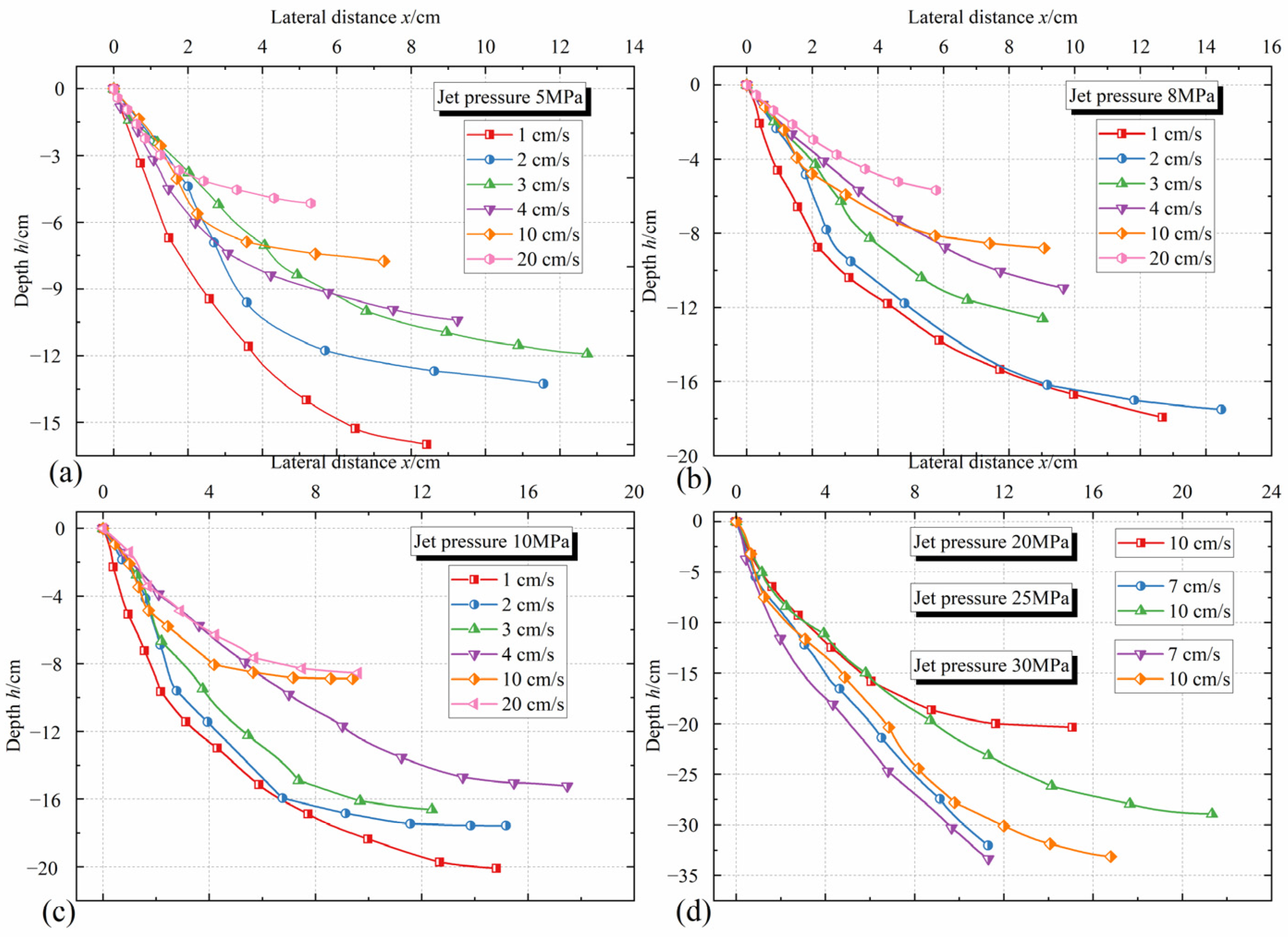
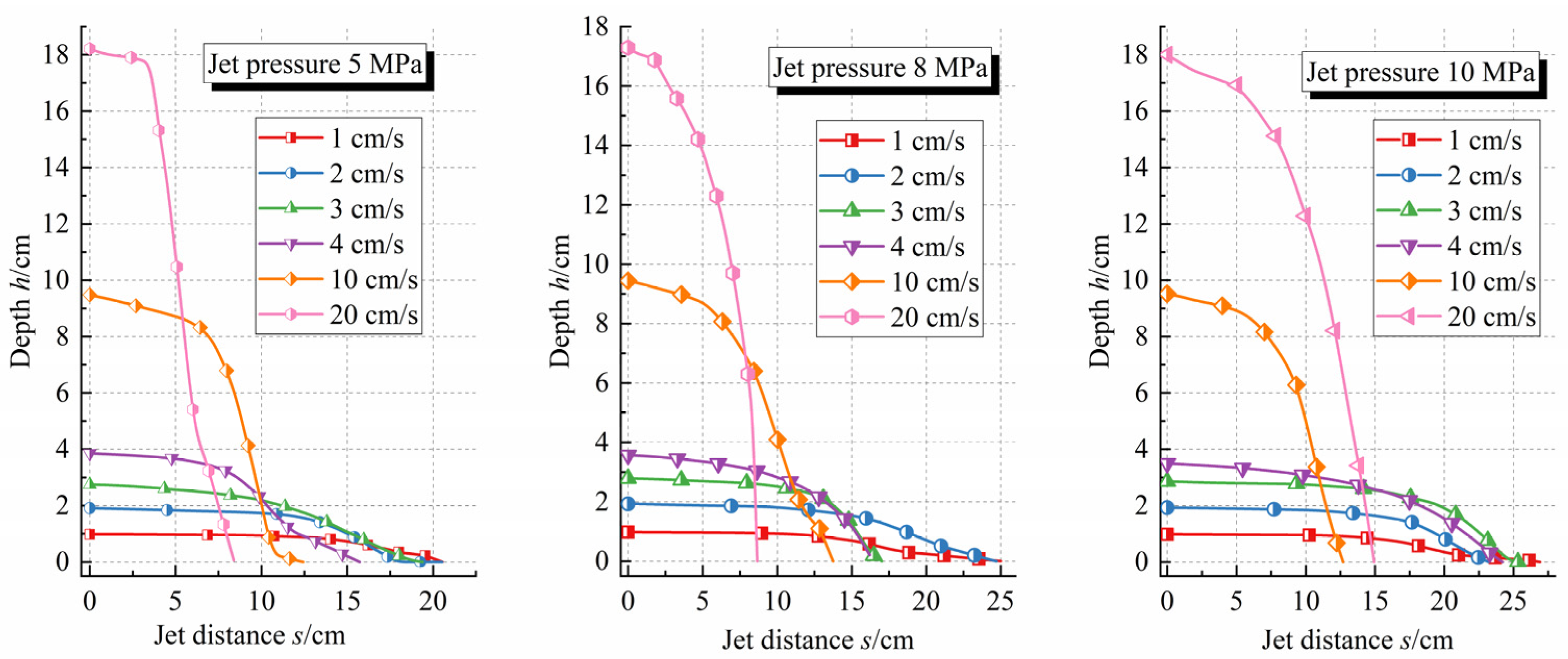
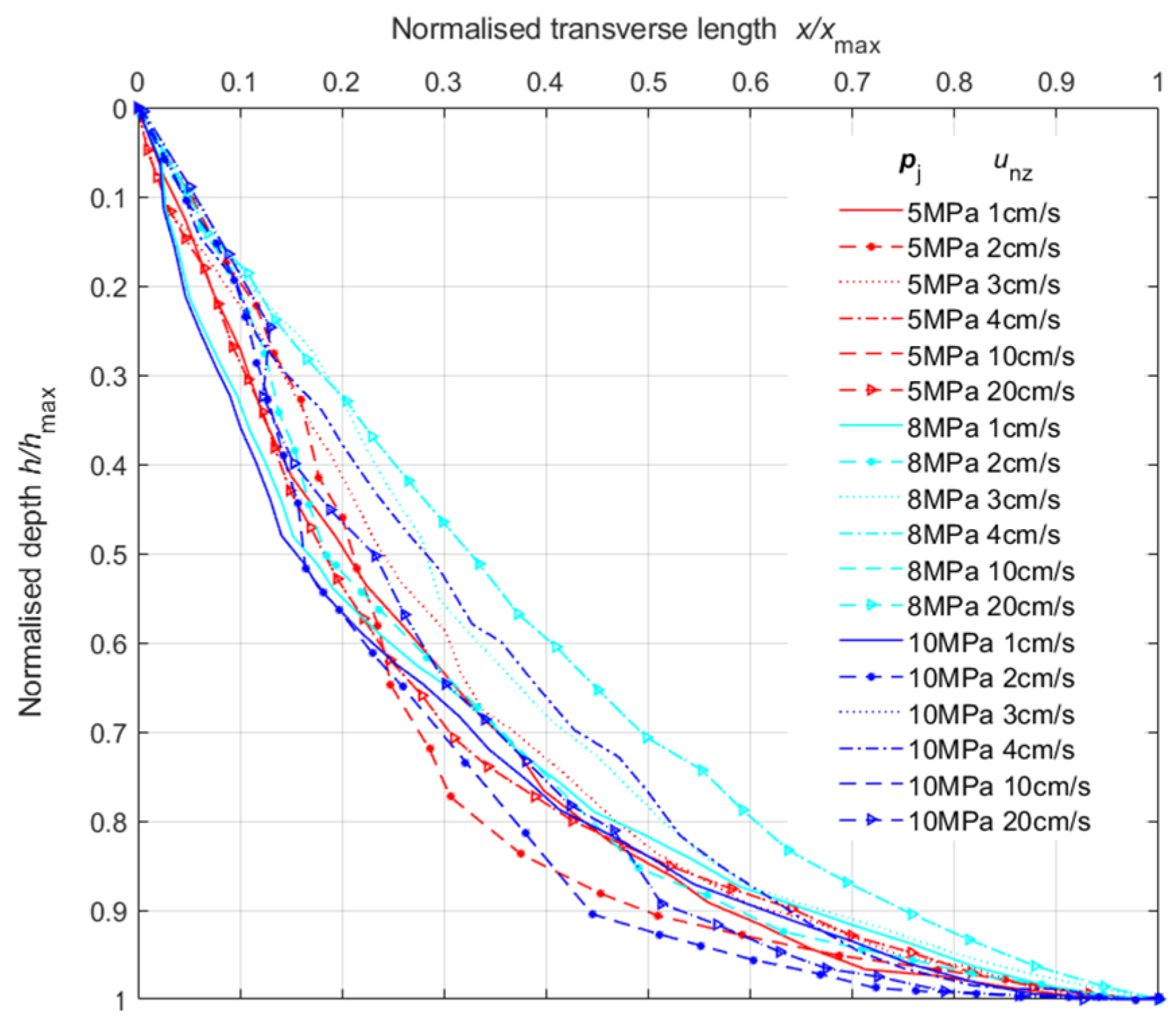
3.1. Morphological Characteristics of Erosion Surface
3.2. Mechanism of Surface Erosion
3.3. Prediction of the Erosion Surface Geometry
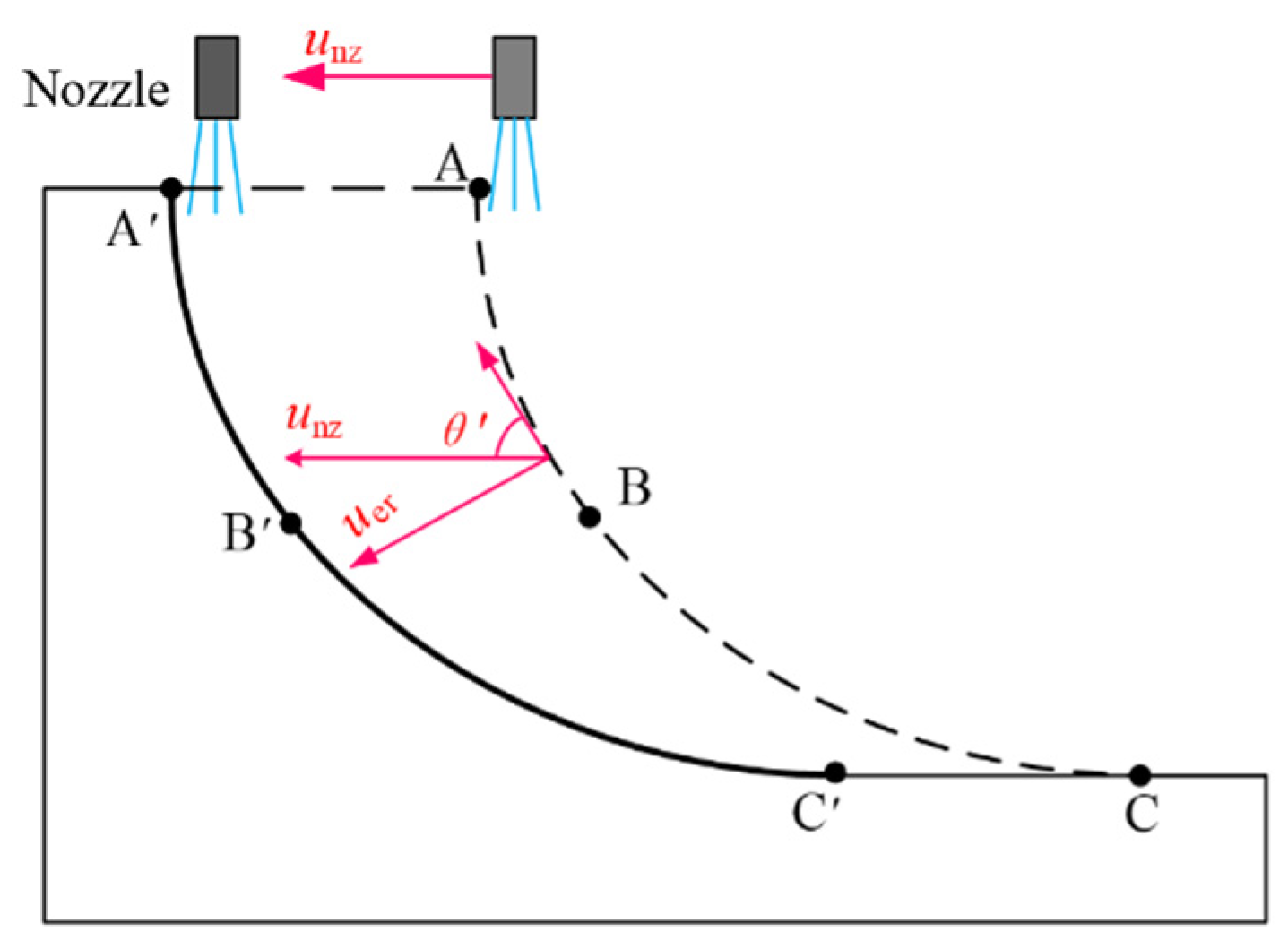
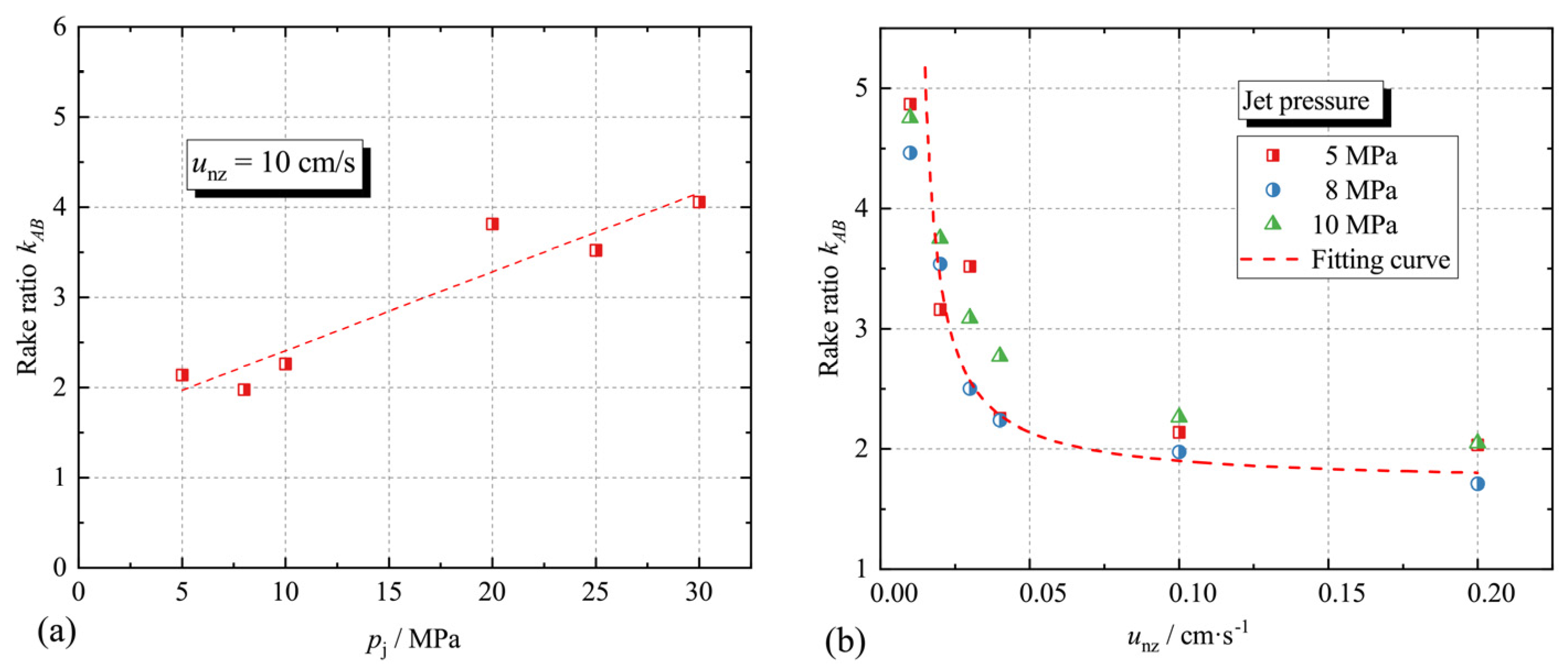
3.3.1. Segmentation of the Erosion Surface Curve
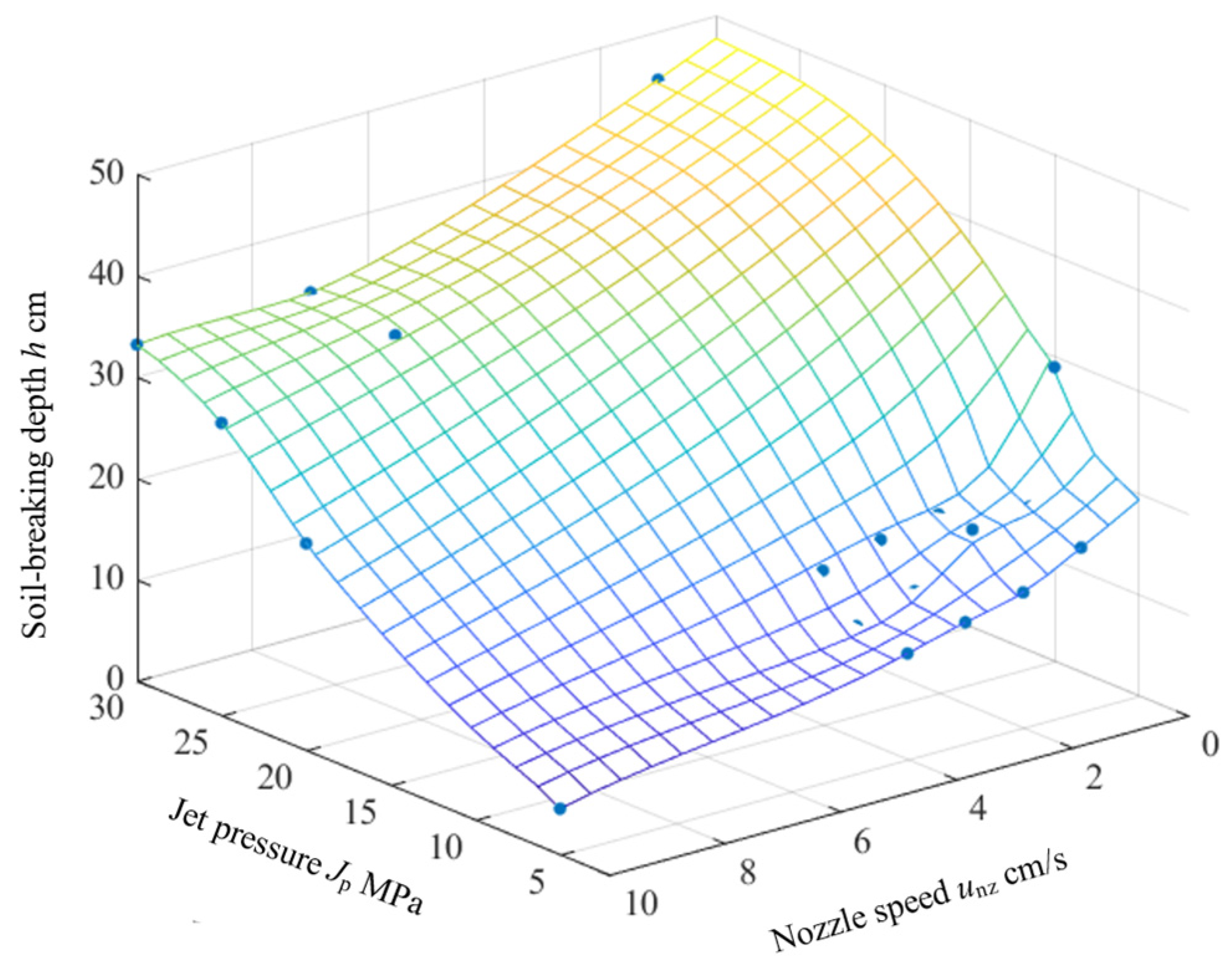
3.3.2. Prediction of Maximum Soil-Breaking Depth
3.3.3. Determination of the Maximum Lateral Distance
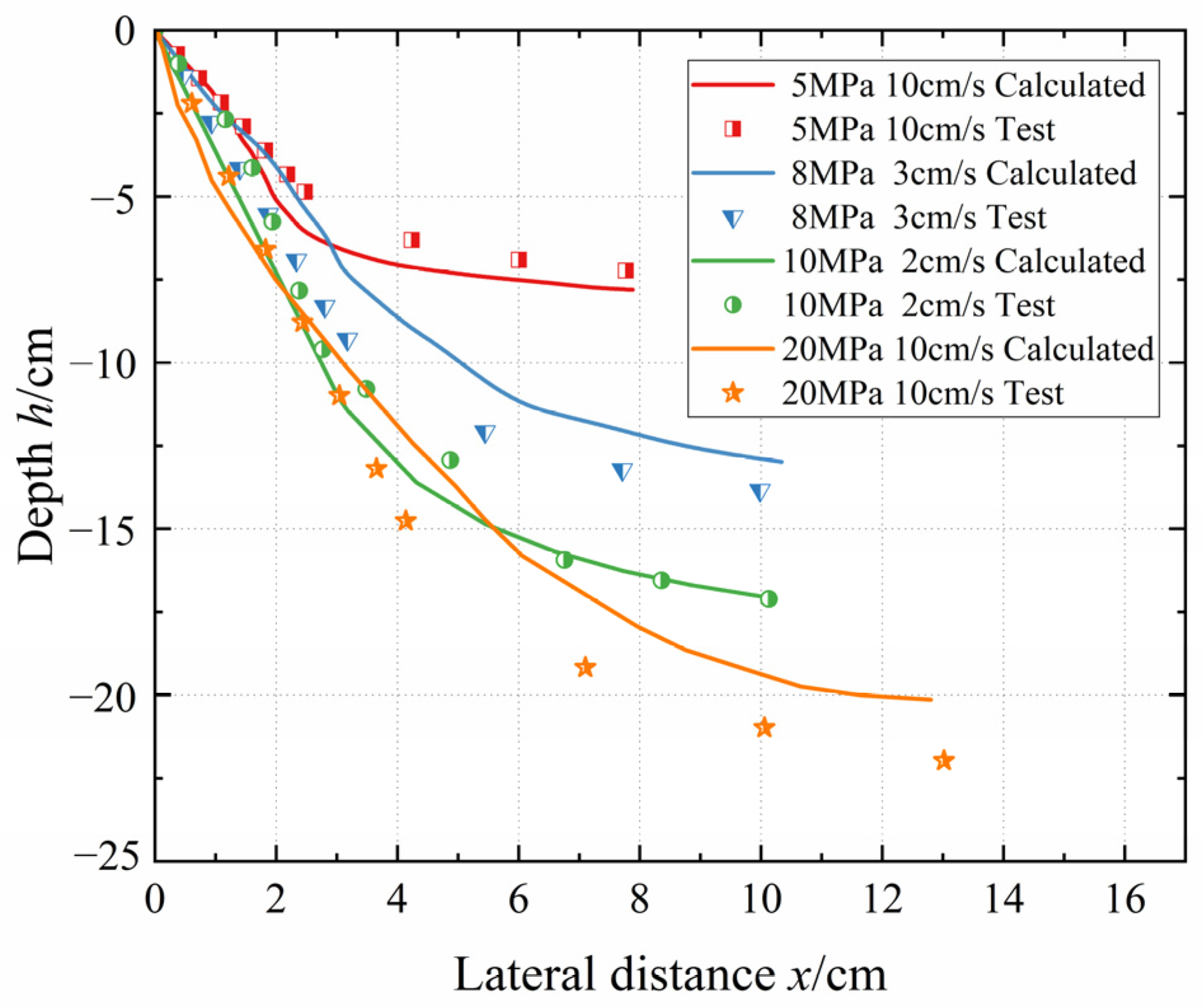
3.3.4. Prediction and Effect of Geometric Shape
4. Conclusions and Future Work
4.1. Conclusions
4.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kartal, F. A Review of the Current State of Abrasive Water-Jet Turning Machining Method. Int. J. Adv. Manuf. Technol. 2017, 88, 495–505. [Google Scholar] [CrossRef]
- Sharma, D.R.; Maurya, D.S.; Saini, D.R. A Review Paper on Current Research and Development in Abrasive Waterjet Machining. Math. Stat. Eng. Appl. 2022, 71, 4160–4169. [Google Scholar]
- Mardi, K.; Dixit, A.; Pramanik, A.; Basak, A.K. Tribology in (Abrasive) Water Jet Machining: A Review. In Machining and Tribology; Elsevier: Amsterdam, The Netherlands, 2022; pp. 113–125. ISBN 978-0-12-819889-6. [Google Scholar]
- Wen, J.; Chen, C.; Campos, U. Experimental Research on the Performances of Water Jet Devices and Proposing the Parameters of Borehole Hydraulic Mining for Oil Shale. PLoS ONE 2018, 13, e0199027. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Tang, J.; Ge, Z.; Xia, B.; Liu, Y. Hard Rock Drilling Technique with Abrasive Water Jet Assistance. Int. J. Rock Mech. Min. Sci. 2013, 60, 47–56. [Google Scholar] [CrossRef]
- Njock, P.G.A.; Shen, J.S.; Modoni, G.; Arulrajah, A. Recent Advances in Horizontal Jet Grouting (HJG): An Overview. Arab. J. Sci. Eng. 2018, 43, 1543–1560. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, C.; Ge, T. Experimental Prediction of the Noncontact Jet Trencher’s Excavation Depth in Clay. Mar. Georesources Geotechnol. 2017, 35, 300–304. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, M.; Ge, T.; Wang, C. Experimental Research on Trenching in Stiff Clay by Submerged Vertical Traveling Jets. J. Coast. Res. 2016, 318, 365–373. [Google Scholar] [CrossRef]
- Yu, J.; Liu, J.; Wang, G.; Luo, S.; Wang, J. Correction of Realizable k-ε model for high pressure submerged water jets. Sci. Technol. Eng. 2021, 21, 5024–5030. [Google Scholar]
- Rajaratnam, N.; Beltaos, S. Erosion by Impinging Circular Turbulent Jets. J. Hydraul. Div. 1977, 103, 1191–1205. [Google Scholar] [CrossRef]
- Hogg, A.J.; Huppert, H.E.; Dade, W.B. Erosion by Planar Turbulent Wall Jets. J. Fluid Mech. 1997, 338, 317–340. [Google Scholar] [CrossRef] [Green Version]
- Mazurek, K.A.; Rajaratnam, N.; Sego, D.C. Scour of Cohesive Soil by Submerged Circular Turbulent Impinging Jets. J. Hydraul. Eng. 2001, 127, 598–606. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, L.; Gong, Y.; Ning, D.; Zhang, Z. Theoretical and Experimental Study of Scour Depth by Submerged Water Jet. Adv. Mech. Eng. 2016, 8, 1687814016682392. [Google Scholar] [CrossRef]
- Jun, D.; Wei-lin, X.U.; Zhong-chao, Y.; Jin-xue, Q.U. Numerical simulation of scouring on bedrock. Skxjz 2005, 16, 47–51. [Google Scholar]
- Nguyen, D.; Uh Zapata, M.; Gauthier, G.; Gondret, P.; Pham Van Bang, D. A Two Phase Numerical Model For The Water Injection Dredging (WID) Technology: An Unified Formulation For Continuum Mechanic. CUNY Academic Works 17–21 August 2014. Available online: https://academicworks.cuny.edu/cc_conf_hic/437/ (accessed on 11 November 2022).
- Epely-Chauvin, G.; De Cesare, G.; Schwindt, S. Numerical Modelling of Plunge Pool Scour Evolution In Non-Cohesive Sediments. Eng. Appl. Comput. Fluid Mech. 2014, 8, 477–487. [Google Scholar] [CrossRef] [Green Version]
- Kuang, S.B.; LaMarche, C.Q.; Curtis, J.S.; Yu, A.B. Discrete Particle Simulation of Jet-Induced Cratering of a Granular Bed. Powder Technol. 2013, 239, 319–336. [Google Scholar] [CrossRef]
- Perng, A.T.H.; Capart, H. Underwater Sand Bed Erosion and Internal Jump Formation by Travelling Plane Jets. J. Fluid Mech. 2008, 595, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Yeh, P.-H.; Chang, K.-A.; Henriksen, J.; Edge, B.; Chang, P.; Silver, A.; Vargas, A. Large-Scale Laboratory Experiment on Erosion of Sand Beds by Moving Circular Vertical Jets. Ocean Eng. 2009, 36, 248–255. [Google Scholar] [CrossRef]
- Dong, C.; Zhao, P.; Yu, G.; Zhang, M. Laboratory Flume Experiments on Cohesive Sediment Erosion by Oscillating Wall Jet. J. Coast. Res. 2020, 37, 179–190. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, G.; La Rovere, A.; Ranzi, R. Erodibility of Fluidized Cohesive Sediments in Unidirectional Open Flows. Ocean Eng. 2017, 130, 523–530. [Google Scholar] [CrossRef]
- Benahmed, N.; Bonelli, S. Investigating Concentrated Leak Erosion Behaviour of Cohesive Soils by Performing Hole Erosion Tests. Eur. J. Environ. Civ. Eng. 2012, 16, 43–58. [Google Scholar] [CrossRef]
- Aderibigbe, O.O.; Rajaratnam, N. Erosion of Loose Beds by Submerged Circular Impinging Vertical Turbulent Jets. J. Hydraul. Res. 1996, 34, 19–33. [Google Scholar] [CrossRef]
- Al-Madhhachi, A.-S.; Hanson, G.; Fox, G.; Tyagi, A.; Bulut, R. Deriving Parameters of a Fundamental Detachment Model for Cohesive Soils from Flume and Jet Erosion Tests. Trans. ASABE 2013, 56, 489–504. [Google Scholar] [CrossRef]
- Utley, B.C.; Wynn, T.M. Cohesive Soil Erosion: Theory and Practice. In Proceedings of the World Environmental and Water Resources Congress 2008, American Society of Civil Engineers, Honolulu, HI, USA, 12–16 May 2008; pp. 1–10. [Google Scholar]
- Wang, B.; van Rhee, C.; Nobel, A.; Keetels, G. Modeling the Hydraulic Excavation of Cohesive Soil by a Moving Vertical Jet. Ocean Eng. 2021, 227, 108796. [Google Scholar] [CrossRef]
- Hanson, G.J. Surface erodibility of earthern channels at high stresses. Part I—Open channel testing. Trans. ASAE 1990, 33, 127–131. [Google Scholar] [CrossRef]
- ASTM D2487; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). Annual Book of ASTM Standards. American Society for Testing Materials: West Conshohocken, PA, USA, 2006.
- Partheniades, E. Erosion and Deposition of Cohesive Soils. J. Hydraul. Div. 1965, 91, 105–139. [Google Scholar] [CrossRef]
- Knapen, A.; Poesen, J.; Govers, G.; Gyssels, G.; Nachtergaele, J. Resistance of Soils to Concentrated Flow Erosion: A Review. Earth-Sci. Rev. 2007, 80, 75–109. [Google Scholar] [CrossRef]



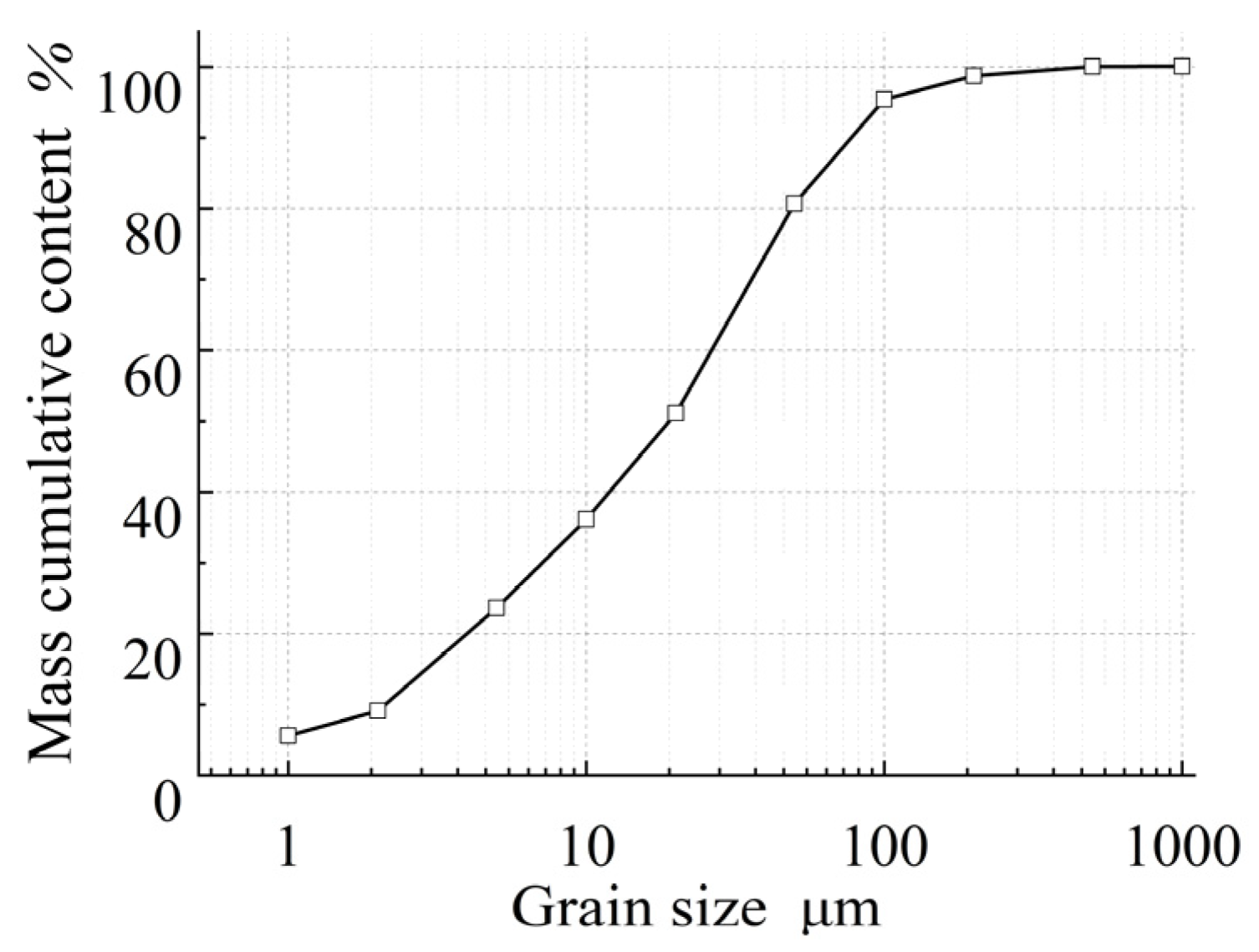


| Sample Location | Distribution of Soil Particle Size/% | Soil Texture | ||
|---|---|---|---|---|
| Sand (>0.05~2 mm) | Silt (0.002~0.05 mm) | Clay (<0.002 mm) | ||
| Pingnan | 52.76 | 38.37 | 8.87 | Loam |
| Parameter | Testing Means | Value | Unit |
|---|---|---|---|
| Relative density | Pycnometer method | 2.70 | g/cm3 |
| density | Cutting ring method | 1.73 | g/cm3 |
| Water content | Drying method | 18 | % |
| Shear strength | Miniature vane | 10.6 | kPa |
| Cohesion | GDS triaxial apparatus | 23 | kPa |
| Internal friction angle | GDS triaxial apparatus | 23.6 | ° |
| Permeability coefficient | Column leaching test | 0.16 | m/d |
| Plasticity index | Liquid–plastic limit combined method | 9.6 | / |
| Test Conditions | Jet Pressure MPa | Nozzle Traversal Speed cm/s | Test Conditions | Jet Pressure MPa | Nozzle Traversal Speed cm/s |
|---|---|---|---|---|---|
| T1-1 | 5 | 1 | T3-1 | 10 | 1 |
| T1-2 | 5 | 2 | T3-2 | 10 | 2 |
| T1-3 | 5 | 3 | T3-3 | 10 | 3 |
| T1-4 | 5 | 4 | T3-4 | 10 | 4 |
| T1-5 | 5 | 10 | T3-5 | 10 | 10 |
| T1-6 | 5 | 20 | T3-6 | 10 | 20 |
| T2-1 | 8 | 1 | T4-1 | 20 | 10 |
| T2-2 | 8 | 2 | T5-1 | 25 | 7 |
| T2-3 | 8 | 3 | T5-2 | 25 | 10 |
| T2-4 | 8 | 4 | T6-1 | 30 | 7 |
| T2-5 | 8 | 10 | T6-2 | 30 | 10 |
| T2-6 | 8 | 20 |
| Serial Number | Jet Pressure MPa | Nozzle Traversal Speed cm/s | Horizontal Ratio xL/xmax % | Depth Ratio hL/hmax % | Distance Ratio sL/smax % | Initial Slope k0 |
|---|---|---|---|---|---|---|
| T1-1 | 5 | 1 | 27.5 | 60.6 | 50.2 | 4.92 |
| T1-2 | 5 | 2 | 30.0 | 66.9 | 48.0 | 3.19 |
| T1-3 | 5 | 3 | 34.5 | 65.4 | 47.6 | 2.28 |
| T1-4 | 5 | 4 | 23.0 | 56.3 | 40.9 | 3.56 |
| T1-5 | 5 | 10 | 30.0 | 66.9 | 46.9 | 2.97 |
| T1-6 | 5 | 20 | 23.0 | 56.3 | 38.9 | 3.07 |
| T2-1 | 8 | 1 | 20.5 | 51.9 | 40.4 | 4.53 |
| T2-2 | 8 | 2 | 28.0 | 61.4 | 46.8 | 3.58 |
| T2-3 | 8 | 3 | 51.0 | 78.4 | 65.6 | 2.51 |
| T2-4 | 8 | 4 | 54.5 | 74.6 | 64.5 | 1.99 |
| T2-5 | 8 | 10 | 28.0 | 61.4 | 43.8 | 2.87 |
| T2-6 | 8 | 20 | 54.5 | 74.6 | 63.2 | 1.72 |
| T3-1 | 10 | 1 | 20.5 | 53.8 | 41.6 | 4.82 |
| T3-2 | 10 | 2 | 27.0 | 65.3 | 47.1 | 3.79 |
| T3-3 | 10 | 3 | 34.5 | 68.4 | 52.1 | 3.11 |
| T3-4 | 10 | 4 | 47.0 | 74.7 | 57.3 | 1.78 |
| T3-5 | 10 | 10 | 27.0 | 65.3 | 44.2 | 3.10 |
| T3-6 | 10 | 20 | 34.5 | 68.4 | 46.6 | 2.07 |
| Average value | 33.1 | 65.0 | 49.2 | 3.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Lan, X.; Wang, G.; Luo, S.; Yang, Z. Study on the Erosion Morphology of Cohesive Soil under the Vertical Impact of a High-Pressure Moving Water Jet. Appl. Sci. 2022, 12, 12343. https://doi.org/10.3390/app122312343
Liu J, Lan X, Wang G, Luo S, Yang Z. Study on the Erosion Morphology of Cohesive Soil under the Vertical Impact of a High-Pressure Moving Water Jet. Applied Sciences. 2022; 12(23):12343. https://doi.org/10.3390/app122312343
Chicago/Turabian StyleLiu, Jian, Xiongdong Lan, Guanshi Wang, Sihai Luo, and Zhipeng Yang. 2022. "Study on the Erosion Morphology of Cohesive Soil under the Vertical Impact of a High-Pressure Moving Water Jet" Applied Sciences 12, no. 23: 12343. https://doi.org/10.3390/app122312343
APA StyleLiu, J., Lan, X., Wang, G., Luo, S., & Yang, Z. (2022). Study on the Erosion Morphology of Cohesive Soil under the Vertical Impact of a High-Pressure Moving Water Jet. Applied Sciences, 12(23), 12343. https://doi.org/10.3390/app122312343






