Modeling the Submergence Depth of Oil Well States and Its Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Submergence Depth Model Construction
2.1.1. Oil Well Full-Pumping State Model
2.1.2. Oil Well Nonfull-Pumping State Model
2.2. Submergence Depth Model Analysis
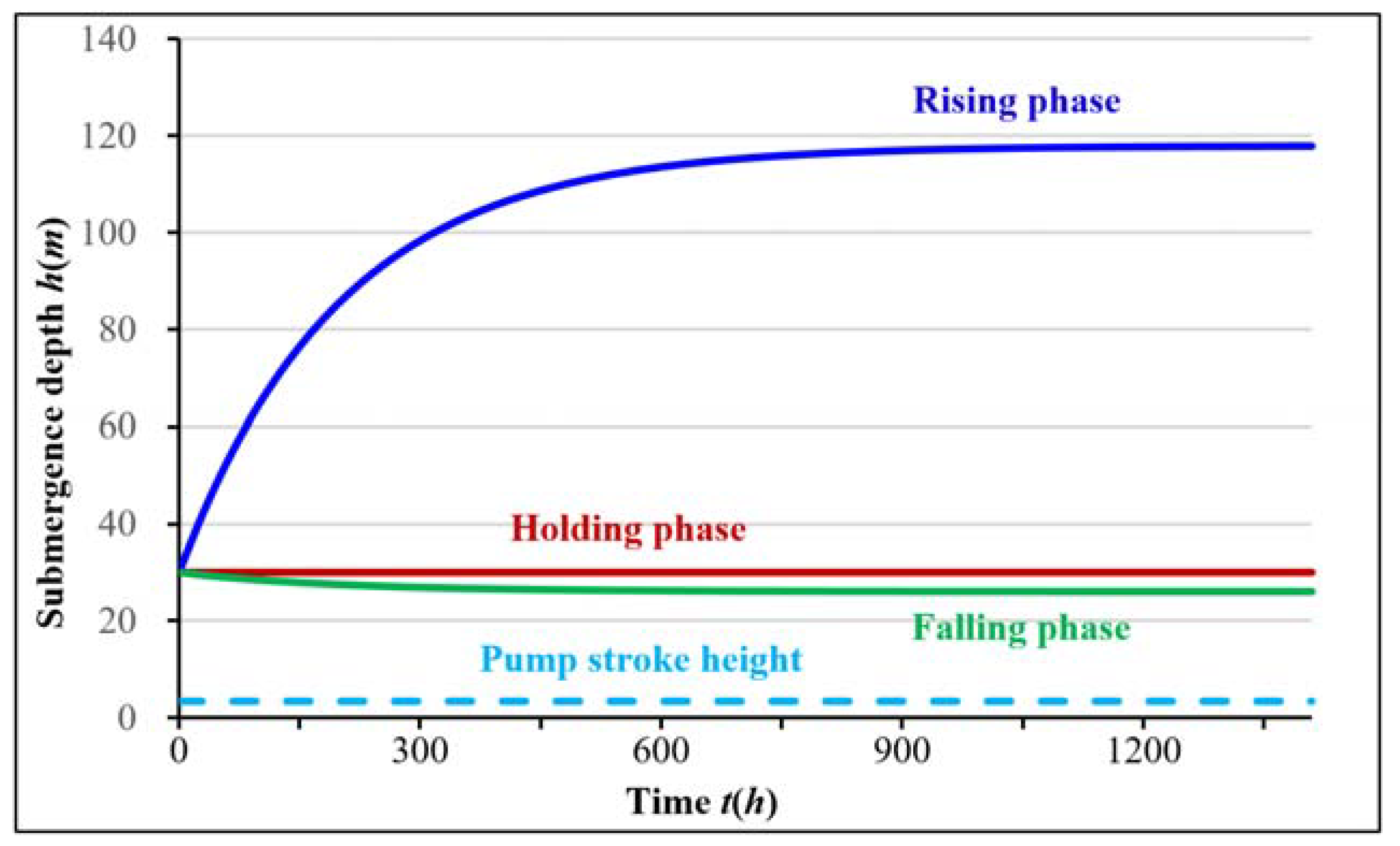
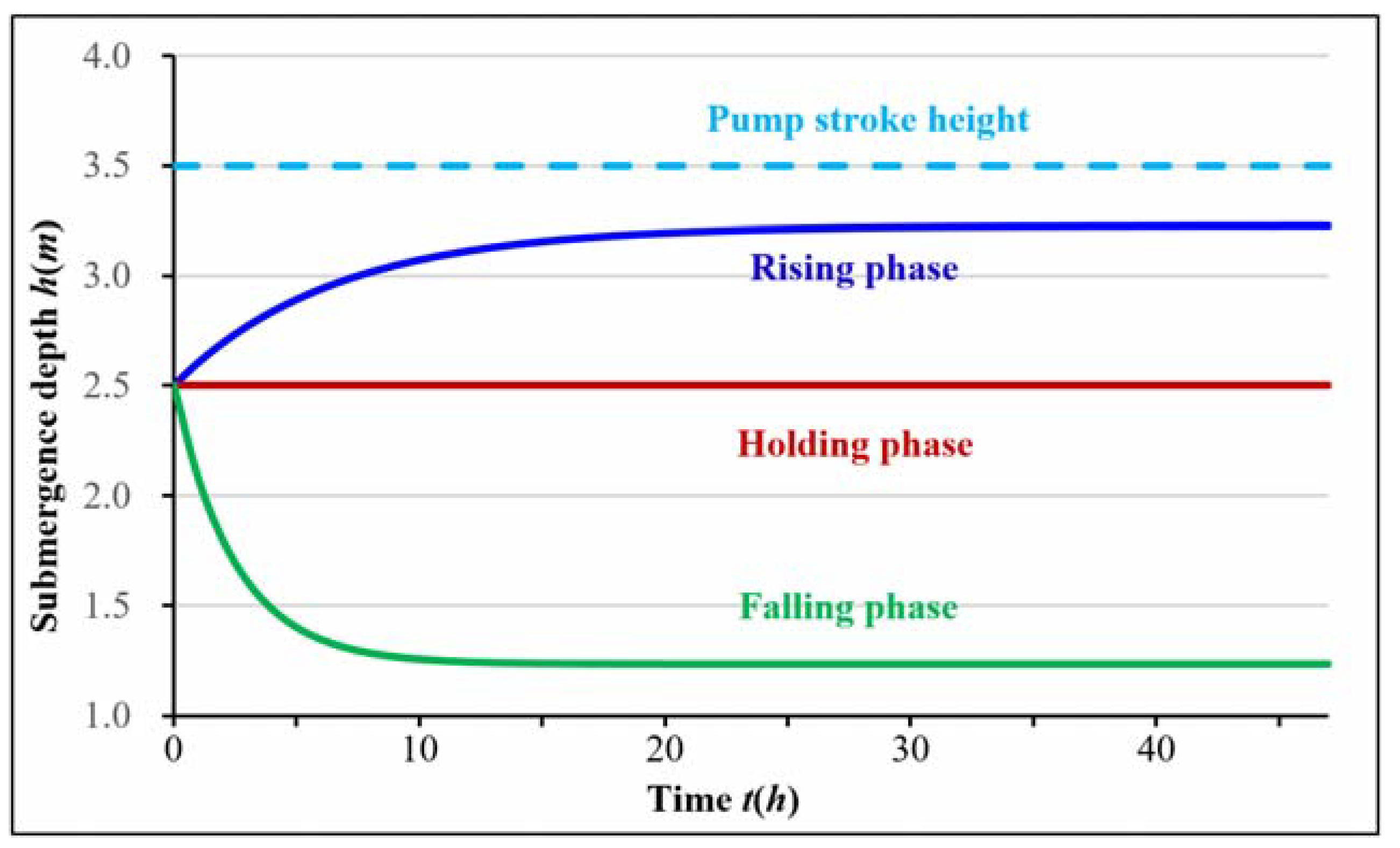
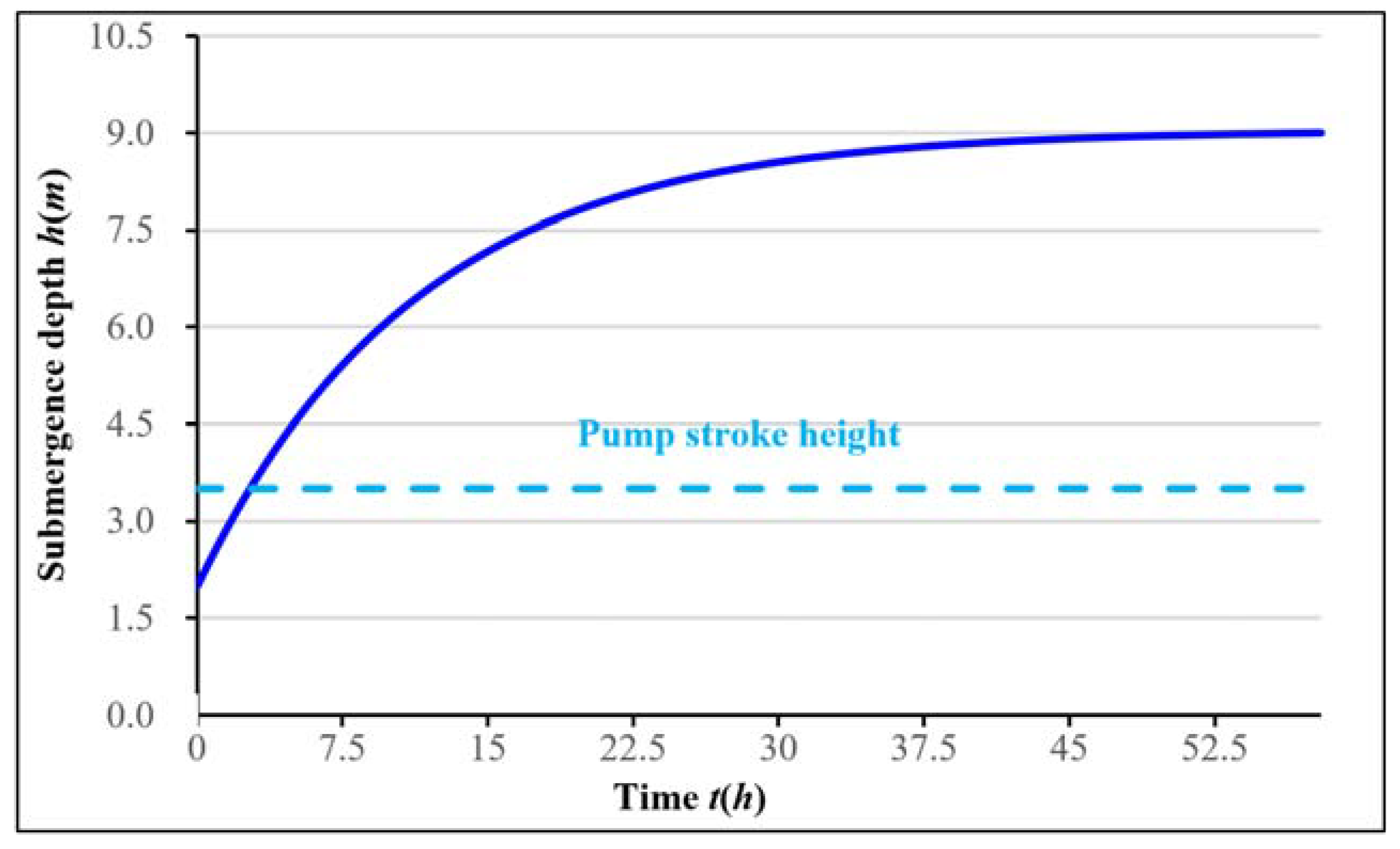
2.2.1. Trends of Change in the Submergence Depth
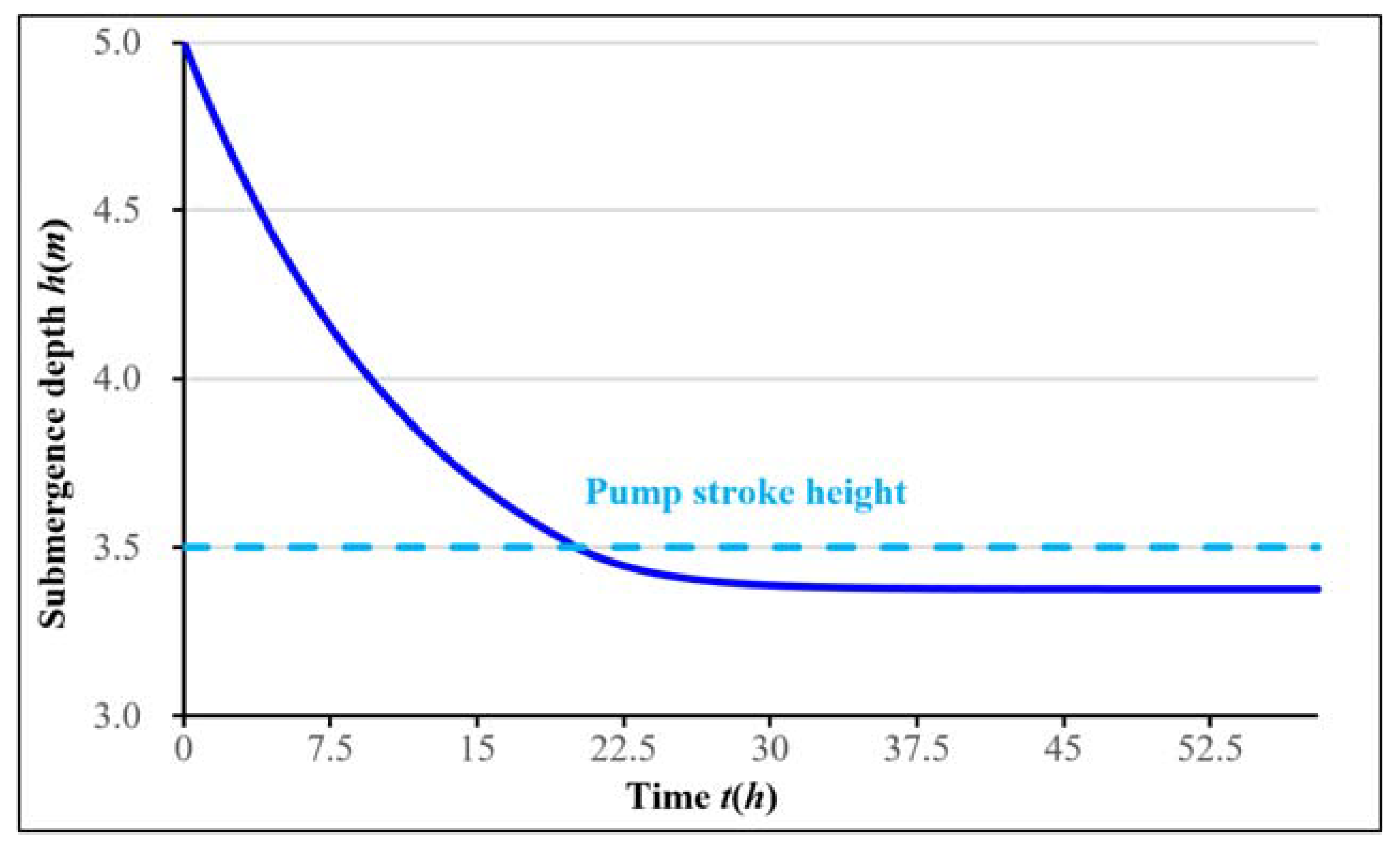
2.2.2. Pumping State Transition
3. Results
3.1. Submergence Depth Models’ Numerical Solutions
3.1.1. Nonlinear-Interpolation Method
3.1.2. Least Squares Curve-Fitting Method
3.2. Error Analysis
3.2.1. Number of Iterations and Error Estimation
3.2.2. Application Analysis of the Nonlinear-Interpolation Method
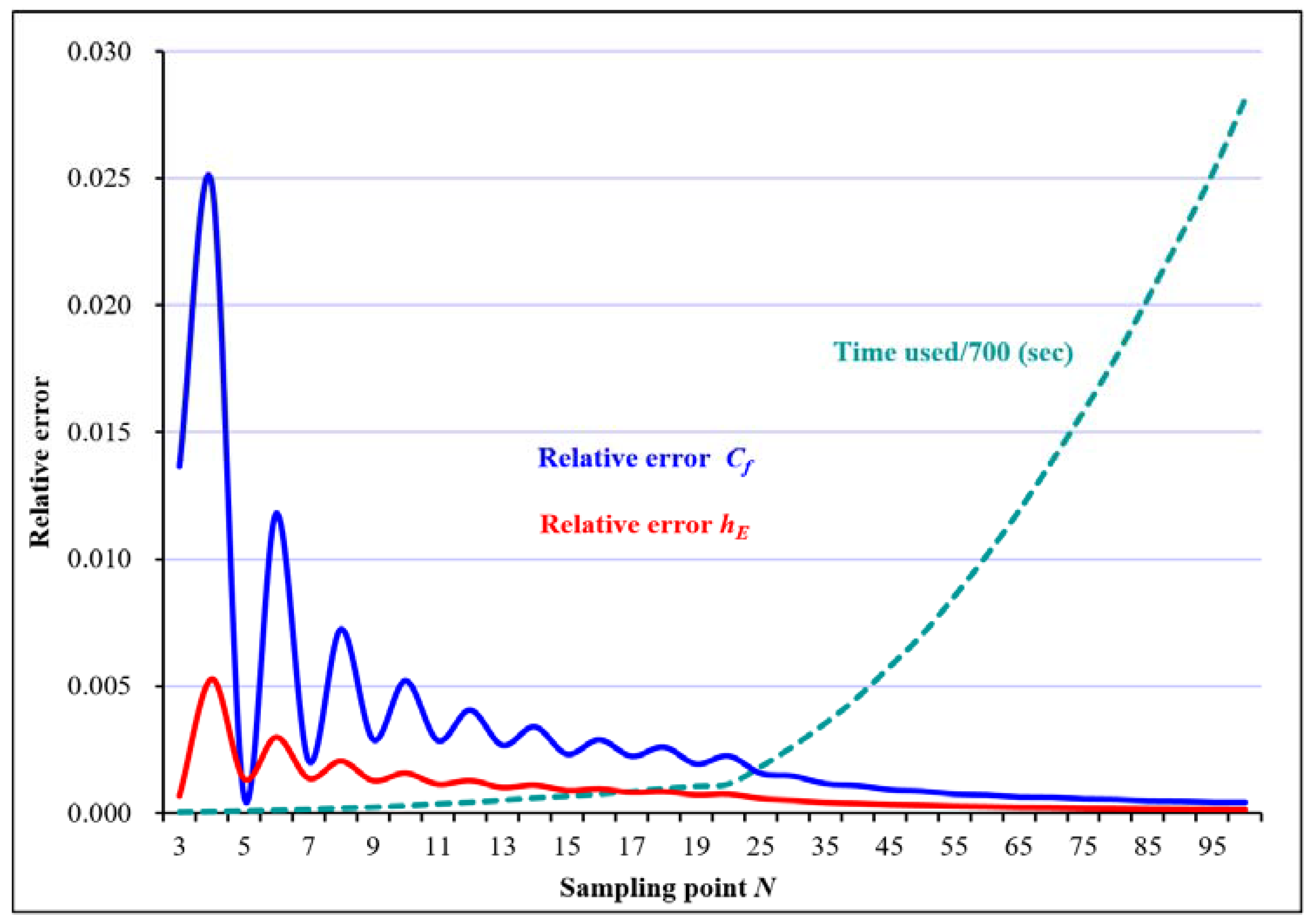
3.2.3. Application Analysis of the Least Squares Curve-Fitting Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, Y.; Song, X.; Li, K.; Yan, X. Hybrid modeling for submergence depth of the pumping well using stochastic configuration networks with random sampling. J. Pet. Sci. Eng. 2021, 208, 109423. [Google Scholar] [CrossRef]
- Xin, L.; Zhu-hong, Z. Research on Depth of Oil Well Moving Liquid Surface Based on Short-term Energy and LSTM. Comput. Mod. 2021, 04, 15–19. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B. Determination of rational submergence depth of oil well pump. Oil Drill. Prod. Technol. 1999, 21, 62–65. [Google Scholar] [CrossRef]
- Qu, B.; Xu, H.; Ma, W.; Xu, Y. Impacts of submergence depth on overall performance of sucker rod pumping system. China Pet. Mach. 2015, 43, 89–93. [Google Scholar] [CrossRef]
- Dong, H.; Wu, T.; Liao, Q.; Chang, Z. Relationship between suitable submergence depth with pump efficiency. Inn. Mong. Petrochem. Ind. 2010, 36, 36–39. [Google Scholar] [CrossRef]
- Lin, X. Analysis of relation between sucker-rod working condition and submergence depth. Petrochem. Ind. Technol. 2016, 23, 99. [Google Scholar] [CrossRef]
- Wu, Q.; Han, L.; Wang, Y.; Fu, S. Influence factors of pump efficiency and determination of pump depth in deep well. Spec. Oil Gas Reserv. 2005, 12, 82–84. [Google Scholar] [CrossRef]
- He, L.; Jiashan, G.; Xueyan, W. Research on Reasonable Intermittent pumping System of oil Pumping Well. Oil Drill. Prod. Technol. 1900, 22, 69–72. [Google Scholar] [CrossRef]
- Fuchao, S.; Xiaohan, P.; Longda, L.; Fanfu, L.; Weina, J. Correction model research on oil well downhole flowrate test based on venturi. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 6664–6667. [Google Scholar] [CrossRef]
- Wang, H.B.; Dong, S.M.; Gan, Q.M.; Xin, H.; Zhu, G. Dynamic parameter simulation model of low-production pumping well and the ways to improve system efficiency. J. Acta Pet. Sin. 2018, 39, 1299–1307. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, X.; Shao, J. Fluid flow through anisotropic and deformable double porosity media with ultra-low matrix permeability: A continuum framework. J. Pet. Sci. Eng. 2021, 200, 108349. [Google Scholar] [CrossRef]
- Liu, T.; Zheng, M.; Song, X.; Wu, Y.; Zhang, R. Submergence depth modeling of oil well reservoirs and applications. J. Pet. Sci. Eng. 2021, 208, 109234. [Google Scholar] [CrossRef]
- Liu, T.; Lou, H.; Gao, X. Research on construction and application method of oil pumping speed control model. J. Xi’an Shiyou Univ. Nat. Sci. Ed. 2022, 37, 125–130. [Google Scholar] [CrossRef]
- Yu, D.; Qi, W.; Deng, S.; Zhang, Y.; Zhang, F.; Wang, X. Submergence forecasting of a submersible plunger pump based on the support vector machine. Acta Pet. Sin. 2011, 32, 53–538. [Google Scholar] [CrossRef]
- Li, X.; Tan, C.D.; Tan, P.F.; Zhang, S.L. Application of ARIMA Model in Time Series Analysisto Predict the Efficiency of Pumping Well Production System. Peak Data Sci. 2017, 6, 41–44. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, Y.; Huang, Y. Research on the Submergence Depth Model of Oil Well Pumping. In Proceedings of the 2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xian, China, 9–11 April 2021; pp. 213–216. [Google Scholar]
- Liu, T.; Dong, Y. Research on numerical solution of one-sided monotonic function dichotomy. J. Phys. Conf. Ser. 2021, 2012. [Google Scholar] [CrossRef]
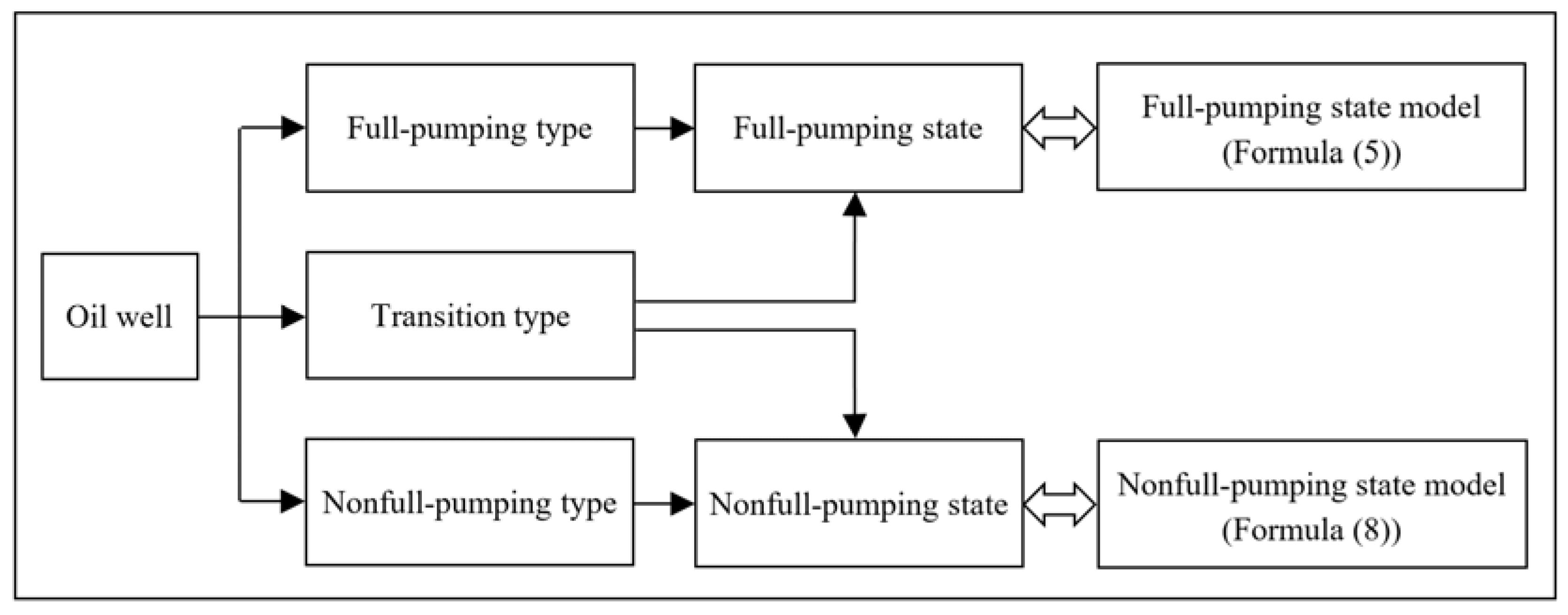
| Oil Well Type | Condition | Pumping Model |
|---|---|---|
| Full-pumping type | Full-pumping state Model (5) | |
| Transition type | 1. If the size relationship between h and hp remains unchanged, keep the original state model. | |
| Otherwise, take and restart the timing: | ||
| 2. When condition becomes , use Model (5); | ||
| 3. When condition becomes , use Model (8). | ||
| Nonfull-pumping type | Nonfull-pumping state Model (8) | |
| ε | Error Cf | Error hE |
|---|---|---|
| 1.00 × 10−01 | 2.31 × 10−03 | 7.29 × 10+02 |
| 1.00 × 10−02 | 1.93 × 10−04 | 3.16 × 10+01 |
| 1.00 × 10−03 | 3.64 × 10−05 | 6.22 × 10+00 |
| 1.00 × 10−04 | 8.73 × 10−07 | 1.48 × 10−01 |
| 1.00 × 10−05 | 2.02 × 10−07 | 3.43 × 10−02 |
| 1.00 × 10−06 | 2.17 × 10−08 | 3.68 × 10−03 |
| 1.00 × 10−07 | 2.08 × 10−09 | 3.52 × 10−04 |
| 1.00 × 10−08 | 3.27 × 10−10 | 5.54 × 10−05 |
| 1.00 × 10−09 | 2.03 × 10−11 | 3.44 × 10−06 |
| 1.00 × 10−10 | 1.14 × 10−12 | 2.00 × 10−07 |
| 1.00 × 10−11 | 1.15 × 10−13 | 2.00 × 10−08 |
| 1.00 × 10−12 | 1.36 × 10−14 | 2.30 × 10−09 |
| h0 ± Δh0 | h1 ± Δh1 | h2 ± Δh2 | Relative Error Cf | Relative Error hE |
|---|---|---|---|---|
| + | + | + | 2.71 × 10−12 | 9.88 × 10−03 |
| − | − | − | 2.71 × 10−12 | 9.88 × 10−03 |
| 0 | + | − | 2.05 × 10−01 | 1.29 × 10−01 |
| 0 | − | + | 2.02 × 10−01 | 1.92 × 10−01 |
| No | h0 ± Δh0 | hi ± Δhi | Relative Error Cf | Relative Error hE | |||
|---|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | 2.72 × 10−12 | 9.88 × 10−03 |
| 2 | − | − | − | − | − | 2.72 × 10−12 | 9.88 × 10−03 |
| 3 | 0 | − | + | − | + | 1.18 × 10−01 | 1.03 × 10−01 |
| 4 | 0 | + | − | + | − | 1.18 × 10−01 | 8.11 × 10−02 |
| 5 | 0 | + | − | − | + | 1.67 × 10−01 | 1.49 × 10−01 |
| 6 | 0 | − | + | + | − | 1.63 × 10−01 | 1.04 × 10−01 |
| 7 | 0 | + | + | − | − | 2.20 × 10−01 | 2.06 × 10−01 |
| 8 | 0 | − | − | + | + | 2.11 × 10−01 | 2.06 × 10−01 |
| No. | h0 ± Δh0 | hi ± Δhi | Relative Error Cf | Relative Error hE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | + | + | + | + | + | + | + | 8.56 × 10−11 | 9.88 × 10−03 |
| 2 | − | − | − | − | − | − | − | − | − | − | − | − | 2.86 × 10−11 | 9.88 × 10−03 |
| 3 | 0 | + | − | + | − | + | − | + | − | + | − | + | 7.79 × 10−03 | 9.76 × 10−03 |
| 4 | 0 | − | + | − | + | − | + | − | + | − | + | − | 7.79 × 10−03 | 9.91 × 10−03 |
| 5 | 0 | + | + | − | − | + | + | − | − | + | + | − | 1.99 × 10−02 | 1.48 × 10−02 |
| 6 | 0 | + | + | + | − | − | − | + | + | + | − | − | 7.94 × 10−02 | 5.66 × 10−02 |
| 7 | 0 | + | + | + | + | + | 0 | − | − | − | − | − | 1.95 × 10−01 | 1.28 × 10−01 |
| 8 | 0 | − | − | − | − | − | 0 | + | + | + | + | + | 1.86 × 10−01 | 1.80 × 10−01 |
| Sampling Point N | Relative Error Cf | Relative Error hE | Time Used (s) |
|---|---|---|---|
| 3 | 1.37 × 10−02 | 6.78 × 10−04 | 0.02 |
| 4 | 2.48 × 10−02 | 5.28 × 10−03 | 0.03 |
| 5 | 6.75 × 10−04 | 1.35 × 10−03 | 0.05 |
| 6 | 1.18 × 10−02 | 2.99 × 10−03 | 0.08 |
| 7 | 2.07 × 10−03 | 1.37 × 10−03 | 0.10 |
| 8 | 7.26 × 10−03 | 2.05 × 10−03 | 0.13 |
| 9 | 2.90 × 10−03 | 1.28 × 10−03 | 0.16 |
| 10 | 5.23 × 10−03 | 1.57 × 10−03 | 0.19 |
| 11 | 2.87 × 10−03 | 1.13 × 10−03 | 0.24 |
| 12 | 4.07 × 10−03 | 1.28 × 10−03 | 0.29 |
| 13 | 2.68 × 10−03 | 1.01 × 10−03 | 0.35 |
| 14 | 3.41 × 10−03 | 1.11 × 10−03 | 0.40 |
| 15 | 2.33 × 10−03 | 8.85 × 10−04 | 0.46 |
| 16 | 2.91 × 10−03 | 9.48 × 10−04 | 0.51 |
| 17 | 2.25 × 10−03 | 8.14 × 10−04 | 0.59 |
| 18 | 2.62 × 10−03 | 8.51 × 10−04 | 0.66 |
| 19 | 1.95 × 10−03 | 7.24 × 10−04 | 0.74 |
| 20 | 2.27 × 10−03 | 7.55 × 10−04 | 0.79 |
| 25 | 1.58 × 10−03 | 5.69 × 10−04 | 1.27 |
| 30 | 1.48 × 10−03 | 5.03 × 10−04 | 1.84 |
| 35 | 1.17 × 10−03 | 4.16 × 10−04 | 2.47 |
| 40 | 1.10 × 10−03 | 3.78 × 10−04 | 3.19 |
| 45 | 9.28 × 10−04 | 3.28 × 10−04 | 4.04 |
| 50 | 8.78 × 10−04 | 3.03 × 10−04 | 4.92 |
| 55 | 7.63 × 10−04 | 2.70 × 10−04 | 5.98 |
| 60 | 7.31 × 10−04 | 2.53 × 10−04 | 7.11 |
| 65 | 6.41 × 10−04 | 2.28 × 10−04 | 8.33 |
| 70 | 6.28 × 10−04 | 2.17 × 10−04 | 9.67 |
| 75 | 5.64 × 10−04 | 1.99 × 10−04 | 11.07 |
| 80 | 5.47 × 10−04 | 1.90 × 10−04 | 12.56 |
| 85 | 4.94 × 10−04 | 1.75 × 10−04 | 14.20 |
| 90 | 4.84 × 10−04 | 1.69 × 10−04 | 15.90 |
| 95 | 4.44 × 10−04 | 1.57 × 10−04 | 17.65 |
| 100 | 4.37 × 10−04 | 1.52 × 10−04 | 19.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Tian, X.; Liu, L.; Gu, X.; Zhao, Y.; Zhang, L.; Song, X. Modeling the Submergence Depth of Oil Well States and Its Applications. Appl. Sci. 2022, 12, 12373. https://doi.org/10.3390/app122312373
Liu T, Tian X, Liu L, Gu X, Zhao Y, Zhang L, Song X. Modeling the Submergence Depth of Oil Well States and Its Applications. Applied Sciences. 2022; 12(23):12373. https://doi.org/10.3390/app122312373
Chicago/Turabian StyleLiu, Tianshi, Xue Tian, Liwen Liu, Xiaoyu Gu, Yun Zhao, Liumei Zhang, and Xinai Song. 2022. "Modeling the Submergence Depth of Oil Well States and Its Applications" Applied Sciences 12, no. 23: 12373. https://doi.org/10.3390/app122312373
APA StyleLiu, T., Tian, X., Liu, L., Gu, X., Zhao, Y., Zhang, L., & Song, X. (2022). Modeling the Submergence Depth of Oil Well States and Its Applications. Applied Sciences, 12(23), 12373. https://doi.org/10.3390/app122312373






