Vehicle Load Identification on Orthotropic Steel Box Beam Bridge Based on the Strain Response Area
Abstract
1. Introduction
2. Identification Method
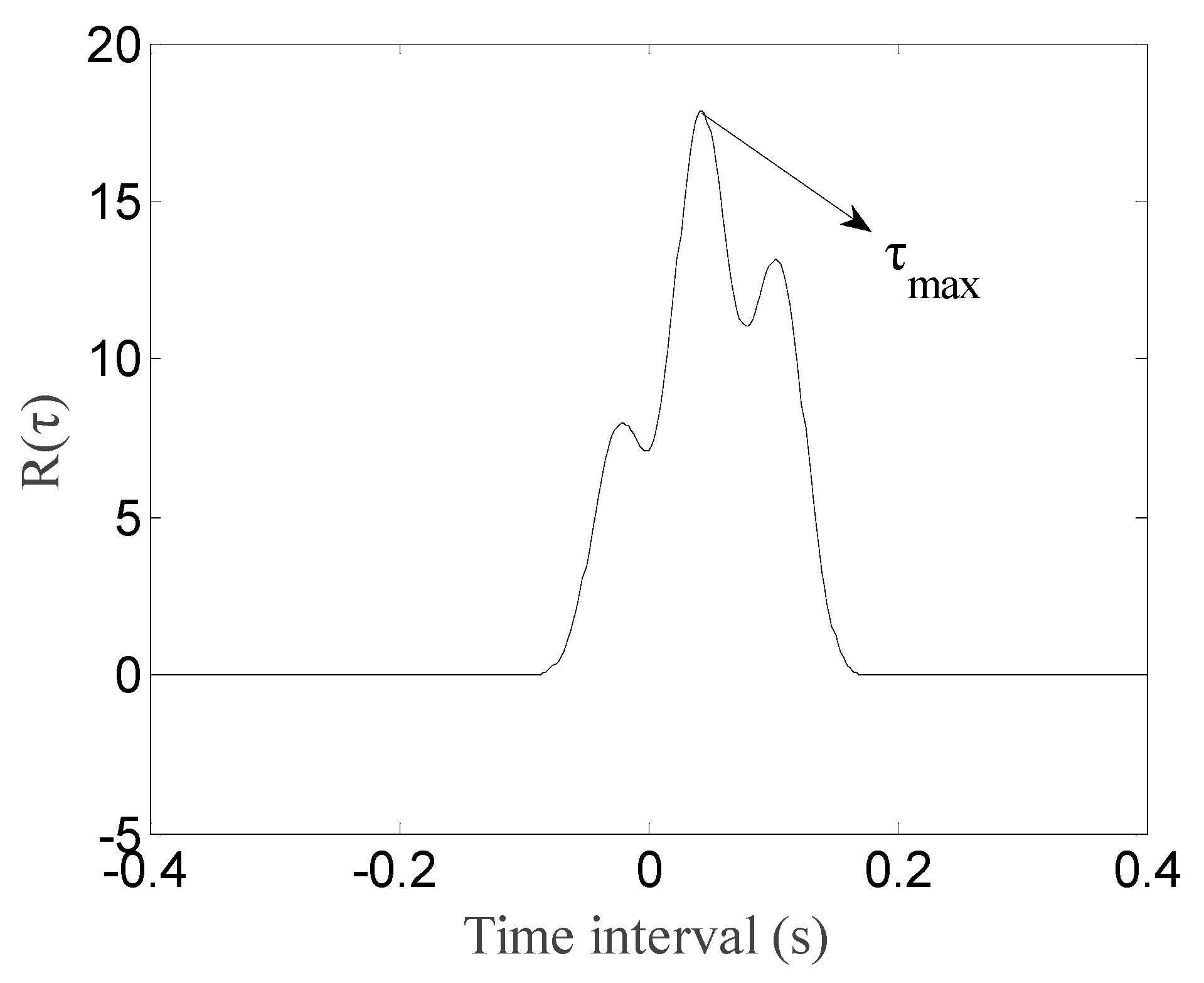
2.1. Identification of Vehicle Speed
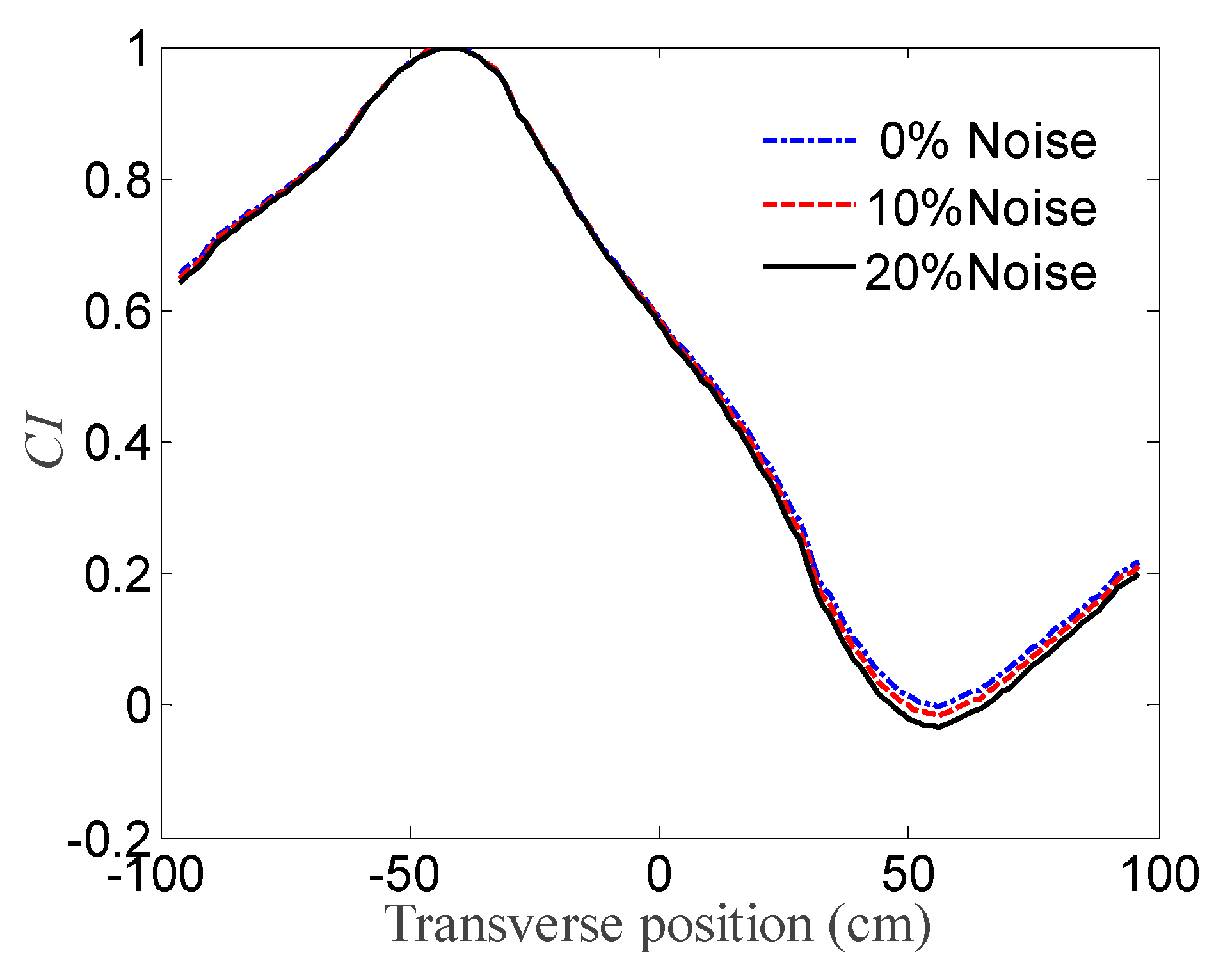
2.2. Identification of the Transverse Position
2.3. Identification of Gross Vehicle Weight
3. Numerical Simulation
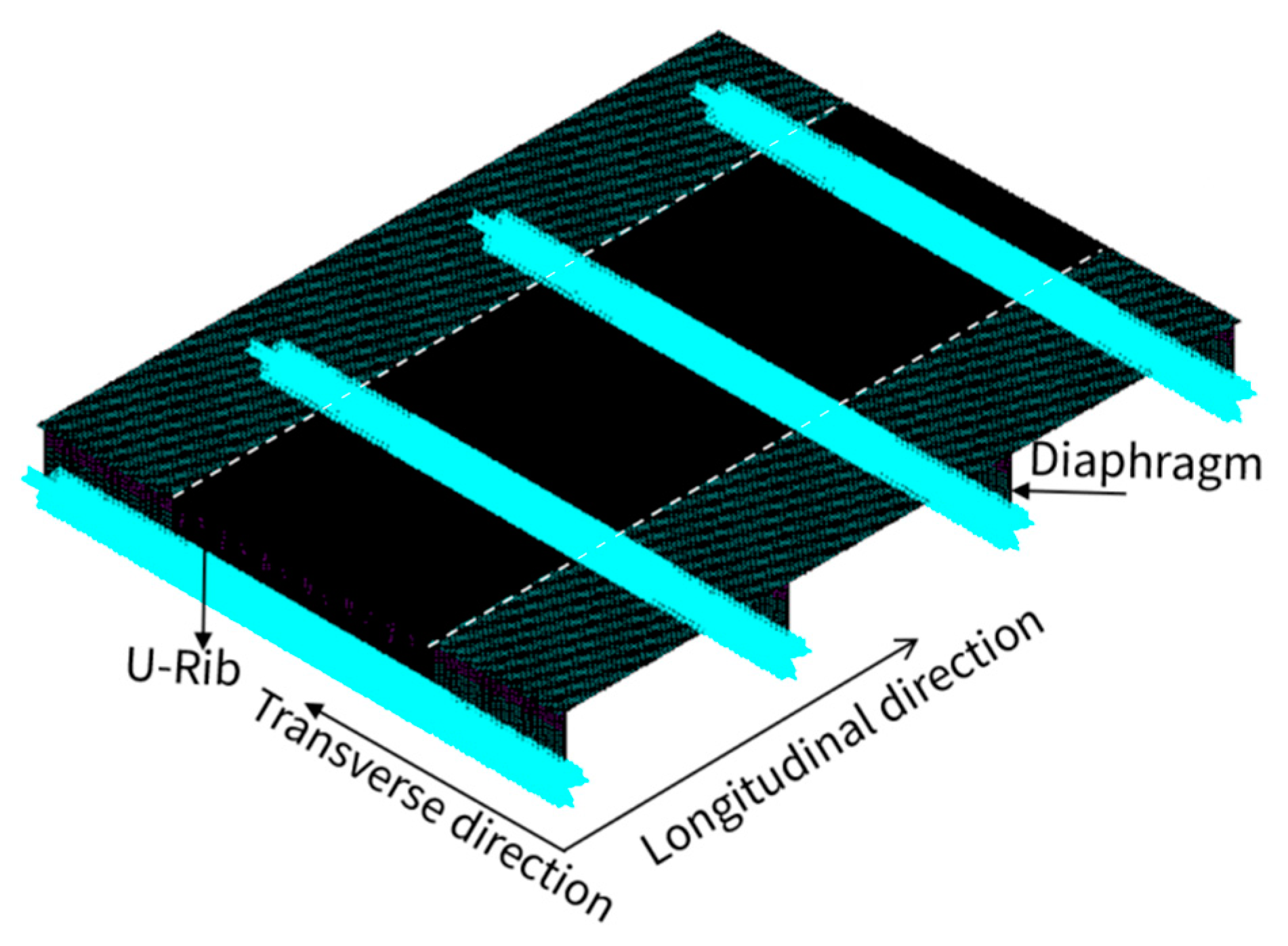
3.1. Model Introduction
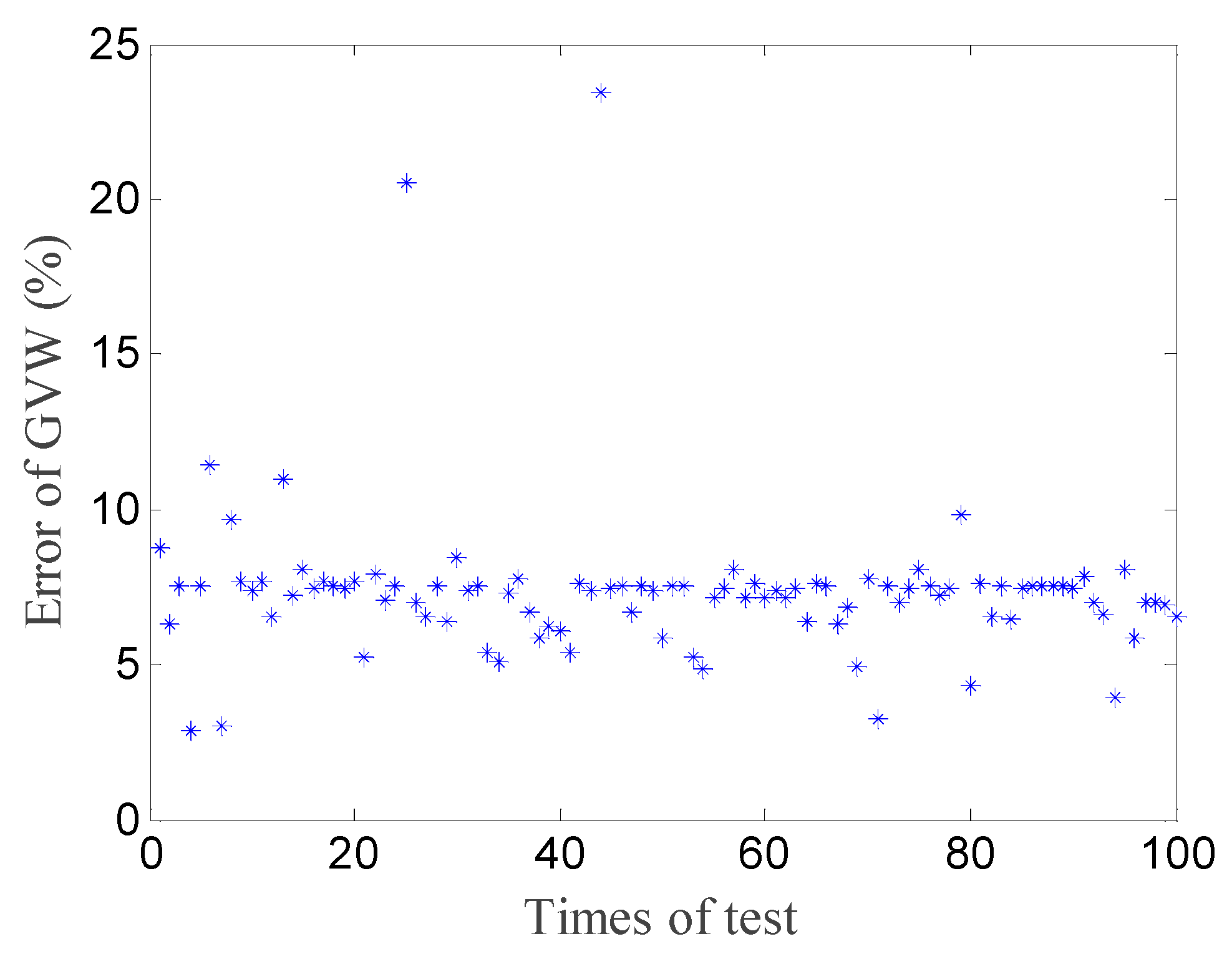
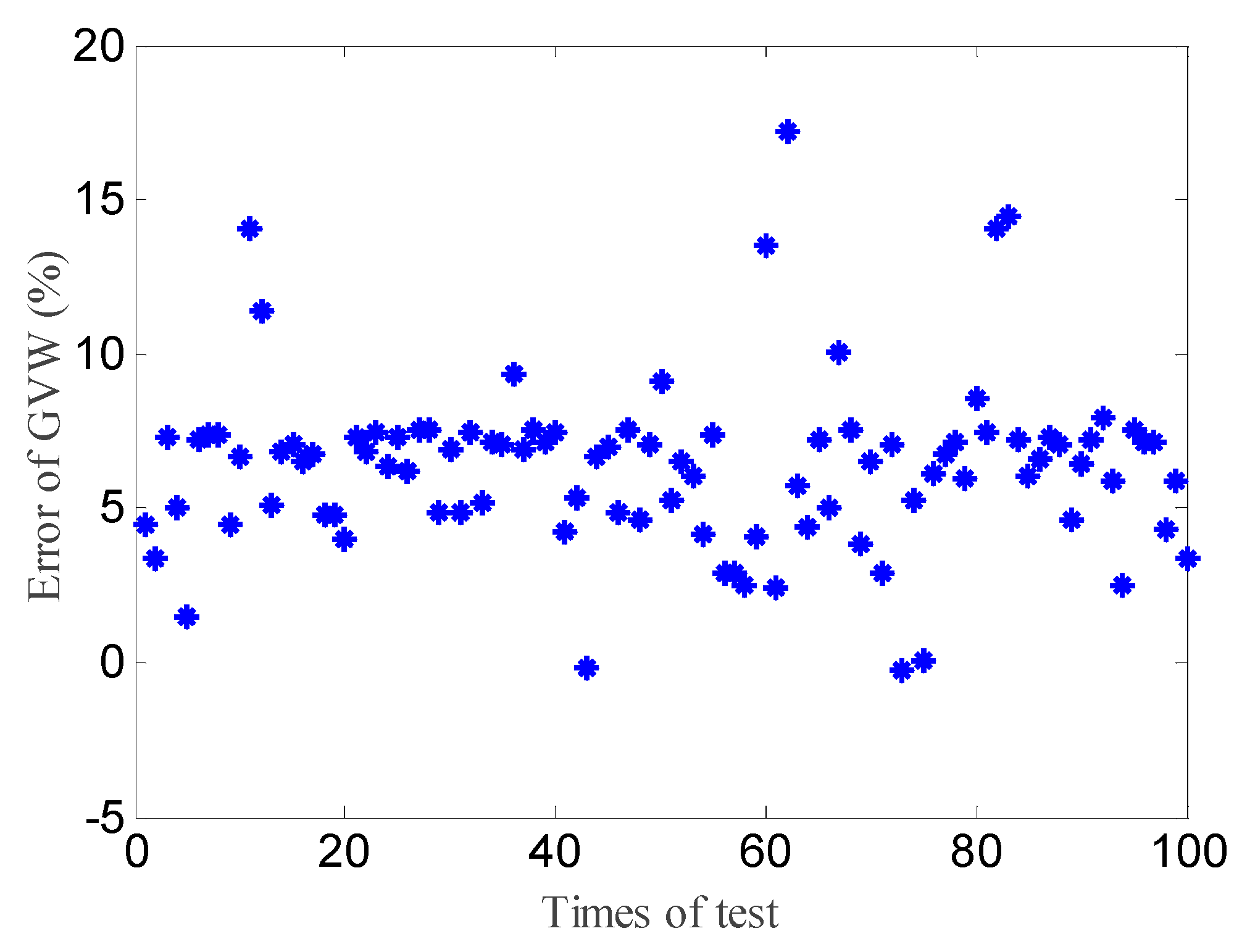
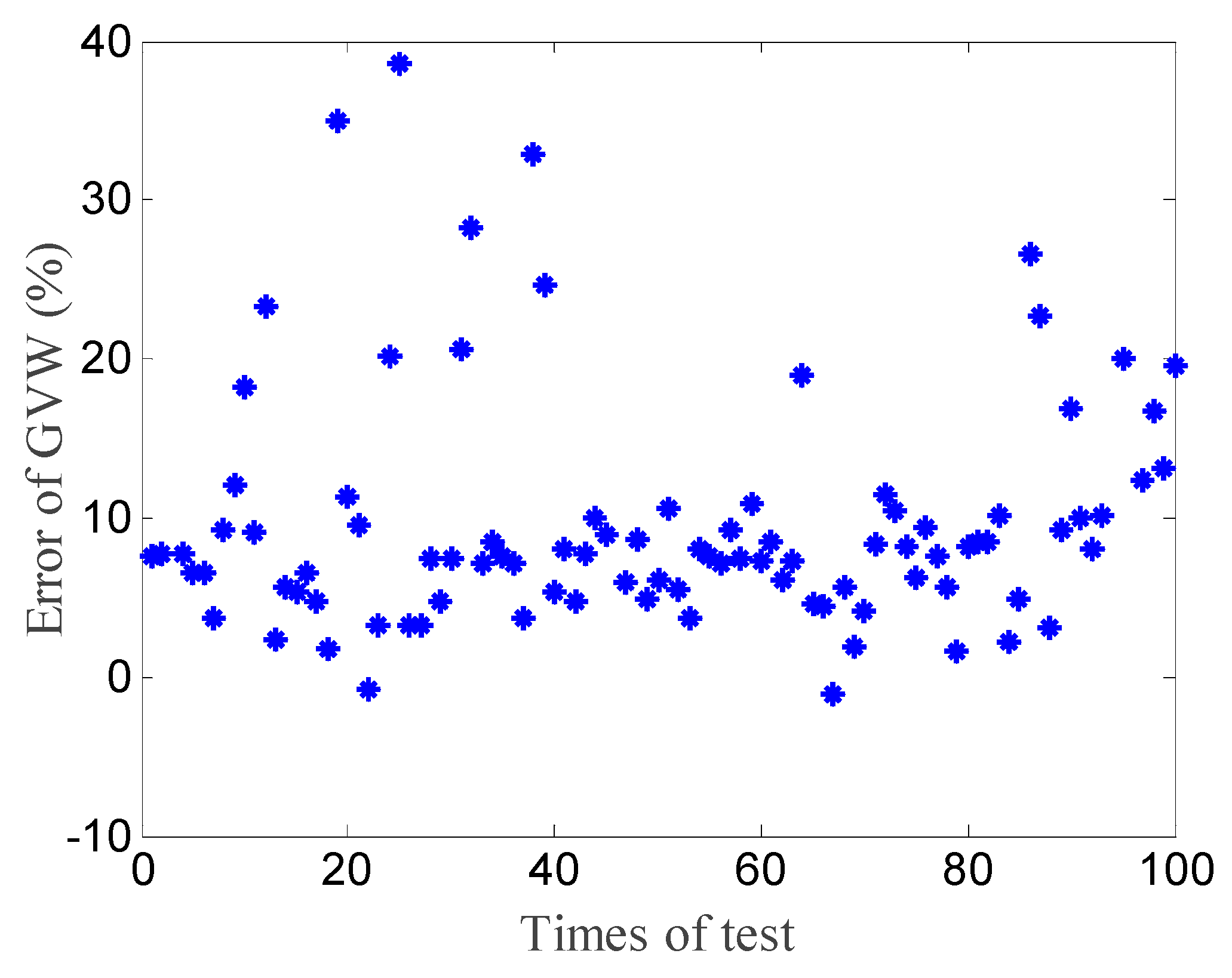
3.2. Gross Weight Identification
- (1)
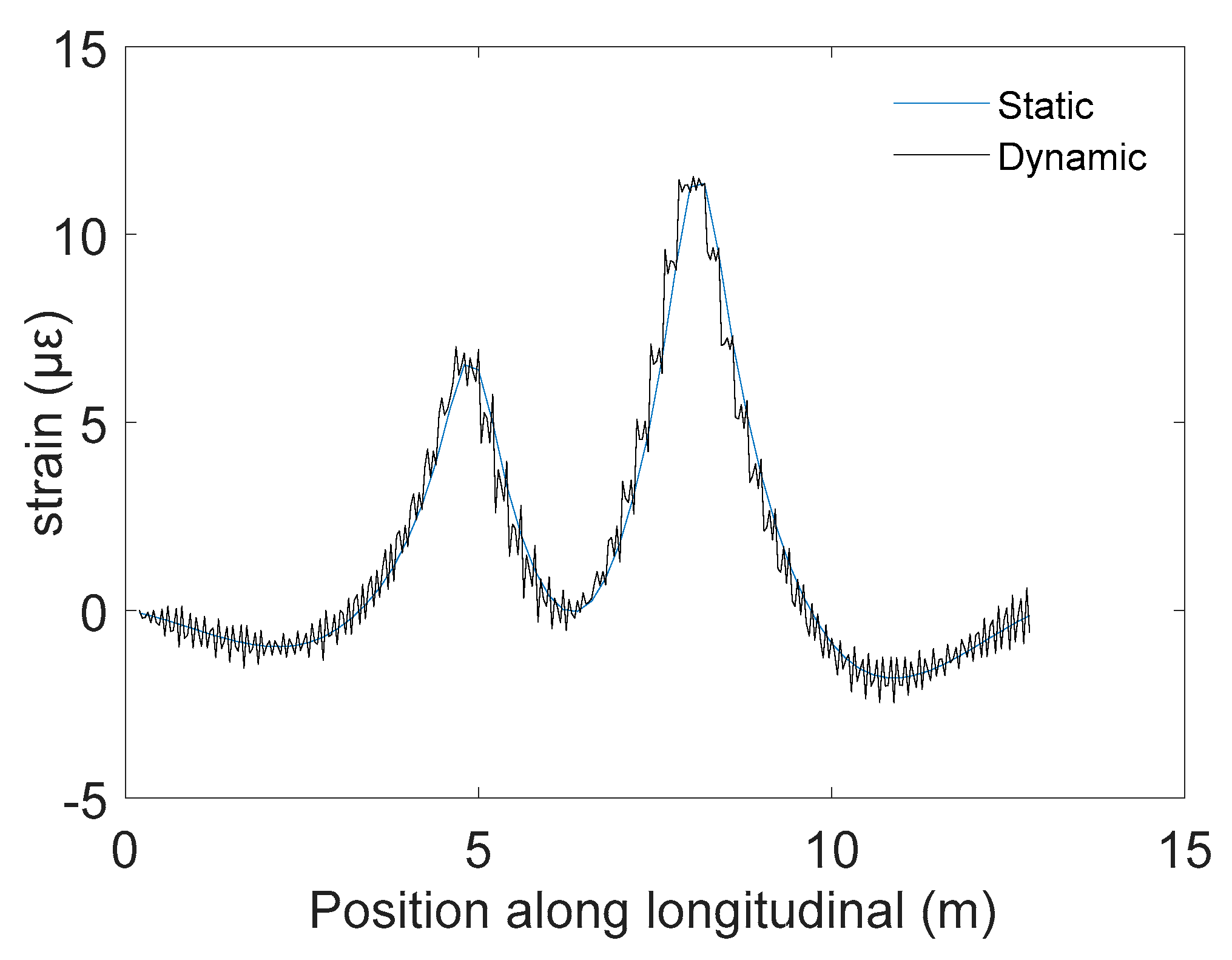
- Calibration of the strain response area
- (2)
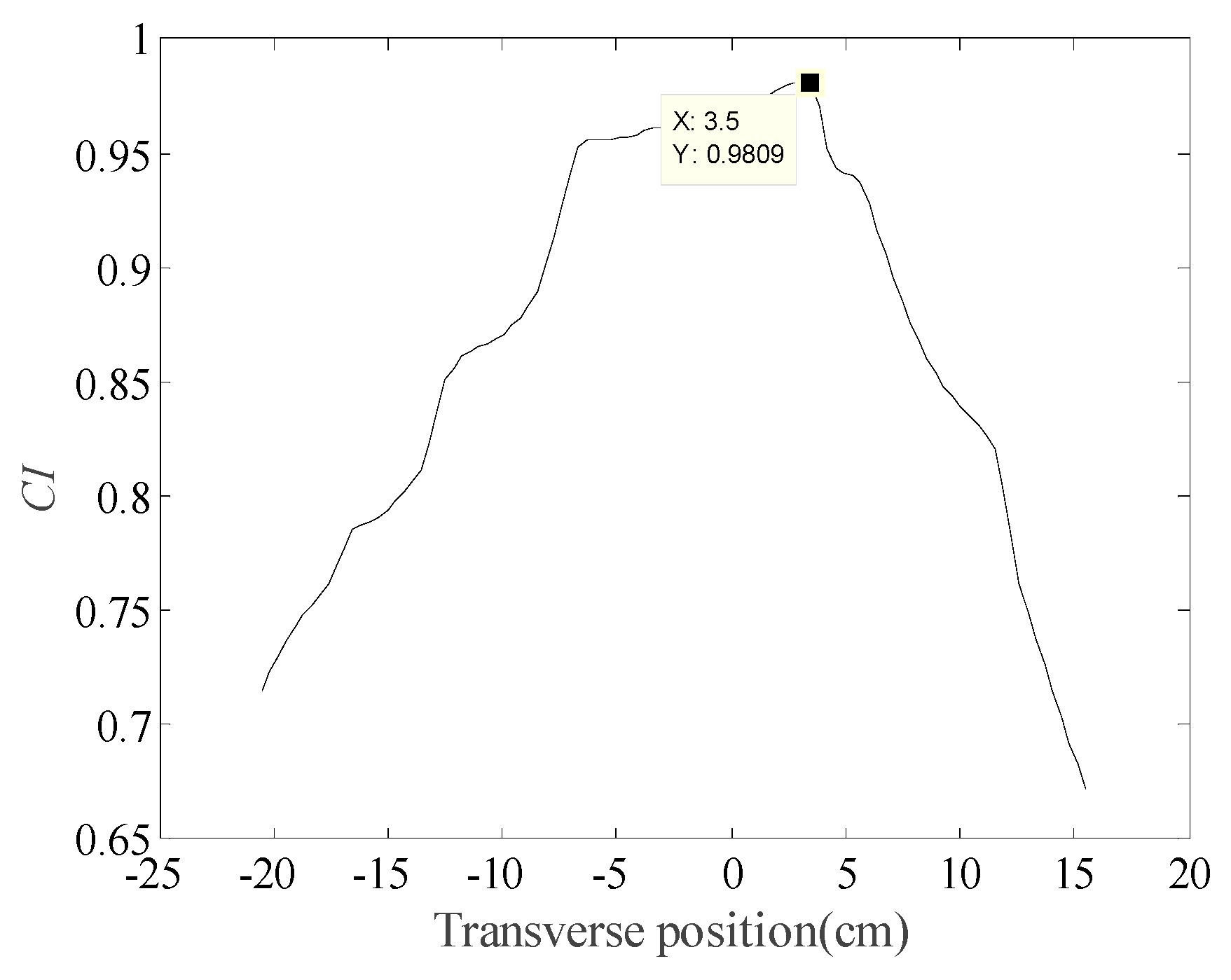
- Locating the transverse position
- (3)
- Evaluating the gross vehicle weight
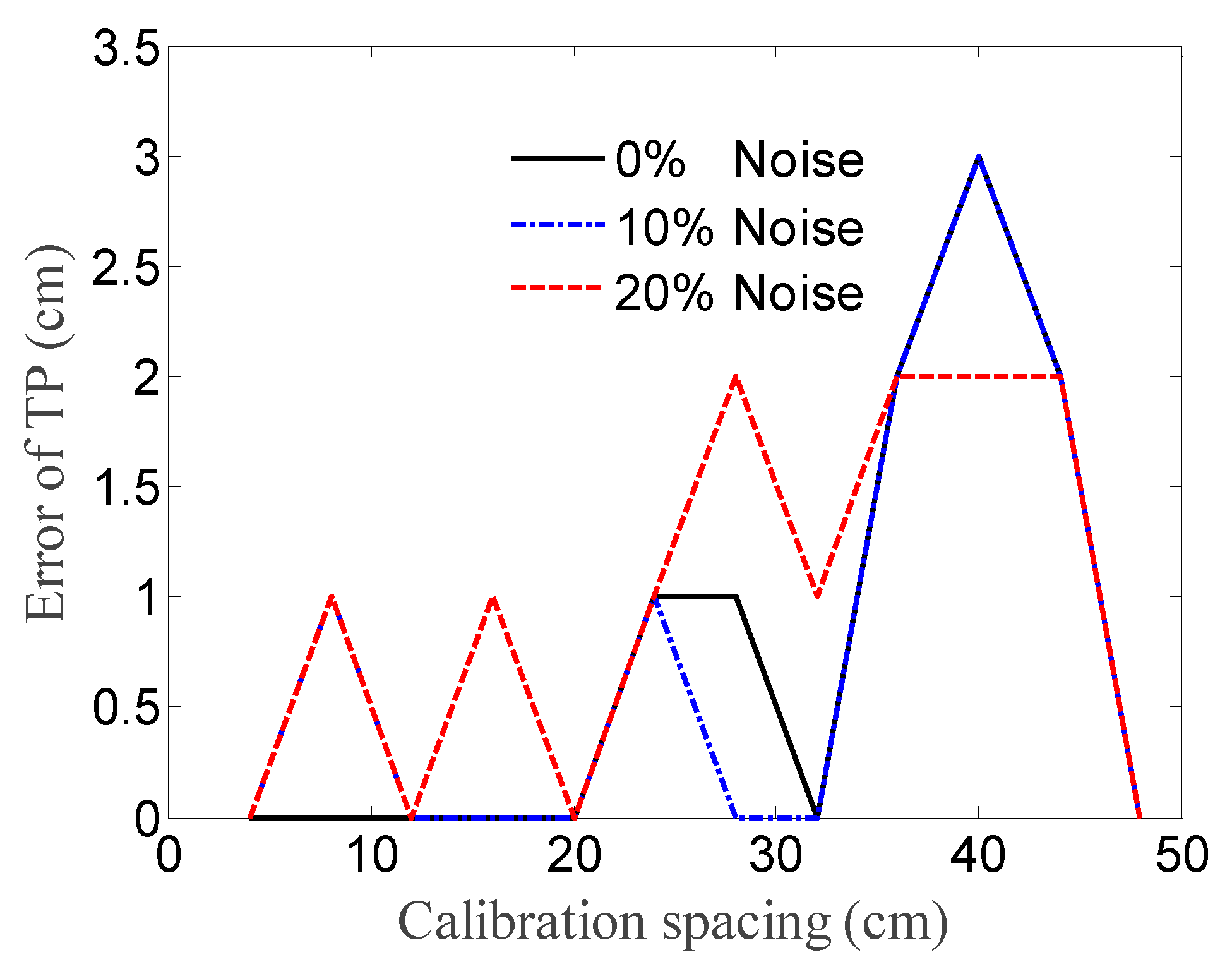
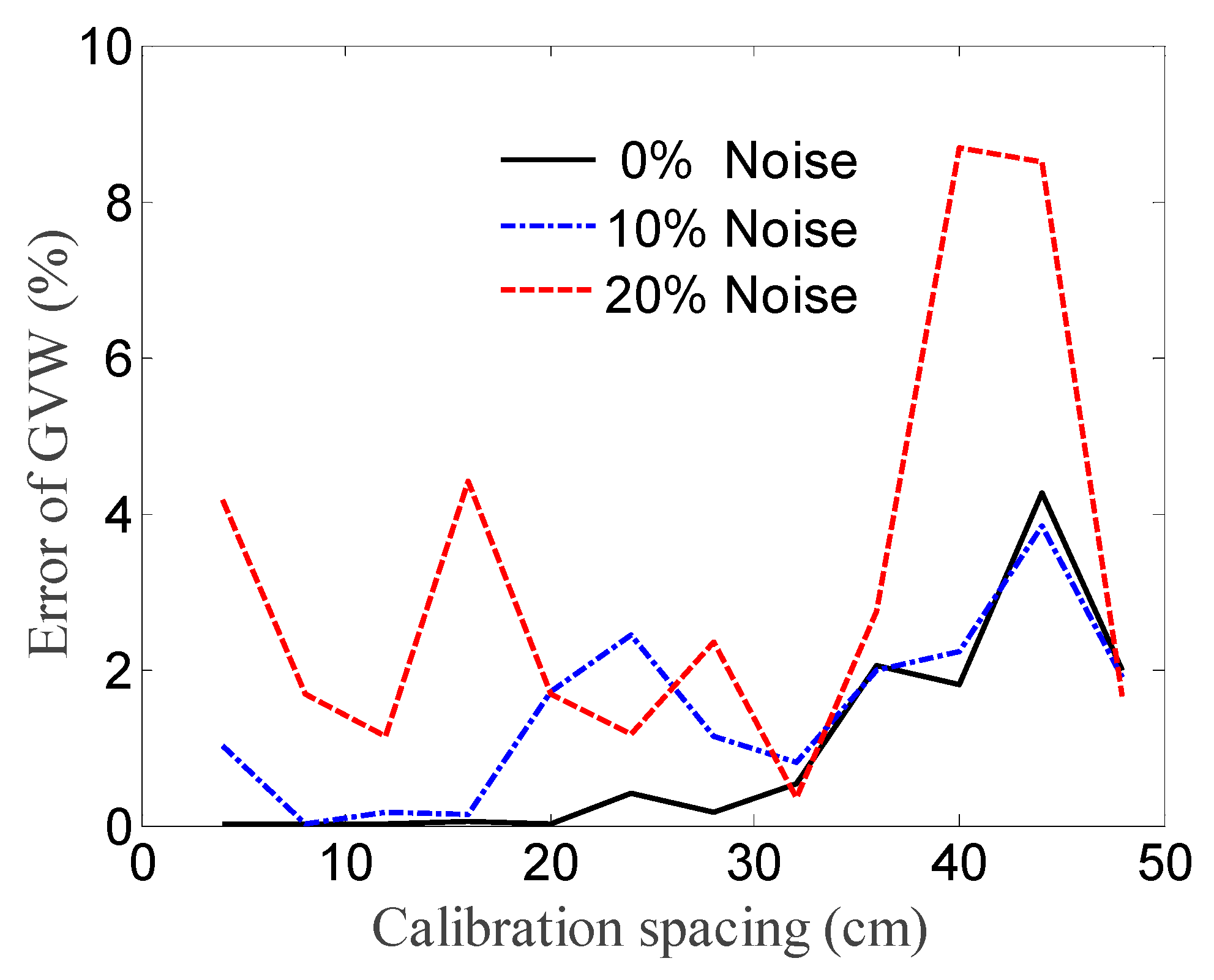
3.3. Influence of Calibration Spacing
- (1)
- Constant calibration spacing
- (2)
- Variable calibration spacing
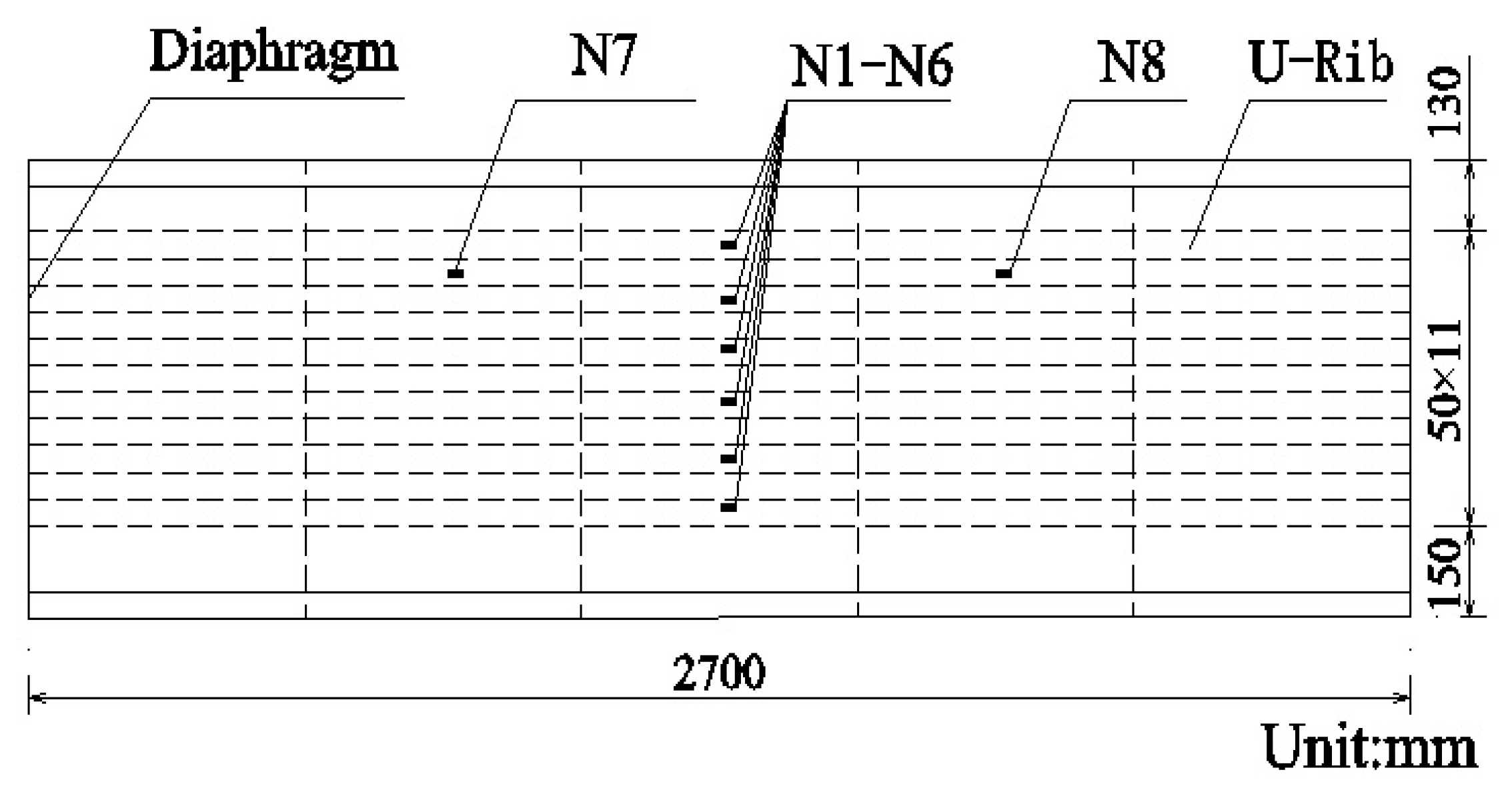
4. Experimental Test
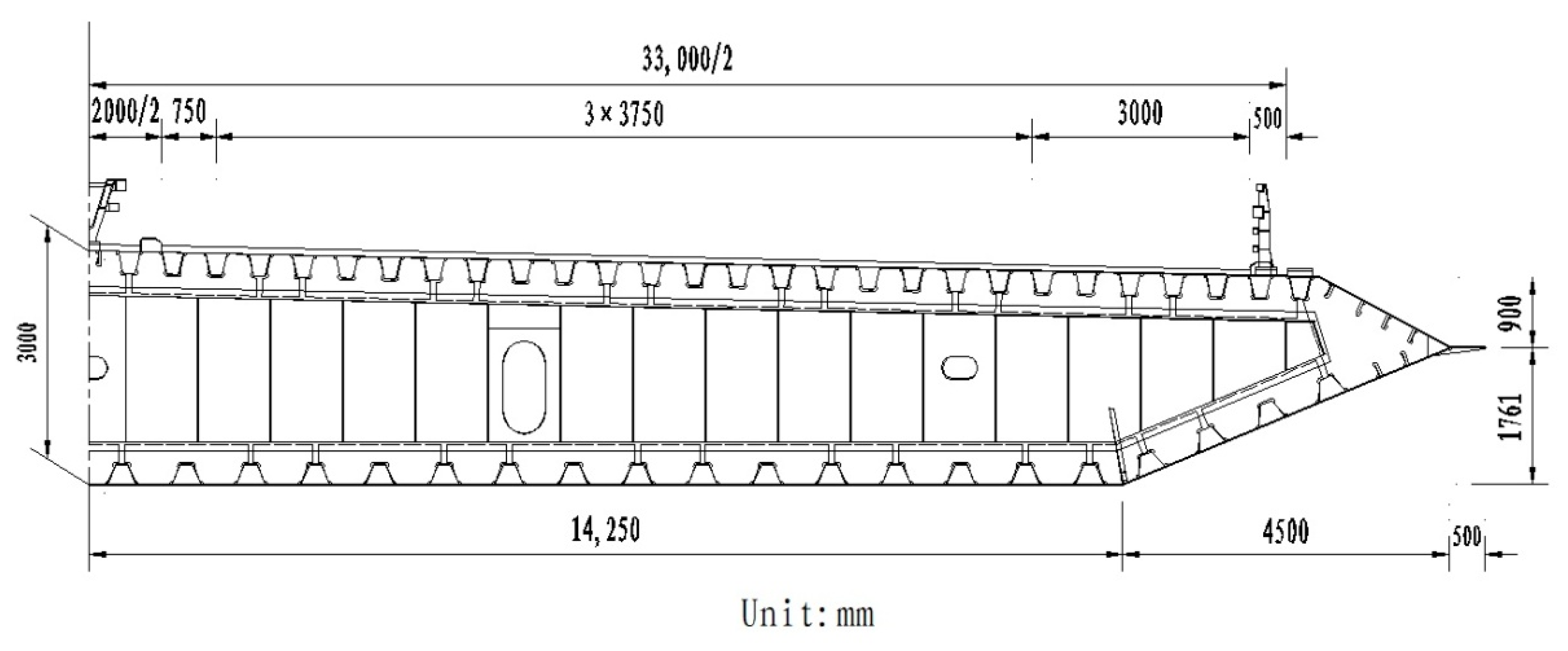
4.1. Experimental Model
4.2. Load Calibration
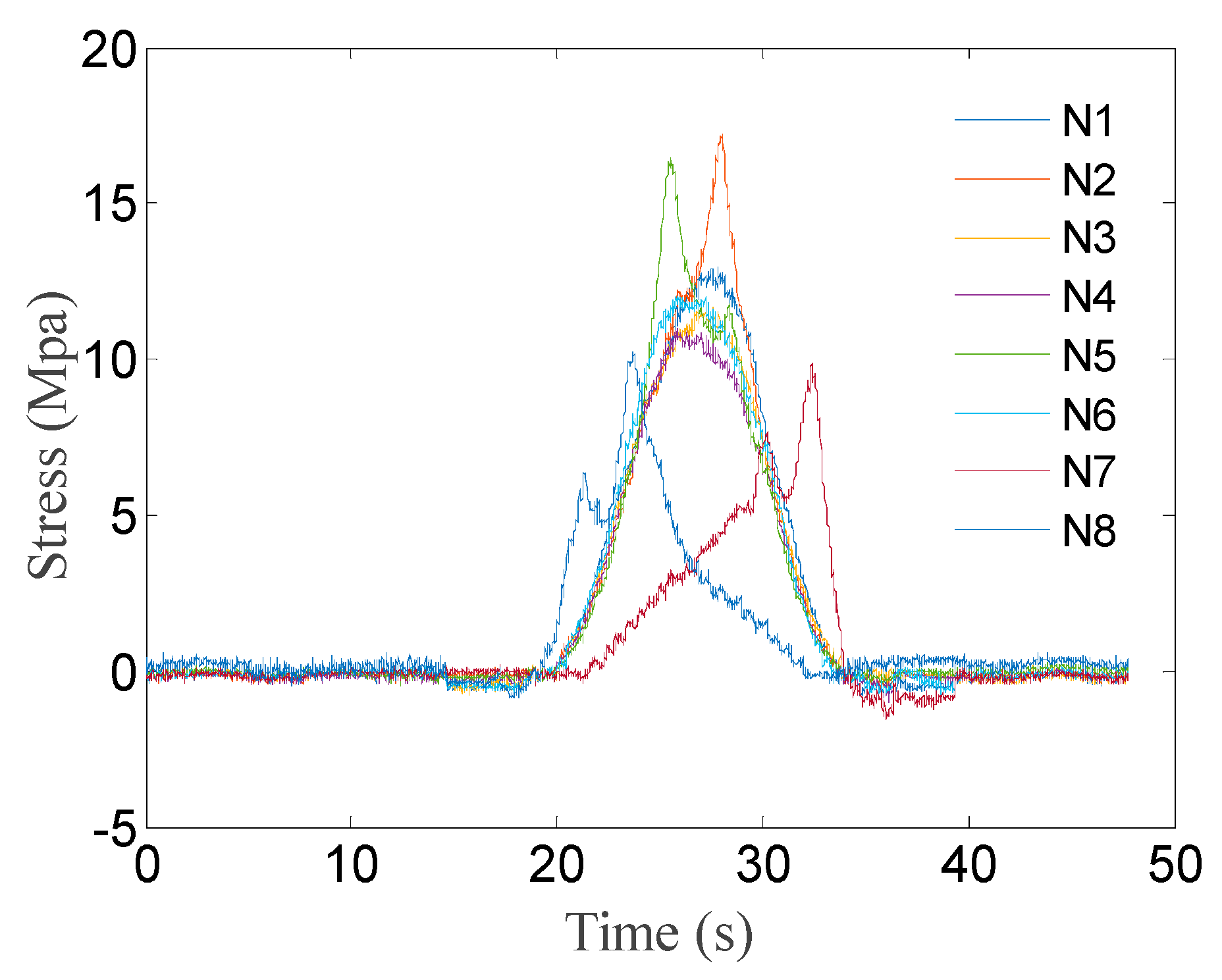
4.3. Load Identification
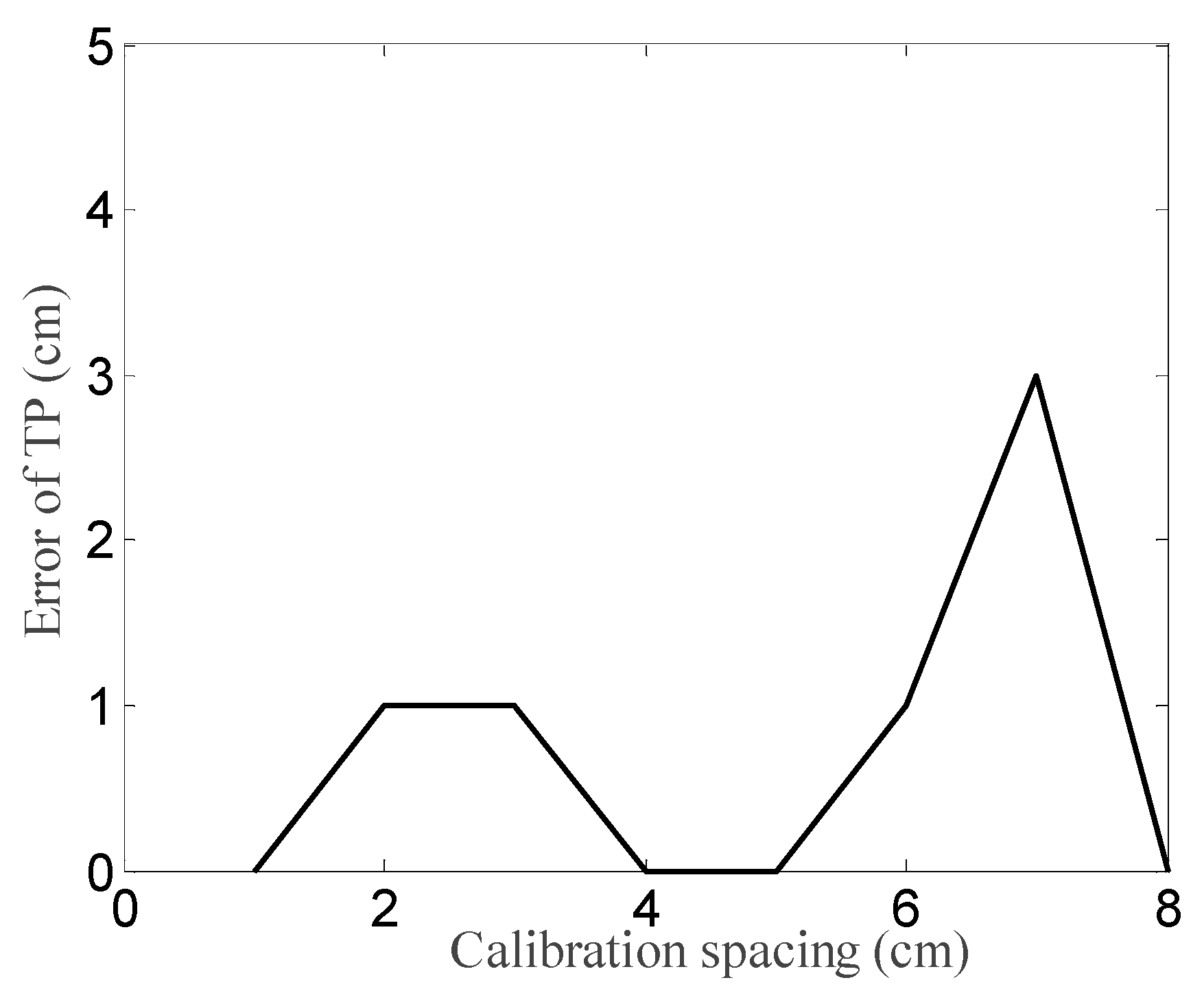
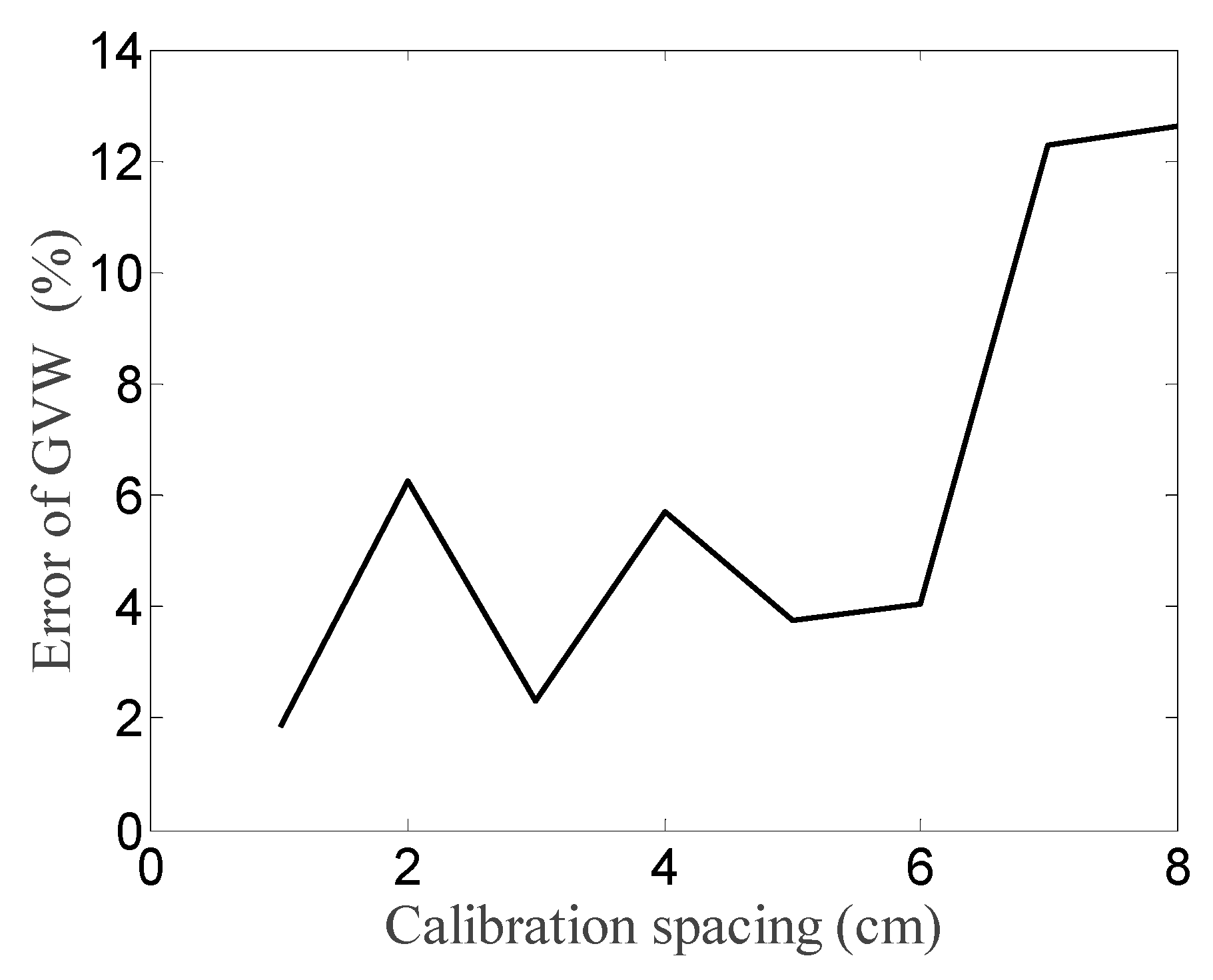
4.4. Effect of Calibration Spacing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.S.; Zhao, H.; Zhu, C.Y.; Li, J.H. Extre value prediction of effect of simply supported beam bridge under heavy vehicle load. J. Huazhong Univ. Sci. Technol. 2021, 49, 95–100. [Google Scholar]
- Sujon, M.; Dai, F. Application of weigh-in-motion technologies for pavement and bridge response monitoring: State-of-the-art review. Autom. Constr. 2021, 130, 103844. [Google Scholar] [CrossRef]
- Ge, L.F.; Dan, D.H.; Li, H. An accurate and robust monitoring method of full-bridge traffic load distribution based on YOLO-v3 machine vision. Struct. Control Health Monit. 2020, 27, e2636. [Google Scholar] [CrossRef]
- Martini, A.; Tronci, E.M.; Feng, M.Q.; Leung, R.Y. A computer vision-based method for bridge model updating using displacement influence lines. Eng. Struct. 2022, 259, 114129. [Google Scholar] [CrossRef]
- Wen, J.S.; Wu, T.; Ni, Z.J.; Zhang, L.L. Influence of common factors on vehicle bridge coupling vibration. Vibroeng. Procedia 2021, 36, 60–65. [Google Scholar] [CrossRef]
- Chen, S.S.; Luo, H.; Song, Y. Studies on Vibration Response of the Continuous Girder Highway Bridge under Horizontal Multi-Vehicle Loads. IOP Conf. Ser. Earth Environ. Sci. 2020, 455, 012133. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, L.B.; Zhao, K.; Yang, H.L. Development of a novel piezoelectric sensing system for pavement dynamic load identification. Sensors 2019, 19, 4668. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.B.; Ren, W.X.; Wan, H.P. Bridge weigh-in-motion and its optimization algorithm based on dynamic strain. J. Vib. Shock 2013, 32, 116–120. [Google Scholar]
- Ojio, T.; Carey, C.H.; Obrien, E.J.; Doherty, C.; Taylor, S.E. Contactless bridge weigh-in-motion. J. Bridge Eng. 2016, 21, 4016032. [Google Scholar] [CrossRef]
- Ren, W.X.; Zuo, X.H.; Wang, N.B.; He, L.X. Review of Non-pavement Bridge Weigh-in-motion. China J. Highw. Transp. 2014, 27, 45–53. [Google Scholar]
- Zhang, Q.H.; Li, J.; Guo, Y.W.; Yuan, D.Y.; Bu, Y.Z. Fatigue failure modes and resistance evaluation of orthotropic steel bridge deck structural system. China Civ. Eng. J. 2019, 52, 71–81. [Google Scholar]
- Ojio, T.; Yamada, K. Bridge weigh-in-motion systems using stringers of plate girder bridges. In Proceedings of the 3rd International Conference on Weigh-In-Motion (ICWIM3), Orlando, FL, USA, 13–15 May 2002; pp. 209–218. [Google Scholar]
- Chen, W.Z.; Yang, G. Theory and case study of vehicle load identification based on BWIM of steel truss bridge. Stahlbau 2013, 82, 214–222. [Google Scholar] [CrossRef]
- Zhang, L.W.; Wang, J.Q.; Chen, N.; Sun, H.X. Theoretical and experimental study on a bridge weigh-in-motion iterative algorithm. J. Vib. Shock 2021, 40, 171–176. [Google Scholar]
- Zhao, H.; Uddin, N.; Shao, X.D.; Zhu, P.; Tan, C.J. Field-calibrated influence lines for improved axle weight identification with a bridge weigh-in-motion system. Struct. Infrastruct. Eng. 2015, 11, 721–743. [Google Scholar] [CrossRef]
- Quilligan, M.; Karoumi, R. Bridge Weigh-in-Motion: Development of a 2-D multi-vehicle algorithm. Trita-BKN Bull. 2003, 69, A-144. [Google Scholar]
- Zhao, H.; Uddin, N.; O’Brien, E.J.; Shao, X.; Zhu, P. Identification of Vehicular Axle Weights with a Bridge Weigh-in-motion System Considering Transverse Distribution of Wheel Loads. J. Bridge Eng. 2013, 19, 4013008. [Google Scholar] [CrossRef]
- Zhang, L.W.; Zhao, H.; Obrien, E.J.; Shao, X.D. Virtual Monitoring of orthotropic steel deck using bridge weigh-in-motion algorithm: Case study. Struct. Health Monit. 2019, 18, 610–620. [Google Scholar] [CrossRef]
- Ma, P.F.; An, J.H.; Zhang, B.; Zhu, P.; Zhao, H. Research on Axle Identification with Lateral Influence Line of U-ribs. Highway Eng. 2020, 45, 1–8+14. [Google Scholar]

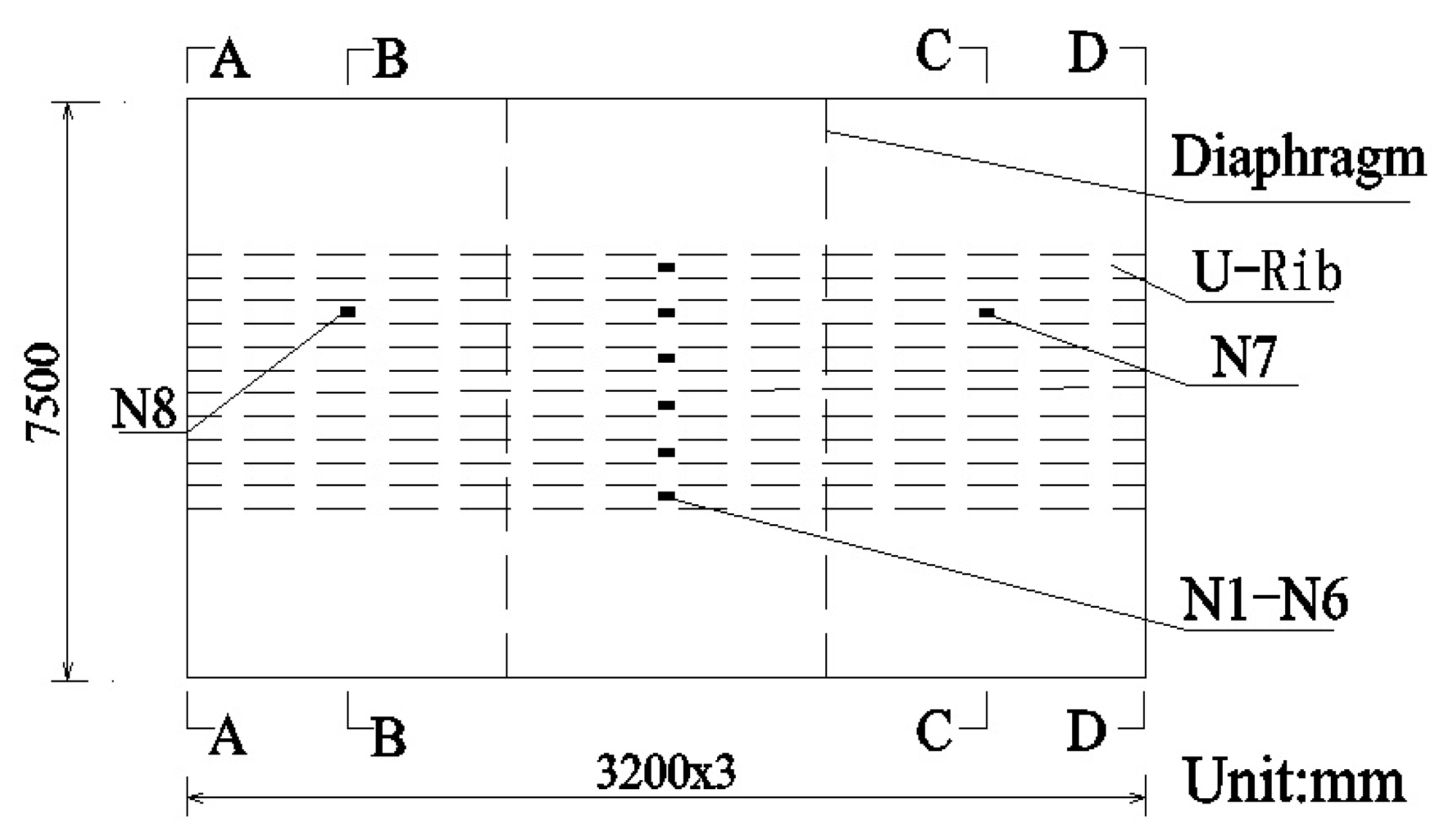


| Type of Vehicle | Number of Axles | D2 (m) | D3 (m) | D4 (m) | D5 (m) | D6 (m) |
|---|---|---|---|---|---|---|
| V1 | 2 | 2.6 | - | - | - | - |
| V2 | 3 | 3.0 | 1.4 | - | - | - |
| V3 | 4 | 2.0 | 4.0 | 1.4 | - | - |
| V4 | 5 | 3.2 | 1.4 | 6.0 | 1.4 | - |
| V5 | 6 | 3.2 | 1.4 | 7.0 | 1.4 | 1.4 |
| Type of Vehicle | A1 (kN) | A2 (kN) | A3 (kN) | A4 (kN) | A5 (kN) | A6 (kN) | GVW (kN) |
|---|---|---|---|---|---|---|---|
| V1 | 14 | 14 | - | - | - | - | 28 |
| V2 | 14 | 14 | 14 | - | - | - | 42 |
| V3 | 14 | 14 | 14 | 28 | - | - | 70 |
| V4 | 14 | 14 | 14 | 14 | 28 | - | 84 |
| V5 | 14 | 14 | 14 | 14 | 28 | 28 | 112 |
| Type of Vehicle | Noise Level | Practical TP (cm) | Identified TP (cm) | Absolute Error of TP (cm) | Identified GVW (kN) | Error of GVW (%) |
|---|---|---|---|---|---|---|
| V1 | 0% | −57 | −58 | 1 | 28.02 | 0.10 |
| 10% | −58 | 1 | 27.39 | −2.17 | ||
| 20% | −58 | 1 | 28.79 | 2.81 | ||
| V2 | 0% | 31 | 31 | 0 | 41.99 | −0.03 |
| 10% | 30 | 1 | 41.35 | −1.55 | ||
| 20% | 31 | 0 | 40.71 | −3.07 | ||
| V3 | 0% | −50 | −50 | 0 | 70.06 | 0.08 |
| 10% | −50 | 0 | 69.83 | −0.24 | ||
| 20% | −51 | 1 | 71.47 | 2.10 | ||
| V4 | 0% | 2 | 2 | 0 | 84.09 | 0.11 |
| 10% | 2 | 0 | 85.66 | 1.97 | ||
| 20% | 3 | 1 | 85.04 | 1.24 | ||
| V5 | 0% | −54 | −54 | 0 | 111.98 | −0.01 |
| 10% | −54 | 0 | 112.16 | 0.14 | ||
| 20% | −54 | 0 | 114.09 | 1.87 |
| Cases | Practical TP (cm) | Identified TP (cm) | Error of TP (cm) | Identified GVW (kg) | Error of GVW (%) |
|---|---|---|---|---|---|
| 1 | −15.5 | −15.5 | 0 | 96.9 | 3.37 |
| 2 | −6.5 | −5.5 | 1 | 96.9 | 1.2 |
| 3 | −3 | −2.5 | 0.5 | 96.9 | 3.83 |
| 4 | 3.7 | 3.5 | 0.2 | 96.9 | 4.69 |
| 5 | −16.3 | −16.5 | 0.2 | 106.6 | 2.6 |
| 6 | −16.5 | −16.5 | 0 | 106.6 | 2.32 |
| 7 | 4 | 3.5 | 0.5 | 106.6 | 4.19 |
| 8 | 11.7 | 11.5 | 0.2 | 106.6 | 2.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.-H.; Wang, C.; Qi, T.-Y.; Zhou, Z.-S. Vehicle Load Identification on Orthotropic Steel Box Beam Bridge Based on the Strain Response Area. Appl. Sci. 2022, 12, 12394. https://doi.org/10.3390/app122312394
Zhu J-H, Wang C, Qi T-Y, Zhou Z-S. Vehicle Load Identification on Orthotropic Steel Box Beam Bridge Based on the Strain Response Area. Applied Sciences. 2022; 12(23):12394. https://doi.org/10.3390/app122312394
Chicago/Turabian StyleZhu, Jun-He, Chao Wang, Tian-Yu Qi, and Zhuo-Sheng Zhou. 2022. "Vehicle Load Identification on Orthotropic Steel Box Beam Bridge Based on the Strain Response Area" Applied Sciences 12, no. 23: 12394. https://doi.org/10.3390/app122312394
APA StyleZhu, J.-H., Wang, C., Qi, T.-Y., & Zhou, Z.-S. (2022). Vehicle Load Identification on Orthotropic Steel Box Beam Bridge Based on the Strain Response Area. Applied Sciences, 12(23), 12394. https://doi.org/10.3390/app122312394





