Performance Study on a Soft X-ray Betatron Radiation Source Realized in the Self-Injection Regime of Laser-Plasma Wakefield Acceleration
Abstract
:1. Introduction
2. Fluctuations of the Plasma Source and the Electron Beams
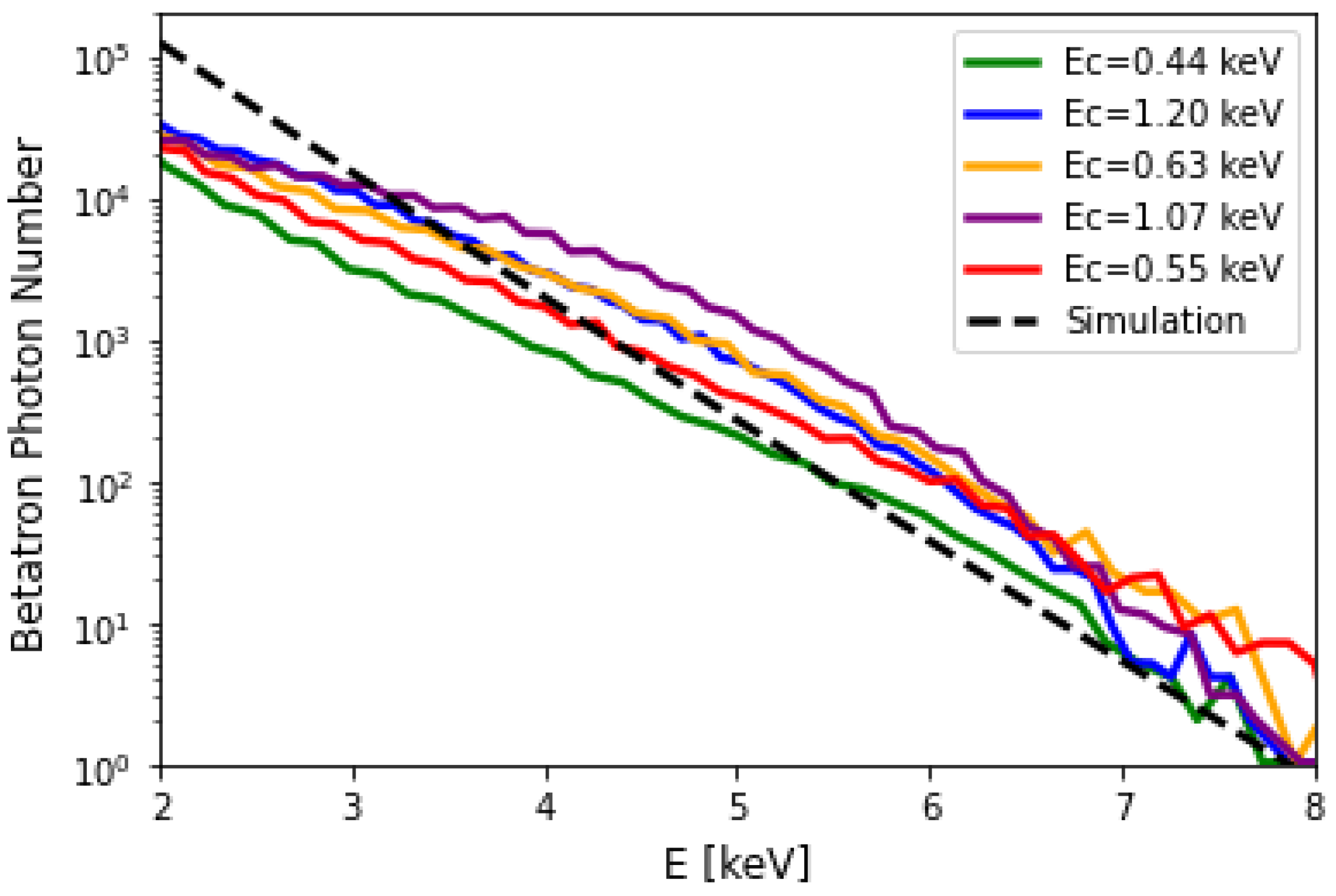
3. Betatron Radiation Sources
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 434, 267. [Google Scholar] [CrossRef] [Green Version]
- Curcio, A.; Giulietti, D. Laser-Plasma Acceleration and Secondary em Radiation; Aracne: Rome, Italy, 2019. [Google Scholar]
- Hogan, M.J.; Raubenheimer, T.O.; Seryi, A.; Muggli, P.; Katsouleas, T.; Huang, C.; Lu, Y.; An, W.; Marsh, K.A.; Mori, W.B.; et al. Plasma wakefield acceleration experiments at FACET. New J. Phys. 2010, 12, 055030. [Google Scholar] [CrossRef]
- Barov, N.; Rosenzweig, J.B.; Conde, M.E.; Gai, W.; Power, J.G. Observation of plasma wakefield acceleration in the underdense regime. Phys. Rev. Spec.-Top. Beams 2000, 3, 011301. [Google Scholar] [CrossRef]
- Loisch, G.; Asova, G.; Boonpornprasert, P.; Brinkmann, R.; Chen, Y.; Engel, J.; Good, J.; Gross, M.; Grüner, F.; Huck, H.; et al. Observation of high transformer ratio plasma wakefield acceleration. Phys. Rev. Lett. 2018, 121, 064801. [Google Scholar] [CrossRef] [Green Version]
- Amiranoff, F.; Baton, S.; Bernard, D.; Cros, B.; Descamps, D.; Dorchies, F.; Jacquet, F.; Malka, V.; Marquès, J.R.; Matthieussent, G.; et al. Observation of laser wakefield acceleration of electrons. Phys. Rev. Lett. 1998, 81, 995. [Google Scholar] [CrossRef] [Green Version]
- Lifschitz, A.F.; Faure, J.; Malka, V.; Mora, P. GeV wakefield acceleration of low energy electron bunches using petawatt lasers. Phys. Plasmas 2005, 12, 093104. [Google Scholar] [CrossRef]
- Chen, P.; Dawson, J.M.; Huff, R.W.; Katsouleas, T. Acceleration of electrons by the interaction of a bunched electron beam with a plasma. Phys. Rev. Lett. 1985, 54, 693. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, K.; Kawakubo, T.; Nakanishi, H.; Ogata, A.; Kato, Y.; Kitagawa, Y.; Kodama, R.; Mima, K.; Shiraga, H.; Suzuki, K.; et al. A proof-of-principle experiment of laser wakefield acceleration. Phys. Scr. 1994, 1994, 61. [Google Scholar] [CrossRef]
- Giulietti, D.; Galimberti, M.; Giulietti, A.; Gizzi, L.A.; Numico, R.; Tomassini, P.; Borghesi, M.; Malka, V.; Fritzler, S.; Pittman, M.; et al. Production of ultracollimated bunches of multi-MeV electrons by 35 fs laser pulses propagating in exploding-foil plasmas. Phys. Plasmas 2002, 9, 3655–3658. [Google Scholar] [CrossRef]
- Zhang, X.; Tajima, T.; Farinella, D.; Shin, Y.; Mourou, G.; Wheeler, J.; Taborek, P.; Chen, P.; Dollar, F.; Shen, B. Particle-in-cell simulation of X-ray wakefield acceleration and betatron radiation in nanotubes. Phys. Rev. Accel. Beams 2016, 19, 101004. [Google Scholar] [CrossRef]
- Blumenfeld, I.; Clayton, C.E.; Decker, F.J.; Hogan, M.J.; Huang, C.; Ischebeck, R.; Iverson, R.; Joshi, C.; Katsouleas, T.; Kirby, N.; et al. Energy doubling of 42 GeV electrons in a metre-scale plasma wakefield accelerator. Nature 2007, 445, 741–744. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229. [Google Scholar] [CrossRef]
- Lu, W.; Huang, C.; Zhou, M.; Tzoufras, M.; Tsung, F.S.; Mori, W.B.; Katsouleas, T. A nonlinear theory for multidimensional relativistic plasma wave wakefields. Phys. Plasmas 2006, 13, 056709. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Plenum Press: New York, NY, USA, 1984; Volume 1. [Google Scholar]
- Oubrerie, K.; Leblanc, A.; Kononenko, O.; Lahaye, R.; Andriyash, I.A.; Gautier, J.; Goddet, J.-P.; Martelli, L.; Tafzi, A.; Phuoc, K.T.; et al. Controlled acceleration of GeV electron beams in an all-optical plasma waveguide. Light. Sci. Appl. 2022, 11, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.L.; Chen, M.; Weng, S.M.; Yu, T.P.; Wang, W.M.; He, F.; Sheng, Z.-M.; McKenna, P.; Jaroszynski, D.A.; Zhang, J. Extremely brilliant GeV γ-rays from a two-stage laser-plasma accelerator. Sci. Adv. 2020, 6, eaaz7240. [Google Scholar] [CrossRef] [PubMed]
- Gonsalves, A.J.; Nakamura, K.; Daniels, J.; Benedetti, C.; Pieronek, C.; de Raadt, T.C.H.; Steinke, S.; Bin, J.H.; Bulanov, S.S.; van Tilborg, J.; et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide. Phys. Rev. Lett. 2019, 122, 084801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karlovets, D.V.; Potylitsyn, A.P. Universal description for different types of polarization radiation. arXiv 2009, arXiv:0908.2336. [Google Scholar]
- Curcio, A.; Ehret, M.; Perez-Hernandez, J.A.; Gatti, G. Observation of tunable parametric X-ray radiation emitted by laser-plasma electron beams interacting with crystalline structures. Phys. Rev. Accel. Beams 2022, 25, 063403. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Esarey, E.; Shadwick, B.A.; Catravas, P.; Leemans, W.P. Synchrotron radiation from electron beams in plasma-focusing channels. Phys. Rev. E 2002, 65, 056505. [Google Scholar] [CrossRef] [Green Version]
- Kostyukov, I.; Kiselev, S.; Pukhov, A. X-ray generation in an ion channel. Phys. Plasmas 2003, 10, 4818–4828. [Google Scholar] [CrossRef]
- Curcio, A.; Anania, M.; Bisesto, F.; Chiadroni, E.; Cianchi, A.; Ferrario, M.; Filippi, F.; Giulietti, D.; Marocchino, A.; Mira, F.; et al. First measurements of betatron radiation at FLAME laser facility. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 402, 388–392. [Google Scholar] [CrossRef]
- Curcio, A.; Anania, M.; Bisesto, F.; Chiadroni, E.; Cianchi, A.; Ferrario, M.; Filippi, F.; Giulietti, D.; Marocchino, A.; Petrarca, M.; et al. Trace-space reconstruction of low-emittance electron beams through betatron radiation in laser-plasma accelerators. Phys. Rev. Accel. Beams 2017, 20, 012801. [Google Scholar] [CrossRef] [Green Version]
- Fourmaux, S.; Corde, S.; Phuoc, K.T.; Leguay, P.M.; Payeur, S.; Lassonde, P.; Gnedyuk, S.; Lebrun, G.; Fourment, C.; Malka, V.; et al. Demonstration of the synchrotron-type spectrum of laser-produced Betatron radiation. New J. Phys. 2011, 13, 033017. [Google Scholar] [CrossRef]
- Ta Phuoc, K.; Fitour, R.; Tafzi, A.; Garl, T.; Artemiev, N.; Shah, R.; Albert, F.; Boschetto, D.; Rousse, A.; Kim, D.-E.; et al. Demonstration of the ultrafast nature of laser produced betatron radiation. Phys. Plasmas 2007, 14, 080701. [Google Scholar] [CrossRef]
- Curcio, A.; Gatti, G. Time-domain study of the synchrotron radiation emitted from electron beams in plasma focusing channels. Phys. Rev. E 2022, 105, 025201. [Google Scholar] [CrossRef] [PubMed]
- Schnell, M.; Sävert, A.; Landgraf, B.; Reuter, M.; Nicolai, M.; Jäckel, O.; Peth, C.; Thiele, T.; Jansen, O.; Pukhov, A.; et al. Deducing the electron-beam diameter in a laser-plasma accelerator using X-ray betatron radiation. Phys. Rev. Lett. 2012, 108, 075001. [Google Scholar] [CrossRef] [PubMed]
- Curcio, A.; Giulietti, D.; Dattoli, G.; Ferrario, M. Resonant interaction between laser and electrons undergoing betatron oscillations in the bubble regime. J. Plasma Phys. 2015, 81, 495810513. [Google Scholar] [CrossRef]
- Yu, C.; Liu, J.; Wang, W.; Li, W.; Qi, R.; Zhang, Z.; Qin, Z.; Liu, J.; Fang, M.; Feng, K.; et al. Enhanced betatron radiation by steering a laser-driven plasma wakefield with a tilted shock front. Appl. Phys. Lett. 2018, 112, 133503. [Google Scholar] [CrossRef] [Green Version]
- Ta Phuoc, K.; Esarey, E.; Leurent, V.; Cormier-Michel, E.; Geddes, C.G.R.; Schroeder, C.B.; Rousse, A.; Leemans, W.P. Betatron radiation from density tailored plasmas. Phys. Plasmas 2008, 15, 063102. [Google Scholar] [CrossRef]
- Corde, S.; Phuoc, K.T.; Lambert, G.; Fitour, R.; Malka, V.; Rousse, A.; Beck, A.; Lefebvre, E. Femtosecond X rays from laser-plasma accelerators. Rev. Mod. Phys. 2013, 85, 1. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical electrodynamics. Am. J. Phys. 1999, 67, 841. [Google Scholar] [CrossRef]
- Kroupp, E.; Tata, S.; Wan, Y.; Levy, D.; Smartsev, S.; Levine, E.Y.; Seemann, O.; Adelberg, M.; Piliposian, R.; Queller, T.; et al. Commissioning and first results from the new 2× 100 TW laser at the WIS. Matter Radiat. Extrem. 2022, 7, 044401. [Google Scholar] [CrossRef]
- Rousse, A.; Phuoc, K.T.; Shah, R.; Pukhov, A.; Lefebvre, E.; Malka, V.; Kiselev, S.; Burgy, F.; Rousseau, J.-P.; Umstadter, D.; et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys. Rev. Lett. 2004, 93, 135005. [Google Scholar] [CrossRef] [Green Version]
- Huang, T.W.; Robinson, A.P.L.; Zhou, C.T.; Qiao, B.; Liu, B.; Ruan, S.C.; He, X.T.; Norreys, P.A. Characteristics of betatron radiation from direct-laser-accelerated electrons. Phys. Rev. E 2016, 93, 063203. [Google Scholar] [CrossRef] [PubMed]
- Cipiccia, S.; Islam, M.R.; Ersfeld, B.; Shanks, R.P.; Brunetti, E.; Vieux, G.; Yang, X.; Issac, R.C.; Wiggins, S.M.; Welsh, G.H.; et al. Gamma-rays from harmonically resonant betatron oscillations in a plasma wake. Nat. Phys. 2011, 7, 867–871. [Google Scholar] [CrossRef]
- Albert, F.; Lemos, N.; Shaw, J.L.; King, P.M.; Pollock, B.B.; Goyon, C.; Schumaker, W.; Saunders, A.M.; Marsh, K.A.; Pak, A.; et al. Betatron X-ray radiation in the self-modulated laser wakefield acceleration regime: Prospects for a novel probe at large scale laser facilities. Nucl. Fusion 2018, 59, 032003. [Google Scholar] [CrossRef]
- Lee, S.; Lee, T.H.; Gupta, D.N.; Uhm, H.S.; Suk, H. Enhanced betatron oscillations in laser wakefield acceleration by off-axis laser alignment to a capillary plasma waveguide. Plasma Phys. Control. Fusion 2015, 57, 075002. [Google Scholar] [CrossRef]
- Du, B.; Wang, X.F. Influence of an external axial magnetic field on betatron radiation from the interaction of a circularly polarized laser with plasma. Phys. Plasmas 2017, 24, 093106. [Google Scholar] [CrossRef]
- Nam, I.; Hur, M.S.; Uhm, H.S.; Hafz, N.A.; Suk, H. Controlling the betatron oscillations of a wakefield-accelerated electron beam by temporally asymmetric laser pulses. Phys. Plasmas 2011, 18, 043107. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Cheng, Z.; Liu, S.; Ning, X.N.; Zhang, J.; Pai, C.H.; Hua, J.F.; Chu, H.H.; Wang, J.; Lu, W. Enhancement of laser-driven betatron X-rays by a density-depressed plasma structure. Plasma Phys. Control. Fusion 2019, 61, 035003. [Google Scholar] [CrossRef]
- Ferri, J.; Davoine, X. Enhancement of betatron X rays through asymmetric laser wakefield generated in transverse density gradients. Phys. Rev. Accel. Beams 2018, 21, 091302. [Google Scholar] [CrossRef]
- Lamač, M.; Chaulagain, U.; Jurkovič, M.; Nejdl, J.; Bulanov, S.V. Two-color nonlinear resonances in betatron oscillations of laser accelerated relativistic electrons. Phys. Rev. Res. 2021, 3, 033088. [Google Scholar] [CrossRef]
- Lécz, Z.; Andreev, A.; Hafz, N. Substantial enhancement of betatron radiation in cluster targets. Phys. Rev. E 2020, 102, 053205. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.M.; Yan, W.C.; Li, D.Z.; Hu, Z.D.; Zhang, L.; Wang, W.M.; Hafz, N.; Mao, J.Y.; Huang, K.; Ma, Y.; et al. Bright betatron X-ray radiation from a laser-driven-clustering gas target. Sci. Rep. 2013, 3, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curcio, A.; Cianchi, A.; Costa, G.; Demurtas, F.; Ehret, M.; Ferrario, M.; Galletti, M.; Giulietti, D.; Pérez-Hernández, J.A.; Gatti, G. Performance Study on a Soft X-ray Betatron Radiation Source Realized in the Self-Injection Regime of Laser-Plasma Wakefield Acceleration. Appl. Sci. 2022, 12, 12471. https://doi.org/10.3390/app122312471
Curcio A, Cianchi A, Costa G, Demurtas F, Ehret M, Ferrario M, Galletti M, Giulietti D, Pérez-Hernández JA, Gatti G. Performance Study on a Soft X-ray Betatron Radiation Source Realized in the Self-Injection Regime of Laser-Plasma Wakefield Acceleration. Applied Sciences. 2022; 12(23):12471. https://doi.org/10.3390/app122312471
Chicago/Turabian StyleCurcio, Alessandro, Alessandro Cianchi, Gemma Costa, Francesco Demurtas, Michael Ehret, Massimo Ferrario, Mario Galletti, Danilo Giulietti, José Antonio Pérez-Hernández, and Giancarlo Gatti. 2022. "Performance Study on a Soft X-ray Betatron Radiation Source Realized in the Self-Injection Regime of Laser-Plasma Wakefield Acceleration" Applied Sciences 12, no. 23: 12471. https://doi.org/10.3390/app122312471
APA StyleCurcio, A., Cianchi, A., Costa, G., Demurtas, F., Ehret, M., Ferrario, M., Galletti, M., Giulietti, D., Pérez-Hernández, J. A., & Gatti, G. (2022). Performance Study on a Soft X-ray Betatron Radiation Source Realized in the Self-Injection Regime of Laser-Plasma Wakefield Acceleration. Applied Sciences, 12(23), 12471. https://doi.org/10.3390/app122312471








