Dirac-Based Quantum Admittance of 2D Nanomaterials at Radio Frequencies
Abstract
:1. Introduction
2. Dirac Equation
3. Spinor Solution
4. Definition of Current
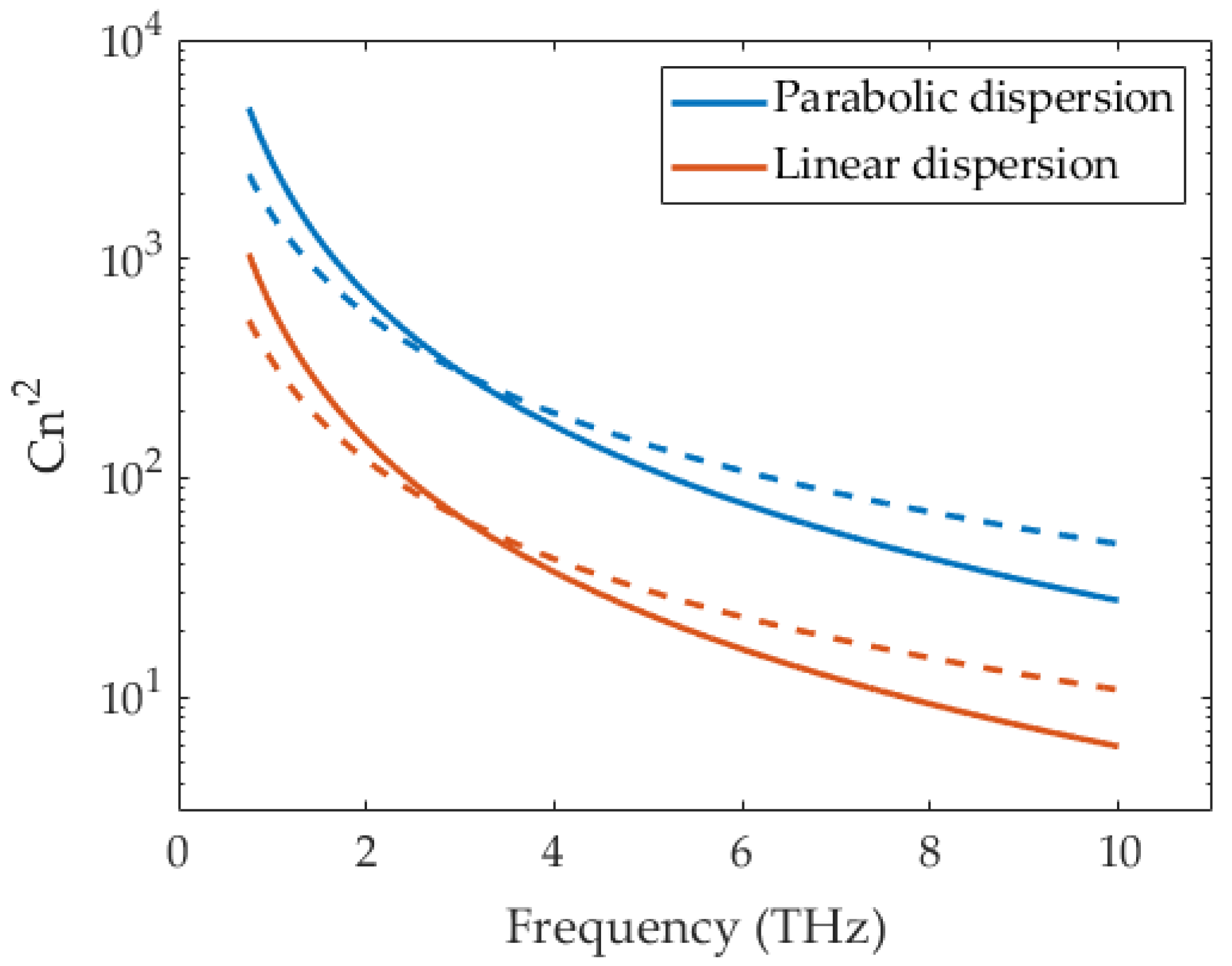
4.1. Graphene
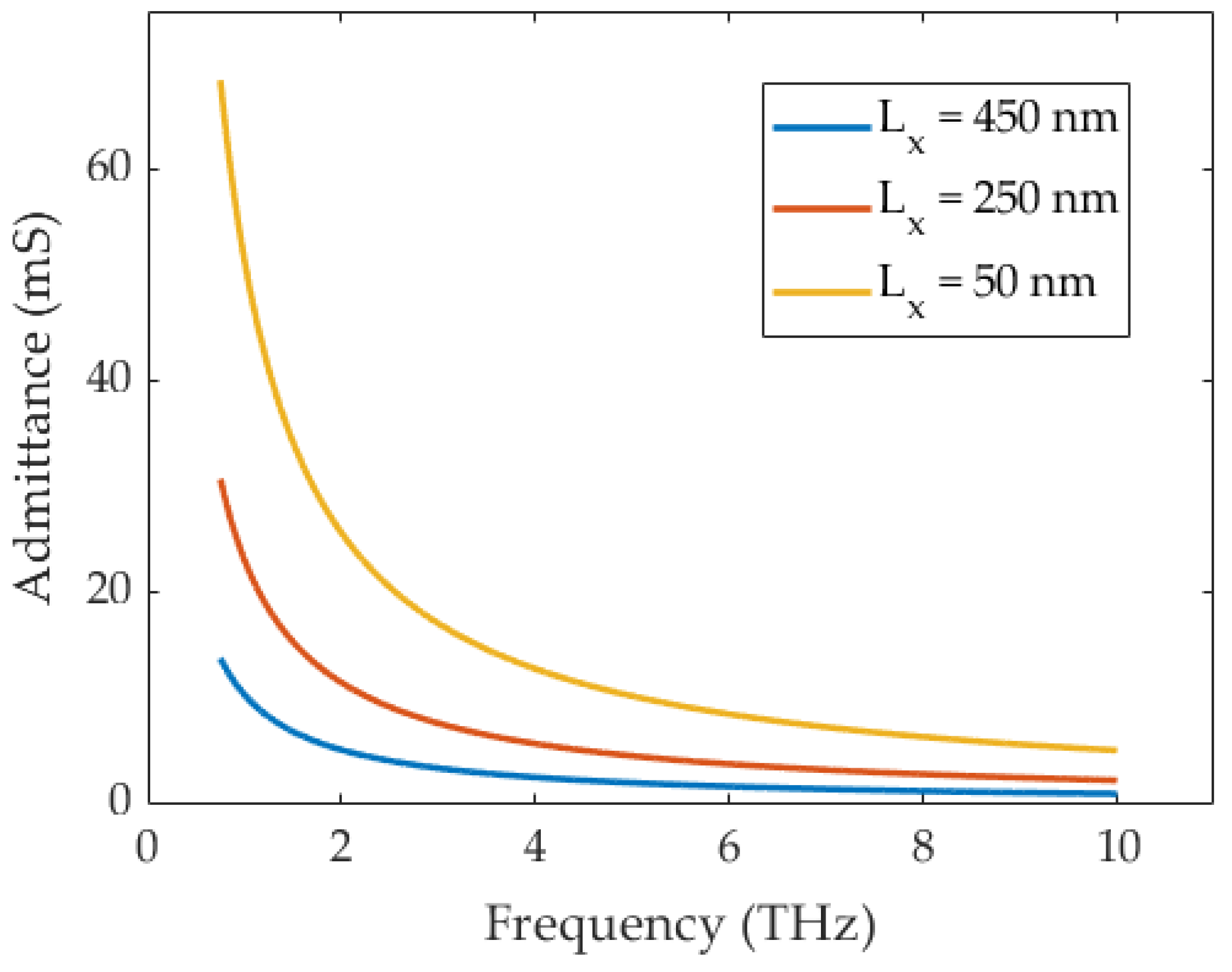
4.2. R.F. Quantum Admittance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Pierantoni, L.; Pelagalli, N.; Mencarelli, D.; Di Donato, A.; Orlandini, M.; Pagliuca, J.; Rozzi, T. Dirac Equation-Based Formulation for the Quantum Conductivity in 2D-Nanomaterials. Appl. Sci. 2021, 11, 2398. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rozzi, T.; Mencarelli, D.; Pierantoni, L. Towards a Unified Approach to Electromagnetic Fields and Quantum Currents From Dirac Spinors. IEEE Trans. Microw. Theory Tech. 2011, 59, 2587–2594. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Chang, D.E.; de Abajo, F.J.G. Graphene Plasmonics: A Platform for Strong Light–Matter Interactions. Nano Lett. 2011, 11, 3370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ju, L.; Geng, B.; Hornh, J.; Girit, C.; Martin, M.; Hao, Z.; Betchel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630. [Google Scholar] [CrossRef] [PubMed]
- Christensen, J.; Manjavacas, A.; Thongrattanasiri, S.; Koppens, F.H.; García de Abajo, F.J. Graphene Plasmon Waveguiding and Hybridization in Individual and Paired Nanoribbons. ACS Nano 2011, 6, 431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartmann, R.R.; Kono, J.; Portnoi, M. Terahertz science and technology of carbon nanomaterials. Nanotechnology 2014, 25, 322001. [Google Scholar] [CrossRef] [PubMed]
- García de Abajo, F.J. Graphene Plasmonics: Challenges and Opportunities. ACS Photonics 2014, 1, 135. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.; Sharapov, S.; Carbotte, J. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 2007, 19, 026222. [Google Scholar] [CrossRef]
- Gusynin, V.; Sharapov, S.; Carbotte, J. Sum rules for the optical and Hall conductivity in graphene. Phys. Rev. B 2007, 75, 165407. [Google Scholar] [CrossRef] [Green Version]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef] [Green Version]
- He, X.Y.; Li, R. Comparison of Graphene-Based Transverse Magnetic and Electric Surface Plasmon Modes. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 62. [Google Scholar]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Bellucci, S. Graphene-based electronically tuneable microstrip attenuator. Nanomater. Nanotechnol. 2014, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Bellucci, S. Microwave Applications of Graphene for Tunable Devices. In Proceedings of the 17th European Microwave Week (EuMW 2014), Rome, Italy, 5–10 October 2014. [Google Scholar]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Bellucci, S. Graphene-based Electronically Tunable Microstrip Attenuator. In Proceedings of the 2014 International Microwave Symposium (IEEE IMS 2014), Microwave Symposium Digest (MTT), Tampa Bay, FL, USA, 1–6 June 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Mencarelli, D.; Rozzi, T.; Pierantoni, L. Coherent carrier transport and scattering by lattice defects in single- and multibranch carbon nanoribbons. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 77, 195435. [Google Scholar] [CrossRef]
- Durkan, C. Current at the Nanoscale; College Press: Joplin, MO, USA, 2007. [Google Scholar]
- Hanson, G.W. Dyadic Green’s Functions for an Anisotropic, Non-Local Model of Biased Graphene. IEEE Trans. Antennas Propag. 2008, 56, 747. [Google Scholar] [CrossRef]
- Pierantoni, L.; Bozzi, M.; Moro, R.; Mencarelli, D.; Bellucci, S. On the use of electrostatically doped graphene: Analysis of microwave attenuators. In Proceedings of the International Conference on Numerical Electromagnetic Modeling and Optimization for RF, Microwave, and Terahertz Applications, NEMO 2014, Pavia, Italy, 14–16 May 2014; p. 6995716. [Google Scholar]
- Lancaster, P. Theory of Matrices; Academic Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Pierantoni, L. RF Nanotechnology-Concept, Birth, Mission and Perspectives. IEEE Microw. Mag. 2010, 11, 130–137. [Google Scholar] [CrossRef]
- Rakhimov, K.; Chaves, A.; Lambin, P. Scattering of Dirac Electrons by Randomly Distributed Nitrogen Substitutional Impurities in Graphene. Appl. Sci. 2016, 6, 256. [Google Scholar] [CrossRef] [Green Version]
- Hanson, G.W. Quasi-transverse electromagnetic modes supported by a graphene parallel-plate waveguide. J. Appl. Phys. 2008, 104, 084314. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| m/s | |
| H/m | |
| C | |
| ℏ | J s |
| kg | |
| 500 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozzi, T.; Mencarelli, D.; Zampa, G.M.; Pierantoni, L. Dirac-Based Quantum Admittance of 2D Nanomaterials at Radio Frequencies. Appl. Sci. 2022, 12, 12539. https://doi.org/10.3390/app122412539
Rozzi T, Mencarelli D, Zampa GM, Pierantoni L. Dirac-Based Quantum Admittance of 2D Nanomaterials at Radio Frequencies. Applied Sciences. 2022; 12(24):12539. https://doi.org/10.3390/app122412539
Chicago/Turabian StyleRozzi, Tullio, Davide Mencarelli, Gian Marco Zampa, and Luca Pierantoni. 2022. "Dirac-Based Quantum Admittance of 2D Nanomaterials at Radio Frequencies" Applied Sciences 12, no. 24: 12539. https://doi.org/10.3390/app122412539






