Analytical and Numerical Solutions to Static Analysis of Moderately Thick Cross-Ply Plates and Shells
Abstract
:1. Introduction
2. Statement of the Problem
3. Solution Methodology
3.1. Boundary Discontinues Fourier Series Method
3.2. Generalized Differantial Quadrature Method
4. Numerical Results and Discussion
4.1. Validation Study
4.2. Convergence Study
4.3. Parametrice Study
5. Conclusions
- ✓
- It is worth noting that almost no difference resulted from changing from moderately deep (R/a = 10) to (R/a = Plate) between BDM and GDQ for the very well-known SS3 type boundary conditions. The relatively small discrepancies between the present methodologies and the finite element method can be predicated to the variation between strong-form and weak-form formulations. Our proposed solution methodologies for BDM and GDQ methods are based on the strong form, as it satisfies the compulsory and natural boundary conditions. In contrast to strong-form, the finite element method uses the weak-form formulation and does not apply natural or force boundary conditions which are imposed on the secondary variable, such as forces and moments.
- ✓
- A rapid and monotonic convergence was observed with the Fourier series for the terms m, n > 10 for displacements and m, n > 20 for stress in the BDM. The stress convergence was higher than the displacement. This is possibly due to the presence of a discontinuity (complementary boundary constraint) in the derivative of the displacement in expression of the stress. The same convergence characteristics were observed for grid numbers m, n = 13 with the generalized differential quadrature method.
- ✓
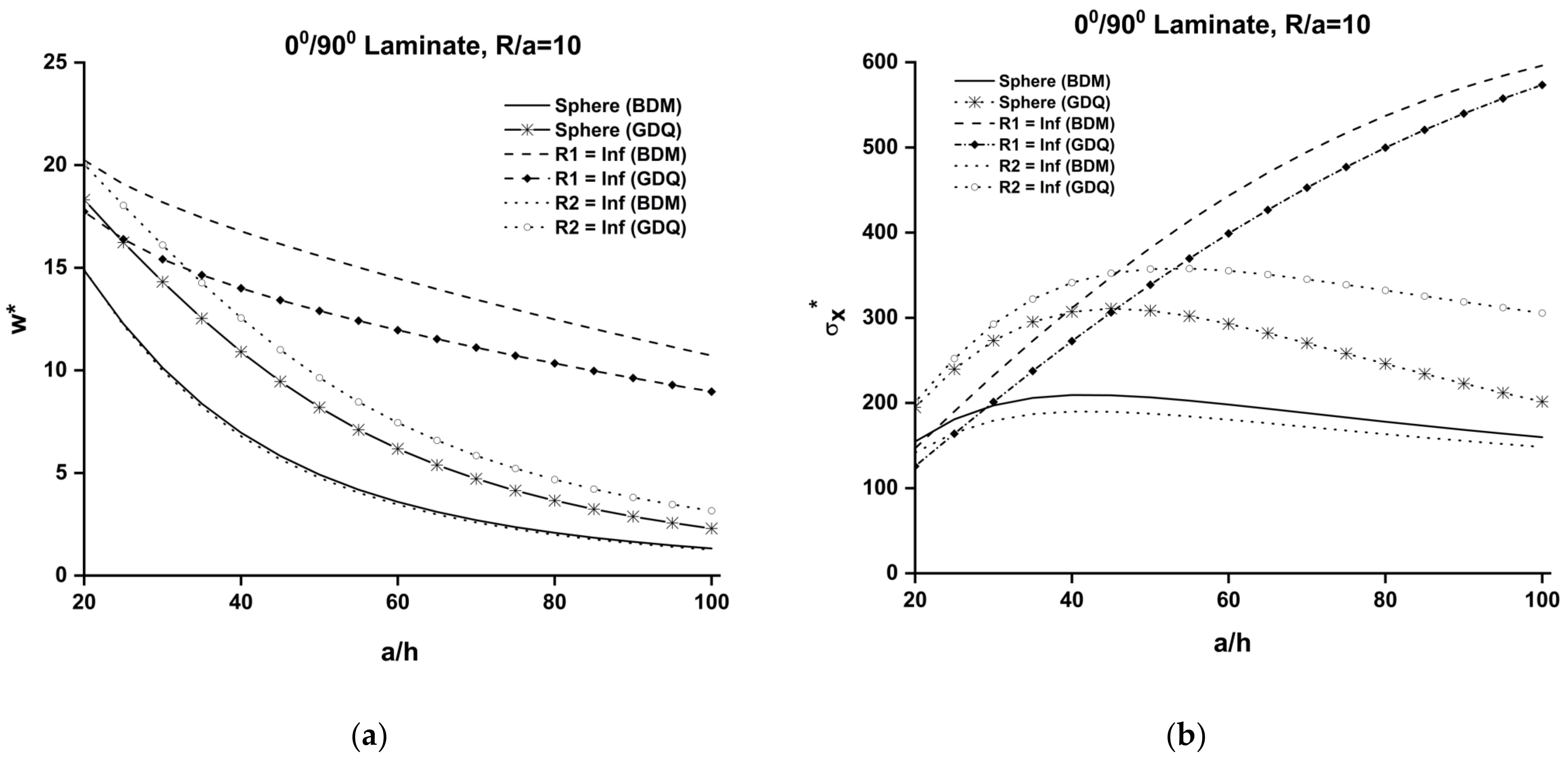
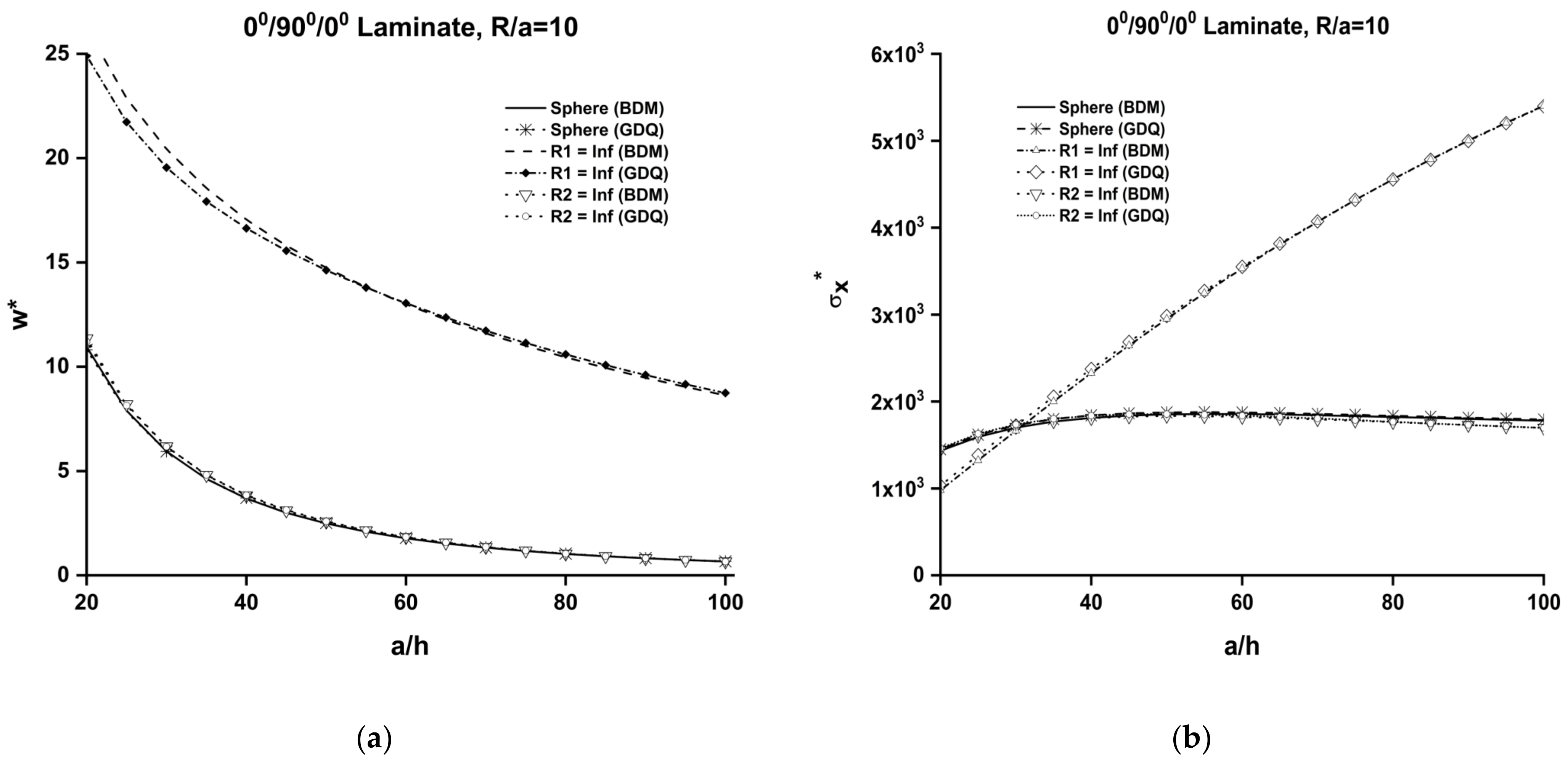
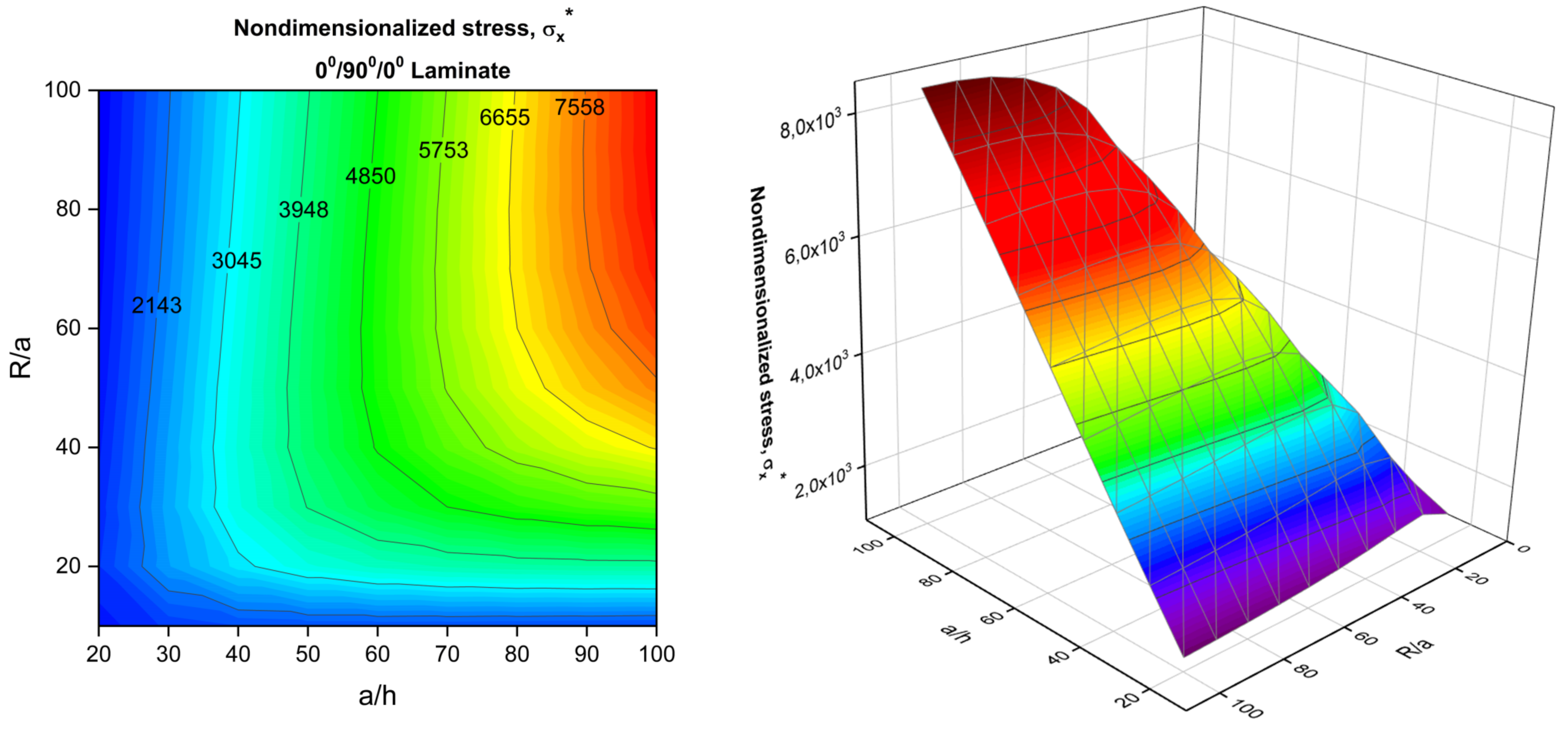
- A difference was seen when changing from the range 11.28% (R/a = Plate) to 18.75% (R/a = 10) for moderately thick (a/h = 20) antisymmetric [0°/90°] plates and shell with the roller skate-type boundary condition prescribed on two opposite edges, while the remaining two edges were subjected to the simply supported constraint between the BDM and GDQ methods. This is possibly due to the presence of a discontinuity in the derivatives which comes from the bending–stretching matrix (B matrix presence) in antisymmetric lamination. However very close results were obtained for symmetric ([0°/90°/0°] plates and shells using the whole range R/a and a/h ratios. It is also important to state that all three methods (BDM, DQM, and FEM) use different formulations, and among them, BDM provides analytical solutions and satisfies boundary conditions exactly, as is shown in Table 2 compared to FEM and DQM.
- ✓
- The difference between BDM and GDQ for an antisymmetric [0°/90°] shell increases with the increase of (E1/E2). The reason for this may be the dominant discontinuity in the bending–stretching matrix (B matrix presence) in antisymmetric lamination.
- ✓
- The effect of the modulus ratio, E1/E2, was more pronounced in the thin laminates (a/h > 50). Furthermore, this effect was increased by the beam–column effect in the case of an antisymmetric laminate. This is because the bending–stretching coupling is dominant in an antisymmetric laminate and produces a softening effect on the beam–column type, which consequently increases the normalized central deflection.
- ✓
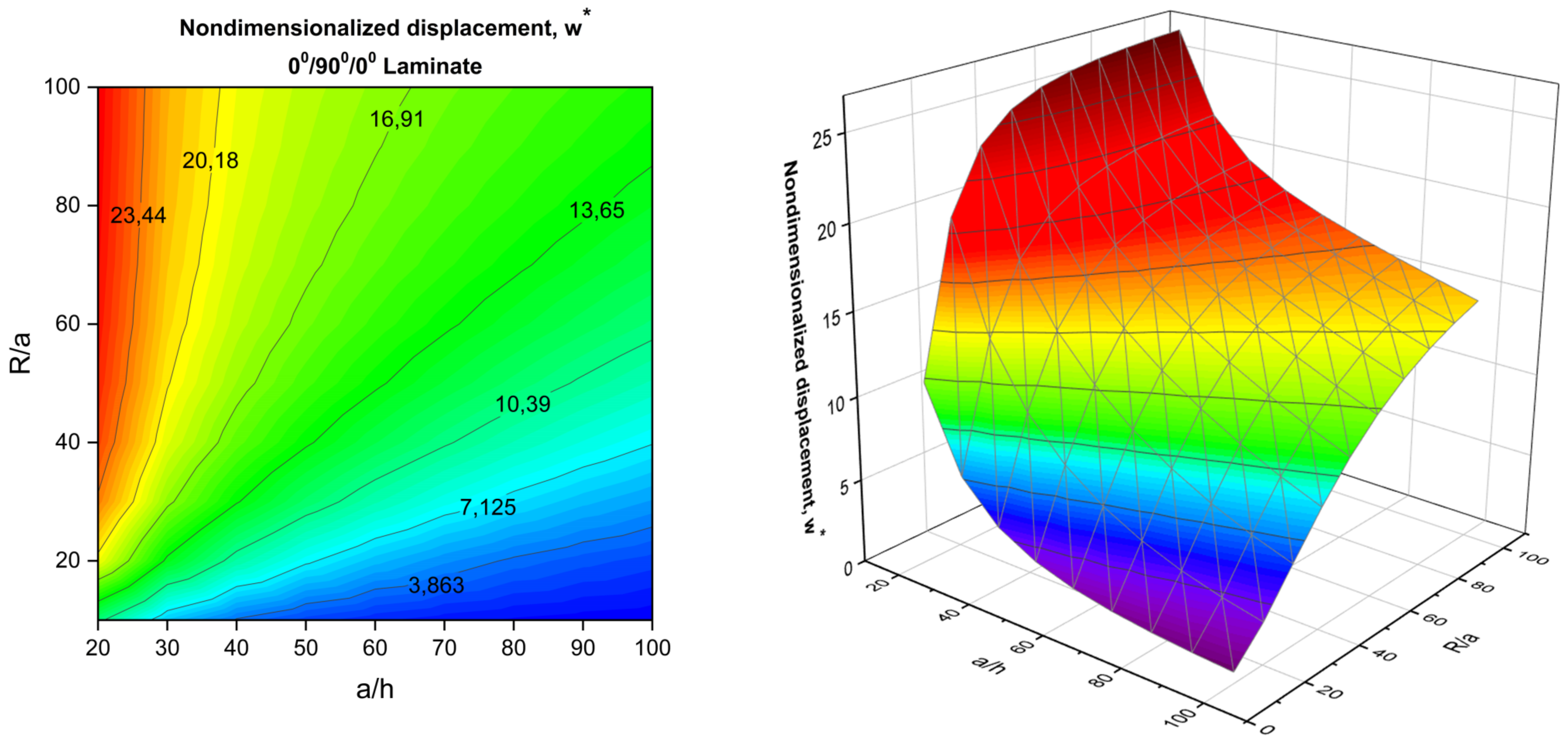
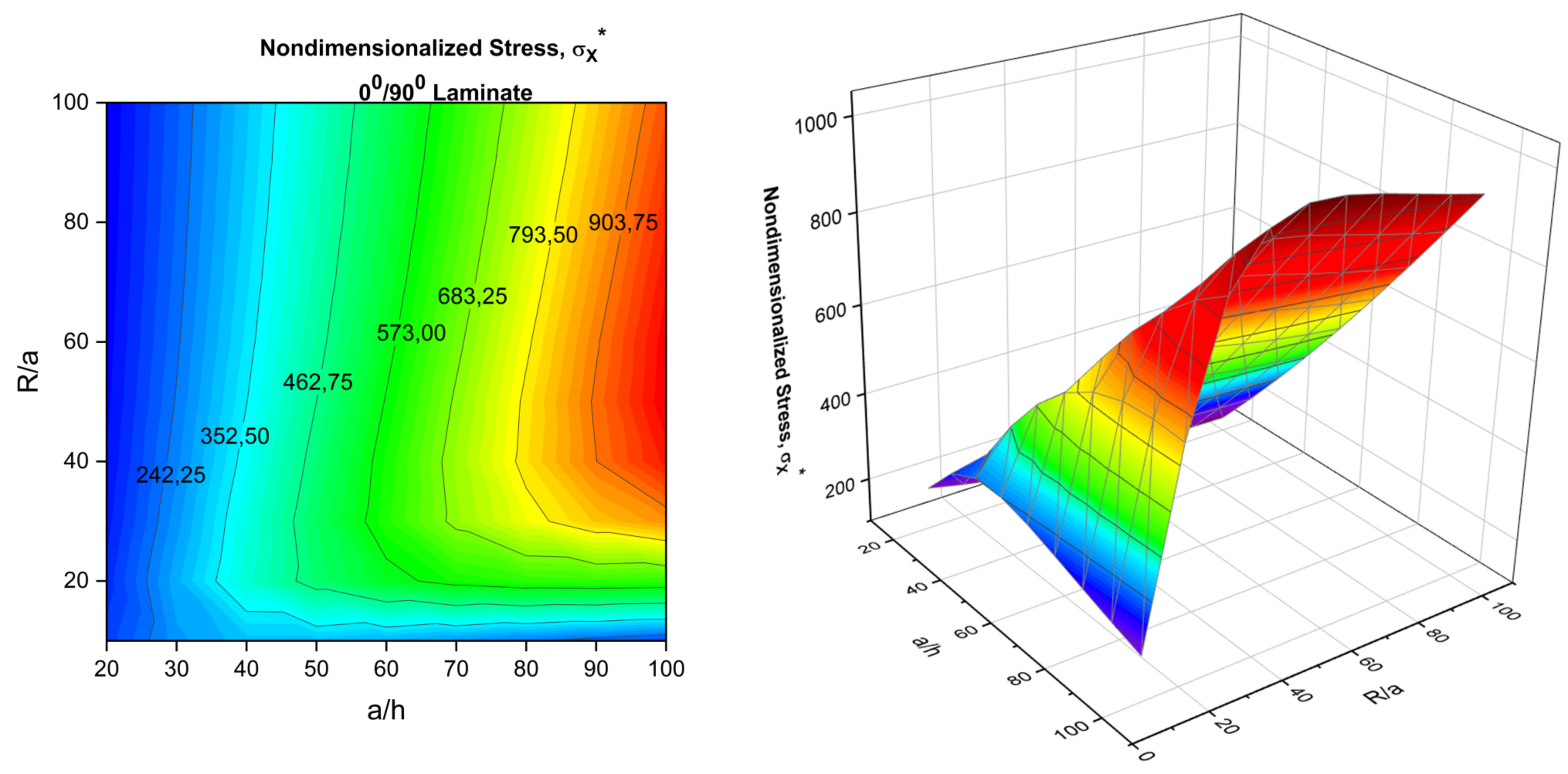
- The effect of the radius-to-length ratio R/a on transverse displacement, w*, also plays a critical role in the thinner shell regime, specifically beginning from the ratio R/a < 40. Bending–stretching coupling is inherited in antisymmetric laminations, and it directly impacts the interaction of membrane action with the beam–column/tie-bar effect. The membrane action due to curvature has a complicated interaction with the stated mechanism. This interaction should be considered during the prior design of composite shells.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 2013; ISBN 1107618096. [Google Scholar]
- Donnell, L.H. A Discussion of Thin Shell Theory. In Proceedings of the 5th International Congress of Applied Mechanics, New York, NY, USA, 12–16 September 1938. [Google Scholar]
- Sanders, J.L. An Improved First-Approximation Theory for Thin Shells; US Government Printing Office: Washington, DC, USA, 1960; Volume 24.
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959; Volume 2. [Google Scholar]
- Reissner, E. A New Derivation of the Equations for the Deformation of Elastic Shells. Am. J. Math. 1941, 63, 177–184. [Google Scholar] [CrossRef]
- Qatu, M.S.; Asadi, E.; Wang, W. Review of Recent Literature on Static Analyses of Composite Shells: 2000–2010. Open J. Compos. Mater. 2012, 2, 61. [Google Scholar] [CrossRef] [Green Version]
- Liew, K.M.; Zhao, X.; Ferreira, A.J.M. A Review of Meshless Methods for Laminated and Functionally Graded Plates and Shells. Compos. Struct. 2011, 93, 2031–2041. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent Development in Modeling and Analysis of Functionally Graded Materials and Structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Van Dung, N.; Tho, N.C.; Ha, N.M.; Hieu, V.T. On the Finite Element Model of Rotating Functionally Graded Graphene Beams Resting on Elastic Foundation. Math. Probl. Eng. 2021, 2021, 1586388. [Google Scholar] [CrossRef]
- Nam, V.H.; van Vinh, P.; van Chinh, N.; van Thom, D.; Hong, T.T. A New Beam Model for Simulation of the Mechanical Behaviour of Variable Thickness Functionally Graded Material Beams Based on Modified First Order Shear Deformation Theory. Materials 2019, 12, 404. [Google Scholar] [CrossRef] [Green Version]
- Bui, T.Q.; Doan, D.H.; van Do, T.; Hirose, S.; Duc, N.D. High Frequency Modes Meshfree Analysis of Reissner–Mindlin Plates. J. Sci. Adv. Mater. Devices 2016, 1, 400–412. [Google Scholar] [CrossRef] [Green Version]
- Pagano, N.J. Exact Solutions for Rectangular Bidirectional Composites and Sandwich Plates. J. Compos. Mater. 1970, 4, 20–34. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, J. Analytical Solutions for Thick, Doubly Curved, Laminated Shells. J. Eng. Mech. 1992, 118, 1338–1356. [Google Scholar] [CrossRef]
- Kumari, P.; Kar, S. Static Behavior of Arbitrarily Supported Composite Laminated Cylindrical Shell Panels: An Analytical 3D Elasticity Approach. Compos. Struct. 2019, 207, 949–965. [Google Scholar] [CrossRef]
- Atashipour, S.R.; Girhammar, U.A.; Al-Emrani, M. Exact Lévy-Type Solutions for Bending of Thick Laminated Orthotropic Plates Based on 3-D Elasticity and Shear Deformation Theories. Compos. Struct. 2017, 163, 129–151. [Google Scholar] [CrossRef]
- Nik, A.M.N.; Tahani, M. Analytical Solutions for Bending Analysis of Rectangular Laminated Plates with Arbitrary Lamination and Boundary Conditions. J. Mech. Sci. Technol. 2009, 23, 2253–2267. [Google Scholar] [CrossRef]
- Whitney, J.M.; Leissa, A.W. Analysis of a Simply Supported Laminated Anisotropic Rectangular Plate. AIAA J. 1970, 8, 28–33. [Google Scholar] [CrossRef]
- Reddy, J.N.; Liu, C. A Higher-Order Shear Deformation Theory of Laminated Elastic Shells. Int. J. Eng. Sci. 1985, 23, 319–330. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, D.-C. Static Analysis of Symmetric Angle-Ply Laminated Plates by Analytical Method. AIAA J. 2006, 44, 667–669. [Google Scholar] [CrossRef]
- Li, H.; Liu, N.; Pang, F.; Du, Y.; Li, S. An Accurate Solution Method for the Static and Vibration Analysis of Functionally Graded Reissner-Mindlin Rectangular Plate with General Boundary Conditions. Shock Vib. 2018, 2018, 4535871. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, R.A. On the Roles of Complementary and Admissible Boundary Constraints in Fourier Solutions to the Boundary Value Problems of Completely Coupled r Th Order PDEs. J. Sound Vib. 2002, 251, 261–313. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. On Boundary-Discontinuous Double Fourier Series Solution to a System of Completely Coupled PDE’s. Int. J. Eng. Sci. 1989, 27, 1005–1022. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kabir, H.R.H. On Analytical Solutions to Boundary-Value Problems of Doubly-Curved Moderately-Thick Orthotropic Shells. Int. J. Eng. Sci. 1989, 27, 1325–1336. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kabir, H.R.H. Sensitivity of the Response of Moderately Thick Cross-Ply Doubly-Curved Panels to Lamination and Boundary Constraint-I. Theory. Int. J. Solids Struct. 1993, 30, 263–272. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kabir, H.R.H. Boundary-Discontinuous Fourier Analysis of Doubly-Curved Panels Using Classical Shallow Shell Theories. Int. J. Eng. Sci. 1993, 31, 1551–1564. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Abu-Arja, K.R. Exact Solution of Shear-Flexible Doubly Curved Anti-Symmetric Angle-Ply Shells. Int. J. Eng. Sci. 1988, 26, 587–604. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Abu-Arja, K.R. Static Analysis of Moderately-Thick Finite Antisymmetric Angle-Ply Cylindrical Panels and Shells. Int. J. Solids Struct. 1991, 28, 1–15. [Google Scholar] [CrossRef]
- Oktem, A.S.; Chaudhuri, R.A. Levy Type Analysis of Cross-Ply Plates Based on Higher-Order Theory. Compos. Struct. 2007, 78, 243–253. [Google Scholar] [CrossRef]
- Oktem, A.S.; Chaudhuri, R.A. Fourier Analysis of Thick Cross-Ply Levy Type Clamped Doubly-Curved Panels. Compos. Struct. 2007, 80, 489–503. [Google Scholar] [CrossRef]
- Oktem, A.S.; Chaudhuri, R.A. Levy Type Fourier Analysis of Thick Cross-Ply Doubly Curved Panels. Compos. Struct. 2007, 80, 475–488. [Google Scholar] [CrossRef]
- Oktem, A.S.; Chaudhuri, R.A. Boundary Discontinuous Fourier Analysis of Thick Cross-Ply Clamped Plates. Compos. Struct. 2008, 82, 539–548. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Soares, C.G. Static and Dynamic Analysis of Laminated Composite and Sandwich Plates and Shells by Using a New Higher-Order Shear Deformation Theory. Compos. Struct. 2011, 94, 37–49. [Google Scholar] [CrossRef]
- Oktem, A.S.; Soares, C.G. Higher Order Theory Based Fourier Analysis of Cross-Ply Plates and Doubly Curved Panels. J. Compos. Mater. 2012, 46, 2675–2694. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Balaraman, K.; Kunukkasseril, V.X. A Combined Theoretical and Experimental Investigation on Free Vibration of Thin Symmetrically Laminated Anisotropic Plates. Compos. Struct. 2005, 67, 85–97. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. Static Analysis of Completely Doubly-Curved Laminated Shells and Panels Using General Higher-Order Shear Deformation Theories. Compos. Struct. 2013, 101, 59–93. [Google Scholar] [CrossRef]
- Asadi, E.; Qatu, M.S. Static Analysis of Thick Laminated Shells with Different Boundary Conditions Using GDQ. Thin-Walled Struct. 2012, 51, 76–81. [Google Scholar] [CrossRef]
- Kurtaran, H. Geometrically Nonlinear Transient Analysis of Moderately Thick Laminated Composite Shallow Shells with Generalized Differential Quadrature Method. Compos. Struct. 2015, 125, 605–614. [Google Scholar] [CrossRef]
- Kurtaran, H. Geometrically Nonlinear Transient Analysis of Thick Deep Composite Curved Beams with Generalized Differential Quadrature Method. Compos. Struct. 2015, 128, 241–250. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method for the Natural Frequencies of Doubly-Curved Shells with Variable Thickness: A General Formulation. Compos. B Eng. 2016, 92, 265–289. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R. Higher Order Theories for the Free Vibration Analysis of Laminated Anisotropic Doubly-Curved Shells of Arbitrary Geometry with General Boundary Conditions. Compos. Struct. 2022, 297, 115740. [Google Scholar] [CrossRef]
- Allahkarami, F.; Tohidi, H.; Dimitri, R.; Tornabene, F. Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation. Appl. Sci. 2020, 10, 1345. [Google Scholar] [CrossRef] [Green Version]
- Zare Jouneghani, F.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Free Vibration Analysis of Functionally Graded Porous Doubly-Curved Shells Based on the First-Order Shear Deformation Theory. Appl. Sci. 2017, 7, 1252. [Google Scholar] [CrossRef] [Green Version]
- Kiarasi, F.; Babaei, M.; Asemi, K.; Dimitri, R.; Tornabene, F. Three-Dimensional Buckling Analysis of Functionally Graded Saturated Porous Rectangular Plates under Combined Loading Conditions. Appl. Sci. 2021, 11, 10434. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E.; Reddy, J.N. A Numerical Investigation on the Natural Frequencies of FGM Sandwich Shells with Variable Thickness by the Local Generalized Differential Quadrature Method. Appl. Sci. 2017, 7, 131. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003; ISBN 0203502809. [Google Scholar]
- Hobson, E.W. The Theory of Functions of a Real Variable and the Theory of Fourier’s Series; The University Press: Cambridge, UK, 1921; Volume 1. [Google Scholar]
- Green, A.E. Double Fourier Series and Boundary Value Problems. Math. Proc. Camb. Philos. Soc. 1944, 40, 222–228. [Google Scholar] [CrossRef]
- Shu, C.; Du, H. A Generalized Approach for Implementing General Boundary Conditions in the GDQ Free Vibration Analysis of Plates. Int. J. Solids Struct. 1997, 34, 837–846. [Google Scholar] [CrossRef]
- Oktem, A.S.; Chaudhuri, R.A. Effect of Inplane Boundary Constraints on the Response of Thick General (Unsymmetric) Cross-Ply Plates. Compos. Struct. 2008, 83, 1–12. [Google Scholar] [CrossRef]







| [0°/90°] | [0°/90°/0°] | [0°/90°/90°/0°] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R/a | BDM | GDQ | Ref. [18] | BDM | GDQ | Ref. [18] | BDM | GDQ | Ref. [18] | |
| 10 | 5.5428 | 5.542 | 5.5428 | 3.644 | 3.644 | 3.6445 | 3.720 | 3.720 | 3.720 | |
| 20 | 11.273 | 11.27 | 11.273 | 5.547 | 5.547 | 5.5473 | 5.661 | 5.661 | 5.661 | |
| 50 | 15.714 | 15.71 | 15.714 | 6.482 | 6.482 | 6.4827 | 6.614 | 6.614 | 6.614 | |
| 100 | 16.645 | 16.64 | 16.645 | 6.642 | 6.642 | 6.6421 | 6.777 | 6.777 | 6.777 | |
| Plate | 16.979 | 16.97 | 16.980 | 6.697 | 6.696 | 6.6970 | 6.833 | 6.833 | 6.842 | |
| R/a | BDM | GDQ | FEM | BDM | GDQ | FEM | BDM | GDQ | FEM | |
| 10 | 420.17 | 420.2 | 418.98 | 4688.6 | 4688.6 | 4678.5 | 4961.8 | 4961.8 | 4954.4 | |
| 20 | 868.116 | 868.1 | 866.180 | 6962.9 | 6963 | 6950 | 7238.2 | 7238.2 | 7227 | |
| 50 | 1196.10 | 1196.1 | 1196 | 7956.6 | 7956.7 | 7985.2 | 8175.8 | 8175.8 | 8209.2 | |
| 100 | 1256.62 | 1256.6 | 1255.6 | 8081.2 | 8081.3 | 8075 | 8271 | 8271 | 8265.9 | |
| Plate | 1268.70 | 1268.7 | 1267.4 | 8073 | 8073 | 8064 | 8229.6 | 8229.5 | 8222.7 | |
| R/a | BDM | GDQ | FEM | |
|---|---|---|---|---|
| 10 | 14.880 | 18.315 | 20.900 | |
| 20 | 20.763 | 20.796 | 22.165 | |
| Plate | 22.152 | 19.901 | 22.603 | |
| 10 | 154.778 | 194.918 | 142.100 | |
| 20 | 172.361 | 176.382 | 129.650 | |
| Plate | 136.668 | 118.459 | 105.135 | |
| 10 | 1850.1 | 2323.4 | 2569.2 | |
| 20 | 2612.8 | 2614.2 | 2684.3 | |
| Plate | 2785.6 | 2466.0 | 2690.4 |
| [0°/90°] | [0°/90°/0°] | [0°/90°/90°/0°] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R/a | a/h | Method | w* | w* | w* | ||||||
| 10 | 20 | BDM | 14.880 | 154.778 | 1850.1 | 10.950 | 1432.6 | 101.046 | 10.999 | 1489.3 | 110.386 |
| GDQ | 18.315 | 194.918 | 2323.4 | 10.811 | 1450.8 | 99.4543 | 10.864 | 1510.8 | 108.887 | ||
| 50 | BDM | 4.9204 | 206.615 | 1460.8 | 2.485 | 1851.6 | 40.88 | 3.1181 | 2394 | 76.979 | |
| GDQ | 8.1924 | 308.405 | 2690 | 2.508 | 1874.7 | 41.746 | 3.1443 | 2419.0 | 78.042 | ||
| 100 | BDM | 1.3248 | 159.760 | 550.63 | 0.666 | 1778.9 | 9.1941 | 0.9236 | 2499.9 | 36.3349 | |
| GDQ | 2.3004 | 201.457 | 1313.9 | 0.671 | 1792.5 | 9.9637 | 0.9304 | 2518.5 | 37.3247 | ||
| Plate | 20 | BDM | 22.147 | 136.554 | 2785 | 28.660 | 944.08 | 269.434 | 20.966 | 769.890 | 200.210 |
| GDQ | 19.901 | 118.459 | 2466.0 | 27.058 | 1004.4 | 252.13 | 20.190 | 828.9 | 191.707 | ||
| 50 | BDM | 19.818 | 399.629 | 6406.5 | 19.598 | 3048.2 | 436.80 | 15.786 | 2680.8 | 390.017 | |
| GDQ | 17.114 | 338.554 | 5439.2 | 19.469 | 3070.2 | 458.07 | 15.853 | 2681.5 | 389.6595 | ||
| 100 | BDM | 19.193 | 837.166 | 1244.5 | 16.799 | 6544.3 | 793.02 | 14.137 | 5893.2 | 703.959 | |
| GDQ | 16.588 | 695.911 | 1058.2 | 17.976 | 6381.6 | 846.779 | 14.98 | 5622.0 | 741.542 | ||
| R/a | a/h | Method | E1/E2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | ||||
| w* | 10 | 20 | BDM | 33.877 | 23.8006 | 17.047 | 13.171 | 10.655 | 8.902 |
| GDQ | 34.559 | 25.9268 | 20.218 | 16.769 | 14.392 | 12.638 | |||
| 50 | BDM | 16.055 | 9.336 | 5.860 | 4.229 | 3.283 | 2.668 | ||
| GDQ | 17.222 | 12.108 | 9.130 | 7.444 | 6.314 | 5.494 | |||
| 100 | BDM | 5.4233 | 2.7262 | 1.6004 | 1.1292 | 0.8699 | 0.705 | ||
| GDQ | 5.8318 | 3.665 | 2.6041 | 2.0677 | 1.7306 | 1.495 | |||
| Plate | 20 | BDM | 41.708 | 31.449 | 24.464 | 20.277 | 17.427 | 15.346 | |
| GDQ | 39.952 | 28.524 | 21.942 | 18.274 | 15.833 | 14.059 | |||
| 50 | BDM | 37.953 | 28.482 | 21.977 | 18.077 | 15.429 | 13.500 | ||
| GDQ | 36.683 | 25.320 | 19.007 | 15.609 | 13.396 | 11.810 | |||
| 100 | BDM | 36.995 | 27.699 | 21.311 | 17.487 | 14.895 | 13.010 | ||
| GDQ | 36.123 | 24.734 | 18.448 | 15.089 | 12.914 | 11.362 | |||
| 10 | 20 | BDM | 408.591 | 268.165 | 181.547 | 134.061 | 104.293 | 84.170 | |
| GDQ | 420.420 | 294.297 | 218.847 | 175.913 | 147.473 | 127.130 | |||
| 50 | BDM | 727.107 | 402.740 | 247.767 | 176.540 | 135.605 | 109.158 | ||
| GDQ | 755.659 | 480.335 | 346.930 | 278.613 | 234.863 | 203.835 | |||
| 100 | BDM | 696.610 | 332.097 | 193.171 | 136.115 | 104.819 | 85.020 | ||
| GDQ | 706.825 | 363.486 | 233.464 | 178.37 | 146.929 | 126.241 | |||
| Plate | 20 | BDM | 344.536 | 231.245 | 159.110 | 118.960 | 93.386 | 75.828 | |
| GDQ | 338.443 | 212.727 | 139.872 | 101.943 | 78.762 | 63.292 | |||
| 50 | BDM | 932.956 | 647.333 | 459.655 | 352.222 | 282.161 | 233.055 | ||
| GDQ | 895.587 | 582.226 | 394.657 | 294.155 | 231.333 | 188.603 | |||
| 100 | BDM | 1905.6 | 1336.1 | 958.7 | 740.8 | 597.8 | 496.9 | ||
| GDQ | 1808.3 | 1183.6 | 807.6 | 605.1 | 478 | 391.2 | |||
| 10 | 20 | BDM | 834.2 | 1380.2 | 1747.4 | 1922.3 | 2009.3 | 2051.6 | |
| GDQ | 858 | 1525.6 | 2111.6 | 2499.8 | 2776.9 | 2984.3 | |||
| 50 | BDM | 1085.2 | 1373.3 | 1453.2 | 1460.3 | 1447.6 | 1428.7 | ||
| GDQ | 1184 | 1894 | 2480.7 | 2866 | 3141.9 | 3350 | |||
| 100 | BDM | 731.916 | 670.952 | 579.850 | 528.011 | 495.387 | 472.958 | ||
| GDQ | 811.3 | 1060.7 | 1244.8 | 1374 | 1474.6 | 1557 | |||
| Plate | 20 | BDM | 967.9 | 1795.5 | 2521.2 | 3006.7 | 3361.3 | 3634.6 | |
| GDQ | 921.1 | 1601.7 | 2225.8 | 2672.7 | 3016.9 | 3293.2 | |||
| 50 | BDM | 2259.0 | 4162.7 | 5810.8 | 6906.9 | 7708.3 | 8329.4 | ||
| GDQ | 2166.5 | 3633 | 4934.7 | 5869.5 | 6600.4 | 7198.3 | |||
| 100 | BDM | 4428 | 8127 | 11,303 | 13,401 | 14,929 | 16,112 | ||
| GDQ | 4285 | 7123 | 9611 | 11,390 | 12,781 | 13,921 | |||
| R/a | a/h | Method | E1/E2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | ||||
| w* | 10 | 20 | BDM | 32.259 | 19.215 | 12.731 | 9.620 | 7.755 | 6.504 |
| GDQ | 31.795 | 18.864 | 12.544 | 9.514 | 7.692 | 6.466 | |||
| 50 | BDM | 13.260 | 5.632 | 3.059 | 2.091 | 1.587 | 1.277 | ||
| GDQ | 13.344 | 5.678 | 3.086 | 2.111 | 1.601 | 1.289 | |||
| 100 | BDM | 4.356 | 1.631 | 0.834 | 0.554 | 0.414 | 0.329 | ||
| GDQ | 4.357 | 1.635 | 0.839 | 0.559 | 0.4177 | 0.332 | |||
| Plate | 20 | BDM | 43.818 | 34.616 | 30.074 | 27.493 | 25.597 | 24.062 | |
| GDQ | 42.631 | 32.968 | 28.419 | 25.954 | 24.192 | 22.785 | |||
| 50 | BDM | 37.065 | 25.627 | 20.850 | 18.653 | 17.263 | 16.240 | ||
| GDQ | 37.146 | 25.559 | 20.728 | 18.520 | 17.132 | 16.116 | |||
| 100 | BDM | 35.240 | 23.015 | 18.047 | 15.883 | 14.585 | 13.674 | ||
| GDQ | 36.173 | 24.169 | 19.235 | 17.042 | 15.701 | 14.742 | |||
| 10 | 20 | BDM | 875.1 | 1245.6 | 1395.2 | 1459.5 | 1496.1 | 1519.9 | |
| GDQ | 886.2 | 1264.1 | 1413.8 | 1477.5 | 1513.6 | 1537.1 | |||
| 50 | BDM | 1550.2 | 1865.4 | 1867 | 1836.2 | 1809.6 | 1788.7 | ||
| GDQ | 1555.8 | 1883.5 | 1889.3 | 1859.8 | 1833.7 | 1813.1 | |||
| 100 | BDM | 1559 | 1798.8 | 1792.4 | 1765.9 | 1743.5 | 1725.8 | ||
| GDQ | 1554.9 | 1802.4 | 1803.4 | 1781.6 | 1762.4 | 1747 | |||
| Plate | 20 | BDM | 699.61 | 927.91 | 956.36 | 931.67 | 895.94 | 858.31 | |
| GDQ | 720.6 | 972.1 | 1011.4 | 991.6 | 958.5 | 922.4 | |||
| 50 | BDM | 1998.1 | 2828.2 | 3033.5 | 3041.7 | 2998.1 | 2936.2 | ||
| GDQ | 1993.2 | 2839 | 3052.9 | 3065.7 | 3025 | 2965.3 | |||
| 100 | BDM | 4140.5 | 5968.8 | 6481.1 | 6559.9 | 6519.6 | 6434.3 | ||
| GDQ | 4059.6 | 5843.3 | 6328 | 6388.9 | 6334.7 | 6237.9 | |||
| 10 | 20 | BDM | 361.159 | 190.887 | 119.383 | 87.688 | 69.430 | 57.484 | |
| GDQ | 357.635 | 187.504 | 117.347 | 86.424 | 68.601 | 56.918 | |||
| 50 | BDM | 409.137 | 127.946 | 54.639 | 32.178 | 22.032 | 16.464 | ||
| GDQ | 412.912 | 129.886 | 55.701 | 32.898 | 22.574 | 16.899 | |||
| 100 | BDM | 265.097 | 51.627 | 14.368 | 6.362 | 3.601 | 2.383 | ||
| GDQ | 264.017 | 52.361 | 15.190 | 7.074 | 4.208 | 2.906 | |||
| Plate | 20 | BDM | 452.400 | 334.082 | 283.944 | 257.786 | 239.216 | 224.367 | |
| GDQ | 440.178 | 316.606 | 266.128 | 241.087 | 223.864 | 210.326 | |||
| 50 | BDM | 993.809 | 632.001 | 496.701 | 439.754 | 405.647 | 381.325 | ||
| GDQ | 992.951 | 627.821 | 491.164 | 433.981 | 399.974 | 375.874 | |||
| 100 | BDM | 1910.4 | 1142 | 859.2 | 746 | 681.9 | 638.5 | ||
| GDQ | 1947.4 | 1193.2 | 913.2 | 799.1 | 733.2 | 687.7 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algül, İ.; Oktem, A.S. Analytical and Numerical Solutions to Static Analysis of Moderately Thick Cross-Ply Plates and Shells. Appl. Sci. 2022, 12, 12547. https://doi.org/10.3390/app122412547
Algül İ, Oktem AS. Analytical and Numerical Solutions to Static Analysis of Moderately Thick Cross-Ply Plates and Shells. Applied Sciences. 2022; 12(24):12547. https://doi.org/10.3390/app122412547
Chicago/Turabian StyleAlgül, İlke, and Ahmet Sinan Oktem. 2022. "Analytical and Numerical Solutions to Static Analysis of Moderately Thick Cross-Ply Plates and Shells" Applied Sciences 12, no. 24: 12547. https://doi.org/10.3390/app122412547






