Reliability of a Global Gait Symmetry Index Based on Linear Joint Displacements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Participants
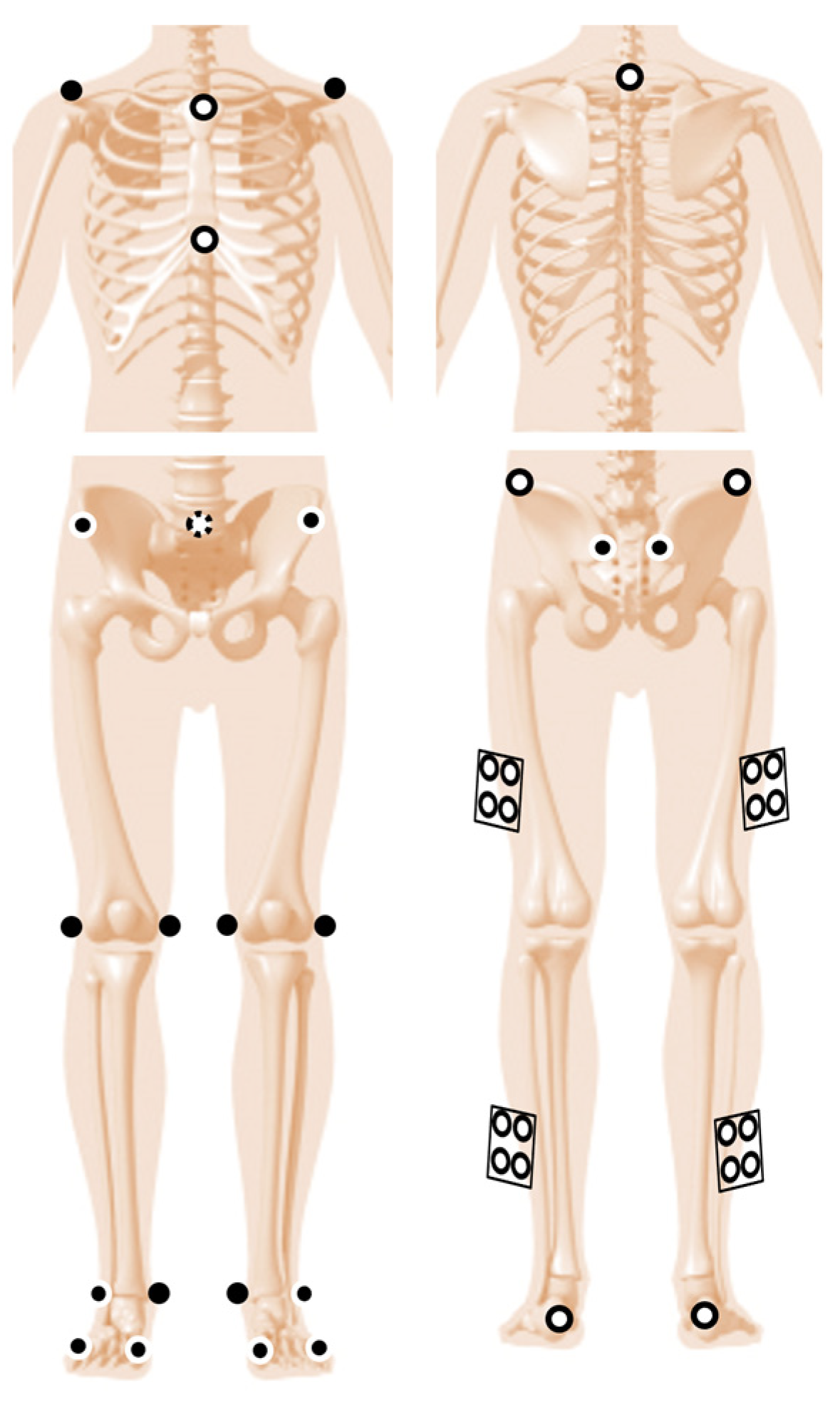
2.3. Protocol
2.4. Data Processing
2.5. Data Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sadeghi, H.; Allard, P.; Prince, F.; Labelle, H. Symmetry and Limb Dominance in Able-Bodied Gait: A Review. Gait Posture 2000, 12, 34–45. [Google Scholar] [CrossRef] [PubMed]
- Patterson, K.K.; Gage, W.H.; Brooks, D.; Black, S.E.; McIlroy, W.E. Evaluation of Gait Symmetry after Stroke: A Comparison of Current Methods and Recommendations for Standardization. Gait Posture 2010, 31, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Shelbourne, K.D.; Klotz, C. What I Have Learned about the ACL: Utilizing a Progressive Rehabilitation Scheme to Achieve Total Knee Symmetry after Anterior Cruciate Ligament Reconstruction. J. Orthop. Sci. 2006, 11, 318–325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patterson, K.K.; Parafianowicz, I.; Danells, C.J.; Closson, V.; Verrier, M.C.; Staines, W.R.; Black, S.E.; McIlroy, W.E. Gait Asymmetry in Community-Ambulating Stroke Survivors. Arch. Phys. Med. Rehabil. 2008, 89, 304–310. [Google Scholar] [CrossRef]
- Archer, K.R.; Castillo, R.C.; MacKenzie, E.J.; Bosse, M.J. Gait Symmetry and Walking Speed Analysis Following Lower-Extremity Trauma. Phys. Ther. 2006, 86, 1630–1640. [Google Scholar] [CrossRef] [Green Version]
- de Vet, H.C.; Terwee, C.B.; Knol, D.L.; Bouter, L.M. When to Use Agreement versus Reliability Measures. J. Clin. Epidemiol. 2006, 59, 1033–1039. [Google Scholar] [CrossRef] [Green Version]
- Klejman, S.; Andrysek, J.; Dupuis, A.; Wright, V. Test-Retest Reliability of Discrete Gait Parameters in Children with Cerebral Palsy. Arch. Phys. Med. Rehabil. 2010, 91, 781–787. [Google Scholar] [CrossRef]
- Mokkink, L.B.; Terwee, C.B.; Patrick, D.L.; Alonso, J.; Stratford, P.W.; Knol, D.L.; Bouter, L.M.; de Vet, H.C.W. The COSMIN Study Reached International Consensus on Taxonomy, Terminology, and Definitions of Measurement Properties for Health-Related Patient-Reported Outcomes. J. Clin. Epidemiol. 2010, 63, 737–745. [Google Scholar] [CrossRef] [Green Version]
- Lewek, M.D.; Randall, E.P. Reliability of Spatiotemporal Asymmetry during Overground Walking for Individuals Following Chronic Stroke. J. Neurol. Phys. Ther. 2011, 35, 116–121. [Google Scholar] [CrossRef]
- Lewek, M.D.; Feasel, J.; Wentz, E.; Brooks, F.P.; Whitton, M.C. Use of Visual and Proprioceptive Feedback to Improve Gait Speed and Spatiotemporal Symmetry Following Chronic Stroke-A Case Series. Phys. Ther. 2012, 92, 748–756. [Google Scholar] [CrossRef]
- Reisman, D.; McLean, H.; Keller, J.; Danks, K.; Bastian, A. Repeated Split-Belt Treadmill Training Improves Poststroke Step Length Asymmetry. Neurorehabil. Neural Repair 2013, 27, 460–468. [Google Scholar] [CrossRef] [Green Version]
- White, S.C.; Lifeso, R.M. Altering Asymmetric Limb Loading after Hip Arthroplasty Using Real-Time Dynamic Feedback When Walking. Arch. Phys. Med. Rehabil. 2005, 86, 1958–1963. [Google Scholar] [CrossRef] [PubMed]
- Senden, R.; Grimm, B.; Heyligers, I.C.; Savelberg, H.H.C.M.; Meijer, K. Acceleration-Based Gait Test for Healthy Subjects: Reliability and Reference Data. Gait Posture 2009, 30, 192–196. [Google Scholar] [CrossRef]
- Cabral, S.; Fernandes, R.; Selbie, W.S.; Moniz-Pereira, V.; Veloso, A.P. Inter-Session Agreement and Reliability of the Global Gait Asymmetry Index in Healthy Adults. Gait Posture 2017, 51, 20–24. [Google Scholar] [CrossRef]
- Roerdink, M.; Roeles, S.; van der Pas, S.C.H.; Bosboom, O.; Beek, P.J. Evaluating Asymmetry in Prosthetic Gait with Step-Length Asymmetry Alone Is Flawed. Gait Posture 2012, 35, 446–451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deluzio, K.J.; Astephen, J.L. Biomechanical Features of Gait Waveform Data Associated with Knee Osteoarthritis: An Application of Principal Component Analysis. Gait Posture 2007, 25, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Nigg, S.; Vienneau, J.; Maurer, C.; Nigg, B.M. Development of a Symmetry Index Using Discrete Variables. Gait Posture 2013, 38, 115–119. [Google Scholar] [CrossRef]
- Pataky, T.C.; Vanrenterghem, J.; Robinson, M.A. The Probability of False Positives in Zero-Dimensional Analyses of One-Dimensional Kinematic, Force and EMG Trajectories. J. Biomech. 2016, 49, 1468–1476. [Google Scholar] [CrossRef] [Green Version]
- Cabral, S.; Resende, R.A.; Clansey, A.C.; Deluzio, K.J.; Selbie, W.S.; Veloso, A.P. A Global Gait Asymmetry Index. J. Appl. Biomech. 2016, 32, 171–177. [Google Scholar] [CrossRef] [PubMed]
- della Croce, U.; Leardini, A.; Chiari, L.; Cappozzo, A. Human Movement Analysis Using Stereophotogrammetry Part 4: Assessment of Anatomical Landmark Misplacement and Its Effects on Joint Kinematics. Gait Posture 2005, 21, 226–237. [Google Scholar] [CrossRef]
- della Croce, U.; Cappozzo, A.; Kerrigan, D.C. Pelvis and Lower Limb Anatomical Landmark Calibration Precision and Its Propagation to Bone Geometry and Joint Angles. Med. Biol. Eng. Comput. 1999, 37, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Cabral, S.; Fernandes, R.; Moniz-Pereira, V.; Selbie, W.S.; Veloso, A.P. The Impact of Joint Kinematics Reliability on the Intersession Agreement and Reliability of Global Gait Symmetry Indices. In Proceedings of the XXVI Congress of the International Society of Biomechanics, Brisbane, Australia, 23–27 July 2017. [Google Scholar]
- Baker, R.; McGinley, J.L.; Schwartz, M.H.; Beynon, S.; Rozumalski, A.; Graham, H.K.; Tirosh, O. The Gait Profile Score and Movement Analysis Profile. Gait Posture 2009, 30, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Lundh, D.; Coleman, S.; Riad, J. Movement Deviation and Asymmetry Assessment with Three Dimensional Gait Analysis of Both Upper- and Lower Extremity Results in Four Different Clinical Relevant Subgroups in Unilateral Cerebral Palsy. Clin. Biomech. 2014, 29, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Troje, N.F. Decomposing Biological Motion-A Framework for Analysis and Synthesis of Human Gait Patterns. J. Vis. 2002, 2, 371–387. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, R.; Armada-da-Silva, P.; Pool-Goudzwaard, A.; Moniz-Pereira, V.; Veloso, A.P. Three Dimensional Multi-Segmental Trunk Kinematics and Kinetics during Gait: Test-Retest Reliability and Minimal Detectable Change. Gait Posture 2016, 46, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, H.C.; Thiemann, S. How Many Subjects? Statistical Power Analysis in Research, 1st ed.; SAGE Publications, Inc.: Newbury Park, CA, USA, 1987. [Google Scholar]
- Robertson, D.G.E.; Caldwell, G.E.; Hamill, J.; Kamen, G.; Whittlesey, S.N. Research Methods in Biomechanics, 2nd ed.; Human kinetics: Champaign, IL, USA, 2014. [Google Scholar]
- Bell, A.L.; Pedersen, D.R.; Brand, R.A. A Comparison of the Accuracy of Several Hip Center Location Prediction Methods. J. Biomech. 1990, 23, 617–621. [Google Scholar] [CrossRef] [PubMed]
- Spoor, C.W.; Veldpaus, F.E. Rigid Body Motion Calculated from Spatial Coordinates of Markers. J. Biomech. 1980, 13, 391–393. [Google Scholar] [CrossRef] [Green Version]
- Stanhope, S.; Kepple, T.; McGuire, D.; Roman, N. Kinematic-Based Technique for Event Time Determination during Gait. Med. Biol. Eng. Comput. 1990, 28, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Mokkink, L.B.; Terwee, C.B.; Patrick, D.L.; Alonso, J.; Stratford, P.W.; Knol, D.L.; Bouter, L.M.; de Vet, H.C.W. The COSMIN Checklist for Assessing the Methodological Quality of Studies on Measurement Properties of Health Status Measurement Instruments: An International Delphi Study. Qual. Life Res. 2010, 19, 539–549. [Google Scholar] [CrossRef] [Green Version]
- Bartlett, J.W.; Frost, C. Reliability, Repeatability and Reproducibility: Analysis of Measurement Errors in Continuous Variables. Ultrasound Obs. Gynecol. 2008, 31, 466–475. [Google Scholar] [CrossRef] [PubMed]
- de Vet, H.C.; Terwee, C.B.; Ostelo, R.W.; Beckerman, H.; Knol, D.L.; Bouter, L.M. Minimal Changes in Health Status Questionnaires: Distinction between Minimally Detectable Change and Minimally Important Change. Health Qual. Life Outcomes 2006, 4, 54–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGraw, K.O.; Wong, S.P. Forming Inferences about Some Intraclass Correlation Coefficients. Psychol. Methods 1996, 1, 30–46. [Google Scholar] [CrossRef]
- Weir, J.P. Quantifying Test-Retest Reliability Using The Intraclass Correlation Coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231–240. [Google Scholar] [PubMed] [Green Version]
- Nunnaly, J.C. Psychometric Theory, 2nd ed.; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Portney, L.G.; Watkins, M.P. Foundations of Clinical Research: Applications to Practice, 3rd ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Bland, J.M.; Altman, D.G. Measuring Agreement in Method Comparison Studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Sigal, L.; Balan, A.; Black, M. HUMANEVA: Synchronized Video and Motion Capture Dataset and Baseline Algorithm for Evaluation of Articulated Human Motion. Int. J. Comput. Vis. 2010, 87, 324–344. [Google Scholar] [CrossRef]

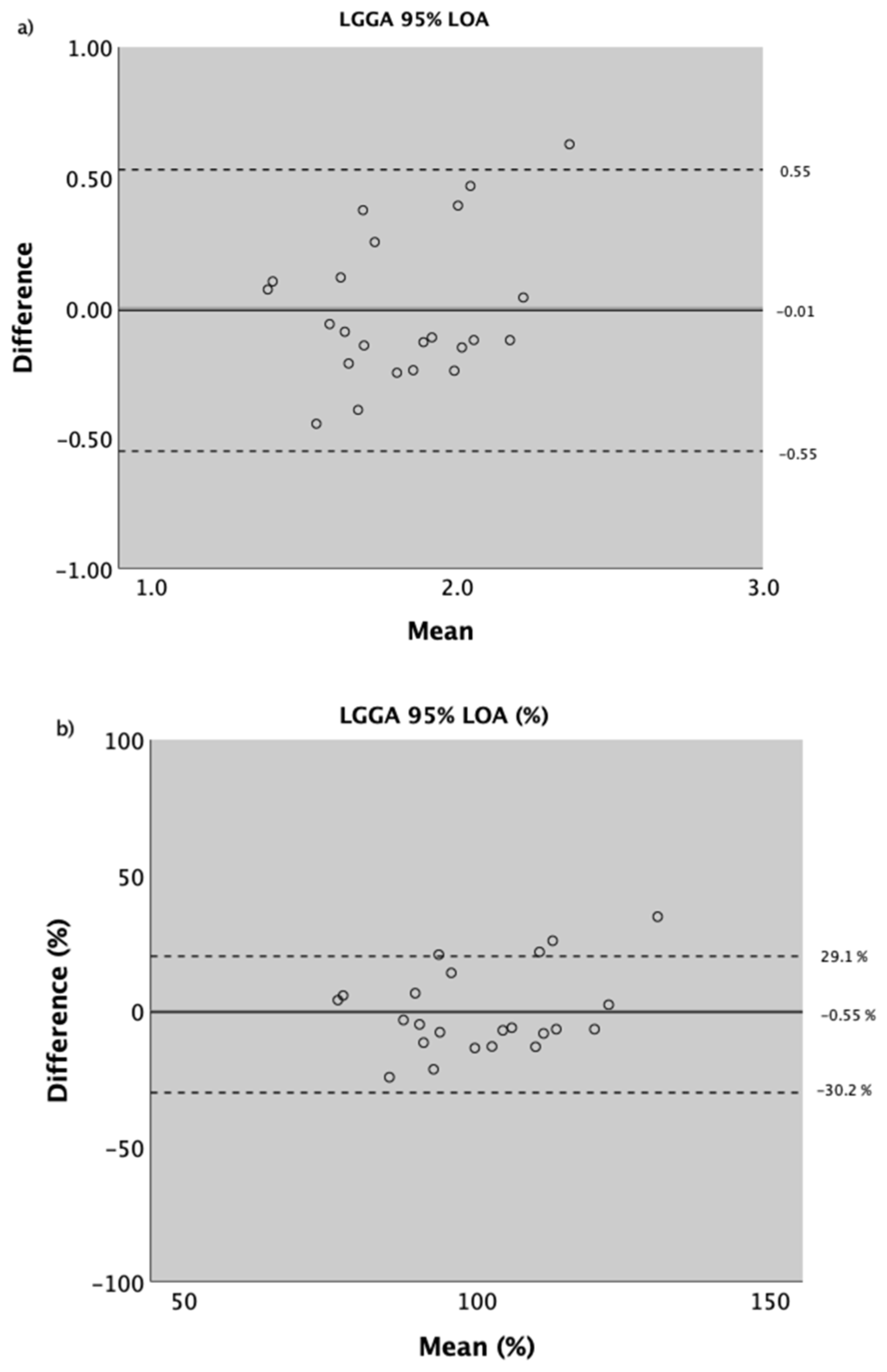
| Mean ± SD 1st Visit | Mean ± SD 2nd Visit | Mean | Diff (%) | SDdiff (%) | 95% CIdiff |
|---|---|---|---|---|---|
| 1.82 ± 0.33 | 1.83 ± 0.25 | 1.82 | −0.01 (−0.55) | 0.28 (15.4) | −0.13 to 0.11 |
| 95% LOA (%) | SEM (%) | SDC (%) | ICC | 95% CIICC |
|---|---|---|---|---|
| −0.55 to 0.55 (−30.2 to 29.1) | 0.20 (10.7) | 0.54 (29.7) | 0.71 | 0.33 to 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabral, S.; Fernandes, R.; Selbie, W.S.; Moniz-Pereira, V.; Veloso, A.P. Reliability of a Global Gait Symmetry Index Based on Linear Joint Displacements. Appl. Sci. 2022, 12, 12558. https://doi.org/10.3390/app122412558
Cabral S, Fernandes R, Selbie WS, Moniz-Pereira V, Veloso AP. Reliability of a Global Gait Symmetry Index Based on Linear Joint Displacements. Applied Sciences. 2022; 12(24):12558. https://doi.org/10.3390/app122412558
Chicago/Turabian StyleCabral, Silvia, Rita Fernandes, William Scott Selbie, Vera Moniz-Pereira, and António P. Veloso. 2022. "Reliability of a Global Gait Symmetry Index Based on Linear Joint Displacements" Applied Sciences 12, no. 24: 12558. https://doi.org/10.3390/app122412558
APA StyleCabral, S., Fernandes, R., Selbie, W. S., Moniz-Pereira, V., & Veloso, A. P. (2022). Reliability of a Global Gait Symmetry Index Based on Linear Joint Displacements. Applied Sciences, 12(24), 12558. https://doi.org/10.3390/app122412558






