Effects of Surface Roughness on Windage Loss and Flow Characteristics in Shaft-Type Gap with Critical CO2
Abstract
1. Introduction
2. Geometry and Numerical Method
2.1. Geometric Model and Boundary Conditions
2.2. Numerical Method
2.3. Windage Loss and Skin Friction Coefficient
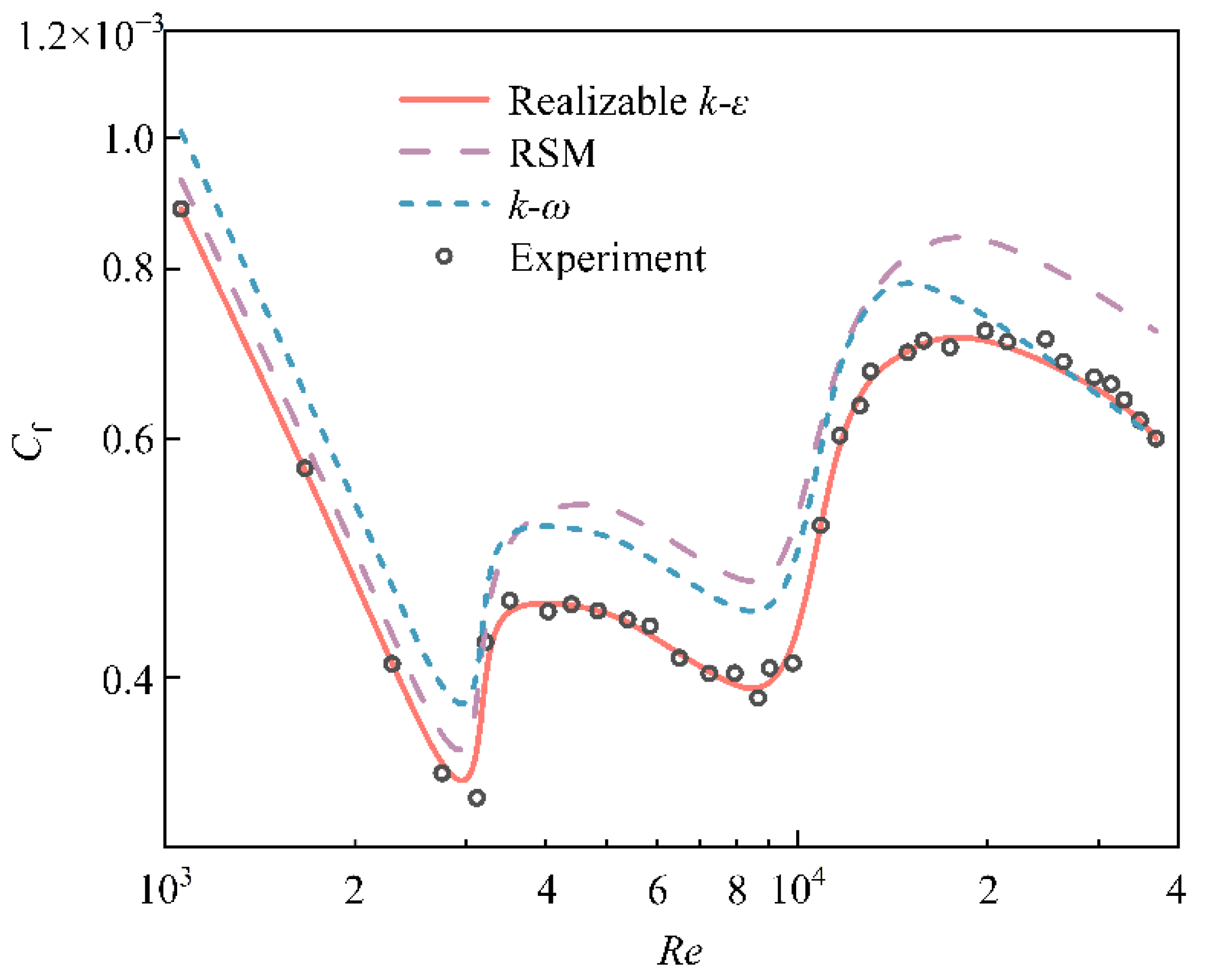
2.4. Turbulence Model Validation
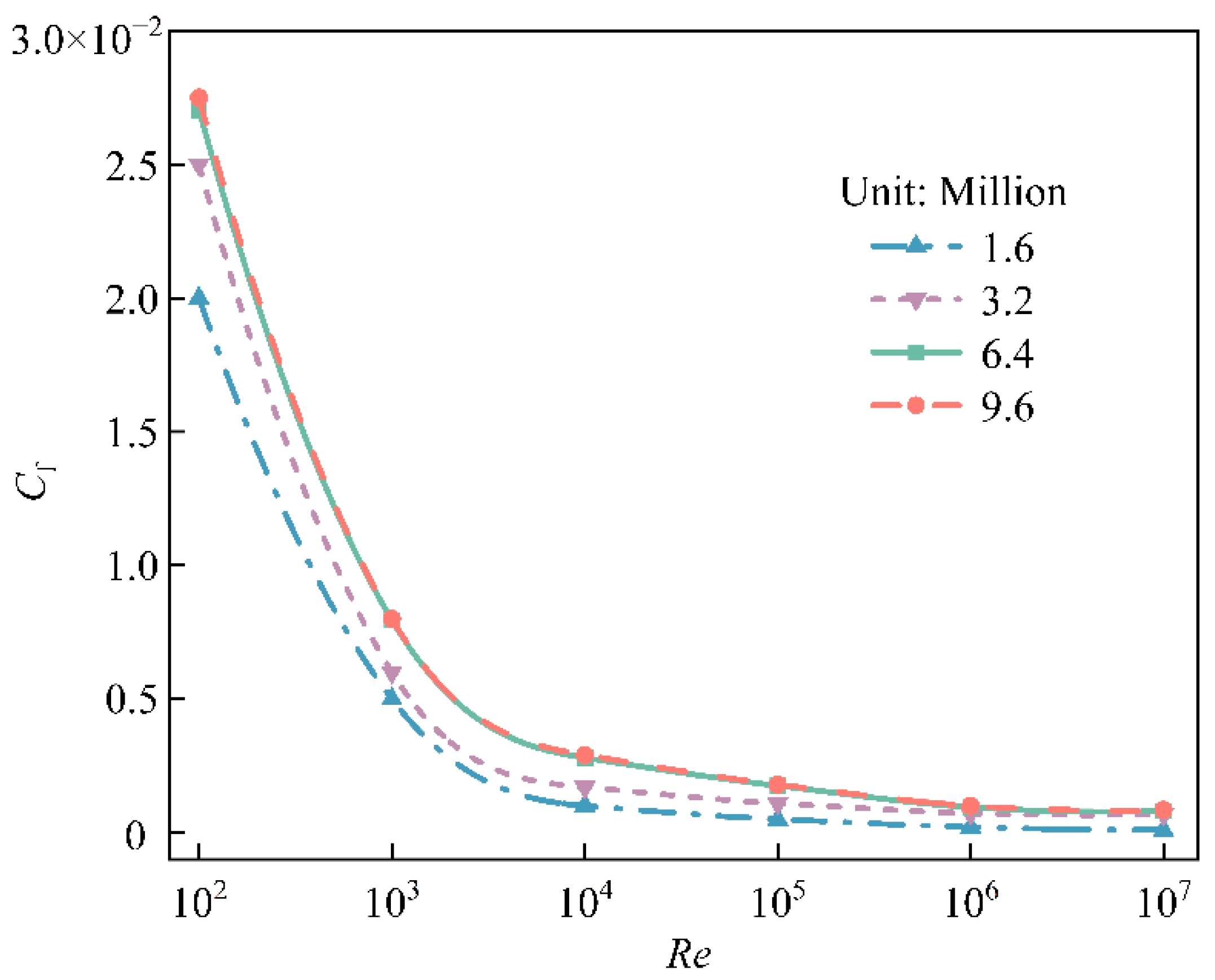
2.5. Grid Independence Validation
3. Results and Discussion
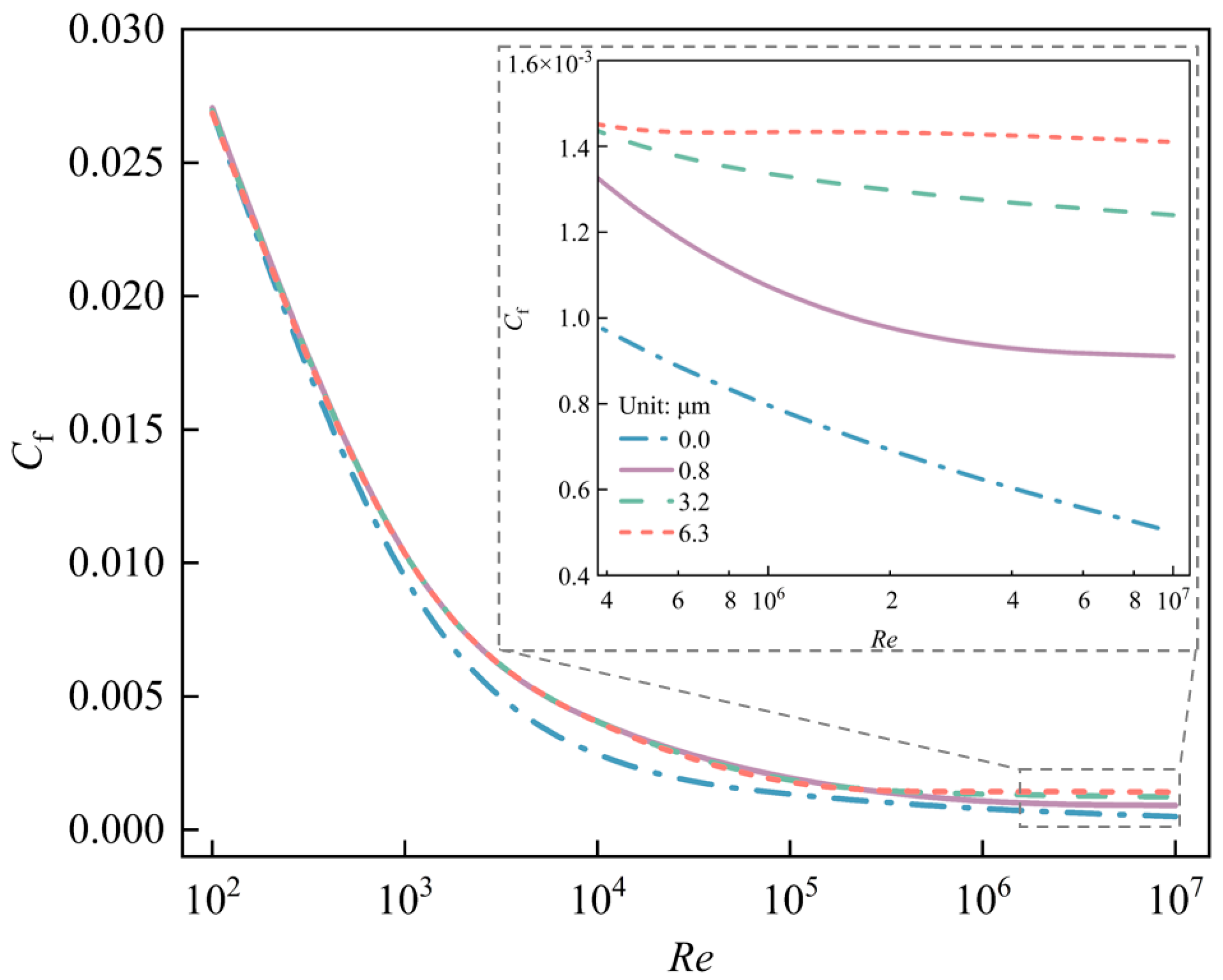
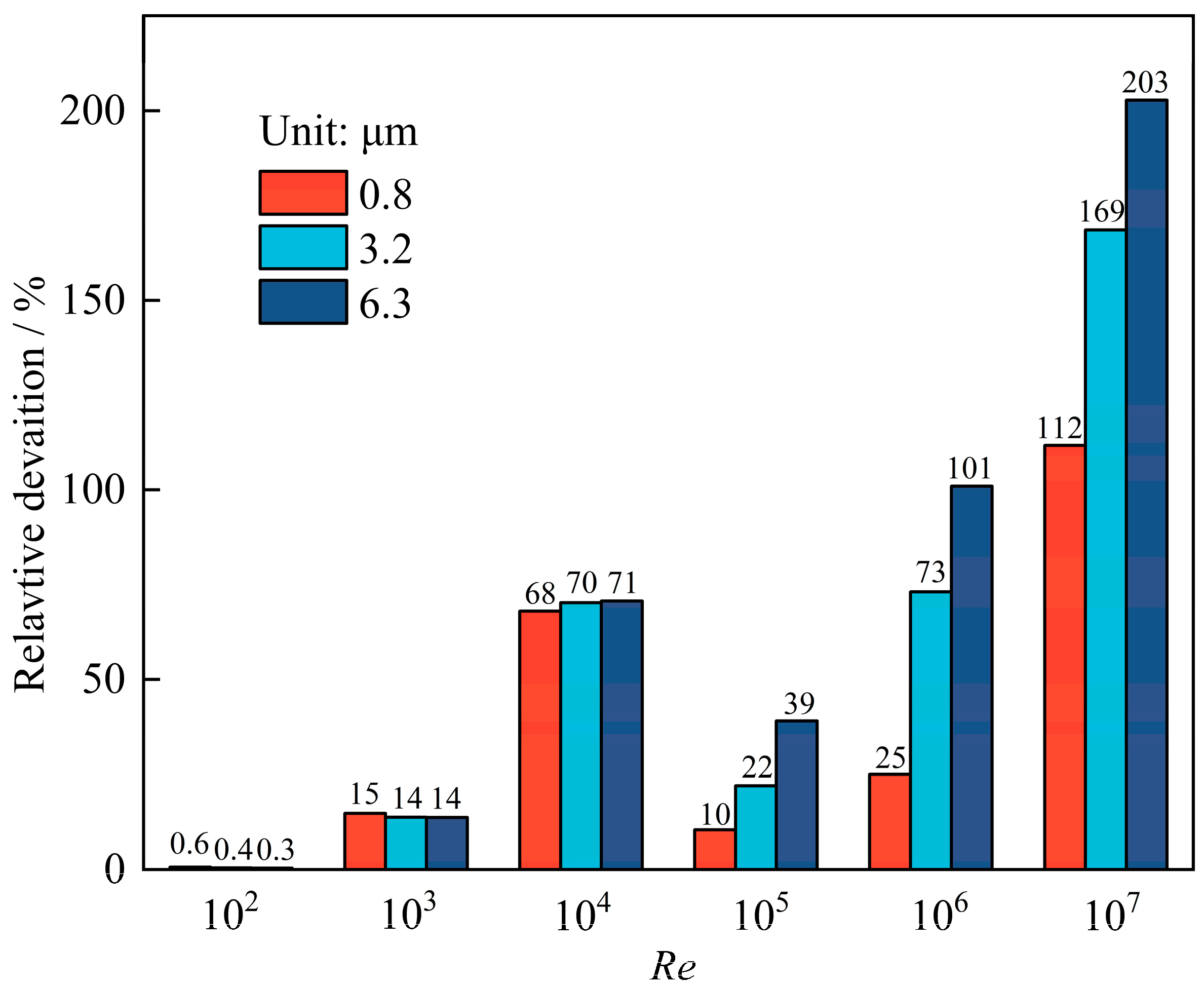
3.1. Effects of Reynolds Number and Surface Roughness on Skin Friction Coefficient
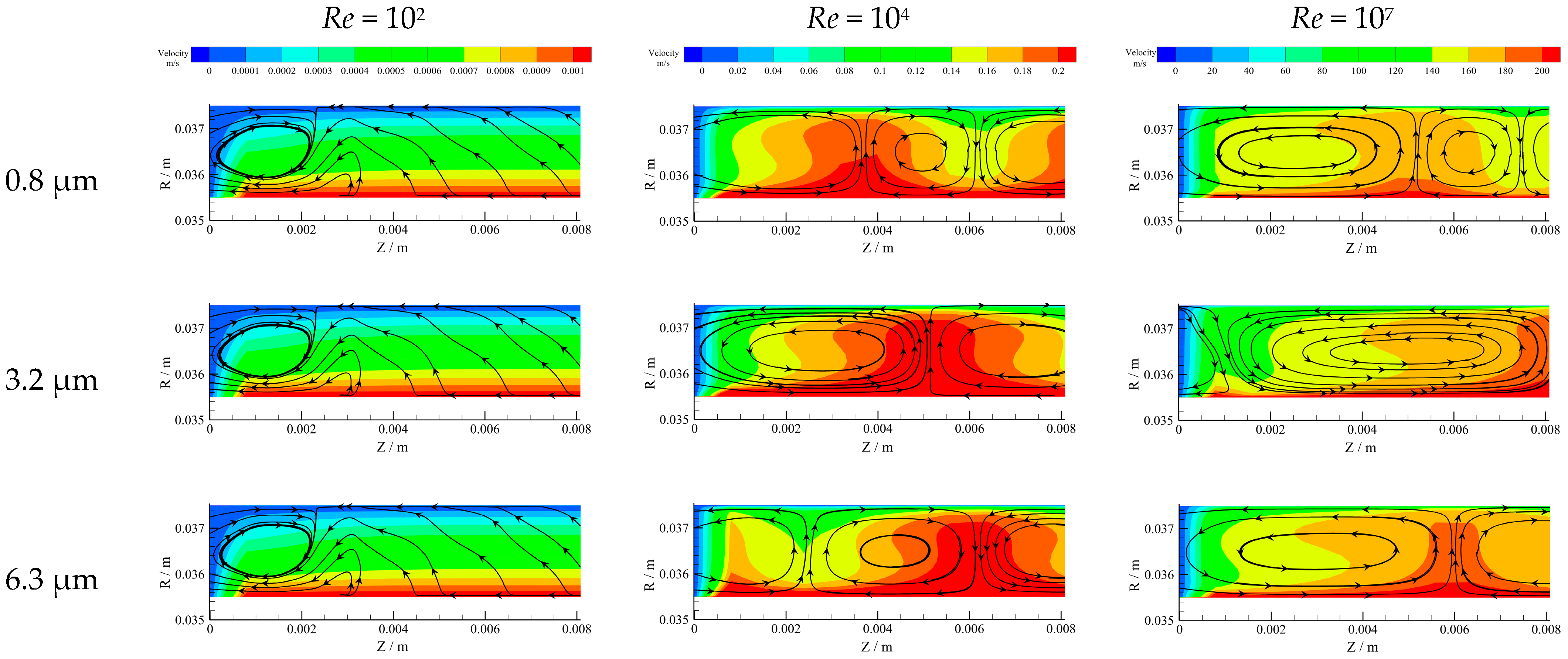
3.2. Effects of Reynolds Number and Surface Roughness on Flow Characteristics
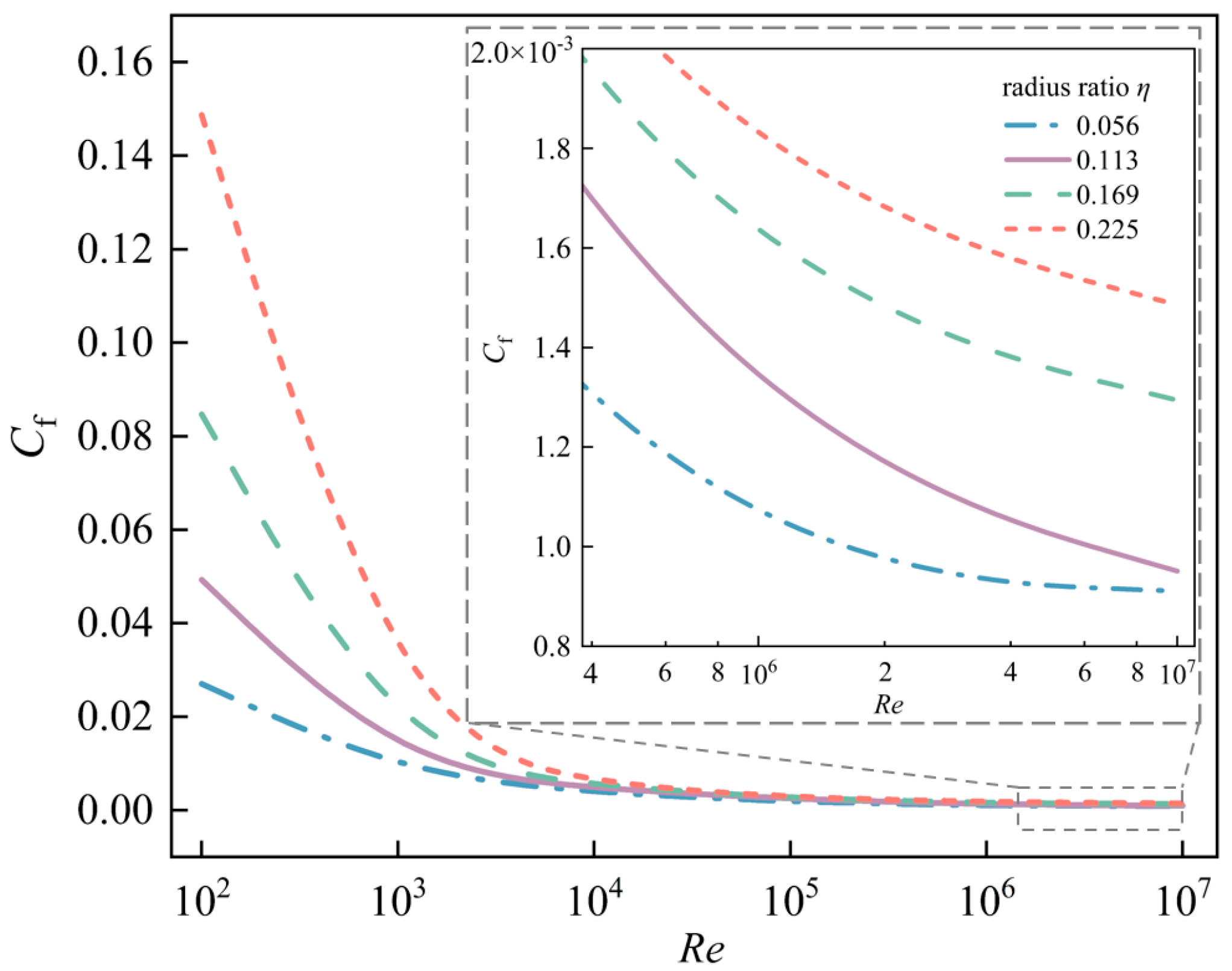
3.3. Effects of Radius Ratio on Skin Friction Coefficient and Flow Characteristics
4. Conclusions
- (1)
- Cf decreased as Re increased, and the rate of decrease was constant at low Re but it gradually decreased at high Re. In addition, for Re = 102, the relative deviations between the skin friction coefficients of smooth and rough walls of 0.3~0.6% indicated that Cf was not influenced by rough walls. However, when Re > 102, the relative deviations increased with Re and Ra, indicating that Cf was influenced by flow and rough walls because the grain was in blending or logarithmic law regions occurred, which impacted the flow.
- (2)
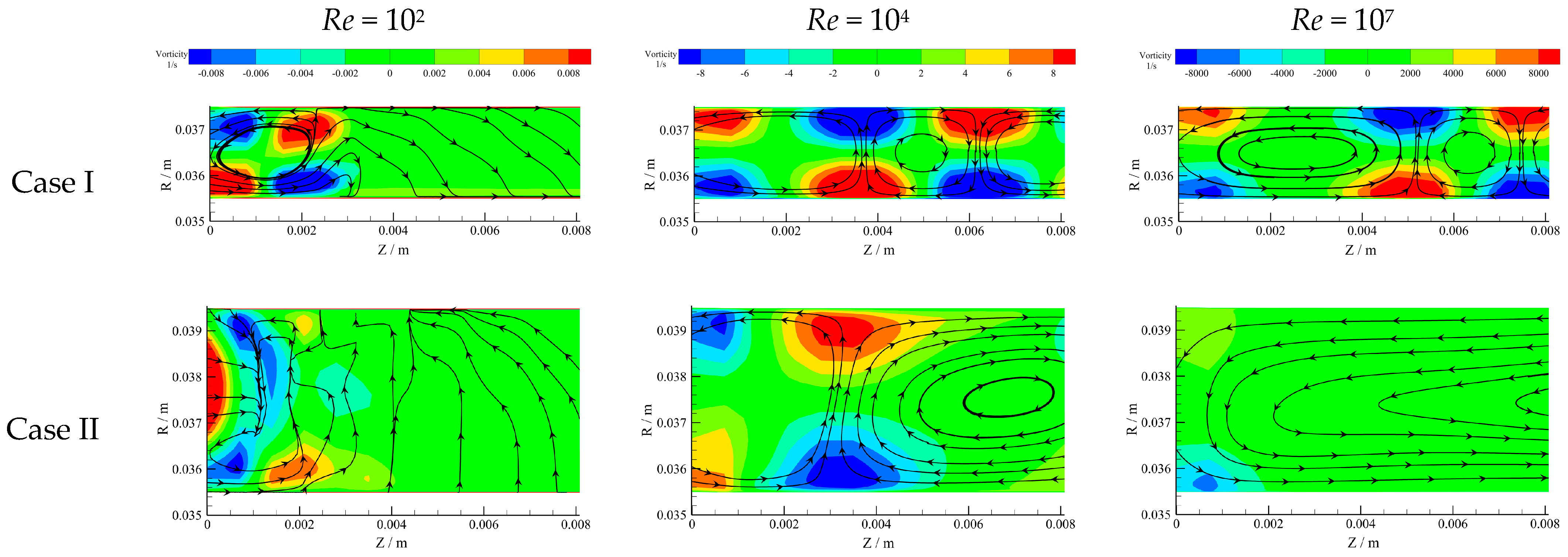
- When Re = 102, the flow was laminar and similar for different Ra, but when Re > 102, it transitioned to TC flow and periodic Taylor vortexes appeared, the number of which increased with Ra. The velocity could be divided into three regions, and the speed-stable region increased with Ra. The velocity gradient in speed-drop regions was larger than that in speed-stable regions. These results indicated that Ra influenced the thickness of the boundary layer and the flow at the center of the gap was more stable.
- (3)
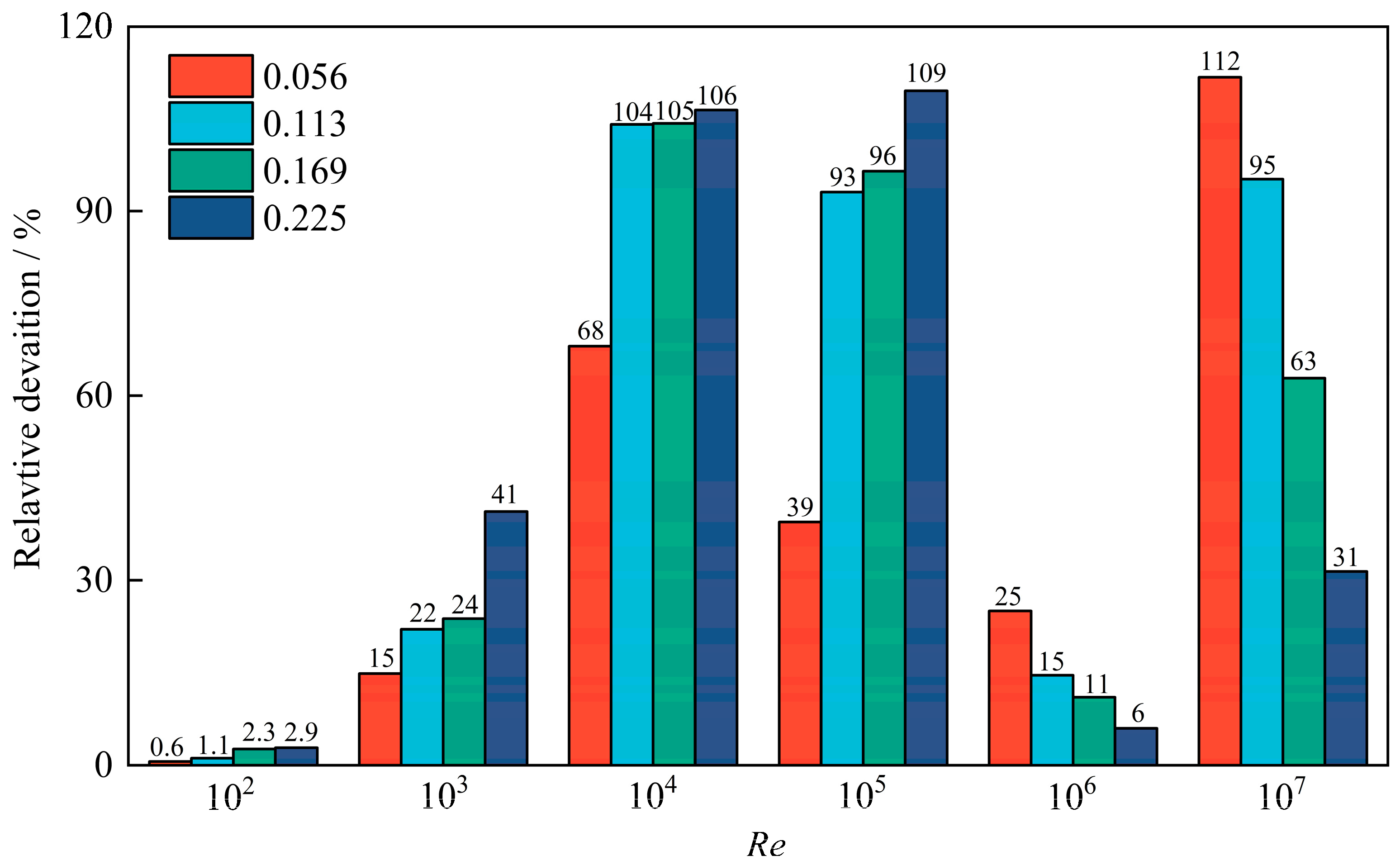
- Cf and the variation rate increased with η, indicating the Cf was seriously influenced by larger η. Moreover, the relative deviations increased with η when Re ≤ 105, which indicated that Cf was more easily influenced by rough walls for larger η under low Re conditions, since the interaction between rough walls and working fluid affected windage loss. However, the opposite was true when Re > 105 because the flow became the primary source of windage loss in a smaller gap width at high Re.
- (4)
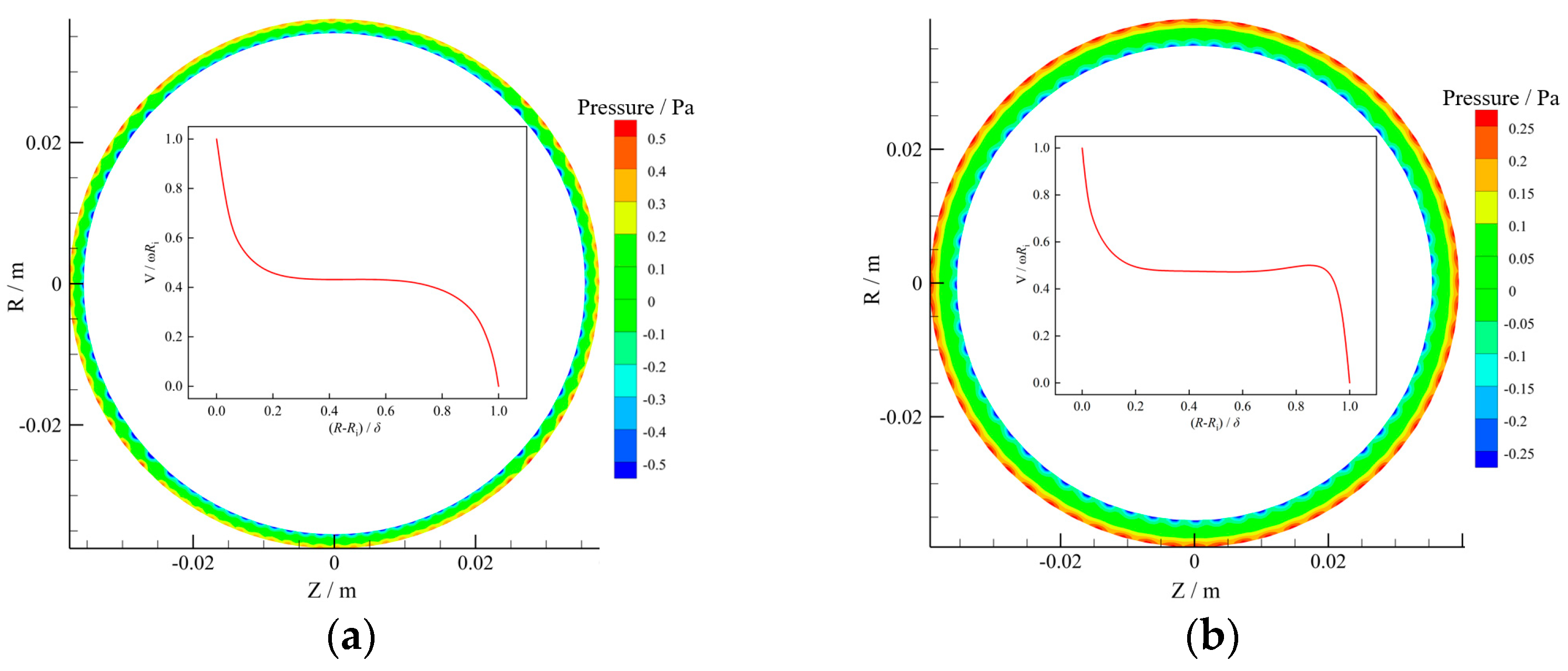
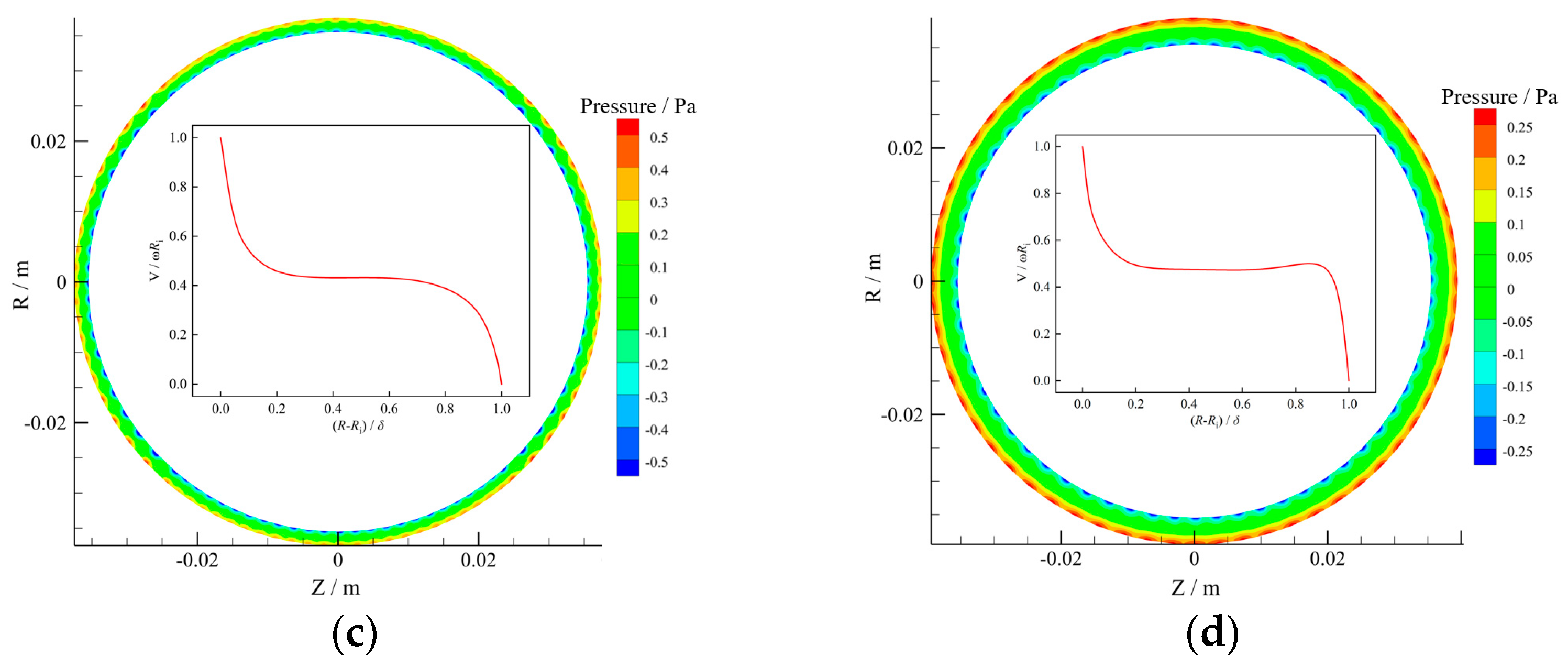
- The size of Taylor vortexes increased with η, leading to fewer vortexes. In addition, the pressure gradually increased from the rotational to stationary walls but decreased with increasing η as a whole. Additionally, there were periodic low-pressure and high-pressure regions near the walls due to Taylor vortexes in the gap, but the periodic high-pressure regions near the stationary walls decreased at larger η, since the number of Taylor vortexes decreased. Moreover, the velocity gradient near the stationary walls for Case IV was smaller than that of other Cases due to the significantly large η.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Sun, E.; Li, M.; Liu, H.; Zhu, B. Key issues and solution strategies for supercritical carbon dioxide coal fired power plant. Energy 2018, 157, 227–246. [Google Scholar] [CrossRef]
- Sathish, S.; Kumar, P. Equation of state based analytical formulation for optimization of sCO2 Brayton cycle. J. Supercrit. Fluids. 2021, 177, 105351. [Google Scholar] [CrossRef]
- Xue, J.; Nie, X.; Zhao, L.; Zhao, R.; Wang, J.; Yang, C.; Lin, A. Molecular dynamics investigation on shear viscosity of the mixed working fluid for supercritical CO2 Brayton cycle. J. Supercrit. Fluids 2022, 182, 105533. [Google Scholar] [CrossRef]
- Cao, R.; Li, Z.; Deng, Q.; Li, J. Design and aerodynamic performance investigations of supercritical carbon dioxide centrifugal compressor. In Proceedings of the ASME Turbo Expo, American Society of Mechanical Engineers (ASME), Virtual, 21–25 September 2020. [Google Scholar] [CrossRef]
- Hu, L.; Deng, Q.; Li, J.; Feng, Z. Model improvement for shaft-type windage loss with CO2. J. Supercrit. Fluids. 2022, 190, 105747. [Google Scholar] [CrossRef]
- Fleming, D.; Conboy, T.; Pash, J.; Rochau, G.; Fuller, R.; Holschuh, T.; Wright, S. Scaling Considerations for a Multi-Megawatt Class Supercritical CO2 Brayton Cycle and Commercialization; Sandia National Laboratory: Albuquerque, NM, USA, 2013.
- Wright, S. Summary of the Sandia Supercritical CO2 Development Program; Sandia National Laboratory: Albuquerque, NM, USA, 2011.
- Quiban, R.; Changenet, C.; Marchesse, Y.; Ville, F. Experimental investigations about the power loss transition between churning and windage for spur gears. J. Tribol. 2020, 143, 024501. [Google Scholar] [CrossRef]
- Zhao, Z.; Song, W.; Jin, Y.; Lu, J. Effect of rotational speed variation on the flow characteristics in the rotor-stator system cavity. Appl. Sci. 2021, 11, 11000. [Google Scholar] [CrossRef]
- Shen, G.; Yao, J.; Lou, W.; Chen, Y.; Guo, Y.; Xing, Y. An experimental investigation of streamwise and vertical wind fields on a typical three-dimensional hill. Appl. Sci. 2020, 10, 1463. [Google Scholar] [CrossRef]
- Conboy, T.; Wright, S.; Pasch, J.; Fleming, D.; Rochau, D.; Fuller, R. Performance characteristics of an operating supercritical CO2 Brayton cycle. J. Eng. Gas Turbines Power. 2012, 134, 111703. [Google Scholar] [CrossRef]
- Anderson, K.; Lin, J.; Namara, M.; Magri, V. CFD study of forced air cooling and windage losses in a high speed electric motor. J. Electron. Cool. Therm. Control. 2015, 5, 27–44. [Google Scholar] [CrossRef]
- Asami, F.; Miyatake, M.; Yoshimoto, S.; Tanaka, E.; Yamauchi, T. A method of reducing windage power loss of a high-speed motor using a viscous vacuum pump. Precis. Eng. 2017, 48, 60–66. [Google Scholar] [CrossRef]
- Kiyota, K.; Kakishima, T.; Chiba, A. Estimation and comparison of the windage loss of a 60 kW switched reluctance motor for hybrid electric vehicles. In Proceedings of the 2014 International Power Electronics Conference, Hiroshima, Japan, 18–21 May 2014. [Google Scholar] [CrossRef]
- Liu, M.; Sixel, W.; Ding, H.; Sarlioglu, B. Investigation of rotor structure influence on the windage loss and efficiency of FSPM machine. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018. [Google Scholar] [CrossRef]
- Sun, D.; Zhou, M.; Zhao, H.; Liu, J.; Fei, C.; Li, H. Numerical and experimental investigations on windage heating effect of labyrinth seals. J. Aerosp. Eng. 2020, 33, 04020057. [Google Scholar] [CrossRef]
- Nachouane, A.; Abdelli, A.; Friedrich, G.; Vivier, S. Estimation of windage losses inside very narrow air gaps of high speed electrical machines without an internal ventilation using CFD methods. In Proceedings of the 2016 International Conference on Electrical Machines, Lausanne, Switzerland, 4–7 September 2016. [Google Scholar] [CrossRef]
- Wendt, V. Turbulente strmungen zwischen zwei rotierenden konaxialen zylinder. Ingenieur-Archiv 1933, 4, 577–595. [Google Scholar] [CrossRef]
- Bilgen, E.; Boulos, R. Functional dependence of torque coefficient of coaxial cylinders on gap width and Reynolds numbers. J. Fluid. Eng. 1973, 95, 122–126. [Google Scholar] [CrossRef]
- Yamada, Y. Torque resistance of a flow between rotating co-axial cylinders having axial flow. Bull. JSME 1962, 186, 634–642. [Google Scholar] [CrossRef]
- Vrancik, J. Prediction of Windage Power Loss in Alternators; NASA: Washington, DC, USA, 1968.
- Deng, Q.; Hu, L.; Zhao, Y.; Yang, G.; Li, J.; Feng, Z. Verification of windage loss model and flow characteristic analysis in shaft-type gap. J. Xi’an Jiaotong. Univ. 2022, 56, 57–66. [Google Scholar] [CrossRef]
- Sarri, J. Thermal Analysis of High-Speed Induction Machines; Helsinki University of Technology: Espoo, Finland, 1998. [Google Scholar]
- Hu, L.; Deng, Q.; Zhao, Z.; Li, J.; Feng, Z. Flow characteristics and windage loss of CO2 in shaft-type rotor-stator gap. J. Eng. Thermophys. 2022, 43, 647–655. [Google Scholar]
- Theodorsen, T.; Regier, A. Experiments on Drag of Revolving Disks, Cylinders, and Streamline Rods at High Speeds; NACA: Boston, MA, USA, 1944.
- Nakabayashi, K.; Yamada, Y.; Kishimoto, T. Viscous frictional torque in the flow between two concentric rotating rough cylinders. J. Fluid Mech. 1982, 119, 409–422. [Google Scholar] [CrossRef]
- Rasmussen, E.; Yellapantula, S.; Martin, M. How equation of state selection impacts accuracy near the critical point: Forced convection supercritical CO2 flow over a cylinder. J. Supercrit. Fluids 2021, 171, 105141. [Google Scholar] [CrossRef]
- NIST Standard Reference Database 23. NIST Thermodynamic and Transport Properties of Refrigerants and Refrigerant Mixtures-REFPROP; Version 6.01; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998. [Google Scholar]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple point temperature to 1100 K at pressures up to 800 MPa. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Qin, K.; Li, D.; Huang, C.; Sun, Y.; Wang, J.; Luo, K. Numerical investigation on heat transfer characteristics of Taylor Couette flows operating with CO2. Appl. Therm. Eng. 2020, 163, 114570. [Google Scholar] [CrossRef]
- Adebayo, D.; Rona, A. Numerical investigation of the three-dimensional pressure distribution in Taylor Couette flow. J. Fluids Eng. 2017, 139, 111201. [Google Scholar] [CrossRef]
- Tao, W. Numerical Heat Transfer, 2nd ed.; Xi’an Jiaotong University Press: Xi’an, China, 2010. [Google Scholar]
- ANSYS. ANSYS Fluent Theory Guide 2020 R2; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]

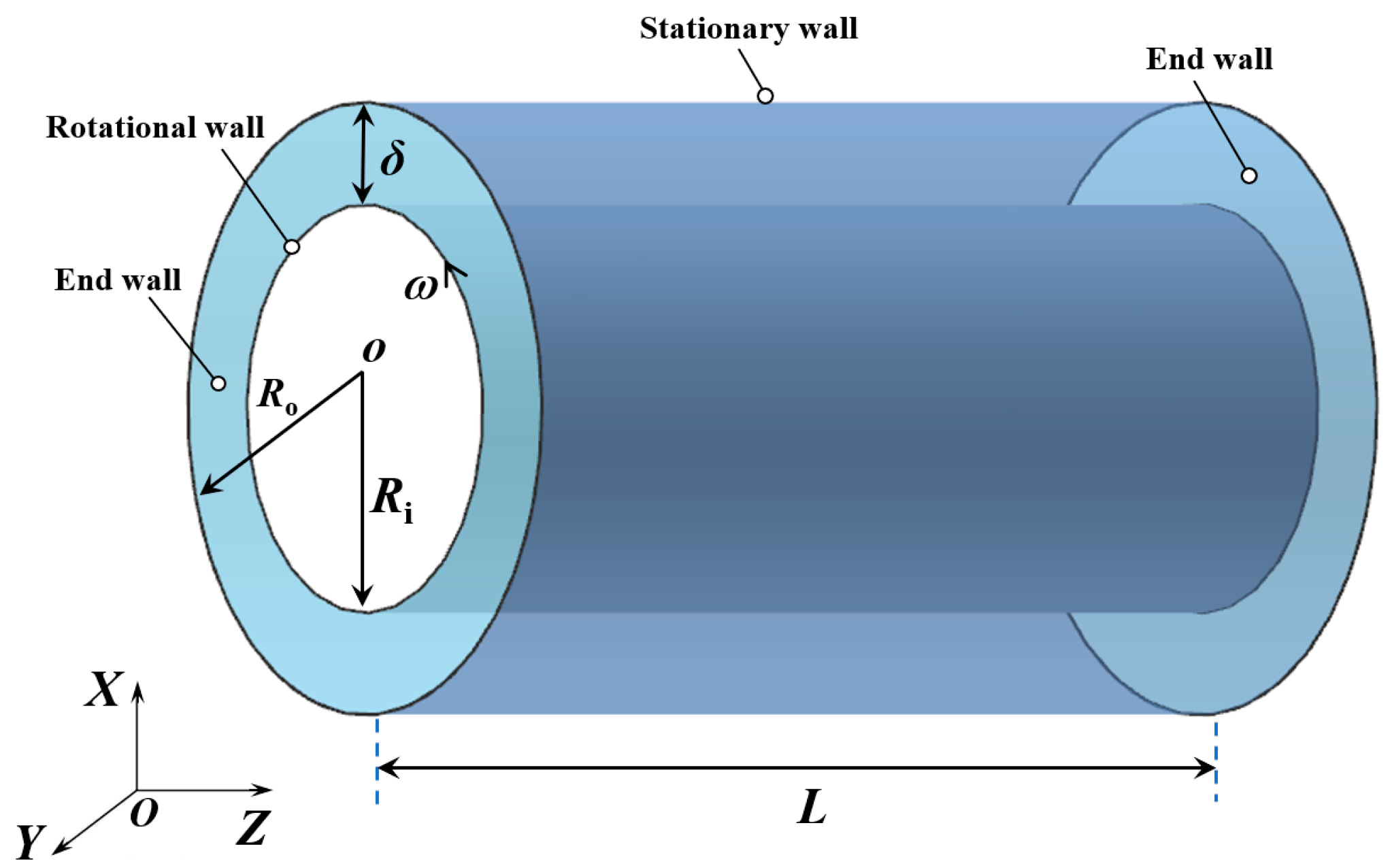
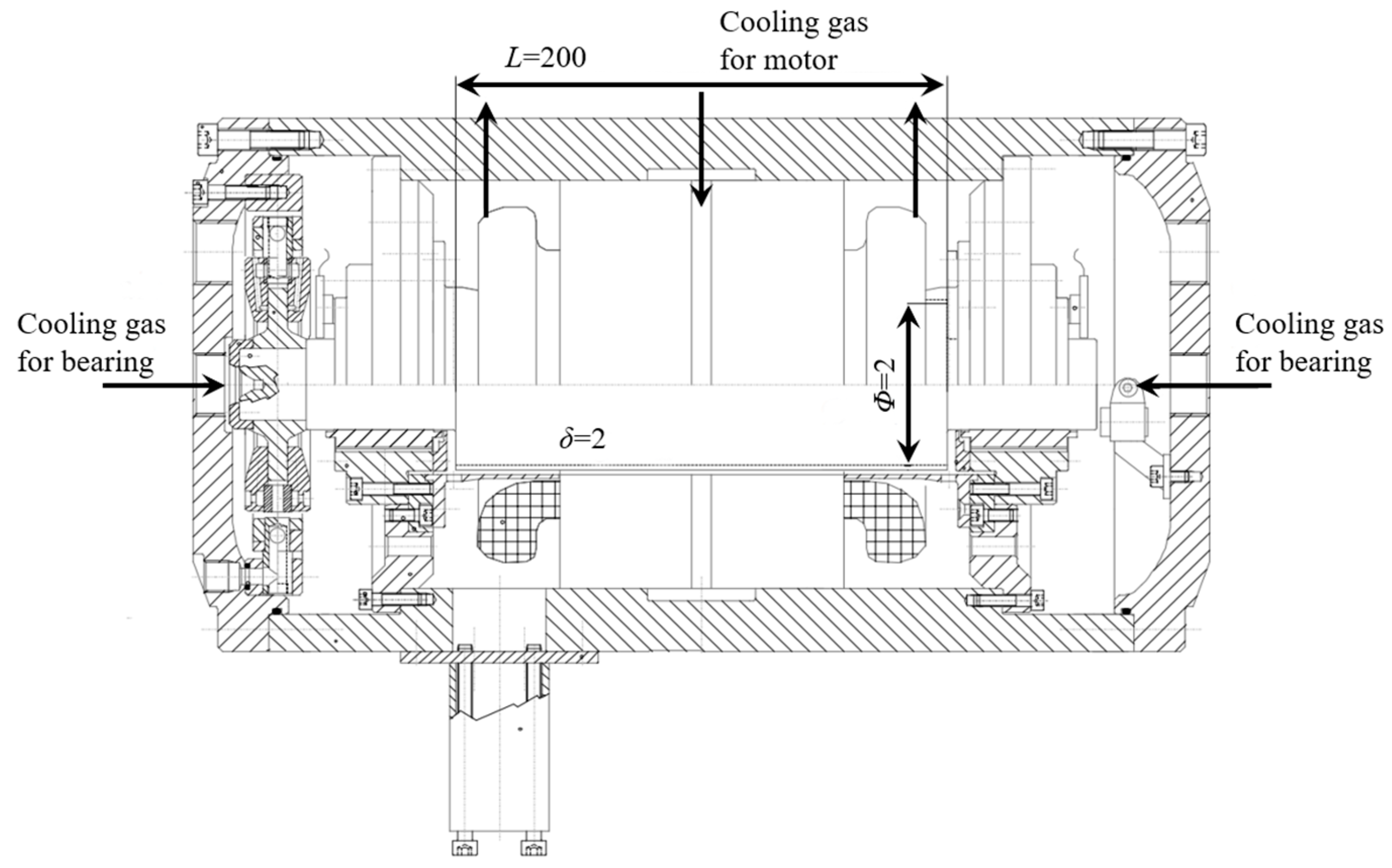



| Description | Case I | Case II | Case III | Case IV | Unit |
|---|---|---|---|---|---|
| Outer radius Ro | 37.5 | 39.5 | 41.5 | 43.5 | mm |
| Gap width δ | 2 | 4 | 6 | 8 | mm |
| Radius ratio η | 0.056 | 0.113 | 0.169 | 0.225 |
| Description | Value | Unit |
|---|---|---|
| Inner radius Ri | 30.7 | mm |
| Outer radius Ro | 33.6 | mm |
| Gap width δ | 2.9 | mm |
| Axial length L | 90 | mm |
| Surface roughness Ra | 0.211 | mm |
| Re | Ra/mm | Cf |
|---|---|---|
| 102 | 0 | 2.69 × 10−2 |
| 0.8 | 2.70 × 10−2 | |
| 3.2 | 2.70 × 10−2 | |
| 6.3 | 2.69 × 10−2 | |
| 103 | 0 | 6.92 × 10−3 |
| 0.8 | 7.96 × 10−3 | |
| 3.2 | 7.88 × 10−3 | |
| 6.3 | 7.88 × 10−3 | |
| 104 | 0 | 2.19 × 10−3 |
| 0.8 | 3.68 × 10−3 | |
| 3.2 | 3.72 × 10−3 | |
| 6.3 | 3.74 × 10−3 | |
| 105 | 0 | 1.26 × 10−3 |
| 0.8 | 1.39 × 10−3 | |
| 3.2 | 1.54 × 10−3 | |
| 6.3 | 1.75 × 10−3 | |
| 106 | 0 | 7.55 × 10−4 |
| 0.8 | 9.44 × 10−4 | |
| 3.2 | 1.31 × 10−3 | |
| 6.3 | 1.52 × 10−3 | |
| 107 | 0 | 4.30 × 10−4 |
| 0.8 | 9.11 × 10−4 | |
| 3.2 | 1.16 × 10−3 | |
| 6.3 | 1.30 × 10−3 |
| Re | Ra/mm | Cf |
|---|---|---|
| 102 | 0.056 | 2.70 × 10−2 |
| 0.113 | 4.93 × 10−2 | |
| 0.169 | 8.47 × 10−2 | |
| 0.225 | 1.49 × 10−1 | |
| 103 | 0.056 | 7.96 × 10−3 |
| 0.113 | 9.11 × 10−3 | |
| 0.169 | 1.09 × 10−2 | |
| 0.225 | 1.56 × 10−2 | |
| 104 | 0.056 | 3.68 × 10−3 |
| 0.113 | 4.55 × 10−3 | |
| 0.169 | 5.16 × 10−3 | |
| 0.225 | 5.49 × 10−3 | |
| 105 | 0.056 | 1.39 × 10−3 |
| 0.113 | 2.35 × 10−3 | |
| 0.169 | 2.54 × 10−3 | |
| 0.225 | 2.68 × 10−3 | |
| 106 | 0.056 | 9.44 × 10−4 |
| 0.113 | 1.19 × 10−3 | |
| 0.169 | 1.50 × 10−3 | |
| 0.225 | 1.71 × 10−3 | |
| 107 | 0.056 | 9.11 × 10−4 |
| 0.113 | 9.51 × 10−4 | |
| 0.169 | 1.29 × 10−3 | |
| 0.225 | 1.49 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Deng, Q.; Liu, Z.; Li, J.; Feng, Z. Effects of Surface Roughness on Windage Loss and Flow Characteristics in Shaft-Type Gap with Critical CO2. Appl. Sci. 2022, 12, 12631. https://doi.org/10.3390/app122412631
Hu L, Deng Q, Liu Z, Li J, Feng Z. Effects of Surface Roughness on Windage Loss and Flow Characteristics in Shaft-Type Gap with Critical CO2. Applied Sciences. 2022; 12(24):12631. https://doi.org/10.3390/app122412631
Chicago/Turabian StyleHu, Lehao, Qinghua Deng, Zhouyang Liu, Jun Li, and Zhenping Feng. 2022. "Effects of Surface Roughness on Windage Loss and Flow Characteristics in Shaft-Type Gap with Critical CO2" Applied Sciences 12, no. 24: 12631. https://doi.org/10.3390/app122412631
APA StyleHu, L., Deng, Q., Liu, Z., Li, J., & Feng, Z. (2022). Effects of Surface Roughness on Windage Loss and Flow Characteristics in Shaft-Type Gap with Critical CO2. Applied Sciences, 12(24), 12631. https://doi.org/10.3390/app122412631






