Artificial Intelligence (AI)-Based Evaluation of Bolt Loosening Using Vibro-Acoustic Modulation (VAM) Features from a Combination of Simulation and Experiments
Abstract
1. Introduction
- The nonlinear coefficients are defined using the amplitudes of the spectral linear and nonlinear components. Consequently, such coefficients may vary inconsistently with the theoretical trend for the CAN model when the amplitudes are affected by the other nonlinear sources.
- The above-mentioned potential nonlinearities and CAN are always affected by the same factors (e.g., contact, temperature, and friction). So, it is challenging to quantitatively decouple the interferences of different mechanisms by controlling the experimental conditions [20].
- Proposing a new theoretical damage index by considering the combined influences of the diverse nonlinear mechanisms needs more effort for accurate modeling.
2. Theoretical Background
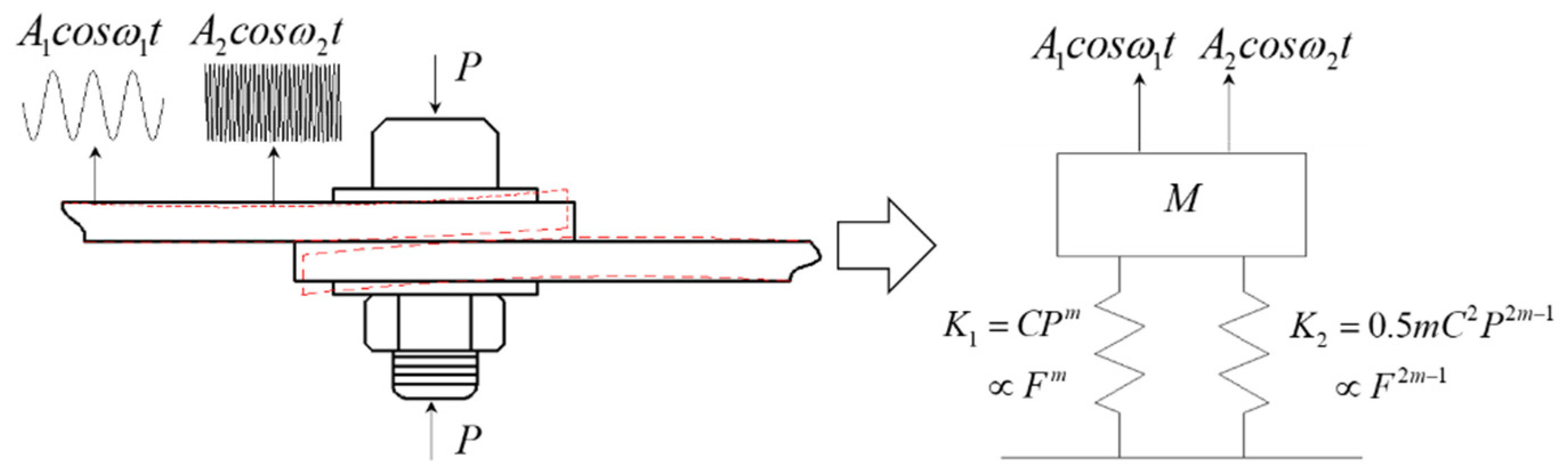
2.1. Contact Acoustic Nonlinearity
2.2. Dissipative Nonlinearity
2.3. Material Intrinsic Nonlinearity
3. Finite Element Model and Experiment
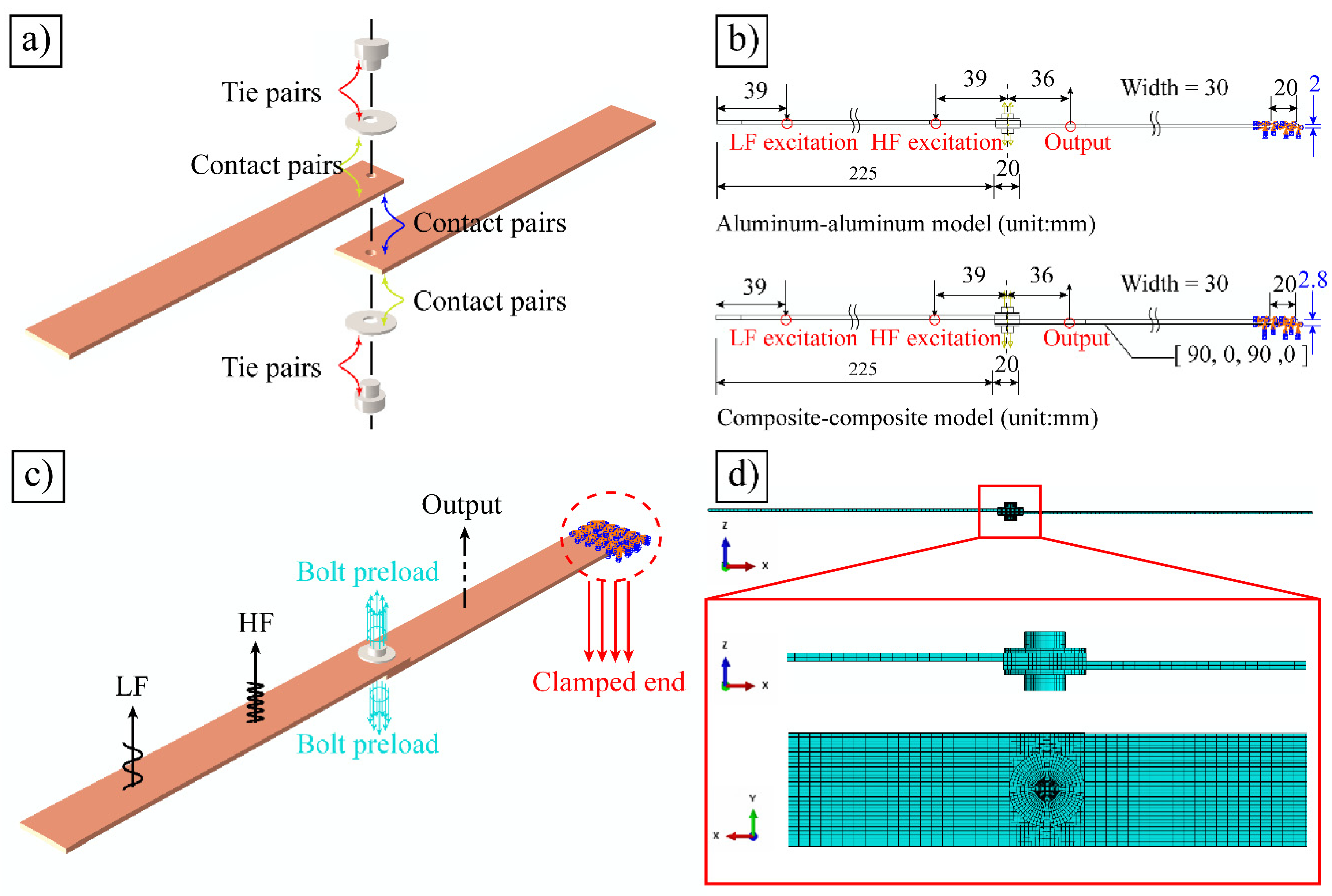
3.1. Finite Element Model
3.2. Experimental Setup
4. VAM Responses of Bolted Joints
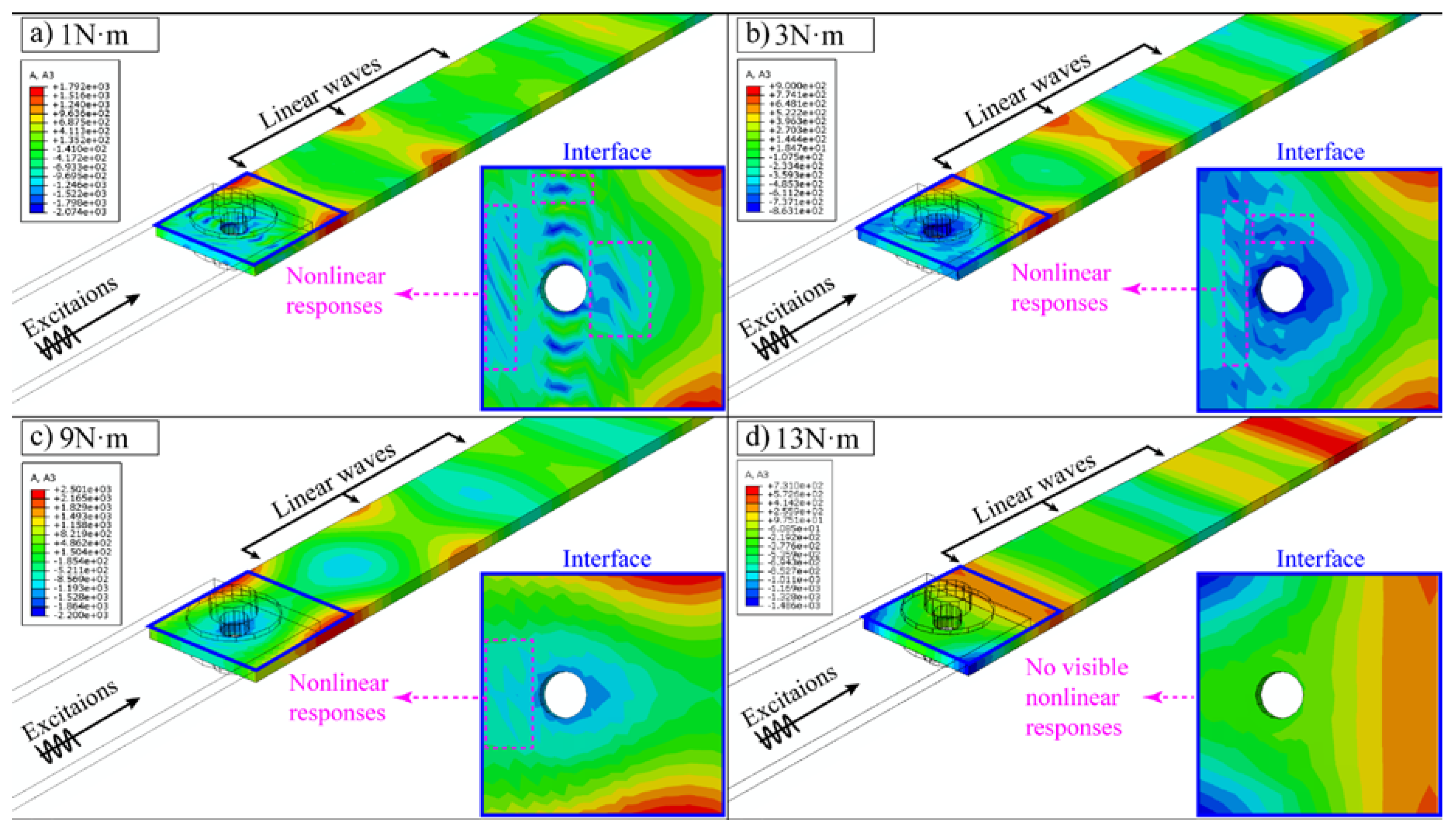
4.1. Acceleration Contour
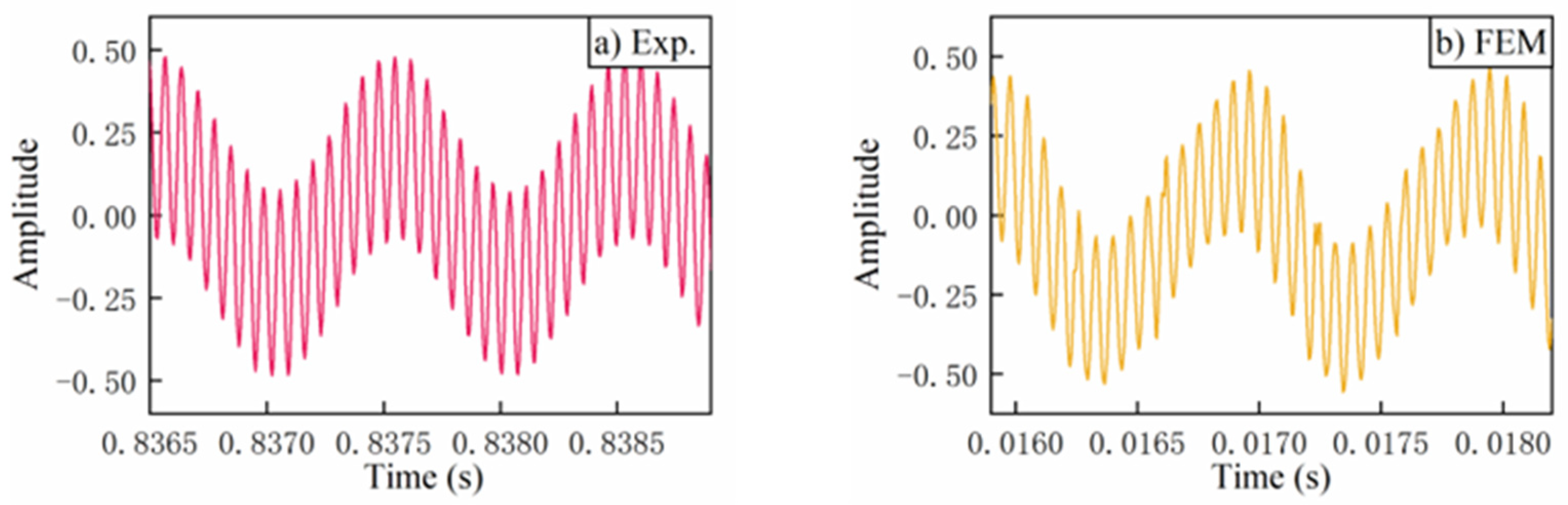
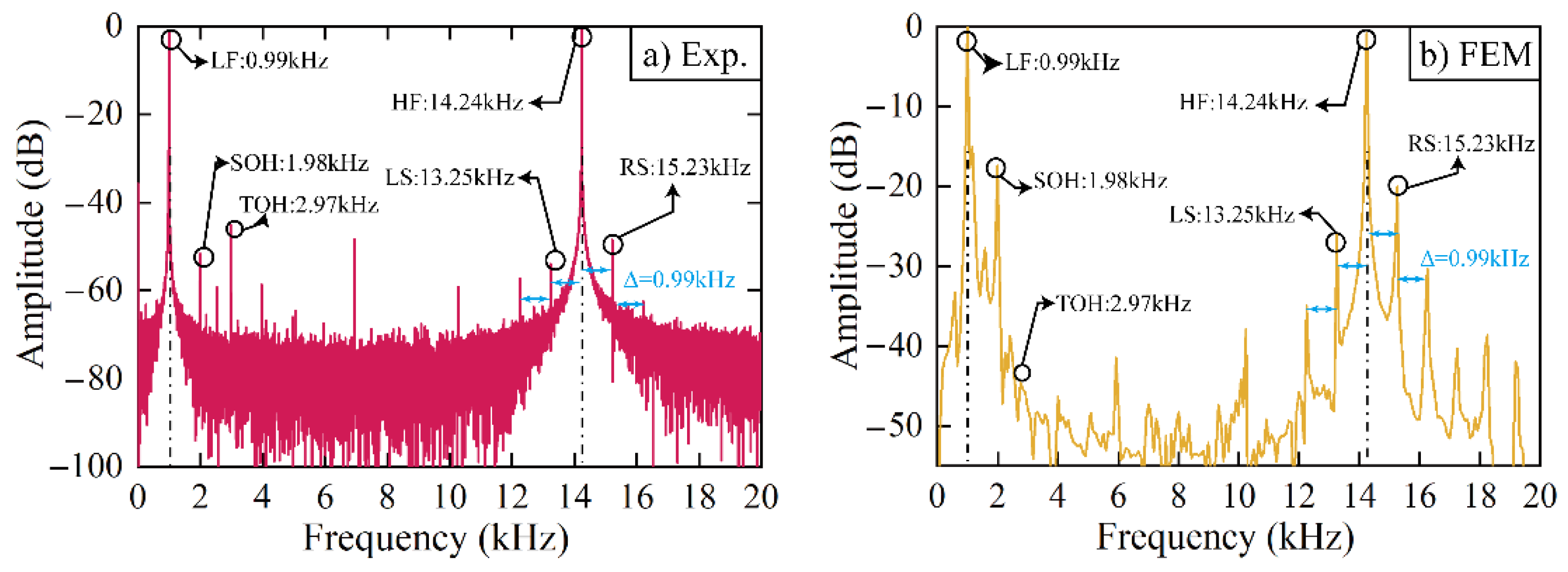
4.2. Collected Signals
5. Nonlinear Coefficients of Joints under Different Preloads
5.1. Influence of Dissipative Nonlinearity
5.2. Influence of Intrinsic Nonlinearity
5.3. Combined Results of Nonlinearities
6. Intelligent Evaluation of Bolt Preload Using SVR
- A mapping relation can be established between the amplitude and preload according to the results in Section 5. The sample consisting of multiple features (i.e., LF, HF, SOH, TOH, and SBs) can improve the accuracy of the load evaluation even when the joint is under the influences of different nonlinearities.
- SVR is a classical machine learning method and has been well tested in long-term applications. Moreover, a fairly simple model without extensive trials and errors can certify the feasibility of the AI evaluation using the nonlinear features.
6.1. Algorithm
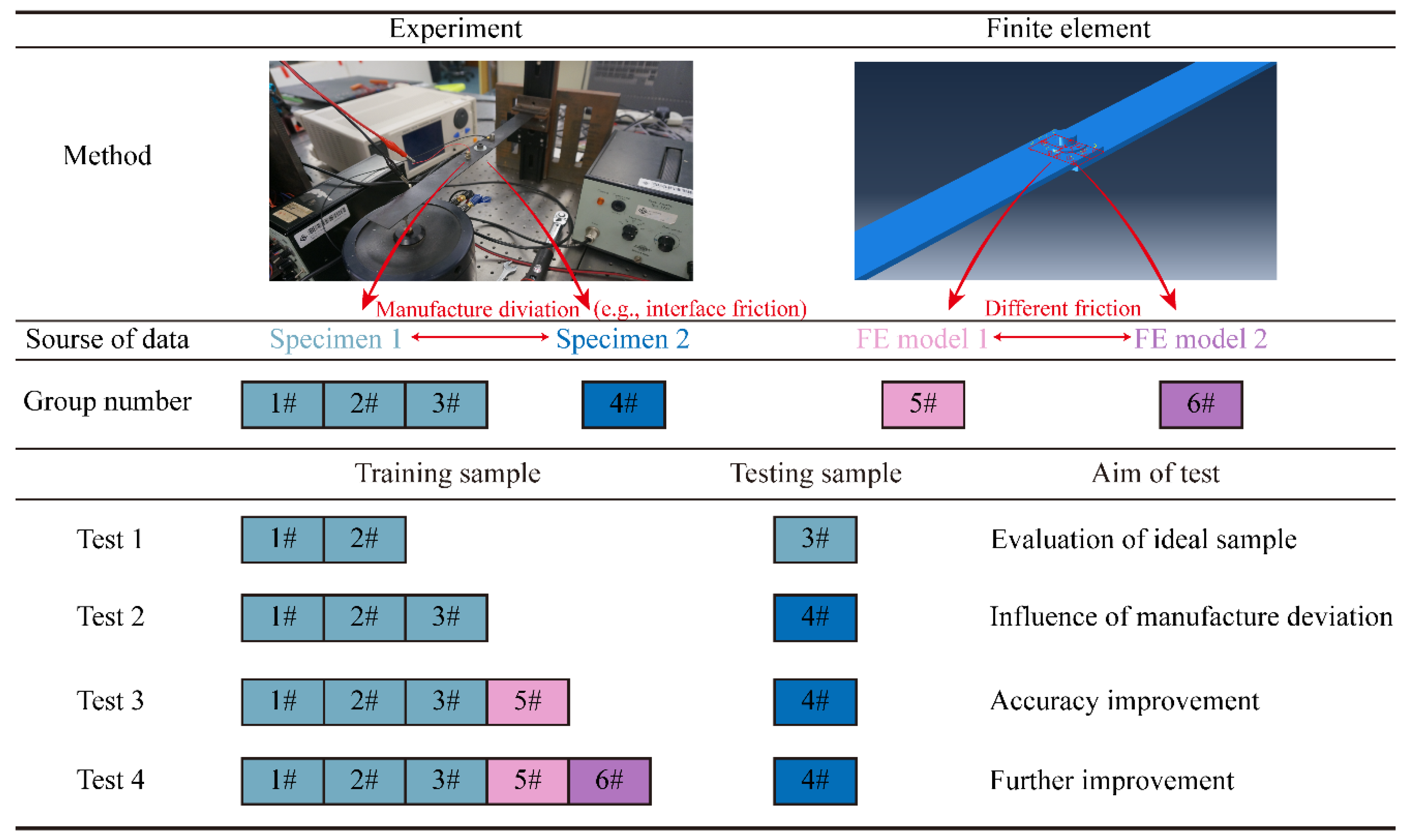
6.2. Arrangement for SVR Modeling and Prediction
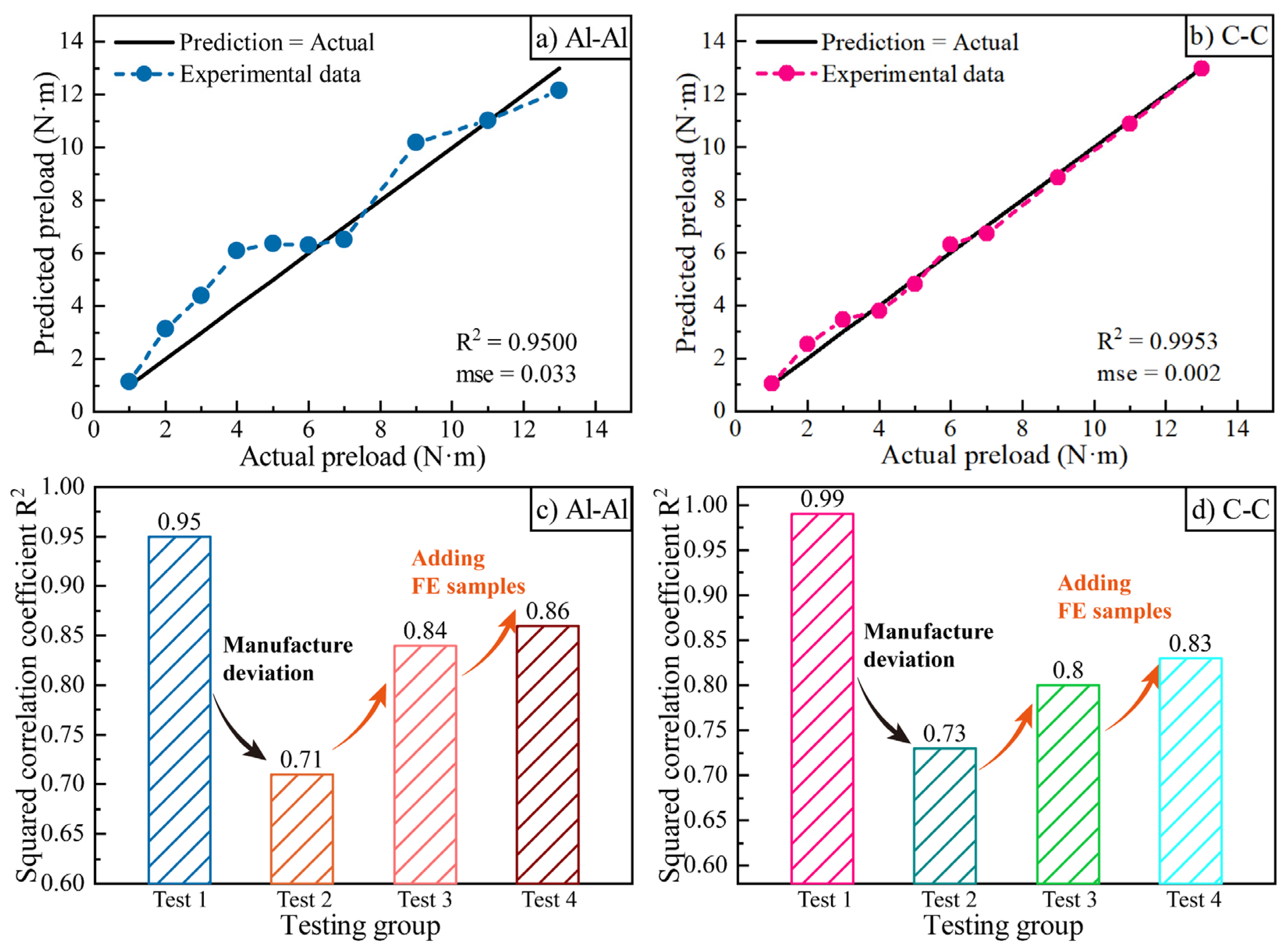
6.3. Results of Intelligent Prediction
6.4. Discussion
- The simulated data have good applicability for considering deviations in the experimental specimens. This method is cost-efficient by avoiding collecting many experimental samples, which are not accessible in certain circumstances (e.g., small-sample applications).
- However, the simulated results can change remarkably with changes in the FE parameters. This is due to the error accumulation during the iterative calculation of FE software. So, it would be better if FE modeling was based on adequate advanced knowledge of the potential influence factors (such as their types and values).
- Despite Point 2, the prediction robustness can still be guaranteed when inputting enough experimental results as training data, which enables the simulated samples to fully consider the different conditions.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yun, H.; Rayhana, R.; Pant, S.; Genest, M.; Liu, Z. Nonlinear ultrasonic testing and data analytics for damage characterization: A review. Measurement 2021, 186, 110155. [Google Scholar] [CrossRef]
- Du, F.; Wu, S.; Xing, S.; Xu, C.; Su, Z. Temperature compensation to guided wave-based monitoring of bolt loosening using an attention-based multi-task network. Struct. Health Monit. 2022. [Google Scholar] [CrossRef]
- Chen, D.; Shen, Z.; Fu, R.; Yuan, B.; Huo, L. Coda wave interferometry-based very early stage bolt looseness monitoring using a single piezoceramic transducer. Smart Mater. Struct. 2022, 31, 035030. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Liao, Y.; Su, Z.; Xiao, Y. Contact acoustic nonlinearity (CAN)-based continuous monitoring of bolt loosening: Hybrid use of high-order harmonics and spectral sidebands. Mech. Syst. Signal Process. 2018, 103, 280–294. [Google Scholar] [CrossRef]
- Guan, R.; Lu, Y.; Wang, K.; Su, Z. Fatigue crack detection in pipes with multiple mode nonlinear guided waves. Struct. Health Monit. 2018, 18, 180–192. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Ostachowicz, W. Impact induced damage assessment by means of Lamb wave image processing. Mech. Syst. Signal Process. 2018, 102, 23–36. [Google Scholar] [CrossRef]
- Solodov, I.Y.; Krohn, N.; Busse, G. CAN: An example of nonclassical acoustic nonlinearity in solids. Ultrasonics 2002, 40, 621–625. [Google Scholar] [CrossRef]
- Yang, Y.; Ng, C.-T.; Kotousov, A. Bolted joint integrity monitoring with second harmonic generated by guided waves. Struct. Health Monit. 2018, 18, 193–204. [Google Scholar] [CrossRef]
- Zhang, M.; Shen, Y.; Xiao, L.; Qu, W. Application of subharmonic resonance for the detection of bolted joint looseness. Nonlinear Dyn. 2017, 88, 1643–1653. [Google Scholar] [CrossRef]
- Croxford, A.J.; Wilcox, P.D.; Drinkwater, B.W.; Nagy, P.B. The use of non-collinear mixing for nonlinear ultrasonic detection of plasticity and fatigue. J. Acoust. Soc. Am. 2009, 126, 117–122. [Google Scholar] [CrossRef]
- Jiao, J.; Meng, X.; He, C.; Wu, B. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates. NDT E Int. 2017, 85, 63–71. [Google Scholar]
- Huan, Q.; Chen, M.; Su, Z.; Li, F. A high-resolution structural health monitoring system based on SH wave piezoelectric transducers phased array. Ultrasonics 2019, 97, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Xu, H.; Liao, Y.; Su, Z.; Xiao, Y. Vibro-acoustic modulation (VAM)-inspired structural integrity monitoring and its applications to bolted composite joints. Compos. Struct. 2017, 176, 505–515. [Google Scholar] [CrossRef]
- Wang, F.; Song, G. Bolt early looseness monitoring using modified vibro-acoustic modulation by time-reversal. Mech. Syst. Signal Process. 2019, 130, 349–360. [Google Scholar] [CrossRef]
- Wang, F.; Song, G. Monitoring of multi-bolt connection looseness using a novel vibro-acoustic method. Nonlinear Dyn. 2020, 100, 243–254. [Google Scholar] [CrossRef]
- Qin, X.; Peng, C.; Zhao, G.; Ju, Z.; Lv, S.; Jiang, M.; Sui, Q.; Jia, L. Full life-cycle monitoring and earlier warning for bolt joint loosening using modified vibro-acoustic modulation. Mech. Syst. Signal Process. 2022, 162, 108054. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveev, L.A.; Matveyev, A.L. Elastic-wave modulation approach to crack detection: Comparison of conventional modulation and higher-order interactions. NDT E Int. 2011, 44, 21–31. [Google Scholar] [CrossRef]
- Klepka, A.; Staszewski, W.; Jenal, R.; Szwedo, M.; Iwaniec, J.; Uhl, T. Nonlinear acoustics for fatigue crack detection—Experimental investigations of vibro-acoustic wave modulations. Struct. Health Monit. 2012, 11, 197–211. [Google Scholar] [CrossRef]
- Li, N.; Sun, J.; Jiao, J.; Wu, B.; He, C. Quantitative evaluation of micro-cracks using nonlinear ultrasonic modulation method. NDT E Int. 2016, 79, 63–72. [Google Scholar] [CrossRef]
- Broda, D.; Staszewski, W.J.; Martowicz, A.; Uhl, T.; Silberschmidt, V.V. Modelling of nonlinear crack–wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Biwa, S.; Nakajima, S.; Ohno, N. On the Acoustic Nonlinearity of Solid-Solid Contact With Pressure-Dependent Interface Stiffness. J. Appl. Mech. 2004, 71, 508–515. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Su, Z.; Xiao, Y. Quantitative evaluation of residual torque of a loose bolt based on wave energy dissipation and vibro-acoustic modulation: A comparative study. J. Sound Vib. 2016, 383, 156–170. [Google Scholar] [CrossRef]
- Fillinger, L.; Zaitsev, V.Y.; Gusev, V.; Castagnede, B. Nonlinear relaxational absorption/transparency for acoustic waves due to thermoelastic effect. Acta Acust. United Acust. 2006, 92, 24–34. [Google Scholar]
- Nazarov, V.E.; Radostin, A.V.; Soustova, I.A. Effect of an intense sound wave on the acoustic properties of a sandstone bar resonator. Experiment. Acoust. Phys. 2002, 48, 76–80. [Google Scholar] [CrossRef]
- Parsons, Z.; Staszewski, W.J. Nonlinear acoustics with low-profile piezoceramic excitation for crack detection in metallic structures. Smart Mater. Struct. 2006, 15, 1110. [Google Scholar] [CrossRef]
- Zimenkov, S.V.; Nazarov, V.E. The dependence of damping of ultrasound by sound in annealed copper on the frequency of the sound. Sov. Phys.-Acoust. 1992, 38, 4. [Google Scholar]
- Meo, M.; Polimeno, U.; Zumpano, G. Detecting Damage in Composite Material Using Nonlinear Elastic Wave Spectroscopy Methods. Appl. Compos. Mater. 2008, 15, 115–126. [Google Scholar] [CrossRef]
- Zaitsev, V.; Gusev, V.; Castagnede, B. Luxemburg-gorky effect retooled for elastic waves: A mechanism and experimental evidence. Phys. Rev. Lett. 2002, 89, 105502. [Google Scholar] [CrossRef]
- Solodov, I.; Wackerl, J.; Pfleiderer, K.; Busse, G. Nonlinear self-modulation and subharmonic acoustic spectroscopyfor damage detection and location. Appl. Phys. Lett. 2004, 84, 5386–5388. [Google Scholar] [CrossRef]
- He, Y.; Xiao, Y.; Su, Z.; Pan, Y.; Zhang, Z. Contact acoustic nonlinearity effect on the vibro-acoustic modulation of delaminated composite structures. Mech. Syst. Signal Process. 2022, 163, 108161. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Y.; He, Y.; Zhang, Z. A detailed finite element analysis of composite bolted joint dynamics with multiscale modeling of contacts between rough surfaces. Compos. Struct. 2020, 236, 111874. [Google Scholar] [CrossRef]
- Dao, P.B.; Klepka, A.; Pieczonka, Ł.; Aymerich, F.; Staszewski, W.J. Impact damage detection in smart composites using nonlinear acoustics—Cointegration analysis for removal of undesired load effect. Smart Mater. Struct. 2017, 26, 035012. [Google Scholar] [CrossRef]


| Material Type | Elasticity Modulus E(GPa) | Poisson’s Ratio ν | Density (kg/m3) ρ | Friction Coefficient τ |
|---|---|---|---|---|
| Aluminum | 75.6 | 0.33 | 2700 | 0.1 |
| Composites | E1/E2/E3 | ν11/ν13/ν23 | 1700 | 0.2 |
| 130/7/7 | 0.32/0.32/0.45 |
| Test 1 | Test 2 | Test 3 | Test 4 | ||
|---|---|---|---|---|---|
| Al–Al | c | 11.3137 | 181 | 256 | 1.414 |
| σ | 0.0884 | 0.0221 | 0.02 | 0.25 | |
| C–C | c | 181 | 5.657 | 2.828 | 4 |
| σ | 0.1768 | 0.125 | 0.5 | 0.354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; He, Y.; Li, Q.; Zhang, Z. Artificial Intelligence (AI)-Based Evaluation of Bolt Loosening Using Vibro-Acoustic Modulation (VAM) Features from a Combination of Simulation and Experiments. Appl. Sci. 2022, 12, 12920. https://doi.org/10.3390/app122412920
Li J, He Y, Li Q, Zhang Z. Artificial Intelligence (AI)-Based Evaluation of Bolt Loosening Using Vibro-Acoustic Modulation (VAM) Features from a Combination of Simulation and Experiments. Applied Sciences. 2022; 12(24):12920. https://doi.org/10.3390/app122412920
Chicago/Turabian StyleLi, Jianbin, Yi He, Qian Li, and Zhen Zhang. 2022. "Artificial Intelligence (AI)-Based Evaluation of Bolt Loosening Using Vibro-Acoustic Modulation (VAM) Features from a Combination of Simulation and Experiments" Applied Sciences 12, no. 24: 12920. https://doi.org/10.3390/app122412920
APA StyleLi, J., He, Y., Li, Q., & Zhang, Z. (2022). Artificial Intelligence (AI)-Based Evaluation of Bolt Loosening Using Vibro-Acoustic Modulation (VAM) Features from a Combination of Simulation and Experiments. Applied Sciences, 12(24), 12920. https://doi.org/10.3390/app122412920





