Language Inclusion Checking of Timed Automata Based on Property Patterns

Abstract

The language inclusion checking of timed automata is described as the following: given two timed automata M and N, where M is a system model and N is a specification model (which represents the properties that the system needs to satisfy), check whether the language of M is included in the language of N. The language inclusion checking of timed automata can detect whether a system model satisfies a given property under the time constraints. There exist excellent studies on verifying real-time systems using timed automata. However, there is no thorough method of timed automata language inclusion checking for real-life systems. Therefore, this paper proposes a language inclusion checking method of timed automata based on the property patterns. On the one hand, we summarize commonly used property patterns described by timed automata, which can guide people to model the properties with time constraints. On the other hand, the system model M often contains a large number of events, but in general, the property N only needs to pay attention to the sequences and time limits of a few events. Therefore, the timed automata language inclusion checking algorithm is improved so that only the concerned events are required. Our method is applied to a water disposal system and it is also evaluated using benchmark systems. The determinization problem of timed automata is undecidable, which may lead to an infinite state space. However, our method is still practical because the properties established according to property patterns are often deterministic.

1. Introduction

Timed automata [1] have been one of the most popular formal models to specify and verify real-time systems. The main purpose of timed automata language inclusion checking [2] is to check whether the system model and the specification model (which represents the properties that the system needs to satisfy) have the relation of language inclusion. It can also be described as whether the system behaviors satisfy a certain property under the time constraints. There are already some studies that apply the theories and methods of timed automata to real-time systems, such as modeling and verification of cyber physical systems [3,4], networked systems [5], the security of smart cities [6,7], etc. However, most of them use verification based on reachability or temporal logics (such as TLTL, TCTL). There is no thorough method for timed automata language inclusion checking that can be applied to real-life systems.

Formal modeling of real-time systems is an error-prone job. Usually the developers or testers are not familiar with formal modeling methods; therefore, they experience obstacles in describing the properties that the system should satisfy using timed automata. On the other hand, in order to verify the system correctness, the model checking tools must use the system models and property models as inputs. The property patterns can be used to close the gap between the users and the model checking tools [8]. Currently, there is a lack of study on property patterns which can be applied in language inclusion checking of timed automata. Current approaches often allow one to construct a system model which can be automatically transformed from other high-level languages to the language supported by a model checker. However, they do not illustrate how to specify the properties to be verified. On this basis, we propose a set of commonly used property patterns described by timed automata. It provides a guidance to users to model the properties for language inclusion checking.

Due to the infinity of the time points, it is impossible to directly search the state space for timed automata. Therefore, verification of timed automata (for instance, reachability) can be solved by using the region graph [1]. However, verification based on region graphs is inefficient. Reference [9] proposed the zone-based method to efficiently check the safety and liveness properties. The verification tools for real-time systems often use zone graphs, such as PAT [10] and UPPAAL [11]. Our previous work [2] first gave a method based on zone abstraction to solve the language inclusion problem of timed automata. The method constructs a synchronous product (which can be seen as the generation of the state space) of two timed automata and then converts the language inclusion checking into a reachability problem on the synchronous product. During this process, the timed automata need to be determinized. In real-life systems, the system models are often complicated and contain a large amount of events, while the property models only need to pay attention to the sequences and time limits of a few events. If a property model must have the same set of events as the system model due to the definition of language inclusion, it will bring great difficulties to the property modeling. On the other hand, the algorithm will often not stop because the determinization of the timed automata is undecidable. Therefore, we improve the algorithm, so that it only needs to consider the concerned events in the property models in critical steps. This improvement makes the algorithm feasible in reality.

The main contributions of this paper are as follows. Firstly, we summarize commonly used property patterns of timed automata, including: Absence, Universality, Existence, Response, Precedence, Chain and Occurrence times. Secondly, an improved language inclusion checking algorithm of timed automata is given, which does not need to consider the events not in the property models in critical steps. The determinization of the timed automata is undecidable, which may lead to an infinite state space by the algorithm. However, our method is practical since the properties established according to property patterns are often deterministic. Finally, our method is applied to a water disposal system [12] and the algorithm is also evaluated using benchmark systems.

The chapters of this paper are organized as follows. Section 2 gives the background of timed automata. Section 3 summarizes several commonly used property patterns for the language inclusion checking. Section 4 gives a detailed description of our algorithm. Section 5 takes the water disposal system as an example and uses our method to verify the system using the property patterns. Section 6 is the related work. Finally, the summary of this paper and future work are given.

2. Background of Timed Automata

Firstly, some related definitions for timed automata [1] are given. Let C be a set of clocks, and $\mathrm{\Phi }\left(C\right)$ be a set of clock constraints. A clock constraint is defined as follows: $\delta :=\mathit{true}\mid x\sim n\mid {\delta }_1\wedge {\delta }_2\mid \neg {\delta }_1$, where $\sim \in \{=,\le ,\ge ,<,>\}$, where x is a clock in C and n is a non-negative integer. The set of downward constraints obtained with $\sim \in \{\le ,<\}$ is denoted as ${\mathrm{\Phi }}_{\le ,<}\left(C\right)$. A clock valuation v for a set of clocks C is a function which assigns a real value to each clock. If the clock valuation v makes the clock constraint $\delta$ true, then v satisfies $\delta$ based on $C(v\mid =\delta )$. For any $d\in R^{+}$, let $v+d$ denote the clock valuation $v^{\prime }$ such that $v^{\prime }\left(c\right)=v\left(c\right)+d$ for all $c\in C$. For a set of clocks $X\subseteq C$, let the clock resetting notion $[X\mapsto 0]v$ denote the valuation $v^{\prime }$ such that $v^{\prime }\left(c\right)=v\left(c\right)$ for any $c\in C\wedge c\notin X$ and $v^{\prime }\left(x\right)=0$ for all $x\in X$.

Definition 1

(Timed Automata). A Timed Automaton is a tuple $A=(S,Init,\mathrm{\Sigma },C,L,T)$, where S is a finite set of states; $Init\subseteq S$ is a set of initial states; Σ is a set of events; C is a finite set of clocks; $L:S\to {\mathrm{\Phi }}_{\le ,<}\left(C\right)$ is a function that gives a state invariant ${\mathrm{\Phi }}_{\le ,<}\left(C\right)$ to each state; and $T\subseteq S\times \mathrm{\Sigma }\times \mathrm{\Phi }\left(C\right)\times 2^C\times S$ is a transition with a set of clock constraints $\mathrm{\Phi }\left(C\right)$.

Based on the concrete semantics, the Timed Automaton A is a transition system. Each node is a pair $(s,v)$, where $s\in S$ is a state and v is a clock valuation which satisfies $v\mid =L\left(s\right)$. A run of A is a finite sequence $▵=⟨(s_0,v_0),(d_0,e_0),(s_1,v_1),(d_1,e_1),\cdots ,(s_i,v_i),(d_i,e_i),\cdots ⟩$, where $s_0\in Init$; $v_0$ resets each clock to zero; for all $i\ge 0$, there is a transition $(s_i,e_i,\delta ,X,s_{i+1})\in T$, such that $v_i+d_i\mid =L\left(s_i\right)$, $v_i+d_i\mid =\delta$, $v_{i+1}=[X\mapsto 0](v_i+d_i)$ and $v_{i+1}\mid =L\left(s_{i+1}\right)$. Given a run $▵$, we can get its timed language $⟨(d_0,e_0),(d_1,e_1),\cdots ,(d_i,e_i),\cdots ⟩$. We use $Lan\left(A\right)$ to denote all the languages of A. If the languages of two timed automata are the same, they are equivalent.

Due to the infinity of time, the Timed Automaton A is essentially a transition system with infinite nodes. To make the verification possible, it must be transformed into a graph with finite transitions. The most commonly used abstraction technique is the zone abstraction. We can obtain a zone graph with finite nodes after zone abstraction. A zone is a linear inequality or a conjunction of linear inequalities defined on C, such as $x-y\le 5$, $y>3\wedge x<7$, etc., where $x,y\in C$. Given a zone $\delta$, let ${\delta }^{\uparrow }$ denote the zone obtained from $\delta$ by delaying any time.

Definition 2

(Zone Graph). Given a Timed Automaton $A=(S,Init,\mathrm{\Sigma },C,L,T)$, the zone graph $ZG\left(A\right)$ is a tuple $(S_z,Ini{t}_z,\mathrm{\Sigma },T_z)$, such that $S_z$ denotes a set of nodes $(s,\delta )$ where $s\in S$ and δ is a clock constraint; $Ini{t}_z=\{(init,{({\wedge }_{c\in C}c=0)}^{\uparrow }\wedge L\left(init\right))\mid init\in Init\}$ is a set of initial nodes; $T_z:S_z\times \mathrm{\Sigma }\times S_z$ is a transition relation such that $((s_1,{\delta }_1),e,(s_2,{\delta }_2))\in T_z$ iff $(s_1,e,\delta ,X,s_2)\in T$, ${\delta }_1\wedge \delta$ is not empty, $[X\mapsto 0]({\delta }_1\wedge \delta )\wedge L\left(s_2\right)$ is not empty and ${\delta }_2=D({\left([X\mapsto 0]({\delta }_1\wedge \delta )\right)}^{\uparrow }\wedge L\left(s_2\right))$. (D is a normalization function [1]).

Figure 1 shows a Timed Automaton example which is a switch, where the initial state is Off. When the event Press occurs, the system transits to the state On and resets the clock x. Because of the state invariant $x\le 2$ on the state On, the system must transit to the state Off in two time units.

Figure 1. An example of a Timed Automaton.

In order to facilitate the modeling of the timed systems, we also use the following expressions in addition to Definition 1. For more information on the modeling, please refer to the paper  [13] (the model checking tool PAT).

• Constants and variables: the constants will not be modified when the model is running, e.g., the expression #define A 10, which defines the value of a constant A to be 10; the variables can be modified, expressed as var B:{0..100} = 50, which defines the variable B, where the initial value is 50 and the range of B is 0 to 100.
• Channel events: the channel events indicate the processes sending or accepting messages. Assume c is the channel name, then $c!$ represents that a message is sent and $c?$ represents the acceptance of a message.
• Transitions: the complete representation is ‘Clock: <clock constraint> [transition condition] event {operations} Clockreset:{clocks}’. The event will be executed when the clock constraint and the transition condition are satisfied. Some operations can be performed at the same time, e.g., changing the values of the variables. Clockreset means to reset the clocks in {} to zero.

3. Property Patterns Based on Timed Automata

A pattern can give a general way of solving one kind of problem. Since modeling properties that the system needs to satisfy is a necessary step, we need to explore the patterns of the verification properties. Property patterns in previous works can infer the occurrence and sequence of events (e.g., the occurrence of event a must follow event b) and can also describe the logical behaviors of time-related events. On this basis, we propose common property patterns represented by timed automata.

The property patterns are shown in the following figures. In the figures, a , b, c are all the events, x is a clock and k is any non-negative integer. The property patterns only have one clock. We can use a single pattern or a combination of multiple patterns to model a property, which may have multiple clocks. The property patterns are described one by one as follows.

• Name of property pattern: Absence
  Problem to be solved: An event must not occur within a certain amount of time.
  Solution: The patterns Absence-1 and Absence-2 are shown in Figure 2. For the self-transition in Absence-1, there is a clock constraint x > k which means that event a can only occur after k time units. The difference between Absence-2 and Absence-1 is whether the clock x is reset on the self-transition, which means that the time between two occurrences of event a must be larger than k time units. Event a may occur many times and also may never occur because there is no state invariant on $Stat{e}_1$ or $Stat{e}_2$.
  

  Figure 2. Property pattern of Absence.
• Name of property pattern: Existence
  Problem to be solved: An event must occur within a certain amount of time.
  Solution: The patterns Existence-1, Existence-2 and Existence-3 are shown in Figure 3. Due to the state invariant x ≤ k on the states and the clock constraint x ≤ k on the transitions, we can make sure that event a occurs within k time units. Existence-1 indicates that event a can occur many times and the time between two successive occurrences must be within k time units due to the resetting of the clock x. In the patterns Existence-2 and Existence-3, the first occurrence of event a must be within k time units. Event a only occurs once within k time units in Existence-2, while it can happen many time in Existence-3 after the first occurrence.
  

  Figure 3. Property pattern of Existence.
• Name of property pattern: Response
  Problem to be solved: An event must always be followed by another event within a certain amount of time.
  Solution: The patterns Response-1 and Response-2 are shown in Figure 4. The state invariant x ≤ k on the states and the clock constraint x ≤ k on the transitions denotes the inevitability of the situation that event b follows event a within k time units. In addition, Response-1 indicates that event b can only occur after event a, while the self-transition on $Stat{e}_3$ in Response-2 indicates that even if the event a does not occur, event b can occur separately.
  

  Figure 4. Property pattern of Response.
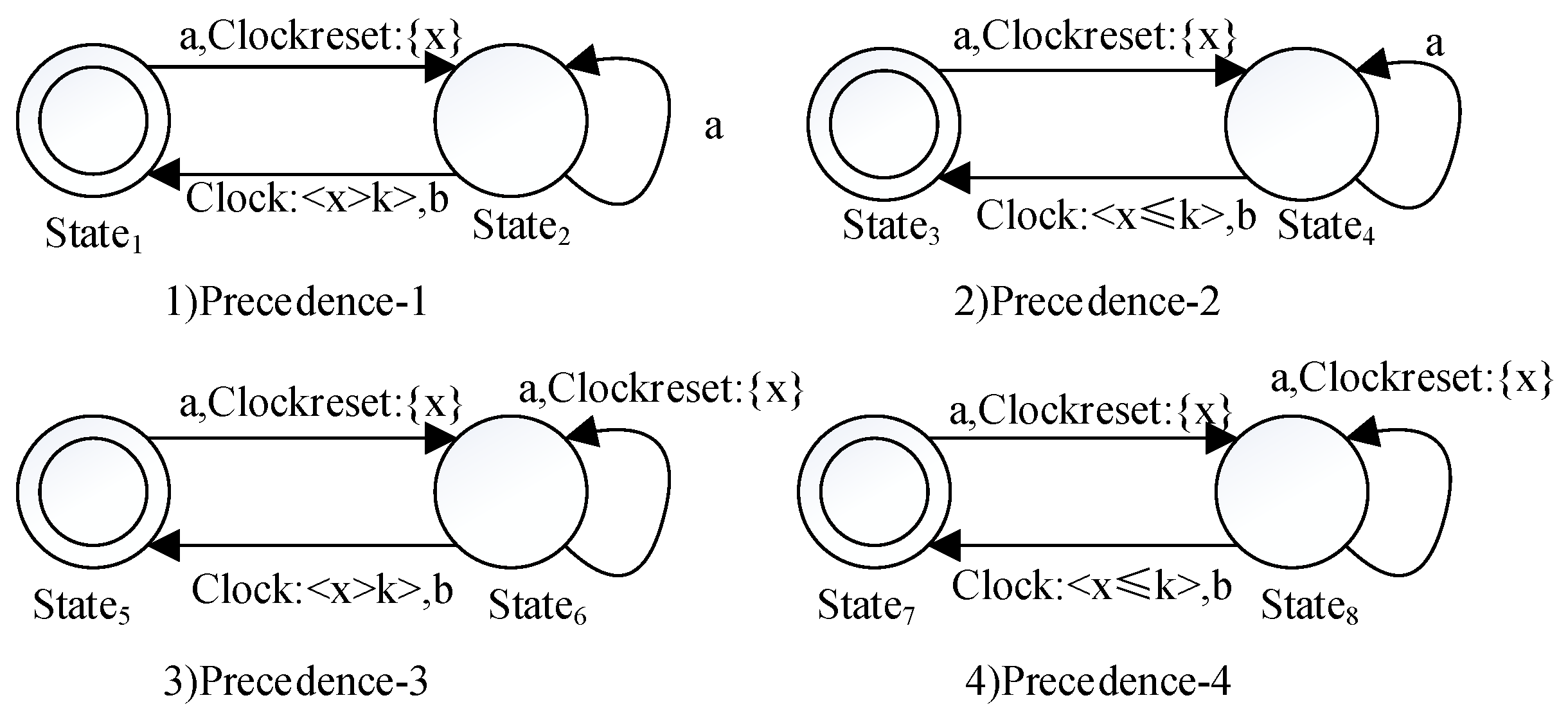
• Name of property pattern: Precedence
  Problem to be solved: An event must always be preceded by another event within a certain amount of time.
  Solution: The patterns Precedence-1, Precedence-2, Precedence-3 and Precedence-4 are shown in Figure 5. Precedence-1 denotes that when event a occurs, the clock x is reset to zero. After that, if event b occurs, it must not be within k clock units, during which event a may continue to happen multiple times because of the self-transition on $Stat{e}_2$. Precedence-2 denotes that after event a, if event b occurs, it must be within k time units, during which event a can also occur many times. Precedence-3 and Precedence-4 are similar to the above. The only difference is that the occurrence time point of event b is related to the last occurrence of event a due to the clock resetting on the self-transitions from $Stat{e}_4$ and $Stat{e}_8$.
  

  Figure 5. Property pattern of Precedence.
• Name of property pattern: Chain
  Problem to be solved: A sequence of events must occur in order within a certain amount of time.
  Solution: The pattern Chain is shown in Figure 6. The state invariant x ≤ k on $Stat{e}_1$ , $Stat{e}_2$ and $Stat{e}_3$ and the clock constraint x ≤ k on the transitions (together with events a, b and c sequentially) ensure that the system will finally transit to $Stat{e}_4$ within k time units. Before or after the sequence happens, events a, b and c can occur arbitrarily.
  

  Figure 6. Property pattern of Chain.
• Name of property pattern: Occurrence times
  Problem to be solved: An event must occur several times in a certain amount of time.
  Solution: The pattern Occurrence times is shown in Figure 7. There are state invariants x ≤ k on the states and clock constraint x ≤ k on the transitions, which indicates that event a must occur three times within k clock units. After that, event a can happen arbitrarily.
  

  Figure 7. Property pattern of Occurrence times.

4. Language Inclusion Checking of Timed Automata

Timed automata language inclusion checking is defined as: given two timed automata M and N, if $Lan\left(M\right)\subseteq Lan\left(N\right)$, then the language inclusion is satisfied. The above definition is based on the concrete semantics of timed automata. Due to the infinity of the time points, it cannot be used in practice. The work in [2] gave a method based on the zone abstraction, making it possible to apply this type of verification method to real-life problems. Our method uses zone abstraction to establish synchronous product of two timed automata (which is the state space) and the language inclusion checking is turned into the reachability checking in the synchronous product. As stated in the introduction, the method is improved so that it only needs to consider the concerned events during the verification.

4.1. The Transformation before the Verification

There are state invariants on the states of timed automata. A Timed Automaton can be converted into an equivalent automaton without state invariants and the language defined in Section 2 is not changed [2]. The state invariant on a state is moved to the transitions which lead to or leave the state. If there is a Timed Automaton $A=(S,Init,\mathrm{\Sigma },C,L,T)$, for any state $s\in S$ and its state invariant $L\left(s\right)$, we have the two operations:

• Convert the transition $(s,e,\delta ,X,s^{\prime })$ to $(s,e,\delta \wedge L\left(s\right),X,s^{\prime })$;
• For any transition $(s^{\prime },e,\delta ,X,s)$ and any clock constraint $x\sim n$ in $L\left(s\right)$, if $x\notin X$, then $x\sim n$ is conjuncted with $\delta$; otherwise, it is ignored.

We use two timed automata $M=(S_m,Ini{t}_m,{\mathrm{\Sigma }}_m,C_m,L_m,T_m)$ and $N=(S_n,Ini{t}_n,{\mathrm{\Sigma }}_n,C_n,L_n,T_n)$ in the next section, where only N needs the above conversion.

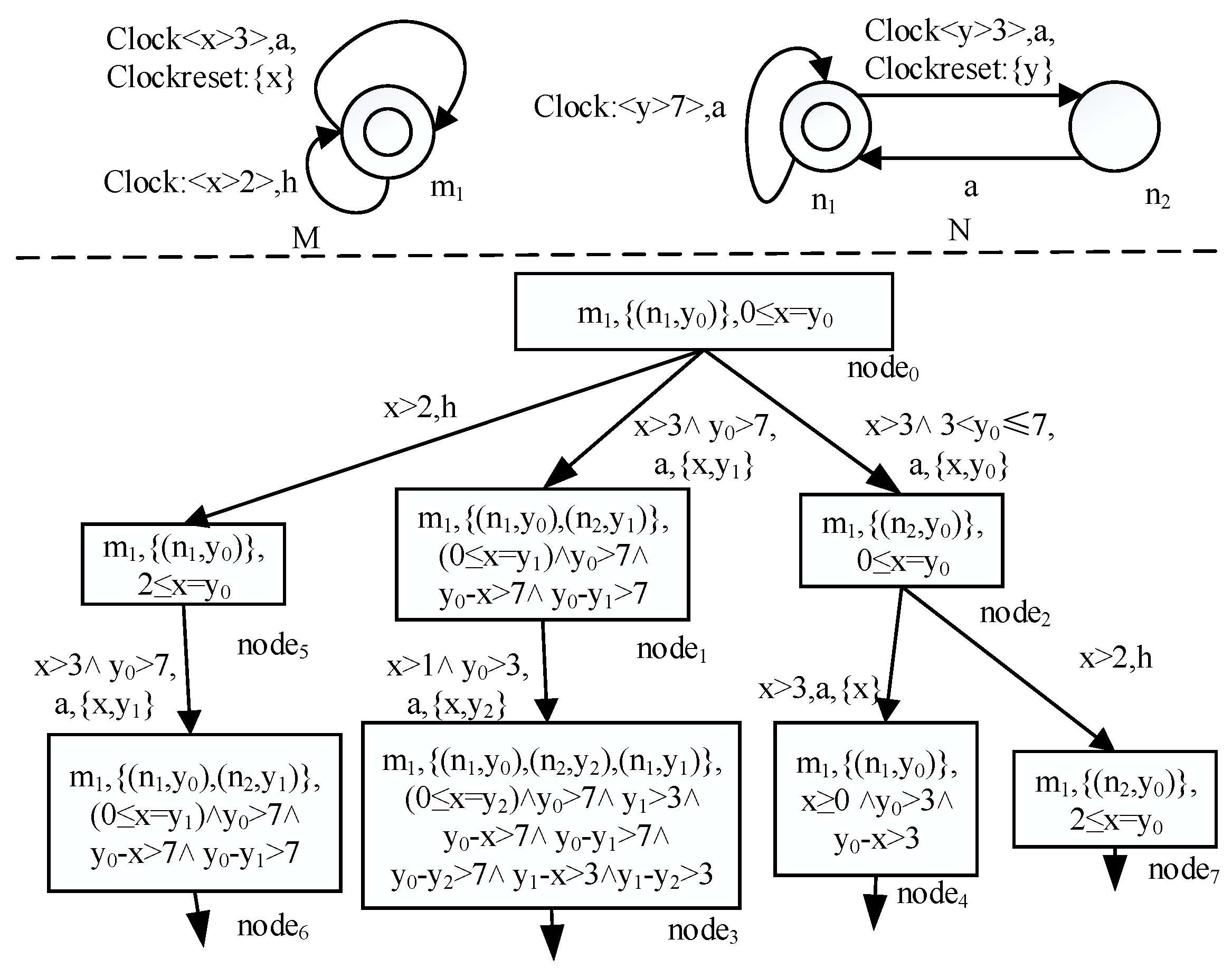
4.2. Synchronous Product with Concerned Events

Firstly, some definitions are given. For a clock c, $c^{*}=\{c_0,c_1,c_2,\cdots ,c_i,\cdots \}$ is an infinite clock set, where any clock in $c^{*}$ is a copy of the clock c. For any $c\in C_n$, a function ${\lambda }_n\left(c\right)$ is defined to represent the mapping of the clock c to a unique clock $c_i$ from $c^{*}$(written as ${\lambda }_n\left(c\right)=c_i$). We use ${\lambda }_n$ to indicate that every $c\in C_n$ is mapped to a unique clock $c_i$ from $c^{*}$ and ${\lambda }_n^0$ to indicate that every $c\in C_n$ is written as $c_0$. For instance, for the clocks $x,y\in C_n$, ${\lambda }_n\left(x\right)=x_2$ and ${\lambda }_n\left(y\right)=y_3$ are both possible.

The synchronous product with concerned events is actually a zone graph $Zone(M\otimes N)=(S,Init,\mathrm{\Sigma },T)$. Any $s\in S$ is a node with the form $(s_m,X_n,\delta )$, where $s_m\in S_m$ and $X_n$ is a set, in which each element is of the form $(s_n,{\lambda }_n)$ where $s_n\in S_n$. For any $(s_n,{\lambda }_n)\in X_n$, ${\lambda }_n$ denotes a set of all active clocks in $s_n$, which will be further illustrated during the construction of T. $ActClock\left(X_n\right)$ is used to represent the set of all the active clocks in $X_n$, i.e., $\{t\mid \exists (s_n,{\lambda }_n)\in X_n,c\in C_n,t={\lambda }_n\left(c\right)\}$. $\delta$ is the clock constraint of all the clocks in $ActClock\left(X_n\right)\cup C_m$. The $Init$ in the zone graph is defined as $\{(s_m,X_n,{((ActClock\left(X_n\right)\cup C_m)=0)}^{\uparrow })\mid s_m\in Ini{t}_m\wedge X_n=\{(s_n,{\lambda }_n^0)\mid s_n\in Ini{t}_n\}\}$. $\mathrm{\Sigma }$ is equal to ${\mathrm{\Sigma }}_m$.

Next, given a node $(s_m,X_n,\delta )$, T is defined by describing how to generate the successors with the following two steps.

(1)

For $s_m$ and the transition $(s_m,e,g_m,Y,s_m^{\prime })$ from $s_m$, if $e\in {\mathrm{\Sigma }}_m\wedge e\notin {\mathrm{\Sigma }}_n$, then its successor is $(s_m^{\prime },X_n,{\delta }^{\prime })$ such that ${\delta }^{\prime }={\left(D([Y\mapsto 0](g_m\wedge \delta )\wedge L\left(s_m^{\prime }\right))\right)}^{\uparrow }$. In this case, $suc{c}_1(node,Zone(M\otimes N))$ is used to represent the successors of $node$.

(2)

For $s_m$ and the transition $(s_m,e,g_m,Y,s_m^{\prime })$ from $s_m$, if $e\in {\mathrm{\Sigma }}_m\wedge e\in {\mathrm{\Sigma }}_n$:

(a)

A set of transitions is represented by $Tran(e,X_n)$ as follows. For any $(s_n,{\lambda }_n)\in X_n$ and any transition $(s_n,e,g_n,Y,s_n^{\prime })$ in $Tran(e,X_n)$, the $((s_n,{\lambda }_n),e,g_n^{\prime },Y^{\prime },(s_n^{\prime },{\lambda }_n^{\prime }))$ is added into $Tran(e,X_n)$. For any $c\in g_n$, the corresponding name of the clock in $g_n^{\prime }$ is ${\lambda }_n\left(c\right)$; for any $c\in Y$, the corresponding one in $Y^{\prime }$ is ${\lambda }_n\left(c\right)$. For any $c\in C$, if ${\lambda }_n\left(c\right)\notin Y^{\prime }$, then ${\lambda }_n^{\prime }\left(c\right)={\lambda }_n\left(c\right)$; otherwise, ${\lambda }_n^{\prime }\left(c\right)=R$. The pending R will be explained in step c.

(b)

Since N needs to be determinized, the clock constraints of all the transitions in $Tran(e,X_n)$ should be mutually exclusive. $Exclusive(e,X_n)$ is a set of clock constraints in which each element is a clock constraint. For every transition in $Tran(e,X_n)$, $Exclusive(e,X_n)$ conjuncts either the transition guard or the negation. As a result, the elements in $Exclusive(e,X_n)$ are mutually exclusive. If a clock constraint on a transition is negated, this transition is disabled; otherwise, it is enabled.

(c)

For each $g\in Exclusive(e,X_n)$, the successors of $(s_m^{\prime },X_n^{\prime },{\delta }^{\prime })$ are generated as follows: (i) For any $(s_n,{\lambda }_n)\in X_n$ and any transition $((s_n,{\lambda }_n),e,g_n,Y^{\prime },(s_n^{\prime },{\lambda }_n^{\prime }))\in Tran(e,X_n)$, if $\delta \wedge g_m\wedge g\wedge g_n$ is true, then $(s_n^{\prime },{\lambda }_n^{\prime })\in X_n^{\prime }$. (ii) Two clock sets are used here: $Reset$ and $Active$. For any $(s_n^{\prime },{\lambda }_n^{\prime })\in X_n^{\prime }$ and any clock $c\in C_n$, if ${\lambda }_n^{\prime }\left(c\right)\ne Active$ and ${\lambda }_n^{\prime }\left(c\right)\ne R$ hold, add c into $Active$; if $c\notin Reset$ and ${\lambda }_n\left(c\right)=R$ hold, add c into $Reset$. (iii) For any clock c in $Reset$, a clock $c_x$ in $c^{*}$ satisfying $c_x\notin Reset$ is chosen. For any $(s_n^{\prime },{\lambda }_n^{\prime })\in X_n^{\prime }$, if ${\lambda }_n^{\prime }\left(c\right)=R$ holds, then ${\lambda }_n^{\prime }\left(c\right)$ is modified to $c_x$. (iv) Let ${\delta }^{temp}=\delta \wedge g\left[Active\right]\wedge g_m$, with which ${\delta }^{\prime }=D\left(\left([X_m\mapsto 0]{((Reset=0)\wedge {\delta }^{temp})}^{\uparrow }\right)\right)$.

The successors of a $node$ in $Zone(M\otimes N)$ generated by the above step 2 are denoted as $suc{c}_2(node,Zone(M\otimes N))$. For (b) in step 2, one of the clock constraints in $Exclusive(e,X_n)$ takes all the clock constraints on the transitions in $Tran(e,X_n)$ to be negative, which is denoted as $negAll$. The successor generated by $negAll$ is $(s_m^{\prime },X_n^{\prime },{\delta }^{\prime })$. Obviously $X_n^{\prime }$ is empty because all the transitions are disabled. However, if ${\delta }^{\prime }$ is not false, M can execute an event at some time point, whereas N cannot in this situation. As a result, there is a trace which is in M but not in N and the language inclusion relation is false.

Theorem 1.

$Lan\left(M\right)\subseteq Lan\left(N\right)$ iff there is no reachable state $(s_m,\varnothing ,\delta )$ in $Zone(M\otimes N)$ where δ is true.

Given two nodes $(s_m,X_n,\delta )$ and $(s_m^{\prime },X_n^{\prime },{\delta }^{\prime })$ in $Zone(M\otimes N)$, because of different clock names, we cannot examine the relation between them directly. For instance, the nodes $(m_1,\{(n_1,y_1),(n_2,y_4)\},x=y_1>3\wedge y_4<7)$ and $(m_1,\{(n_1,y_4),(n_2,y_1)\},x=y_4>3\wedge y_1<7)$ are actually equivalent, since in the latter $y_1$ and $y_4$ can be exchanged. Therefore, the names of clocks in $ActClock\left(X_n\right)$ or $ActClock\left(X_n^{\prime }\right)$ are not important, as long as the mapping relationship is found. If $s_m=s_m^{\prime }$ and there exists a bijection between $X_n$ and $X_n^{\prime }$, such that for any $(s_n,{\lambda }_n)\in X_n$, there is a unique $(s_n^{\prime },{\lambda }_n^{\prime })\in X_n^{\prime }$ satisfying $s_n=s_n^{\prime }$ (and vice versa), then we go to check the equivalence. That is, we need to find a bijective function $bij$ from $ActClock\left(X_n\right)$ to $ActClock\left(X_n^{\prime }\right)$: $ActClock\left(X_n\right)\to ActClock\left(X_n^{\prime }\right)$. Let $bij\left(\delta \right)$ denote the clock constraint with renamed clocks. Then $bij\left(\delta \right)={\delta }^{\prime }$ means that the two nodes are equivalent.

It should be noted that, according to [2], the number of nodes in $Zone(M\otimes N)$ may be infinite, because it is possible to generate infinite clocks during the determinization of N. As a result, the state space grows unboundedly and the search is unable to terminate. Fortunately, all the property patterns summarized in Section 2 can be determinized. Therefore the verification will not encounter the above situation with the properties built by property patterns. When modeling and verifying real-life systems, most of the properties can be established by using the property patterns or their mutations, which reflects the feasibility of our method.

Example 1.

The example in Figure 8 illustrates how to generate the synchronous product with concerned events. Above the dashed line, there are the time automata M and N, while the below one is the zone graph $Zone(M\otimes N)$. Let $nod{e}_0=(m_1,\left\{(n_1,y)\right\},0\le x=y_0)$ be the initial node and the other nodes are as shown in the figure.

Figure 8. Synchronous product based on zone abstraction.

The event h in M is an unconcerned event, and a is the concerned event. $nod{e}_5$ is a successor of $nod{e}_0$ with the unconcerned event h, where $m_1$ does not change after event h. Since N does not need to run, $(n_1,y_0)$ in $nod{e}_5$ is the same as $nod{e}_0$. The clock constraint is $2\le x=y_0$ because of the clock condition $x>2$. Similarly, $nod{e}_7$ is the successor of $nod{e}_2$ by event h. (Step 1).

For $(n_1,y_0)$ in $nod{e}_0$, there are two transitions from $n_1$ with clock constraints $y>7$ or $y>3$, respectively. Because for the clock y, the initial active clock is $y_0$, the transitions $((n_1,y_0),a,y_0>3,\left\{y_0\right\},(n_2,R))$ and $((n_1,y_0),a,y_0>7,\varnothing ,(n_1,y_0))$ are added into $Tran(a,(n_1,y_0))$. R in the former transition can be determined in the subsequent steps (Step 2 a).

Four clock constraints $y_0>7\wedge y_0>3$,$y_0>7\wedge y_0\le 3$,$y_0\le 7\wedge y_0>3$ and $y_0\le 7\wedge y_0\le 3$ can be obtained from $Tran(a,(n_1,y_0))$, which constitutes the $Exclusive(a,(n_1,y_0))$. Among them, $y_0>7$ and $3<y_0\le 7$ are feasible. $y_0\le 3$ belongs to $negAll$ and is used to verify whether the language inclusion is satisfied or not, which will be explained later. For $y_0>7$, both transitions from $n_1$ in N are enabled; therefore, there are two elements in the set about N in $nod{e}_1$. For $3<y_0\le 7$, only the transition from $n_1$ to $n_2$ is enabled, so that there is only one element in the set about N in $nod{e}_2$. (Step 2 b).

From $nod{e}_0$ to $nod{e}_1$, the clock $y_0$ is not reset in the self-transition of $n_1$; thus, $(n_1,y_0)$ does not change in $nod{e}_1$ and $y_0$ is still in use. For the transition from $n_1$ to $n_2$, the clock $y_0$ is reset but is active in $(n_1,y_0)$; thus, a new clock $y_1$ (notice that now $R=y_1$) is enabled in $nod{e}_1$. From $nod{e}_0$ to $nod{e}_2$, only the transition from $n_1$ to $n_2$ is enabled; then, the clock $y_0$ can be reused in $nod{e}_2$. The clock constraints in $nod{e}_1$ and $nod{e}_2$ are calculated from the initial zone, the clock conditions on the transitions and the reset clocks. Thus, the synchronous product with concerned events is constructed step by step (Step 2 c).

For the judgment concerning the language inclusion, the $negAll$ in $Exclusive(a,(n_1,y_0))$ of $nod{e}_0$ is $y_0\le 3$. The result of the conjunction of $0\le x=y_0$ (in $nod{e}_0$), $x>3$ (the transition guard in M) and $negAll$ is false, so $(s_m,\varnothing ,\delta )$ cannot be generated from $nod{e}_0$. Other nodes can also be handled in this manner (in Figure 8, the language inclusion checking of M and N is true).

4.3. Timed Automata Language Inclusion Checking Algorithm with Concerned Events

Algorithm 1 is the language inclusion checking algorithm of timed automata. There are two data structures in the algorithm, i.e., the $visiting$ stores for the nodes to be searched in the zone graph $Zone(M\otimes N)$ and $visited$ stores for the nodes which have been searched. The initial element in $visiting$ is the initial node of $Zone(M\otimes N)$, while $visited$ is an empty set. For the loop from line 3 to line 18, in each loop the current node is deleted from $visiting$ and then added into $visited$; if this node is the target one in the form of $(s_m,\varnothing ,\delta )$, then the algorithm returns $false$ at line 7. Lines 9 to 17 check whether event e on the transition from the current node is an unconcerned event. If event e only belongs to the event set ${\mathrm{\Sigma }}_m$ but not ${\mathrm{\Sigma }}_n$, which means that e is an unconcerned event, then the nodes in $suc{c}_1(node,Zone(M\otimes N))$ are added into $visiting$. If event e belongs to both ${\mathrm{\Sigma }}_m$ and ${\mathrm{\Sigma }}_n$, then all the nodes in $suc{c}_2(node,Zone(M\otimes N))$ are added into $visiting$. Finally, if all the nodes have been visited without any node in the form of $(s_m,\varnothing ,\delta )$, then the algorithm returns $true$ at line 19.

Algorithm 1 Timed Automata Language Inclusion Checking Algorithm with Concerned Events

Input: timed automata M and N Output: verification result ($true$ or $false$) 1: let $visiting:=Init$; 2: let $visited:=\varnothing$; 3: while $visiting\ne \varnothing$do 4:    remove $node:=(s_m,X_n,\delta )$ from $visiting$; 5:    add $node$ into $visited$; 6:    if $X_n=\varnothing$ then 7:      return false; 8:    end if 9:    for all $(s_m,e,g_m,Y,s_m^{\prime })$ do 10:      if $e\in {\mathrm{\Sigma }}_m\wedge e\notin {\mathrm{\Sigma }}_n$ then 11:        add $suc{c}_1(node,Zone(M\otimes N))$ into $visiting$; 12:      else if $e\in {\mathrm{\Sigma }}_m\wedge e\in {\mathrm{\Sigma }}_n$ then 13:         for all $(s_m^{\prime },X_n^{\prime },{\delta }^{\prime })\in suc{c}_2(node,Zone(M\otimes N))$do 14:            add $(s_m^{\prime },X_n^{\prime },{\delta }^{\prime })$ into $visiting$; 15:         end for 16:       end if 17:     end for 18: end while 19: return true;

5. Case Study

In this section, we use the water disposal system [12] as an example to show the application of our proposed algorithm. The algorithm is based on the model checking tool PAT [10]. Firstly, the system is modeled by timed automata. Then we use property patterns to model the properties and give the verification results. We use a PC (Intel(R) Core(TM) i7-12700 CPU at 2.10 GHz and 32.0 GB RAM) to obtain the experimental results.

5.1. Modeling of the Water Disposal System

Figure 9 gives the architecture and models of the water disposal system. In the figure, (1) is the architecture of the system and (2)∼(7) are the timed automata for each component of the system. The system consists of five components: Actuator, Controller (CtrlWithAct and CtrlWithCon), Heater, Sensor and Configuration. In addition, we add an Attacker which executes command injection attacks to the system. The Attacker (Figure 9(8)) can simulate a message (a malicious command) sending to the Controller like the Configuration. The maximal water level is set as 100. The Configuration can set the range of the water level: in order to ensure safety, the highest water level is 90 (i.e., SH = 90) and the lowest water level is 10 (i.e., SL = 10). If this range is exceeded, the system is not safe. The Controller checks up on the real-time water level to make sure that the water level is within the normal range (i.e., L = 40 < water level < H = 60) and sometimes sends controlling messages to the Actuator. The Actuator opens or closes the valve according to the messages from the Controller and gives the current water level to the Sensor periodically. If the valve is opened, the water level can increase by 4 every time unit. The water level always drops by 1 every time unit regardless of the valve status. The Sensor receives the data from the Actuator and then sends them to the Controller at once. The components of the system operate independently and communicate with each other if necessary. We use the interleaving [10] to combine the components as a whole system model: System = Heater $\left|\right||$ Sensor $\left|\right||$ CtrlWithAct $\left|\right||$ Actuator.

Figure 9. Architecture and timed automata models of water disposal system.

The Attacker sends error messages to the Controller periodically. It changes the values of the normal range of the water level (i.e., change H to 95 and L to 5) such that the values exceed the safe water line. There will be an accident if the system does not find it in time. In order to solve this problem, the Controller detects whether the values of H and L are abnormal periodically: if so, it sends a request to the Configuration to obtain the correct values. Then the Configuration sends the right values to the Controller (with the assumption that the values in the Configuration are unmodifiable). The complete system is shown as follows: SystemWithAttacker=Attacker $\left|\right||$ Configuration $\left|\right||$ CtrlWithAct $\left|\right||$ CtrlWithCon $\left|\right||$ Actuator $\left|\right||$ Heater $\left|\right||$ Sensor. In addition, the variables, the constants and the channel declarations of the system are shown in Figure 10.

Figure 10. Declarations of the system.

5.2. Models and Verification of System Properties

In this section, we first give the verification without time requirements, such as the deadlock checking and the checking with Linear Temporal Logic (LTL). Next, we model some properties with time requirements based on proposed property patterns and verify them with our algorithm embedded in the tool PAT.

The verification results of deadlock and LTL checking are shown as follows:

• The verification results of the assertions #assert System deadlockfree and #assert SystemWithAttacker deadlockfree are both true (through 184 states and 230 transitions and 91,146 states and 178,546 transitions, respectively), indicating that the deadlocks never occur in System and SystemWithAttacker.
• The verification result of the assertion #assert System ∣=[](WLToSen-$><>$WLToCtrl) is true (through 184 states and 230 transitions), indicating that the event WLToCtrl always happens after WLToSen, which means that the occurrence of WLToCtrl is inevitable after the event WLToSen.
• If an attack with the event FalseHL happens, the values of H or L will exceed the warning water levels. Then the event CorrectHL in the Configuration will recover the H and L. The verification result of the assertion #assert SystemWithAttacker∣=[](FalseHL-$><>$ CorrectHL) is true (through 81,544 states and 206,839 transitions). This indicates that the event CorrectHL always happens after the event FalseHL, which means that the values of H and L can be recovered after an attack.
• If the attacks always happen, the CtrlWithCon will often send a message to the Configuration with the event ObtainHL to obtain the correct values of H and L. The verification result of the assertion #assert SystemWithAttacker ∣=[]$<>$ObtainHL is true (through 81,770 states and 183,929 transitions). This indicates that the event ObtainHL can always happen, which means that CtrlWithCon can detect the attacks.

Next, we model three properties (Figure 11) using the property patterns and obtain the verification results.

Figure 11. Property models of the system.

• The property Resp is modeled by using the property pattern Resp-1, which detects whether the Sensor can send the messages to the Controller in time. The assertion in the PAT is: #assert System refines<T> Resp. The verification result is true (through 184 states and 230 transitions), indicating that when the Sensor receives the message WLToSen sent from the Heater, it can send the message WLToCtrl to the Controller in one time unit. If the clock constraint $x\le 1$ is changed to $x<1$, the verification result is false. The above verification with LTL (#assert System ∣=[](WLToSen-$><>$WLToCtrl)) gives the result that the event WLToCtrl always happens after WLToSen. This verification further shows that the event WLToCtrl always happens after WLToSen in one time unit.
• The property Pre is modeled based on the property pattern Precedence-2. In Figure 9, we set the attack interval to be at least five time units and the detecting interval of the CtrlWithCon to be six time units. As the CtrlWithCon shown in Figure 9, if the conditions H > SH or L < SL are met, the Configuration will receive a message from CtrlWithCon to obtain the correct values of H and L and reply with the event CorrectHL. The property Pre verifies whether the controller could receive the messages with correct values of H and L, after the Attacker sends error messages, i.e., the event FalseHL. FalseHL can occur many times before CtrlWithCon notices it (i.e., the event ObtainHL), because the attacker can launch the attacks continuously (see the self-transition on the state Recover). The clock x is ticking after the first occurrence of FalseHL. The assertion is: #assert SystemWithAttacker refines<T> Pre. The verification result is true (through 36,094 states and 71,836). If the number in the clock constraint $x\le 7$ is changed to a smaller one, then the verification result is false. This means that the system is able to recover within seven time units after being attacked. The above verification with LTL (#assert SystemWithAttacker∣=[](FalseHL-$><>$ CorrectHL)) gives the result that the event CorrectHL always happens after the event FalseHL. This verification further shows that the event CorrectHL always happens after the event FalseHL in seven time units.
• The property Existence is modeled based on the property pattern Existence-1. The assertion is: #assert SystemWithAttacker refines<T> Existence. The verification result of the property Existence is true (through 33,889 states and 67,375 transitions). This means that the system is able to examine whether the system is under attack within six time units, which shows that the system can automatically recover after being attacked. The above verification with LTL (#assert SystemWithAttacker ∣=[]$<>$ObtainHL) gives the result that the event ObtainHL can always happen if the attacker exists. This verification further shows that the time between two successive occurrences of the event ObtainHL is at most six time units.

5.3. Evaluation of the Algorithm

We use some timed benchmark systems to evaluate our algorithm. The benchmark systems [2] include FIS (Fischer’s mutual exclusion protocol), RW (railway control system), LYN (Lynch–Shavit’s mutual exclusion protocol), FDDI (fiber distributed data interface) and CSMA (CSMA/CD protocol).

Table 1 shows the tests with benchmark systems. A1 is the algorithm from [2] and A2 is the algorithm in this paper. The system models and the property models are represented with a set of processes. For example, LYN×5(2) indicates that there are five processes in the system model and two clocks in the property model. The properties are modeled using the patterns in this paper. All of them are deterministic or can be determinized. As a result, the algorithms can terminate. Algorithm A2 can improve the performance a little, because the property models are simplified (only need to pay attention to the concerned events) which reduces some calculations in the algorithm. The performance cannot be improved a lot, since the amount of visited states of A2 are the same as A1. However, we emphasise that the main contribution of A2 is to make the property models easy to understand and model, as indicated in the introduction.

Table 1. Tests on the algorithms with benchmark systems.

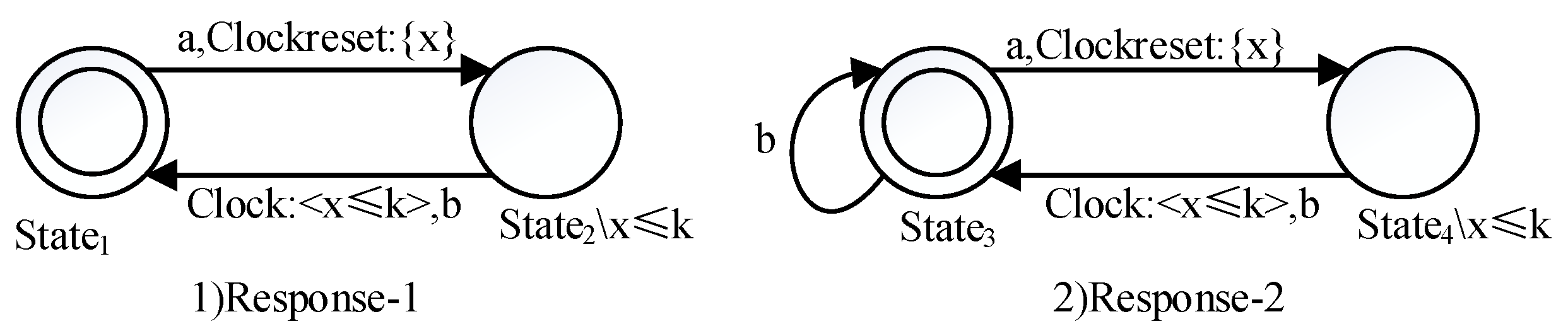
System	Time (in s) (A1)	Visited States (A1)	Time (in s) (A2)	Visited States (A2)
FIS×7(1)	3.7	20.0 K	3.3	20.0 K
FIS×8(1)	23.8	91.6 K	20.5	91.6 K
RW×6(6)	5.6	23.3 K	4.9	23.3 K
RW×7(1)	10.3	99.5 K	9.1	99.5 K
LYN×5(2)	1.8	8.1 K	1.7	8.1 K
LYN×6(1)	3.2	16.8 K	2.8	16.8 K
FDDI×7(7)	6.3	1.2 K	5.7	1.2 K
CSMA×5(1)	0.2	0.9 K	0.2	0.9 K

6. Related Work

Alur and Dill [1] first proposed the timed automata language inclusion problem, where the determinization of timed automata is a core issue. Later, some works on special time automata emerged, e.g., event-clock timed automata [14,15], Timed Automaton with single clock [16,17,18], integer resets timed automata [19] and they all can be determinized. The paper [20] introduces a new form of automata and gives the conditions that the timed automata can be determinized without changing the zones. The work in [21] first proposes a method for bounded determination of single timed automata, which expands the timed automata into a bounded tree and bounds the states to an observable depth k. The bounded determination of timed automata network [22] is also realized, with an on-the-fly algorithm which only needs to traverse the state space once. The paper [23,24] discusses the decision and computation problems for parametric timed automata. The work in [2] gives a zone based determinization and language inclusion checking method which can be applied to any timed automata. Based on [2], this paper improves the method, making it more applicable.

We also notice the works on handling the uncertainties about timing constants, i.e., they are represented as parameters in a parametric Timed Automaton. Then the parameter synthesis methods [24,25] are used to find suitable values to obtain a resultant Timed Automaton which meets the specification. The robustness of timed automata [26,27] is explored considering non-ideal implementations, e.g., measuring errors, imprecise clocks, etc. In recent works, repair of timed automata [28,29] has been studied, with the goal of modifying a given Timed Automaton to satisfy the specification.

The paper [30] collects more than 500 property models and establishes a pattern system for the representation, coding and reuse of properties for finite state verification. The work in [31] gives a set of property patterns with time requirements. It constructs observer automata for every pattern, which can be applied in some timed model checking tools directly. Based on three commonly used real-time temporal logics, the paper [32] creates real-time specification patterns, with an analysis of timed requirements of several industrial embedded systems. Based on a hierarchical framework in time-enriched process algebras, the work in [33] defines several compositional timed automata patterns for complex systems. The work in [34] proposes a set of specification patterns which can be used to describe real-time requirements in reactive systems. The work in [35] defines a set of atomic property patterns for qualitative and quantitative real-time requirements. Our work describes a set of property patterns to facilitate the timed automata language inclusion checking.

7. Conclusions

In this paper, a complete timed automata language inclusion checking method based on property patterns is proposed. We describe commonly used property patterns of timed automata in detail. The patterns provide guidance for specifying the properties, which is not mentioned much in the previous work. Furthermore, an improved language inclusion algorithm of timed automata is given, with which we only need to consider the sequences and time requirements of concerned events, so that the modeling of the property model is simplified. Finally, we use the water disposal system to illustrate our method. Three different properties are modeled based on the patterns and the system is verified using the model checker PAT. The verification results show a potential attack and the effectiveness of recovery mechanism. Although the determinization of timed automata is undecidable, our algorithm is still practical because the properties established according to property patterns are often deterministic.

As for future work, we will study the optimization of the proposed algorithm, for example, the method of handing diagonal constraints in timed automata to reduce the state space. On the other hand, we will continue to explore how a language inclusion algorithm can better solve real-life problems, e.g., the robustness of timed automata.