An Example-Guide for Rapid Seismic Assessment and FRP Strengthening of Substandard RC Buildings
Abstract
:1. Introduction
2. Synopsis of the Methodology
3. Assessment
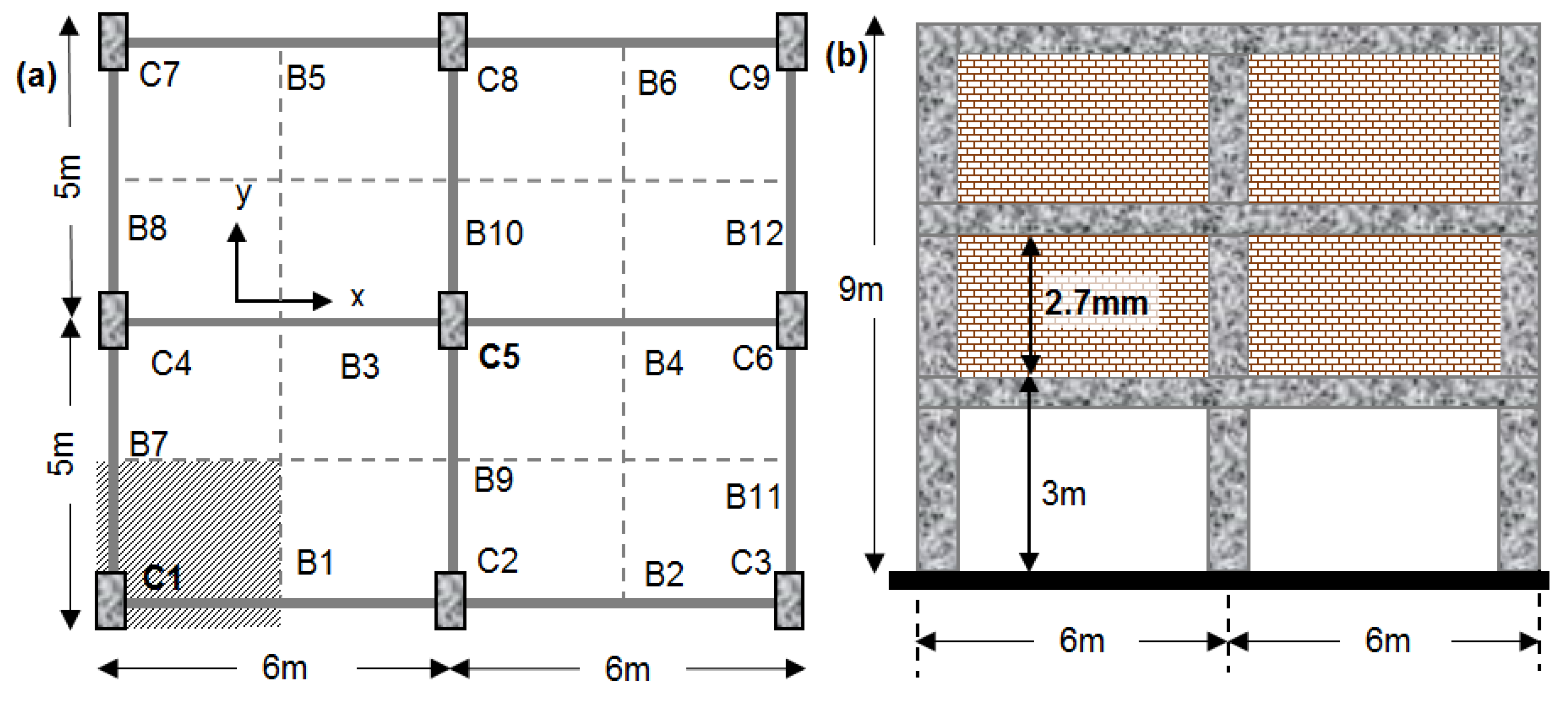
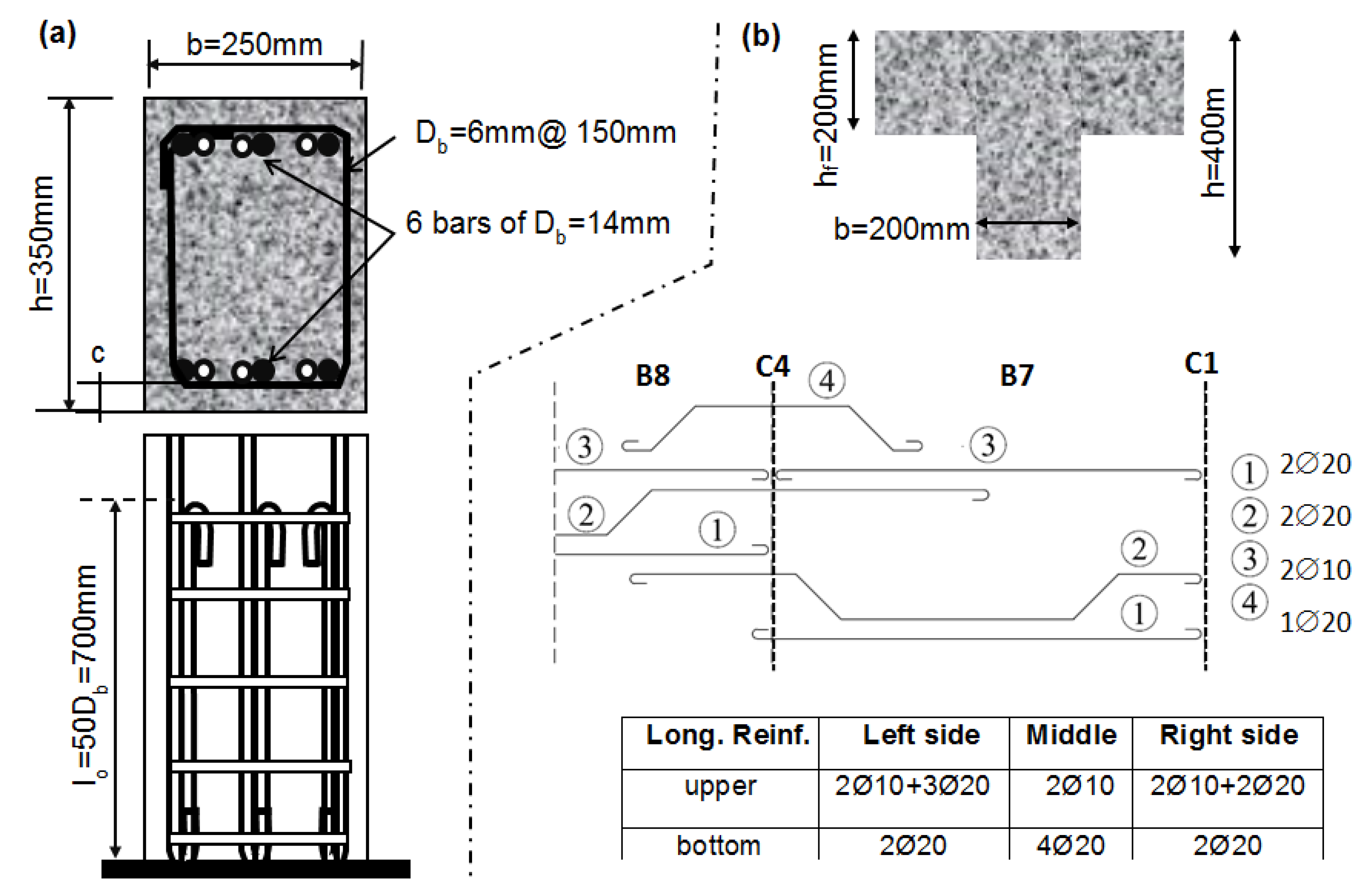
3.1. Description of the Building: Materials and Detailing
3.2. Assessment of Pilotis Columns
3.2.1. Slenderness
3.2.2. Deformation and Strength Indices from Flexure
- (a)
- From basic mechanics:
- (b)
- Empirically, by following the proposed Equation (4a,b):
- (c)
- The value of the plastic part of the chord rotation capacity of concrete members under cyclic loading is given by the following calibrated Equation (5) (from [33]):
3.2.3. Brittle Mechanisms: Shear and Lap-Splices
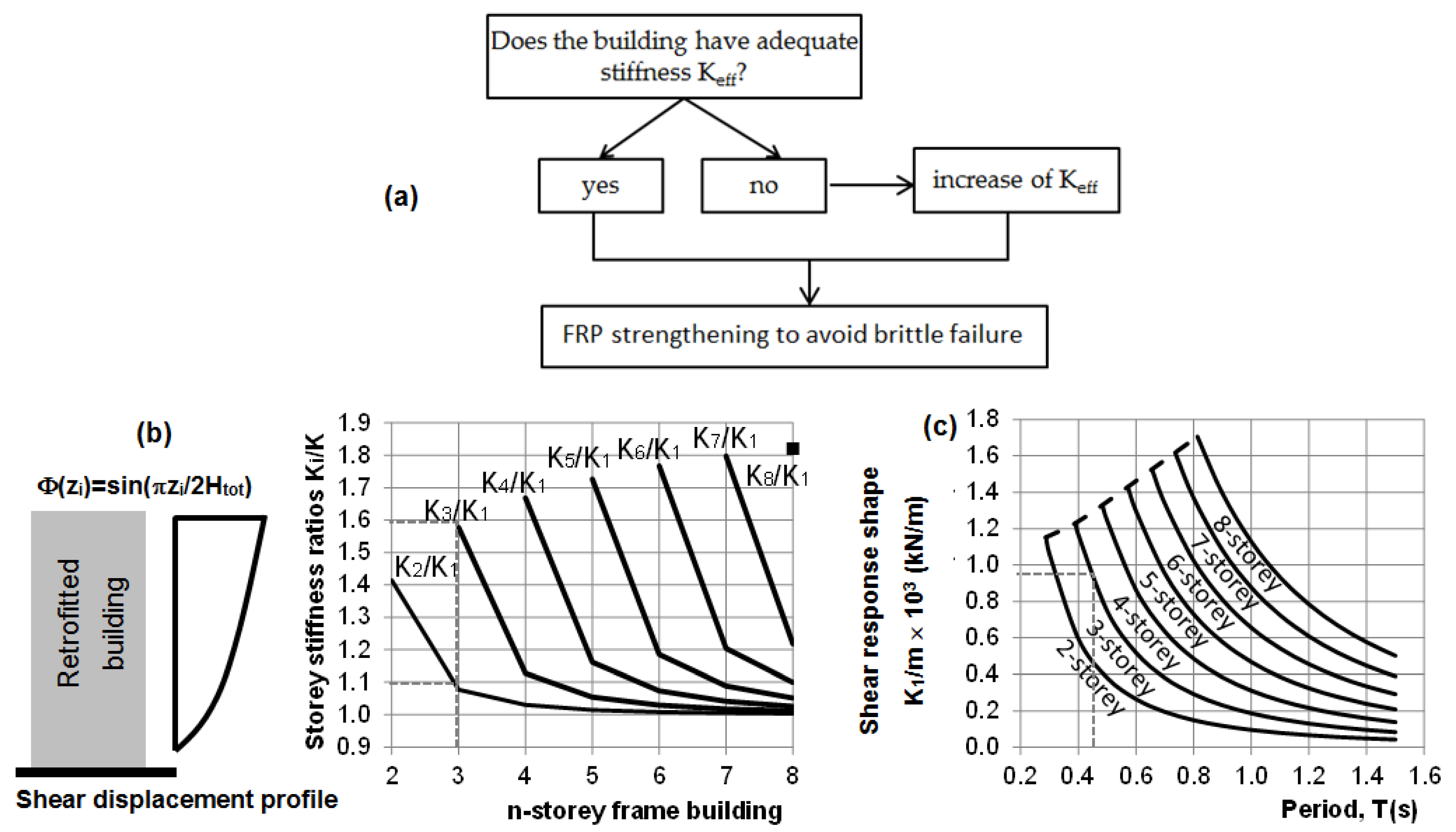
4. Global Strengthening Requirements
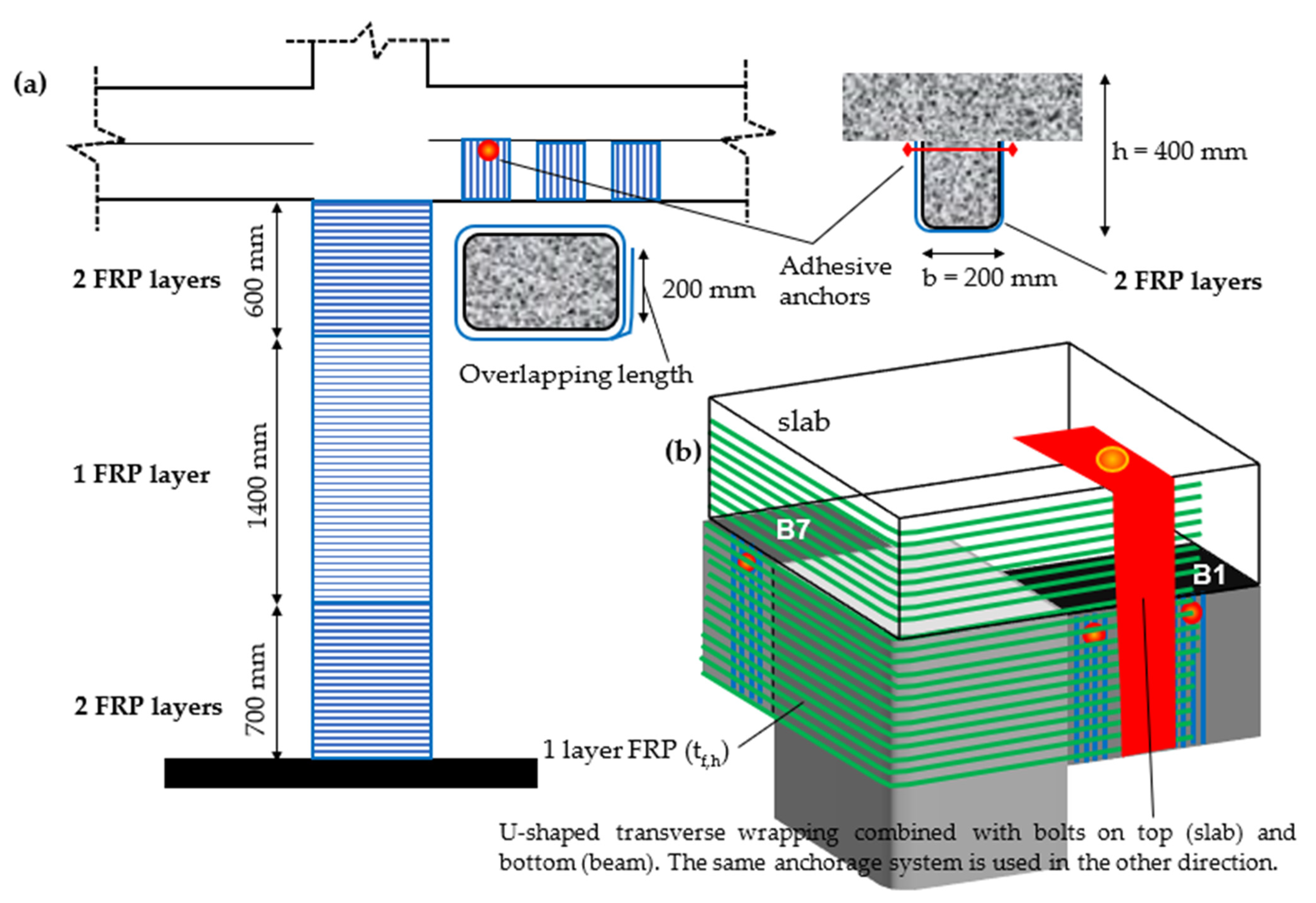
5. Local Strengthening through FRP Jacketing
- -
- Factor η1 accounts for the radius of chamfer R (= c + 0.5Db = 20 + 7 = 27 mm), at the corners of the member: η1 = 0.25 + 2(2R + Db)/h′ = 0.25 + 2(2 × 27 + 14)/(350 − 2 × 27) = 0.71 < 1 (h′ is the straight part of the largest cross section side).
- -
- Factor η2 = 1 accounts for the sufficiency of the wrap development length: the straight parts of the cross section sides h′ ≈ 300 mm and b′ ≈ 200 mm suffice to accommodate the minimum anchorage length of the external FRP layer lbmin = 0.5π√(Ef × to × so/τa)= 0.5π√(165,000 × 0.12 × 0.5/5) ≈ 70 mm (so and τa are slip and bond strength values, provided by the resin manufacturer); to this end the external layer of the FRP jacket can be anchored over the column’s shorter side.
- -
- Factor η3 = 1 for fully wrapped jacket (considers the redundancy of the jacket against debonding).
Beam-Column Joint Strengthening
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| Ag | gross area of concrete |
| As | total area of longitudinal steel reinforcement |
| Db | diameter of longitudinal steel reinforcement |
| Db,st | diameter of transverse steel reinforcement |
| Ec | modulus of elasticity of concrete |
| Ef | modulus of elasticity of FRP |
| Es | modulus of elasticity of steel |
| H | clear height of column |
| Htot | Height of building |
| Kj | translational stiffness of the column |
| Lv | shear span |
| NEd | Axial load of column |
| My | moment at yielding |
| MRdo | the flexural strength |
| Nb | number of tensile splice pairs |
| Lprov | provided anchorage length of beam longitudinal reinforcement |
| R | radius of rounded corner |
| Tref/eff/trg | reference, effective or target period |
| VRd | design shear resistance |
| VRd,c | the contribution of the concrete compression zone to the shear strength of the original member |
| VRd,f | shear strength of the FRP jacket |
| VRd,o | shear strength of the original member |
| VRd,s | the contribution of the web reinforcement to the shear strength of the original member |
| Vfl | lateral force at flexural strength (=MRdo/Lv) |
| Wtot | total weight of the building due to the seismic combination G + 0.3Q |
| avz | the tension shift of the bending moment diagram |
| b | width of cross section (b’ after chambering) |
| bf | width of FRP strip |
| bo | width of confined core in a column (to centerline of hoops) |
| c | the clear cover |
| d | effective depth of the member |
| fc | concrete strength |
| fcm | mean value of the concrete compressive strength |
| fctk | the concrete tensile strength |
| ffd | design value of the FRP tensile strength |
| fym | mean value of the longitudinal steel yield strength, also referred as fsy |
| fyw | the mean yield strength of the shear reinforcement, also referred as fy,st |
| h | total depth of the member (h’ after chamfering) |
| hslab | total depth of the slab |
| lpl | plastic hinge length |
| lo | splice length |
| i | radius of gyration for the cross section |
| n | the number of FRP layers placed in the jacket |
| nl | the number of longitudinal reinforcing bars in the cross section |
| nfloor | the total number of floors of the building |
| s | spacing of hoops/stirrups |
| tf | thickness of FRP |
| to | the thickness of a single layer |
| vEd | axial load ratio |
| x | depth of the compression zone |
| z | internal lever arm |
| ϕu | curvature at ultimate |
| ϕy | yield curvature |
| α | angle between fibres and the member axis perpendicular to the shear force |
| αf | confinement effectiveness factor defined for FRP |
| αw | confinement effectiveness factor defined for stirrups |
| γel | factor, greater than 1.00 for primary seismic members |
| γf | material safety factor for the FRP |
| εcu,c | the maximum compression strain demand |
| εcu | ultimate concrete strain |
| εfu,h | ultimate strain of the FRP jacket in the hoop direction |
| εs,crit | the strain at which the bar will become unstable |
| εsy | yield strain of the steel reinforcement |
| θu | ultimate chord rotation |
| θy | chord rotation at yielding |
| θupl | plastic part of the chord rotation capacity |
| μΔ | displacement ductility |
| μθ | chord rotation ductility |
| μΦ | curvature ductility |
| vd,max | the maximum axial load ratio |
| ξ = x/d | relative depth of the compression zone |
| ρs | longitudinal steel reinforcement ratio |
| ρsw | transverse steel reinforcement ratio |
| ρfv | the volumetric ratio of FRP reinforcement |
| ρsv | the volumetric ratio of transverse reinforcement |
| τb | bond strength |
Appendix A
| Formulae | Computation |
|---|---|
| masonry weight per floor: Wmasonry = specific weight × masonry thickness × perimeter × height | Wmasonry = 1200 Kgr/m3 × 12 cm (that is the total thickness of a two-layer bricks of breadth 6 cm) × 2 × (9.95 + 11.25) m × 2.7 m ≈ 165 kN |
| slenderness effect: (i) the radius of gyration for the cross section of the column with respect to the weak axis y-y is i = √(Ig/Ag) ≈ 0.3b and (ii) the slenderness is λ = (βo∙H)/I and λ < λlim = max{25; 15/√vEd} | Calculations for central column with vEd = 0.52: i = √(Ig/Ag) ≈ 0.3b = 0.3 × 250 = 75 mm λ = (βo∙H)/i = (1 × 2700)/75 = 36 and λ = 36 > λlim = max{25; 15/√0.52 = 20.8} = 25 |
| Flexural strength: My = Asl,1 × fym × jd + NEd × (0.5 h − 0.4 × 0.25∙d) | For corner columns (NEd = 181.3 kN): My = 462 × 500 × 0.85 × 323 + 181.3 × 103 × (0.5 × 350 − 0.4 × 0.25 × 323) ≈ 89 kNm |
| plastic hinge length lpl (three alternatives): Equation (3a) Equation (3b) Equation (3c) | lpl(3.a) = 0.1 × 1350 + 0.17 × 350 + 0.24 × (14 × 500)/√16 = 615 mm lpl(3.b) = 0.2 × 350 × [1 + 1/3 min(9,1.35/0.35)] = 160 mm lpl(3.c) = 0.5 × 323 = 161.5 mm |
| ultimate chord rotation θu: θu = 1/γel [θy + (ϕu − ϕy) lpl (1 − 0.5 lpl/LV)] | For corner columns: θu(lpl = 615 mm) = 1/1.5 × [0.64% + (0.05 − 0.0143) × 0.615 × (1 − 0.5 × 0.615/1.35)] = 1.6%, or θu(lpl = 160 mm) = 1/1.5 × [0.64% + (0.05 − 0.0143) × 0.16 × (1 − 0.5 × 0.16/1.35)] = 0.8% |
| Curvature ductility: Equation (4a) Equation (4b) μθ value shall be multiplied by 1.5 to account for the contribution of reinforcement pullout to the rotation capacity. | for corner columns (νEd = 0.13 < 0.2): μϕ = 0.45 × 0.0035/0.0025 × 350/(0.9 × 0.24 × 323) = 3.16 and μθ = 1.5 × [0.5 × (3.16 + 1)] = 3.1 and θu =3.1 × 0.64% = 2% |
| Equation (5b) Equation (5a) | al = (1 − 150/(2 × 210))∙(1 − 150/(2 × 310)) × 4/6 = 0.32 lou,min = 14 × 500/[1.05 + 14.5 × 0.32 × 0.00151 × 240/16 × √16] = 1513 m |
| Equation (6b) Equation (6c) Equation (6a) | for corner columns: VRd,c = 0.41√16 × 250 × 0.9 × 0.24 × 323/1000 ≈ 29 kN for peripheral: VRd,c = 0.41√16 × 250 × 0.9 × 0.27 × 323/1000 ≈ 32 kN VRd,s = 2 × (π × 622/4)/(150 × 210) × 210 × 310 × 240/1000 = 28 kN VRd,o|corner = 1/1.15{(350 − 0.9 × 0.24 × 323)/(2 × 1350) × min(181.25,0.55 × 250 × 350 × 16/1000) + 0.89 × (29 + 28)} ≈ 60 kN < 1.5 Vfl = 1.5 × 66 = 99 kN VRd,o|periph. = 1/1.15{(350 − 0.9 × 0.27 × 323)/(2 × 1350) × min(362.5,0.55 × 250 × 350 × 16/1000) + 0.92 × (32 + 28)} = 80 kN < 1.5Vfl = 1.5 × 85 ≈ 128 kN |
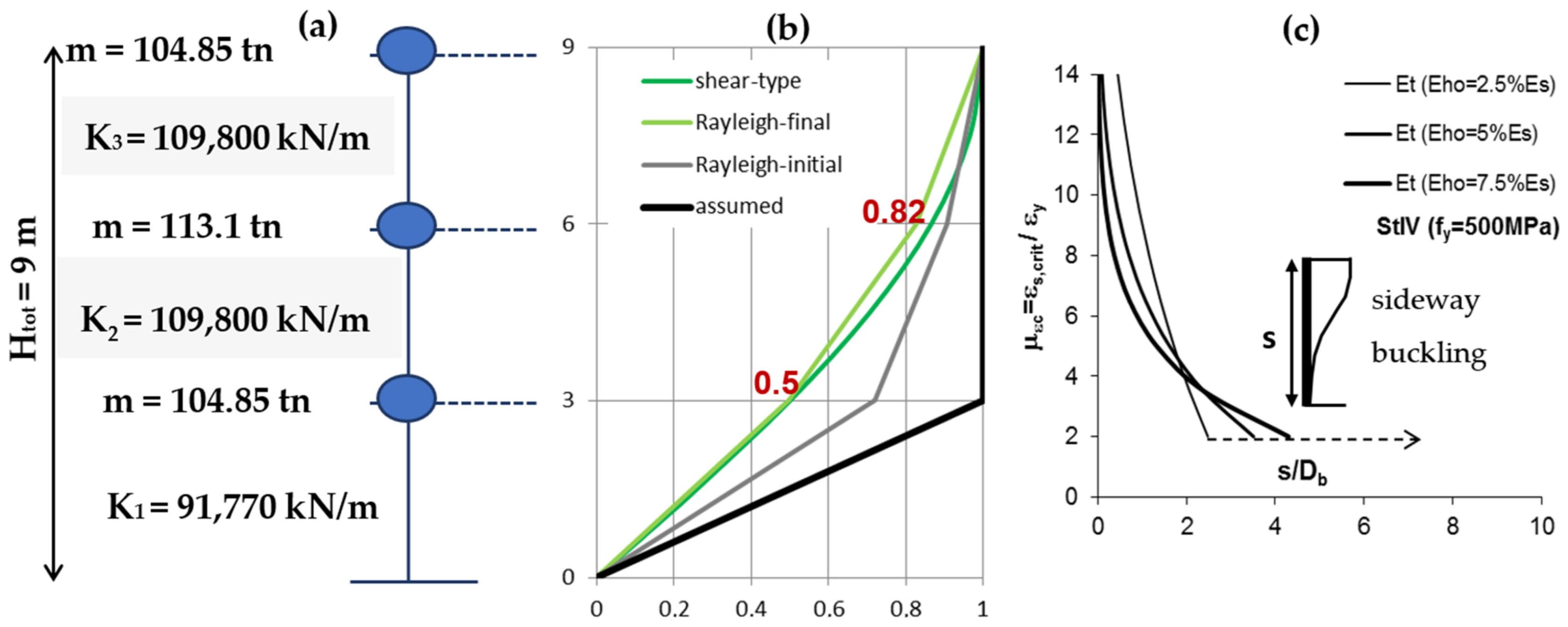
| translational stiffness of the ground storey (soft storey): Keff = ∑i=1nKi ΔΦi2 = K1 × 12 = K1 | Keff = 4 (corner columns) × 3810 kN/m + 4 (per. columns) × 4910 kN/m + (central column) × 3810 kN/m ≈ 38690 kN/m |
| FRP as shear reinforcement: For simplicity: 1.5Vfl = max(1.5Vfl,corner,1.5Vfl,peripheral) VRd,o = min(VRd,o,corner,VRd,o,peripheral) VRd,f = 1.5Vfl − VRd,o = (2tf/b) × bh × Ef × εfu,h | 1.5Vfl = max(99 kN, 128 kN) ≈ 128 kN VRd,o = min(60 kN, 80 kN) = 60 kN ΔV = 1.5Vfl − VRd,o = 68 kN ΔV = VRd,f = (2tf/b)·bh·Ef·εfu,h → 68,000 Nt = (2tf/250) × 250 × 350 × 165,000 × 0.0085 → tf = 0.07 mm < to = 0.12 mm → 1 layer |
| Equation (10) | for Db = 14 mm, μfr = 1, Nb = 3, εf,sl = 0.0015, tf = nto, Ast = 2 × π × 62/4 = 56.5 mm2, fy,st = 240 MPa and s = 150 mm: 2.3 = (2 × 1)/(3.14 × 14)(0.33 × 56.5 × 240/(3 × 150) + 2 × tf × 165,000 × 0.0015)/3) → tf = 0.25 = n × 0.12 → n = 2 layers |
| Equation (11b) Equation (11c) Equation (11a) | αf =1 − ((250 − 2∙33)2 + (350 – 2 × 33)2)/(3 × 250 × 350) = 0.56 ρsv= ((2 × 200 + 2 × 300) × 28.26)/(150 × 200 × 300) = 0.00314 εcu,c = 0.005 = 0.0035 + 0.075[1(0.56 × ρfv × 165,000 × 0.0085 + 0.15 × 0.00314 × 240)/16 − 0.1] → ρfv = 0.0023 and ρfv = 2tf(b + h)/(bh) → 0.0023 = 2tf (350 + 250))/(350 × 250) → tf = 0.17 mm tf = nto → 0.17 mm = n × 0.12 mm → n = 2 FRP layers |
| Equation (12) | µΔ = 1.3 + 12.4 × (0.5 × 0.56 × 0.0033 × 165000 × 0.0085/16 − 0.1) = 1.06 ≥ 1.3 thus µΔ = 1.3 |
| The load from the slabs is assumed to be transferred to beam B1. Conservatively, it is assumed that the loads transferred from the slab to B1 correspond to a quarter of the area of the slab. Hence, the total linear load for the seismic combination is: g = [((1/4 × 6 × 5 × 0.2))⁄6]slab × 25 + (0.2 × 0.2)beam × 25 + [((1/4 × 6 × 5))⁄6]slab × 2 = 9.75 kN⁄m, q = [((1/4 × 6 × 5))⁄6]slab × 3.5 = 4.38 kN⁄m and g + 0.3q = 9.75 + 0.3 × 4.38 = 11.06 kN⁄m, (Vg+ψq,b)l = (g + 0.3q)l/2 = (11.06 × 6)/2 = 33.19 kN. Equation (13): Vj,v = ΣMyc(1/jdc − 1/Lb,n × Hn/H) + 1/2|(Vg+ψq,b)l − (Vg+ψq,b)r| = 101 × 103(1/((250 − 2∙30)) − 1/3000 × 3000/2700) + 1/2 × |33.19 − 0| = 510.8 kN | |
| Equation (14) | Vj,h = 134 × 103(1/(0.9 × 370) − 1/3000 × 2500/2325) = 354.4 kN |
References
- Fib Bulletin 14. Externally Bonded FRP Reinforcement for r.c. Structures; Report by Task Group 9.3; Fédération Internationale du Béton (fib): Lausanne, Switzerland, 2001; p. 130. [Google Scholar]
- Ruggieri, S.; Calo, M.; Cardellicchio, A.; Uva, G. Analytical-mechanical based framework for seismic overall fragility analysis of existing RC buildings in town compartments. Bull. Earthq. Eng. 2022, 20, 8179–8216. [Google Scholar] [CrossRef]
- Leggeri, V.; Ruggieri, S.; Zagari, G.; Uva, G. Appraising seismic vulnerability of masonry aggregates through an automated mechanical-typological approach. Autom. Constr. 2021, 132, 103972. [Google Scholar] [CrossRef]
- fib Bulletin 90. Externally Applied FRP Reinforcement for Concrete Structures; Technical Report, Task Group 5.1; Fédération Internationale du Béton (fib): Lausanne, Switzerland, 2019; ISBN 978-2-88394-131-1. [Google Scholar]
- Pantazopoulou, S.; Tastani, S.P.; Thermou, G.; Triantafillou, T.; Monti, G.; Bournas, D.; Guadagnini, M. Background to European seismic design provisions for the retrofit of R.C. elements using FRP materials. Fib Struct. Concr. 2015, 17, 194–219. [Google Scholar] [CrossRef]
- Bilotta, A.; Ceroni, F.; Di Ludovico, M.; Nigro, E.; Pecce, M.; Manfredi, G. Bond Efficiency of EBR and NSM FRP Systems for Strengthening Concrete Members. ASCE J. Compos. Constr. 2011, 15, 757–772. [Google Scholar] [CrossRef]
- Bournas, D.; Triantafillou, T. Flexural strengthening of reinforced concrete columns with near-surface-mounted FRP or stainless steel. ACI Struct. J. 2009, 106, 495–505. [Google Scholar]
- Coelho, M.; Sena-Cruz, J.; Neves, L. A review on the bond behavior of FRP NSM systems in concrete. Constr. Build. Mater. 2015, 93, 1157–1169. [Google Scholar] [CrossRef] [Green Version]
- Dias, S.; Barros, J. Shear strengthening of RC beams with NSM CFRP laminates: Experimental research and analytical formulation. Compos. Struct. 2013, 99, 477–490. [Google Scholar] [CrossRef] [Green Version]
- Novidis, D.; Pantazopoulou, S. Bond Tests of Short NSM—FRP & Steel Bar Anchorages. ASCE J. Compos. Constr. 2008, 12, 323–333. [Google Scholar]
- Sharaky, I.; Torres, L.; Baena, M.; Miàs, C. An experimental study of different factors affecting the bond of NSM FRP bars in concrete. Compos. Struct. 2013, 99, 350–365. [Google Scholar] [CrossRef]
- Thermou, G.; Pantazopoulou, S. Criteria and methods for redesign and retrofit of old structures. In Proceedings of the 10th U.S. National Conference on Earthquake Engineering, Frontiers of Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Pantazopoulou, S.; Guadagnini, M.; D’Antino, T.; Lignola, G.; Napoli, A.; Relafonzo, R.; Pellegrino, C.; Prota, A.; Balafas, I.; Tastani, S.; et al. Confinement of RC elements by means of EBR-FRP Systems, Chapter 5. In Design Procedures for the Use of Composites in Strengthening of Reinforced Concrete Structures—State of the Art Report of RILEM TC 234-DUC; Pellegrino, C., Sena-Cruz, J., Eds.; RILEM STAR Book Series; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Tastani, S.; Pantazopoulou, S.; Zdoumba, D.; Plakantaras, V.; Akritidis, E. Limitations of FRP jacketing in confining old-type reinforced concrete members in axial compression. ASCE J. Compos. Constr. 2006, 10, 13–25. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Analytical model for FRP confinement of concrete columns with and without internal steel reinforcement. ASCE J. Compos. Constr. 2010, 14, 693–705. [Google Scholar] [CrossRef]
- Biskinis, D.; Fardis, M. Models for FRP-wrapped rectangular RC Columns with Continuous or Lap-Spliced Bars under Cyclic Lateral Loading. Eng. Struct. 2013, 57, 199–212. [Google Scholar] [CrossRef]
- Tastani, S.; Balafas, I.; Dervisis, A.; Pantazopoulou, S. Effect of Core Compaction on Deformation Capacity of FRP-Jacketed Concrete. Constr. Build. Mater. 2013, 47, 1078–1092. [Google Scholar] [CrossRef]
- Bousselham, A. State of Research on Seismic Retrofit of RC Beam-Column Joints with Externally Bonded FRP. ASCE J. Compos. Constr. 2010, 14, 49–61. [Google Scholar] [CrossRef]
- Akguzel, U.; Pampanin, S. Assessment and Design Procedure for the Seismic Retrofit of Reinforced Concrete Beam-Column Joints using FRP Composite Materials. ASCE J. Compos. Constr. 2012, 16, 21–34. [Google Scholar] [CrossRef]
- Del Vecchio, C.; Di Ludovico, M.; Balsamo, A.; Prota, A.; Manfredi, G.; Dolce, M. Experimental Investigation on Exterior RC Beam-Column Joints Retrofitted with FRP Systems. ASCE J. Compos. Constr. 2014, 18, 1–13. [Google Scholar] [CrossRef]
- Del Vecchio, C.; Di Ludovico, M.; Prota, A.; Manfredi, G. Analytical Model and Design Approach for FRP Strengthening of non-Conforming RC Corner Beam–Column Joints. Eng. Struct. 2015, 87, 8–20. [Google Scholar] [CrossRef]
- Frascadore, R.; Di Ludovico, M.; Prota, A.; Verderame, G.; Manfredi, G.; Dolce, M.; Cosenza, E. Local Strengthening of RC Structures as a Strategy for Seismic Risk Mitigation at Regional Scale. Earthq. Spectra 2015, 31, 1083–1102. [Google Scholar] [CrossRef] [Green Version]
- Tureyen, A.; Frosch, R. Concrete Shear Strength: Another Perspective. ACI Struct. J. 2003, 100, 609–615. [Google Scholar]
- Richart, F.; Brandtzaeg, A.; Brown, R. Study of Failure of Concrete under Combined Compressive Stresses; Engineering Experiment Station, No. 185; University of Illinois: Urbana, IL, USA, 1928. [Google Scholar]
- Clough, R.; Penzien, J. Dynamics of Structures, 2nd ed.; McGraw-Hill International Editions: New York, NY, USA, 1993. [Google Scholar]
- Rozman, M.; Fajfar, P. Seismic response of RC frame building designed according to old and modern practices. Bull. Earthq. Eng. 2009, 7, 779–799. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Alternative retrofitting strategies to prevent the failure of an under-designed reinforced concrete frame. Eng. Fail. Anal. 2018, 89, 271–285. [Google Scholar] [CrossRef]
- EN 1998-3 NEN SC8 PT3; Eurocode 8–Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings and Bridges. European Committee for Standardization (CEN): Brussels, Belgium, 2021.
- EN 13791; Assessment of In-Situ Compressive Strength in Structures and Precast Concrete Components. European Committee for Standardization (CEN): Brussels, Belgium, 2019.
- ACI CODE-318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members. Ph.D. Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2000; p. 184. [Google Scholar]
- Thermou, G.E.; Pantazopoulou, S.J.; Elnashai, A.S. Global interventions for seismic upgrading of substandard rc buildings. ASCE J. Struct. Eng. 2012, 138, 387–401. [Google Scholar] [CrossRef]
- EN 1998-3; Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- Dai, K.Y.; Yu, X.H.; Lu, D.G. Phenomenological hysteretic model for corroded RC columns. Eng. Struct. 2020, 210, 110315. [Google Scholar] [CrossRef]
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Greek Seismic Assessment and Retrofit Code, Earthquake Planning and Protection Organization, 2017. Official Government Gazette 2984 B, 30-8-2017. Available online: www.oasp.gr (accessed on 11 December 2022).

| Cross Section Analysis: Approximations | Chord Rotation from Procedures (a–c) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Column | ϕy = 2εsy/h (1/m) | My (kNm) | K (kNm−1) | ϕu (1/m) − ξ from Figure 3 | θy (%) | (a): θu (%) (µθ = θu/θy) | (b): θu (%) (µθ = θu/θy) | (c): θu (%) (µθ = θu/θy) | |
| lpl = 160 mm | lpl = 615 mm | ||||||||
| 1/3/7/9 vEd = 0.13 | 0.0143 | 89 | 3810 | 0.05–0.24 | 0.64 | 0.8 (1.2) | 1.6 (2.4) | 2 (3.1) | 1.7 (2.7) |
| 2/4/6/8 vEd = 0.26 | 115 | 4910 | 0.044–0.27 | 0.73 (1.1) | 1.4 (2.2) | 1.7 (2.6) | 1.8 (2.8) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tastani, S.; Thermou, G. An Example-Guide for Rapid Seismic Assessment and FRP Strengthening of Substandard RC Buildings. Appl. Sci. 2022, 12, 12950. https://doi.org/10.3390/app122412950
Tastani S, Thermou G. An Example-Guide for Rapid Seismic Assessment and FRP Strengthening of Substandard RC Buildings. Applied Sciences. 2022; 12(24):12950. https://doi.org/10.3390/app122412950
Chicago/Turabian StyleTastani, Sousana, and Georgia Thermou. 2022. "An Example-Guide for Rapid Seismic Assessment and FRP Strengthening of Substandard RC Buildings" Applied Sciences 12, no. 24: 12950. https://doi.org/10.3390/app122412950
APA StyleTastani, S., & Thermou, G. (2022). An Example-Guide for Rapid Seismic Assessment and FRP Strengthening of Substandard RC Buildings. Applied Sciences, 12(24), 12950. https://doi.org/10.3390/app122412950







