Study on the Correspondence of Vortex Structures and Vortex-Induced Pressures for a Streamlined Box Girder
Abstract
:1. Introduction
2. Method and Model
2.1. Governing Equations
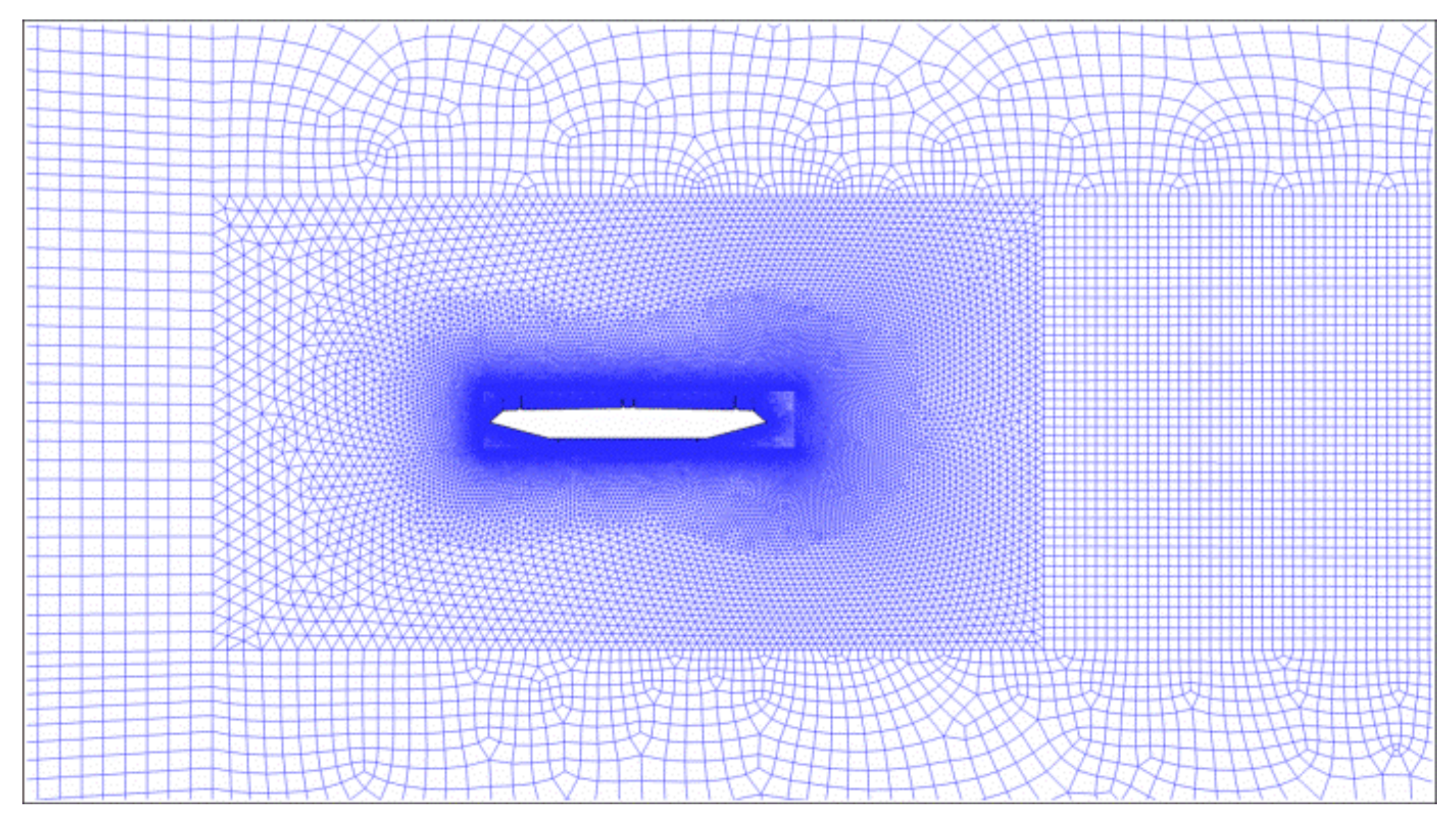
2.2. Simulation Model
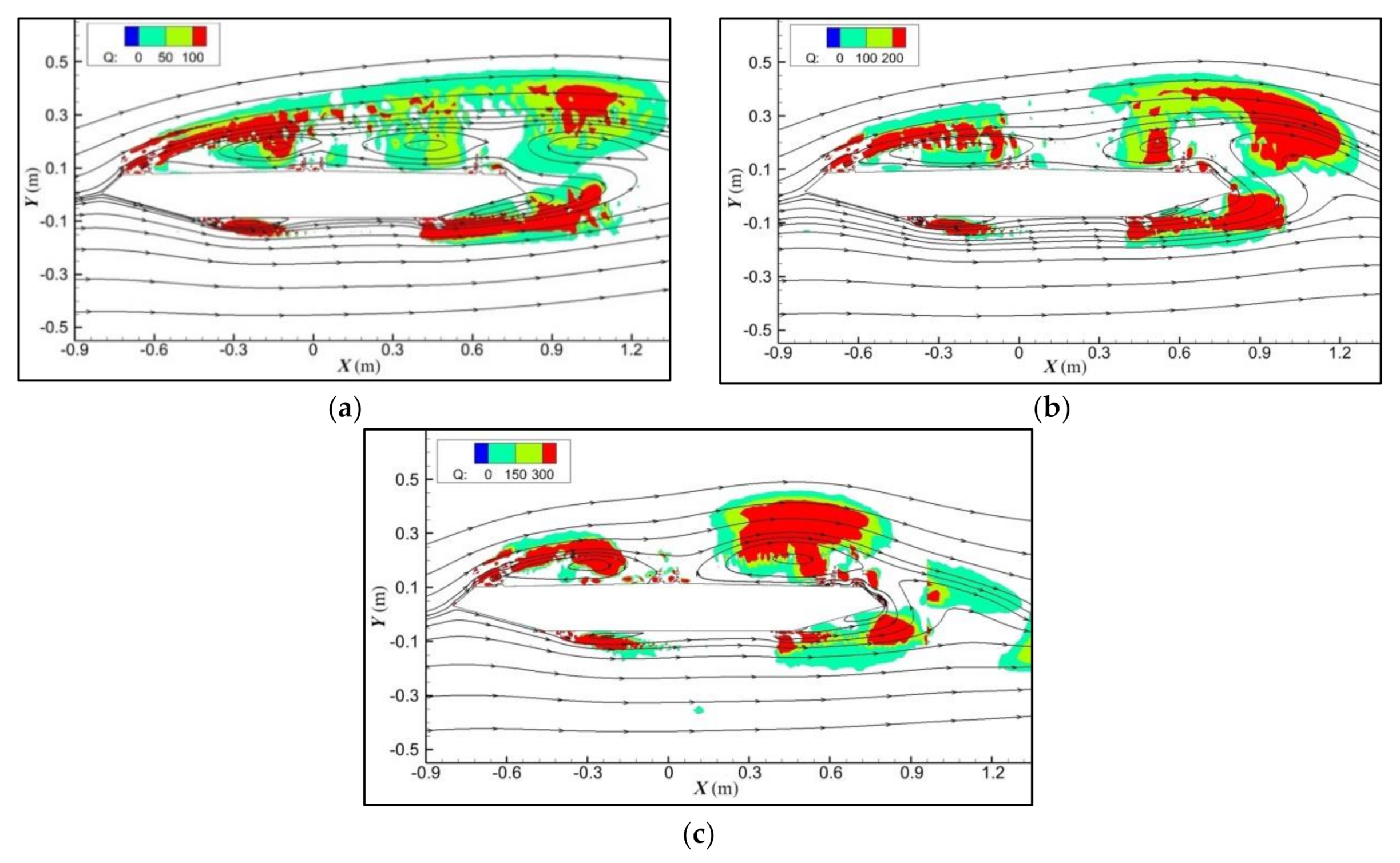
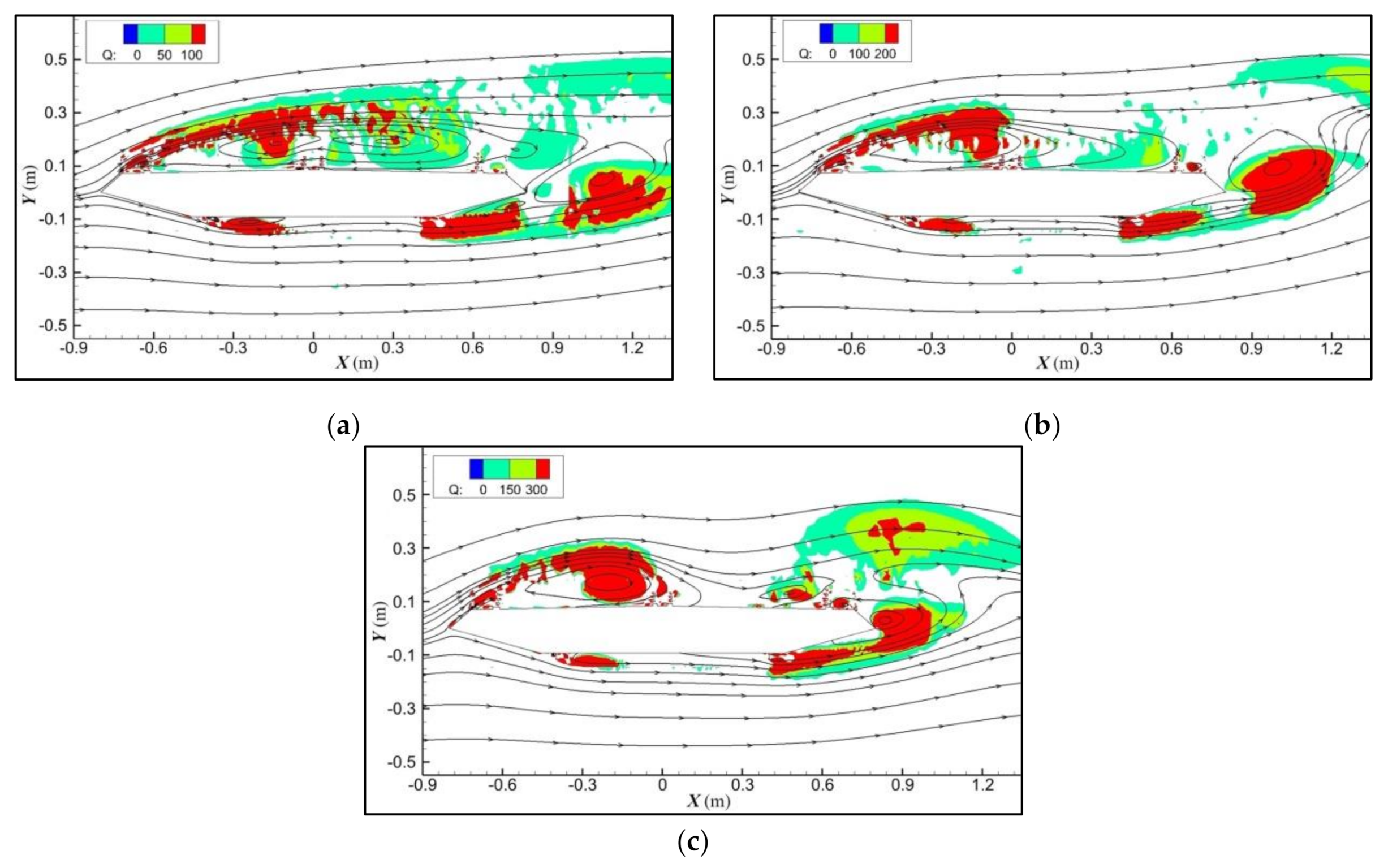
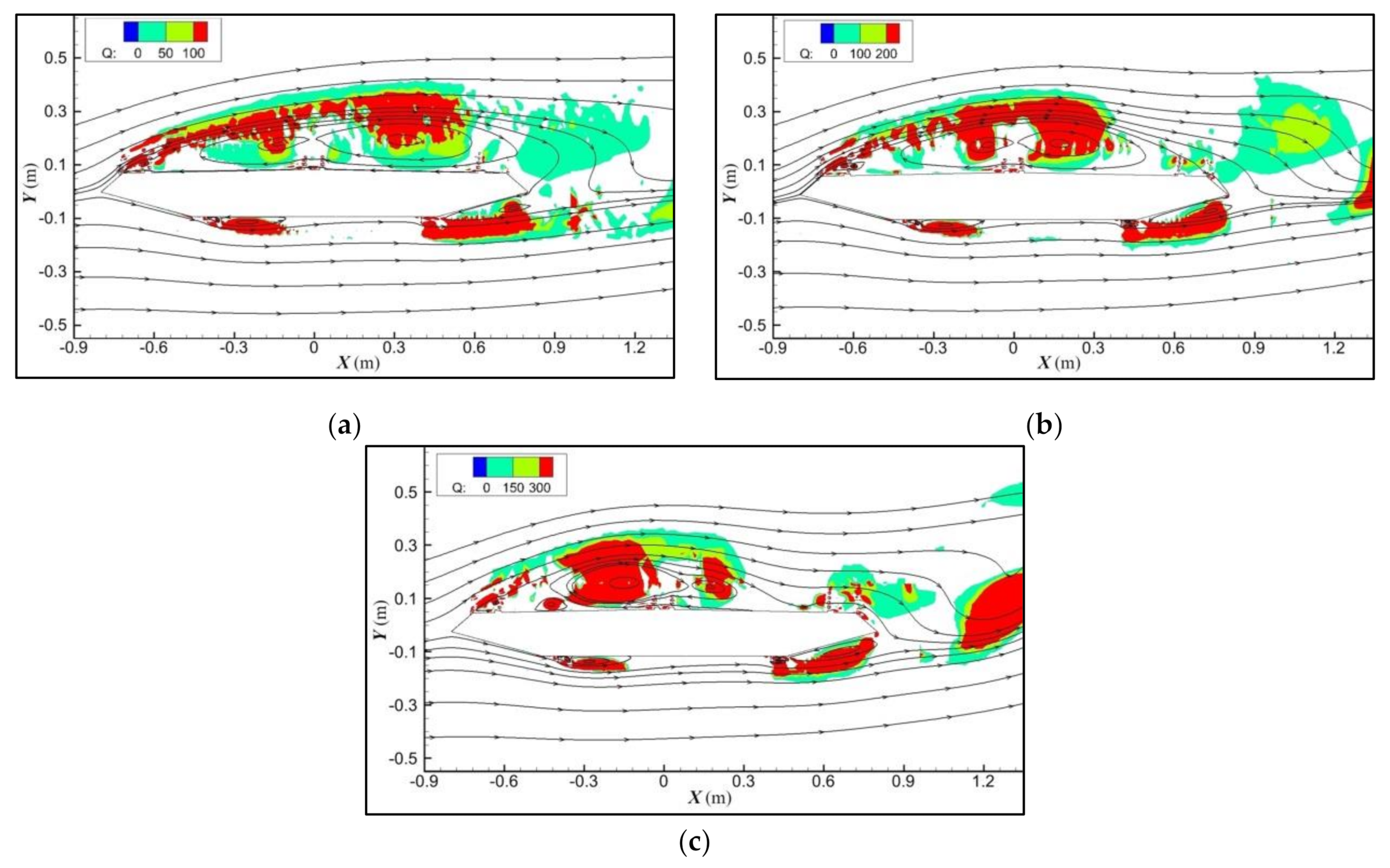
3. Distribution and Evolution of Vortex Structures
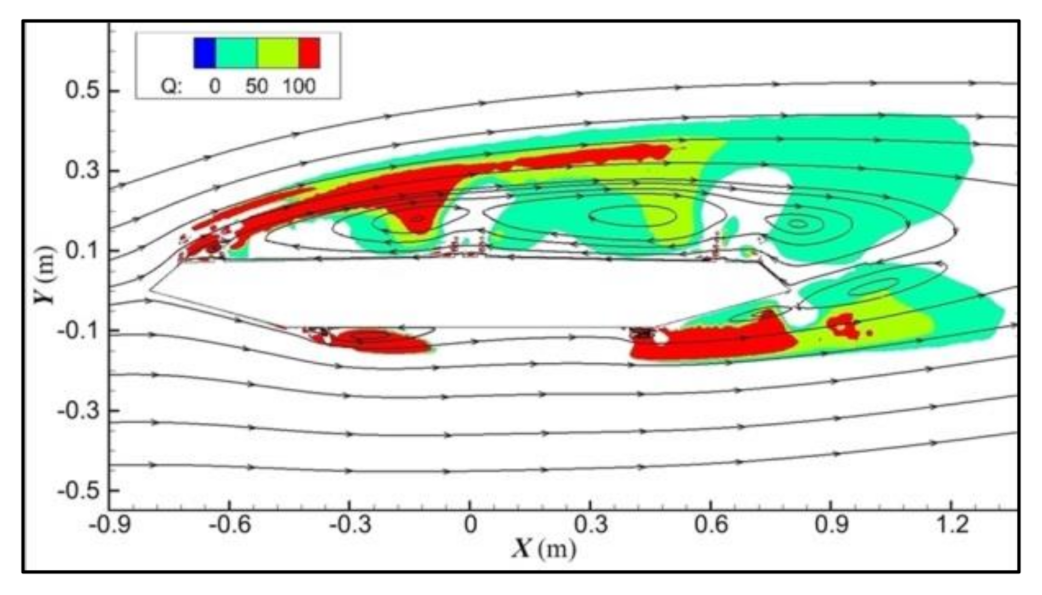
3.1. Determination of Vortex Structures
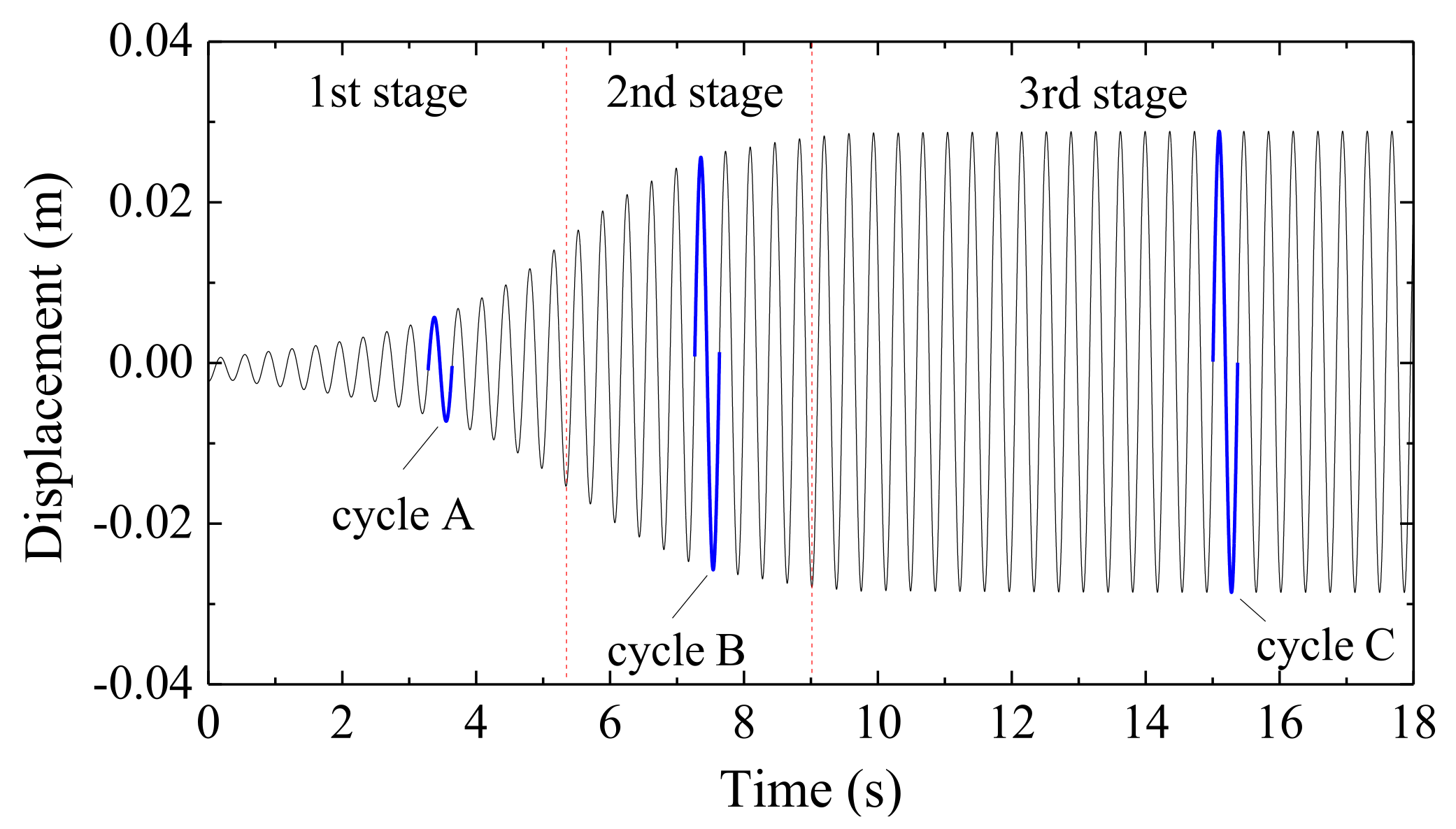
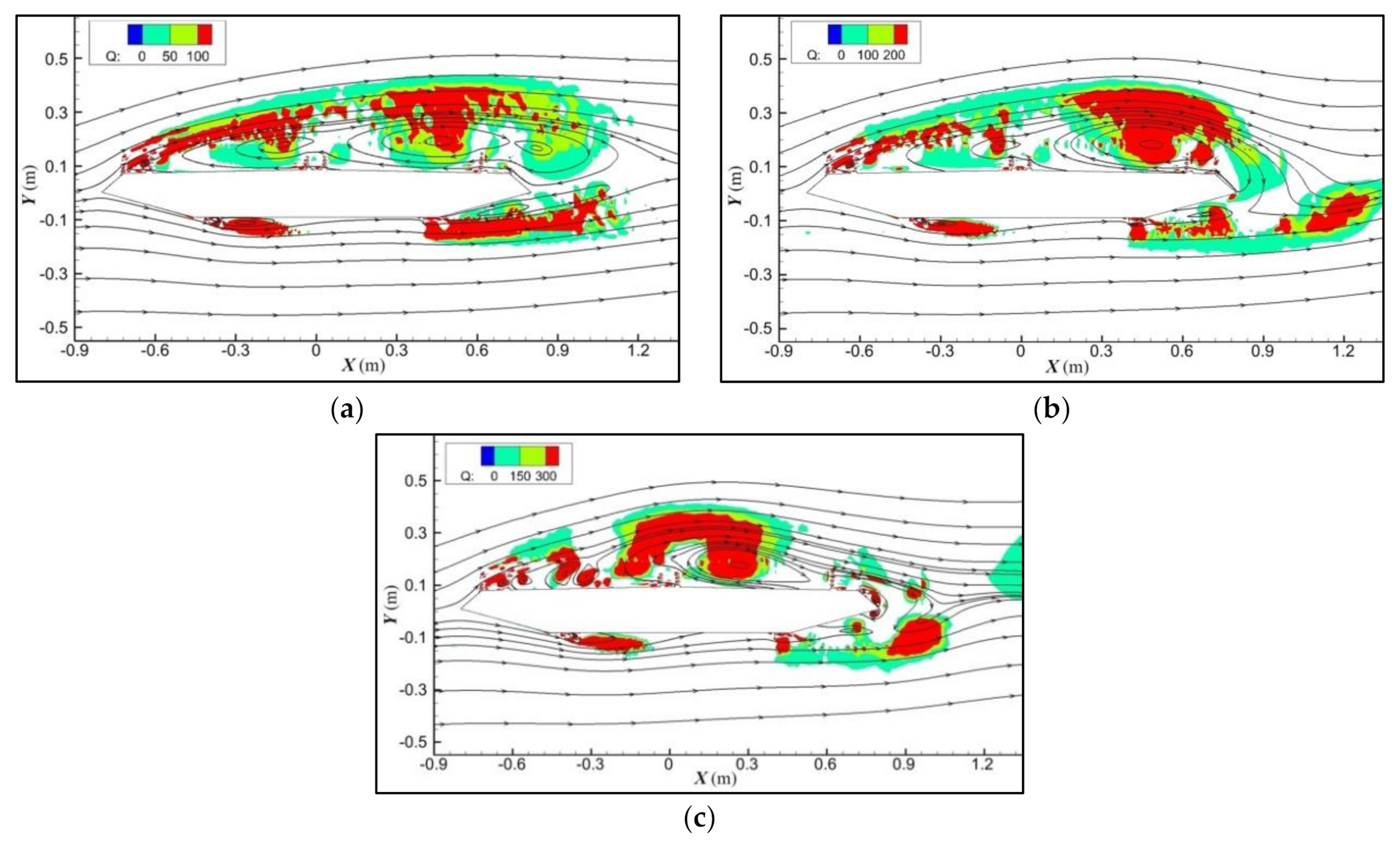
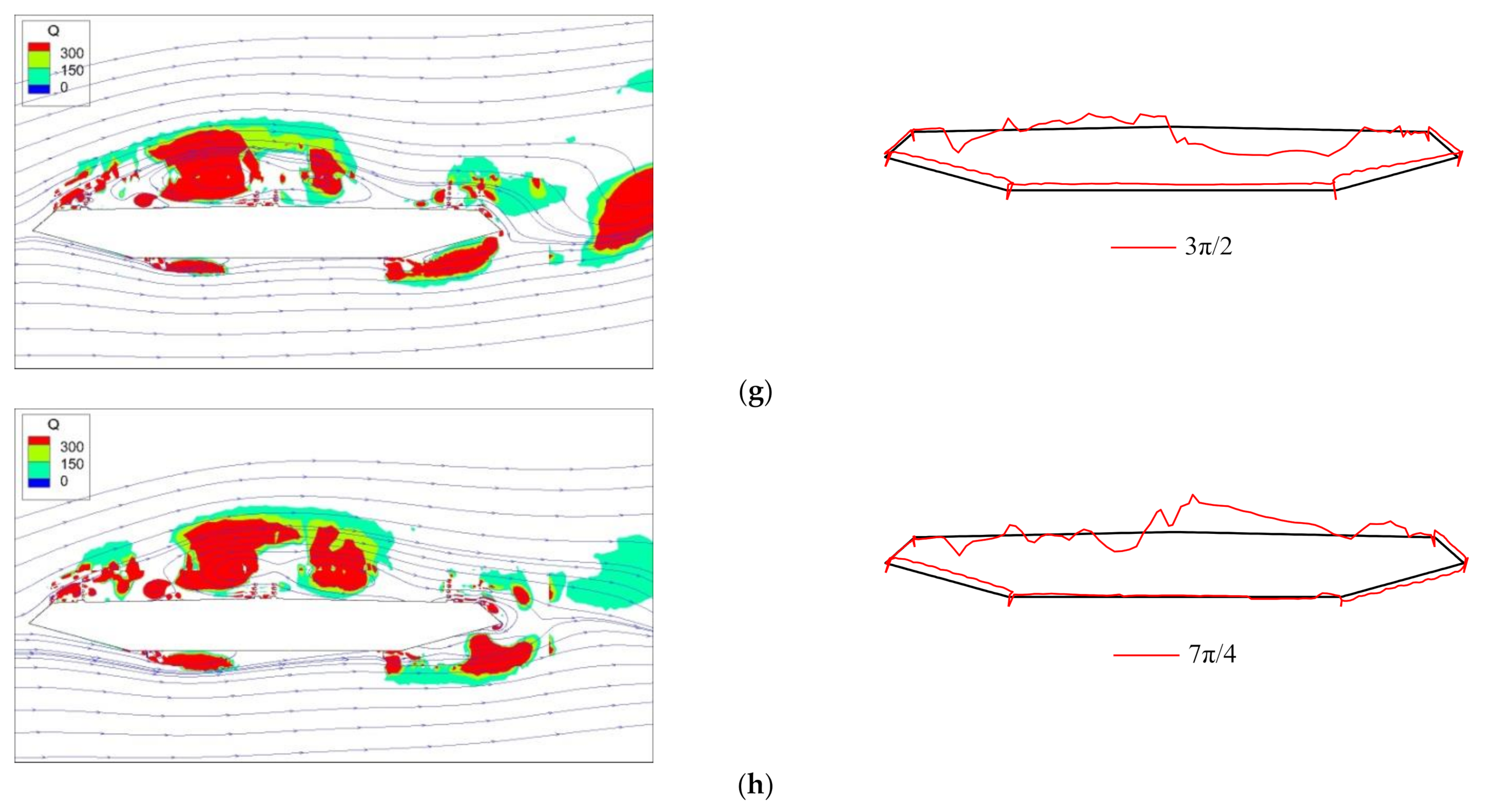
3.2. Evolution of Vortex Structures in the Whole Process of VIV
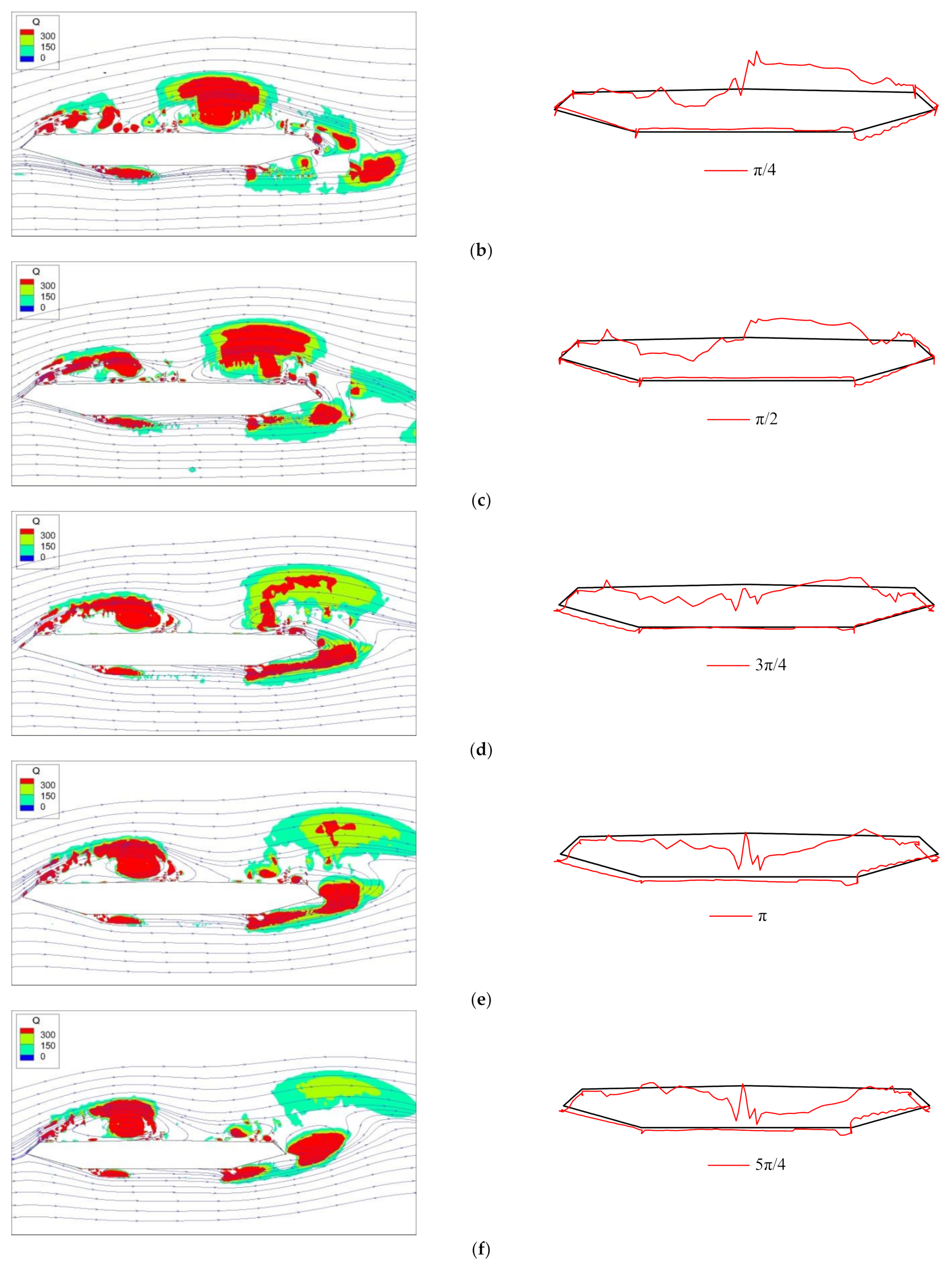
4. Correspondence of Vortex Structures and Vortex-Induced Pressures
4.1. Determination of Vortex-Induced Pressures of Each Point
4.2. Relation between Vortex Structures and VIPs at the Stable Stage of VIV
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matsumoto, M.; Yagi, T.; Shigemura, Y.; Tsushima, D. Vortex-induced cable vibration of cable-stayed bridges at high reduced wind velocity. J. Wind Eng. Ind. Aerod. 2001, 89, 633–647. [Google Scholar] [CrossRef]
- Zhou, T.M.; Razali, S.F.M.; Hao, Z.; Cheng, L. On the study of vortex-induced vibration of a cylinder with helical strakes. J. Fluid Struct. 2011, 27, 903–917. [Google Scholar] [CrossRef]
- Tumkur, R.K.R.; Pearlstein, A.J.; Masud, A.; Gendelman, O.V.; Blanchard, A.B.; Bergman, L.A.; Vakakis, A.F. Effect of an internal nonlinear rotational dissipative element on vortex shedding and vortex-induced vibration of a sprung circular cylinder. J. Fluid Mech. 2017, 828, 196–235. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Hargreaves, D.M.; Owen, J.S. Vortex-induced vibration of a 5:1 rectangular cylinder: A comparison of wind tunnel sectional model tests and computational simulations. J. Wind Eng. Ind. Aerod. 2018, 175, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, T.; Li, T. Numerical study on suppression of vortex-induced vibration of circular cylinder by helical wires. J. Wind Eng. Ind. Aerod. 2020, 197, 104081. [Google Scholar] [CrossRef]
- Tamura, Y. Mathematical models for understanding phenomena: Vortex-induced vibrations. JPN Archit. Rev. 2020, 3, 398–422. [Google Scholar] [CrossRef]
- Zhao, M.; Murphy, J.M.; Kwok, K. Numerical simulation of vortex-induced vibration of two rigidly connected cylinders in side-by-side and tandem arrangements using RANS model. J. Fluid Eng. 2016, 138, 021102. [Google Scholar] [CrossRef]
- Zhou, S.; Zou, Y.F.; Hua, X.G.; Liu, Z. Comparison of Two-Dimensional and Three-Dimensional Responses for Vortex-Induced Vibrations of a Rectangular Prism. Appl. Sci. 2020, 10, 7996. [Google Scholar] [CrossRef]
- Badhurshah, R.; Bhardwaj, R.; Bhattacharya, A. Numerical simulation of Vortex-Induced Vibration with bistable springs: Consistency with the Equilibrium Constraint. J. Fluid Struct. 2021, 1, 103280. [Google Scholar] [CrossRef]
- Zhu, L.D.; Meng, X.L.; Guo, Z.S. Nonlinear mathematical model of vortex-induced vertical force on a flat closed-box bridge deck. J. Wind Eng. Ind. Aerod. 2013, 122, 69–82. [Google Scholar] [CrossRef]
- Mashnad, M.; Jones, N.P. A model for vortex-induced vibration analysis of long-span bridges. J. Wind Eng. Ind. Aerod. 2014, 134, 96–108. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Yang, T.; Ding, Q.S.; Ge, Y.J. Mechanism on suppression in vortex-induced vibration of bridge deck with long projecting slab with countermeasures. Wind Struct. 2015, 20, 643–660. [Google Scholar] [CrossRef]
- He, H.X.; Li, J.W. Study on the Effect and Mechanism of Aerodynamic Measures for the Vortex-Induced Vibration of Separate Pairs of Box Girders in Cable-Stayed Bridges. Shock Vib. 2015, 2015, 792957. [Google Scholar] [CrossRef]
- Xu, K.; Ge, Y.J.; Zhao, L.; Du, X.L. Calculating Vortex-Induced Vibration of Bridge Decks at Different Mass-Damping Conditions. J. Bridge. Eng. 2018, 23, 4017149. [Google Scholar] [CrossRef]
- Ma, C.M.; Wang, J.X.; Li, Q.S.; Qin, H.; Liao, H.L. Vortex-Induced Vibration Performance and Suppression Mechanism for a Long Suspension Bridge with Wide Twin-Box Girder. J. Struct. Eng. 2018, 144, 4018202. [Google Scholar] [CrossRef]
- Yang, W.H.; Chen, W.L.; Li, H. Suppression of vortex-induced vibration of single-box girder with various angles of attack by self-issuing jet method. J. Fluid Struct. 2020, 96, 103017. [Google Scholar] [CrossRef]
- Chen, X.Y.; Li, Y.L.; Xu, X.Y.; Tang, H.J.; Wang, B. Evolution laws of distributed vortex-induced pressures and energy of a streamlines box girder via numerical simulation. Adv. Struct. Eng. 2020, 23, 2776–2788. [Google Scholar] [CrossRef]
- Oh, S.; Seo, S.I.; Lee, H.; Lee, H.E. Prediction of wind velocity to raise vortex-induced vibration through a road-rail bridge with truss-shaped girder. Shock Vib. 2018, 2018, 2829640. [Google Scholar] [CrossRef] [Green Version]
- Mao, W.; Zhou, Z.; Huilin, A. Ground effects on the vortex-induced vibration of bridge decks. KSCE J. Civ. Eng. 2019, 23, 1248–1258. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Y.; Hua, X.; Chen, Z.; Wen, Q. Automatic identification of bridge vortex-induced vibration using random decrement method. Appl. Sci. 2019, 9, 2049. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Zheng, S.; Yan, Z. Vortex-induced Vibration and Control of Split Three-Box Girder Bridges. Struct. Eng. Int. 2021, 1–10. [Google Scholar] [CrossRef]
- Xin, D.; Zhan, J.; Zhang, H.; Ou, J.P. Control of Vortex-Induced Vibration of a Long-Span Bridge by Inclined Railings. J. Bridge Eng. 2021, 26, 04021093. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z. VIV Properties of π-Shaped Bridge Sectional Model: Dependence on Torsional-Bending Frequency Ratio. J. Bridge Eng. 2021, 26, 06021003. [Google Scholar] [CrossRef]
- Bruno, L.; Khris, S. The validity of 2D numerical simulations of vortical structures around a bridge deck. Math. Comput. Model. 2003, 37, 795–828. [Google Scholar] [CrossRef]
- Sarwar, M.W.; Ishihara, T. Numerical study on suppression of vortex-induced vibrations of box girder bridge section by aerodynamic countermeasures. J. Wind Eng. Ind. Aerod. 2010, 98, 701–711. [Google Scholar] [CrossRef]
- Kwok, K.C.; Qin, X.R.; Fok, C.H.; Hitchcock, P.A. Wind-induced pressures around a sectional twin-deck bridge model: Effects of gap-width on the aerodynamic forces and vortex shedding mechanisms. J. Wind Eng. Ind. Aerod. 2012, 110, 50–61. [Google Scholar] [CrossRef]
- Chen, X.Y.; Wang, B.; Zhu, L.D.; Li, Y.L. Numerical study on surface distributed vortex-induced force on a flat-steel-box girder. Eng. Appl. Comp. Fluid 2018, 12, 41–56. [Google Scholar] [CrossRef]
- Haque, M.N.; Katsuchi, H.; Yamada, H.; Nishio, M. Investigation of edge fairing shaping effects on aerodynamic response of long-span bridge deck by unsteady RANS. Arch. Civ. Mech. Eng. 2016, 16, 888–900. [Google Scholar] [CrossRef]
- Tang, H.J.; Li, Y.L.; Shum, K.M. Flutter performance and aerodynamic mechanism of plate with central stabilizer at large angles of attack. Adv. Struct. Eng. 2018, 21, 335–346. [Google Scholar] [CrossRef]
- Tang, H.J.; Li, Y.L.; Chen, X.Z.; Shum, K.M.; Liao, H.L. Flutter performance of central-slotted plate at large angles of attack. Wind Struct. 2017, 24, 447–464. [Google Scholar] [CrossRef]
- Xu, X.Y.; Wang, Y.L.; Chen, X.Y.; Zheng, X.L.; Zeng, Y.P. Vortex-induced vibration characteristics and equivalent static force calculation method of circular steel hangers on arch bridge. KSCE J. Civ. Eng. 2020, 24, 1276–1284. [Google Scholar] [CrossRef]
- Mannini, C.; Sbragi, G.; Schewe, G. Analysis of self-excited forces for a box-girder bridge deck through unsteady RANS simulations. J. Fluid Struct. 2016, 63, 57–76. [Google Scholar] [CrossRef]
- Hu, C.X.; Zhao, L.; Ge, Y.J. A simplified vortex model for the mechanism of vortex-induced vibrations in a streamlined closed-box girder. Wind Struct. 2021, 32, 309–319. [Google Scholar]
- Zhang, T.Y.; Sun, Y.G.; Li, M.S.; Yang, X.W. Experimental and numerical studies on the vortex-induced vibration of two-box edge girder for cable-stayed bridges. J. Wind Eng. Ind. Aerod. 2020, 206, 104336. [Google Scholar] [CrossRef]
- Noguchi, K.; Ito, Y.; Yagi, T. Numerical evaluation of vortex-induced vibration amplitude of a box girder bridge using forced oscillation method. J. Wind Eng. Ind. Aerod. 2020, 196, 104029. [Google Scholar] [CrossRef]
- Fang, C.; Hu, R.J.; Tang, H.J.; Li, Y.L.; Wang, Z.W. Experimental and numerical study on vortex-induced vibration of a truss girder with two decks. Adv. Struct. Eng. 2021, 24, 841–855. [Google Scholar] [CrossRef]
- Chen, W.L.; Li, H.; Hu, H. An experimental study on the unsteady vortices and turbulent flow structures around twin-box-girder bridge deck models with different gap ratios. J. Wind Eng. Ind. Aerod. 2014, 132, 27–36. [Google Scholar] [CrossRef]
- Dubief, Y.; Delcayre, F. On coherent-vortex identification in turbulence. J. Turbul. 2000, 1, 11. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. In Proceeding of the Summer Program in Center for Turbulence Research; Report CTR-S88; Stanford University: Stanford, CA, USA, 1988. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Shen, M.; Song, X.; Chen, X.; Lv, M.; Jia, S. Study on the Correspondence of Vortex Structures and Vortex-Induced Pressures for a Streamlined Box Girder. Appl. Sci. 2022, 12, 1075. https://doi.org/10.3390/app12031075
Wei Z, Shen M, Song X, Chen X, Lv M, Jia S. Study on the Correspondence of Vortex Structures and Vortex-Induced Pressures for a Streamlined Box Girder. Applied Sciences. 2022; 12(3):1075. https://doi.org/10.3390/app12031075
Chicago/Turabian StyleWei, Zhaolan, Minghui Shen, Xiaodong Song, Xingyu Chen, Mengting Lv, and Shaomin Jia. 2022. "Study on the Correspondence of Vortex Structures and Vortex-Induced Pressures for a Streamlined Box Girder" Applied Sciences 12, no. 3: 1075. https://doi.org/10.3390/app12031075
APA StyleWei, Z., Shen, M., Song, X., Chen, X., Lv, M., & Jia, S. (2022). Study on the Correspondence of Vortex Structures and Vortex-Induced Pressures for a Streamlined Box Girder. Applied Sciences, 12(3), 1075. https://doi.org/10.3390/app12031075





