Computational Studies of the Photogeneration from Dihydrosanguinarine and the Probable Cytotoxicity Mechanism of Sanguinarine
Abstract
:1. Introduction
2. Computational Details
2.1. Molecular Dynamic Simulations
2.2. Quantum Mechanical Calculations
3. Results and Discussion
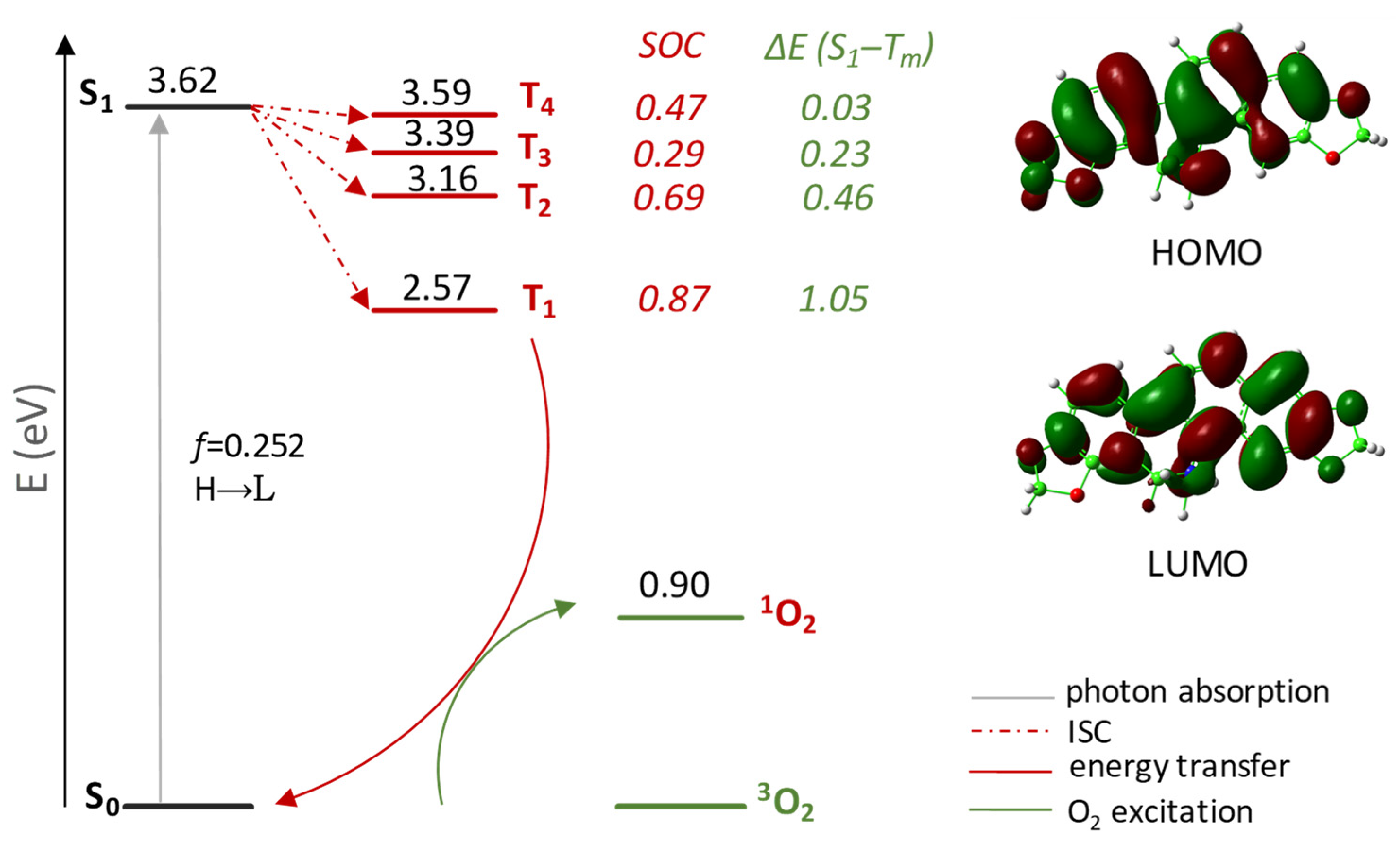
3.1. Photophysical Properties of DHSAN
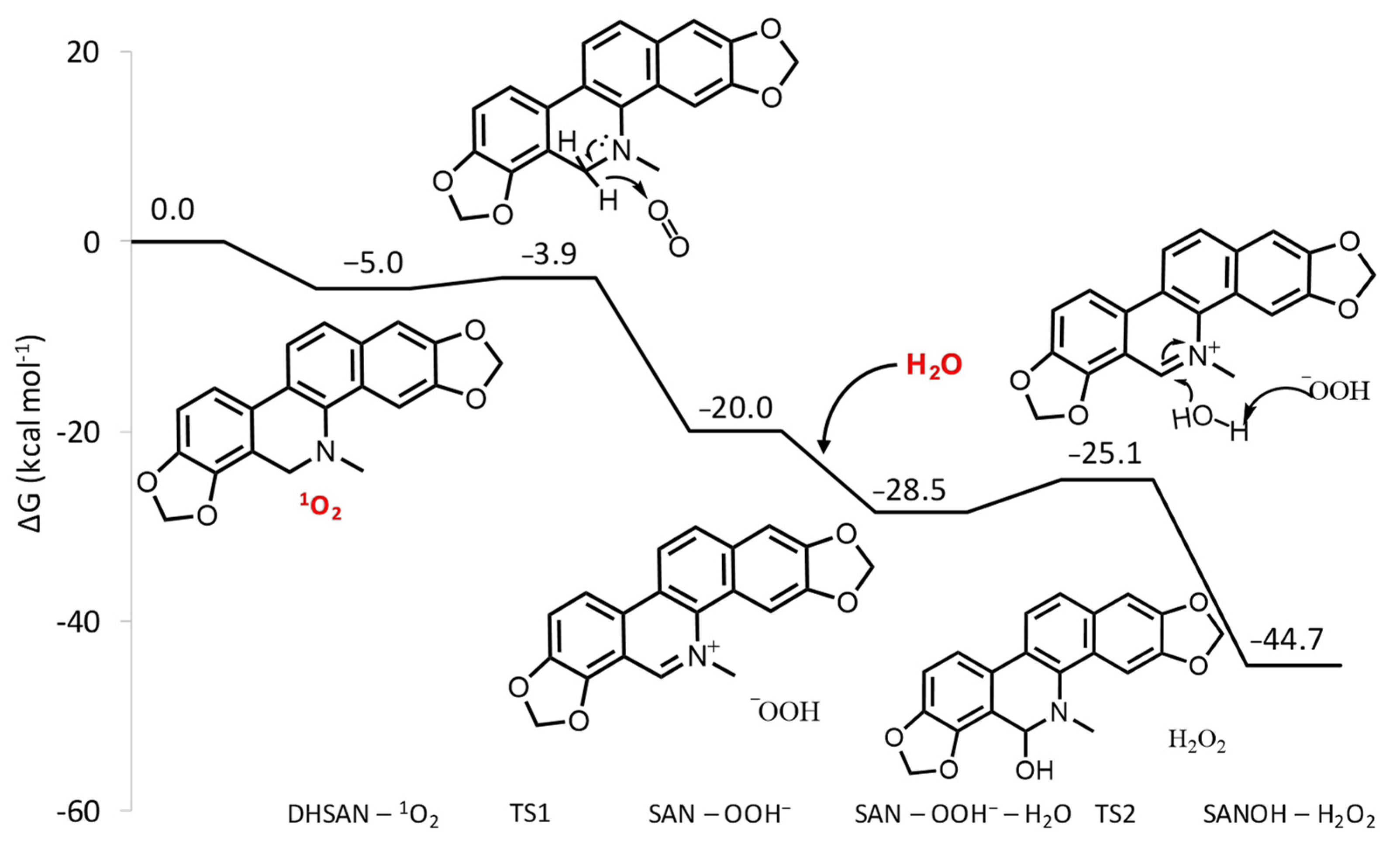
3.2. Photoconversion Mechanism of DHSAN into SAN
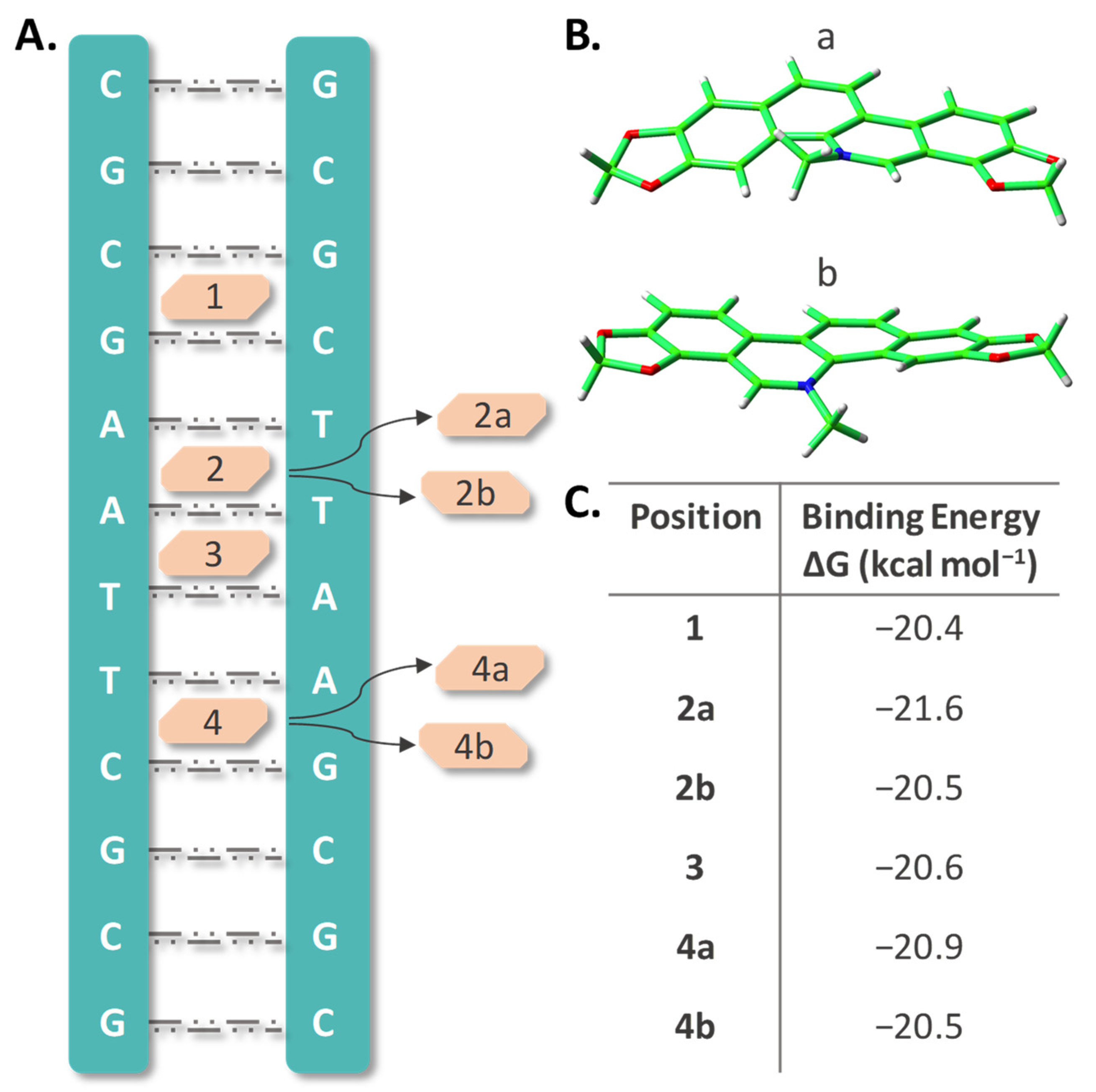
3.3. Structures and Dynamics of SAN Intercalation into DNA
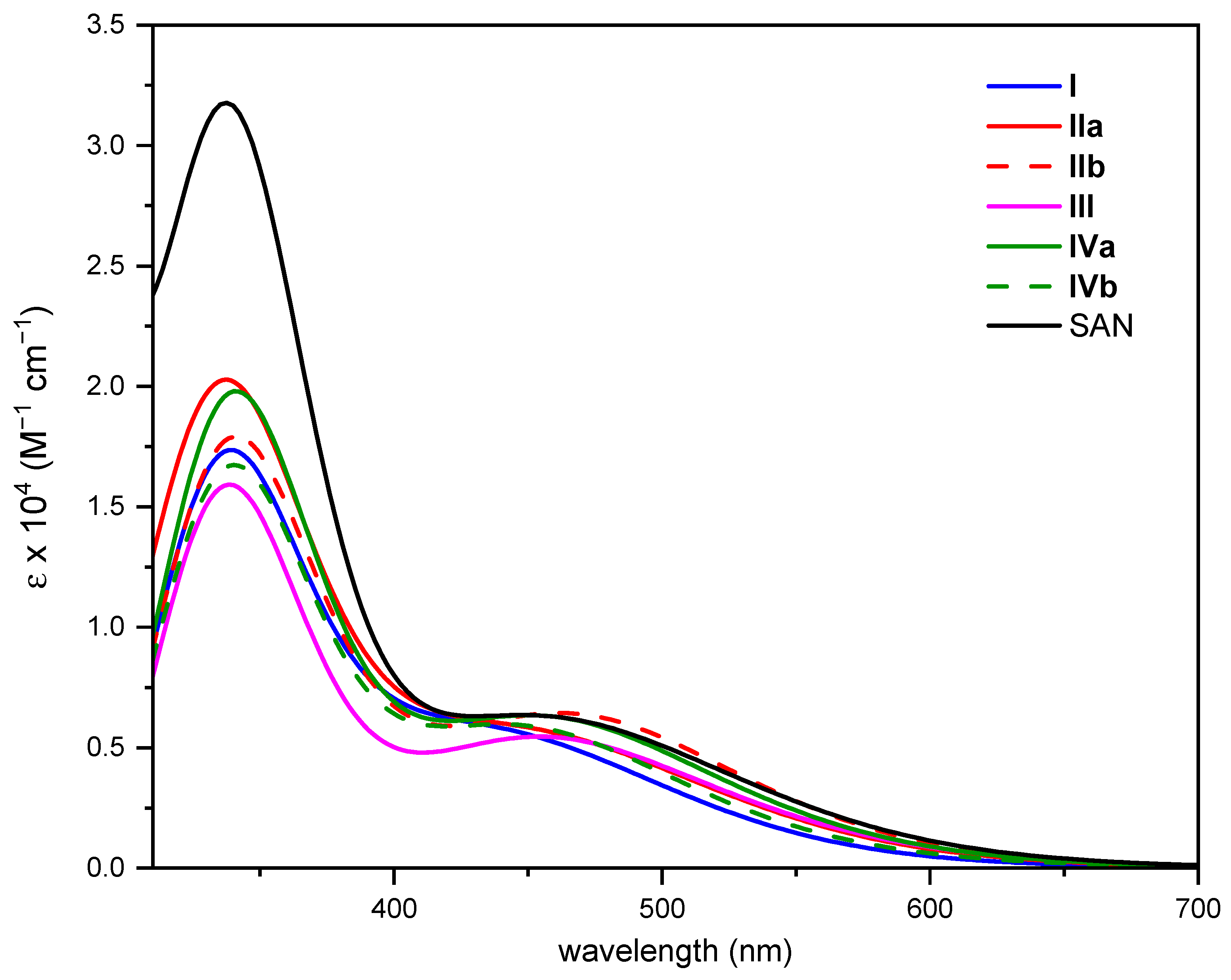
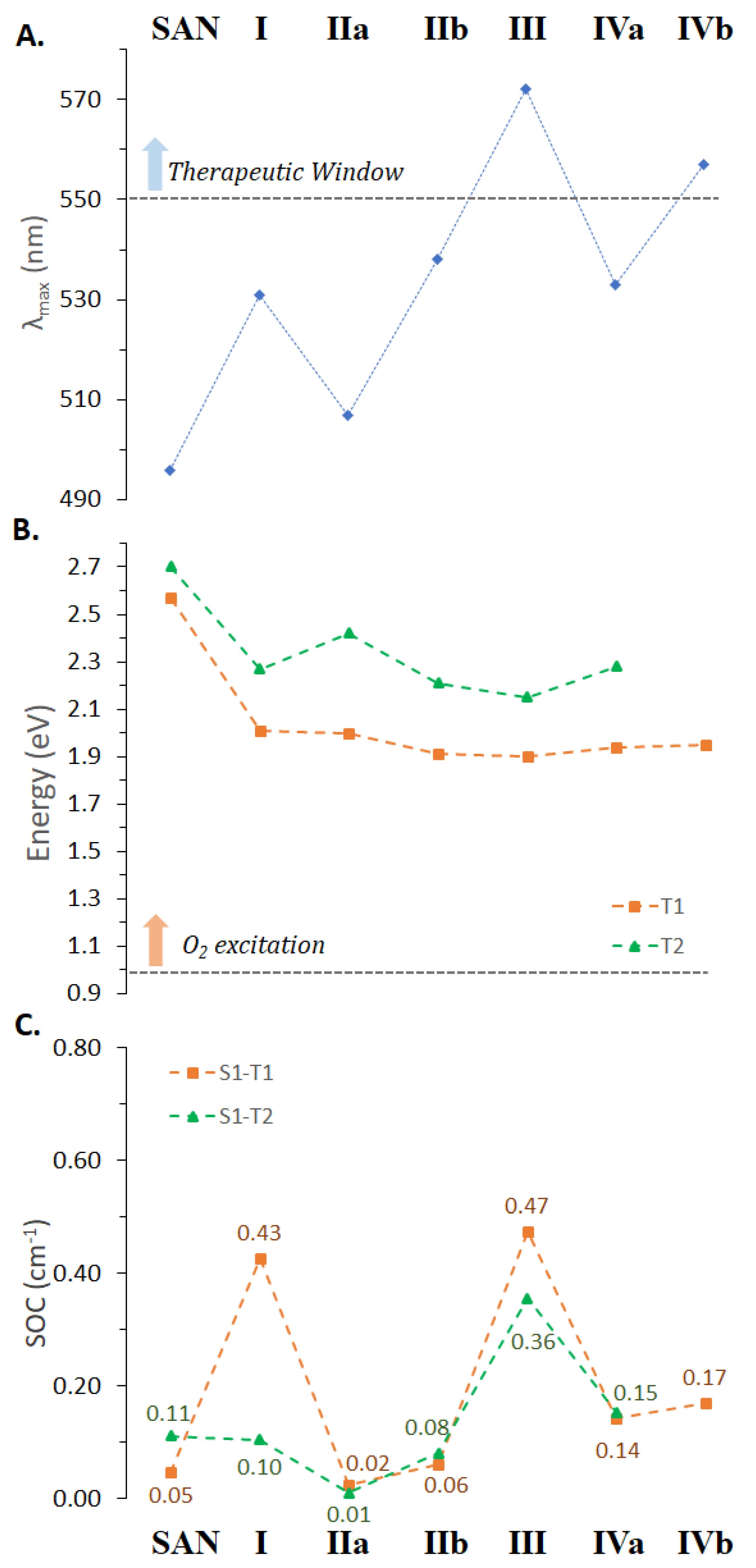
3.4. Photophysical Properties of SAN
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lenfeld, J.; Kroutil, M.; Marsalek, E.; Slavík, J.; Preininger, V.; Simánek, V. Antiinflammatory activity of quaternary benzophenanthridine alkaloids from Chelidonium majus. Planta Med. 1981, 43, 161–165. [Google Scholar] [CrossRef] [PubMed]
- Godowski, K.C. Antimicrobial action of sanguinarine. J. Clin. Dent. 1989, 1, 96–101. [Google Scholar] [PubMed]
- Obiang-Obounou, B.W.; Kang, O.H.; Choi, J.G.; Keum, J.H.; Kim, S.B.; Mun, S.H.; Shin, D.W.; Kim, K.W.; Park, C.B.; Kim, Y.G.; et al. The mechanism of action of sanguinarine against methicillin-resistant staphylococcus aureus. J. Toxicol. Sci. 2011, 36, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Adhami, V.M.; Aziz, M.H.; Reagan-Shaw, S.R.; Nihal, M.; Mukhtar, H.; Ahmad, N. Sanguinarine causes cell cyle blockade and apoptosis of human prostate carcinoma cells via modulation of cylin kinase inhibitor-cyclin-cyclin-dependent kinase machinery. Mol. Cancer Ther. 2004, 3, 933–940. [Google Scholar]
- Croaker, A.; King, G.J.; Pyne, J.H.; Anoopkumar-Dukie, S.; Liu, L. Sanguinaria canadensis: Traditional Medicine, Phytochemical Composition, Biological Activities and Current Uses. Int. J. Mol. Sci. 2016, 17, 1414. [Google Scholar] [CrossRef] [Green Version]
- Galadari, S.; Rahman, A.; Pallichankandy, S.; Thayyullathil, F. Molecular targets and anticancer potential of sanguinarine—a benzophenanthridine alkaloid. Phytomedicine 2017, 34, 143–153. [Google Scholar] [CrossRef]
- Ling, X.; Huang, L.; Li, Y.; Wan, Q.; Wang, Z.; Qin, A.; Gao, M.; Tang, B.Z. Photoactivatable dihydroalkaloids for cancer cell imaging and chemotherapy with high spatiotemporal resolution. Mater. Horiz. 2020, 7, 2696–2701. [Google Scholar] [CrossRef]
- Bonnet, S. Why develop photoactivated chemotherapy? Dalton Trans. 2018, 47, 10330–10343. [Google Scholar] [CrossRef]
- Slunská, Z.; Gelnarová, E.; Hammerová, J.; Táborská, E.; Slaninová, I. Effect of quaternary benzo[c]phenanthridine alkaloids sanguilutine and chelilutine on normal and cancer cells. Toxicol. Vitr. 2010, 24, 697–706. [Google Scholar] [CrossRef] [PubMed]
- Malíková, J.; Zdařilová, A.; Hlobilková, A.; Ulrichová, J. The effect of chelerythrine on cell growth, apoptosis, and cell cycle in human normal and cancer cells in comparison with sanguinarine. Cell Biol. Toxicol. 2006, 22, 439–453. [Google Scholar] [CrossRef]
- Dvorak, Z.; Simanek, V. Metabolism of Sanguinarine: The Facts and The Myths. Curr. Drug Metab. 2007, 8, 173–176. [Google Scholar] [CrossRef] [PubMed]
- Maiti, M.; Nandi, R.; Chaudhuri, K. Sanguinarine: A monofunctional intercalating alkaloid. FEBS Lett. 1982, 142, 280–284. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.; Kumar, G.S. DNA binding of benzophenanthridine compounds sanguinarine versus ethidium: Comparative binding and thermodynamic profile of intercalation. J. Chem. Thermodyn. 2009, 41, 764–774. [Google Scholar] [CrossRef]
- Bajaj, N.P.S.; McLean, M.J.; Waring, M.J.; Smekal, E. Sequence-selective, pH-dependent binding to DNA of benzophenanthridine alkaloids. J. Mol. Recognit. 1990, 3, 48–54. [Google Scholar] [CrossRef]
- Sen, A.; Ray, A.; Maiti, M. Thermodynamics of the interactions of sanguinarine with DNA: Influence of ionic strength and base composition. Biophys. Chem. 1996, 59, 155–170. [Google Scholar] [CrossRef]
- Bai, L.P.; Zhao, Z.Z.; Cai, Z.; Jiang, Z.H. DNA-binding affinities and sequence selectivity of quaternary benzophenanthridine alkaloids sanguinarine, chelerythrine, and nitidine. Bioorgan. Med. Chem. 2006, 14, 5439–5445. [Google Scholar] [CrossRef] [PubMed]
- An, Y.W.; Jin, H.T.; Yuan, B.; Wang, J.C.; Wang, C.; Liu, H.Q. Research progress of berberine mediated photodynamic therapy (Review). Oncol. Lett. 2021, 21, 1–10. [Google Scholar] [CrossRef]
- Warowicka, A.; Łukasz, P.; Grażyna, B.; Oskar, M.; Litowczenko, J.; Dorota, K.; Robert, N.; Stefan, J.; Anna, G.J. Protoberberine compounds extracted from Chelidonium majus L. as novel natural photosensitizers for cancer therapy. Phytomedicine 2019, 64, 152919. [Google Scholar] [CrossRef]
- Arnason, J.T.; Guèrin, B.; Kraml, M.M.; Mehta, B.; Redmond, R.W.; Scaiano, J.C. Phototoxic and Photochemical Properties of Sanguinarine. Photochem. Photobiol. 1992, 55, 35–38. [Google Scholar] [CrossRef] [PubMed]
- Maiti, M.; Chatterjee, A. Production of singlet oxygen by sanguinarine and berberine. Curr. Sci. 1995, 68, 734–736. [Google Scholar]
- Agostinis, P.; Berg, K.; Cengel, K.A.; Foster, T.H.; Girotti, A.W.; Gollnick, S.O.; Hahn, S.M.; Hamblin, M.R.; Juzeniene, A.; Kessel, D.; et al. Photodynamic therapy of cancer: An update. CA. Cancer J. Clin. 2011, 61, 250–281. [Google Scholar] [CrossRef] [PubMed]
- Dąbrowski, J.M.; Arnaut, L.G. Photodynamic therapy (PDT) of cancer: From local to systemic treatment. Photochem. Photobiol. Sci. 2015, 14, 1765–1780. [Google Scholar] [CrossRef]
- Drew, H.R.; Wing, R.M.; Takano, T.; Broka, C.; Tanaka, S.; Itakura, K.; Dickerson, R.E. Structure of a B-DNA dodecamer: Conformation and dynamics. Proc. Natl. Acad. Sci. USA 1981, 78, 2179–2183. [Google Scholar] [CrossRef] [Green Version]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pk prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myers, J.; Grothaus, G.; Narayanan, S.; Onufriev, A. A simple clustering algorithm can be accurate enough for use in calculations of pKs in macromolecules. Proteins Struct. Funct. Genet. 2006, 63, 928–938. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. G16_C01 2016, Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Bayly, C.I.; Cieplak, P.; Cornell, W.D.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general Amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Case, A.D.; Betz, R.M.; Cerutti, D.S.; Cheatham, T.E.; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W..; Homeyer, N.; et al. AMBER; University of California: San Francisco, CA, USA, 2016. [Google Scholar]
- Ivani, I.; Dans, P.D.; Noy, A.; Pérez, A.; Faustino, I.; Hospital, A.; Walther, J.; Andrio, P.; Goñi, R.; Balaceanu, A.; et al. Parmbsc1: A refined force field for DNA simulations. Nat. Methods 2015, 13, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef]
- Mahoney, M.W.; Jorgensen, W.L. Diffusion constant of the TIP5P model of liquid water. J. Chem. Phys. 2001, 114, 363–366. [Google Scholar] [CrossRef] [Green Version]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Miller, B.R.; McGee, T.D.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA.py: An efficient program for end-state free energy calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef] [PubMed]
- Roe, D.R.; Cheatham, T.E. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Gonzalez, C.; Bernhard Schlegel, H. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef] [PubMed]
- McQuarrie, D.A.; Simon, J.D. Molecular Thermodynamics; University Science Books: Sausalito, CA, USA, 1999; Volume 17, ISBN 978-1891389054. [Google Scholar]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
- Da Chai, J.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burke, K.; Perdew, J.P.; Wang, Y. Derivation of a Generalized Gradient Approximation: The PW91 Density Functional. In Electronic Density Functional Theory; Springer: Boston, MA, USA, 1998; pp. 81–111. [Google Scholar]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Aidas, K.; Angeli, C.; Bak, K.L.; Bakken, V.; Bast, R.; Boman, L.; Christiansen, O.; Cimiraglia, R.; Coriani, S.; Dahle, P.; et al. The Dalton quantum chemistry program system: The Dalton program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 269–284. [Google Scholar] [CrossRef]
- Kumar, G.S.; Hazra, S. Sanguinarine, a promising anticancer therapeutic: Photochemical and nucleic acid binding properties. RSC Adv. 2014, 4, 56518–56531. [Google Scholar] [CrossRef]
- Alberto, M.E.; Marino, T.; Quartarolo, A.D.; Russo, N. Photophysical origin of the reduced photodynamic therapy activity of temocene compared to Foscan®: Insights from theory. Phys. Chem. Chem. Phys. 2013, 15, 16167–16171. [Google Scholar] [CrossRef]
- Robbins, E.; Leroy-Lhez, S.; Villandier, N.; Samoć, M.; Matczyszyn, K. Prospects for More Efficient Multi-Photon Absorption Photosensitizers Exhibiting Both Reactive Oxygen Species Generation and Luminescence. Molecules 2021, 26, 6323. [Google Scholar] [CrossRef]
- Maiti, M.; Nandi, R.; Chaudhuri, K. The Effect of pH on the Absoprtion and Fluorescence Spectra of Sanguinarine. Photochem. Photobiol. 1983, 38, 245–249. [Google Scholar] [CrossRef]
- Maiti, M.; Kumar, G.S. Biophysical aspects and biological implications of the interaction of benzophenanthridine alkaloids with DNA. Biophys. Rev. 2009, 1, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Sen, A.; Maiti, M. Interaction of sanguinarine iminium and alkanolamine form with calf thymus DNA. Biochem. Pharmacol. 1994, 48, 2097–2102. [Google Scholar] [CrossRef]
- D’Amico, M.L.; Paiotta, V.; Secco, F.; Venturini, M. A kinetic study of the intercalation of ethidium bromide into Poly(A)·Poly(U). J. Phys. Chem. B 2002, 106, 12635–12641. [Google Scholar] [CrossRef]
- Scoditti, S.; Dabbish, E.; Russo, N.; Mazzone, G.; Sicilia, E. Anticancer Activity, DNA Binding, and Photodynamic Properties of a N^C^N-Coordinated Pt(II) Complex. Inorg. Chem. 2021, 60, 10350–10360. [Google Scholar] [CrossRef]
- Dabbish, E.; Russo, N.; Sicilia, E. Rationalization of the Superior Anticancer Activity of Phenanthriplatin: An In-Depth Computational Exploration. Chem. Eur. J. 2020, 26, 259–268. [Google Scholar] [CrossRef] [Green Version]
- Scoditti, S.; Dabbish, E.; Sicilia, E. Is the cytotoxic activity of phenanthriplatin dependent on the specific size of the phenanthridine ligand π system? J. Inorg. Biochem. 2021, 219, 111447. [Google Scholar] [CrossRef] [PubMed]
- Biver, T. Use of UV-vis spectrometry to gain information on the mode of binding of small molecules to DNAs and RNAs. Appl. Spectrosc. Rev. 2012, 47, 272–325. [Google Scholar] [CrossRef]

| ΔE (eV) | λ (nm) | ||
|---|---|---|---|
| 3.47 | 715 | 1,490,000 | 6550 |
| 3.80 | 653 | 3400 | 18 |
| 3.94 | 629 | 2490 | 14 |
| 4.19 | 592 | 2400 | 15 |
| 4.29 | 578 | 11,400 | 77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scoditti, S.; Bruno, S.; Sicilia, E.; Mazzone, G. Computational Studies of the Photogeneration from Dihydrosanguinarine and the Probable Cytotoxicity Mechanism of Sanguinarine. Appl. Sci. 2022, 12, 1095. https://doi.org/10.3390/app12031095
Scoditti S, Bruno S, Sicilia E, Mazzone G. Computational Studies of the Photogeneration from Dihydrosanguinarine and the Probable Cytotoxicity Mechanism of Sanguinarine. Applied Sciences. 2022; 12(3):1095. https://doi.org/10.3390/app12031095
Chicago/Turabian StyleScoditti, Stefano, Simone Bruno, Emilia Sicilia, and Gloria Mazzone. 2022. "Computational Studies of the Photogeneration from Dihydrosanguinarine and the Probable Cytotoxicity Mechanism of Sanguinarine" Applied Sciences 12, no. 3: 1095. https://doi.org/10.3390/app12031095






