Modeling and Control of an Articulated Multibody Aircraft
Abstract
:1. Introduction
1.1. Related Work
1.1.1. Moving Masses in Insect Flight
1.1.2. Moving-Mass Control in Spacecraft and Aircraft
1.1.3. Control Design for Multibody Aircraft
1.2. A Dragonfly Biomimetic Aircraft Model
1.3. Scope and Contributions
2. Development of the Multibody Equations of Motion
2.1. Preliminaries
2.2. Reference Frames and Coordinate Systems
- (a)
- The inertial reference frame : The Earth frame is assumed to be the inertial frame with its origin, I fixed at an arbitrary point relative to the Earth’s surface. The orientation of the inertial frame is such that the axis is positive facing North, axis is positive facing East and axis is positive downwards towards Earth’s center of gravity.
- (b)
- The body-fixed reference frame : The origin is located at the center of mass of the central body, point b. The body frame is oriented such that axis lies on the plane of symmetry of the aircraft and points in the forward direction towards the head of the aircraft. The axis is perpendicular to the axis, pointing towards the right side of the aircraft and the axis is positive downwards and lies on the plane of symmetry.
- (c)
- The abdominal/tail reference frame : This reference frame originates from the center of mass of the tail with its orientation the same as that of the body frame coordinate system when the tail is not deflected.
2.3. Reference Points
2.4. Orientation and Transformation Matrices
2.5. Kinematics
2.6. Multibody Equations of Motion
2.6.1. Translational Dynamics
2.6.2. Rotational Dynamics
2.6.3. Abdominal Motion
2.7. Forces and Moments
2.8. Control Effectors
3. Control System Design
3.1. System Description
Controllability and Observability
3.2. Optimal Linear Quadratic Regulator Control Theory
3.3. Linear Quadratic Integral (LQI) Control
4. Simulation and Results
4.1. Aircraft Specification
4.2. Model Validation: Single-Body vs. Multibody
4.3. Linearized Aircraft Model
4.4. Effect of Abdomen Mass on Longitudinal Stability
4.5. Control Design
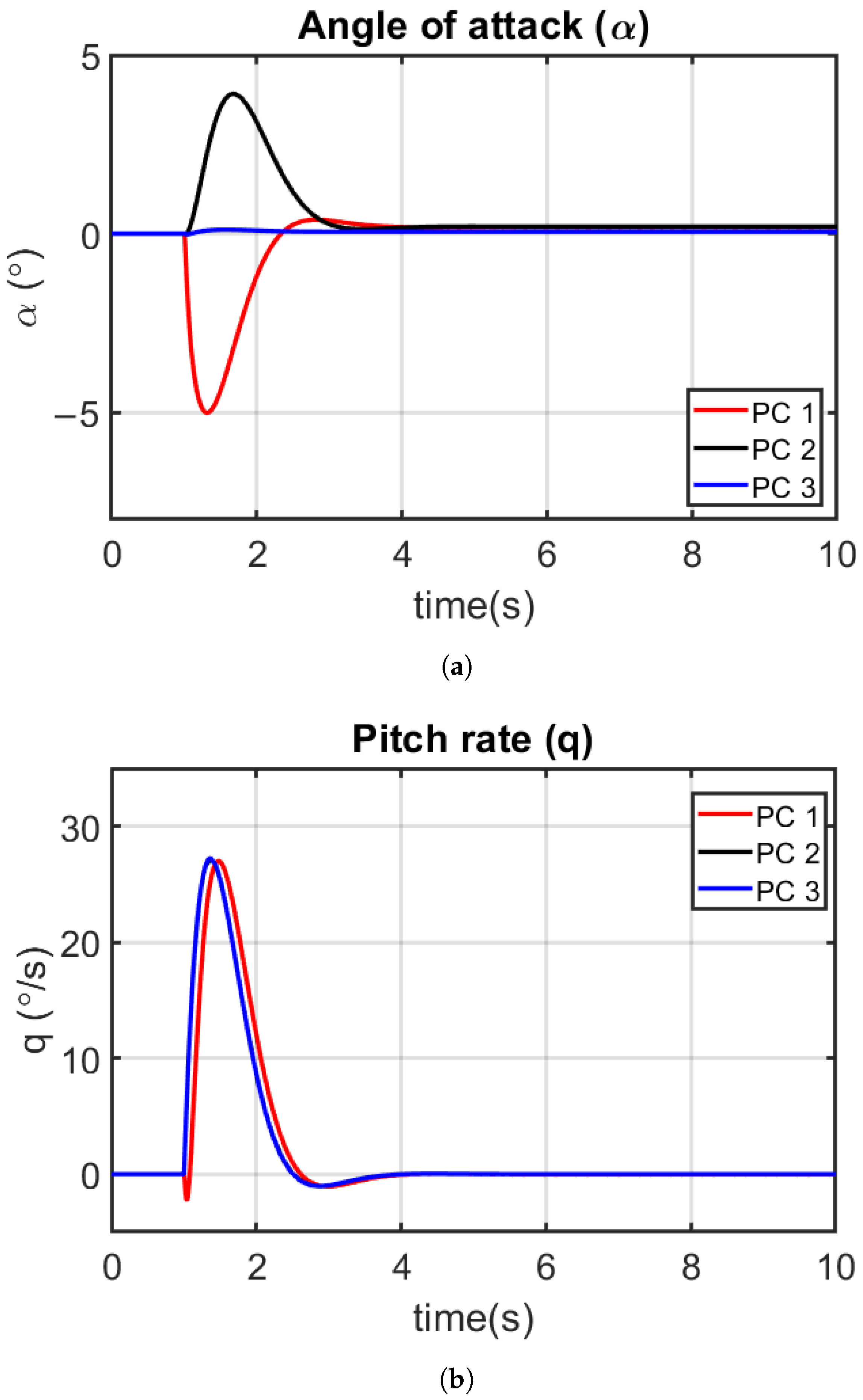
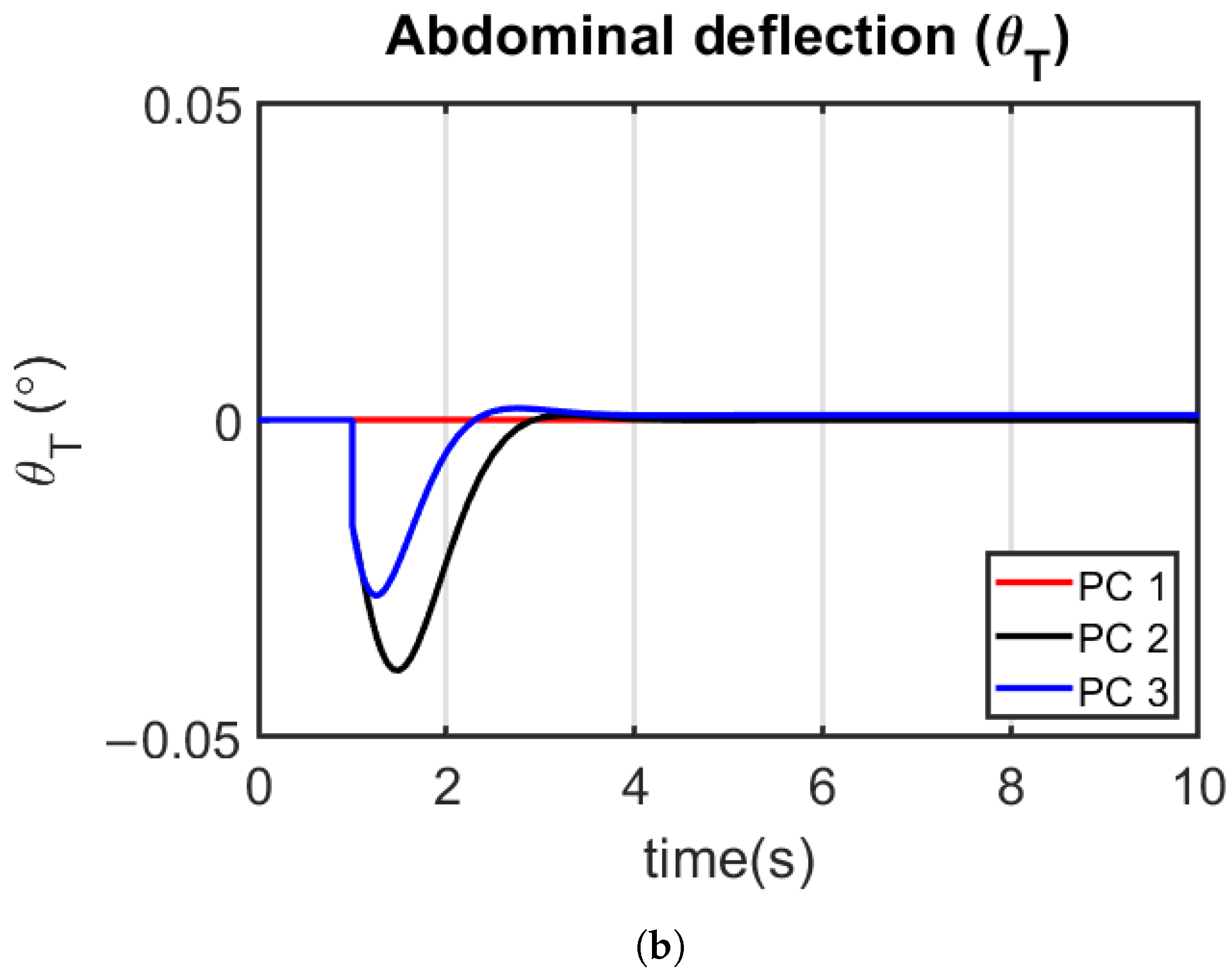
4.5.1. Longitudinal Control Simulation Study
- PC 1 —Prioritized use of elevator for pitch angle control, interpreted as cheap elevator cost and expensive abdominal pitch cost.
- PC 2—Prioritized use of abdominal pitch for pitch angle control, interpreted as expensive elevator cost and cheap abdominal pitch cost.
- PC 3—Relatively evenly prioritized use of elevator and abdominal pitch for pitch angle control, interpreted as cheap elevator cost, cheap abdominal pitch cost.
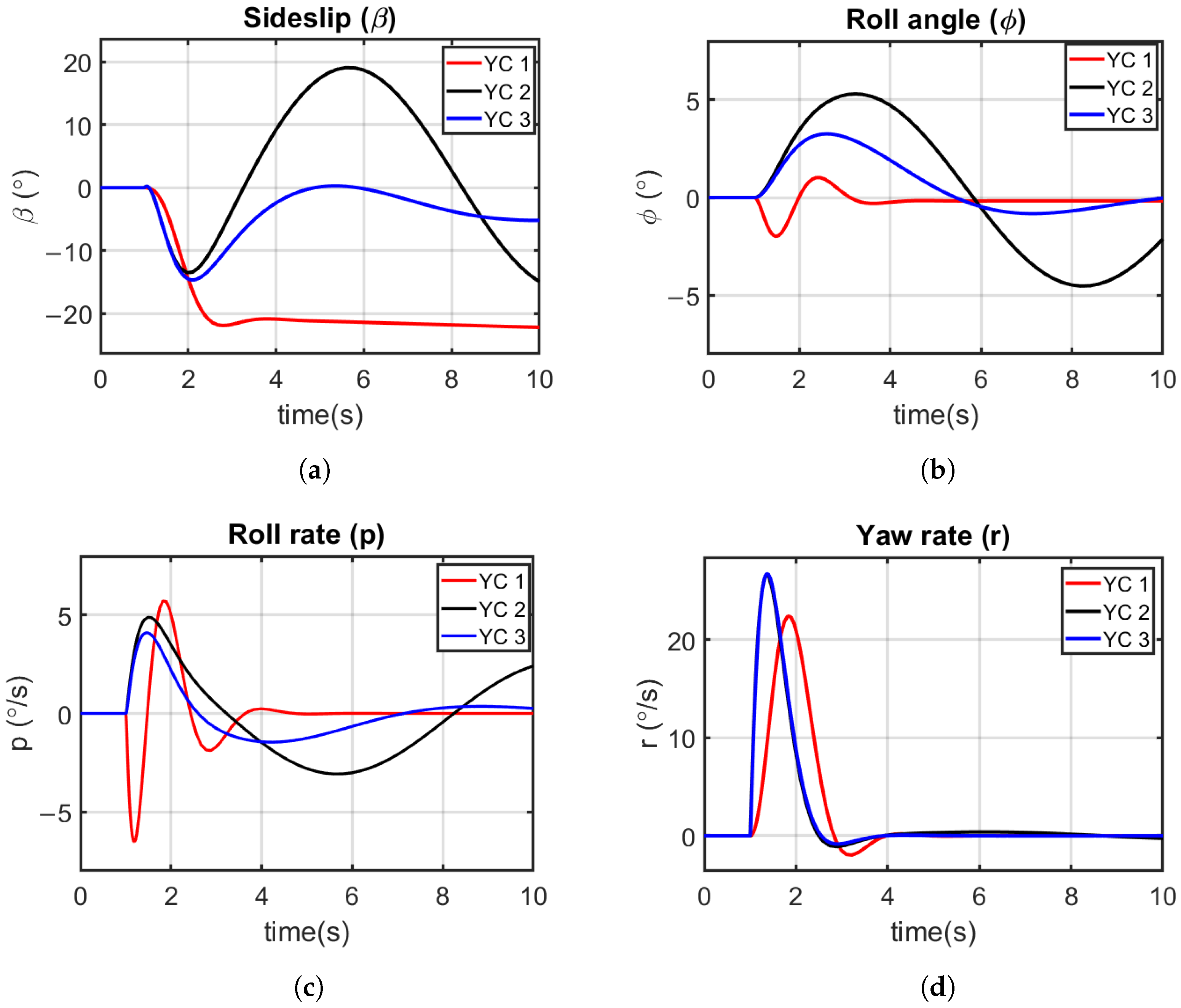
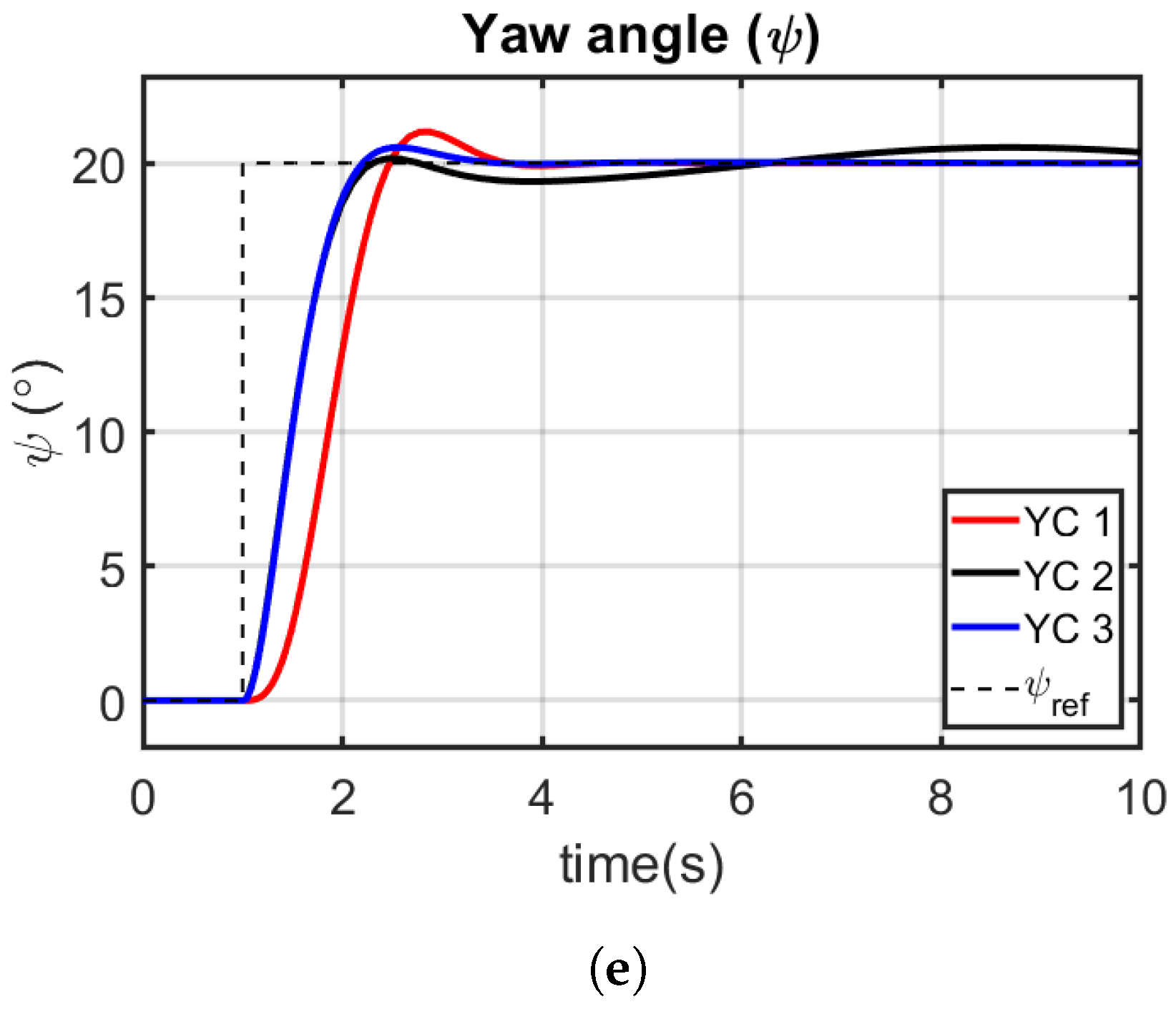
4.5.2. Lateral–Directional Simulation Study
- YC 1—Prioritized use of aileron for yaw angle control, interpreted as cheap aileron cost, expensive abdominal yaw cost.
- YC 2—Prioritized use of abdominal yaw for yaw angle control, interpreted as expensive aileron cost, cheap abdominal yaw cost.
- YC 3—Relatively evenly prioritized use of elevator and abdominal pitch for yaw angle control, interpreted as cheap aileron cost, cheap abdominal yaw cost.
5. Discussion
5.1. Model Validation: Single-Body vs. Multibody
5.2. Effect of Abdominal Mass on Longitudinal Stability
5.3. Pitch Attitude Control
5.4. Yaw Attitude Control
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| AoA | Angle of Attack |
| ARE | Algebraic Riccati Equation |
| ARP | Aerodynamic Reference Point |
| AVL | Athena Vortex Lattice |
| CA | Control Allocation |
| CoM | Center of Mass |
| cg | Center of Gravity |
| DISWA | Dragonfly-Inspired Straight-Wing Aircraft |
| DoF | Degree of Freedom |
| EoM | Equation of Motion |
| LHS | Left-hand Side |
| LQI | Linear Quadratic Integral |
| LQR | Linear Quadratic Regulator |
| MAV | Micro-Aerial Vehicle |
| MIMO | Multiple-input Multiple-output |
| MMC | Moving Mass Control |
| MPC | Model Predictive Control |
| NP | Neutral Point |
| PC | Pitch Control |
| PID | Proportional Integral Derivative |
| RHS | Right-Hand Side |
| SM | Static Margin |
| SMC | Sliding Mode Control |
| SUAV | Mini Unmanned Aerial Vehicle |
| wrt | With Respect To |
| YC | Yaw Control |
| Nomenclature | |
| A,O | Arbitrary rigid bodies A and O (Central body (B), abdomen (T) or aircraft (C) in text) (–), Body-fixed frames associated with rigid bodies A and O (–) |
| a,o | First-order tensors (equivalent to a vector) associated with frames A and O (–) |
| Mass of rigid bodies A and O, respectively (kg) | |
| m | Total mass (kg) |
| Vector or tensor expressed in reference frame A (–) | |
| Displacement vector of point a relative to point b (m) | |
| Skew symmetric matrix of (m) | |
| Velocity of rigid body A relative to point of (m/s) | |
| Angular velocity of frame A relative to frame O (rad/s) | |
| Skew symmetric matrix of (rad/s) | |
| Inertia tensor of rigid body A about at point a (kg ) | |
| Transformation matrix from frame A to O (–) | |
| Rotational time derivative of a vector or tensor * with respect to frame A (–) | |
| Ordinary time derivative of * (–) | |
| e | Output error of additional integral state (–) |
| g | Acceleration due to gravity () |
| i | Imaginary unit (–) |
| H | Altitude/height (m) |
| F | External force vector (N) |
| M | External moment vector (Nm) |
| V | Airspeed (m/s) |
| Propulsive thrust (N) | |
| Reference wing chord (m) | |
| Reference wing span (m) | |
| Reference wing area () | |
| Dimensionless aerodynamic coefficients for axial, side and normal force, respectively (–) | |
| Dimensionless aerodynamic coefficients for roll, pitch and yaw moment, respectively (–) | |
| Velocity vector components (m/s) | |
| Angular velocity vector components (rad/s) | |
| Position vector components (m) | |
| Angle of Attack and sideslip angle (rad) | |
| Elevator deflection angle (rad) | |
| Aileron deflection angle (rad) | |
| Elevon deflection angle (rad) | |
| Damping constant (Nms) | |
| Air density () | |
| Load torque due to gravity (Nm) | |
| Actuator torque (Nm) | |
| Roll, pitch and yaw Euler angles (rad) | |
| state, input, output vector (–) | |
| Reference input signal, output signal (–) | |
| System state, control, output and feedforward matrices (–) | |
| Optimal gain matrix (–) | |
| State-weighting matrix (–) | |
| Control weighting matrix (–) | |
| Cost function (–) | |
| Algebraic Riccati Equation solution (–) | |
| Subscripts | |
| 0 | Initial/nominal value |
| i | Additional integral states |
| k | rigid body |
| B, T | Central rigid body, abdomen rigid body |
| I, B, T | Inertial, central body and abdominal reference frames systems |
| l, r | left, right |
| lat | Lateral–directional motion |
| long | Longitudinal motion |
| Superscripts | |
| First-order time derivative | |
| Second-order time derivative | |
| Augmented matrix | |
| Transpose of parameter | |
| Inverse of parameter |
Appendix A. Athena Vortex Lattice File for Aerodynamic Data
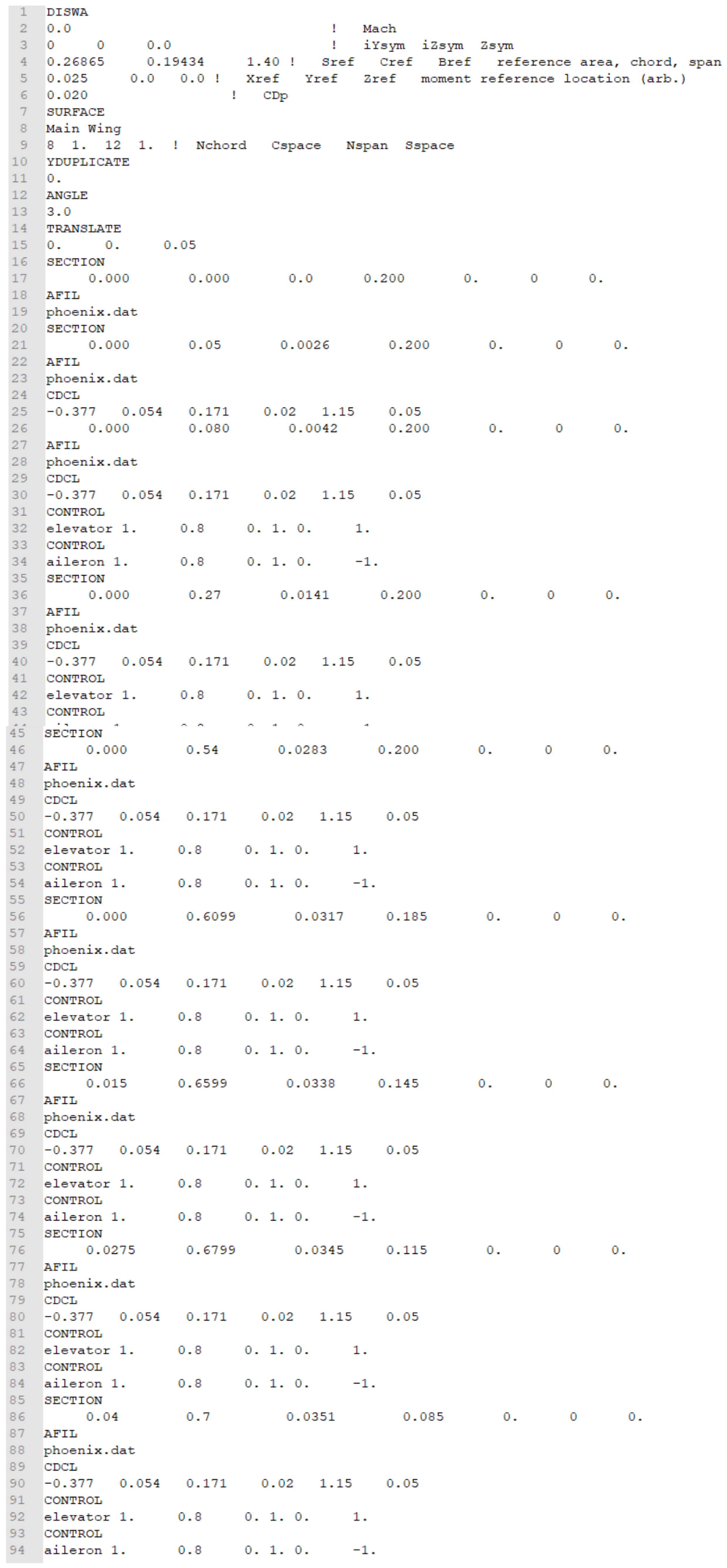
References
- Ramesh, P.; Jeyan, M.L. Mini Unmanned Aerial Systems (UAV)—A Review of the Parameters for Classification of a Mini UAV. Int. J. Aviat. Aeronaut. Aerosp. 2020, 7, 5. [Google Scholar]
- Alexander, R.M. Principles of Animal Locomotion; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Ellington, C.P. The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms. Philos. Trans. R. Soc. Lond. Biol. Sci. 1984, 305, 79–113. [Google Scholar]
- Ellington, C.P. The aerodynamics of hovering insect flight. VI. Lift and power requirements. Philos. Trans. R. Soc. Lond. Biol. Sci. 1984, 305, 145–181. [Google Scholar]
- Pennycuick, C.J. A wind-tunnel study of gliding flight in the pigeon Columba livia. J. Exp. Biol. 1968, 49, 509–526. [Google Scholar] [CrossRef]
- Pennycuick, C.J. Control of gliding angle in Rüppell’s griffon vulture Gyps rueppelli. J. Exp. Biol. 1971, 55, 39–46. [Google Scholar] [CrossRef]
- Cook, M.; Spottiswoode, M. Modelling the flight dynamics of the hang glider. Aeronaut. J. 2005, 109, I–XX. [Google Scholar] [CrossRef] [Green Version]
- Libby, T.; Moore, T.Y.; Chang-Siu, E.; Li, D.; Cohen, D.J.; Jusufi, A.; Full, R.J. Tail-assisted pitch control in lizards, robots and dinosaurs. Nature 2012, 481, 181. [Google Scholar] [CrossRef]
- Chahl, J.; Chitsaz, N.; McIvor, B.; Ogunwa, T.; Kok, J.M.; McIntyre, T.; Abdullah, E. Biomimetic Drones Inspired by Dragonflies Will Require a Systems Based Approach and Insights from Biology. Drones 2021, 5, 24. [Google Scholar] [CrossRef]
- Götz, K.G.; Hengstenberg, B.; Biesinger, R. Optomotor control of wing beat and body posture in Drosophila. Biol. Cybern. 1979, 35, 101–112. [Google Scholar] [CrossRef]
- Zanker, J. On the mechanism of speed and altitude control in Drosophila melanogaster. Physiol. Entomol. 1988, 13, 351–361. [Google Scholar] [CrossRef]
- Berthé, R.; Lehmann, F.O. Body appendages fine-tune posture and moments in freely manoeuvring fruit flies. J. Exp. Biol. 2015, 218, 3295–3307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanker, J.M.; Egelhaaf, M.; Warzecha, A.K. On the coordination of motor output during visual flight control of flies. J. Comp. Physiol. 1991, 169, 127–134. [Google Scholar] [CrossRef] [Green Version]
- Combes, S.A.; Dudley, R. Turbulence-driven instabilities limit insect flight performance. Proc. Natl. Acad. Sci. USA 2009, 106, 9105–9108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, B.; Deng, X.; Hedrick, T.L. The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta). J. Exp. Biol. 2011, 214, 4092–4106. [Google Scholar] [CrossRef] [Green Version]
- Hedrick, T.L.; Daniel, T.L. Flight control in the hawkmoth Manduca sexta: The inverse problem of hovering. J. Exp. Biol. 2006, 209, 3114–3130. [Google Scholar] [CrossRef] [Green Version]
- Luu, T.; Cheung, A.; Ball, D.; Srinivasan, M.V. Honeybee flight: A novel ‘streamlining’ response. J. Exp. Biol. 2011, 214, 2215–2225. [Google Scholar] [CrossRef] [Green Version]
- Sridhar, M.; Kang, C.K.; Lee, T. Geometric Formulation for the Dynamics of Monarch Butterfly with the Effects of Abdomen Undulation. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1962. [Google Scholar]
- Rüppell, G.; Hilfert-Rüppell, D.; Schneider, B.; Dedenbach, H. On the firing line–interactions between hunting frogs and Odonata. Int. J. Odonatol. 2020, 23, 1–19. [Google Scholar] [CrossRef]
- Bode-Oke, A.T.; Zeyghami, S.; Dong, H. Flying in reverse: Kinematics and aerodynamics of a dragonfly in backward free flight. J. R. Soc. Interface 2018, 15, 20180102. [Google Scholar] [CrossRef]
- Zanker, J.M. How does lateral abdomen deflection contribute to flight control of Drosophila melanogaster? J. Comp. Physiol. 1988, 162, 581–588. [Google Scholar] [CrossRef]
- Dyhr, J.P.; Morgansen, K.A.; Daniel, T.L.; Cowan, N.J. Flexible strategies for flight control: An active role for the abdomen. J. Exp. Biol. 2013, 216, 1523–1536. [Google Scholar] [CrossRef] [Green Version]
- Hinterwirth, A.J.; Daniel, T.L. Antennae in the hawkmoth Manduca sexta (Lepidoptera, Sphingidae) mediate abdominal flexion in response to mechanical stimuli. J. Comp. Physiol. 2010, 196, 947–956. [Google Scholar] [CrossRef] [PubMed]
- Frye, M.A. Effects of stretch receptor ablation on the optomotor control of lift in the hawkmoth Manduca sexta. J. Exp. Biol. 2001, 204, 3683–3691. [Google Scholar] [CrossRef] [PubMed]
- Dyhr, J.P.; Cowan, N.J.; Colmenares, D.J.; Morgansen, K.A.; Daniel, T.L. Autostabilizing airframe articulation: Animal inspired air vehicle control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3715–3720. [Google Scholar]
- Arbas, E.A. Control of hindlimb posture by wind-sensitive hairs and antennae during locust flight. J. Comp. Physiol. 1986, 159, 849–857. [Google Scholar] [CrossRef] [PubMed]
- Camhi, J.M. Sensory control of abdomen posture in flying locusts. J. Exp. Biol. 1970, 52, 533–537. [Google Scholar] [CrossRef]
- Camhi, J.M. Yaw-correcting postural changes in locusts. J. Exp. Biol. 1970, 52, 519–531. [Google Scholar] [CrossRef]
- Tejaswi, K.; Kang, C.k.; Lee, T. Dynamics and control of a flapping wing uav with abdomen undulation inspired by monarch butterfly. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 66–71. [Google Scholar]
- Tejaswi, K.; Sridhar, M.K.; Kang, C.k.; Lee, T. Effects of abdomen undulation in energy consumption and stability for monarch butterfly. Bioinspir. Biomimetic 2021, 16, 046003. [Google Scholar]
- Jang, J.; Tomlin, C. Longitudinal stability augmentation system design for the DragonFly UAV using a single GPS receiver. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; p. 5592. [Google Scholar]
- Couceiro, M.S.; Ferreira, N.; Tenreiro Machado, J.A. Modeling and control of a dragonfly-like robot. J. Control. Sci. Eng. 2010, 2010, 643045. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, Q.V.; Chan, W.L.; Debiasi, M. Design, fabrication, and performance test of a hovering-based flapping-wing micro air vehicle capable of sustained and controlled flight. In Proceedings of the IMAV 2014: International Micro Air Vehicle Conference and Competition 2014, Delft, The Netherlands, 12–15 August 2014; Delft University of Technology: Delft, The Netherlands, 2014. [Google Scholar]
- Siqueira, J.C.D.C. Modeling of Wind Phenomena and Analysis of Their Effects on UAV Trajectory Tracking Performance. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, 2017. [Google Scholar]
- Gebert, G.; Gallmeier, P.; Evers, J. Equations of motion for flapping flight. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, USA, 6 August 2002; p. 4872. [Google Scholar]
- Erturk, S.A. Performance Analysis, Dynamic Simulation and Control of Mass-Actuated Airplane. Ph.D. Thesis, University of Texas at Arlington, Arlington, TX, USA, 2016. [Google Scholar]
- Haixu, L.; Xiangju, Q.; Weijun, W. Multi-body motion modeling and simulation for tilt rotor aircraft. Chin. J. Aeronaut. 2010, 23, 415–422. [Google Scholar] [CrossRef] [Green Version]
- Sakhaei, A. Dynamic Modelling and Predictive Control for Insect-like Flapping Wing Aerial Micro Robots. Ph.D. Thesis, Ryerson University, Toronto, ON, Canada, 2010. [Google Scholar]
- Grauer, J.; Ulrich, E.; Hubbard, J.; Pines, D.; Humbert, J. System identification of an ornithopter aerodynamics model. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Toronto, ON, Canada, 2–5 August 2010; p. 7632. [Google Scholar]
- Grauer, J.; Ulrich, E.; Hubbard Jr, J.; Pines, D.; Humbert, J.S. Testing and system identification of an ornithopter in longitudinal flight. J. Aircr. 2011, 48, 660–667. [Google Scholar]
- Orlowski, C.; Girard, A.; Shyy, W. Open loop pitch control of a flapping wing micro-air vehicle using a tail and control mass. In Proceedings of the 2010 American Control Conference, Baltimore, MA, USA, 30 June–2 July 2010; pp. 536–541. [Google Scholar]
- Caetano, J.; Weehuizen, M.; De Visser, C.; De Croon, G.; De Wagter, C.; Remes, B.; Mulder, M. Rigid vs. flapping: The effects of kinematic formulations in force determination of a free flying Flapping Wing Micro Air Vehicle. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 949–959. [Google Scholar]
- Bolender, M. Rigid multi-body equations-of-motion for flapping wing mavs using kane’s equations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 11 August 2009; p. 6158. [Google Scholar]
- Su, J.; Su, C.; Xu, S.; Yang, X. A multibody model of tilt-rotor aircraft based on Kane’s method. Int. J. Aerosp. Eng. 2019, 2019, 9396352. [Google Scholar] [CrossRef] [Green Version]
- Lasek, M.; Sibilski, K. Modelling and simulation of flapping wing control for a micromechanical flying insect (entomopter). In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4973. [Google Scholar]
- Sibilski, K.; Loroch, L.; Buler, W.; Zyluk, A. Modeling and simulation of the nonlinear dynamic behavior of a flapping wings micro-aerial-vehicle. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004; p. 541. [Google Scholar]
- Grauer, J.A.; Hubbard, J.E., Jr. Multibody model of an ornithopter. J. Guid. Control Dyn. 2009, 32, 1675–1679. [Google Scholar] [CrossRef]
- Sun, M.; Wang, J.; Xiong, Y. Dynamic flight stability of hovering insects. Acta Mech. Sin. 2007, 23, 231–246. [Google Scholar] [CrossRef]
- Loh, K.; Cook, M.; Thomasson, P. An investigation into the longitudinal dynamics and control of a flapping wing micro air vehicle at hovering flight. Aeronaut. J. 2003, 107, 743–753. [Google Scholar]
- Orlowski, C.T. Flapping Wing Micro Air Vehicles: An Analysis of the Importance of the Mass of the Wings to Flight Dynamics, Stability, and Control. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2011. [Google Scholar]
- Du, C.; Xu, J.; Zheng, Y. Modeling and control of a dragonfly-like micro aerial vehicle. Adv. Robot Autom. S 2015, 2, 2. [Google Scholar]
- Grubin, C. Dynamics of a vehicle containing moving parts. J. Appl. Mech. 1962, 29, 486–488. [Google Scholar] [CrossRef]
- Janssens, F.L.; van der Ha, J.C. Stability of spinning satellite under axial thrust, internal mass motion, and damping. J. Guid. Control Dyn. 2015, 38, 761–771. [Google Scholar] [CrossRef]
- Mingori, D.; Yam, Y. Nutational stability of a spinning spacecraft with internal mass motion and axial thrust. In Proceedings of the Astrodynamics Conference, Vail, CO, USA, 12 August 1986; p. 2271. [Google Scholar]
- Mingori, D.; Halsmer, D.; Yam, Y. Stability of spinning rockets with internal mass motion. NASA Sti/Recon Tech. Rep. 1993, 95, 199–209. [Google Scholar]
- Yam, Y.; Mingori, D.; Halsmer, D. Stability of a spinning axisymmetric rocket with dissipative internal mass motion. J. Guid. Control Dyn. 1997, 20, 306–312. [Google Scholar] [CrossRef]
- Salimov, G. Motion of a spacecraft containing a moving element in a gravitational field. Mekhanika Tverd. Tela 1974, 9, 35–41. [Google Scholar]
- Leshchenko, D. Motion of a rigid body with movable point mass. Mekhanika Tverd. Tela 1976, 11, 37–40. [Google Scholar]
- Salimov, G. Stability of rotating space station containing a moving element. Mekhanika Tverd. Tela 1975, 10, 52–56. [Google Scholar]
- Chernousko, F.L.; Akulenko, L.D.; Leshchenko, D.D. Evolution of Motions of a Rigid Body about Its Center of Mass; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Han, J.; Hong, G. Modeling of aircraft with time-varying inertia properties. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Dallas, TX, USA, 23 June 2015; p. 1133. [Google Scholar]
- Roberson, R.E. Torques on a satellite vehicle from internal moving parts. J. Appl. Mech. 1958, 25, 196–200. [Google Scholar] [CrossRef]
- Chanute, O. Progress in Flying Machines. Republication of the Work First Published in 1884; Dover Publications: New York, NY, USA, 1997. [Google Scholar]
- Wolko, H.S.; Anderson, J. The Wright Flyer: An Engineering Perspective; Smithsonia: Birmingham, UK, 1983. [Google Scholar]
- Qin, L.; Yang, M. Moving mass attitude law based on neural networks. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; Volume 5, pp. 2791–2795. [Google Scholar]
- Gao, F.J.; Zhao, L.Y. Adaptive sliding mode control with backstepping approach for a moving mass hypersonic spinning missile. In Proceedings of the International Conference on Applied Science and Engineering Innovation (ASEI 2015), Jinan, China, 30–31 August 2015; pp. 834–837. [Google Scholar]
- Yi, Y.; Zhou, F. Variable centroid control scheme over hypersonic tactical missile. Sci. China Ser. 2003, 46, 561–569. [Google Scholar]
- Rogers, J.; Costello, M. A variable stability projectile using an internal moving mass. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2009, 223, 927–938. [Google Scholar] [CrossRef]
- Rogers, J. Applications of Internal Translating Mass Technologies to Smart Weapons Systems; Georgia Institute of Technology: Atlanta, GA, USA, 2009. [Google Scholar]
- Rogers, J.; Costello, M. Control authority of a projectile equipped with a controllable internal translating mass. J. Guid. Control Dyn. 2008, 31, 1323–1333. [Google Scholar] [CrossRef]
- Wang, S.; Yang, M.; Wang, Z. Moving-mass trim control system design for spinning vehicles. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 1, pp. 1034–1038. [Google Scholar]
- Chen, L.; Zhou, G.; Yan, X.; Duan, D. Composite control of stratospheric airships with moving masses. J. Aircr. 2012, 49, 794–801. [Google Scholar] [CrossRef]
- Vengate, S.R.; Erturk, S.A.; Dogan, A. Development and flight test of moving-mass actuated unmanned aerial vehicle. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Washington, DC, USA, 13 June 2016; p. 3713. [Google Scholar]
- Haus, T.; Orsag, M.; Bogdan, S. Mathematical modelling and control of an unmanned aerial vehicle with moving mass control concept. J. Intell. Robot. Syst. 2017, 88, 219. [Google Scholar] [CrossRef]
- Haus, T.; Orsag, M.; Bogdan, S. Design considerations for a large quadrotor with moving mass control. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems, Arlington, VA, USA, 7–10 June 2016; pp. 1327–1334. [Google Scholar]
- Bouabdallah, S.; Siegwart, R.; Caprari, G. Design and control of an indoor coaxial helicopter. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 2930–2935. [Google Scholar]
- Bermes, C.; Leutenegger, S.; Bouabdallah, S.; Schafroth, D.; Siegwart, R. New design of the steering mechanism for a mini coaxial helicopter. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 7 September 2008; pp. 1236–1241. [Google Scholar]
- Canuto, E.; Novara, C.; Carlucci, D.; Montenegro, C.P.; Massotti, L. Spacecraft Dynamics and Control: The Embedded Model Control Approach; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Virgili-Llop, J.; Polat, H.C.; Romano, M. Attitude stabilization of spacecraft in very low earth orbit by center-of-mass shifting. Front. Robot. 2019, 6, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Childs, D. An Investigation of a Movable Mass-Attitude Stabilization System for Artificial-G Space. J. Spacecr. 1972, 8, 8. [Google Scholar]
- Childs, D.W.; Hardison, T.L. A Movable-Mass Attitude Stabilization System For Cable-Connected Artificial-G Space Stations. J. Spacecr. Rocket. 1974, 11, 165–172. [Google Scholar] [CrossRef]
- Childs, D.W. A movable-mass attitude-stabilization system for artificial-g space stations. J. Spacecr. Rocket. 1971, 8, 829–834. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhou, Z. Stability of Moving Mass Control Spinning Missiles with Angular Rate Loops. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Gao, C.; Li, C.; Jing, W. A survey on moving mass control technology. Aerosp. Sci. Technol. 2018, 82, 594–606. [Google Scholar] [CrossRef]
- Gao, C.; Jing, W.; Wei, P. Research on application of single moving mass in the reentry warhead maneuver. Aerosp. Sci. Technol. 2013, 30, 108–118. [Google Scholar] [CrossRef]
- Su, X.L.; Yu, J.Q.; Wang, Y.F.; Wang, L.l. Moving mass actuated reentry vehicle control based on trajectory linearization. Int. J. Aeronaut. Space Sci. 2013, 14, 247–255. [Google Scholar] [CrossRef] [Green Version]
- Candel, S. Concorde and the future of supersonic transport. J. Propuls. Power 2004, 20, 59–68. [Google Scholar] [CrossRef]
- Turner, H. Fuel management for Concorde: A brief account of the fuel system and the fuel pumps developed for the aircraft. Aircr. Eng. Aerosp. Technol. 1971, 43, 36–39. [Google Scholar] [CrossRef]
- Collard, D. Concorde airframe design and development. SAE Trans. 1991, 100, 2620–2641. [Google Scholar]
- Seisan, F.Z. Modeling and Control of a Co-Axial Helicopter; University of Toronto (Canada): Toront, ON, Canada, 2012. [Google Scholar]
- Graver, J.G. Underwater Gliders: Dynamics, Control and Design. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2005. [Google Scholar]
- Zhang, X.Y.; Zhao, Y.X.; Xu, D.X.; He, K.P. Sliding mode control for mass moment aerospace vehicles using dynamic inversion approach. Math. Probl. Eng. 2013, 2013, 284869. [Google Scholar] [CrossRef]
- Kunciw, B.G. Optimal Detumbling of a Large Manned Spacecraft Using an Internal Moving Mass; The Pennsylvania State University: State College, PA, USA, 1973. [Google Scholar]
- Ross, I.M. Mechanism for precision orbit control with applications to formation keeping. J. Guid. Control Dyn. 2002, 25, 818–820. [Google Scholar] [CrossRef]
- Beyer, E.W. Design, Testing, and Performance of a Hybrid Micro Vehicle—The Hopping Rotochute; Georgia Institute of Technology: Atlanta, GA, USA, 2009. [Google Scholar]
- Nelson, R.C. Flight Stability and Automatic Control; WCB/McGraw Hill: New York, NY, USA, 1998; Volume 2. [Google Scholar]
- Chrif, L.; Kadda, Z.M. Aircraft control system using LQG and LQR controller with optimal estimation-Kalman filter design. Procedia Eng. 2014, 80, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Shaji, J.; Aswin, R. Pitch control of flight system using dynamic inversion and pid controller. Int. J. Eng. Res. Technol. 2015, 4, 1–5. [Google Scholar] [CrossRef]
- Lungu, R.; Lungu, M.; Grigorie, L.T. Automatic control of aircraft in longitudinal plane during landing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1338–1350. [Google Scholar] [CrossRef]
- Islam, M.T.; Alam, M.S.; Laskar, M.A.R.; Garg, A. Modeling and simulation of longitudinal autopilot for general aviation aircraft. In Proceedings of the 2016 5th International Conference on Informatics, Electronics and Vision (ICIEV), Piscataway, NJ, USA, 3–14 May 2016; pp. 490–495. [Google Scholar]
- Wahid, N.; Hassan, N. Self-tuning fuzzy PID controller design for aircraft pitch control. In Proceedings of the 2012 Third International Conference on Intelligent Systems Modelling and Simulation, Kota Kinabalu, Malaysia, 8–10 February 2012; pp. 19–24. [Google Scholar]
- Vishal; Ohri, J. GA tuned LQR and PID controller for aircraft pitch control. In Proceedings of the 2014 IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–6. [Google Scholar]
- Ibrahim, I.; Al Akkad, M. Exploiting an intelligent fuzzy-PID system in nonlinear aircraft pitch control. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Russia, Moscow, 12–14 May 2016; pp. 1–7. [Google Scholar]
- Babar, M.; Ali, S.; Shah, M.; Samar, R.; Bhatti, A.; Afzal, W. Robust control of UAVs using H∞ control paradigm. In Proceedings of the 2013 IEEE 9th International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 9–10 December 2013; pp. 1–5. [Google Scholar]
- López, J.; Dormido, R.; Dormido, S.; Gómez, J. A robust controller for an UAV flight control system. Sci. World J. 2015, 2015, 403236. [Google Scholar] [CrossRef] [Green Version]
- Doyle, J.; Glover, K.; Kh&gaoeSar, P.; Francis, B. StateSpace Solutions to Standard Hi aid Control Problems. IEEE Trans. Autom. Control 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Polas, M.; Fekih, A. A multi-gain sliding mode based controller for the pitch angle control of a civil aircraft. In Proceedings of the 2010 42nd Southeastern Symposium on System Theory (SSST), Tyler, TX, USA, 7–9 March 2010; pp. 96–101. [Google Scholar]
- Promtun, E.; Seshagiri, S. Sliding mode control of pitch-rate of an f-16 aircraft. IFAC Proc. Vol. 2008, 41, 1099–1104. [Google Scholar] [CrossRef] [Green Version]
- MacKunis, W.; Patre, P.M.; Kaiser, M.K.; Dixon, W.E. Asymptotic tracking for aircraft via robust and adaptive dynamic inversion methods. IEEE Trans. Control. Syst. Technol. 2010, 18, 1448–1456. [Google Scholar] [CrossRef] [Green Version]
- Wahid, N.; Rahmat, M.F. Pitch control system using LQR and Fuzzy Logic Controller. In Proceedings of the 2010 IEEE Symposium on Industrial Electronics and Applications (ISIEA), Penang, Malaysia, 3–5 October 2010; pp. 389–394. [Google Scholar]
- Călugăru, G.; Dănişor, E.A. Improved aircraft attitude control using generalized predictive control method. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 29 May–1 June 2016; pp. 101–106. [Google Scholar]
- Härkegård, O. Backstepping and Control Allocation with Applications to Flight Control. Ph.D. Thesis, Linköpings Universitet, Linköping, Sweden, 2003. [Google Scholar]
- Härkegård, O. Quadratic Programming Control Allocation Toolbox(Qcat). Mar. Available online: http://research.harkegard.se/qcat (accessed on 12 June 2020).
- Luo, Y.; Serrani, A.; Yurkovich, S.; Oppenheimer, M.W.; Doman, D.B. Model-predictive dynamic control allocation scheme for reentry vehicles. J. Guid. Control Dyn. 2007, 30, 100–113. [Google Scholar] [CrossRef]
- Bolender, M.A.; Doman, D.B. Nonlinear control allocation using piecewise linear functions: A linear programming approach. J. Guid. Control Dyn. 2005, 28, 558–562. [Google Scholar] [CrossRef] [Green Version]
- Durham, W.; Bordignon, K.A.; Beck, R. Aircraft Control Allocation; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Buffington, J.M.; Enns, D.F. Lyapunov stability analysis of daisy chain control allocation. J. Guid. Control Dyn. 1996, 19, 1226–1230. [Google Scholar] [CrossRef]
- Rupp, A. Control Allocation for Over-Actuated Road Vehicles; University of Graz: Graz, Austria, 2013; pp. 13–26. [Google Scholar]
- Oppenheimer, M.W.; Doman, D.B.; Bolender, M.A. Control allocation for over-actuated systems. In Proceedings of the 2006 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–26 June 2006; pp. 1–6. [Google Scholar]
- Nel, A.; Prokop, J.; Pecharová, M.; Engel, M.S.; Garrouste, R. Palaeozoic giant dragonflies were hawker predators. Sci. Rep. 2018, 8, 12141. [Google Scholar] [CrossRef] [PubMed]
- May, M.L. A critical overview of progress in studies of migration of dragonflies (Odonata: Anisoptera), with emphasis on North America. J. Insect Conserv. 2013, 17, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Azuma, A.; Watanabe, T. Flight performance of a dragonfly. J. Exp. Biol. 1988, 137, 221–252. [Google Scholar] [CrossRef]
- Wakeling, J.; Ellington, C.P. Dragonfly flight. I. Gliding flight and steady-state aerodynamic forces. J. Exp. Biol. 1997, 200, 543–556. [Google Scholar] [CrossRef] [PubMed]
- Newman, B. Model test on a wing section of a dragonfly. In Scale Effects in Animal Locomotion; Academic Press: London, UK, 1977; pp. 445–477. [Google Scholar]
- Zipfel, P.H. Modeling and Simulation of Aerospace Vehicle Dynamics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
- Wrede, R.C. Introduction to Vector and Tensor Analysis; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Prentice, NJ, USA, 2012. [Google Scholar]
- Anderson, B.D.; Moore, J.B. Optimal Control Linear Quadratic Methods; Prentice Hall International: Prentice, NJ, USA, 1989; Volume 7632. [Google Scholar]
- Dorato, P.; Cerone, V.; Abdallah, C. Linear Quadratic Control: An Introduction; Krieger Pub Co.: Malabar, FL, USA, 2000. [Google Scholar]
- MATLAB. 9.7.0.1190202 (R2019b); The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Ogunwa, T.; McIvor, B.; Jumat, N.A.; Abdullah, E.; Chahl, J. Longitudinal Actuated Abdomen Control for Energy Efficient Flight of Insects. Energies 2020, 13, 5480. [Google Scholar] [CrossRef]
- Drela, M.; Youngren, H. AVL 3.36 User Primer. 2017. Available online: http://web.mit.edu/drela/Public/web/avl/avl_doc.txt (accessed on 10 June 2020).
- Budziak, K. Aerodynamic Analysis with Athena Vortex Lattice (AVL); Aircraft Design and Systems Group (AERO), Department of Automotive: Hamburg, Germany, 2015. [Google Scholar]
- Bacon, B.; Gregory, I. General equations of motion for a damaged asymmetric aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 20 August 2007; p. 6306. [Google Scholar]
- De Castro, H.V. The Longitudinal Static Stability of Tailless Aircraft; CoA Report No 0018/1; College of Aeronautics, Cranfield University: Bedford, UK, 2001. [Google Scholar]
- Anderson, J. Aircraft Performance and Design; McGraw-Hill International Editions: Aerospace Science/Technology Series; WCB/McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Drela, M.; Youngren, H. AVL Overview. [Online Product Brochure]. Available online: http://web.mit.edu/drela/Public/web/avl/ (accessed on 12 June 2020).
- Drela, M.; Youngren, H. XFOIL manual. 2001. Available online: http://web.mit.edu/aeroutil_v1.0/xfoil_doc.txt (accessed on 10 June 2020).
- Deperrois, A. Analysis of foils and wings operating at low Reynolds numbers. Guidel. Xflr5 2009, 4, 58. [Google Scholar]
- Bryson, A.E. Control of Spacecraft and Aircraft; Princeton University Press Princeton: Princeton, NJ, USA, 1993; Volume 41. [Google Scholar]
- Hamada, A.; Sultan, A.; Abdelrahman, M. Design, Build and Fly a Flying Wing. Athens J. Technol. Eng. 2018, 5, 223–250. [Google Scholar] [CrossRef]
- Coates, E.M.; Fossen, T.I. Geometric reduced-attitude control of fixed-wing uavs. Appl. Sci. 2021, 11, 3147. [Google Scholar] [CrossRef]
- Markin, S. Multiple Simultaneous Specification Attitude Control of a Mini Flying-Wing Unmanned Aerial Vehicle. Ph.D. Thesis, University of Toronto (Canada), Toronto, ON, Canada, 2010. [Google Scholar]
- Alexander, D.E. Wind tunnel studies of turns by flying dragonflies. J. Exp. Biol. 1986, 122, 81–98. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (kg) | 0.325 | (kg) | 0.06 |
| Body length, (m) | 0.3 | Tail length, (m) | 0.4 |
| Max. body diameter, (m) | 0.14 | Tail diameter, (m) | 0.05 |
| (kg) | 0.00187 | (m) | 1.4 |
| (kg) | 0.01117 | (m) | 0.19434 |
| (kg) | 0.00934 | () | 0.26865 |
| (m) | [−0.064; 0; 0.003] | (m) | [0.025; 0; 0] |
| (m/s) | (m) | () | Model Type | () | () | (N) | (Nm) |
|---|---|---|---|---|---|---|---|
| 10 | 100 | 0 | Single-body | −11.35 | 0.228 | 0.679 | - |
| Multibody | −11.35 | 0.228 | 0.679 | −0.235 | |||
| −10 | Single-body | −10.66 | 0.0707 | 0.683 | - | ||
| Multibody | −10.66 | 0.0707 | 0.683 | −0.232 | |||
| −30 | Single-body | −6.02 | −0.96 | 0.708 | - | ||
| Multibody | −6.02 | −0.96 | 0.708 | −0.204 |
| State () | Control Input () | ||
|---|---|---|---|
| = 10 (m/s) | = 0 (/s) | = 0.228 () | = 0 () |
| = 0 (m/s) | = 0 (/s) | = 0 () | = 0 () |
| = −0.198 (m/s) | = 0 (/s) | = 0.68 (N) | = 0 () |
| = 0 (m) | = 0 () | ||
| = 0 (m) | = −1.13 () | ||
| = −100 (m) | = 0 () | ||
| Percentage of Central Body Mass (%) | Static Margin (%) | Eigenvalues | Dynamic Stability |
|---|---|---|---|
| 6 | 37.3 | −20.80 ± 28.21i | Stable |
| −0.22 ± 0.95i | |||
| 11 | 24.6 | −18.81 ± 23.02i | Stable |
| −0.20 ± 0.69 | |||
| 16 | 9.5 | −18.00 ± 20.39 | Stable |
| −0.16 ± 0.41 | |||
| 21 | −2.7 | −17.52 ± 18.91i | Unstable |
| −0.34 | |||
| 0.06 | |||
| 26 | −13.9 | −17.24 ± 17.77i | Unstable |
| −0.55 | |||
| 0.385 |
| Pitch Control (PC) Case | ||
|---|---|---|
| PC 1 | diag [ ] | |
| PC 2 | diag [ ] | |
| PC 3 | diag [ ] |
| Characteristic | PC 1 | PC 2 | PC 3 |
|---|---|---|---|
| Settling time (s) | 3.08 | 2.97 | 2.96 |
| Overshoot (%) | 3.84 | 3.82 | 3.81 |
| Steady-state error (%) | 0 | 0 | 0 |
| Roll Control (YC) Case | ||
|---|---|---|
| YC 1 | diag [18 ] | |
| YC 2 | diag [ 2] | |
| YC 3 | diag [10 10] |
| Characteristic | YC 1 | YC 2 | YC 3 |
|---|---|---|---|
| Settling time (s) | 3.33 | 6.25 | 2.29 |
| Overshoot (%) | 5.80 | 0.89 | 2.95 |
| Steady-state error (%) | 0 | 2.00 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogunwa, T.; Abdullah, E.; Chahl, J. Modeling and Control of an Articulated Multibody Aircraft. Appl. Sci. 2022, 12, 1162. https://doi.org/10.3390/app12031162
Ogunwa T, Abdullah E, Chahl J. Modeling and Control of an Articulated Multibody Aircraft. Applied Sciences. 2022; 12(3):1162. https://doi.org/10.3390/app12031162
Chicago/Turabian StyleOgunwa, Titilayo, Ermira Abdullah, and Javaan Chahl. 2022. "Modeling and Control of an Articulated Multibody Aircraft" Applied Sciences 12, no. 3: 1162. https://doi.org/10.3390/app12031162






