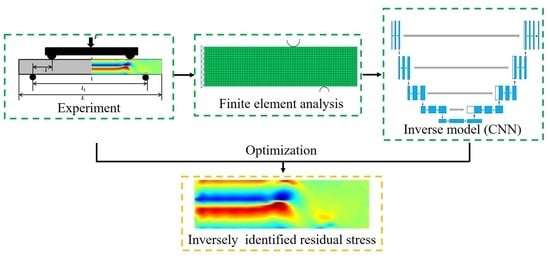
Inverse Identification of Residual Stress Distribution in Aluminium Alloy Components Based on Deep Learning
Abstract
:1. Introduction
2. Inverse Method
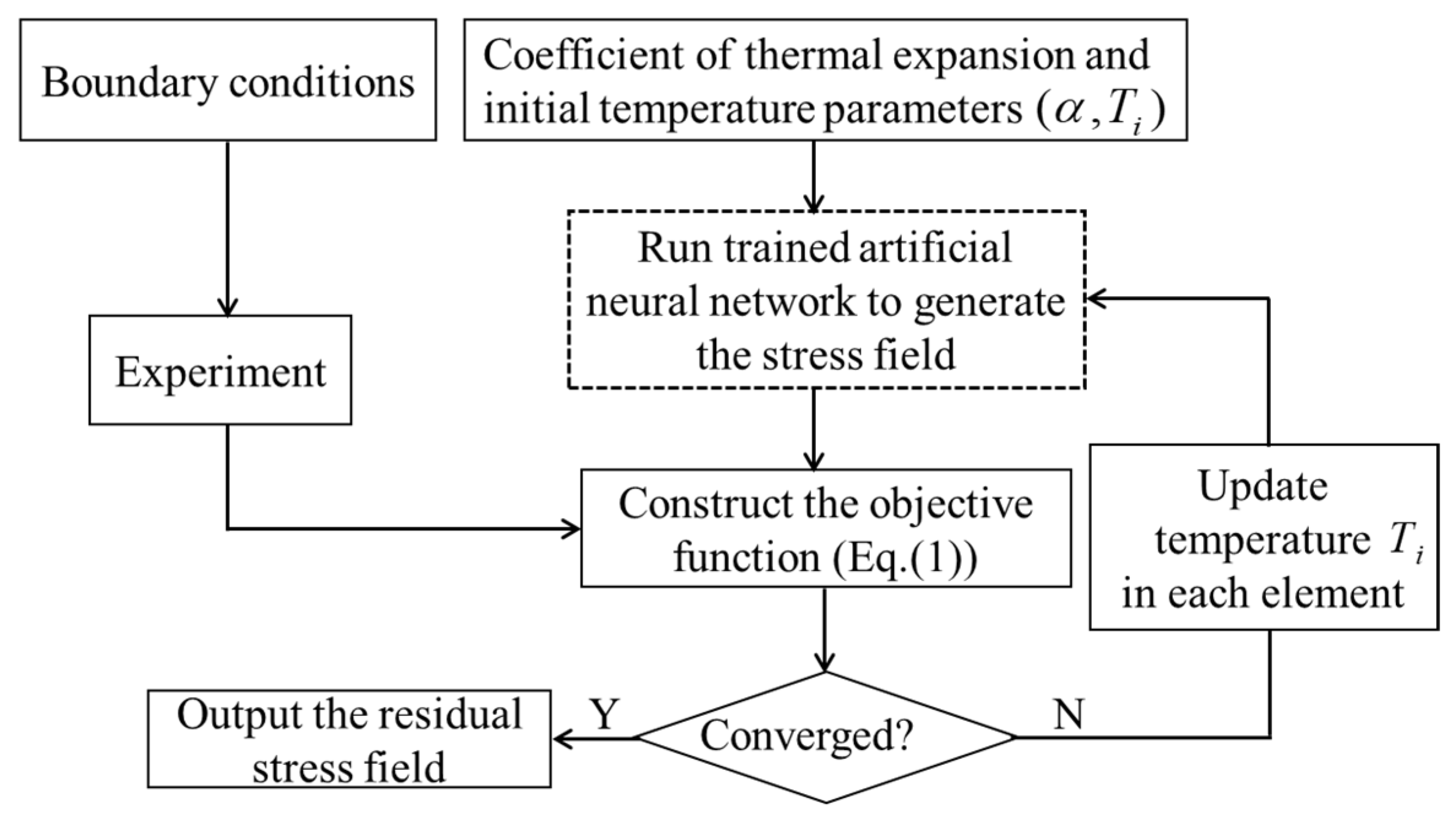
2.1. Inverse Strategy
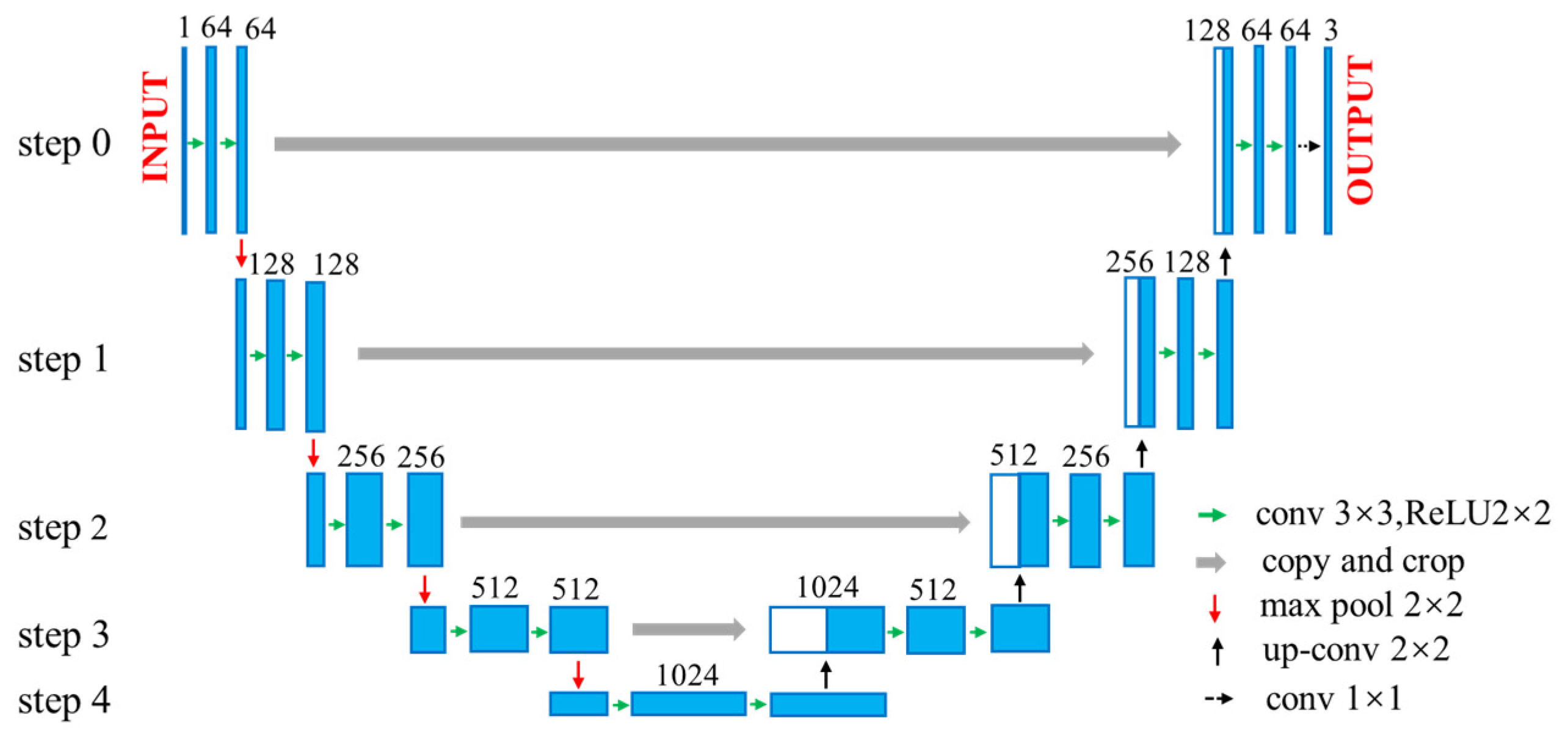
2.2. U-Net Architecture
2.3. Database and U-Net Training Strategy
3. Results
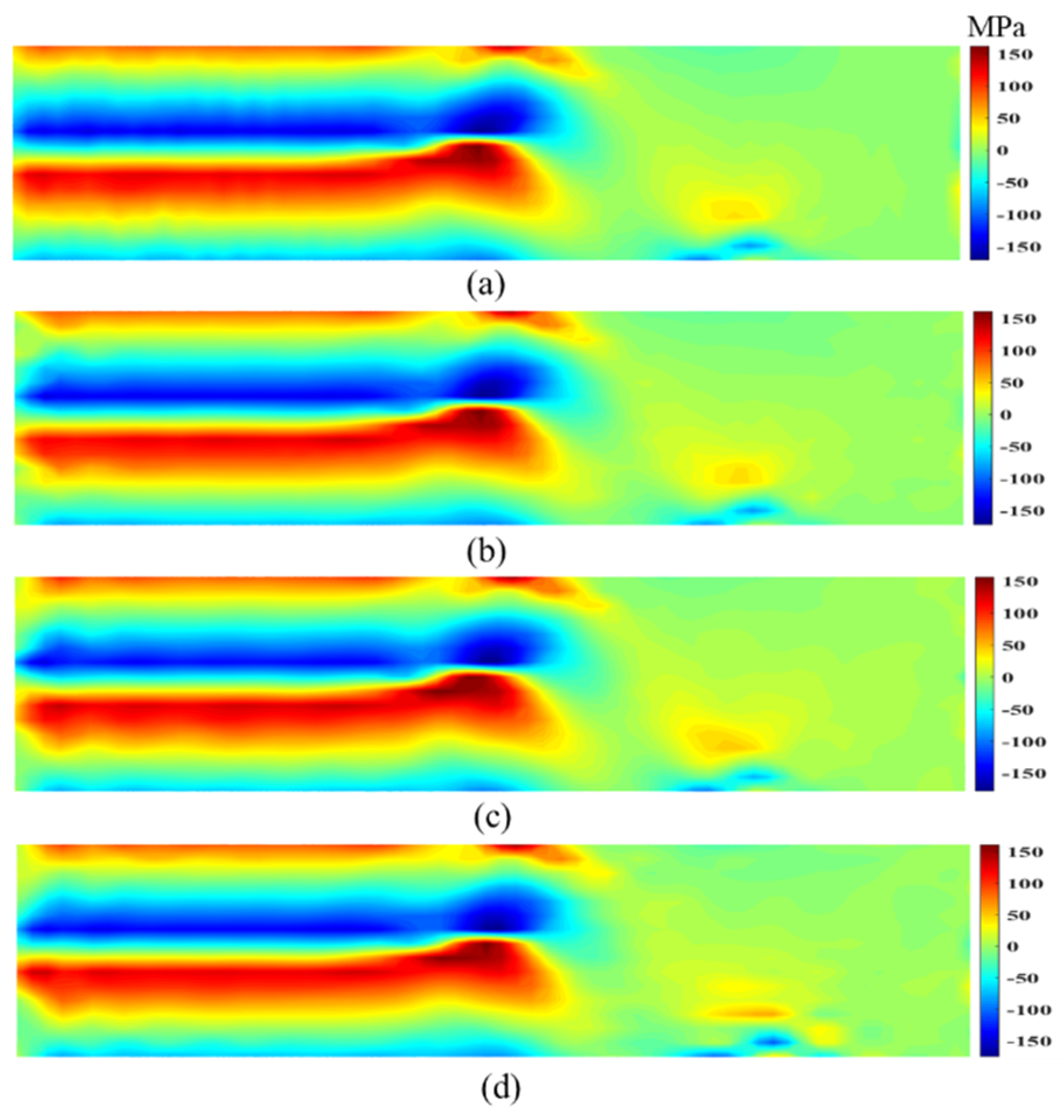
3.1. Residual Stress Field of Simulated Four-Point Bending Experiment
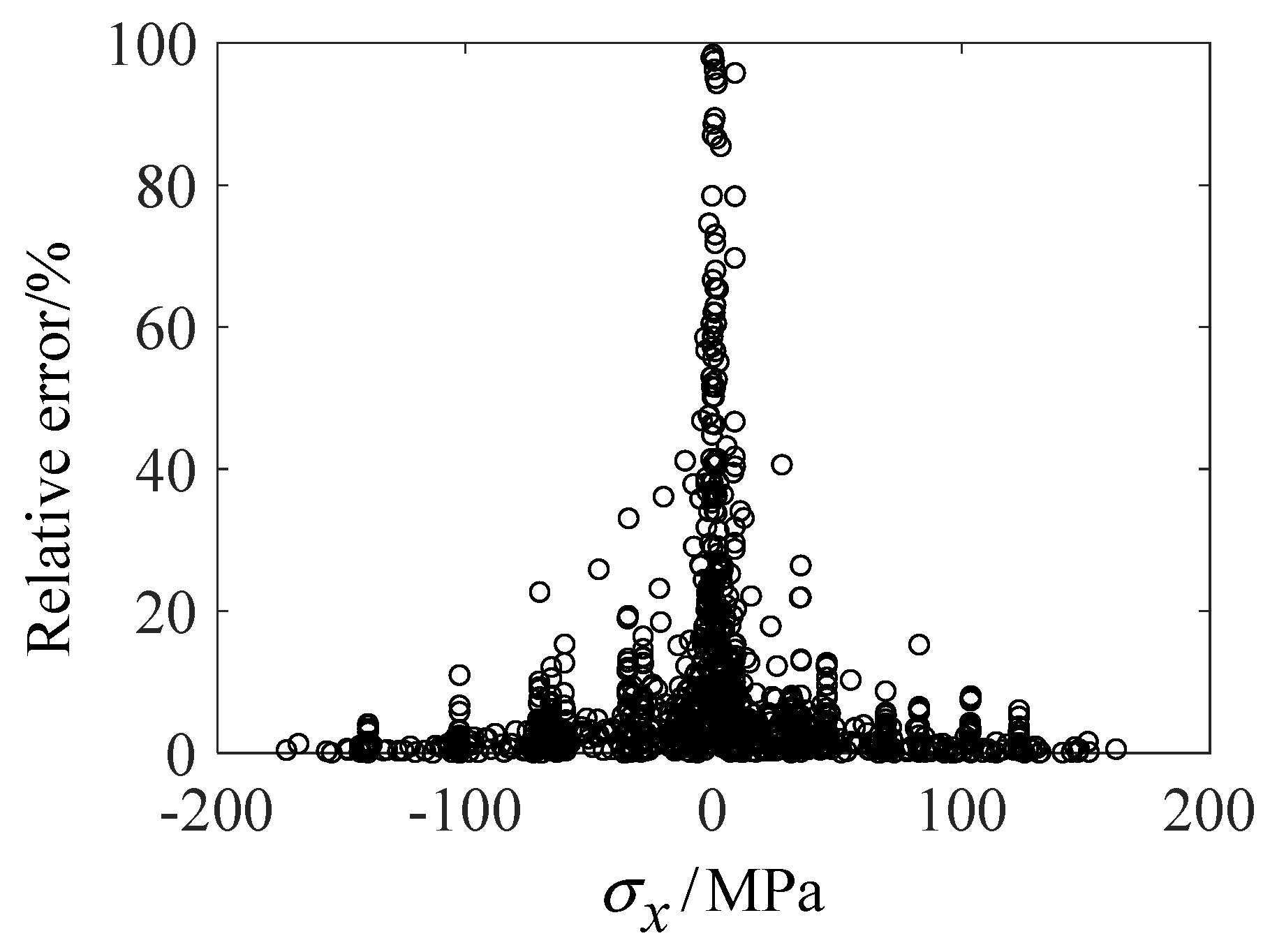
3.2. Residual Stress Prediction Based on UNet Architecture
4. Discussion
4.1. Influence of Initial Values on Stability of the Inverse Algorithm
4.2. Comparison of CPU Running Time of Different Inverse Algorithms
5. Conclusions
- (1)
- The machining process and conditions of structural components need not be known and the full-field residual stress satisfying mechanical constrains can be inversely determined from limited measurement points.
- (2)
- In the proposed method, the U-Net architecture trained by the temperature and stress fields exhibited superior performance in predicting residual stress field and greatly improved the computational efficiency. In fact, the residual stress determined by this method reached an accuracy close to that of the X-ray diffraction method.
- (3)
- Moreover, the proposed inverse method based on neural networks is not only suitable for the residual stress prediction but can also undertake inverse identification of various material parameters such as damage factors.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akhtar, N.; Afzal, M.; Awais, M.; Akbar, M. Optimizing cold compression deformation to remove residual stresses in die forged disc of Al-Mg-Si alloy. Key Eng. Mater. 2018, 778, 53–60. [Google Scholar] [CrossRef]
- Tao, X.; Gao, Y. Influences of thermal effects on residual stress fields of an aluminium-lithium alloy induced by shot peening. Int. J. Adv. Manuf. Technol. 2021, 112, 3105–3116. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, R.L.; Wang, X.-L.; McGreevy, R. Grain-orientation-dependent residual stress and the effect of annealing in cold-rolled stainless steel. Acta Mater. 2002, 50, 1717–1734. [Google Scholar] [CrossRef]
- Li, X.; Qi, C.; Zhang, P. A micro-macro confined compressive fatigue creep failure model in brittle solids. Int. J. Fatigue 2020, 130, 105278. [Google Scholar] [CrossRef]
- Zhang, Z.; Tan, Q.; Cui, Y.; Tian, Y.; Wang, Y.; Qin, H.; Bi, Z.; Wang, Y. Experimental validation of residual stress thermomechanical simulation in as-quenched superalloy discs by using diffraction and incremental hole-drilling methods. Mater. Today Commun. 2021, 27, 102229. [Google Scholar] [CrossRef]
- Gadallah, R.; Tsutsumi, S.; Yonezawa, T.; Shimanuki, H. Residual stress measurement at the weld root of rib-to-deck welded joints in orthotropic steel bridge decks using the contour method. Eng. Struct. 2020, 219, 110946. [Google Scholar] [CrossRef]
- Zhu, K.Y.; Li, Z.Q.; Fan, G.L.; Xu, R.; Jiang, C.H. Thermal relaxation of residual stress in shot-peened CNT/Al–Mg–Si alloy composites. J. Mater. Res. Technol. 2019, 8, 2201–2208. [Google Scholar] [CrossRef]
- Marciszko, M.; Baczmański, A.; Klaus, M.; Genzel, C.; Oponowicz, A.; Wroński, S.; Wróbel, M.; Braham, C.; Sidhom, H.; Wawszczak, R. A multireflection and multiwavelength residual stress determination method using energy dispersive diffraction. J. Appl. Crystallogr. 2018, 51, 732–745. [Google Scholar] [CrossRef] [Green Version]
- Marola, S.; Bosia, S.; Veltro, A.; Fiore, G.; Manfredi, D.; Lombardi, M.; Amato, G.; Baricco, M.; Battezzati, L. Residual stresses in additively manufactured AlSi10Mg: Raman spectroscopy and X-ray diffraction analysis. Mater. Des. 2021, 202, 109550. [Google Scholar] [CrossRef]
- Schoderböck, P.; Köstenbauer, H. Residual stress determination in thin films by X-ray diffraction and the widespread analytical practice applying a biaxial stress model: An outdated oversimplification? Appl. Surf. Sci. 2020, 541, 148531. [Google Scholar] [CrossRef]
- Faghidian, S.A. New framework for Bayesian statistical analysis and interpolation of residual stress measurements. Mech. Res. Commun. 2013, 50, 17–21. [Google Scholar] [CrossRef]
- Jiang, X.; Li, H.; Wang, Y.; Ding, Z. An approach to predict the distortion of thin-walled parts affected by residual stress during the milling process. Int. J. Adv. Manuf. Technol. 2017, 93, 4203–4216. [Google Scholar] [CrossRef]
- Oliveira, A.L.R.D.; Rego, R.R.; de Faria, A.R. Residual stresses prediction in machining: Hybrid FEM enhanced by assessment of plastic flow. J. Mater. Process. Technol. 2020, 275, 116332. [Google Scholar] [CrossRef]
- Chukkan, J.R.; Wu, G.; Fitzpatrick, M.E.; Jones, S.; Kelleher, J. An iterative technique for the reconstruction of residual stress fields in a butt-welded plate from experimental measurement, and comparison with welding process simulation. Int. J. Mech. Sci. 2019, 160, 421–428. [Google Scholar] [CrossRef]
- Jun, T.-S.; Korsunsky, A.M. Evaluation of residual stresses and strains using the Eigenstrain Reconstruction Method. Int. J. Solids Struct. 2010, 47, 1678–1686. [Google Scholar] [CrossRef] [Green Version]
- Markiewicz, É.; Langrand, B.; Notta-Cuvier, D. A review of characterisation and parameters identification of materials constitutive and damage models: From normalised direct approach to most advanced inverse problem resolution. Int. J. Impact Eng. 2017, 110, 371–381. [Google Scholar] [CrossRef]
- Liu, G.; Wang, L.; Yi, Y.; Sun, L.; Shi, L.; Ma, S. Inverse identification of graphite damage properties under complex stress states. Mater. Des. 2019, 183, 108135. [Google Scholar] [CrossRef]
- Aguir, H.; Belhadjsalah, H.; Hambli, R. Parameter identification of an elasto-plastic behaviour using artificial neural networks–genetic algorithm method. Mater. Des. 2011, 32, 48–53. [Google Scholar] [CrossRef]
- Ali, U.; Muhammad, W.; Brahme, A.; Skiba, O.; Inal, K. Application of artificial neural networks in micromechanics for polycrystalline metals. Int. J. Plast. 2019, 120, 205–219. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, G.; Xu, X.; Li, G.; Huang, X.; Shen, J.; Li, Q. Identification of material parameters for aluminum foam at high strain rate. Comput. Mater. Sci. 2013, 74, 65–74. [Google Scholar] [CrossRef]
- Fan, J.; Xu, W.; Wu, Y.; Gong, Y. Human Tracking Using Convolutional Neural Networks. IEEE Trans. Neural Netw. 2010, 21, 1610–1623. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation, International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Mendizabal, A.; Márquez-Neila, P.; Cotin, S. Simulation of hyperelastic materials in real-time using deep learning. Med. Image Anal. 2020, 59, 101569. [Google Scholar] [CrossRef] [PubMed]
- Koeppe, A.; Bamer, F.; Markert, B. An intelligent nonlinear meta element for elastoplastic continua: Deep learning using a new Time-distributed Residual U-Net architecture. Comput. Methods Appl. Mech. Eng. 2020, 366, 113088. [Google Scholar] [CrossRef]
- Donovan, D.; Burrage, K.; McCourt, T.; Thompson, B.; Yazici, E. Estimates of the coverage of parameter space by Latin Hypercube and Orthogonal Array-based sampling. Appl. Math. Model. 2018, 57, 553–564. [Google Scholar] [CrossRef] [Green Version]
- Chollet, F. Keras: The Python Deep Learning Library. Astrophysics Source Code Library. 2018. Available online: https://github.com/keras-team/keras (accessed on 7 December 2021).
- Coules, H.; Smith, D.; Venkata, K.A.; Truman, C. A method for reconstruction of residual stress fields from measurements made in an incompatible region. Int. J. Solids Struct. 2014, 51, 1980–1990. [Google Scholar] [CrossRef] [Green Version]

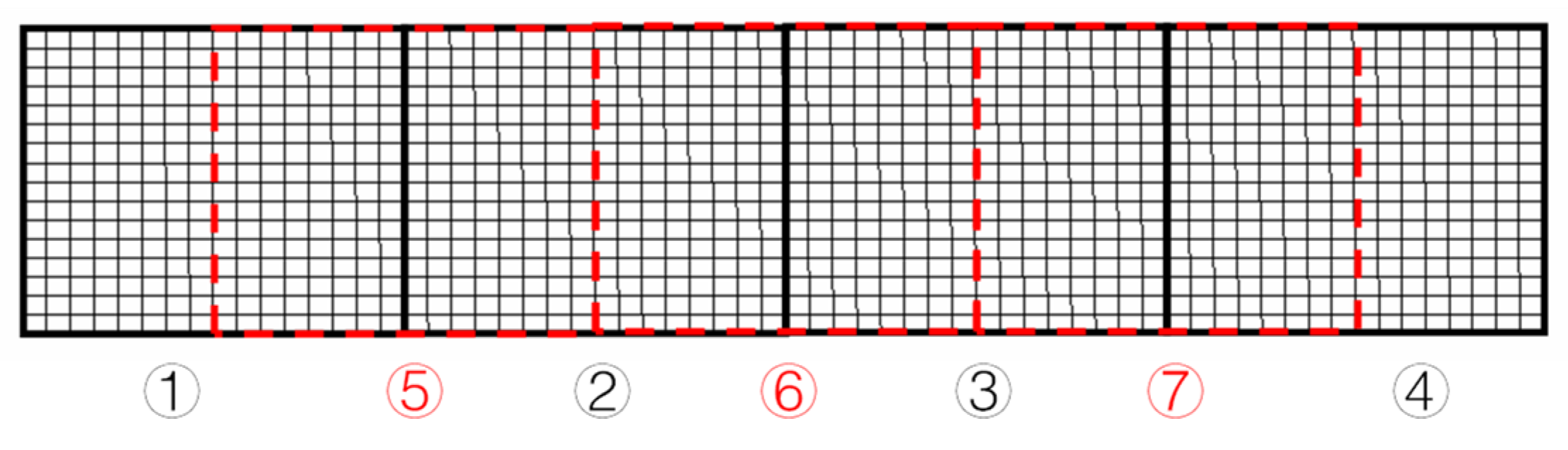

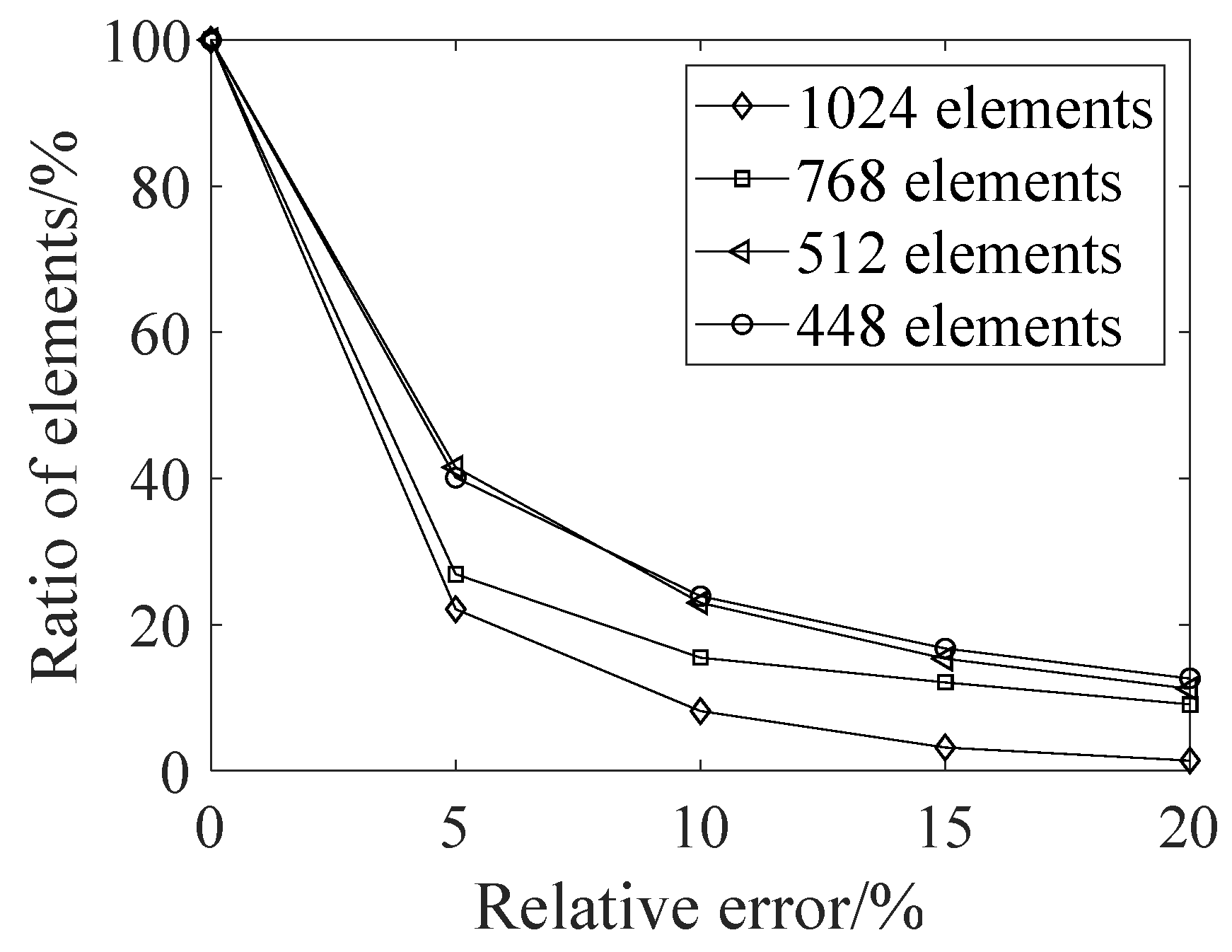
| Measurement Points | 1024 | 768 | 512 | 448 |
|---|---|---|---|---|
| Row | 1:1:16 | 1:2:16; 2:2:16 | 1:1:16 | 1:1:16 |
| Column | 1:1:64 | 1:1:64; 1:2:64 | 1:2:64 | 1:2:40; 41:3:64 |
| Initial Values | 0.2 | 0.5 | 0.8 |
|---|---|---|---|
| RMSE (MPa) | 7.82 | 7.45 | 7.61 |
| Iteration times | 2.5 × 106 | 106 | 2.3 × 106 |
| Procedure | Time | |
|---|---|---|
| CNN-Based | FEMU-Based | |
| Each iteration | 0.08 s | 21 s |
| Training | 22.91 h | 0 |
| Sampling | 59.85 h | 0 |
| Total | 82.76 h | 5833.33 h (estimated) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, T.; Wang, L.; Gao, X.; Liu, G. Inverse Identification of Residual Stress Distribution in Aluminium Alloy Components Based on Deep Learning. Appl. Sci. 2022, 12, 1195. https://doi.org/10.3390/app12031195
Xiong T, Wang L, Gao X, Liu G. Inverse Identification of Residual Stress Distribution in Aluminium Alloy Components Based on Deep Learning. Applied Sciences. 2022; 12(3):1195. https://doi.org/10.3390/app12031195
Chicago/Turabian StyleXiong, Tulin, Lu Wang, Xianzhi Gao, and Guangyan Liu. 2022. "Inverse Identification of Residual Stress Distribution in Aluminium Alloy Components Based on Deep Learning" Applied Sciences 12, no. 3: 1195. https://doi.org/10.3390/app12031195
APA StyleXiong, T., Wang, L., Gao, X., & Liu, G. (2022). Inverse Identification of Residual Stress Distribution in Aluminium Alloy Components Based on Deep Learning. Applied Sciences, 12(3), 1195. https://doi.org/10.3390/app12031195