Nonlinear Dynamics Suppression of Bending Deflection in a Composite Laminated Plate Using a Beam Stiffener Due to Critical Buckling Load and Shear Force
Abstract
:1. Introduction
2. Experiment Test
3. Analytic Solution of Bending Deflection
4. Special Case Using the Navier Solution
5. Different Boundary Conditions
6. Numerical Simulation
7. Largest Lyapunov Exponent Parameter
8. Power Density Function of Fast Fourier Transfer (FFT)
9. Results and Discussion
10. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
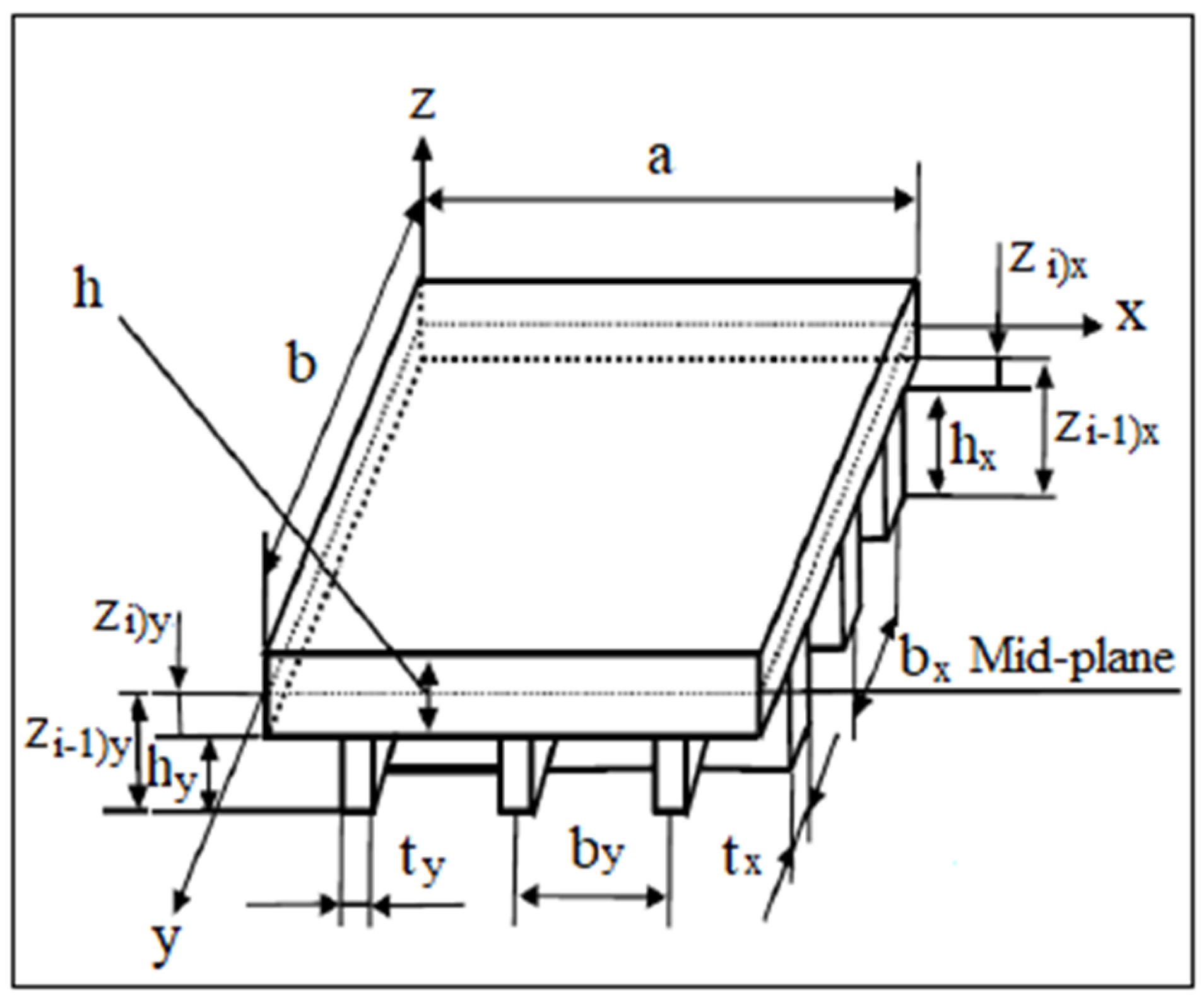
Nomenclature
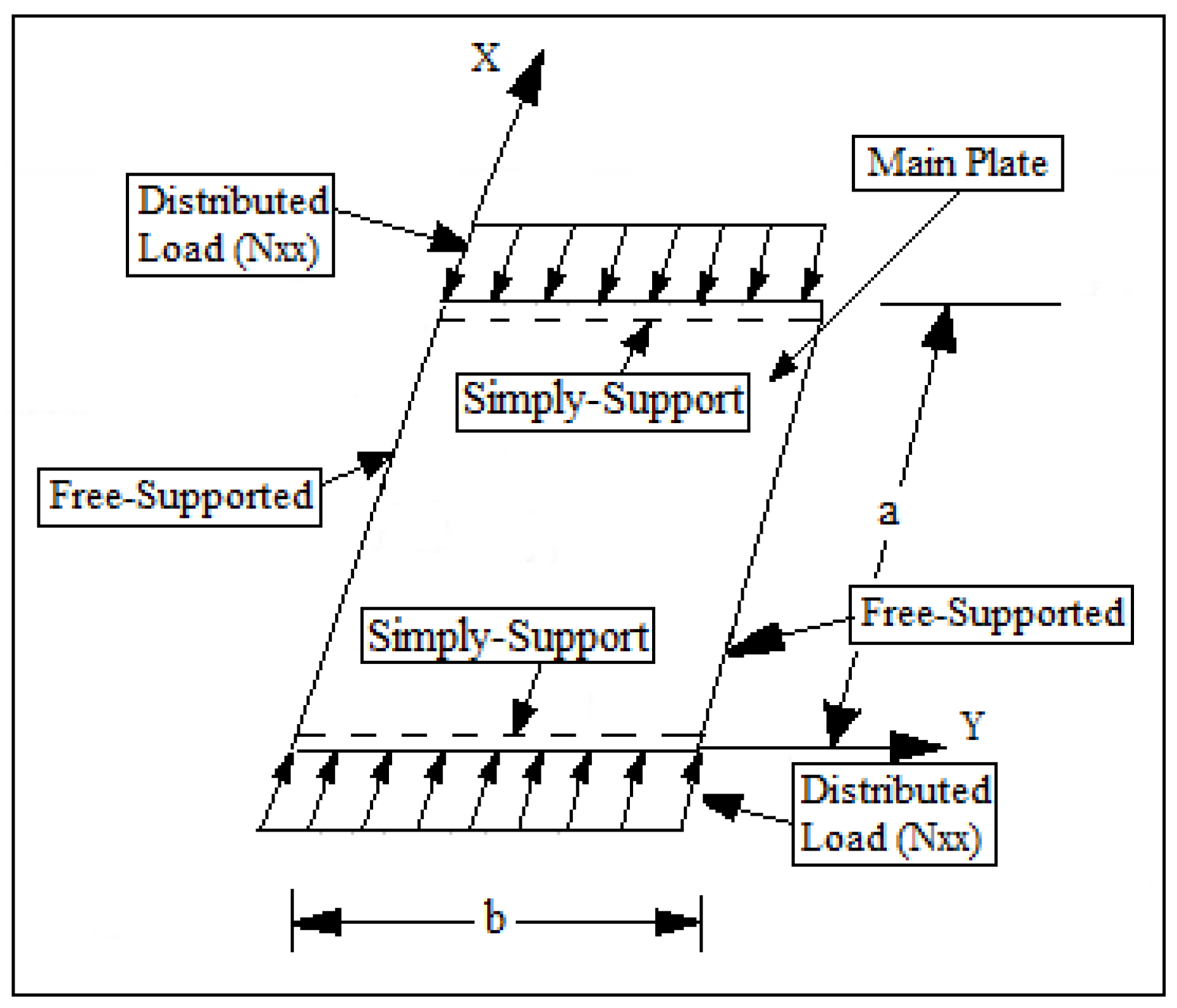
| a | Length of large span of rectangular plate, mm |
| b | Length of small span of rectangular plate, mm |
| h | Thickness of the composite plate, mm |
| , | Lamina stresses field vector, N/mm2 |
| , | Extensional strain vector |
| , | Flexural (bending) strain vector |
| , | Displacement components in the 2-D coordinate system, mm |
| Reduced stiffness elements, N/mm2 | |
| Mid plane deflection along z-direction, mm | |
| Volume fraction for the fiber | |
| Fiber weight fraction | |
| Mass density for the fiber, kg | |
| Mass density for the composite, kg | |
| , | Modulus of elasticity along (x and y) directions, respectively, N/mm2 |
| , | Poisson’s ratio in plane 1-2 and the perpendicular plane 2-1, respectively |
| Thickness, depth, distance between stiffeners when the stiffener placed along x-axis, mm | |
| Thickness, depth, distance between stiffeners when the stiffener placed along y-axis, mm | |
| Critical buckling load, N | |
| Mass per unit area of the composite plate, kg/m2 | |
| m, n | Double trigonometric of Fourier series |
| Natural frequency of the composite laminated plate | |
| Buckling factor | |
| GFNN | Global false nearest neighbors for extracting embedding dimensions |
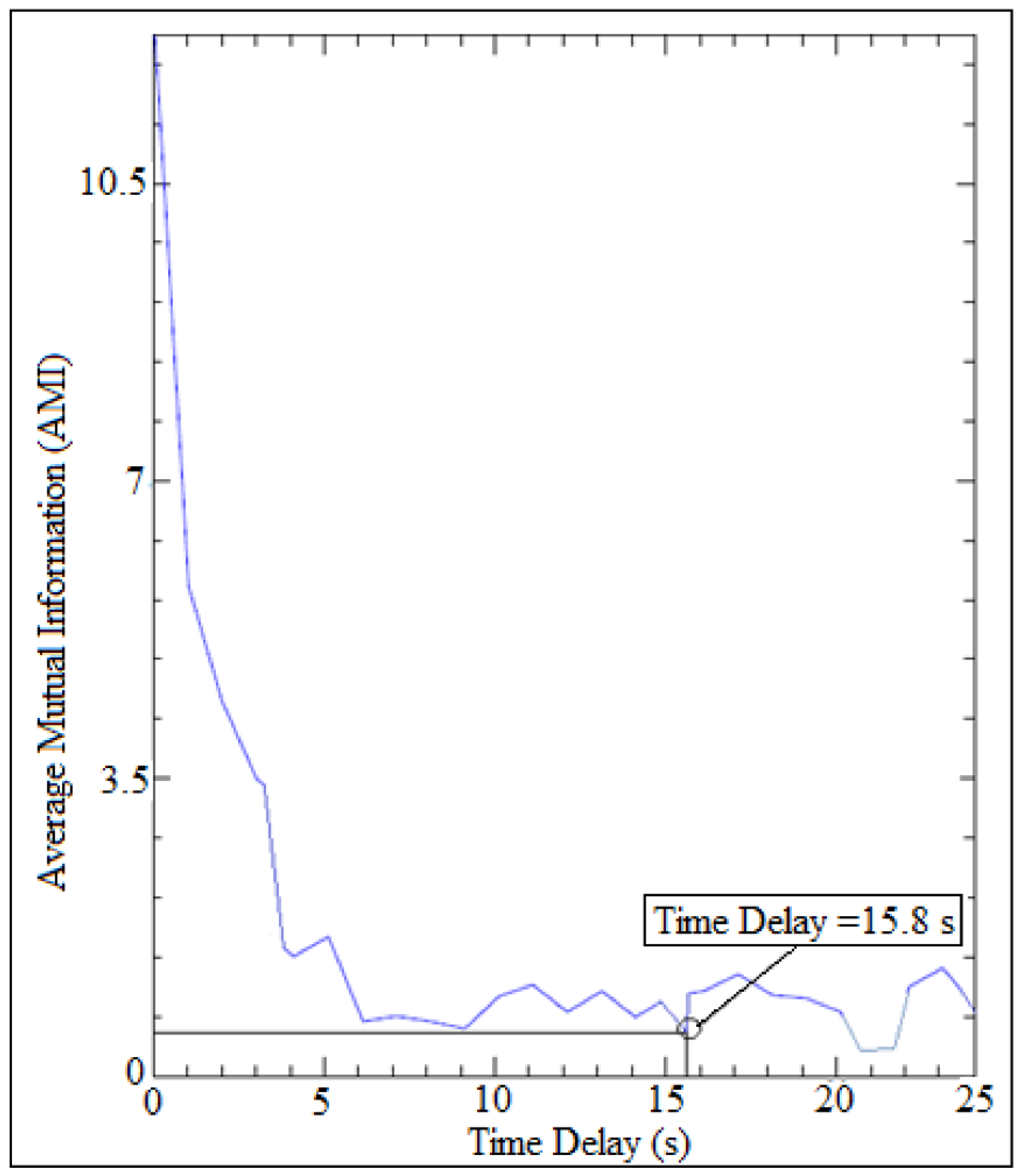
| AMI | Average mutual information algorithm for quantifying time delay |
| D | Distance between trajectories |
| d(t) | Percentage of variation in the distance between trajectories |
| Distance between the pair (j-th) at nearest neighbors (i) of the trajectories | |
| t | Time strides |
| y(i) | Data of follower displacement after curve fitting |
| Δt | Various time strides |
| λ | Largest Lyapunov exponent parameter |
| S-S-S-S | Simply-simply-simply-simply supported boundary conditions |
| S-F-S-F | Simply-free-simply-free supported boundary conditions |
| S-C-S-C | Simply-clamped-simply-clamped supported boundary conditions |
| S-F-S-S | Simply-free-simply-simply supported boundary conditions |
| S-F-S-C | Simply-free-simply-clamped supported boundary conditions |
| S-C-S-S | Simply-clamped-simply-simply supported boundary conditions |
Appendix A
Appendix B
- (1)
- (S-C-S-C) Boundary Conditions:
- (2)
- (S-C-S-S) Boundary Conditions:
- (3)
- (S-F-S-C) Boundary Conditions:
- (4)
- (S-F-S-S) Boundary Conditions:
References
- Keshav, V.; Patel, S.N. Non-Linear dynamic pulse buckling of laminated composite curved panels. J. Struct. Eng. Mech. 2020, 73, 181–190. [Google Scholar]
- Mondal, S.; Ramachandra, L.S. Nonlinear Dynamic Pulse Buckling of Imperfect Laminated Composite Plate with Delamination. Int. J. Solids Struct. 2020, 198, 170–182. [Google Scholar]
- Taczała, M.; Buczkowski, R.; Kleiber, M. Nonlinear buckling and post-buckling response of stiffened FGM plates in thermal environments. J. Compos. Part B Eng. 2017, 109, 238–247. [Google Scholar]
- Tao, Z.; Tu-guang, L.; Yao, Z.; Luo, J. Nonlinear dynamic buckling of stiffened plates under in-plane impact load. J. Zhejiang Univ. Sci. A 2004, 5, 609–617. [Google Scholar]
- Yousuf, L.S. Nonlinear dynamics investigation of flexural stiffness of composite laminated plate under the effect of temperature and combined loading using Lyapunov exponent parameter. J. Compos. Part B Eng. 2021, 219, 108926. [Google Scholar] [CrossRef]
- Yousuf, L.S. Nonlinear dynamics simulation of bending deflection for composite laminated plate under varied temperature using Lyapunov exponent parameter. In Proceedings of the ASME 2021 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2021, Online, 17–19 August 2021. [Google Scholar]
- Hegaze, M.H. Nonlinear Dynamic Analysis of Stiffened and Unstiffened Laminated Composite Plates Using a High-order Element. J. Compos. Mater. 2009, 44, 327–346. [Google Scholar] [CrossRef]
- Less, H.; Abramovich, H. Dynamic buckling of a laminated composite stringer–stiffened cylindrical panel. J. Compos. Part B Eng. 2012, 43, 2348–2358. [Google Scholar] [CrossRef]
- Aboudi, J.; Gilat, R. The Lyapunov exponents as a quantitative criterion for the dynamic buckling of composite plates. Int. J. Solids Struct. 2002, 39, 467–481. [Google Scholar]
- Chai, Y.Y.; Li, F.M.; Song, Z.G. Nonlinear Vibration Behaviors of Composite Laminated Plates with Time-Dependent Base Excitation and Boundary Conditions. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 145–161. [Google Scholar] [CrossRef]
- Borkowski, L. Numerical analysis of dynamic stability of an isotropic plate by applying tools used in dynamics. Dyn. Syst. Theory Appl. 2017, 248, 63–73. [Google Scholar]
- Kim, H.G. Experimental nonlinear dynamics and snap-through of post-buckled composite plates. Nonlinear Dyn. 2017, 1, 21–35. [Google Scholar]
- Pan, N. Theoretical determination of the optimal fiber volume fraction and fiber-matrix property compatibility of short fiber composites. Polym. Compos. 1993, 14, 85–93. [Google Scholar] [CrossRef] [Green Version]
- Gopalan, V.; Suthenthiraveerappa, V.; David, J.S.; Subramanian, J.; Annamalai, A.R.; Jen, C.P. Experimental and Numerical Analyses on the Buckling Characteristics of Woven Flax/Epoxy Laminated Composite Plate under Axial Compression. Polymers 2021, 13, 995. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.T. Mechanics of Aircraft Structures, 2nd ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Thompsom, M.K.; Thompson, J.M. ANSYS Mechanical APDL for Finite Element Analysis; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Parlitz, U. Estimating lyapunov exponents from time series. In Chaos Detection and Predictability; Springer: Berlin/Heidelberg, Germany, 2016; Volume 915, pp. 1–34. [Google Scholar]
- Terrier, P.; Fabienne, R. Maximum Lyapunov exponent revisited: Long-term attractor divergence of gait dynamics is highly sensitive to the noise structure of stride intervals. Gait Posture 2018, 66, 236–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hussain, V.S.; Spano, M.L.; Lockhart, T.E. Effect of data length on time delay and embedding dimension for calculating the Lyapunov exponent in walking. J. R. Soc. Interface 2020, 17, 20200311. [Google Scholar] [CrossRef] [PubMed]
- Garcia, M.M.; Morales, I.; Rodriguez, J.M.; Marin, M.R. Selection of embedding dimension and delay time in phase space reconstruction via symbolic dynamics. Entropy 2021, 23, 221. [Google Scholar] [CrossRef] [PubMed]
- Stoica, P.; Moses, R.L. Spectral analysis of signals. In Digital Signal Processing; Rao, K.D., Swamy, M.N.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 721–751. [Google Scholar]
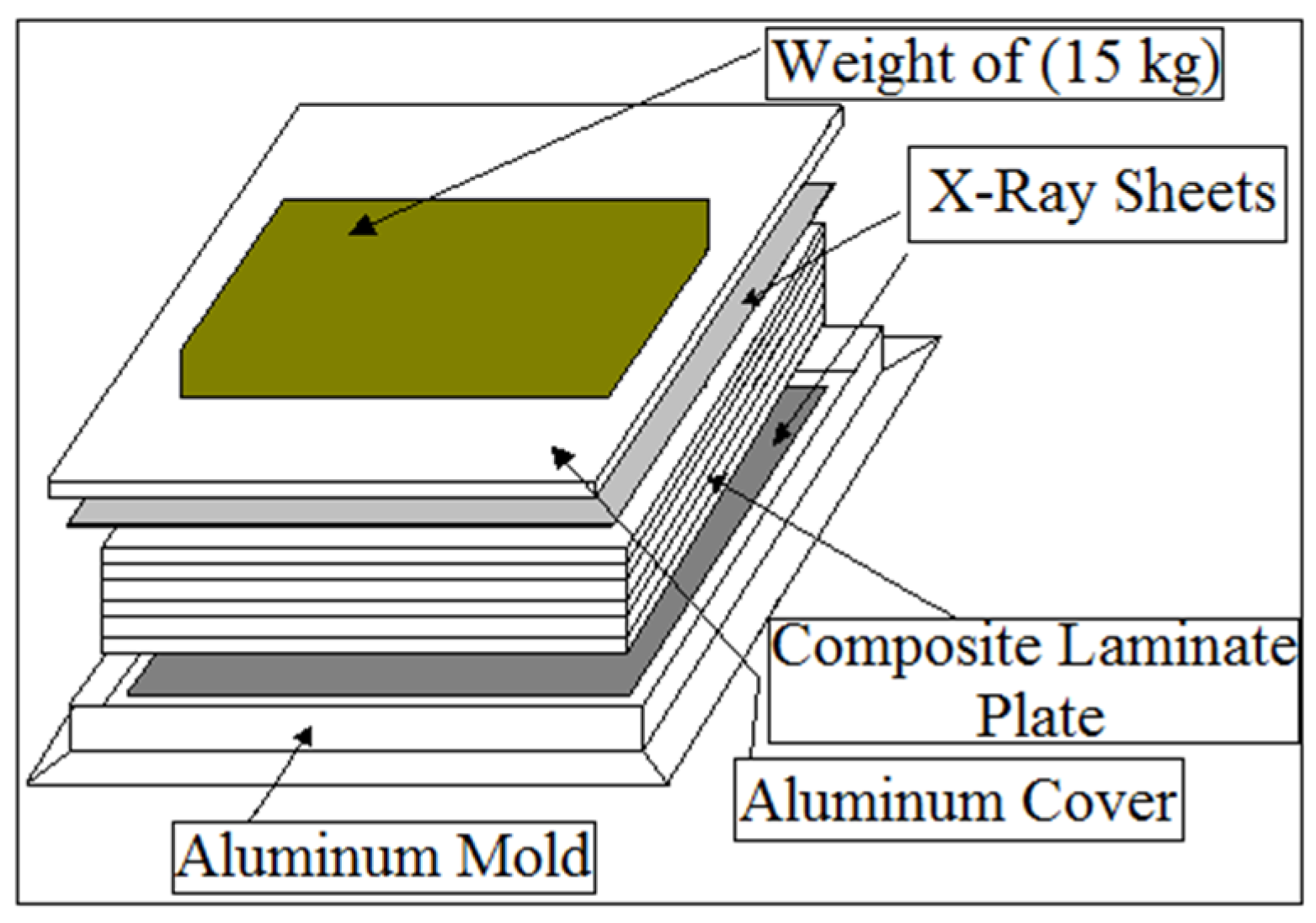




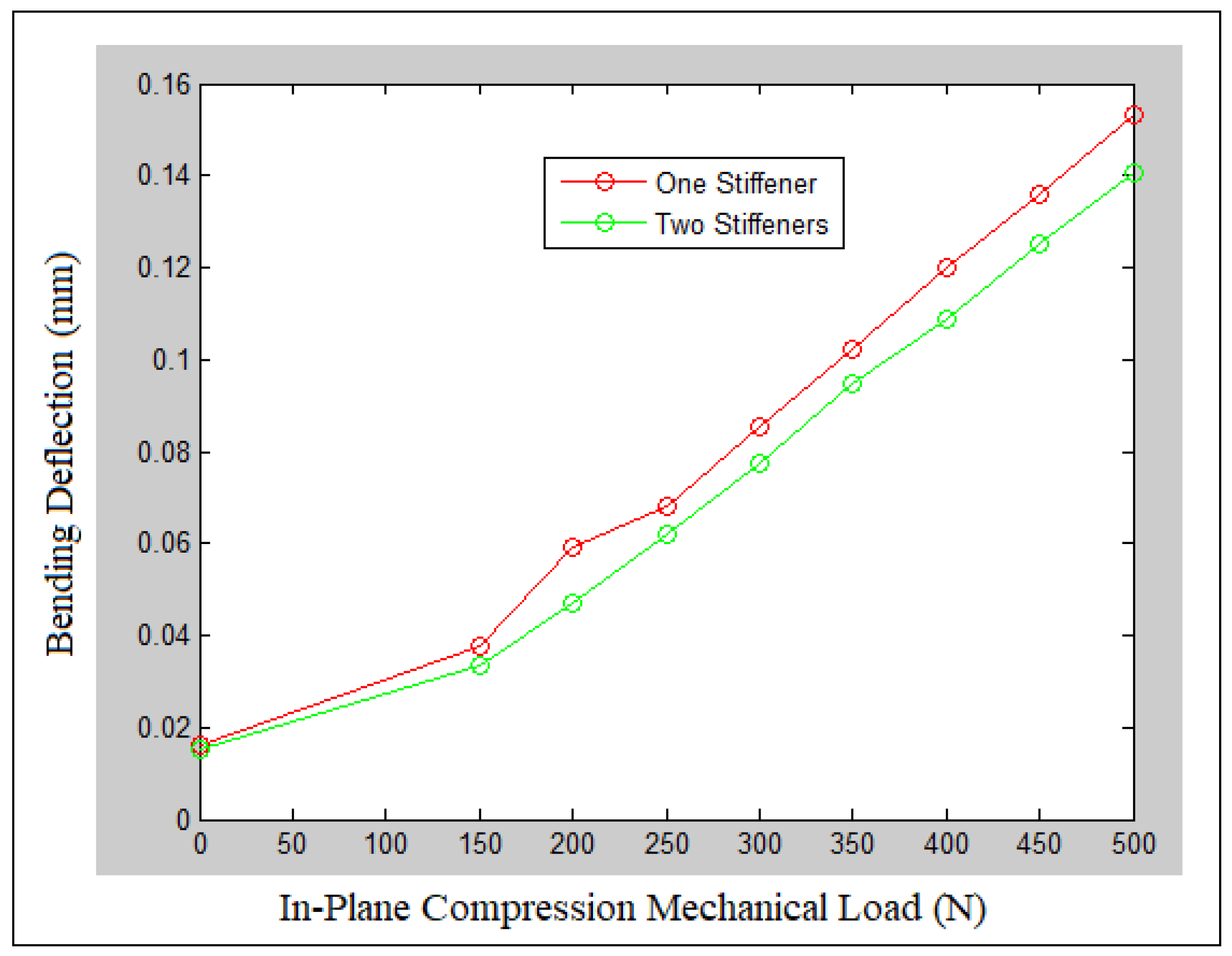
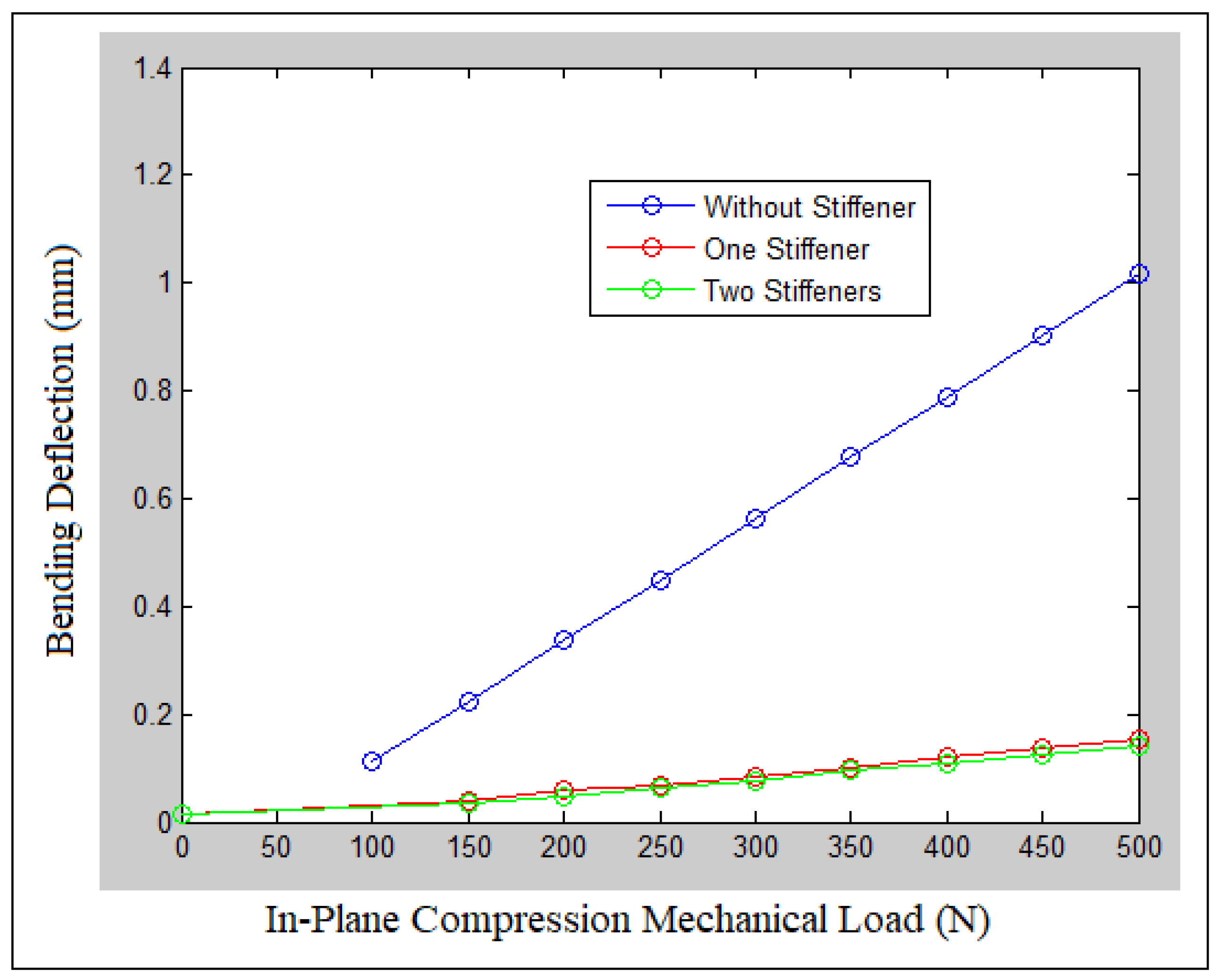


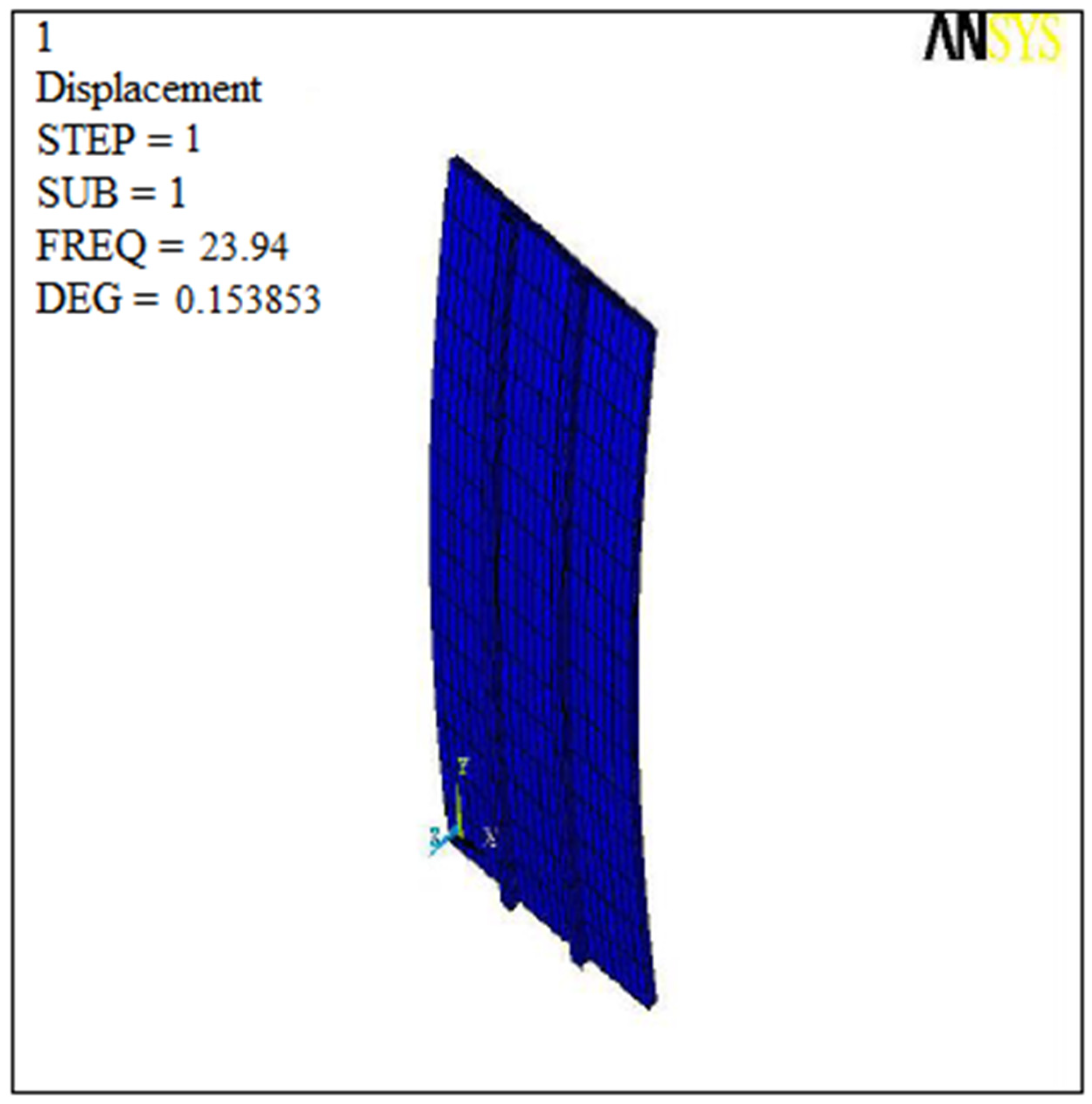

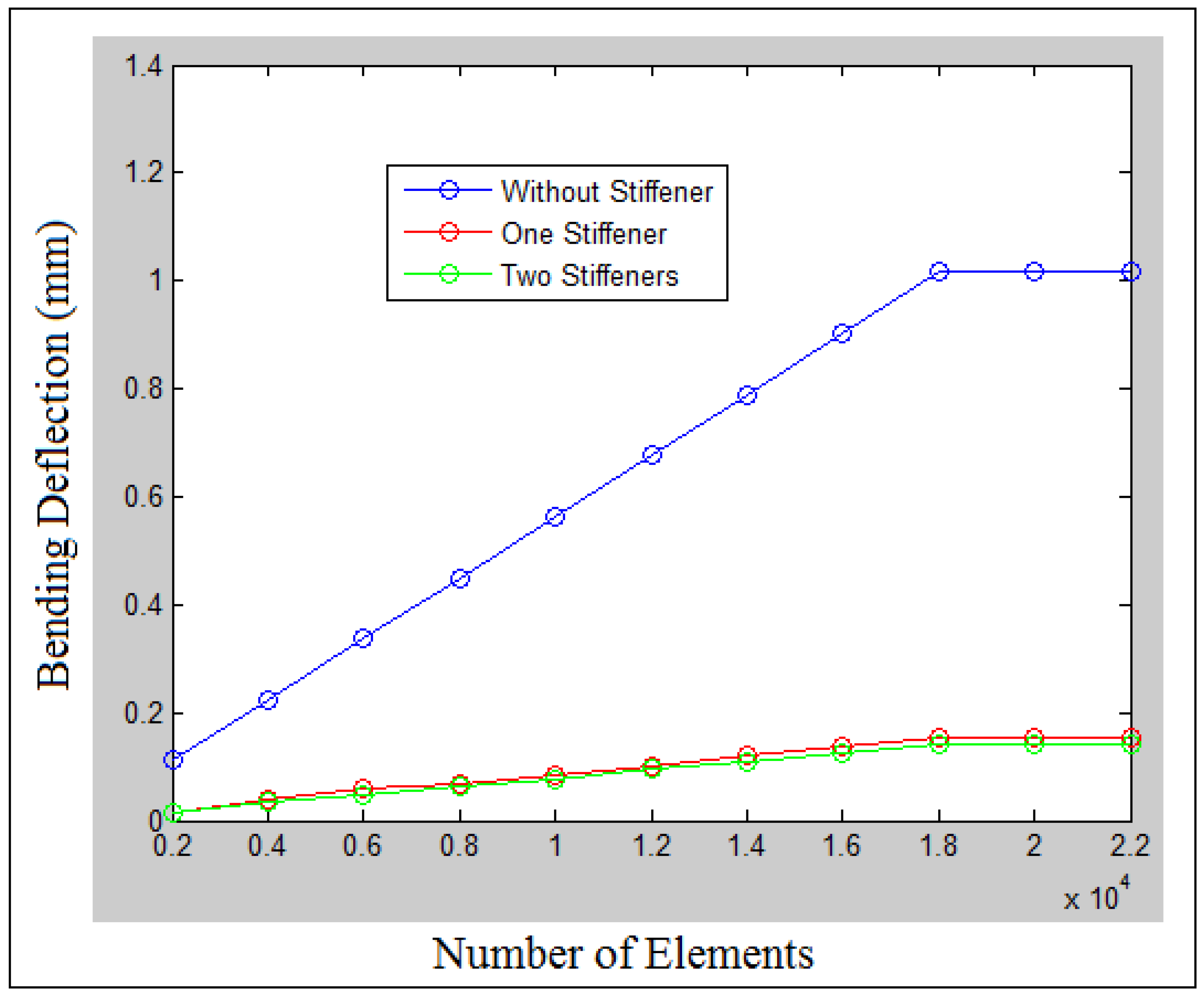

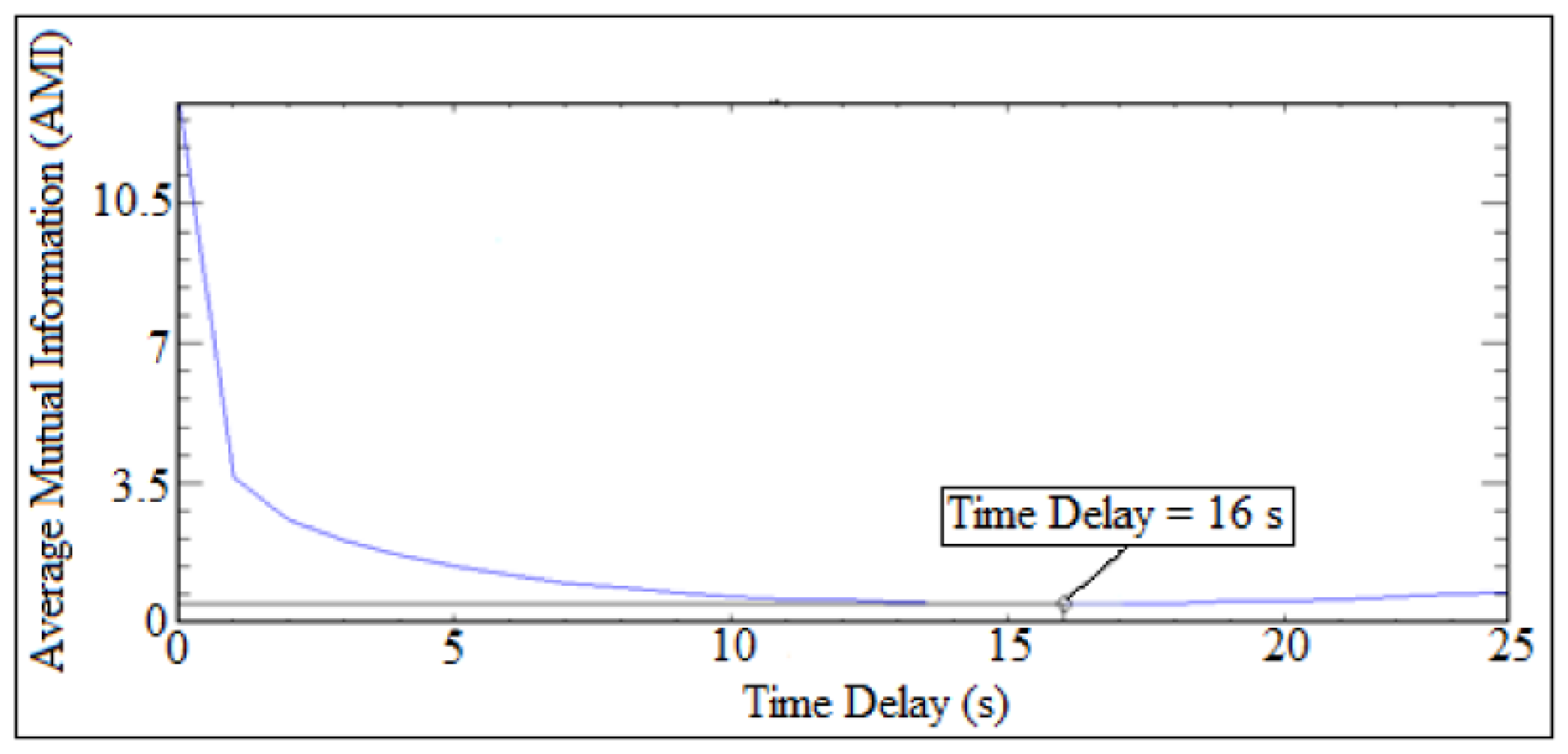
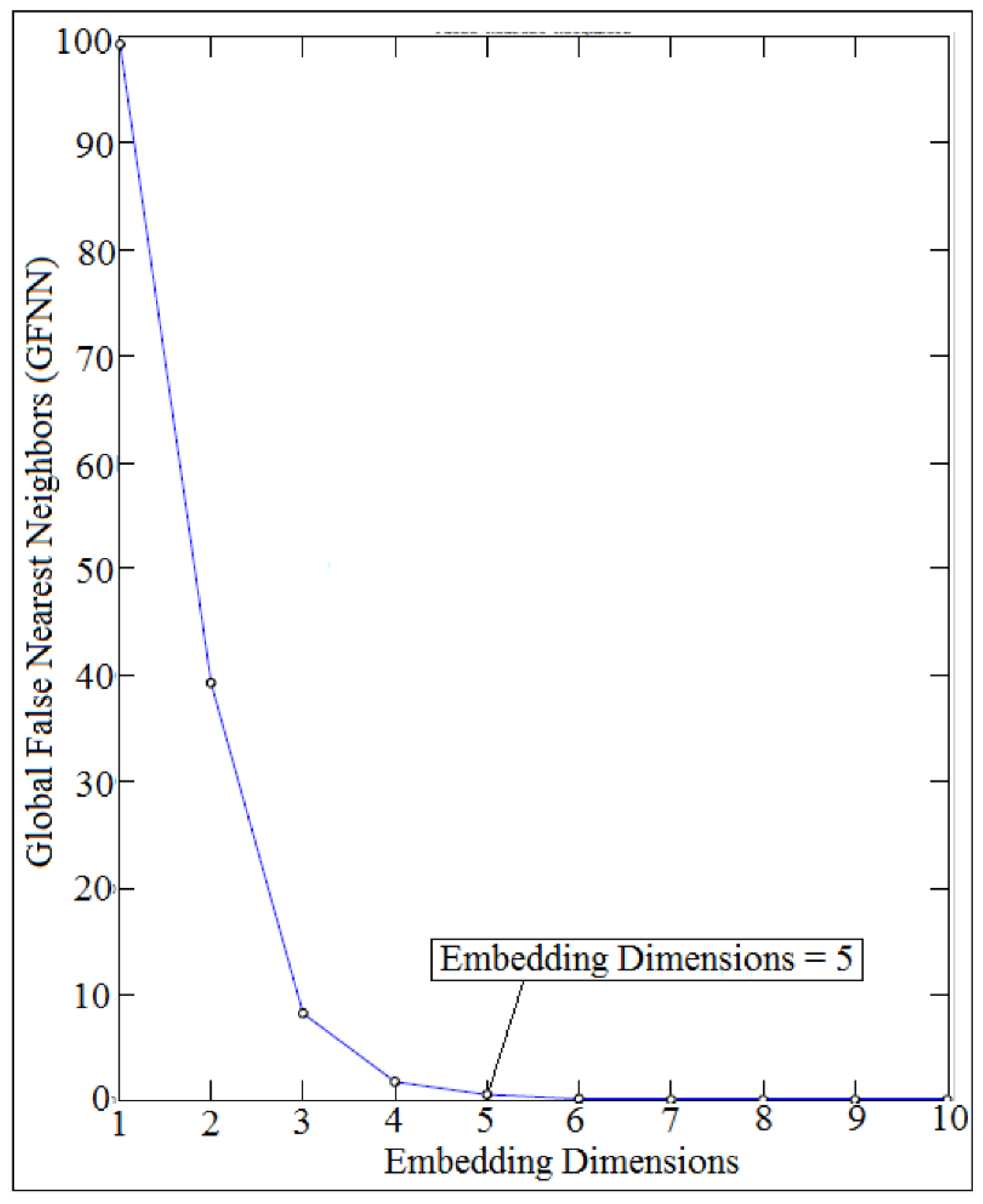

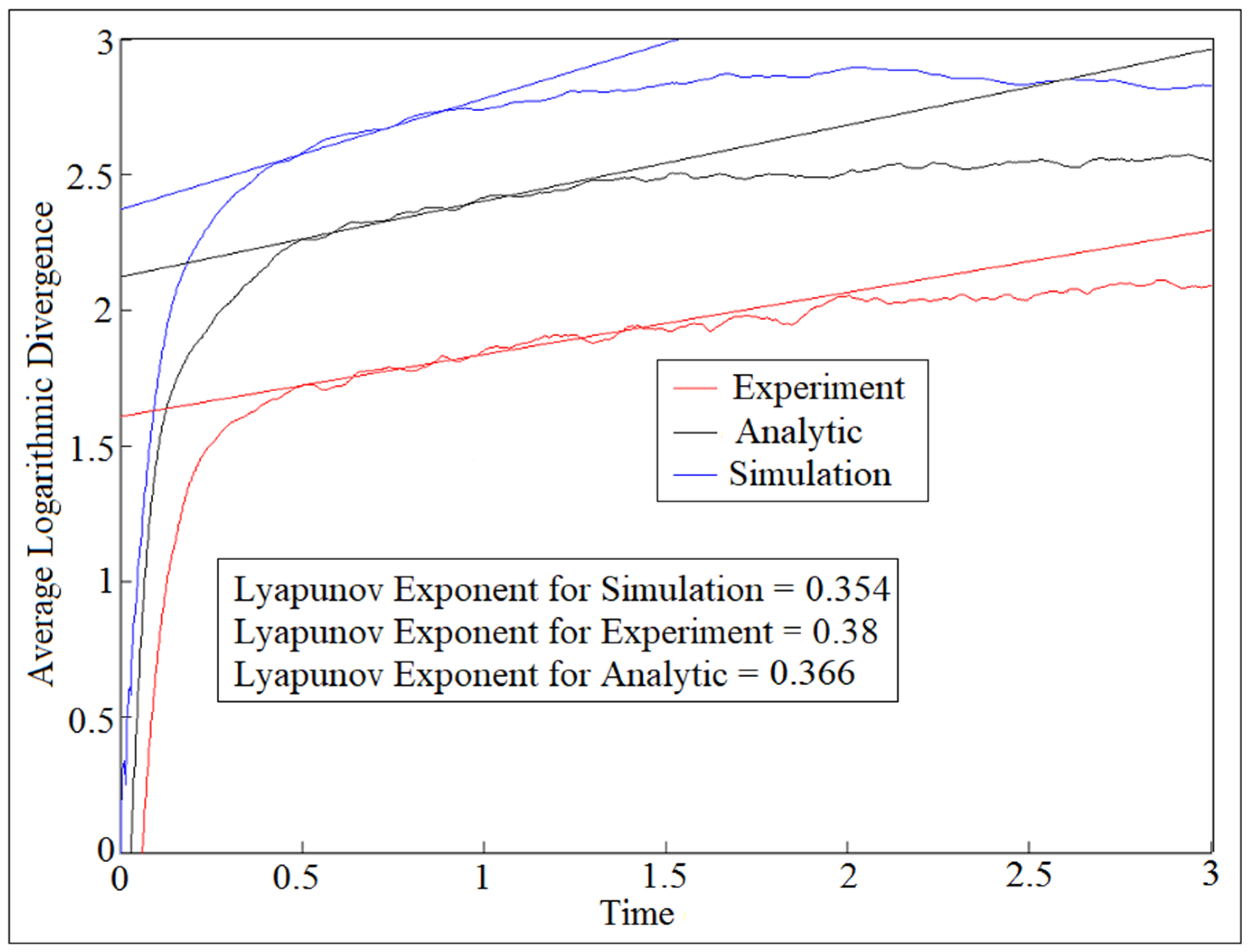
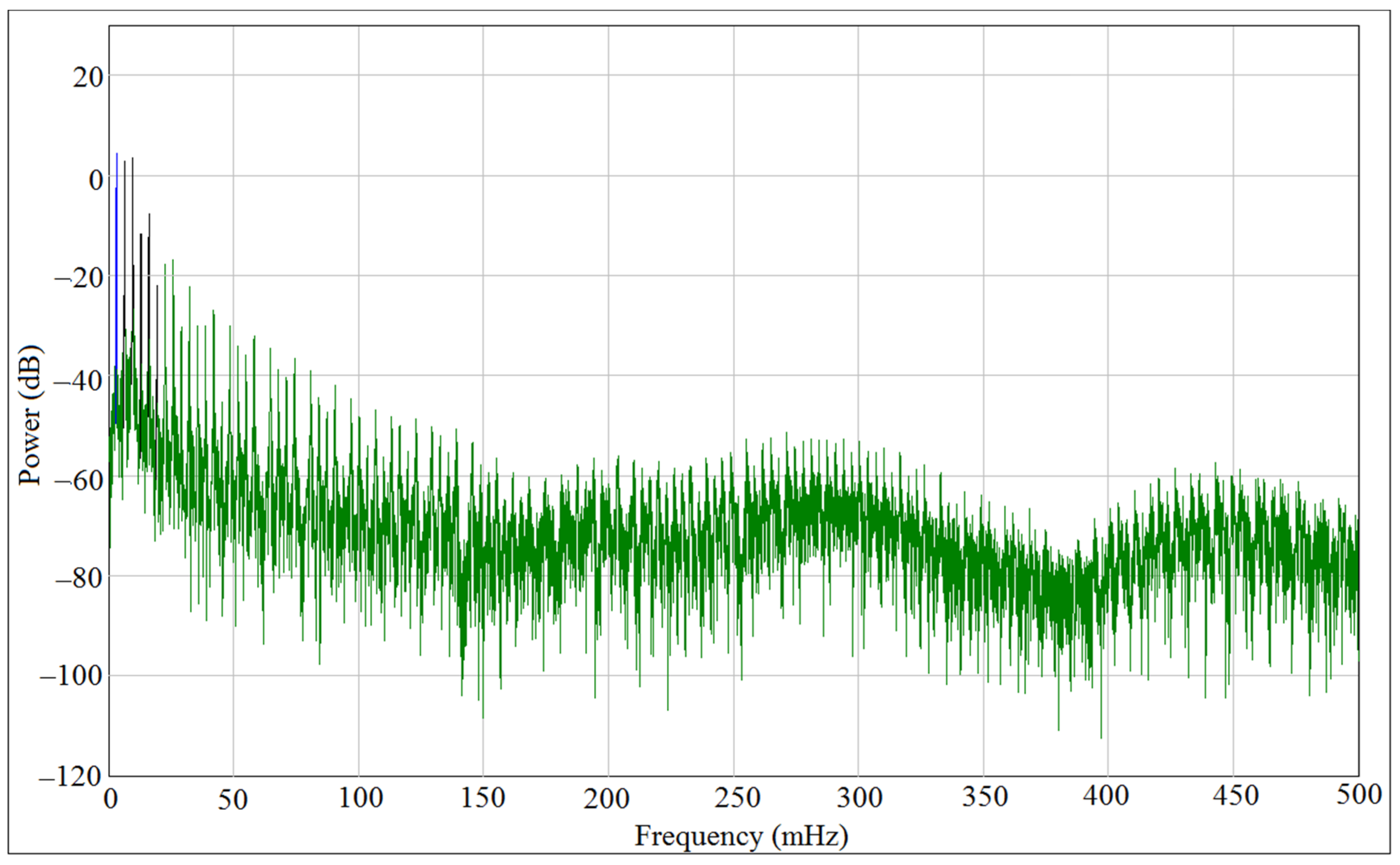
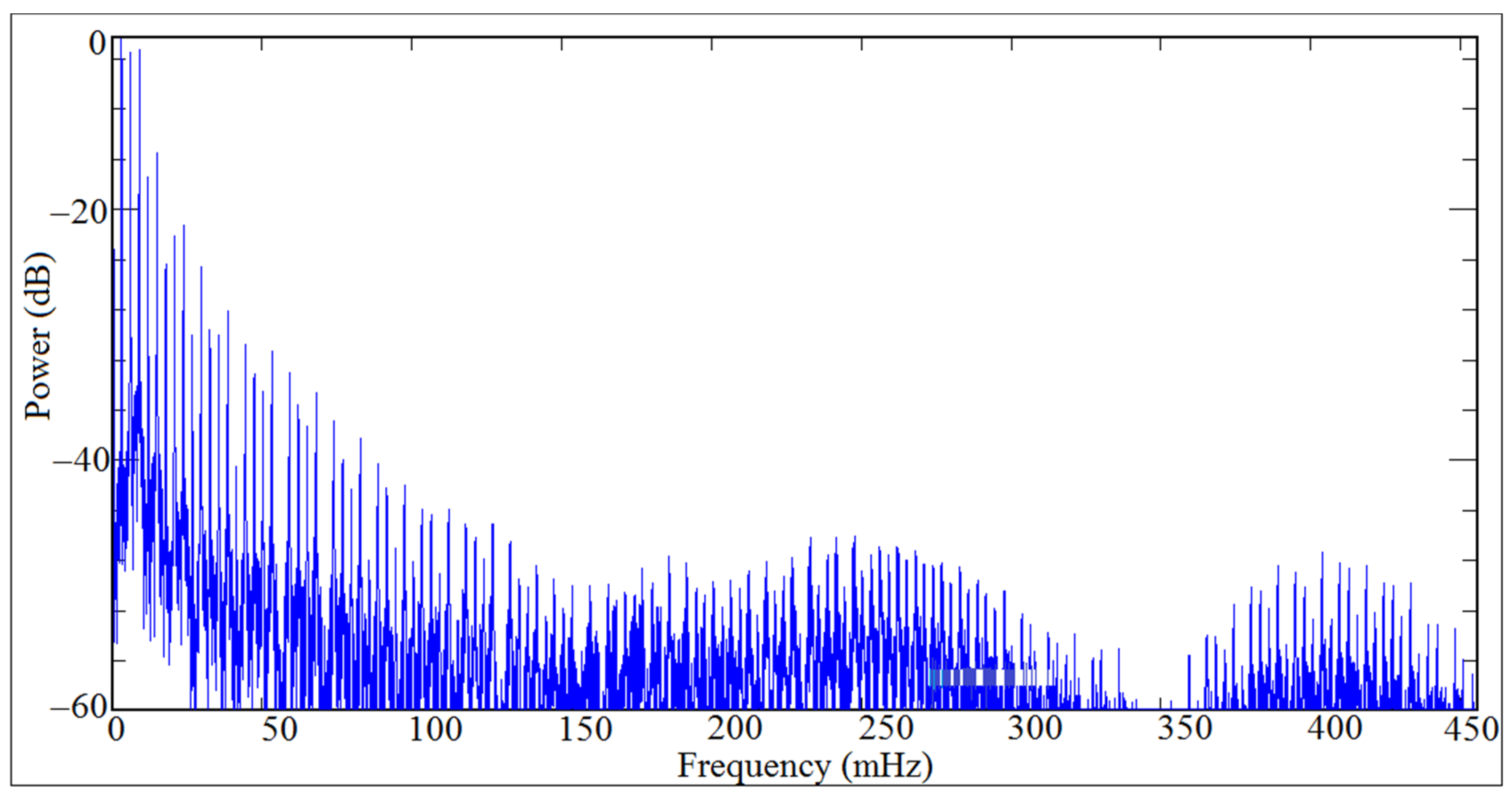
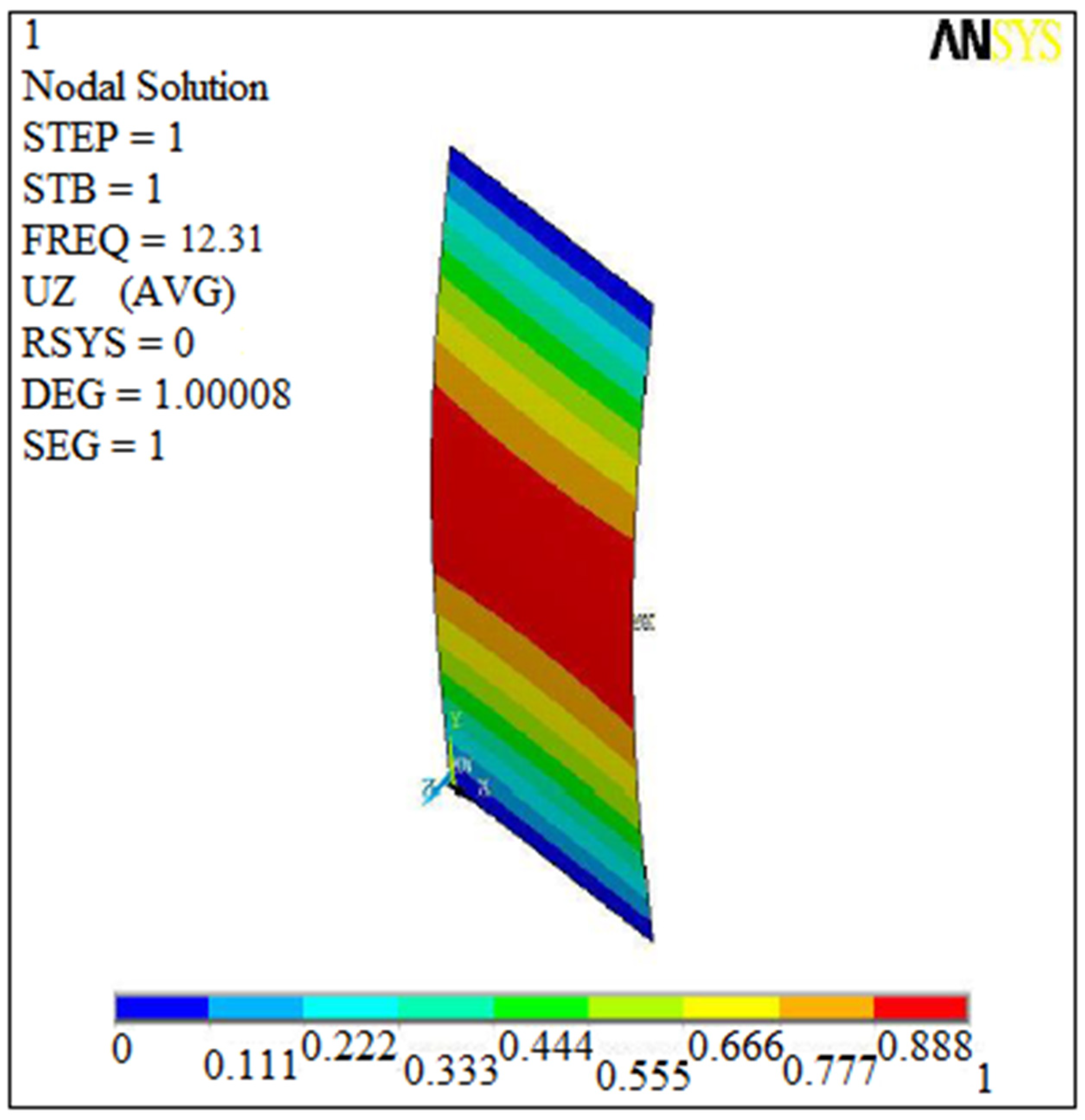

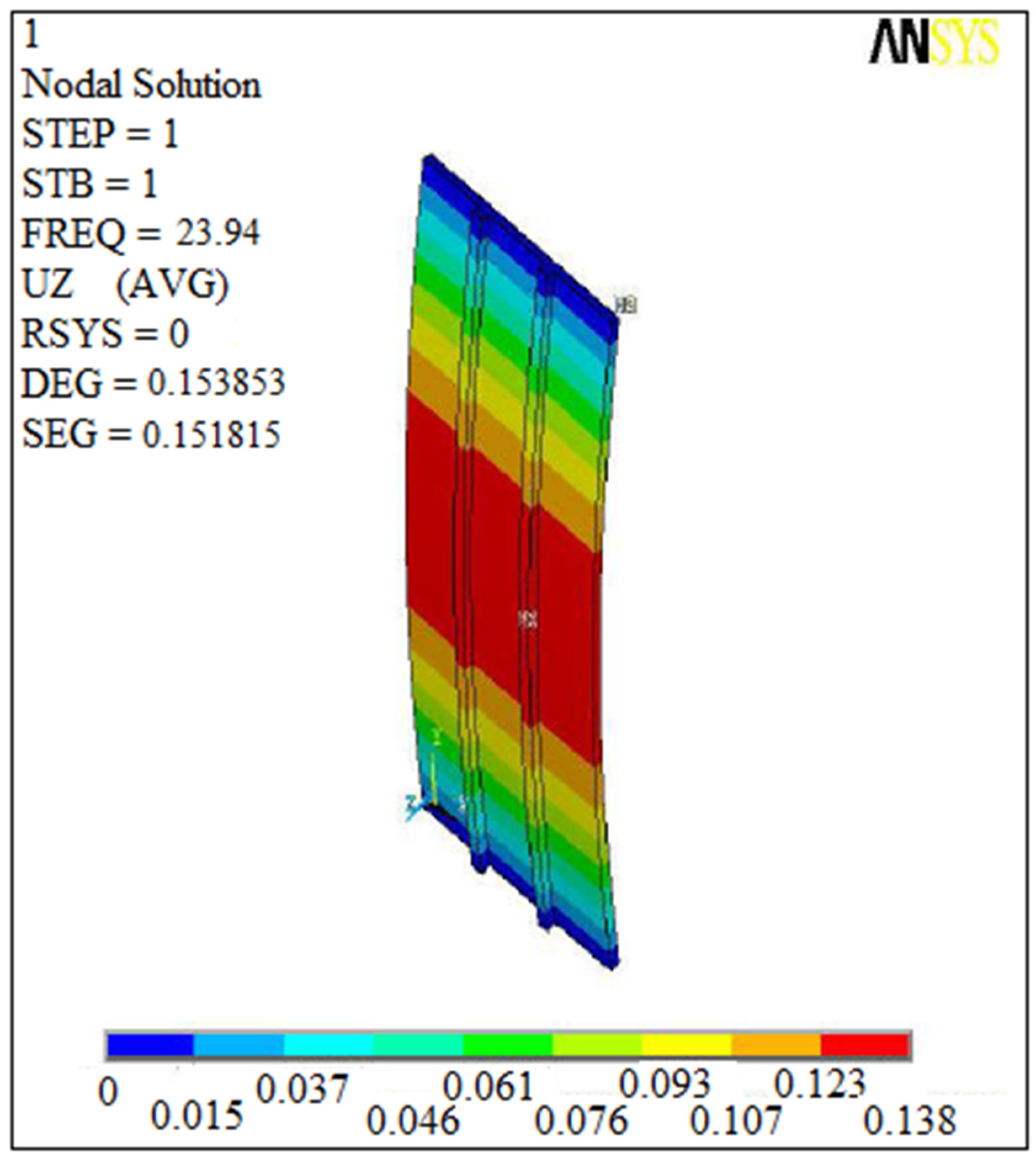

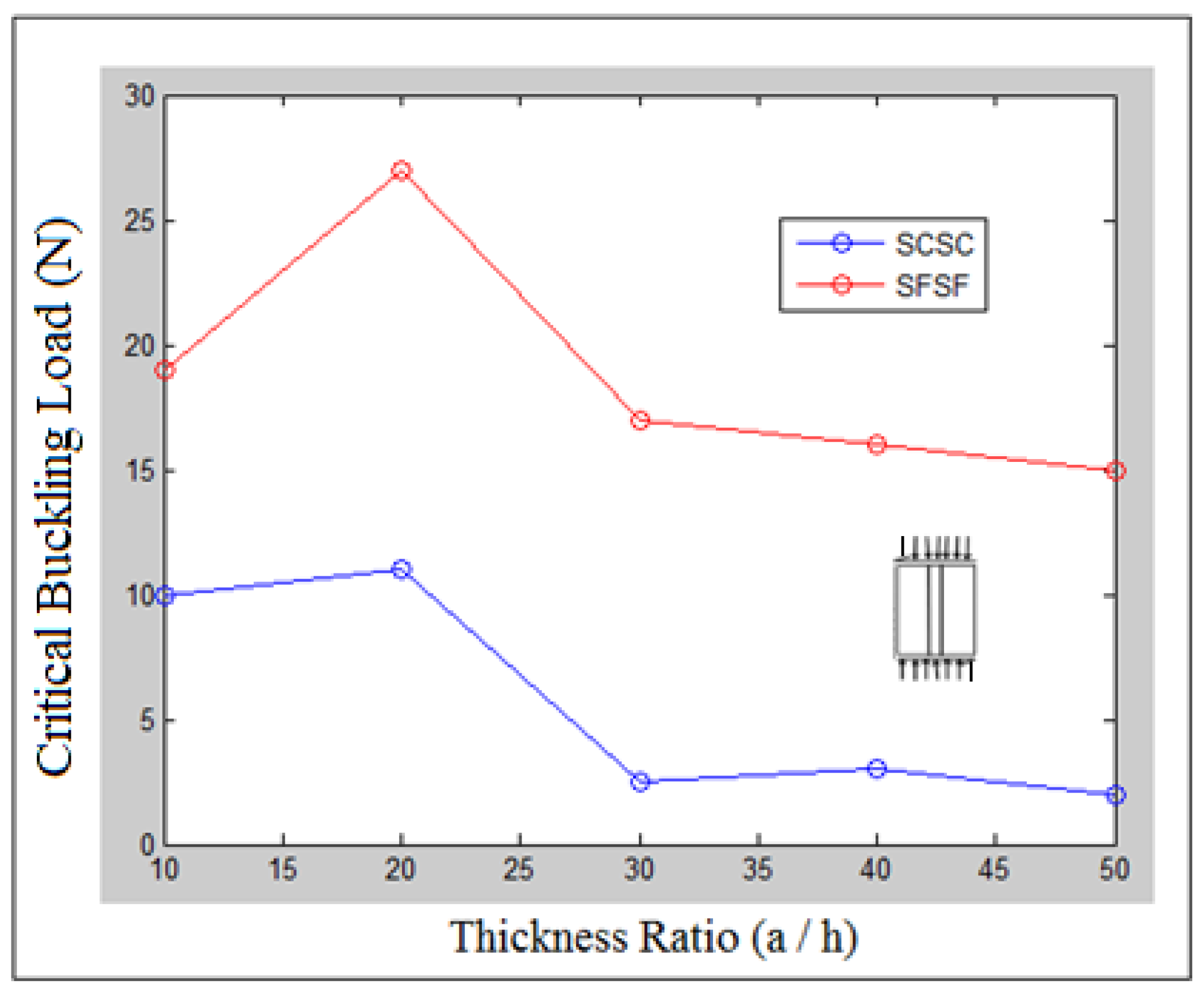
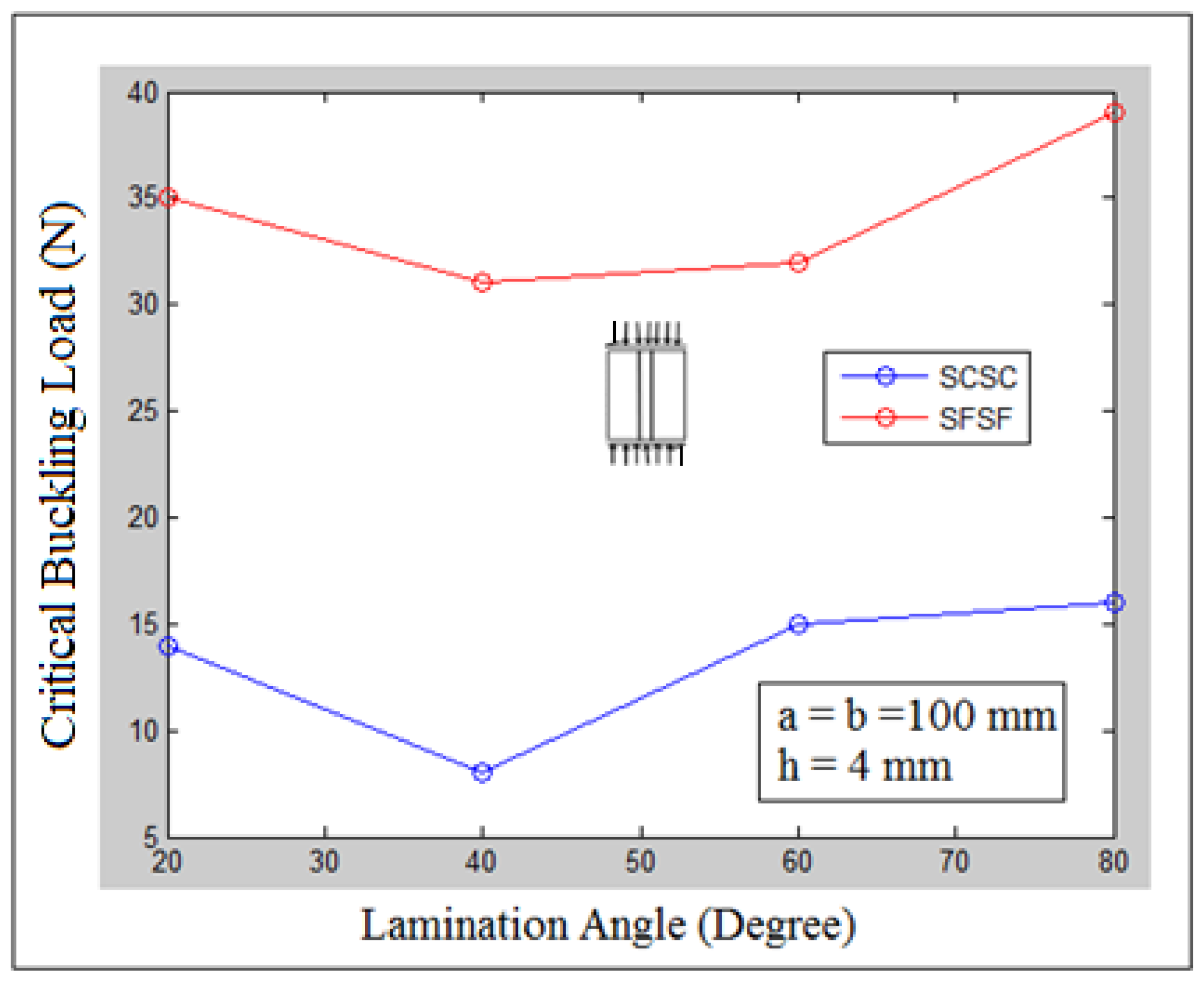
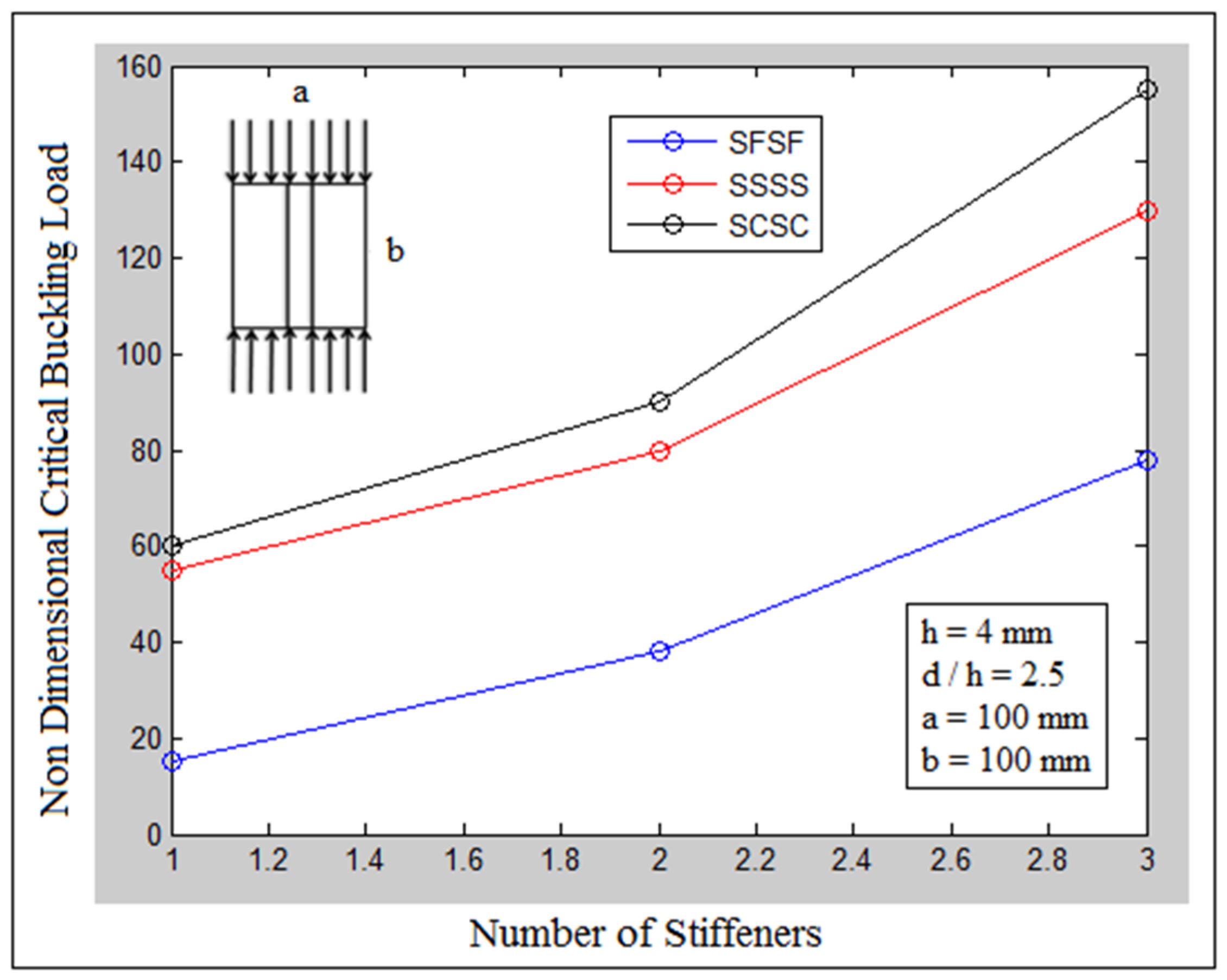
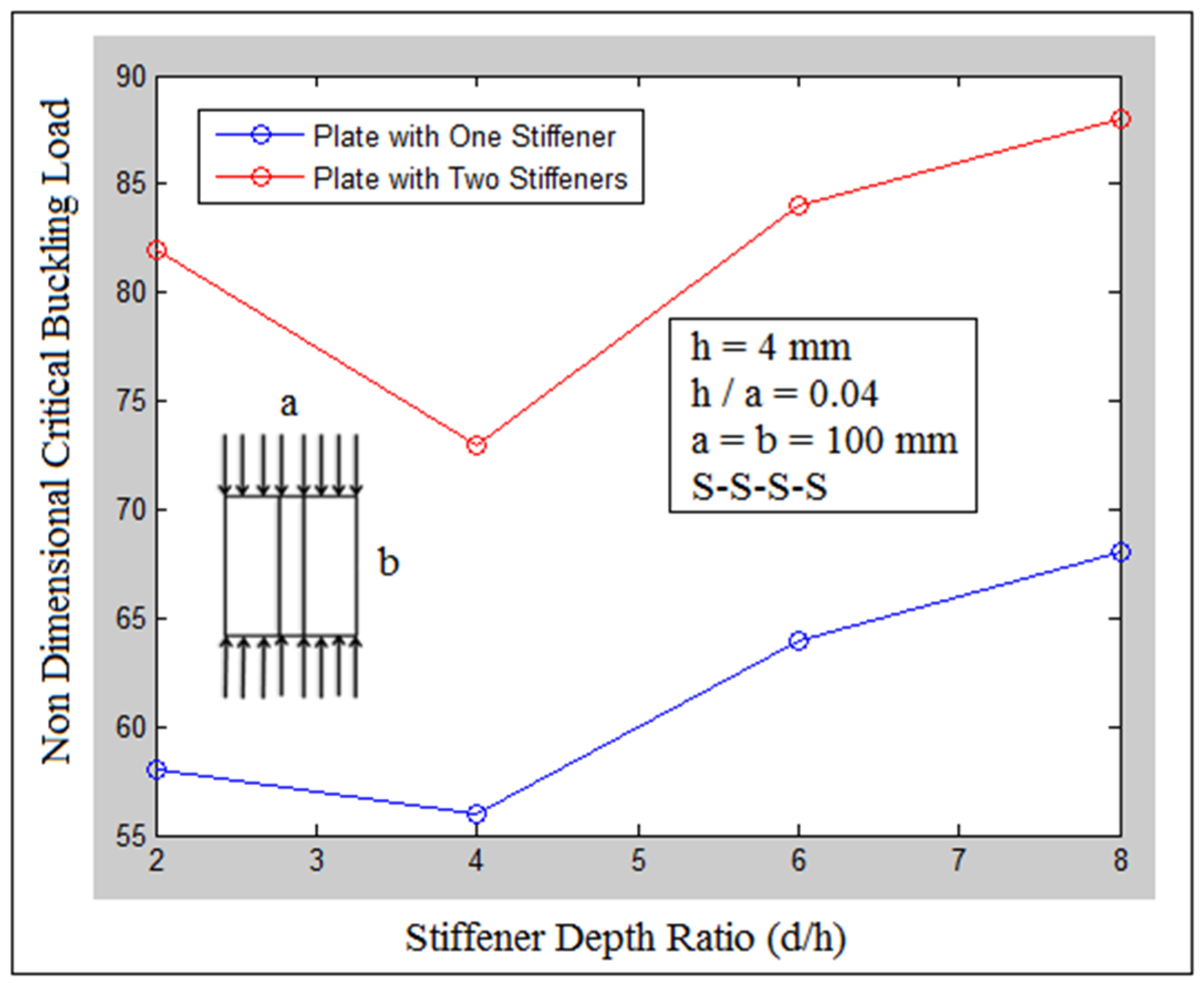
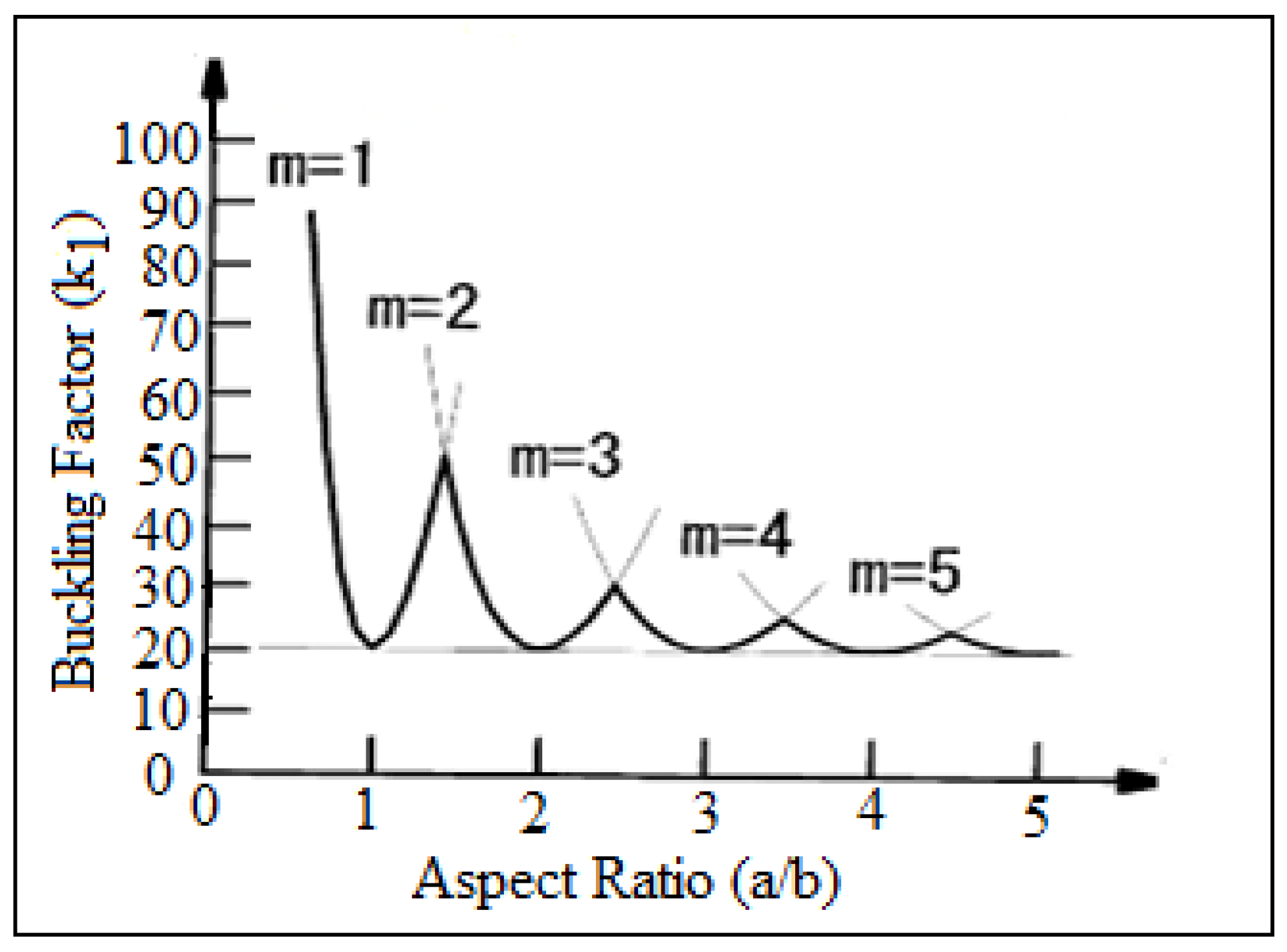
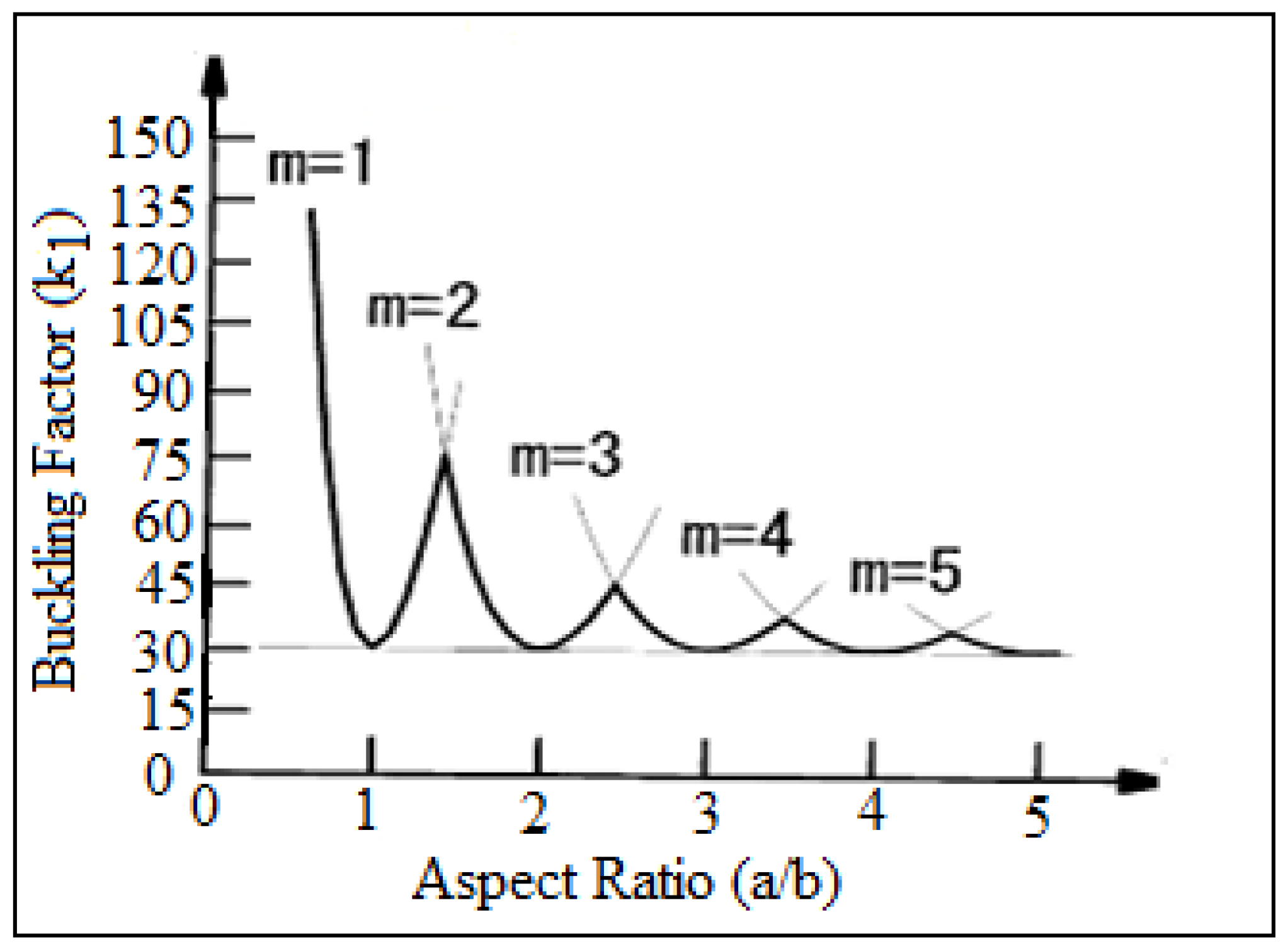
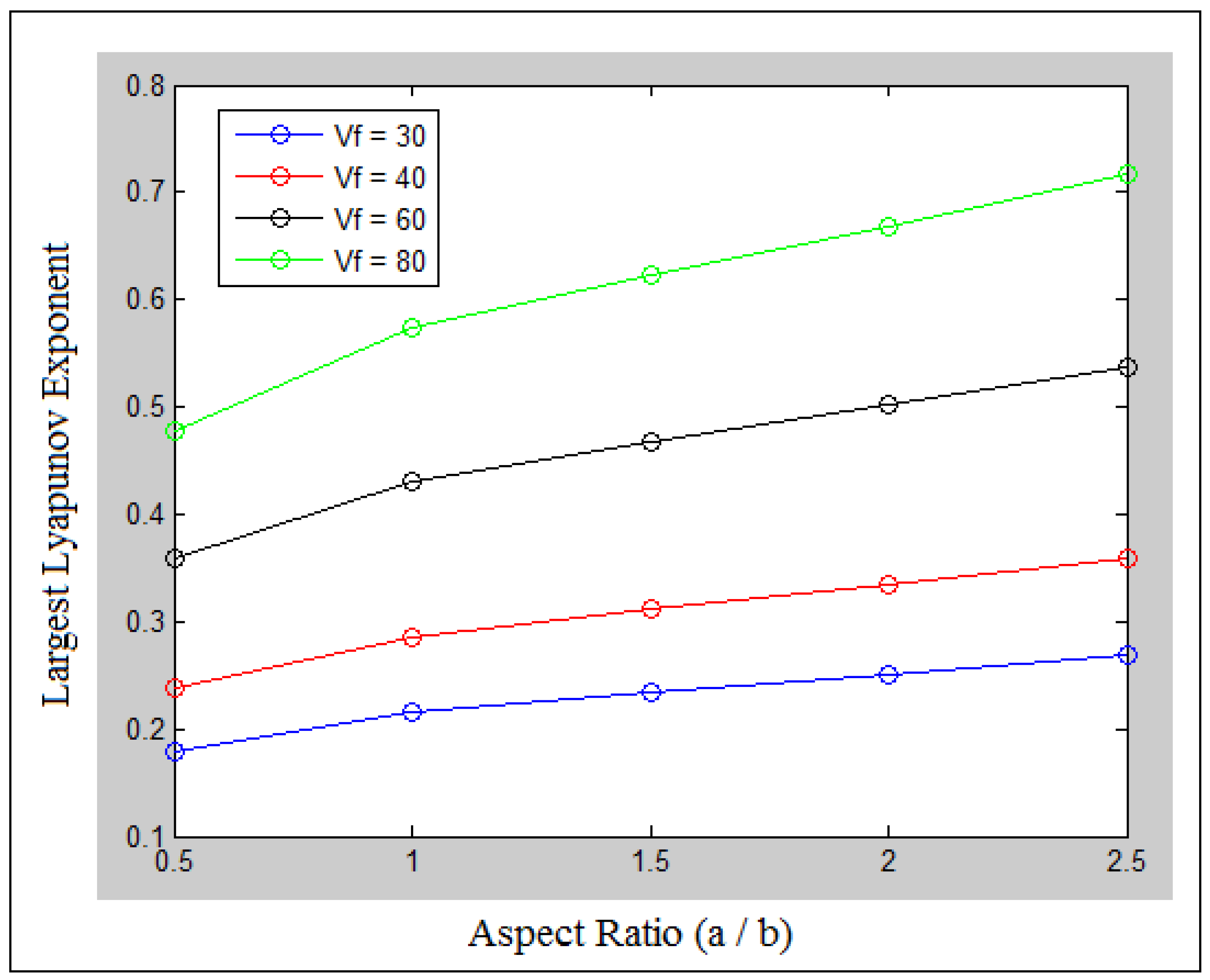
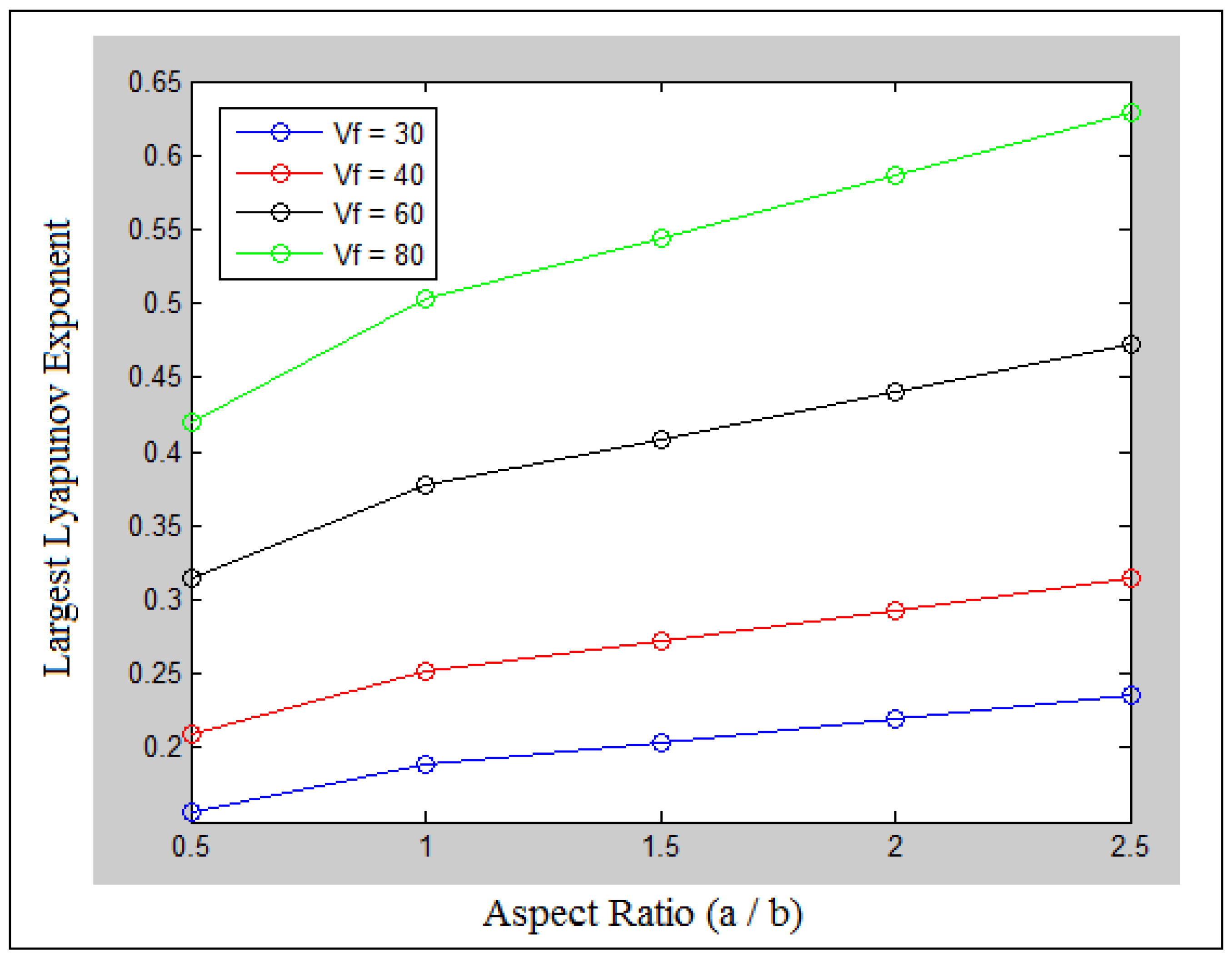
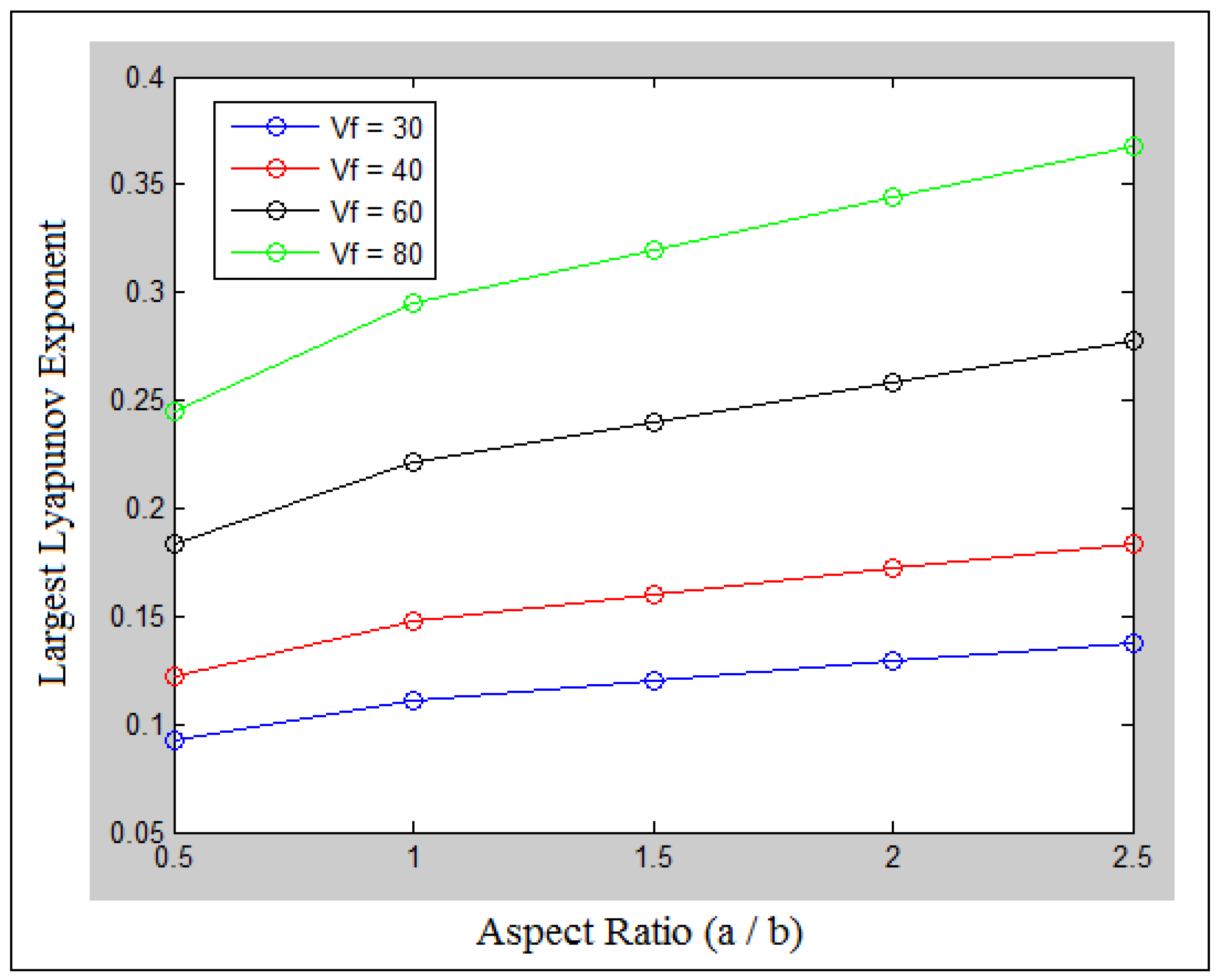


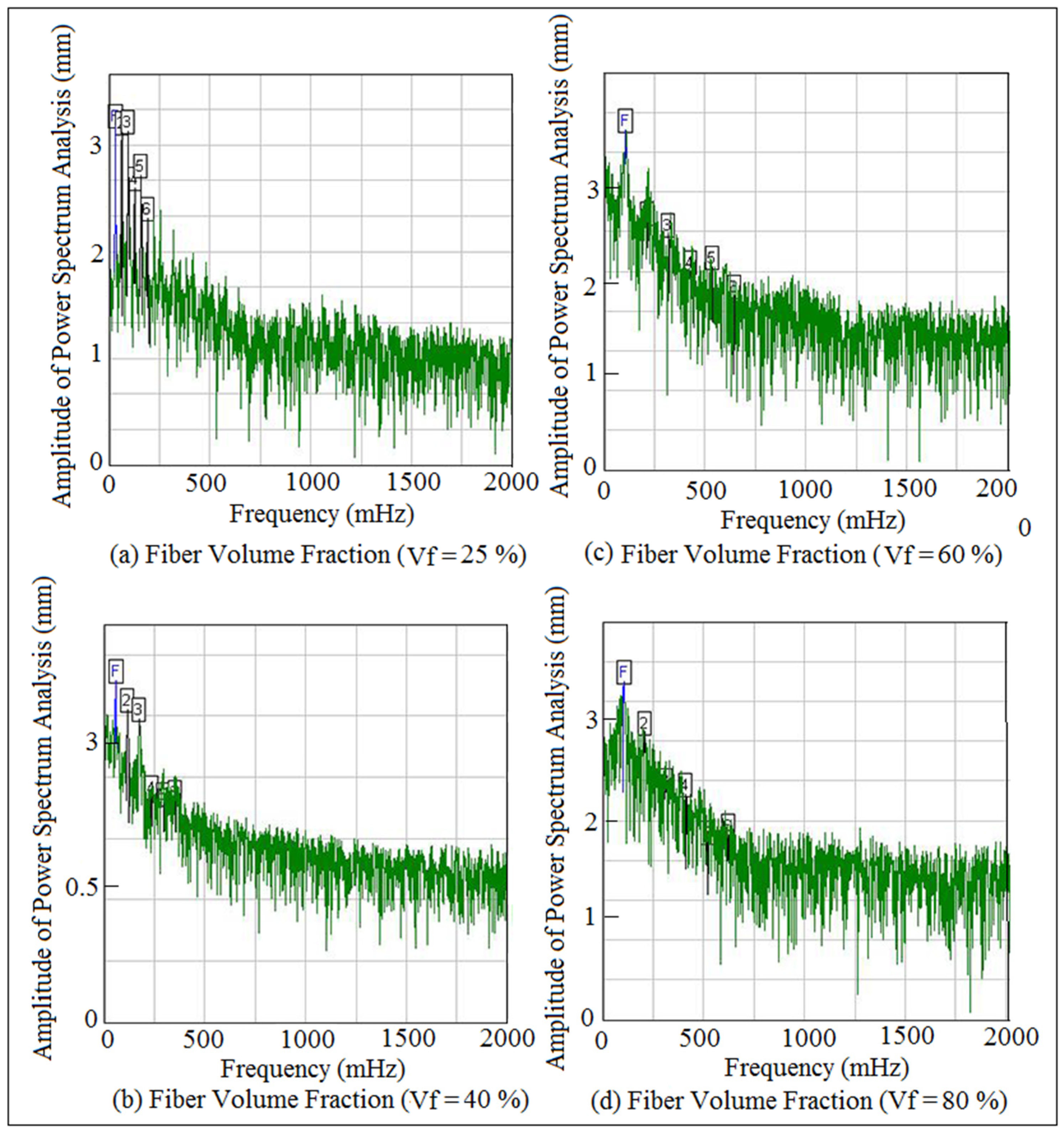

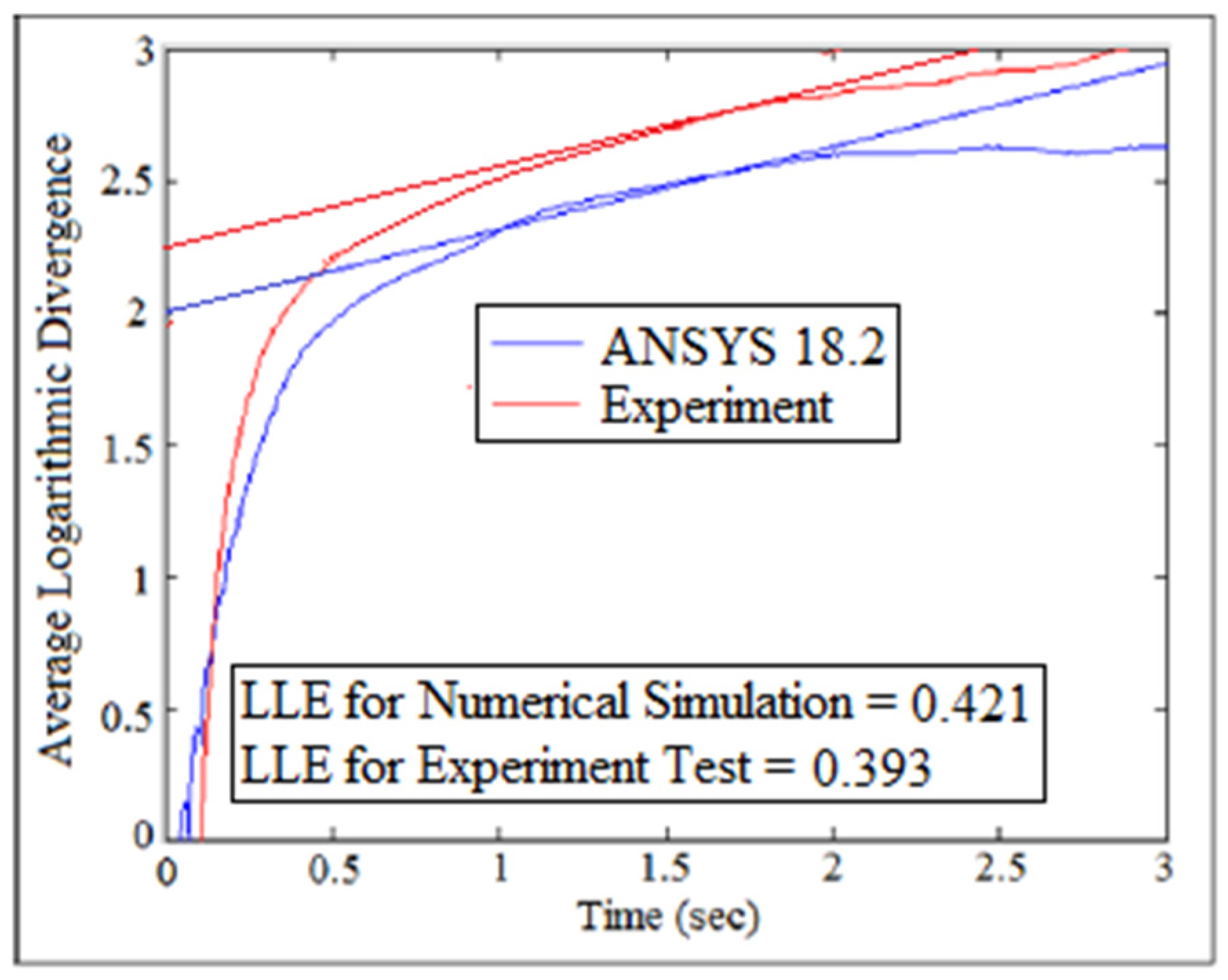
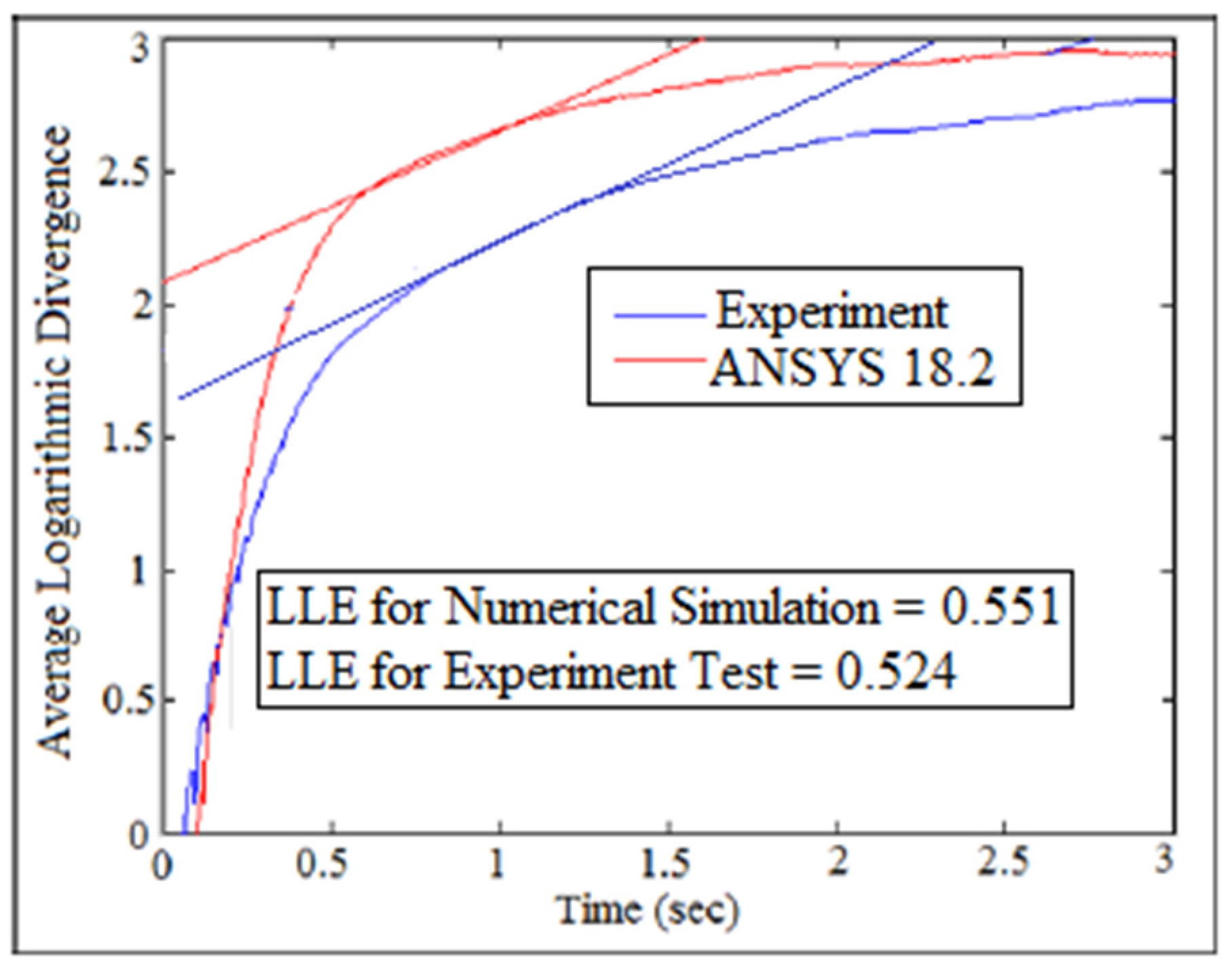
| Stiffeners | Orientation | Experiment | Numerical | Analytic |
|---|---|---|---|---|
| One Stiffener | 0/90 | 12.07 | 11.645 | 11.923 |
| 0/90/0 | 13.274 | 12.249 | 13.03 | |
| 0/90/0/90 | 29.94 | 28.944 | 29.53 | |
| 0/90/90/0 | 30.387 | 29.26 | 29.856 | |
| Two Stiffeners | 0/90 | 14.016 | 13.334 | 13.738 |
| 0/90/0 | 15.446 | 14.665 | 15.127 | |
| 0/90/0/90 | 34.046 | 33.337 | 33.691 | |
| 0/90/90/0 | 44.366 | 43.603 | 43.752 |
| The Support | One Stiffener | Two Stiffeners | ||
|---|---|---|---|---|
| Numerical | Analytic | Numerical | Analytic | |
| S-C-S-C | 247.5 | 245.23 | 264.25 | 260.18 |
| S-C-S-S | 245.1 | 242.52 | 279.74 | 276.24 |
| S-S-S-S | 220.6 | 218.24 | 228.33 | 225.79 |
| S-F-S-C | 100.8 | 97.1 | 131.25 | 126.34 |
| S-F-S-S | 118.2 | 114.97 | 133.55 | 130.25 |
| S-F-S-F | 7.43 | 7.25 | 14.544 | 13.176 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousuf, L.S. Nonlinear Dynamics Suppression of Bending Deflection in a Composite Laminated Plate Using a Beam Stiffener Due to Critical Buckling Load and Shear Force. Appl. Sci. 2022, 12, 1204. https://doi.org/10.3390/app12031204
Yousuf LS. Nonlinear Dynamics Suppression of Bending Deflection in a Composite Laminated Plate Using a Beam Stiffener Due to Critical Buckling Load and Shear Force. Applied Sciences. 2022; 12(3):1204. https://doi.org/10.3390/app12031204
Chicago/Turabian StyleYousuf, Louay S. 2022. "Nonlinear Dynamics Suppression of Bending Deflection in a Composite Laminated Plate Using a Beam Stiffener Due to Critical Buckling Load and Shear Force" Applied Sciences 12, no. 3: 1204. https://doi.org/10.3390/app12031204





