Corrected Tilt Calculation for Atmospheric Pressure-Induced Seismic Noise
Abstract
:Featured Application
Abstract
1. Introduction
2. Theory
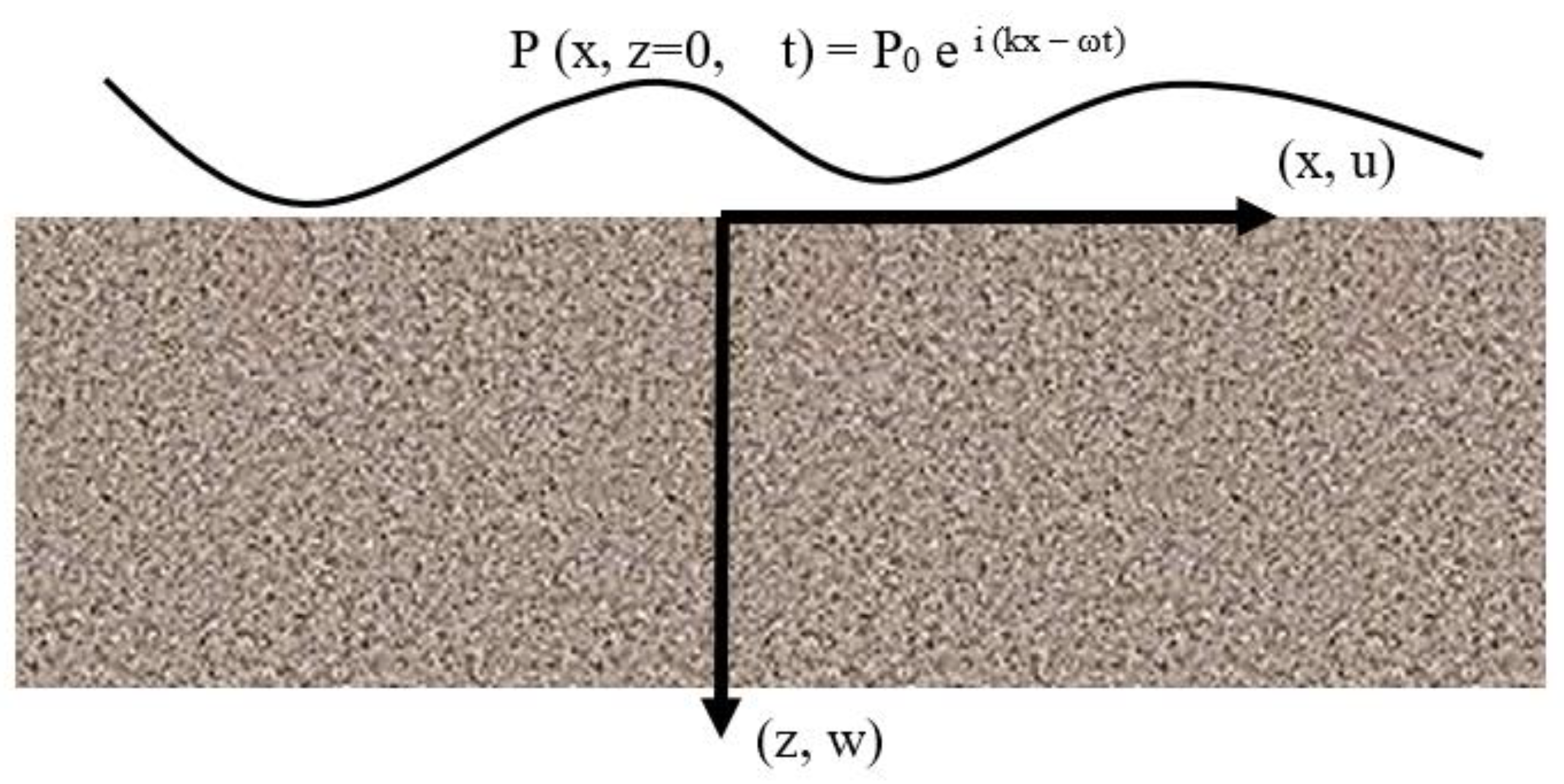
2.1. Displacement
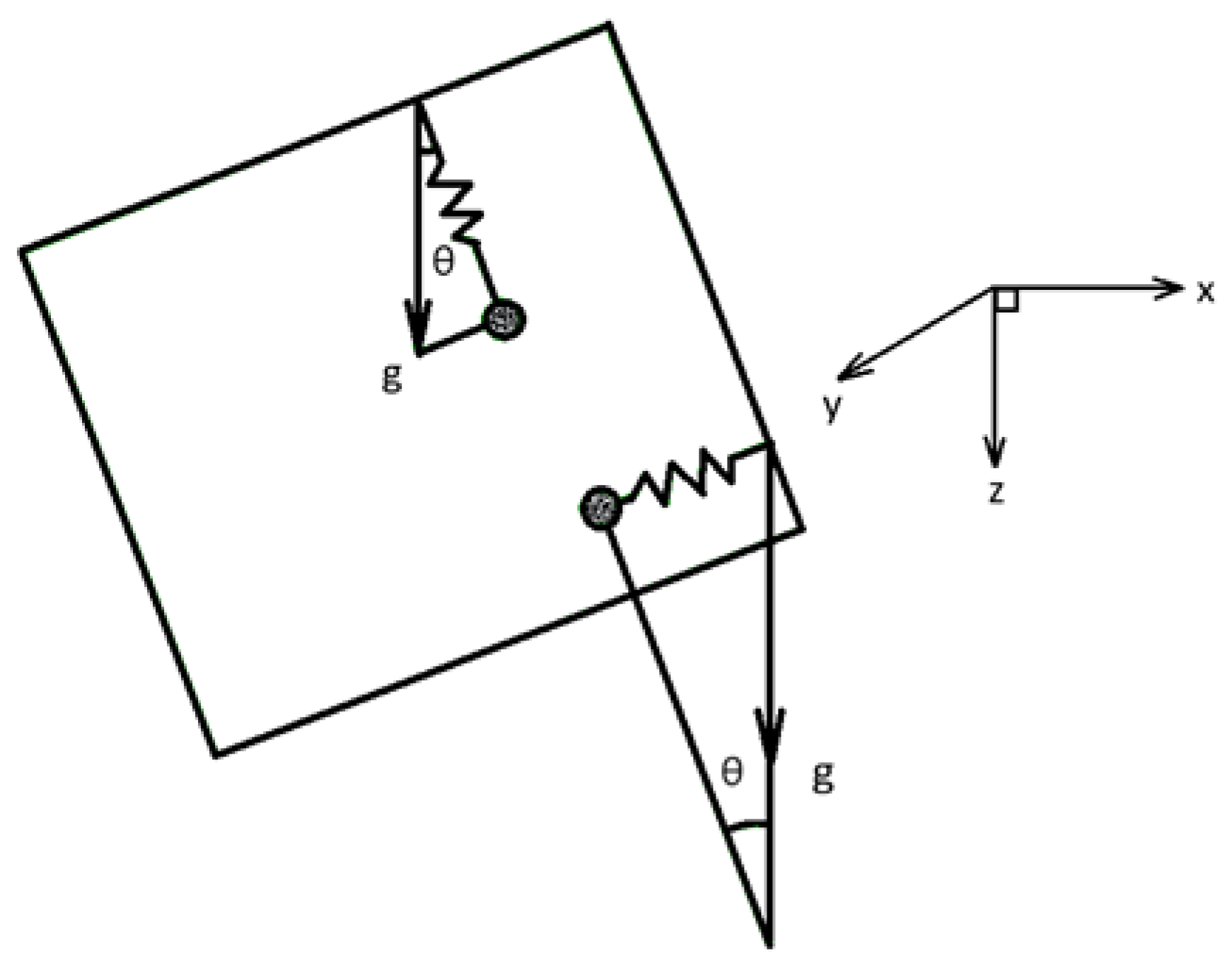
2.2. Apparent Horizontal Displacement Due to Tilt
2.3. Analytic Approximations
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Naderyan, V.; Hickey, C.J.; Raspet, R. Wind-induced ground motion. J. Geophys. Res. Solid Earth 2016, 121, 917–930. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, M.; Hickey, C.J.; Raspet, R.; Naderyan, V. Wind-induced ground motion: Dynamic model and nonuniform structure for ground. J. Geophys. Res. Solid Earth 2019, 124, 8478–8490. [Google Scholar] [CrossRef]
- Sorrells, G.G. A preliminary investigation into the relationship between long-period seismic noise and local fluctuations in the atmospheric pressure field. Geophys. J. R. Astr. Soc. 1971, 26, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Tanimoto, T.; Wang, J. Theory for deriving shallow elasticity structure from collocated seismic and pressure data. J. Geophys. Res. Solid Earth 2019, 124, 5811–5835. [Google Scholar] [CrossRef]
- Brekhovskikh, L.M. Plane Waves in Discretely Layered Media. In Waves in Layered Media, 2nd ed.; Frankiel, F.N., Temple, G., Eds.; Beyer, R.T., Translator; Academic Press: San Diego, CA, USA, 1980; pp. 1–129. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Elastic Continua. In Theoretical Mechanics of Particles and Continua; Zappa, C.R., Eichberg, M., Eds.; McGraw-Hill: New York, NY, USA, 1980; pp. 459–479. [Google Scholar]
- Release, S.T. MATLAB; The MathWorks: Natick, MA, USA, 2018. [Google Scholar]
- Altmann, J. Acoustic-seismic detection of ballistic-missile launches for cooperative early warning of nuclear attack. Sci. Glob. Secur. 2005, 13, 129–168. [Google Scholar] [CrossRef]
- Ansari, A.; Hosseini, K.A. Broadband seismic network of Iran and increasing quality of seismic recordings. Seismol. Res. Lett. 2014, 85, 878–888. [Google Scholar] [CrossRef]
- Anthony, R.E.; Aster, R.C.; Ryan, S.; Rathburn, S.; Baker, M.G. Measuring mountain river discharge using seismographs emplaced within the hyporheic zone. J. Geophys. Res. Earth Surf. 2018, 123, 210–228. [Google Scholar] [CrossRef]
- Anthony, R.E.; Aster, R.C.; Weins, D.; Nyblade, A.; Anandakrishnan, S.; Huerta, A.; Winberry, J.P.; Wilson, T.; Rowe, C. The seismic noise environment of Antarctica. Seismol. Res. Lett. 2014, 86, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Barruol, G.; Reymond, D.; Fontaine, F.R.; Hyvernaud, O.; Maurer, V.; Maamaatuaiahutapu, K. Characterizing swells in the southern Pacific from seismic and infrasonic noise analyses. Geophys. J. Int. 2006, 164, 516–542. [Google Scholar] [CrossRef] [Green Version]
- Beauduin, R.; Lognonné, P.; Montagner, J.P.; Cacho, S.; Karczewski, J.F.; Morand, M. The effects of the atmospheric pressure changes on seismic signals or how to improve the quality of a station. Bull. Seismol. Soc. Am. 1996, 86, 1760–1769. [Google Scholar] [CrossRef]
- Block, B.; Dratler, J., Jr. Improvements in the wide-band vertical quartz torsion accelerometer. J. Geophys. Res. 1972, 77, 3678–3689. [Google Scholar] [CrossRef]
- Bodin, P.; Smith, K.; Horton, S.; Hwang, H. Microtremor observations of deep sediment resonance in metropolitan Memphis, Tennessee. Eng. Geol. 2001, 62, 159–168. [Google Scholar] [CrossRef]
- Díaz, J. On the origin of the signals observed across the seismic spectrum. Earth-Sci. Rev. 2016, 161, 224–232. [Google Scholar] [CrossRef] [Green Version]
- Díaz, J.; Villaseñor, A.; Morales, J.; Pazos, A.; Córdoba, D.; Pulgar, J.; García-Lobón, J.L.; Harnafi, M.; Carbonell, R.; Gallart, J. Background noise characteristics at the IberArray broadband seismic network. Bull. Seismol. Soc. Am. 2010, 100, 618–628. [Google Scholar] [CrossRef] [Green Version]
- Dratler, J.; Block, B. A wide band horizontal accelerometer with preliminary Earth normal mode and seismic investigations. Geophys. J. Int. 1972, 27, 337–367. [Google Scholar] [CrossRef] [Green Version]
- Duputel, Z.; Rivera, L.; Fukahata, Y.; Kanamori, H. Uncertainty estimations for seismic source inversions. Geophys. J. Int. 2012, 190, 1243–1256. [Google Scholar] [CrossRef] [Green Version]
- Gebauer, A.; Kroner, C.; Jahr, T. The influence of topographic and lithologic features on horizontal deformations. Geophys. J. Int. 2009, 177, 586–602. [Google Scholar] [CrossRef] [Green Version]
- Gebauer, A.; Steffen, H.; Kroner, C.; Jahr, T. Finite element modelling of atmosphere loading effects on strain, tilt and displacement at multi-sensor stations. Geophys. J. Int. 2010, 181, 1593–1612. [Google Scholar] [CrossRef] [Green Version]
- Goodman, D.; Yamamoto, T.; Trevorrow, M.; Abbott, C.; Turgut, A.; Badiey, M.; Ando, K. Directional spectra observations of seafloor microseisms from an ocean-bottom seismometer array. J. Acoust. Soc. Am. 1989, 86, 2309–2317. [Google Scholar] [CrossRef]
- Green, D.N.; Le Pichon, A.; Ceranna, L.; Evers, L. Ground Truth Events: Assessing the Capability of Infrasound Networks Using High Resolution Data Analyses. In Infrasound Monitoring for Atmospheric Studies; Le Pichon, A., Blanc, E., Hauchorne, A., Eds.; Springer: Dordrecht, Switzerland, 2010; pp. 599–625. [Google Scholar]
- Hu, W.; Pryor, S.C.; Letson, F.; Tytell, J.; Barthelmie, R.J. Investigation of gust-seismic relationships and applications to gust detection. J. Geophys. Res. Atmos. 2017, 122, 140–151. [Google Scholar] [CrossRef]
- Hutt, C.R.; Ringler, A.T.; Gee, L.S. Broadband seismic noise attenuation versus depth at the Albuquerque seismological laboratory. Bull. Seismol. Soc. Am. 2017, 107, 1402–1412. [Google Scholar] [CrossRef]
- Johnson, C.W.; Meng, H.; Vernon, F.; Ben-Zion, Y. Characteristics of ground motion generated by wind interaction with trees, structures, and other surface obstacles. J. Geophys. Res. Solid Earth 2019, 124, 8519–8539. [Google Scholar] [CrossRef]
- Kroner, C.; Jahr, T.; Kuhlmann, S.; Fischer, K.D. Pressure-induced noise on horizontal seismometer and strainmeter records evaluated by finite element modelling. Geophys. J. Int. 2005, 161, 167–178. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Li, Y.; Yang, B. Seismic exploration random noise on land: Modeling and application to noise suppression. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4668–4681. [Google Scholar] [CrossRef]
- Mauk, F.J.; Mahrer, K.D. Use of long-period seismometers to determine induced fracture geometry. SPE Prod. Eng. 1988, 3, 192–200. [Google Scholar] [CrossRef]
- Mucciarelli, M.; Gallipoli, M.R.; Di Giacomo, D.; Di Nota, F.; Nino, E. The influence of wind on measurements of seismic noise. Geophys. J. Int. 2005, 161, 303–308. [Google Scholar] [CrossRef]
- Panou, A.A.; Theodulidis, N.P.; Hatzidimitriou, P.M.; Savvaidis, A.S.; Papazachos, C.B. Reliability of ambient noise horizontal-to-vertical spectral ratio in urban environments: The case of Thessaloniki City (Northern Greece). Pure Appl. Geophys. 2005, 162, 891–912. [Google Scholar] [CrossRef]
- Ringler, A.T.; Wilson, D.C.; Zürn, W.; Anthony, R.E. Rayleigh wave ellipticity measurement uncertainty across the IRIS/USGS and New China Digital Seismograph Networks. Geophys. J. Int. 2018, 217, 219–237. [Google Scholar] [CrossRef]
- Rohde, M.D.; Ringler, A.T.; Hutt, C.R.; Wilson, D.C.; Holland, A.A.; Sandoval, L.D.; Storm, T. Characterizing local variability in long-period horizontal tilt noise. Seismol. Res. Lett. 2017, 88, 822–830. [Google Scholar] [CrossRef]
- Rouland, D.; Condis, C.; Roult, G. Overlooked earthquakes on and around the Antarctica plate: Identification and location of 1999 shallow depth events. Tectonophysics 2003, 376, 1–17. [Google Scholar] [CrossRef]
- Roult, G.; Crawford, W. Analysis of ‘background’ free oscillations and how to improve resolution by subtracting the atmospheric pressure signal. Phys. Earth Planet. Inter. 2000, 121, 325–338. [Google Scholar] [CrossRef]
- Steffen, H.; Kuhlmann, S.; Jahr, T.; Kroner, C. Numerical modelling of the barometric pressure-induced noise in horizontal components for the observatories Moxa and Schiltach. J. Geodyn. 2006, 41, 242–252. [Google Scholar] [CrossRef]
- Steim, J.M. Theory and Observations-Instrumentation for Global and Regional Seismology. In Treatise on Geophysics: Volume 1 Deep Earth Seismology; Romanowicz, B., Dziewonski, A., Eds.; Elsevier Science: San Diego, CA, USA, 2015; pp. 29–74. [Google Scholar]
- Stutzmann, E.; Roult, G.; Astiz, L. GEOSCOPE station noise levels. Bull. Seismol. Soc. Am. 2000, 90, 690–701. [Google Scholar] [CrossRef]
- Suda, N.; Nawa, K.; Fukao, Y. Earth’s background free oscillations. Science 1998, 279, 2089–2091. [Google Scholar] [CrossRef] [Green Version]
- Tanimoto, T. Interaction of solid Earth, atmosphere, and ionosphere. Treatise Geophys. 2007, 4, 421–444. [Google Scholar]
- Tanimoto, T.; Valovcin, A. Existence of the threshold pressure for seismic excitation by atmospheric disturbances. Geophys. Res. Lett. 2016, 43, 11–202. [Google Scholar] [CrossRef] [Green Version]
- Tape, C.; Christensen, D.; Moore-Driskell, M.M.; Sweet, J.; Smith, K. Southern Alaska Lithosphere and Mantle Observation Network (SALMON): A seismic experiment covering the active arc by road, boat, plane, and helicopter. Seismol. Res. Lett. 2017, 88, 1185–1202. [Google Scholar] [CrossRef]
- Valovcin, A.; Tanimoto, T. Modeling the excitation of seismic waves by the Joplin tornado. Geophys. Res. Lett. 2017, 44, 10–256. [Google Scholar] [CrossRef]
- Vila, J.; Macià, R. The broadband seismic station CADI (Tunel del Cadi, Eastern Pyrenees), part II: Long-period variations of background noise. Bull. Seismol. Soc. Am. 2002, 92, 3329–3334. [Google Scholar] [CrossRef]
- Webb, S.C. Broadband seismology and noise under the ocean. Rev. Geophys. 1998, 36, 105–142. [Google Scholar] [CrossRef]
- Widmer, R.; Zürn, W.; Masters, G. Observation of low-order toroidal modes from the 1989 Macquarie Rise event. Geophys. J. Int. 1992, 111, 226–236. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Ni, S.; Tape, C. Multipathing Rayleigh waves from long-distance noise cross correlation along an ocean-continent boundary (Alaska to California). Geophys. Res. Lett. 2018, 45, 6051–6060. [Google Scholar] [CrossRef]
- Yang, C.F.; Chi, W.C.; Lai, Y.J. Seismically detected ground tilts Induced by precipitation and fluvial processes: An example from Taiwan. J. Geophys. Res. Solid Earth 2018, 123, 4814–4828. [Google Scholar] [CrossRef]
- Yang, Z.; Sheehan, A.F.; Collins, J.A.; Laske, G. The character of seafloor ambient noise recorded offshore New Zealand: Results from the MOANA ocean bottom seismic experiment. Geochem. Geophys. Geosyst. 2012, 13, 10011. [Google Scholar] [CrossRef] [Green Version]
- Adair, R.G.; Orcutt, J.A.; Jordan, T.H. Low-frequency noise observations in the deep ocean. J. Acoust. Soc. Am. 1986, 80, 633–645. [Google Scholar] [CrossRef]
- Custódio, S.; Dias, N.A.; Caldeira, B.; Carrilho, F.; Carvalho, S.; Díaz, J.; Narciso, J.; Madureira, G.; Matias, L.; Haberland, C.; et al. Ambient noise recorded by a dense broadband seismic deployment in western Iberia. Bull. Seismol. Soc. Am. 2014, 104, 2985–3007. [Google Scholar] [CrossRef]
- Doody, C.D.; Ringler, A.T.; Anthony, R.E.; Wilson, D.C.; Holland, A.A.; Hutt, C.R.; Sandoval, L.D. Effects of thermal variability on broadband seismometers: Controlled experiments, observations, and implications. Bull. Seismol. Soc. Am. 2018, 108, 493–502. [Google Scholar] [CrossRef]
- Hayman, M.B. Downhole Seismometers. In Encyclopedia of Earthquake Engineering; Beers, M., Kougioumtzoglou, I.A., Patelli, E., Au, S.-K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–22. [Google Scholar] [CrossRef]
- Li, Y.; Prothero, W., Jr.; Thurber, C.; Butler, R. Observations of ambient noise and signal coherency on the island of Hawaii for teleseismic studies. Bull. Seismol. Soc. Am. 1994, 84, 1229–1242. [Google Scholar] [CrossRef]
- Melton, B.S. The sensitivity and dynamic range of inertial seismographs. Rev. Geophys. 1976, 14, 93–116. [Google Scholar] [CrossRef]
- Montagner, J.-P.; Karczewski, J.-F.; Romanowicz, B.; Bouaricha, S.; Lognonne, P.; Roult, G.; Stutzmann, E.; Thirot, J.-L.; Brion, J.; Dole, B.; et al. The French Pilot Experiment OFM-SISMOBS: First scientific results on noise level and event detection. Phys. Earth Planet. Inter. 1994, 84, 321–336. [Google Scholar] [CrossRef]
- Peterson, J.; Butler, H.M.; Holcomb, L.G.; Hutt, C.R. The seismic research observatory. Bull. Seismol. Soc. Am. 1976, 66, 2049–2068. [Google Scholar] [CrossRef]
- Peterson, J.; Orsini, N.A. Seismic research observatories: Upgrading the worldwide seismic data network. Eos Trans. Am. Geophys. Union 1976, 57, 548–556. [Google Scholar] [CrossRef]
- Ringler, A.T.; Hagerty, M.T.; Holland, J.; Gonzales, A.; Gee, L.S.; Edwards, J.D. The data quality analyzer: A quality control program for seismic data. Comput. Geosci. 2015, 76, 96–111. [Google Scholar] [CrossRef]
- Ringler, A.T.; Steim, J.M.; van Zandt, T.; Hutt, C.R.; Wilson, D.C.; Storm, T.L. Potential improvements in horizontal very broadband seismic data in the IRIS/USGS component of the Global Seismic Network. Seismol. Res. Lett. 2015, 87, 81–89. [Google Scholar] [CrossRef]
- Ringler, A.T.; Wilson, D.C.; Storm, T.; Marshall, B.; Hutt, C.R.; Holland, A.A. Noise reduction in long-period seismograms by way of array summing. Bull. Seismol. Soc. Am. 2016, 106, 1991–1997. [Google Scholar] [CrossRef]
- Webb, S.C.; Lee, W.H.K. Seismic noise on land and on the seafloor. Int. Handb. Earthq. Eng. Seismol. 2002, 81, 305–318. [Google Scholar]
- Kenda, B.; Lognonné, P.; Spiga, A.; Kawamura, T.; Kedar, S.; Banerdt, W.B.; Lorenz, R.; Banfield, D.; Golembek, M. Modeling of ground deformation and shallow surface waves generated by Martian dust devils and perspectives for near-surface structure inversion. Space Sci. Rev. 2017, 211, 501–524. [Google Scholar] [CrossRef]
- Lognonné, P.; Zharkov, V.N.; Karczewski, J.F.; Romanowicz, B.; Menvielle, M.; Poupinet, G.; Brient, B.; Cavoit, C.; Desautez, A.; Dole, R.; et al. The seismic OPTIMISM experiment. Planet. Space Sci. 1998, 46, 739–747. [Google Scholar] [CrossRef]
- Lognonné, P.; Beyneix, J.G.; Banerdt, W.B.; Cacho, S.; Karczewski, J.F.; Morand, M. Ultra broad band seismology on InterMarsNet. Planet. Space Sci. 1996, 44, 1237–1249. [Google Scholar] [CrossRef]
- Lognonné, P.; Johnson, C. Planetary Seismology. In Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2007; Volume 10, pp. 69–122. [Google Scholar]
- Lognonné, P.; Mosser, B. Planetary seismology. Surv. Geophys. 1993, 14, 239–302. [Google Scholar] [CrossRef]
- Lorenz, R.D. Planetary seismology—Expectations for lander and wind noise with application to Venus. Planet. Space Sci. 2012, 62, 86–96. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Kedar, S.; Murdoch, N.; Lognonné, P.; Kawamura, T.; Mimoun, D.; Bruce Banerdt, W. Seismometer detection of dust devil vortices by ground tilt. Bull. Seismol. Soc. Am. 2015, 105, 3015–3023. [Google Scholar] [CrossRef] [Green Version]
- Mège, D.; Gurgurewicz, J.; Grygorczuk, J.; Wiśniewski, Ł.; Thornell, G. The Highland Terrain Hopper (HOPTER): Concept and use cases of a new locomotion system for the exploration of low gravity Solar System bodies. Acta Astronaut. 2016, 121, 200–220. [Google Scholar] [CrossRef]
- Mimoun, D.; Murdoch, N.; Lognonné, P.; Hurst, K.; Pike, W.T.; Hurley, J.; Nébut, T.; Banerdt, W.B.; SEIS Team. The noise model of the SEIS seismometer of the InSight mission to Mars. Space Sci. Rev. 2017, 211, 383–428. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, N.; Kenda, B.; Kawamura, T.; Spiga, A.; Lognonné, P.; Mimoun, D.; Banerdt, W.B. Estimations of the seismic pressure noise on Mars determined from Large Eddy Simulations and demonstration of pressure decorrelation techniques for the InSight mission. Space Sci. Rev. 2017, 211, 457–483. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, N.; Mimoun, D.; Garcia, R.F.; Rapin, W.; Kawamura, T.; Lognonné, P.; Banfield, D.; Banerdt, W.B. Evaluating the wind-induced mechanical noise on the InSight seismometers. Space Sci. Rev. 2017, 211, 429–455. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, N.; Mimoun, D.; Lognonné, P.; Garcia, R.; Kawamura, T. Environmental noise contributors on the InSight seismometers. Eur. Planet. Sci. Congr. 2018, 8, 2. [Google Scholar]
- Murphy, J.; Steakley, K.; Balme, M.; Deprez, G.; Esposito, F.; Kahanpää, H.; Lemmon, M.; Lorenz, R.; Murdoch, N.; Neakrase, L.; et al. Field measurements of terrestrial and Martian dust devils. Space Sci. Rev. 2016, 203, 39–87. [Google Scholar] [CrossRef] [Green Version]
- Pou, L.; Mimoun, D.; Lognonné, P.; Garcia, R.F.; Karatekin, O.; Nonon-Latapie, M.; Llorca-Cejudo, R. High precision SEIS calibration for the InSight mission and its applications. Space Sci. Rev. 2019, 215, 6. [Google Scholar] [CrossRef] [Green Version]
- Reiss, D.; Lorenz, R.D. Dust devil track survey at Elysium Planitia, Mars: Implications for the InSight landing sites. Icarus 2016, 266, 315–330. [Google Scholar] [CrossRef]
- Spiga, A.; Banfield, D.; Teanby, N.A.; Forget, F.; Lucas, A.; Kenda, B.; Manfredi, J.A.R.; Widmer-Schnidrig, R.; Murdoch, N.; Lemmon, M.T.; et al. Atmospheric science with InSight. Space Sci. Rev. 2018, 214, 109. [Google Scholar] [CrossRef] [Green Version]
- Sobolev, G.A.; Zakrzhevskaya, N.A.; Migunov, I.N.; Sobolev, D.G. Migration of pulsations after earthquakes. Izv. Phys. Solid Earth 2017, 53, 493–517. [Google Scholar] [CrossRef]
- Shved, G.M.; Ermolenko, S.I.; Karpova, N.V.; Wendt, S.; Jacobi, C. Detecting global atmospheric oscillations by seismic instruments. Izv. Phys. Solid Earth 2013, 49, 278–288. [Google Scholar] [CrossRef]
- Shved, G.M.; Karpova, N.V.; Petrova, L.N.; Orlov, E.G.; Ermolenko, S.I. Steady-frequency waves at intradiurnal periods from simultaneous co-located microbarometer and seismometer measurements: A case study. Ann. Geophys. 2011, 29, 1153–1167. [Google Scholar] [CrossRef] [Green Version]
- Zürn, W.; Exß, J.; Steffen, H.; Kroner, C.; Jahr, T.; Westerhaus, M. On reduction of long-period horizontal seismic noise using local barometric pressure. Geophys. J. Int. 2007, 171, 780–796. [Google Scholar] [CrossRef]
- Zürn, W.; Meurers, B. Clear evidence for the sign-reversal of the pressure admittance to gravity near 3 mHz. J. Geodyn. 2009, 48, 371–377. [Google Scholar] [CrossRef] [Green Version]
- Zürn, W.; Wielandt, E. On the minimum of vertical seismic noise near 3 mHz. Geophys. J. Int. 2007, 168, 647–658. [Google Scholar] [CrossRef] [Green Version]
- Weber, G. Sonic boom exposure effects II. 1: Structures and terrain. J. Sound Vib. 1972, 20, 505–509. [Google Scholar] [CrossRef]
- Negraru, P.T. Application of seismo-acoustic signals to the study of local site effects. Acta Geophys. 2010, 58, 1021–1039. [Google Scholar] [CrossRef]
- Mauk, F.J. Utilization of seismically recorded infrasonic-acoustic signals to monitor volcanic explosions: The El Chichon Sequence 1982—A case study. J. Geophys. Res. Solid Earth 1983, 88, 10385–10401. [Google Scholar] [CrossRef]
- De Angelis, S.; McNutt, S.R.; Webley, P.W. Evidence of atmospheric gravity waves during the 2008 eruption of Okmok volcano from seismic and remote sensing observations. Geophys. Res. Lett. 2011, 38, L10303. [Google Scholar] [CrossRef] [Green Version]
- Sorrells, G.G.; McDonald, J.A.; Der, Z.A.; Herrin, E. Earth motion caused by local atmospheric pressure changes. Geophys. J. Int. 1971, 26, 83–98. [Google Scholar] [CrossRef]
- Sorrells, G.G.; Goforth, T.T. Low-frequency earth motion generated by slowly propagating partially organized pressure fields. Bull. Seismol. Soc. Am. 1973, 63, 1583–1601. [Google Scholar] [CrossRef]
- Douze, E.J.; Sorrells, G.G. Prediction of pressure-generated earth motion using optimum filters. Bull. Seismol. Soc. Am. 1975, 65, 637–650. [Google Scholar] [CrossRef]
- Dybing, S.N.; Ringler, A.T.; Wilson, D.C.; Anthony, R.E. Characteristics and spatial variability of wind noise on near-surface broadband seismometers. Bull. Seismol. Soc. Am. 2019, 109, 1082–1098. [Google Scholar] [CrossRef]
- De Angelis, S.; Bodin, P. Watching the wind: Seismic data contamination at long periods due to atmospheric pressure-field-induced tilting. Bull. Seismol. Soc. Am. 2012, 102, 1255–1265. [Google Scholar] [CrossRef]
- Wolin, E.; van der Lee, S.; Bollmann, T.A.; Wiens, D.A.; Revenaugh, J.; Darbyshire, F.A.; Fredrickson, A.W.; Stein, S.; Wysession, M.E. Seasonal and diurnal variations in long-period noise at SPREE stations: The influence of soil characteristics on shallow stations’ performance. Bull. Seismol. Soc. Am. 2015, 105, 2433–2452. [Google Scholar] [CrossRef] [Green Version]
- Tanimoto, T.; Wang, J. Low-frequency seismic noise characteristics from the analysis of co-located seismic and pressure data. J. Geophys. Res. Solid Earth 2018, 123, 5853–5885. [Google Scholar] [CrossRef] [Green Version]
- Priestly, J.T. Correlation Studies of Pressure Fluctuations on the Ground Beneath a Turbulent Boundary Layer; National Bureau of Standards Report No. 8942; University of Maryland: Gaithersburg, MA, USA, 1965. [Google Scholar]
- Shields, F.D. Low-frequency wind noise correlation in microphone arrays. J. Acoust. Soc. Am. 2005, 117, 3489–3496. [Google Scholar] [CrossRef]
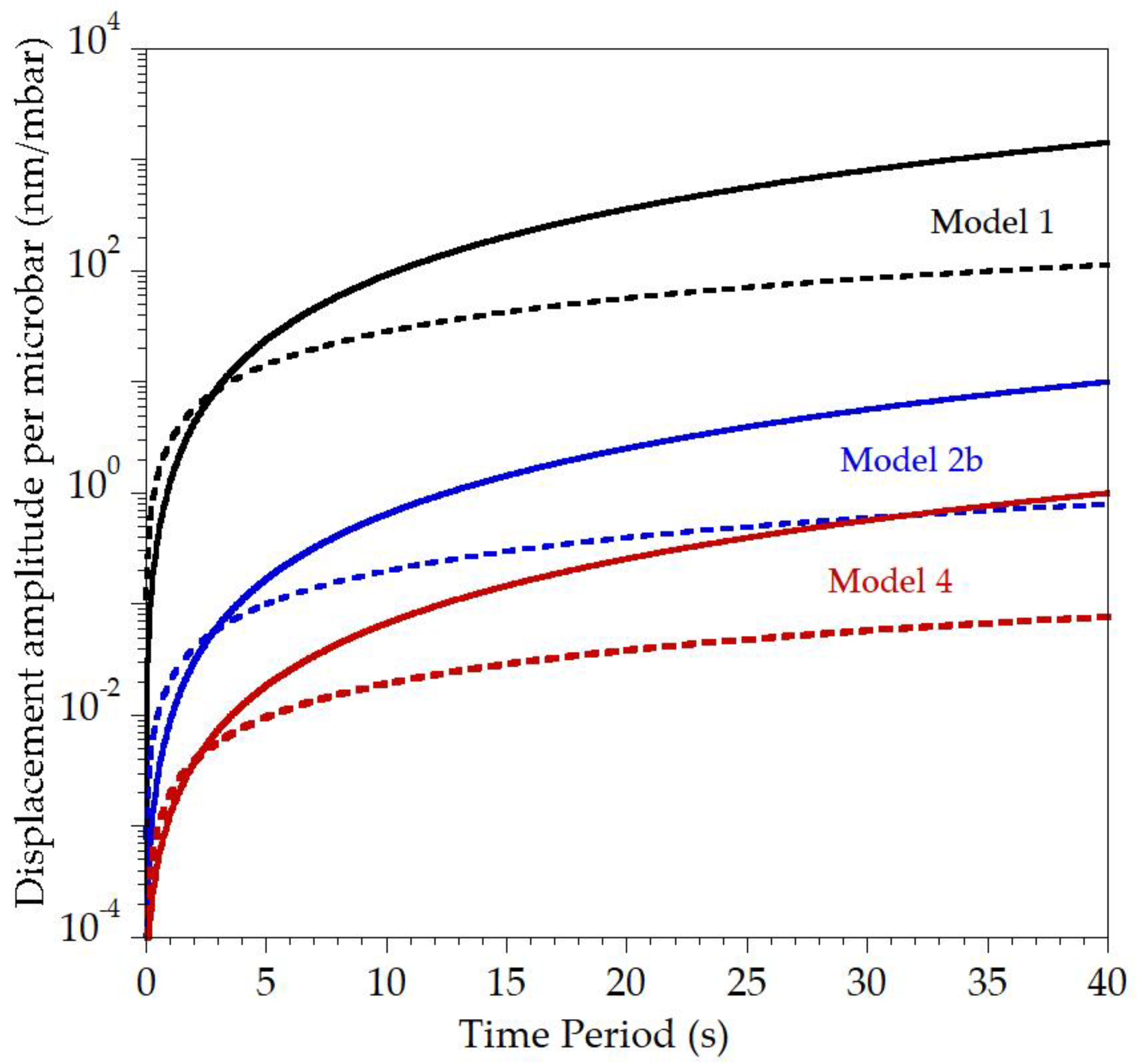
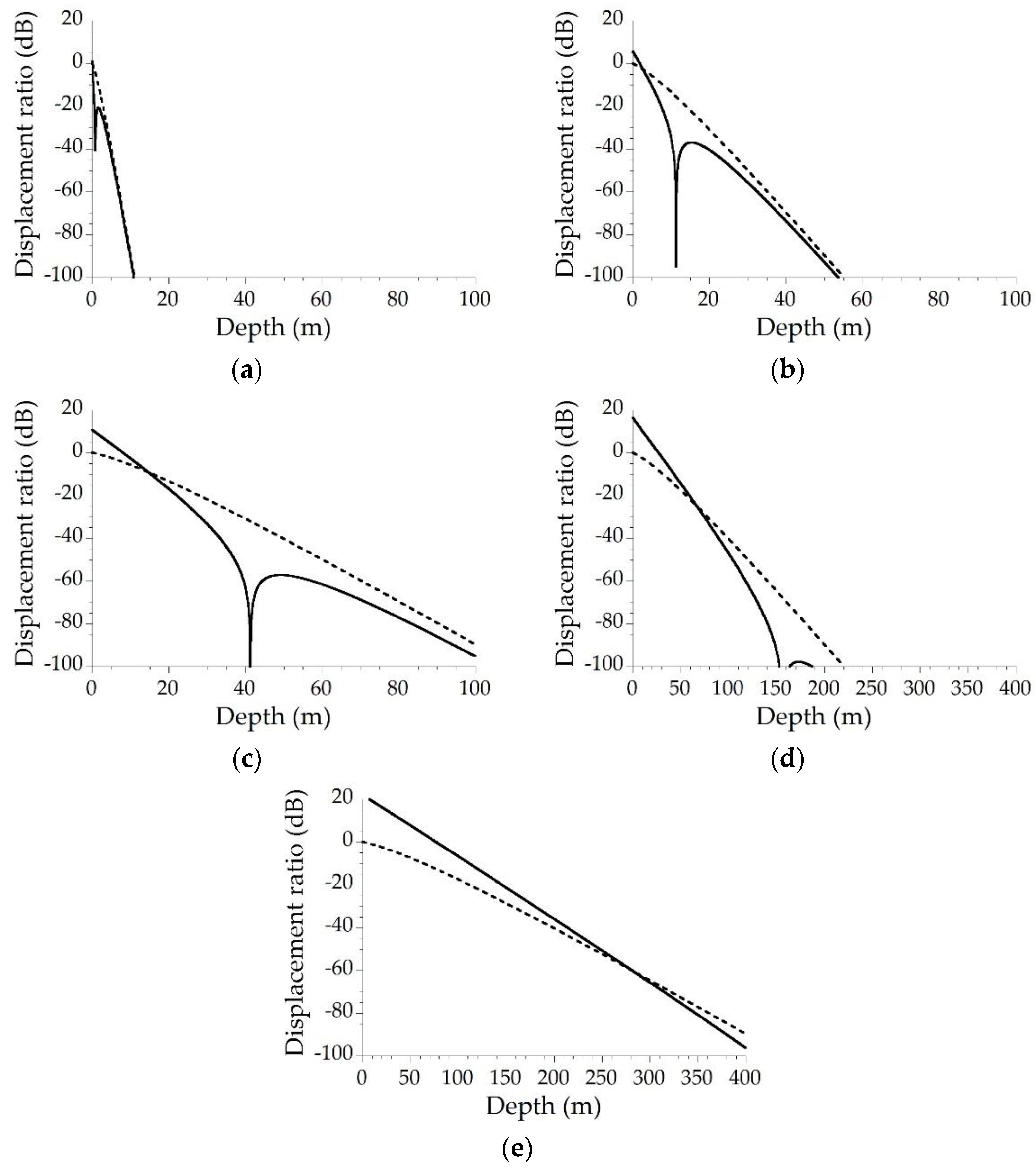
| Model No. | α (km/s) | β (km/s) | ρ (g/cm3) | Geology |
|---|---|---|---|---|
| 1 | 0.3 | 0.1 | 1.6 | Unconsolidated sediments |
| 2b | 2.9 | 1.0 | 2.3 | Sedimentary rock |
| 4 | 5.8 | 3.25 | 2.85 | Granites |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raspet, R.; Hickey, C.J.; Koirala, B. Corrected Tilt Calculation for Atmospheric Pressure-Induced Seismic Noise. Appl. Sci. 2022, 12, 1247. https://doi.org/10.3390/app12031247
Raspet R, Hickey CJ, Koirala B. Corrected Tilt Calculation for Atmospheric Pressure-Induced Seismic Noise. Applied Sciences. 2022; 12(3):1247. https://doi.org/10.3390/app12031247
Chicago/Turabian StyleRaspet, Richard, Craig J. Hickey, and Bipin Koirala. 2022. "Corrected Tilt Calculation for Atmospheric Pressure-Induced Seismic Noise" Applied Sciences 12, no. 3: 1247. https://doi.org/10.3390/app12031247
APA StyleRaspet, R., Hickey, C. J., & Koirala, B. (2022). Corrected Tilt Calculation for Atmospheric Pressure-Induced Seismic Noise. Applied Sciences, 12(3), 1247. https://doi.org/10.3390/app12031247






