Numerical Analysis of Shear Keys for Offshore Wind Turbine Monopile Grouted Connection with Elastomeric Bearings
Abstract
:1. Introduction
2. Methodology and Materials
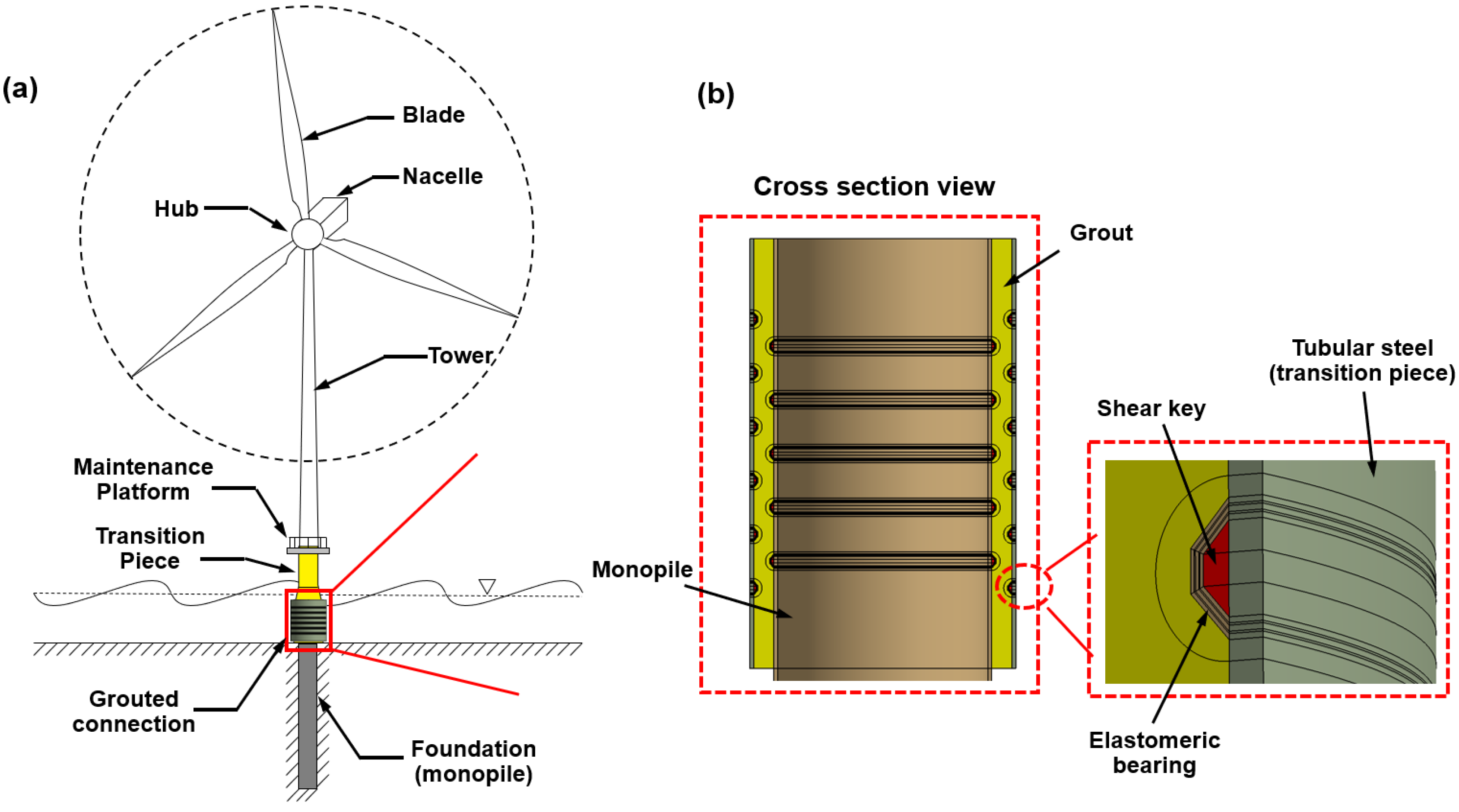
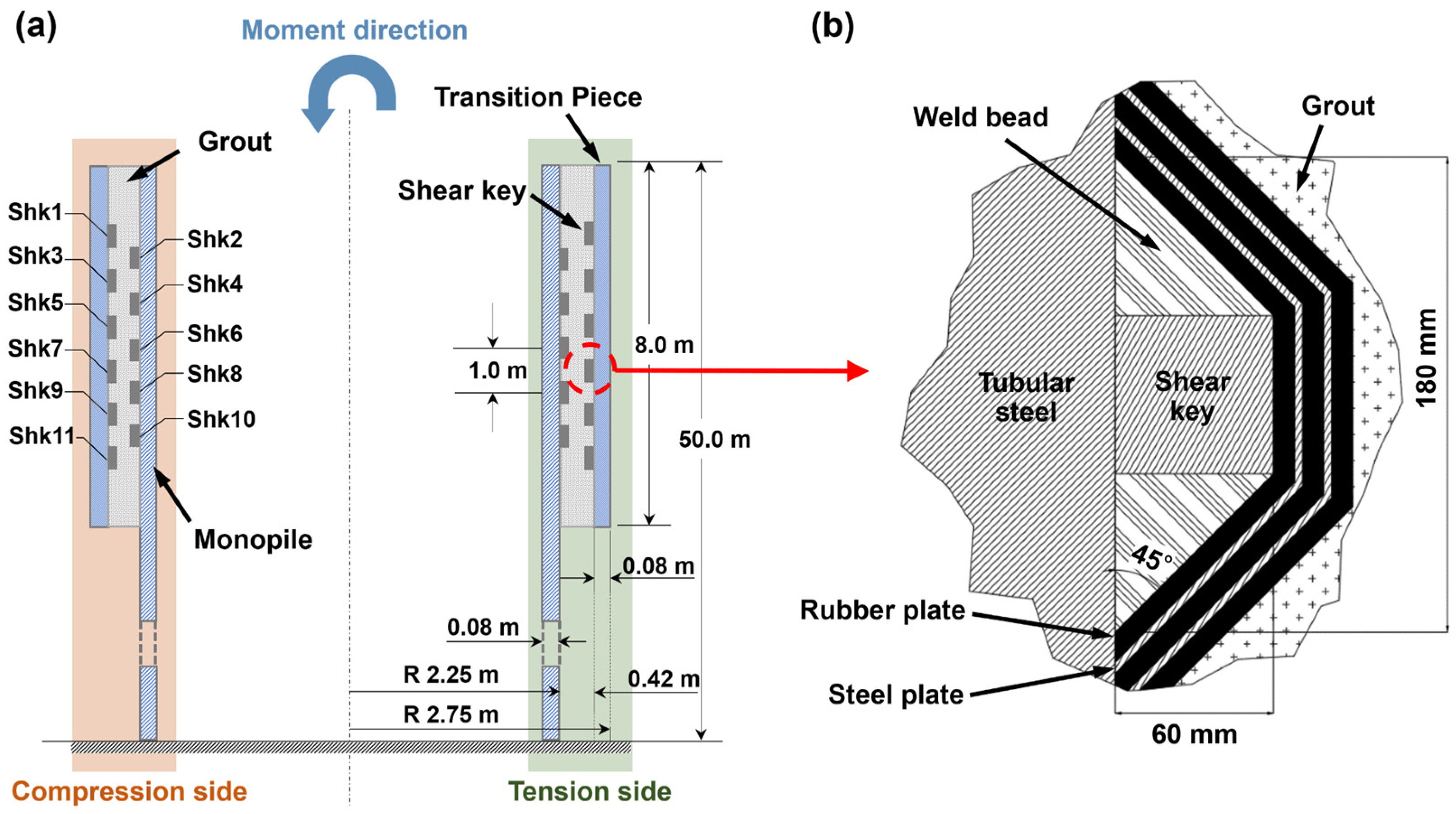
2.1. Design Standard of Monopile Grouted Connection
2.2. Load of Ultimate Condition
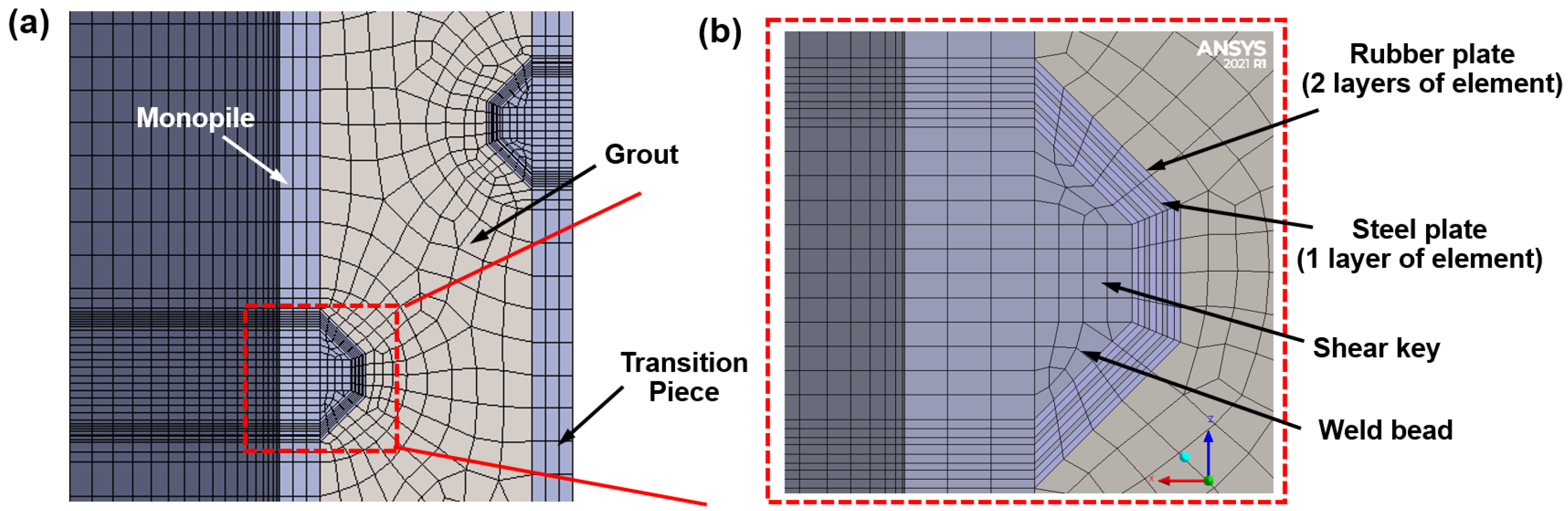
3. Finite Element Model
4. Results and Discussion
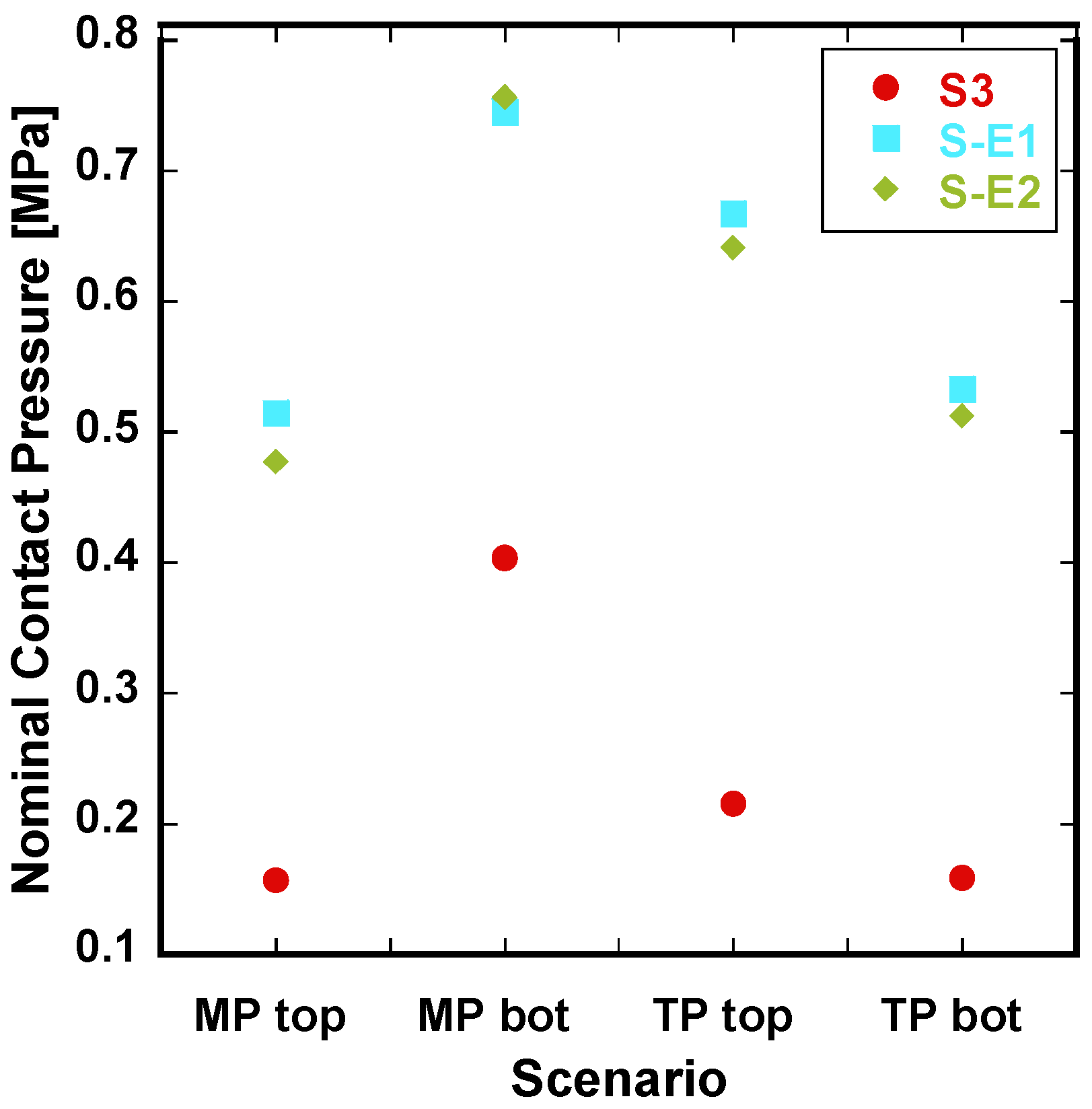
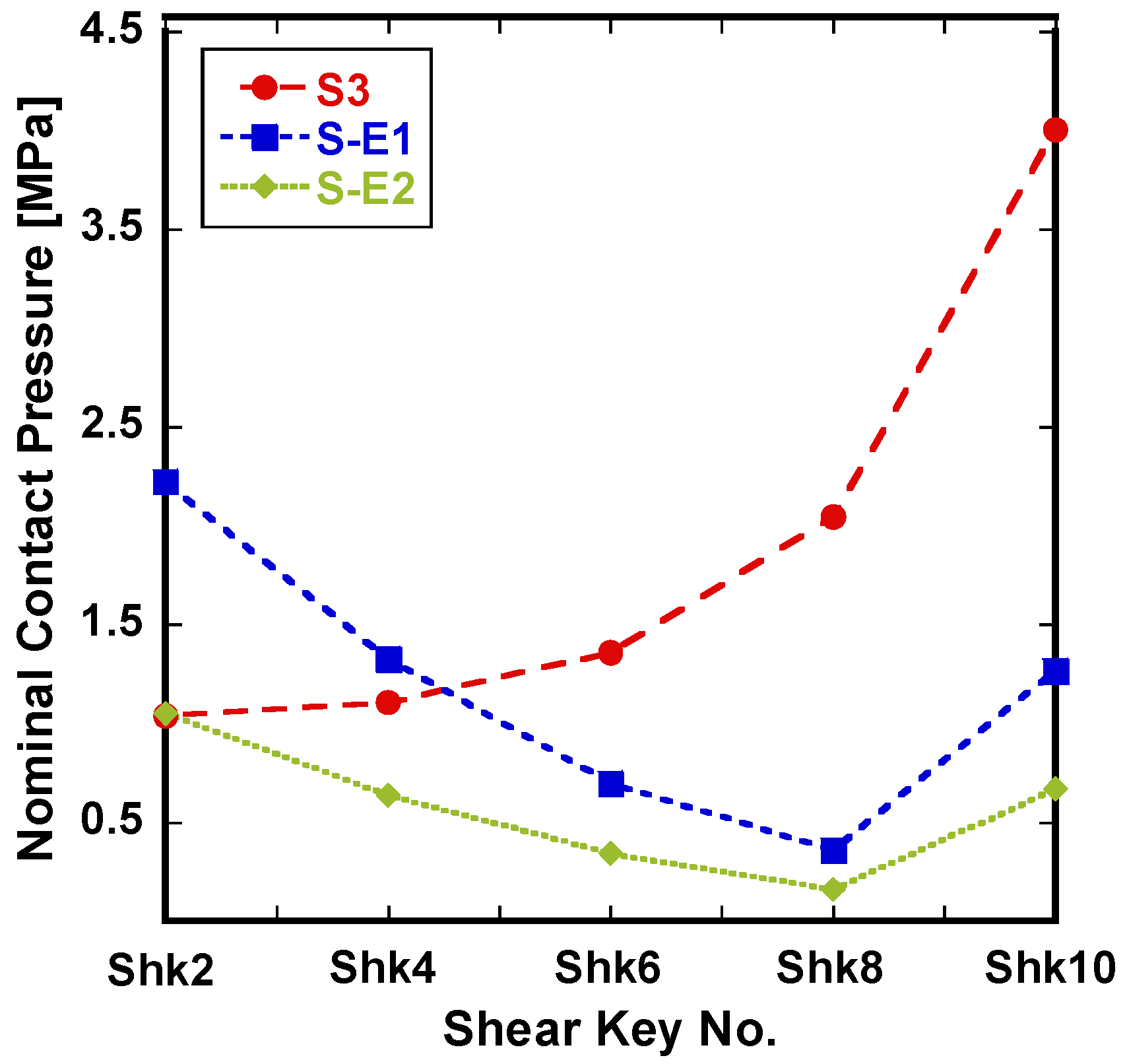
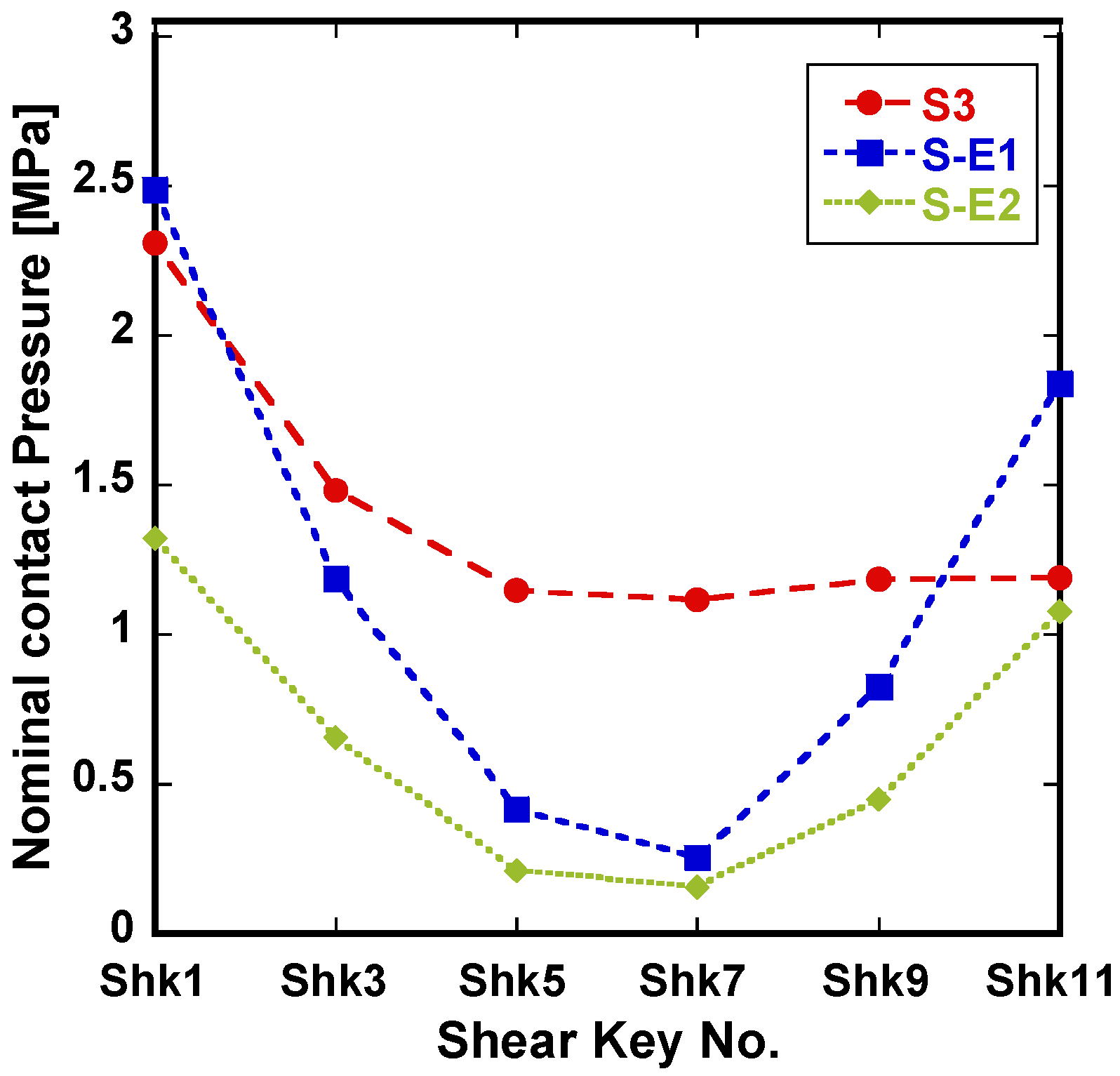
4.1. Contact Pressure
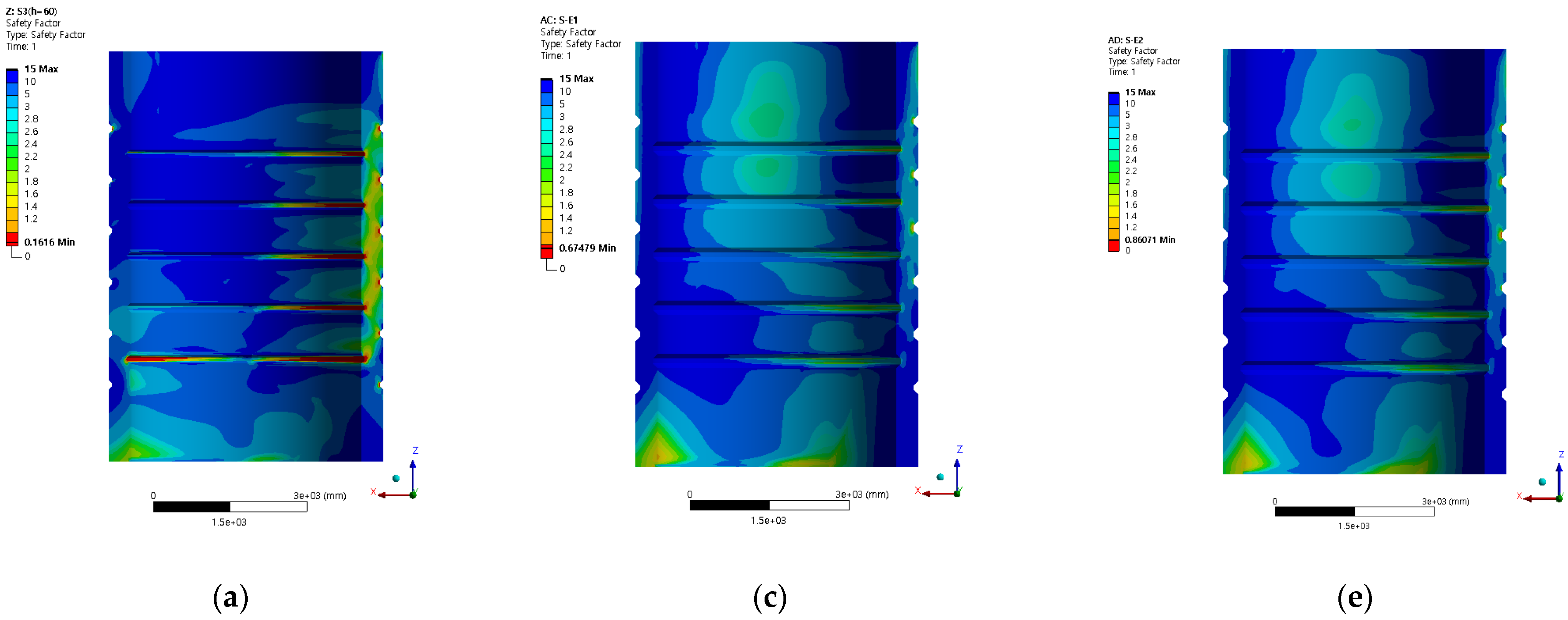
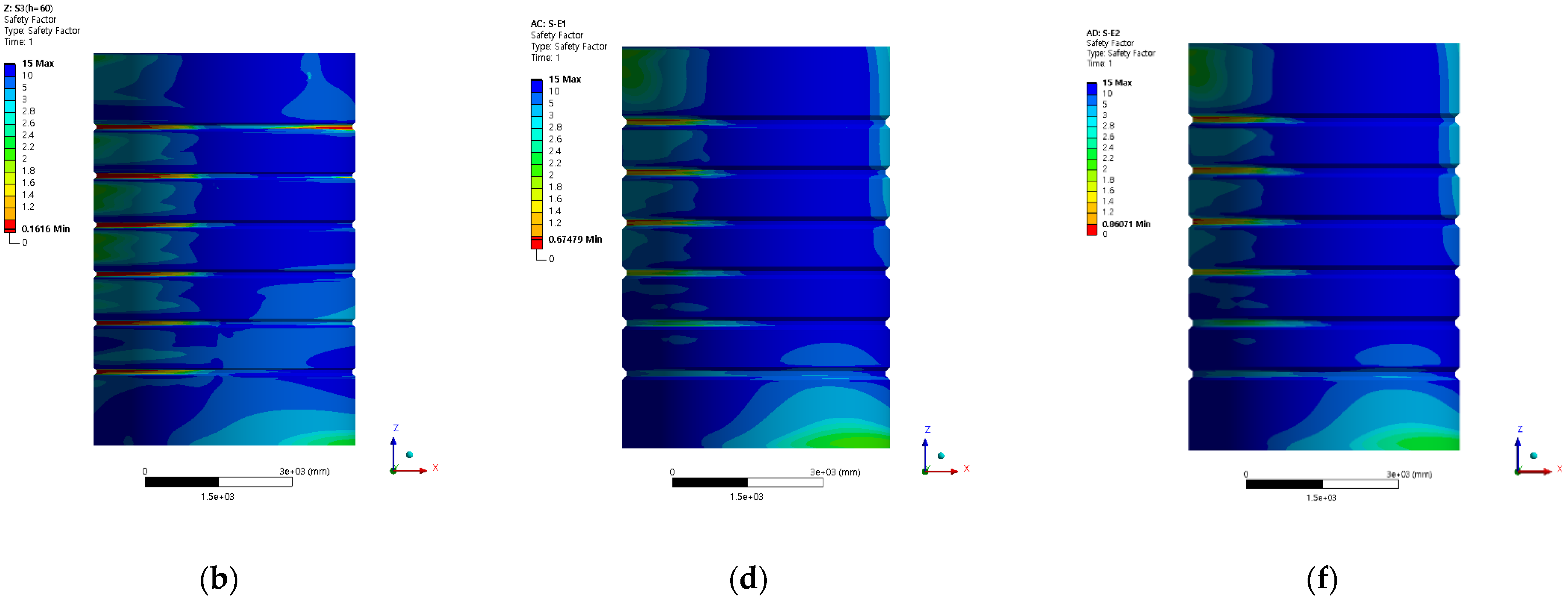
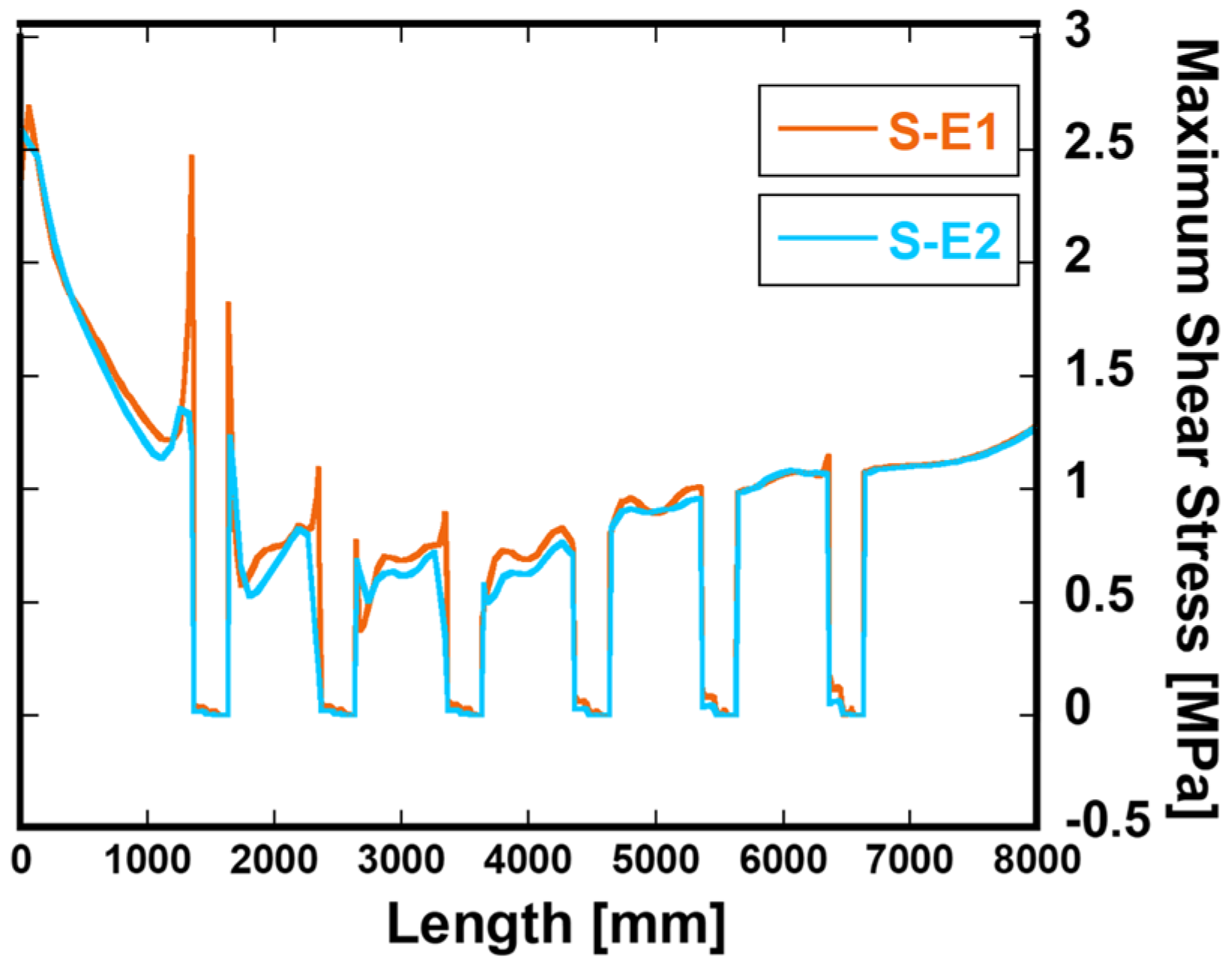
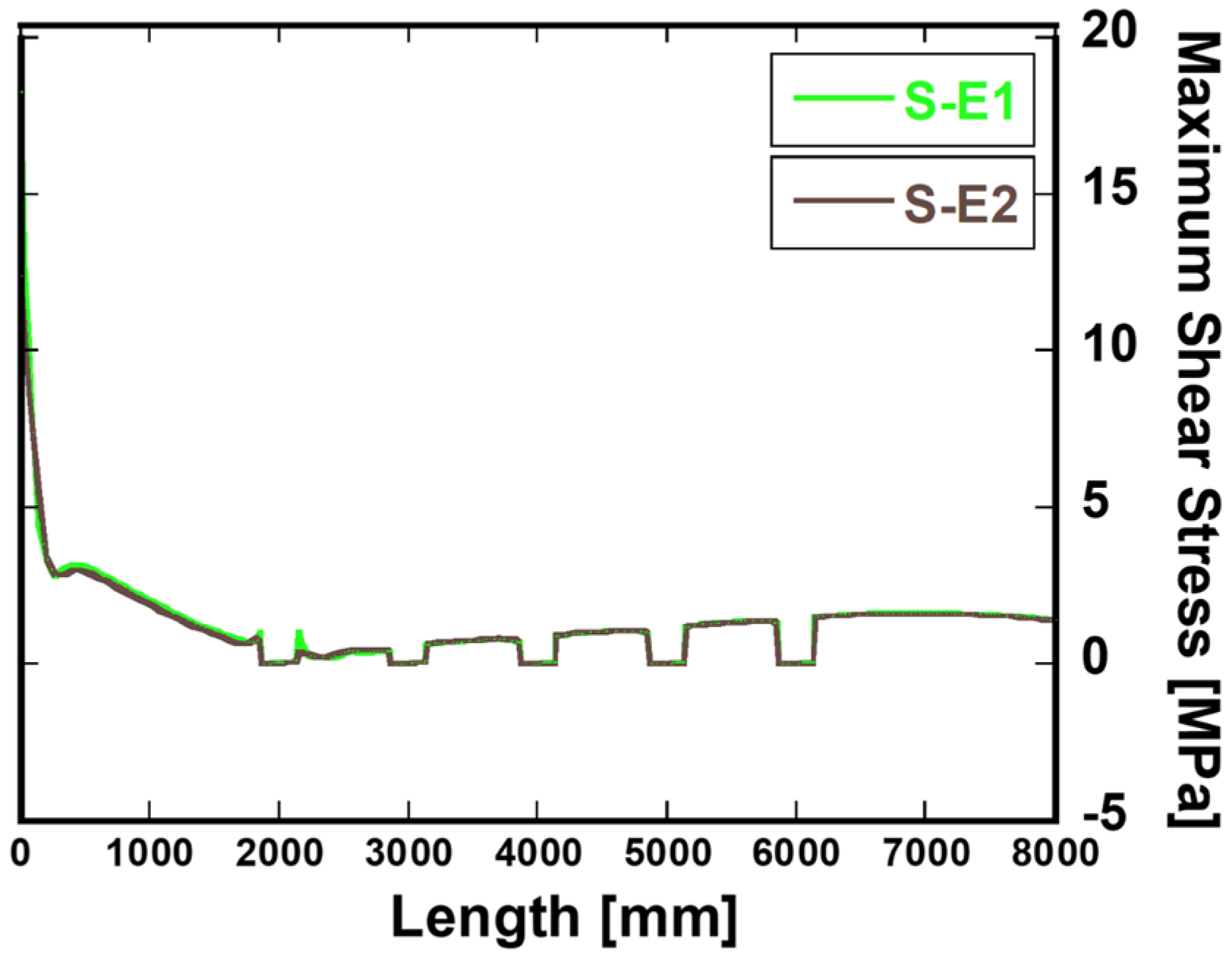
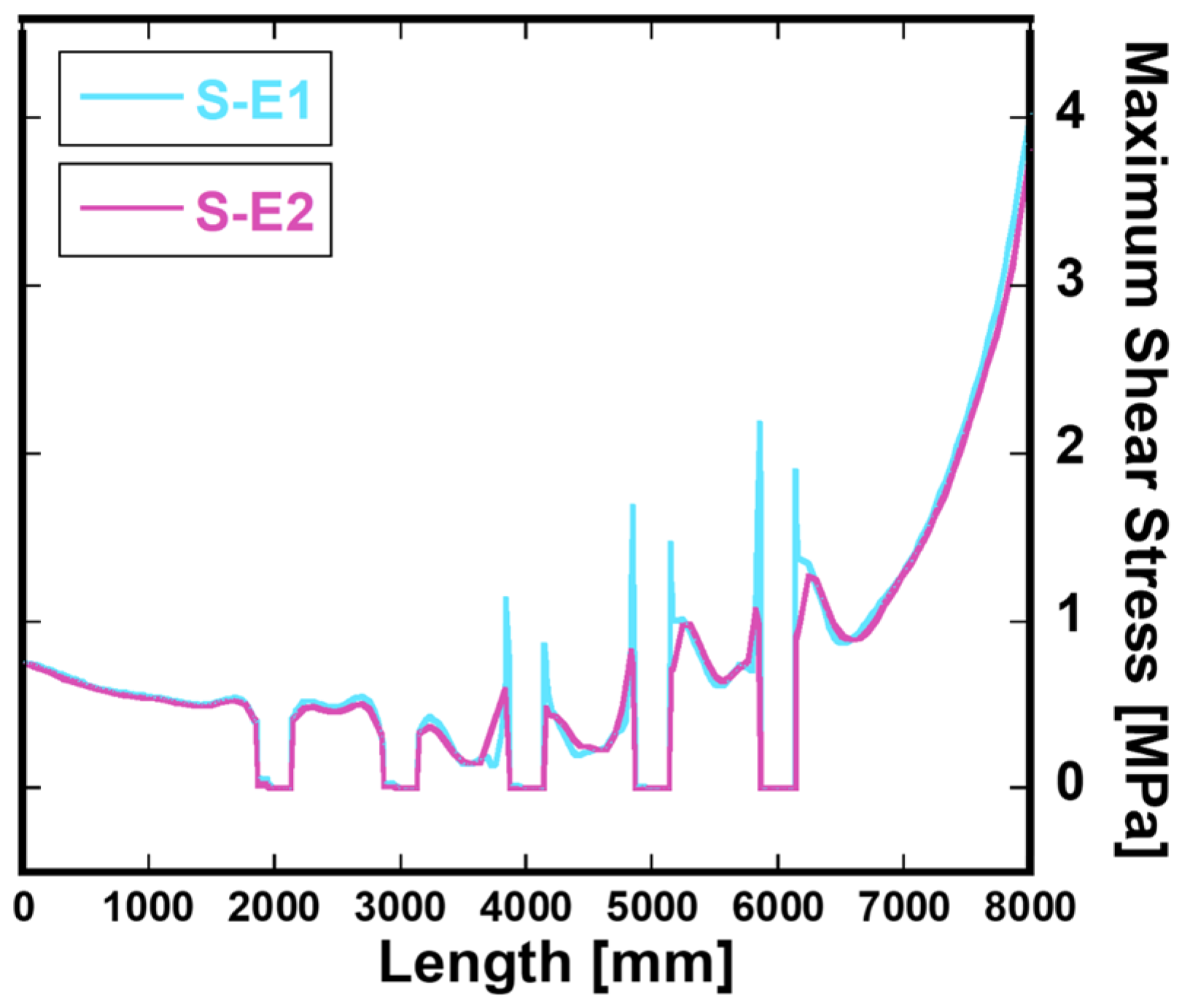
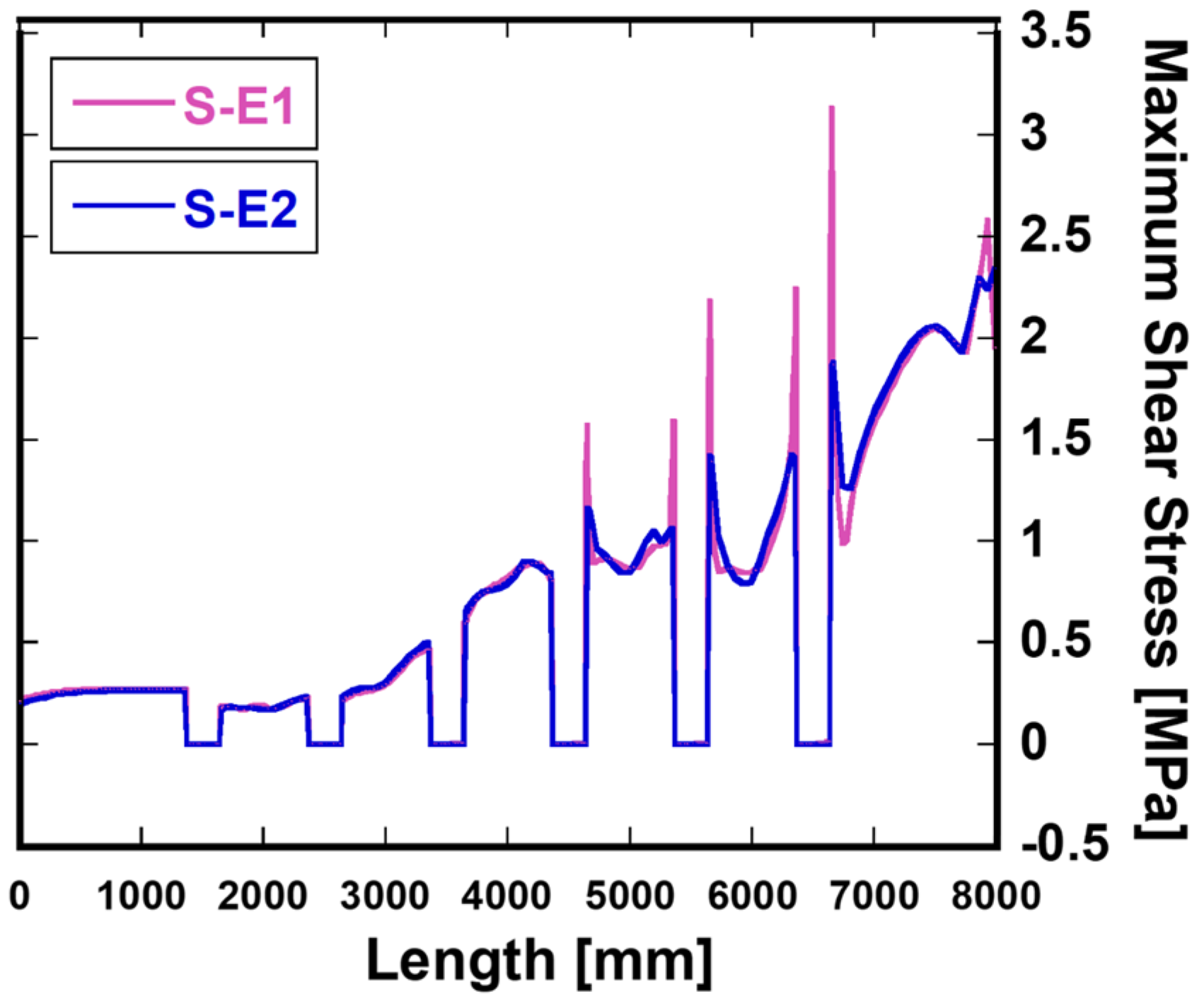
4.2. Shear Stress
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, X.; Huang, D.; Wu, G. The current state of offshore wind energy technology development. Energy 2012, 41, 298–312. [Google Scholar] [CrossRef]
- Weiss, C.V.C.; Guanche, R.; Ondiviela, B.; Castellanos, O.F.; Juanes, J. Marine renewable energy potential: A global perspective for offshore wind and wave exploitation. Energy Convers. Manag. 2018, 177, 43–54. [Google Scholar] [CrossRef]
- Klose, M.; Mittelstaedt, M.; Mulve, A. Grouted connections-offshore standards driven by the wind industry. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Sánchez, S.; López-Gutiérrez, J.-S.; Negro, V.; Esteban, M.D. Foundations in offshore wind farms: Evolution, characteristics and range of use. Analysis of main dimensional parameters in monopile foundations. J. Mar. Sci. Eng. 2019, 7, 441. [Google Scholar] [CrossRef] [Green Version]
- Schallenberg-Rodríguez, J.; García Montesdeoca, N. Spatial planning to estimate the offshore wind energy potential in coastal regions and islands. Practical case: The Canary Islands. Energy 2018, 143, 91–103. [Google Scholar] [CrossRef]
- Nonveiller, E. Grouting Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Schaumann, P.; Bechtel, A.; Lochte-Holtgreven, S. Grouted joints for offshore wind turbine jackets under full reversal axially loading conditions. In Proceedings of the Twenty-third International Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Dallyn, P.; El-Hamalawi, A.; Palmeri, A.; Knight, R. Experimental testing of grouted connections for offshore substructures: A critical review. Structures 2015, 3, 90–108. [Google Scholar] [CrossRef] [Green Version]
- Johnston, C.; Doré, M. Comparison of the Fatigue Performance of Galvanised M72 Bolts With Design Standard Recommendations. In Proceedings of the ASME 2021 40th International Conference on Ocean, Offshore and Arctic Engineering, Online, 21–30 June 2021. [Google Scholar]
- Schaumann, P.; Raba, A.; Bechtel, A. Impact of Contact Interface Conditions on the Axial Load Bearing Capacity of Grouted Connections. In Proceedings of the European Wind Energy Association Conference EWEA 2013, Vienna, Austria, 4–7 February 2013. [Google Scholar]
- Ibrahim, R. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Jie, Y.; Yuan, H.; Zhou, H.; Yu, Y. Bending moment calculations for piles based on the finite element method. J. Appl. Math. 2013, 2013, 784583. [Google Scholar] [CrossRef] [Green Version]
- Khodair, Y.; Abdel-Mohti, A. Numerical analysis of pile–soil interaction under axial and lateral loads. Int. J. Concr. Struct. Mater. 2014, 8, 239–249. [Google Scholar] [CrossRef] [Green Version]
- Achmus, M.; Thieken, K. On the behavior of piles in non-cohesive soil under combined horizontal and vertical loading. Acta Geotech. 2010, 5, 199–210. [Google Scholar] [CrossRef]
- Conte, E.; Pugliese, L.; Troncone, A.; Vena, M. A simple approach for evaluating the bearing capacity of piles subjected to inclined loads. Int. J. Geomech. 2021, 21, 04021224. [Google Scholar] [CrossRef]
- Graine, N.; Hjiaj, M.; Krabbenhoft, K. 3D failure envelope of a rigid pile embedded in a cohesive soil using finite element limit analysis. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 265–290. [Google Scholar] [CrossRef]
- Saigal, R.K.; Dolan, D.; Der Kiureghian, A.; Camp, T.; Smith, C.E. Comparison of design guidelines for offshore wind energy systems. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2007. [Google Scholar]
- Roach, S.; Park, S.M.; Gaertner, E.; Manwell, J.; Lackner, M. Application of the new IEC international design standard for offshore wind turbines to a reference site in the massachusetts offshore wind energy area. J. Phys. Conf. Ser. 2020, 1452, 012038. [Google Scholar] [CrossRef]
- Hopstad, A.L.H.; Ronold, K.O.; Slätte, J. Design Standard for Floating Wind Turbine Structures. Doc. Hist. 2013, 194. Available online: https://www.sintef.no/globalassets/project/deepwind-2013/deepwind-presentations-2013/posters/hopstad_poster.pdf (accessed on 23 November 2021).
- Tziavos, N.I.; Hemida, H.; Metje, N.; Baniotopoulos, C.J. Non-linear finite element analysis of grouted connections for offshore monopile wind turbines. Ocean. Eng. 2019, 171, 633–645. [Google Scholar] [CrossRef] [Green Version]
- Sunday, K.; Brennan, F. A review of offshore wind monopiles structural design achievements and challenges. Ocean. Eng. 2021, 235, 109409. [Google Scholar] [CrossRef]
- Grech, J.; Antunes, E. Zirconia in dental prosthetics: A literature review. J. Mater. Res. Technol. 2019, 8, 4956–4964. [Google Scholar] [CrossRef]
- Krahl, N.W.; Karsan, D.I. Axial strength of grouted pile-to-sleeve connections. J. Struct. Eng. 1985, 111, 889–905. [Google Scholar] [CrossRef]
- DNV GL. STANDARD DNV GL ST 0437: Loads and Site Conditions for Wind Turbines; DNV GL: Oslo, Norway, 2016. [Google Scholar]
- Morison, J.; Johnson, J.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Chen, T.; Wang, X.; Zhao, Q.; Yuan, G. A numerical investigation on grouted connections for offshore wind turbines under combined loads. J. Mar. Eng. Technol. 2019, 18, 134–146. [Google Scholar] [CrossRef]
- Stanton, J.F.; Roeder, C.W. Elastomeric Bearings Design, Construction, and Materials; NCHRP Report; Transportation Research Board: Washington, DC, USA, 1982; p. 248. [Google Scholar]
- Yoon, H.; Kwahk, I.J.; Kim, Y.J. A study on the ultimate performances of elastomeric bearings in Korea. KSCE J. Civ. Eng. 2013, 17, 438–449. [Google Scholar] [CrossRef]
- Wadham-Gagnon, M.; Hubert, P.; Semler, C.; Païdoussis, M.P.; Vézina, M.; Lavoie, D. Hyperelastic modeling of rubber in commercial finite element software (ANSYS). In Proceedings of the Conference on SAMPE 2006, Long Beach, CA, USA, 30 April–4 May 2006; Volume 6. [Google Scholar]
- Schaffer, W.; Seo, J.; Choi, E.; Lee, J. Optimized retrofit design of in-service monopile foundation offshore wind turbine transition zone. Eng. Struct. 2020, 220, 111001. [Google Scholar] [CrossRef]
- Lotsberg, I.; Serednicki, A.; Lervik, A.; Bertnes, H.J.S. Design of grouted connections for monopile offshore structures: Results from two joint industry projects. Stahlbau 2012, 81, 695–704. [Google Scholar] [CrossRef]
- Chen, B.-Q.; Soares, C.G. Experimental and numerical investigation on welding simulation of long stiffened steel plate specimen. Mar. Struct. 2021, 75, 102824. [Google Scholar] [CrossRef]
- Kumar, N.; Rao, V.V. Hyperelastic Mooney-Rivlin model: Determination and physical interpretation of material constants. Parameters 2016, 2, 43–46. [Google Scholar]
| Contents | Value |
|---|---|
| Rated power of turbine | 3.6 MW |
| Hub height | 95 m |
| Weight of rotor nacelle assembly | 234.0 tons |
| Weight of tower | 214.1 tons |
| Mean wind speed | 5.7 m/s |
| Extreme wind speed (50 years) | 55.0 m/s |
| Average water level | 8 mMSL |
| Upper slash zone with respect to LAT | 2.8 mLAT |
| Lower splash zone with respect to LAT | −2.1 mLAT |
| Extreme individual wave height (50 years) | 3.50 m |
| Extreme individual wave height (100 years) | 3.68 m |
| Significant wave height (50 years) | 1.88 m |
| Wave crest height (50 years) | 2.28 m |
| Wave period corresponding to the extreme individual wave height | 4.9–6.3 s |
| Fluid velocity | 0.69 m/s |
| Maximum wind driven current (50 years) | 0.56 m/s |
| Maximum tidal current (50 years) | 0.1335 m/s |
| Current profile (50 years) | 0.1 m/s |
| Division | Subdivision | Value |
|---|---|---|
| ULS turbine load and moment | Scalar load (N) | 5.036 × 106 |
| Vector load (N) | (9.512 × 105, 0, −4.945 × 106) | |
| Scalar moment (N·mm) | 9.202 × 1010 | |
| Vector moment (N·mm) | (0, 9.199 × 1010, 2.401 × 109) | |
| Location of load | Top of TP | |
| Hydrostatic pressure | Hydrostatic pressure (MPa) | 0.026 |
| Location of pressure | Outer surface of TP | |
| ULS wave load | Scalar load (N) | 2.7 × 105 |
| Vector load (N) | (2.7 × 105, 0, 0) | |
| Location of load | Top of TP |
| Contents | Value |
|---|---|
| (mm) | 2250 |
| (mm) | 80 |
| (m) | 50.0 |
| (mm) | 2750 |
| (mm) | 80 |
| (mm) | 2670 |
| (mm) | 420 |
| (m) | 8.0 |
| (mm) | 60 |
| (mm) | 180 |
| (mm) | 1000 |
| (-) | 11 |
| Contents | Steel | Grout Filler | Weld Bead |
|---|---|---|---|
| Compressive strength (MPa) | 250 | 130 | 300 |
| Static modulus of elasticity (GPa) | 200 | 50 | 206 |
| Tensile strength (MPa) | 460 | 7 | 300 |
| Density (kg/m3) | 7850 | 2440 | 7850 |
| Poisson’s ratio (-) | 0.30 | 0.19 | 0.30 |
| Applied part | MP, TP, Shear keys | Grout filler | Weld bead |
| References | [30] | [31] | [32] |
| Material Properties | S-E1 | S-E2 |
|---|---|---|
| Common name | Neoprene (CR) | Natural rubber (NR) |
| Density (kg/m3) | 1265.0 | 949.8 |
| Tensile yield strength (MPa) | 16.97 | 24.25 |
| C10 (Pa) | 210,000 | 160,000 |
| C01 (Pa) | 54,000 | 41,000 |
| d (1/Pa) | 1.2 × 10 −9 | 1.2 × 10 −9 |
| Nominal Contact Pressure | S3 | S-E1 | S-E2 |
|---|---|---|---|
| (MPa) | 0.2401 | 0.6176 | 0.5998 |
| (MPa) | 0.1566 | 0.5150 | 0.4774 |
| (MPa) | 0.4038 | 0.7459 | 0.7564 |
| (MPa) | 0.2151 | 0.6673 | 0.6410 |
| (MPa) | 0.1588 | 0.5331 | 0.5125 |
| (MPa) | 1.6337 | 1.1708 | 0.6117 |
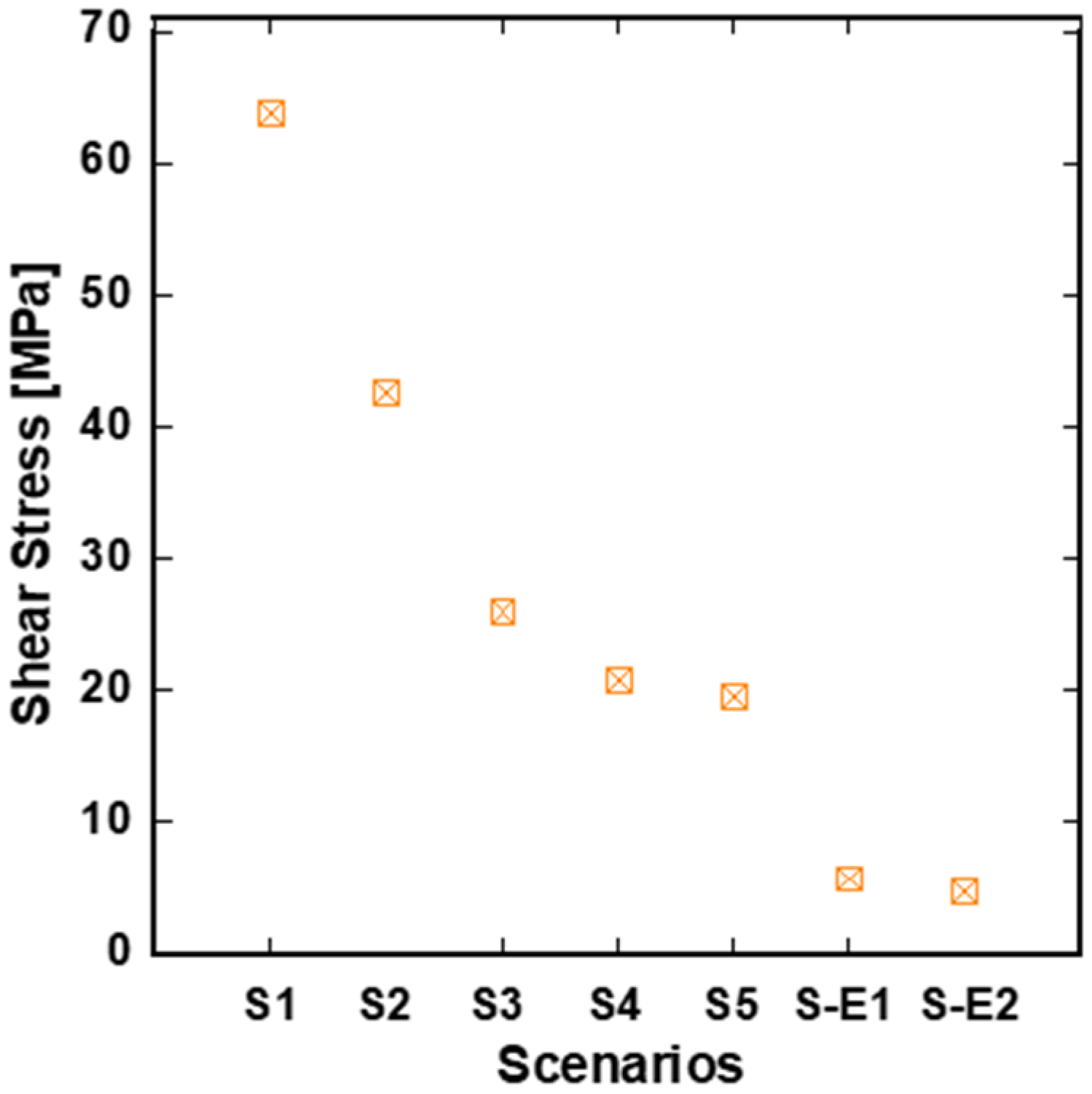
| Shear Stress of Grout | S3 | S-E1 | S-E2 |
|---|---|---|---|
| (MPa) | 25.95 | 5.78 | 4.90 |
| (MPa) | 0.420 | 0.366 | 0.365 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.-S.; Sun, M.-Y. Numerical Analysis of Shear Keys for Offshore Wind Turbine Monopile Grouted Connection with Elastomeric Bearings. Appl. Sci. 2022, 12, 1273. https://doi.org/10.3390/app12031273
You Y-S, Sun M-Y. Numerical Analysis of Shear Keys for Offshore Wind Turbine Monopile Grouted Connection with Elastomeric Bearings. Applied Sciences. 2022; 12(3):1273. https://doi.org/10.3390/app12031273
Chicago/Turabian StyleYou, Young-Suk, and Min-Young Sun. 2022. "Numerical Analysis of Shear Keys for Offshore Wind Turbine Monopile Grouted Connection with Elastomeric Bearings" Applied Sciences 12, no. 3: 1273. https://doi.org/10.3390/app12031273






