An Intelligent Radiomic Approach for Lung Cancer Screening
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset Description
2.2. Methodology Description
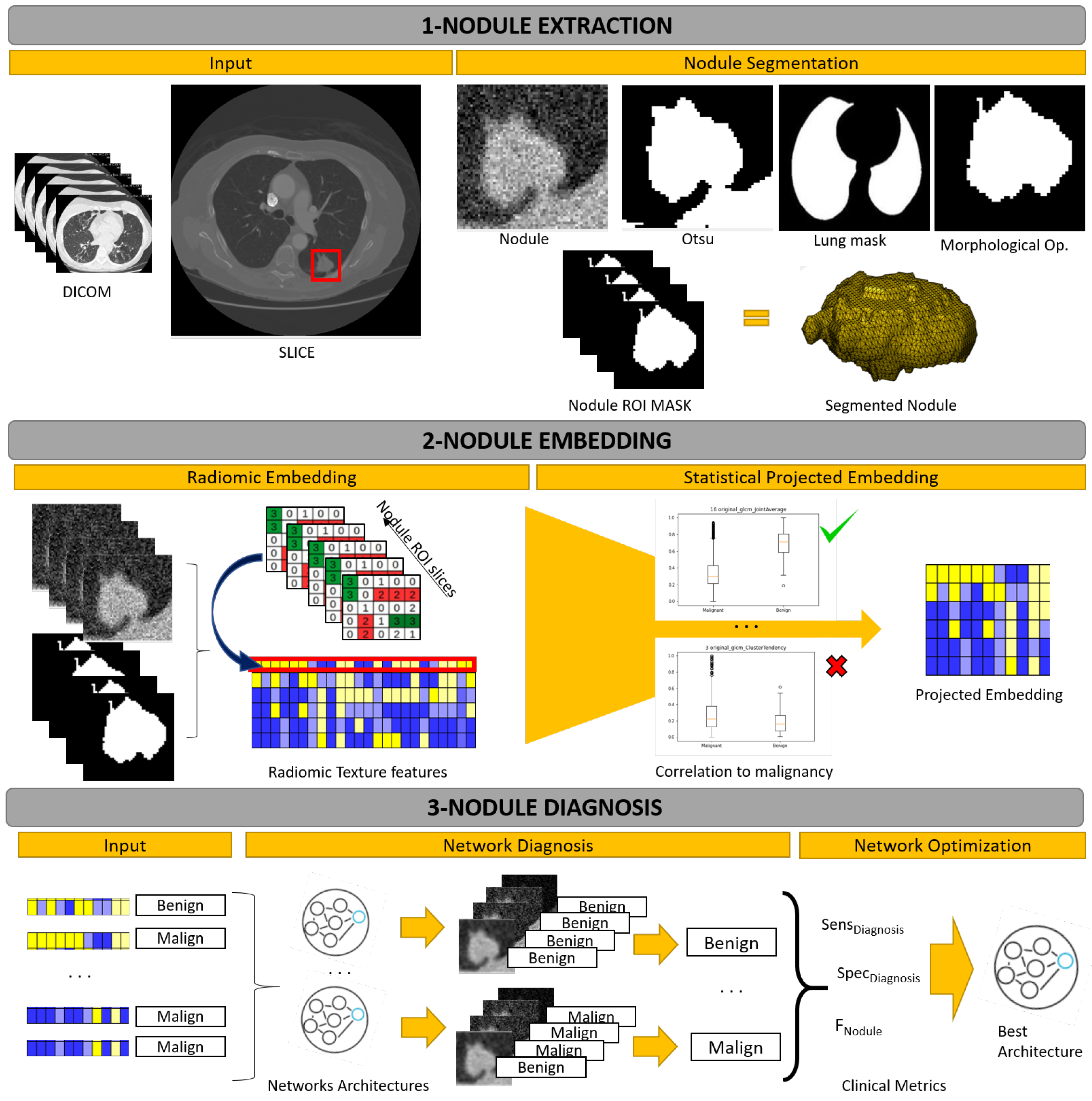
2.3. Nodule Extraction
2.4. Nodule Embedding
2.5. Nodule Diagnosis
2.6. Network Optimization
- 1.
- Diagnostic Sensitivity. This measures the percentage of correctly diagnosed malign nodules:for , denoting, respectively, true positives and false negatives for malignancy detection at nodule level.
- 2.
- Diagnostic Specificity. This measures the percentage of correctly diagnosed benign nodules:for , denoting, respectively, true negatives and false positives for benign detection at nodule level.
- 3.
- Slice Diagnostic Index. This index is an adaptation of the well-known F1-score to measure the percentage of correctly diagnosed slices:being and , the average sensitivity and specificity for the classification of 2D slices at nodule level. Sensitivity is given by:for the number of malign nodules, the true positives for the i-th malign nodule and its number of slices. Specificity is given by:for the number of benign nodules, the true positives for the i-th benign nodule and its number of slices.The score measures the trade-off between benign and malign accuracy at nodule level.
3. Results
- 1.
- Model Optimization. A training and selection of models, which consists in a leave-one-out validation on a training set of patients to select the best model for the benign and malignant classification. In order to assess the benefits of our embedding (labelled t-test), models were also trained using all 24 GLCM features (labelled None) and the selection based on reproducibility (labelled Reproducibility) reported in [31] excluding the shape class (see Table 5).
- 2.
- Model Verification. A testing and assessment of models reproducibility, which is a validation of the best model on an independent set of test patients to assess the reproducibility of results. To assess the advantages of the proposed strategy, the best model selected in the first experiment was compared to state of the art methods.
3.1. Model Optimization
3.2. Model Verification
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AUC | Area Under the Curve |
| CNN | Convolutional Neural Network |
| CT | Computed Tomography |
| GLCM | Gray Level Co-ocurrence Matrix |
| HU | Hounsfield Units |
| PN | Pulmonary Nodule |
| ROI | Region of Interest |
References
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- National Lung Screening Trial Research Team. The national lung screening trial: Overview and study design. Radiology 2011, 258, 243–253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.R.; Xie, X.; de Koning, H.J.; Mali, W.P.; Vliegenthart, R.; Oudkerk, M. NELSON lung cancer screening study. Cancer Imaging 2011, 11, S79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, H.; Yang, D.; Sun, N.; Chen, Z.; Zhang, Y. Automated pulmonary nodule detection in CT images using deep convolutional neural networks. Pattern Recognit. 2019, 85, 109–119. [Google Scholar] [CrossRef]
- de Koning, H.; van der Aalst, C.; de Jong, P. Screening met een thoracale lage-dosis-CT-scan vermindert de sterfte na 10 jaar door longkanker bij mannelijke actieve of ex-rokers. N. Engl. J. Med. 2020, 382, 503–513. [Google Scholar] [CrossRef]
- Zhang, F.; Song, Y.; Cai, W.; Lee, M.Z.; Zhou, Y.; Huang, H.; Shan, S.; Fulham, M.J.; Feng, D.D. Lung nodule classification with multilevel patch-based context analysis. IEEE Trans. Biomed. Eng. 2013, 61, 1155–1166. [Google Scholar] [CrossRef]
- Lee, S.L.A.; Kouzani, A.Z.; Hu, E.J. Random forest based lung nodule classification aided by clustering. Comput. Med. Imaging Graph. 2010, 34, 535–542. [Google Scholar] [CrossRef]
- Shen, W.; Zhou, M.; Yang, F.; Yu, D.; Dong, D.; Yang, C.; Zang, Y.; Tian, J. Multi-crop convolutional neural networks for lung nodule malignancy suspiciousness classification. Pattern Recognit. 2017, 61, 663–673. [Google Scholar] [CrossRef]
- Yan, X.; Pang, J.; Qi, H.; Zhu, Y.; Bai, C.; Geng, X.; Liu, M.; Terzopoulos, D.; Ding, X. Classification of lung nodule malignancy risk on computed tomography images using convolutional neural network: A comparison between 2d and 3d strategies. In Asian Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 91–101. [Google Scholar]
- Zhu, W.; Liu, C.; Fan, W.; Xie, X. Deeplung: Deep 3d dual path nets for automated pulmonary nodule detection and classification. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 673–681. [Google Scholar]
- Jiang, H.; Gao, F.; Xu, X.; Huang, F.; Zhu, S. Attentive and ensemble 3D dual path networks for pulmonary nodules classification. Neurocomputing 2020, 398, 422–430. [Google Scholar] [CrossRef]
- Jiang, H.; Shen, F.; Gao, F.; Han, W. Learning efficient, explainable and discriminative representations for pulmonary nodules classification. Pattern Recognit. 2021, 113, 107825. [Google Scholar] [CrossRef]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1997–2017. [Google Scholar]
- Armato, S.G., III; McLennan, G.; Bidaut, L.; McNitt-Gray, M.F.; Meyer, C.R.; Reeves, A.P.; Zhao, B.; Aberle, D.R.; Henschke, C.I.; Hoffman, E.A.; et al. The lung image database consortium (LIDC) and image database resource initiative (IDRI): A completed reference database of lung nodules on CT scans. Med. Phys. 2011, 38, 915–931. [Google Scholar] [PubMed]
- Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of variable selection methods for random forests and omics data sets. Briefings Bioinform. 2019, 20, 492–503. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J.P.; Luck, M.; Honari, S. Distribution matching losses can hallucinate features in medical image translation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 529–536. [Google Scholar]
- Maicas, G.; Bradley, A.P.; Nascimento, J.C.; Reid, I.; Carneiro, G. Training medical image analysis systems like radiologists. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 546–554. [Google Scholar]
- Bernatowicz, K.; Grussu, F.; Ligero, M.; Garcia, A.; Delgado, E.; Perez-Lopez, R. Robust imaging habitat computation using voxel-wise radiomics features. Sci. Rep. 2021, 11, 20133. [Google Scholar] [CrossRef]
- Kim, Y.J.; Lee, H.J.; Kim, K.G.; Lee, S.H. The effect of CT scan parameters on the measurement of CT radiomic features: A lung nodule phantom study. Comput. Math. Methods Med. 2019, 2019, 8790694. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, L.; Sun, S.H.; Lian, W.; Yang, H.; Schwartz, L.H.; Yang, Z.H.; Zhao, B. Effect of CT image acquisition parameters on diagnostic performance of radiomics in predicting malignancy of pulmonary nodules of different sizes. Eur. Radiol. 2021. [Google Scholar] [CrossRef] [PubMed]
- van Griethuysen, J.J.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.; Fillion-Robin, J.C.; Pieper, S.; Aerts, H.J. Computational radiomics system to decode the radiographic phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef] [Green Version]
- Beig, N.; Khorrami, M.; Alilou, M.; Prasanna, P.; Braman, N.; Orooji, M.; Rakshit, S.; Bera, K.; Rajiah, P.; Ginsberg, J.; et al. Perinodular and intranodular radiomic features on lung CT images distinguish adenocarcinomas from granulomas. Radiology 2019, 290, 783–792. [Google Scholar] [CrossRef]
- Calheiros, J.L.L.; de Amorim, L.B.V.; de Lima, L.L.; de Lima Filho, A.F.; Júnior, J.R.F.; de Oliveira, M.C. The Effects of Perinodular Features on Solid Lung Nodule Classification. J. Digit. Imaging 2021, 34, 798–810. [Google Scholar] [CrossRef]
- Gil, D.; Sanchez, C.; Borras, A.; Diez-Ferrer, M.; Rosell, A. Segmentation of distal airways using structural analysis. PLoS ONE 2019, 14, e0226006. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Tixier, F.; Le Rest, C.C.; Hatt, M.; Albarghach, N.; Pradier, O.; Metges, J.P.; Corcos, L.; Visvikis, D. Intratumor heterogeneity characterized by textural features on baseline 18F-FDG PET images predicts response to concomitant radiochemotherapy in esophageal cancer. J. Nucl. Med. 2011, 52, 369–378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, C.L.; Lian, M.J.; Wu, Y.H.; Chen, W.M.; Chiu, W.T. Identification of Human Ovarian Adenocarcinoma Cells with Cisplatin-Resistance by Feature Extraction of Gray Level Co-Occurrence Matrix Using Optical Images. Diagnostics 2020, 10, 389. [Google Scholar] [CrossRef] [PubMed]
- Leijenaar, R.T.; Nalbantov, G.; Carvalho, S.; Van Elmpt, W.J.; Troost, E.G.; Boellaard, R.; Aerts, H.J.; Gillies, R.J.; Lambin, P. The effect of SUV discretization in quantitative FDG-PET Radiomics: The need for standardized methodology in tumor texture analysis. Sci. Rep. 2015, 5, 11075. [Google Scholar] [CrossRef] [PubMed]
- Pomeroy, M.; Lu, H.; Pickhardt, P.J.; Liang, Z. Histogram-based adaptive gray level scaling for texture feature classification of colorectal polyps. In Medical Imaging 2018: Computer-Aided Diagnosis; International Society for Optics and Photonics: Houston, TX, USA, 2018; Volume 10575, p. 105752A. [Google Scholar]
- Tan, J.; Gao, Y.; Liang, Z.; Cao, W.; Pomeroy, M.J.; Huo, Y.; Li, L.; Barish, M.A.; Abbasi, A.F.; Pickhardt, P.J. 3D-GLCM CNN: A 3-dimensional gray-level Co-occurrence matrix-based CNN model for polyp classification via CT colonography. IEEE Trans. Med. Imaging 2019, 39, 2013–2024. [Google Scholar] [CrossRef] [PubMed]
- Ligero, M.; Torres, G.; Sanchez, C.; Diaz-Chito, K.; Perez, R.; Gil, D. Selection of radiomics features based on their reproducibility. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 403–408. [Google Scholar]
| Description\Manufacturer | GE Medical Systems | Philips |
|---|---|---|
| Model Name | LightSpeed VCT BrightSpeed Optima CT540 Discovery ST | GeminiGXL 16 Brilliance 16 TruFlight Select |
| Convoluton Kernel | SOFT STANDARD LUNG | B YA YB YC |
| Pixel XY size | 0.56–0.87 | 0.36–0.72 |
| Slice Thickness | 0.63–1.25 | 1–2 |
| Benign Nodules | 3 | 6 |
| Malignant Nodules | 21 | 30 |
| Description | Male | Female | Total | |
|---|---|---|---|---|
| Demographic population | Patients Age avg ± std Benign PNs Malign PNs | 36 70.67 ± 6.87 5 31 | 24 63.96 ± 12.35 4 20 | 60 67.98 ± 9.92 9 51 |
| Nodule characterization | Benign Slices min/max/avg Malign Slices min/max/avg | 6/111/48 8/152/45 | 28/39/32 12/82/45 | 6/111/41 8/152/43 |
| GLCM Textural Features | t-Test Selection |
|---|---|
| Autocorrelation | ✓ |
| Cluster Prominence | ✓ |
| Cluster Shade | ✓ |
| Cluster Tendency | ✓ |
| Contrast | × |
| Correlation | ✓ |
| Difference Average | × |
| Difference Entropy | ✓ |
| Difference Variance | × |
| Inverse Difference | ✓ |
| Inverse Difference Moment | ✓ |
| Inverse Difference Moment Normalized | × |
| Informational Measure of Correlation 1 | ✓ |
| Informational Measure of Correlation 2 | ✓ |
| Inverse Difference Normalized | × |
| Inverse Variance | ✓ |
| Joint Average | ✓ |
| Joint Energy | ✓ |
| Joint Entropy | ✓ |
| Maximum Probability | ✓ |
| Maximal Correlation Coefficient | ✓ |
| Sum Average | ✓ |
| Sum Entropy | ✓ |
| Sum Squares | ✓ |
| Num. | Architecture | # Trainable Parameters |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| Class | Feature |
|---|---|
| Fist Order | Entropy TotalEnergy Uniformity |
| GLCM | Inverse Difference Inverse Difference Moment Joint Energy Joint Entropy Maximum Probability |
| GLDM | Dependence Non Uniformity Normalized Dependence Variance Large Dependence Emphasis |
| GLRLM | Run Length Non Uniformity Normalized Run Percentage Short Run Emphasis |
| Model | Radiomic Embedding | Arch. Num. | Arch. Setting | Architecture | # Param. |
|---|---|---|---|---|---|
| Model 1 | None | 1 | 24, 6 | [(24,6),(6,6),(6,2)] | 206 |
| Model 2 | Reproducibility | 1 | 14, 8 | [(14,8),(8,8),(8,2)] | 210 |
| Model 3 | t-test | 1 | 19, 9 | [(19,9),(9,9),(9,2)] | 290 |
| Model 4 | None | 2 | 24, 9 | [(24,9),(9,9),(9,4),(9,2)] | 365 |
| Model 5 | Reproducibility | 2 | 14, 9 | [(14,9),(9,9),(9,4),(9,2)] | 275 |
| Model 6 | t-test | 2 | 19, 9 | [(19,9),(9,9),(9,4),(9,2)] | 320 |
| Model 7 | None | 3 | 24, 8 | [(24,8),(8,8),(8,8),(8,4),(4,2)] | 382 |
| Model 8 | Reproducibility | 3 | 14, 9 | [(14,9),(9,9,(9,9),(9,4),(4,2)] | 362 |
| Model 9 | t-test | 3 | 19, 9 | [(19,9),(9,9),(9,9),(9,4),(4,2)] | 407 |
| Model 10 | None | 4 | 24, 8 | [(24,8),(8,7)(7,6)(6,5),(5,4),(4,2)] | 305 |
| Model 11 | Reproducibility | 4 | 14, 14 | [(14,14),(14,13),(13,12),(12,11), (11,10),(10,2)] | 745 |
| Model 12 | t-test | 4 | 19, 8 | [(19,8),(8,7),(7,6),(6,5),(5,4),(4,2)] | 270 |
| Model | Radiomic Embedding | Weight Init. | Optimizer | Learning Rate | Epochs |
|---|---|---|---|---|---|
| Model 1 | None | Kaiming | RMSProp | 0.001 | 1500 |
| Model 2 | Reproducibility | Orthogonal | Adam | 0.001 | 1500 |
| Model 3 | t-test | Xavier | SGD | 0.001 | 1500 |
| Model 4 | None | Orthogonal | Adam | 0.001 | 1000 |
| Model 5 | Reproducibility | Xavier | Adam | 0.01 | 1000 |
| Model 6 | t-test | Xavier | Adam | 0.001 | 1000 |
| Model 7 | None | Orthogonal | Adam | 0.001 | 1000 |
| Model 8 | Reproducibility | Orthogonal | Adam | 0.001 | 1000 |
| Model 9 | t-test | Kaiming | Adam | 0.001 | 1000 |
| Model 10 | None | Kaiming | Adam | 0.001 | 1000 |
| Model 11 | Reproducibility | Xavier | Adam | 0.001 | 1000 |
| Model 12 | t-test | Orthogonal | Adam | 0.001 | 1000 |
| Model | |||
|---|---|---|---|
| Model 1 | 100 | 100 | 0.856 |
| Model 2 | 93.02 | 75 | 0.683 |
| Model 3 | 100 | 100 | 0.903 |
| Model 4 | 100 | 87.5 | 0.846 |
| Model 5 | 97.67 | 37.5 | 0.595 |
| Model 6 | 100 | 100 | 0.839 |
| Model 7 | 100 | 100 | 0.804 |
| Model 8 | 100 | 37.5 | 0.619 |
| Model 9 | 100 | 100 | 0.834 |
| Model 10 | 100 | 87.5 | 0.840 |
| Model 11 | 100 | 37.5 | 0.617 |
| Model 12 | 100 | 100 | 0.831 |
| Approaches | Accuracy | Sensitivity | Specificity | F1 Score | AUC | Param. (M) |
|---|---|---|---|---|---|---|
| Radiomics | ||||||
| Peikert et al. [5] | – | 90.40 | 85.50 | – | 0.939 | <0.29 |
| Machine Learning | ||||||
| Zhang et al. [6] | 96.09 | 96.84 | 95.34 | – | 0.979 | <0.29 |
| Deep CNN | ||||||
| Multicrop [8] | 87.14 | 77.00 | 93.00 | – | 0.930 | – |
| Nodule-level 2D [9] | 87.30 | 88.50 | 86.00 | 87.23 | 0.937 | – |
| Vanilla 3D [9] | 87.40 | 89.40 | 85.20 | 87.25 | 0.947 | – |
| DeepLung [10] | 90.44 | 81.42 | – | – | – | 141.57 |
| AE-DPN [11] | 90.24 | 92.04 | 88.94 | 90.45 | 0.933 | 678.69 |
| NASLung [12] | 90.77 | 85.37 | 95.04 | 89.04 | – | 16.84 |
| Hybrid | ||||||
| model3 (Our) | 96.30 | 100 | 83.33 | 97.67 | 0.940 | 0.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, G.; Baeza, S.; Sanchez, C.; Guasch, I.; Rosell, A.; Gil, D. An Intelligent Radiomic Approach for Lung Cancer Screening. Appl. Sci. 2022, 12, 1568. https://doi.org/10.3390/app12031568
Torres G, Baeza S, Sanchez C, Guasch I, Rosell A, Gil D. An Intelligent Radiomic Approach for Lung Cancer Screening. Applied Sciences. 2022; 12(3):1568. https://doi.org/10.3390/app12031568
Chicago/Turabian StyleTorres, Guillermo, Sonia Baeza, Carles Sanchez, Ignasi Guasch, Antoni Rosell, and Debora Gil. 2022. "An Intelligent Radiomic Approach for Lung Cancer Screening" Applied Sciences 12, no. 3: 1568. https://doi.org/10.3390/app12031568
APA StyleTorres, G., Baeza, S., Sanchez, C., Guasch, I., Rosell, A., & Gil, D. (2022). An Intelligent Radiomic Approach for Lung Cancer Screening. Applied Sciences, 12(3), 1568. https://doi.org/10.3390/app12031568






