Flexural Behavior of Self-Prestressed RC Slabs with Fe-Based Shape Memory Alloy Rebar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Specimens
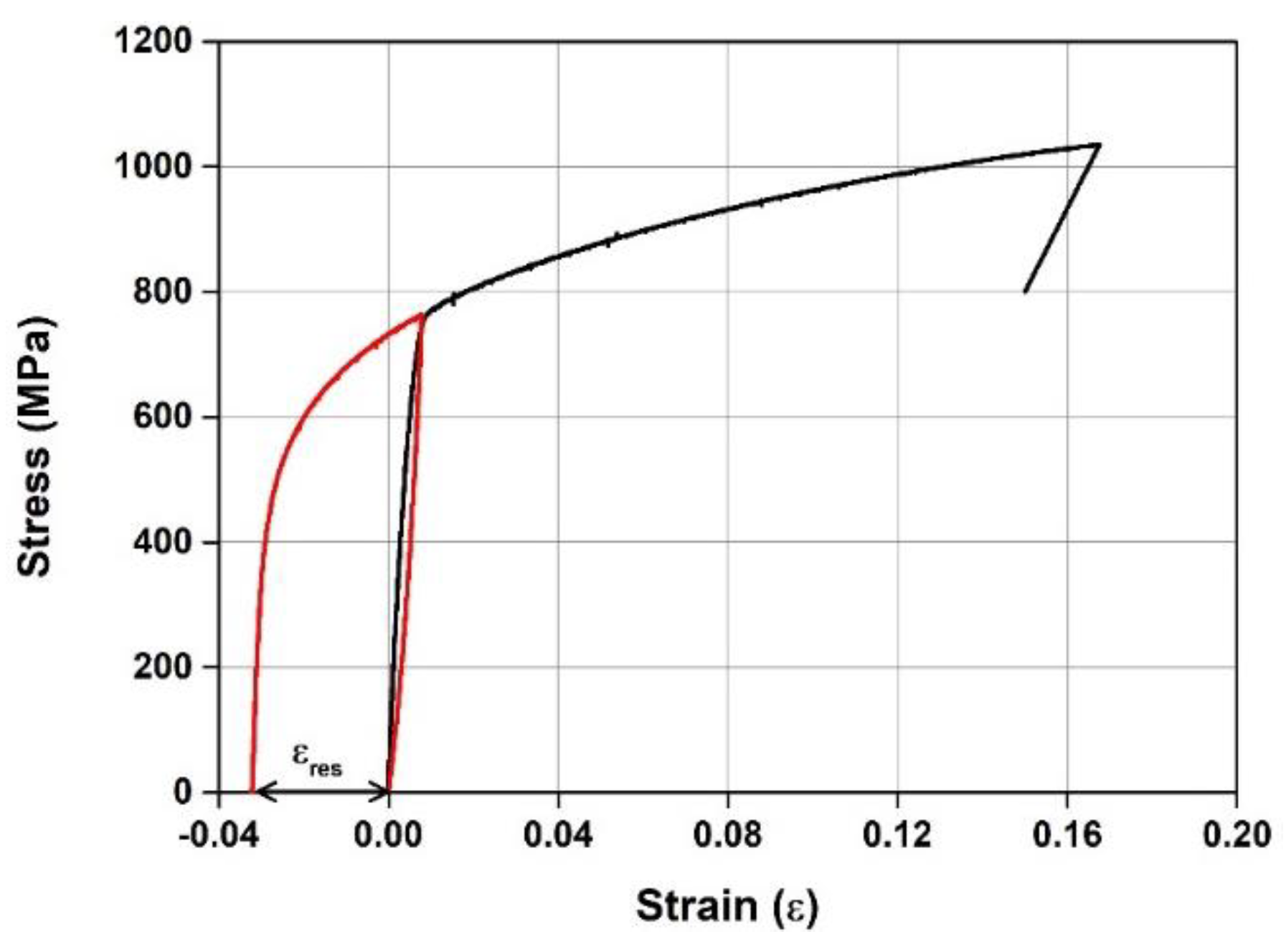
2.2. Materials
2.3. Test Set-Up
3. Experiment Results and Discussion
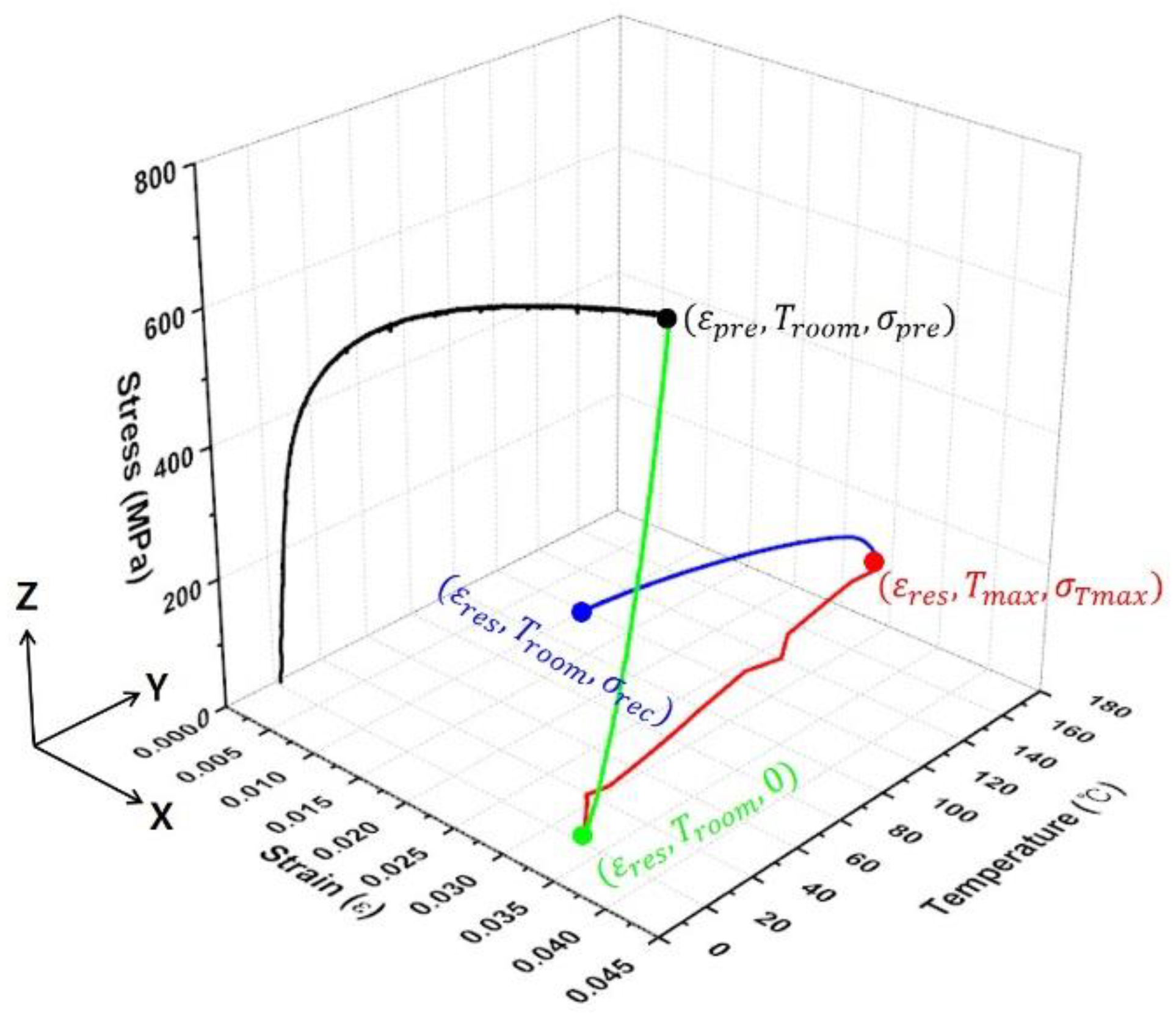
3.1. Activation of Fe-SMA Rebar
3.2. Failure Mode
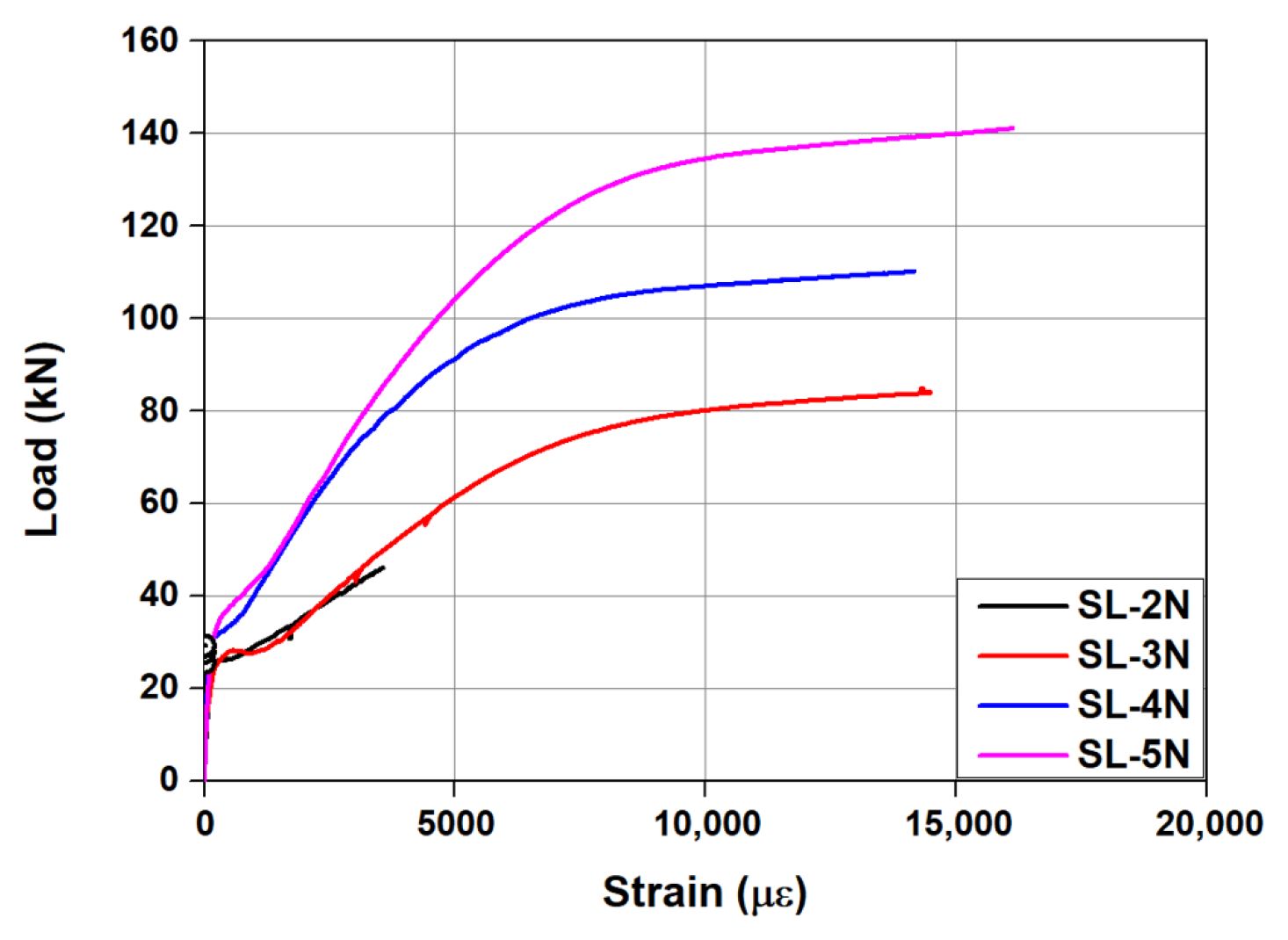
3.3. Load–Fe-SMA Rebar Strain Relationship
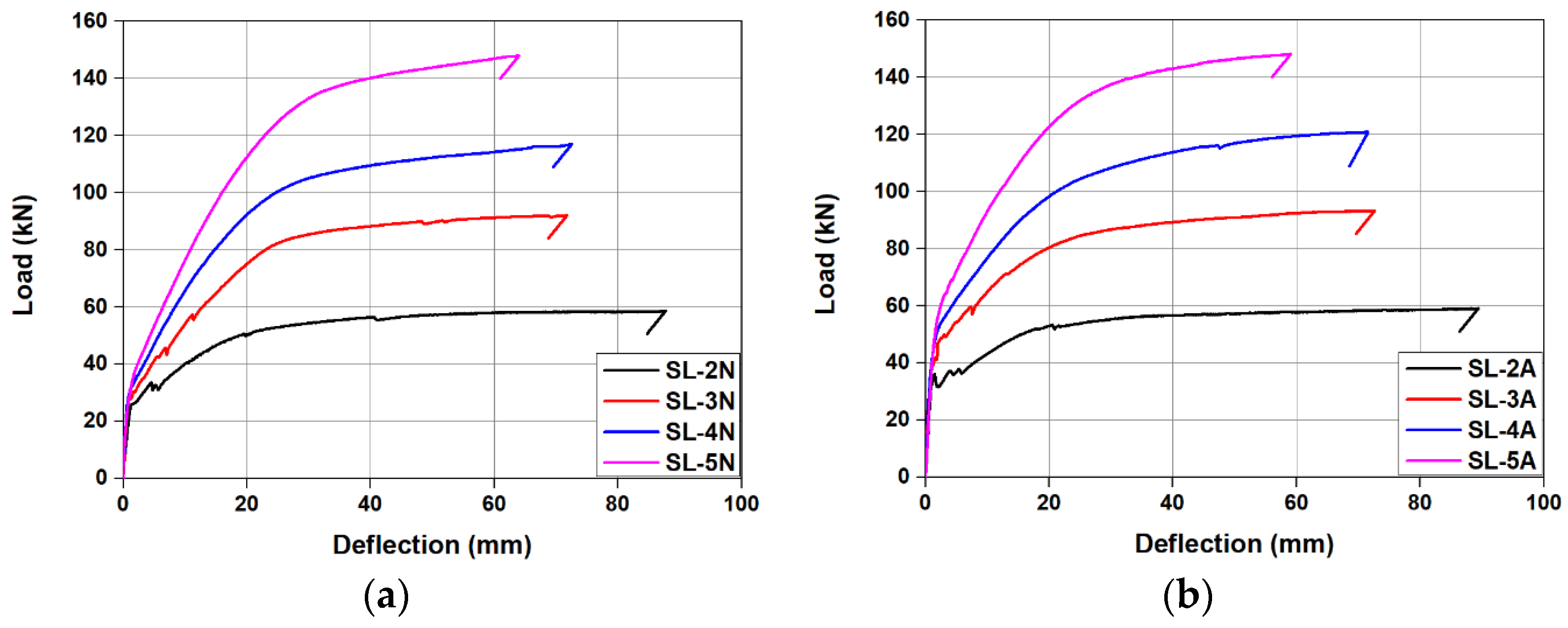
3.4. Load–Deflection Relationship
3.4.1. Effect of the Fe-SMA Rebar Activation
3.4.2. Effect of the Amount of Fe-SMA Rebar
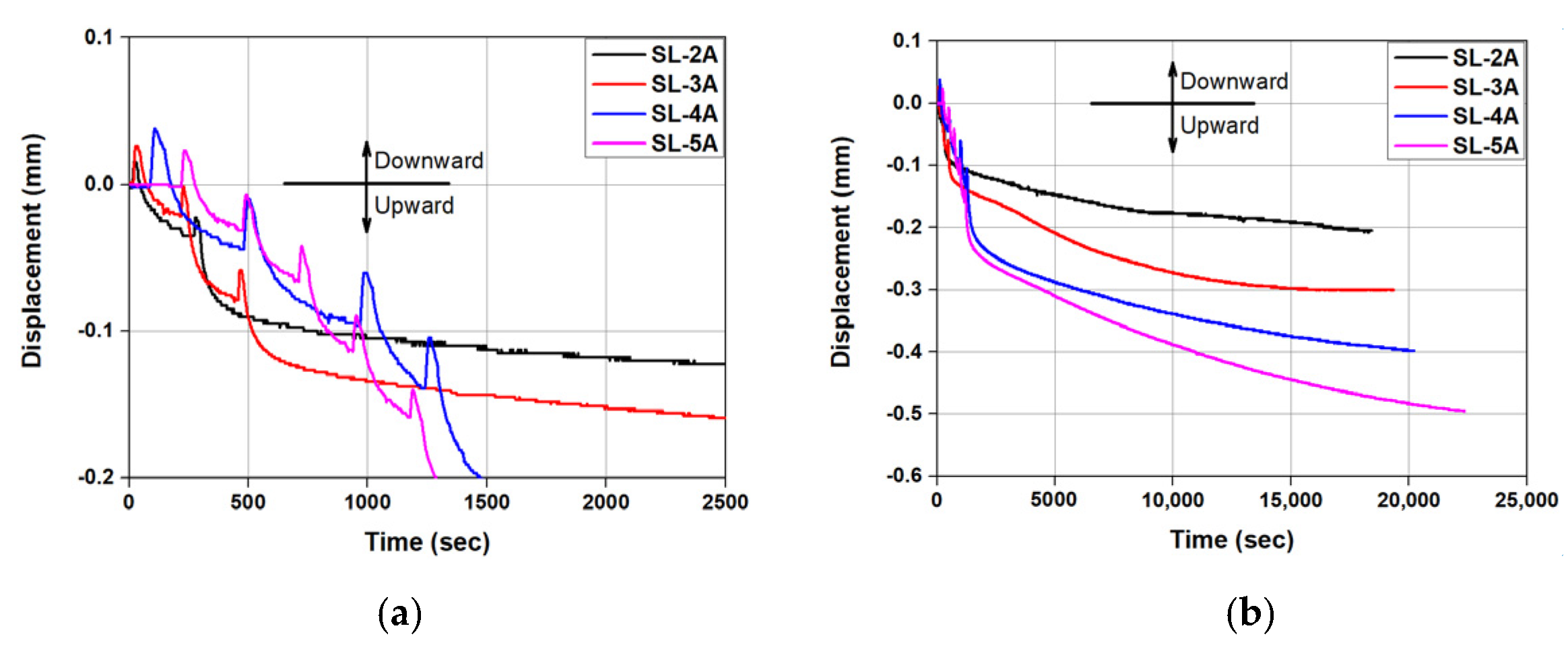
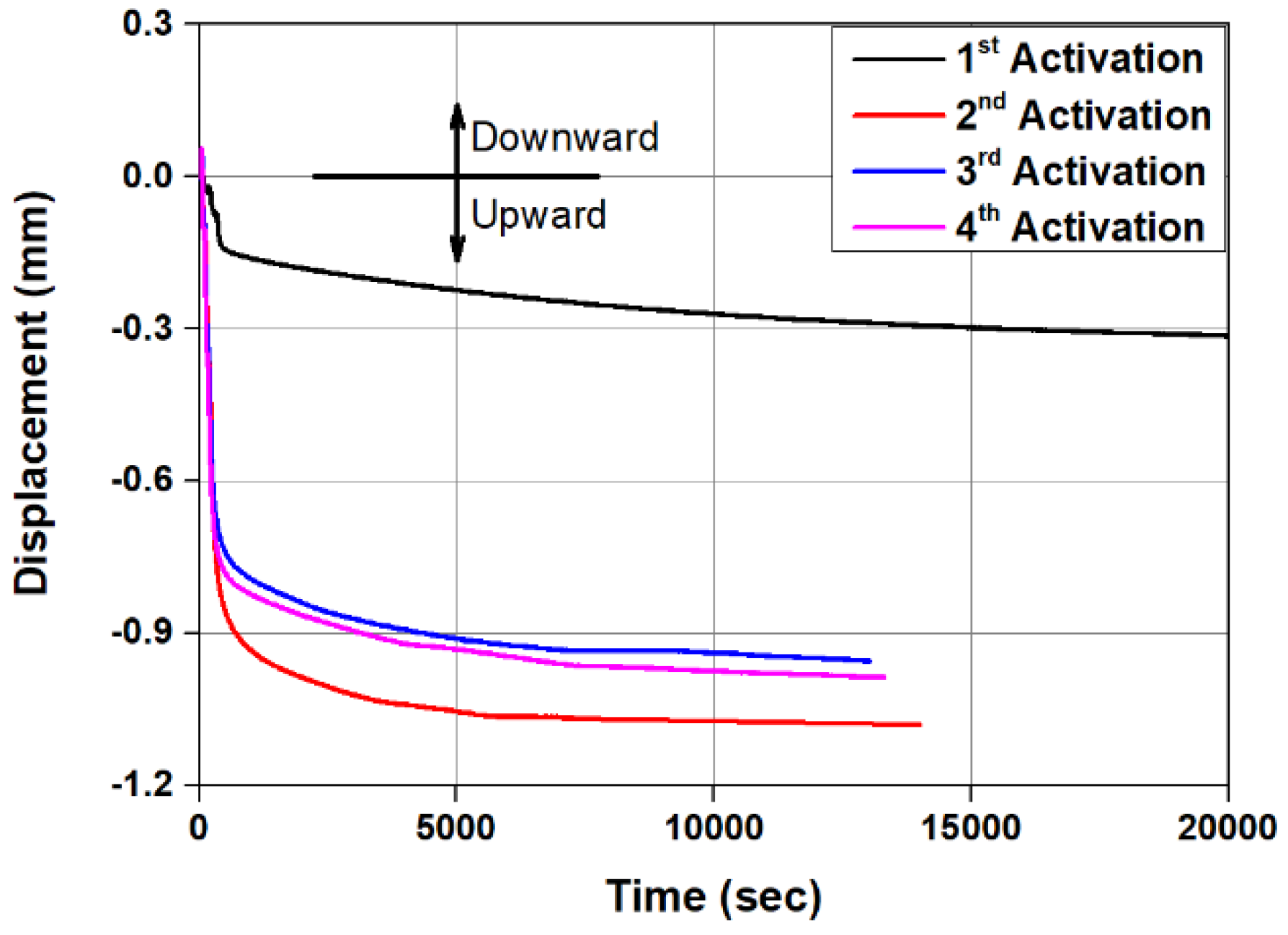
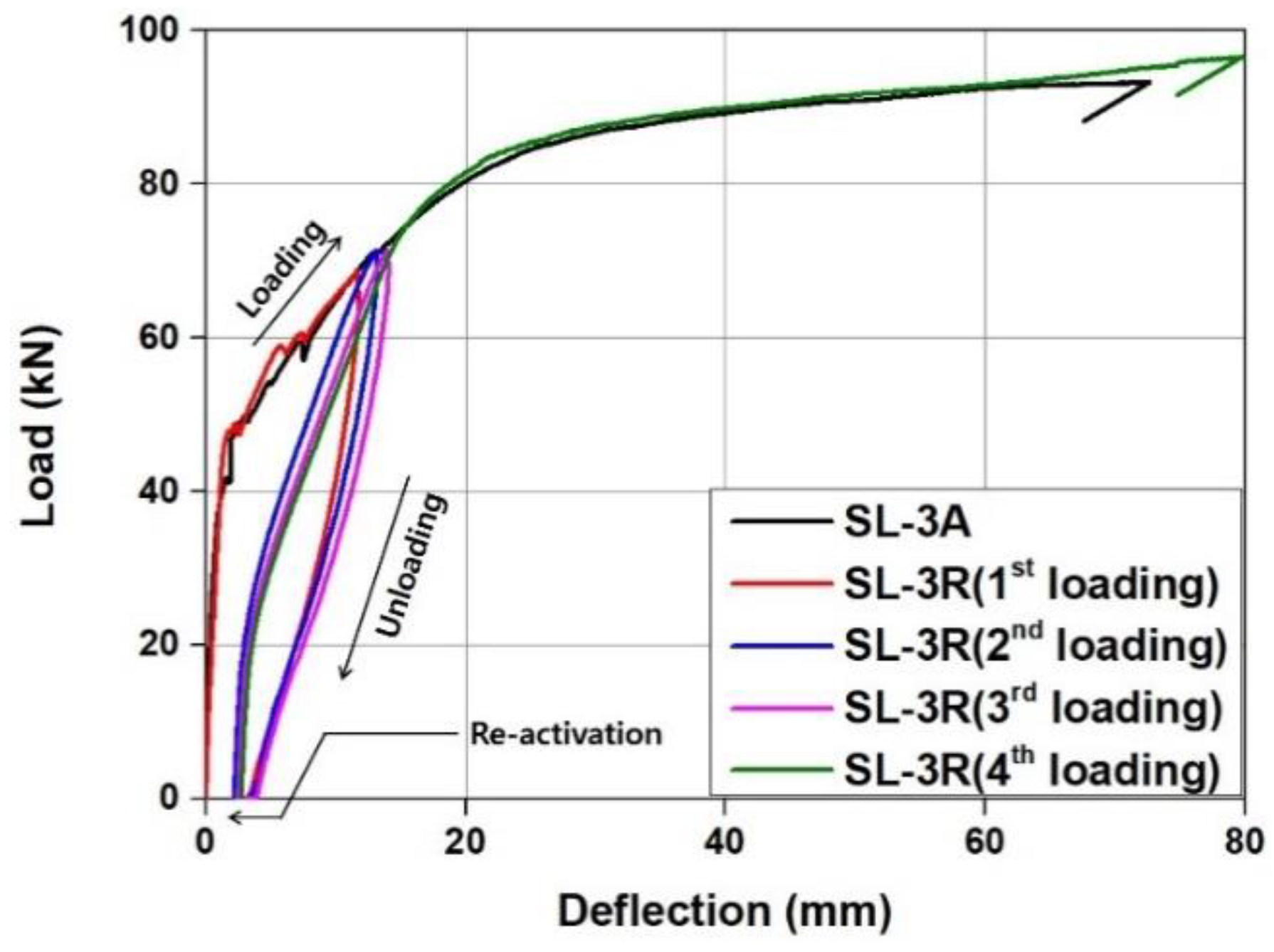
3.4.3. Reactivation of Fe-SMA Rebar
4. Conclusions
- Activation of the Fe-SMA rebar caused camber in the concrete member by applying an eccentric compressive force due to the recovery stress on the cross-section. This camber increased by an average of 0.096 mm when the amount of Fe-SMA reinforcement increased by 100 mm2.
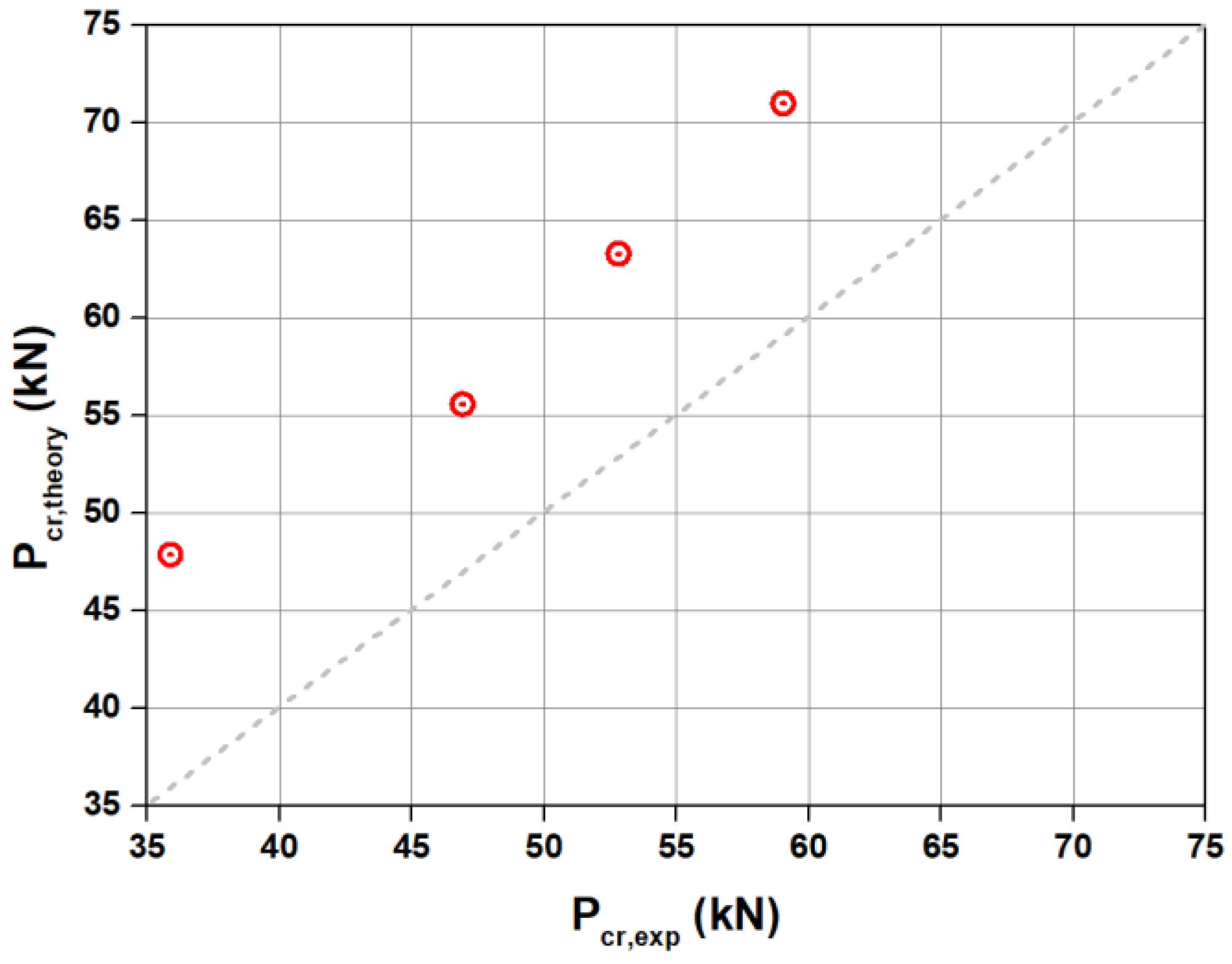
- The initial cracking load of the specimen with the activated Fe-SMA rebar was 40~101% greater than that of the non-activated specimen due to the action of the eccentric compressive load.
- The theoretically calculated initial crack load was 23% larger on average compared with the experimental value. This was considered to be due to the reduction of the recovery stress resulting from the thermal expansion at the Fe-SMA and concrete interface and the concrete hydration heat. Therefore, future studies are needed to quantitatively evaluate the effect of thermal expansion and hydration heat of concrete on the recovery stress of Fe-SMA rebar.
- The effect of the Fe-SMA rebar activation on the ultimate load of the concrete member was negligible. Therefore, it was confirmed that the introduction of prestress by activation of the Fe-SMA rebar, like traditional prestressed concrete, mainly increased the usability of the concrete member.
- The load–displacement relationship of the specimen with Fe-SMA rebars activated four times was similar to that of the specimen with Fe-SMA rebars activated once. Therefore, it was considered that the prestress force of the concrete reinforced with Fe-SMA rebar could be recovered through reactivation even if the prestress force was reduced due to various reasons, such as drying shrinkage and relaxation, unlike the conventional bonded prestressed concrete.
- Through this study, it was confirmed that the concrete prestressing method using the Fe-SMA rebar could solve several disadvantages of conventional prestressed concrete. Therefore, the self-prestressing method using Fe-SMA was expected to have high potential in the field of prestressed concrete for new construction.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, D.-K.; Han, S.-J.; Joo, H.-E.; Kim, K.-S. Control of tensile stress in prestressed concrete members under service loads. Int. J. Concr. Struct. Mater. 2017, 12, 425–437. [Google Scholar] [CrossRef]
- Silva, S.-D.; Mutsuyoshi, H.; Witchukrenangkrai, E. Evaluation of shear crack width in I-shaped prestressed reinforced concrete beams. J. Adv. Concr. Technol. 2008, 6, 443–458. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Zhou, Y.; Feng, C.; Liu, Z.; He, Z. Experimental and simulation analysis of prestressed concrete continuous box girder bridge. Rev. Tec. Ing. Univ. Zulia 2016, 39, 392–398. [Google Scholar]
- Caro, L.A.; Martí-Vargas, J.R.; Serna, P. Prestress losses evaluation in prestressed concrete prismatic specimens. Eng. Struct. 2013, 48, 704–715. [Google Scholar] [CrossRef]
- Lee, D.-S.; Kim, T.-K.; Lee, S.-C. Development and field application of portable tensioning system using segmental CFT member. J. Korean Soc. Civ. Eng. 2014, 34, 965–975. [Google Scholar] [CrossRef]
- Hong, S. Effect of prestress levels and jacking methods on friction losses in curved prestressed tendons. Appl. Sci. 2017, 7, 824. [Google Scholar] [CrossRef] [Green Version]
- Pischulev, A.; Panfilov, D.; Zhiltsov, Y. Experimental investigation of reinforced concrete beams using post-tension. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Abdelhalim, J. Prestressed Concrete Slabs with Bonded and Unbonded Tendons. Master’ Thesis, The American University in Cairo, Cairo, Egypt, 2021. [Google Scholar]
- Sun, X.-T.; He, W.-Y.; Wang, Z.-C.; Ren, W.-X. Grouting quality evaluation in post-tensioning tendon ducts using wavelet packet transform and bayes classifier. Sensors 2019, 19, 5372. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.; Jin, X.; Zhou, Y. Prestressed Concrete Structures; Springer: Berlin/Heidelberg, Germany, 2016; pp. 415–495. [Google Scholar] [CrossRef]
- Abdullah, A.B.M.; Rice, J.A.; Hamilton, H.R. Wire breakage detection using relative strain variation in unbonded posttensioning anchors. J. Bridge Eng. 2015, 20, 04014056. [Google Scholar] [CrossRef]
- Yoon, I.-S.; Kang, H.-K.; Shin, H.-Y. Evaluation of corrosion prevention systems of strands for PSC structures. J. Korea Concr. Inst. 2019, 31, 557–565. [Google Scholar] [CrossRef]
- Rojob, H.; El-Hacha, R. Self-prestressing using iron-based shape memory alloy for flexural strengthening of reinforced concrete beams. ACI Struct. J. 2017, 114, 523–532. [Google Scholar] [CrossRef]
- Debska, A.; Gwozdziewicz, P.; Seruga, A.; Balandraud, X.; Destrebecq, J.F. Prestress state evolution during thermal activation of memory efect in concrete beams strengthened with external SMA wire. Arch. Civ. Mech. Eng. 2020, 20, 142. [Google Scholar] [CrossRef]
- Hong, K.-N.; Yeon, Y.-M.; Shim, W.-B.; Kim, D.-H. Recovery behavior of Fe-based shape memory alloy under different restraints. Appl. Sci. 2020, 10, 3441. [Google Scholar] [CrossRef]
- Lee, W.J.; Weber, B.; Leinenbach, C. Recovery stress formation in a restrained Fe–Mn–Si-based shape memory alloy used for prestressing or mechanical joining. Constr. Build. Mater. 2015, 95, 600–610. [Google Scholar] [CrossRef]
- Kim, M.-S. Mechanical Properties and Shape Memory Properties of Ti50Ni50/Ti50Ni35Cu15 Functionally Graded Shape Memory. Sci. Adv. Mater. 2015, 12, 1586–1590. [Google Scholar] [CrossRef]
- Buehler, W.J.; Gilfrich, L.V.; Wiley, R.C. Effect of Low Temperature Phase Changes on the Mechanical Properties of Alloys Near Composition TiNi. J. Appl. Phys. 1963, 34, 1475–1477. [Google Scholar] [CrossRef]
- Yun, J.-H. Deterministic and Probabilistic Assessment of Seismic Performance of Bridges Retrofitted with Shape Memory Alloy. Doctoral Dissertation, Hanyang University, Seoul, Korea, 2008. [Google Scholar]
- Michels, J.; Shahverdi, M.; Czaderski, C. Flexural strengthening of structural concrete with iron-based shape memory alloy strips. Struct. Concr. 2018, 19, 876–891. [Google Scholar] [CrossRef]
- Shahverdi, M.; Czaderski, C.; Motavalli, M. Iron-based shape memory alloys for prestressed near-surface mounted strengthening of reinforced concrete beams. Constr. Build. Mater. 2016, 112, 28–38. [Google Scholar] [CrossRef]
- Shahverdi, M.; Michels, J.; Czaderski, C.; Motavalli, M. Iron-based shape memory alloy strips for strengthening RC members: Material behavior and characterization. Constr. Build. Mater. 2018, 173, 586–599. [Google Scholar] [CrossRef]
- Abouali, S.; Shahverdi, M.; Ghassemieh, M.; Motavalli, M. Nonlinear simulation of reinforced concrete beams retrofitted by near surface mounted iron based shape memory alloy. Eng. Struct. 2019, 187, 133–148. [Google Scholar] [CrossRef]
- Hong, K.-N.; Lee, S.-G.; Han, S.-H.; Yeon, Y.-M. Evaluation of Fe-based shape memory alloy (Fe-SMA) as strengthening material for reinforced concrete structures. Appl. Sci. 2016, 8, 730. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Kim, Y.; Oak, J.-J.; Lee, J.; Park, C.-H.; Lee, W.; Park, Y. Effect of Ni, C and Ti addition on shape recovery behavior and the mechanical properties of Fe-17Mn-5Si-5Cr shape memory alloy. Korean J. Met. Mater. 2020, 58, 660–671. [Google Scholar] [CrossRef]
- Yeon, Y.-M.; Hong, K.-N.; Shim, W.-B. Iron-based shape memory alloy strips for strengthening RC members: Material behavior and characterization Long-term behaivor of reinforced concrete beams strengthened with near-surface mounted Fe-based shape memory alloy strips. J. Korean. Soc. Adv. Comp. Struc. 2020, 11, 11–17. [Google Scholar] [CrossRef]
- Hosseini, E.; Ghafoori, E.; Leinenbach, C.; Motavalli, M.; Holdsworth, S.R. Stress recovery and cyclic behaviour of an Fe–Mn–Si shape memory alloy after multiple thermal activation. Smart Mater. Struct. 2018, 27, 025009. [Google Scholar] [CrossRef] [Green Version]
- ASTM C39/C39M-17; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017.
- Lee, W.-J.; Partovi-Nia, R.; Suter, T.; Leinenbach, C. Electrochemical Characterization and Corrosion Behavior of an Fe-Mn-Si Shape Memory Alloy in Simulated Concrete Pore Solutions. Mater. Corros. 2015, 67, 839–846. [Google Scholar] [CrossRef]
- Park, S.-J.; Yim, H.-J.; Kwak, H.-G. Evaluation of microcracks in thermal damaged concrete using nonlinear ultrasonic modulation technique. J. Korea Concr. Inst. 2012, 24, 651–658. [Google Scholar] [CrossRef] [Green Version]
- Yeon, Y.-M. Evaluation of Prestressing Effect for Fe-Based Shape Memory Alloy. Master Thesis, Chungbuk National University, Cheongju, Korea, 2018. [Google Scholar]
- ACI. Building Code Requirements for Structural Concrete; ACI 318-08; ACI: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Santhanam, N.; Anbuarasu, G. Experimental Study on High Strength Concrete (M60) with Reused E-Waste Plastics. Mater. Today Proceed. 2019, 22, 919–925. [Google Scholar] [CrossRef]
- Jaung, J.-D.; Cho, H.-D.; Park, S.-W. Properties of hydration heat of high-strength concrete and reduction strategy for heat production. J. Korea Insititute Build. Constr. 2012, 12, 203–210. [Google Scholar] [CrossRef] [Green Version]
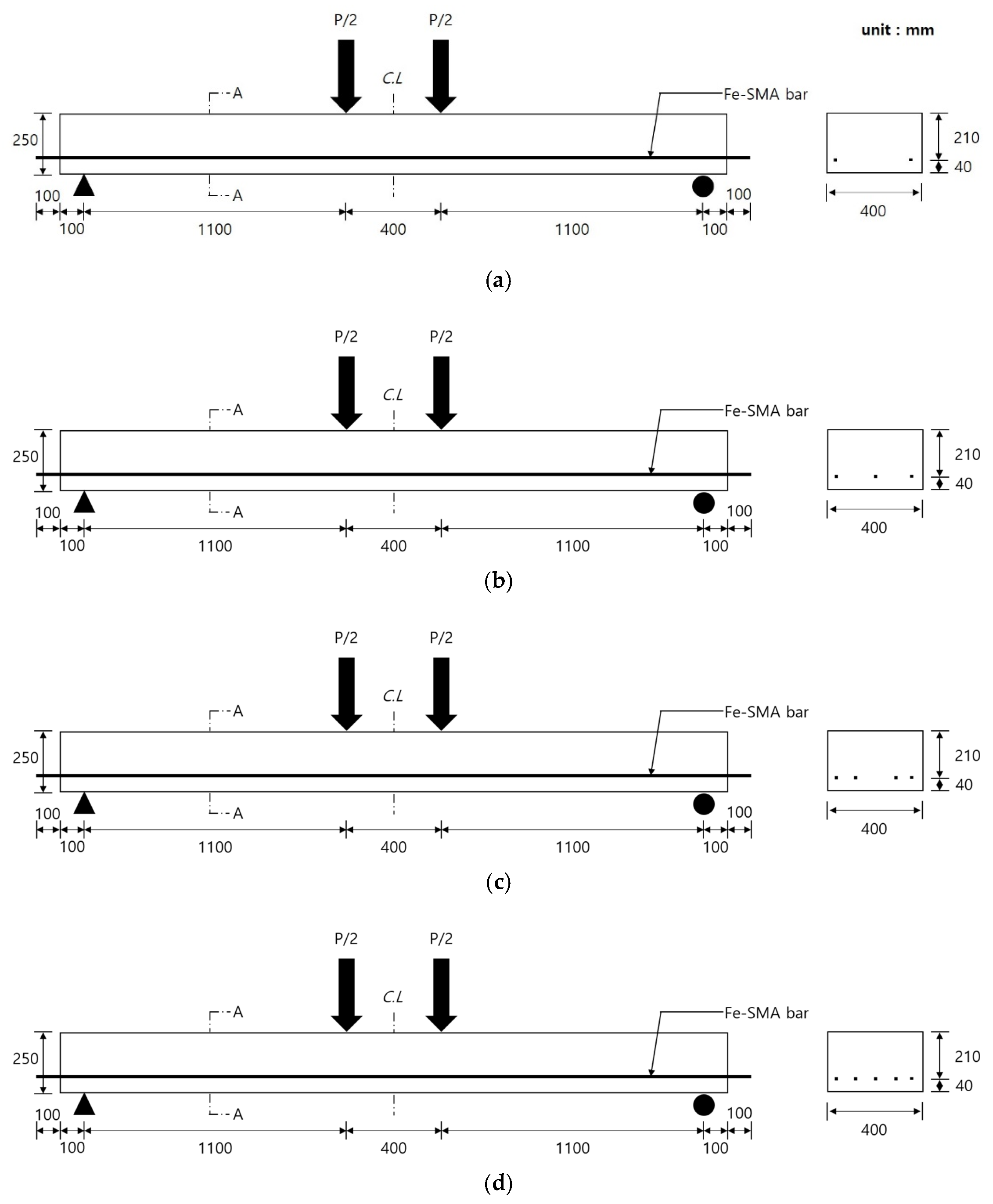





| Specimen | Area of Fe-SMA Rebar (mm2) | Activation |
|---|---|---|
| SL-2N | 200 | Non-activation |
| SL-2A | Activation | |
| SL-3N | 300 | Non-activation |
| SL-3A | Activation | |
| SL-3R | Re-activation | |
| SL-4N | 400 | Non-activation |
| SL-4A | Activation | |
| SL-5N | 500 | Non-activation |
| SL-5A | Activation |
| Slump (cm) | Air Content (%) | W/B (%) | S/a (%) | Weight Per Unit Volume (kg/m3) | ||||
|---|---|---|---|---|---|---|---|---|
| W | C | S | G | AD | ||||
| 12 | 4.5 | 30.7 | 47 | 192 | 625 | 684 | 780 | 4.38 |
| Specimen | Initial Crack | Ultimate | Failure Mode | ||
|---|---|---|---|---|---|
| Deflection (mm) | Load (kN) | Deflection (mm) | Load (kN) | ||
| SL-2N | 1.45 | 25.59 | 87.69 | 58.66 | Flexural |
| SL-2A | 1.42 | 35.88 | 89.34 | 59.05 | |
| SL-3N | 1.2 | 27.73 | 74.73 | 92.04 | |
| SL-3A | 1.99 | 46.92 | 72.59 | 93.23 | |
| SL-3R | 2.35 | 45.66 | 79.77 | 94.87 | |
| SL-4N | 0.88 | 29.06 | 75.52 | 117.01 | |
| SL-4A | 3.24 | 52.81 | 71.53 | 120.82 | |
| SL-5N | 1.00 | 29.28 | 96.95 | 147.91 | |
| SL-5A | 2.33 | 59.03 | 59.03 | 148.09 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeon, Y.-M.; Hong, K.-N.; Ji, S.-W. Flexural Behavior of Self-Prestressed RC Slabs with Fe-Based Shape Memory Alloy Rebar. Appl. Sci. 2022, 12, 1640. https://doi.org/10.3390/app12031640
Yeon Y-M, Hong K-N, Ji S-W. Flexural Behavior of Self-Prestressed RC Slabs with Fe-Based Shape Memory Alloy Rebar. Applied Sciences. 2022; 12(3):1640. https://doi.org/10.3390/app12031640
Chicago/Turabian StyleYeon, Yeong-Mo, Ki-Nam Hong, and Sang-Won Ji. 2022. "Flexural Behavior of Self-Prestressed RC Slabs with Fe-Based Shape Memory Alloy Rebar" Applied Sciences 12, no. 3: 1640. https://doi.org/10.3390/app12031640
APA StyleYeon, Y.-M., Hong, K.-N., & Ji, S.-W. (2022). Flexural Behavior of Self-Prestressed RC Slabs with Fe-Based Shape Memory Alloy Rebar. Applied Sciences, 12(3), 1640. https://doi.org/10.3390/app12031640






