Next Article in Journal
Analysis of Intracerebral Activity during Reflex Locomotion Stimulation According to Vojta’s Principle
Previous Article in Journal
Analytical Design of Fractional-Order PI Controller for Parallel Cascade Control Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 12
Issue 4
10.3390/app12042223
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Laser Vibration Characteristics of Marble Specimens and Failure Criterion

by
Qiang Xie
1,
Jun Duan
1,2,
Yuxin Ban
1,3,*,
Xiang Fu
4,* and
Shilin Liu
5
1
School of Civil Engineering, Chongqing University, 83 Shabei Street, Chongqing 400045, China
2
School of Architecture and Civil Engineering, Chongqing Metropolitan College of Science and Technology, Yongchuan District, Chongqing 402167, China
3
School of Civil Engineering and Architecture, Chongqing University of Science & Technology, Chongqing 401331, China
4
College of River and Ocean Engineering, Chongqing Jiaotong University, 66 Xuefu Street, Chongqing 400074, China
5
Housing and Urban-Rural Construction Bureau of Ping’an District, 190 Ping’an Street, Haidong 810600, China
*
Authors to whom correspondence should be addressed.
Appl. Sci. 2022, 12(4), 2223; https://doi.org/10.3390/app12042223
Submission received: 20 December 2021 / Revised: 4 February 2022 / Accepted: 14 February 2022 / Published: 21 February 2022
Browse Figures
Versions Notes

Abstract

:
Rock failure and instability usually lead to significant engineering disasters. This paper aims to establish an experimental failure criterion to predict rock failure via testing the laser vibration characteristics of marble specimens. Uniaxial compression tests and Brazilian tests were carried out on marble specimens coupled with acoustic emission technology and laser Doppler vibrometry measurement technology. The whole laser vibration waveform of the marble specimen was divided into elastic stage, plastic stage, and failure stage. Although different frequency spectrum characteristics were identified in different waveform phases, a wide frequency spectrum was always present prior to rock failure. Furthermore, the wide frequency band frequency spectra characteristics took place 30.9 s and 21.3 s earlier than the rapid increase of the acoustic emission counts in the uniaxial compression test and Brazilian test, respectively. Taking the wide frequency spectrum as a failure criterion for the failure of loaded marble is quick, convenient, and reasonable. Using laser Doppler vibrometry measurement has the advantages of being remote, non-contacting, and earlier warning. This research can provide a reference for the further study of forecasting rock failure.

1. Introduction

Laser vibration measurement employing Laser Doppler Vibrometers (LDV) is advantageous in the vibration measurement of structural engineering, as it is optical, remote, non-contacting, and highly sensitive [1,2]. However, the application of laser vibration measurement in civil engineering is still limited. For example, Fujino et al. [3] established a vibration measurement system with LDV and detected the damage on a reinforced concrete deck. Chen and Petro [4] tested the tension level of bridge cable via the non-contacting LDV, and they concluded that the technique was much more effective than the traditional contact measurements. Matsuoka et al. [5] established a practical displacement detection method for a railway bridge through the non-contact ion laser Doppler system. De Grassi et al. [6] showed the application of in situ measurements of a slab on the building’s external wall peeling off and falling to the ground.
In geotechnical engineering, new technologies such as LDV are in urgent need for assessing rock stability [7]. Applications of LDV have been commented on in the scientific literature to monitor deformation [8] or to evaluate rockfall hazards [9]. Slope model experiments were conducted to evaluate the influence of discontinuities on rock slope stability. In this type of experiment, a block is put on the slope of a triangular block, and their interfaces are treated as potential slip surfaces. Ma et al. [10] concluded that the LDV could precisely measure the dominant frequency of the block, which was an effective index for evaluating the stability of the rock mass. Du et al. [11] and Jia et al. [12] further considered the freeze-thawing condition and pointed out that the fundamental natural frequency monitored by LVD could be used to calculate the strength reduction factor and accurately describe the rock stability. Frequency response monitoring is a practical and reasonable method to evaluate the stability of hazardous rock blocks.
Acoustic emission (AE) is defined as the transient elastic waveform released by the accumulated localized energy, which is induced by microcrack initiation or expansion [13]. AE technology is now widely used in rock experiments and field monitoring, reflecting the evolution and propagation of cracks [14,15]. It was concluded that the instantaneously sharp increase of AE parameters (e.g., AE rate, AE counts, and AE energy) are representative of rock failure [16]. For example, Zhang et al. [17] divided the AE variation process of rock into a slow growth stage and an accelerated growth stage. Chen et al. [18] found that AE activities were affected by moisture content in rock. The AE counts were stable in the elastic deformation phase, increased rapidly in the plastic phase, and sharply increased in the failure stage. The rapid increase of AE counts represents the rapid development of microcracks, and the sharp increase indicated that the specimens began fracturing. This viewpoint has been verified by many researchers [19,20,21]. Xu et al. [22] pointed out that damage occurred at the high-stress level after sufficient energy was accumulated. Based on laboratory results, AE microearthquake monitoring and early warning equipment was developed to forecast coal and gas outburst dynamic disasters [23].
Recently, researchers have turned to focus on waveform-based frequency spectra characteristics. For example, Manthei et al. [24,25] confirmed that the results possessed conformality by using different AE waveform-based algorithms and pointed out that the AE waveform characteristics could be used to analyze the source mechanism. Ban et al. [13,26] revealed the failure morphology and failure mechanism of shale specimens by distinguishing the high and low AE dominant frequency. Li et al. [27] conducted Brazilian tests on marble discs and reported that the high AE dominant frequency was caused by shear failure and the low AE dominant frequency was caused by tensile failure. Aggelis et al. [28] reported that AE frequency signals could be used as a warning against the failure of steel fiber reinforced concrete. However, the AE frequency spectra characteristics are not used for forecasting rock failure. Consequently, the AE real-time monitor is simultaneously conducted to compare the laser vibration signals and LDV signals in evaluating and forecasting rock failure in this study. Although both laser vibration and AE measurements are waveform-based, they are significantly different in that the AE technology is acoustical and contacting, as the sensors should be attached to the surfaces of the specimens.
Previous research indicates that the non-contacting, remote LDV is effective for evaluating slope stability. However, only the potential sliding surface is considered, while the rupture of loaded rock is not studied. Consequently, the frequency evolution characteristics of marble are tested under uniaxial compression and indirect tensile stress. This study aims to reveal the characteristics of laser vibration waveforms and propose failure criteria for rock failure in the laboratory, which may provide some experimental references for the early warning of geological disasters, such as rock slope slide and collapse.

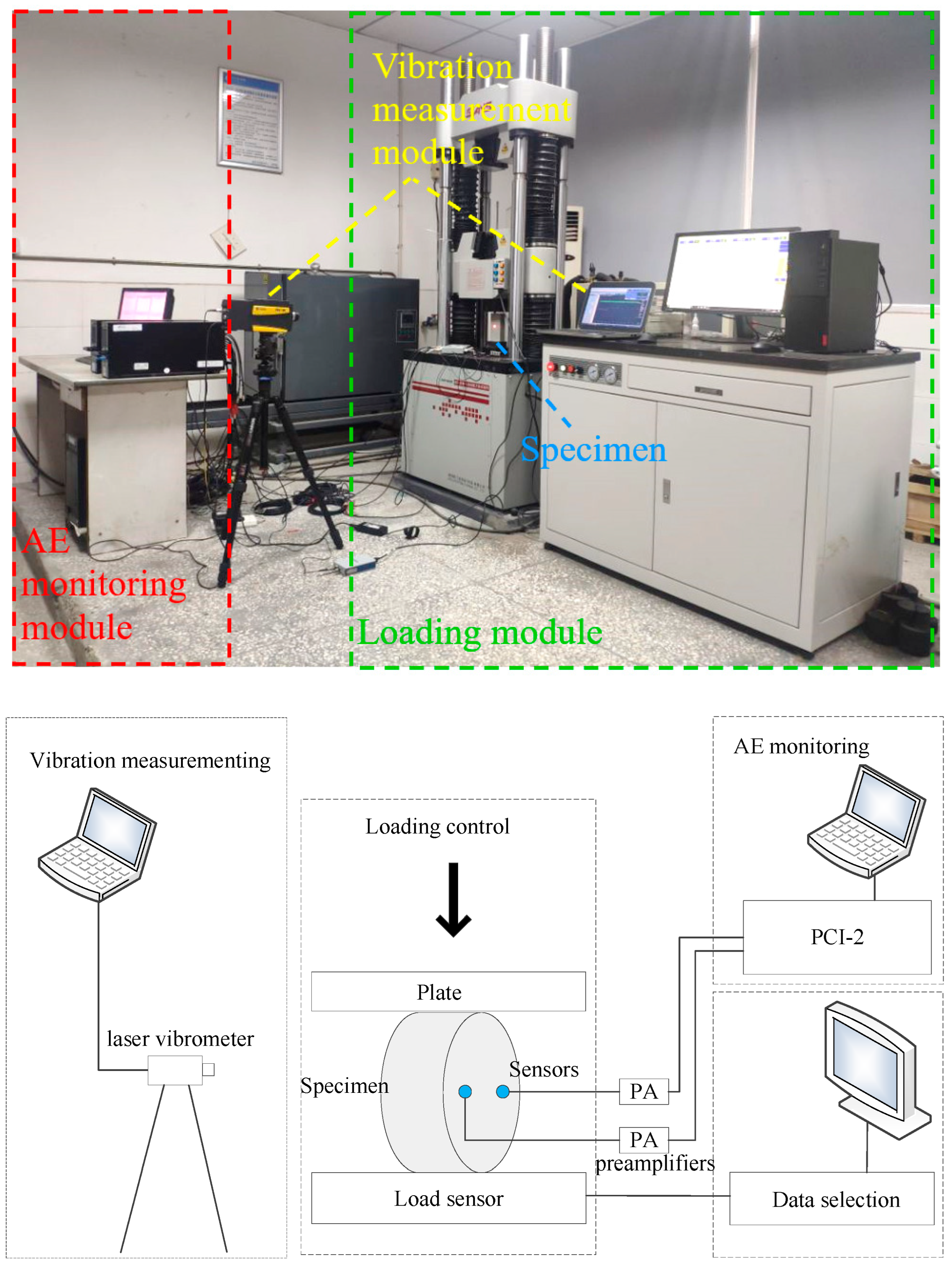
2. Experiment Setup

2.1. Testing System

The loading-acoustical-optical testing system consists of a loading module, real-time AE monitoring module, and a vibration measurement module with a laser, as shown in Figure 1. The SHT-4605 servo-controlled rock mechanics machine from the MTS System (China) Company was used for loading, whose maximum loading was 600 kN and working frequency was as low as approximately 0.6 Hz. The 8-channel PCI-2 AE equipment from PAC Company was adopted. Two wide-frequency WD sensors were attached to the back surface of the rock specimen to monitor the acoustical signals in real time. The sensor exhibits a response frequency range of 125–1000 kHz. The signals from the AE sensors were amplified by 40 dB using preamplifiers. The sampling rate of the AE system was 2 MSPS (Mega Samples per Second), and the sampling threshold was set as 40 dB. The PDV-100 laser vibrometer from Polytec in German was used. The sampling rate of laser measurement was 1 kHz. The loading speeds of uniaxial compression tests and Brazilian tests were 0.5 kN/s and 0.1 kN/s, respectively.

2.2. Specimen Preparation

The marble specimens were processed into 100 × 50 mm discs for Brazilian tests and 152 × 78 × 32 mm prismatic for uniaxial compression tests. The average tensile strength and uniaxial compressive strength of the marble specimens were 9.73 MPa and 94.50 MPa, respectively.

3. Results

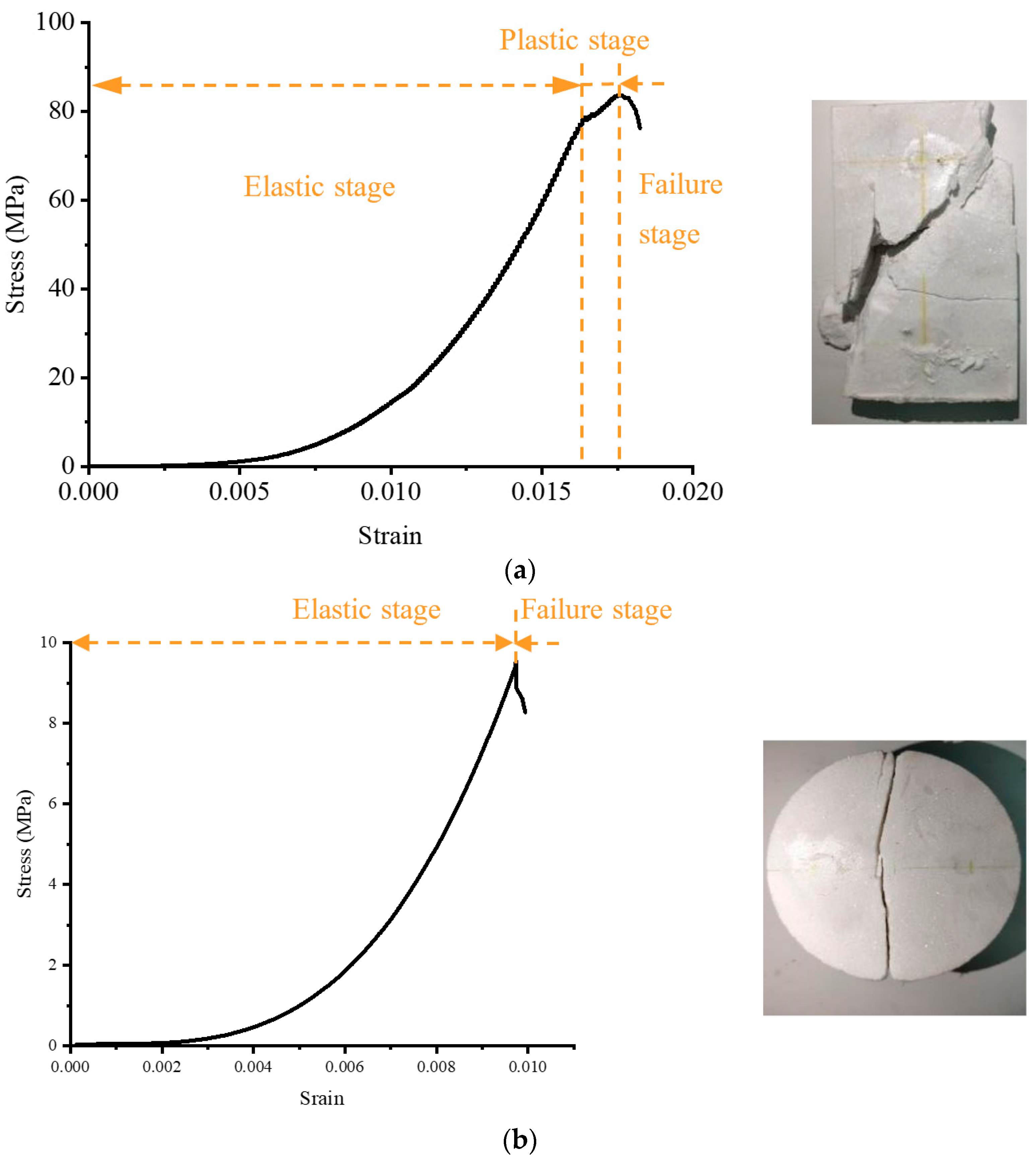
3.1. Failure of Marble Specimens

Figure 2 shows the stress-strain relationship and failure mode of marble in the uniaxial compression test and Brazilian test. The stress-strain curve in a uniaxial compression test can be divided into three stages: elastic stage, plastic stage, and failure stage. In the elastic stage, the stress-strain curves exhibit typical downward convex characteristics, and a linear elastic phenomenon is observed. After that, the strain quickly increases while the stress increases slow down, indicating that the marble specimen enters a plastic deformation stage. Finally, the stress sharply decreases, and the specimen fails. However, the plastic deformation is not reflected by the stress-strain curve in the Brazilian test. This phenomenon is also demonstrated by Sharafisafa et al. [29]; the rock with small blocks exhibits only elastic and failure stages under the effect of indirect tensile stress.
Typical fracture morphologies are obtained for rock brittle failure. An approximate 45° shear failure surface separates the marble specimen, and there is local material spalling on the surface when the specimen is subjected to uniaxial compression stress. The marble specimen broke into two blocks along the central fracture in the Brazilian test, indicating that the central area was subject to lateral tensile stress [30].

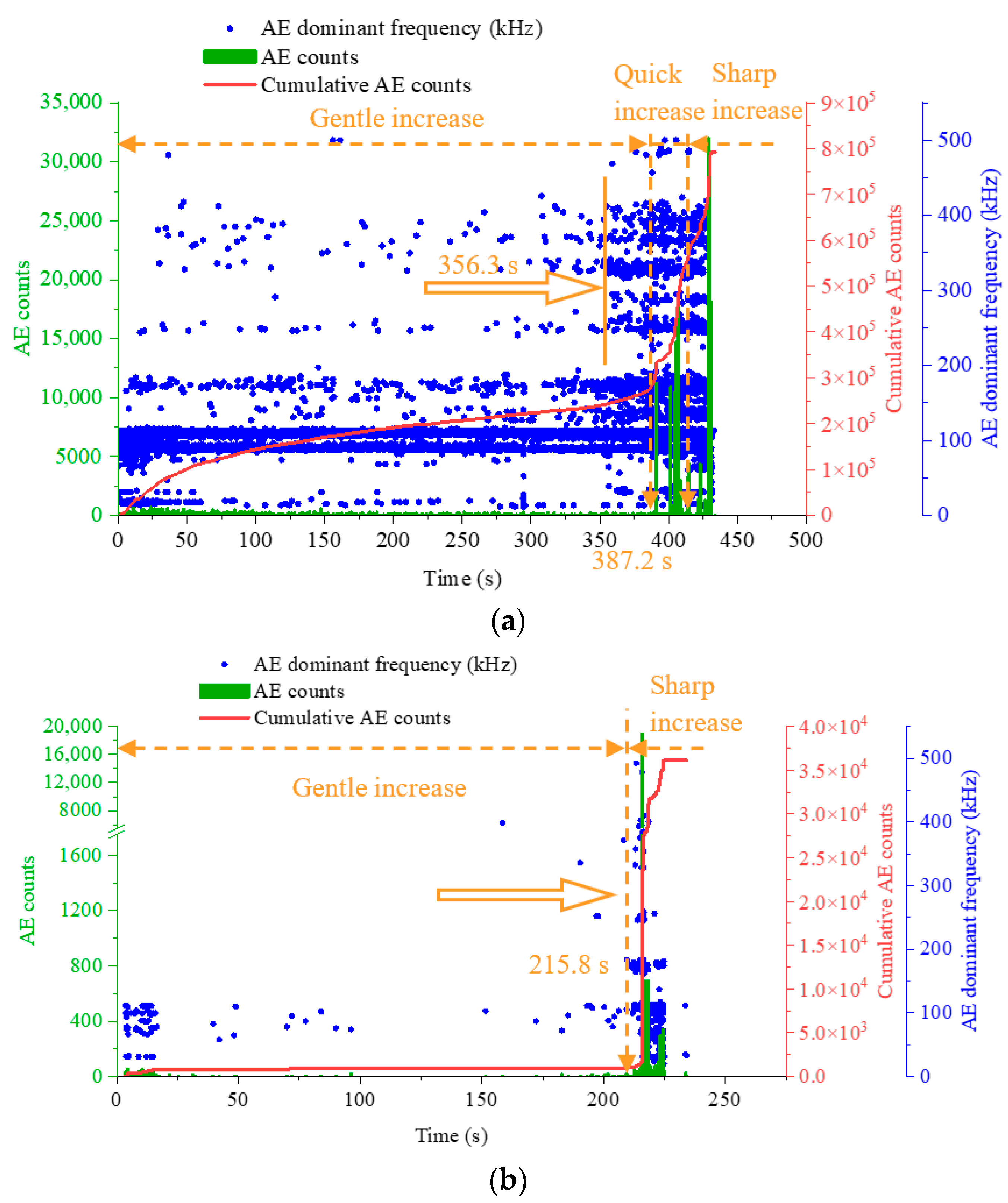
3.2. Characteristics of AE Signals

The parameter-based and waveform-based AE characteristics are plotted in Figure 3. The AE counts and cumulative AE counts curves are AE parameter characteristics, and the dominant frequency is AE waveform-based characteristics.
In Figure 3a, the AE activities in uniaxial compression experience gentle increase stage, quick increase stage, and rapid increase stage. In the gentle stage, the natural holes, cracks, and fissures are compressed as the axial compression stress is small. The AE counts are weak, and the cumulative AE count curves increase gently. As the axial compression stress increases, the AE activities gradually become intensive, and the cumulative AE counts curve quickly increases at 387.2 s, indicating unstable crack propagation. Unstable cracking forecasts the failure of marble specimens. Finally, the AE signals are notably released, and the cumulative AE counts curve sharply increases as the peak stress is achieved.
In Figure 3b, the AE activities are weak in most of the loading process when the specimen is subjected to indirect tensile stress, and only the clam stage and sharp increase stage are identified. The released AE counts are relatively rare in the calm stage, and the cumulative AE counts curve starts to increase at 215.8 s, indicating unstable cracking behaviors.
According to the statistical regularities of AE dominant frequency in this study, the AE dominant frequency higher than 200 kHz is high dominant frequency, while lower than 200 kHz is low dominant frequency. In the uniaxial compression test (Figure 3a), AE dominant frequency-intensive distributed in the low frequency band and dispersedly distributed in the high frequency band, while both low and high AE dominant frequencies became dense after 356.3 s. In the Brazilian tests (Figure 3b), the low AE dominant frequency distributes from initial loading to final failure of the specimen, while the high AE dominant frequency major distributes around the failure moment, i.e., synchronous with the sour of cumulative AE counts curve at 215.8 s.
On the one hand, the AE frequency characteristics can reveal the failure mechanism of rock. Compared Figure 3a,b, the tensile failure component is characterized by low dominant frequency AE signals, and the shear failure component is represented by high dominant frequency AE signals. This finding is consistent with Li et al. [28]. Combined with the failure morphologies in Figure 2, it can be concluded that the marble specimen in the Brazilian test failed due to tensile cracks. However, under uniaxial compression stress, tensile cracks are predominant, while shear cracks are control factors for its failure.
On the other hand, forecasting the failure of rock mass with the AE method is related to the stress conditions. Under uniaxial compression stress, the occurrence of high AE dominant frequency is 30.9 s earlier than the sharp increase of cumulative AE counts (356.3 s and 387.2 s, respectively). However, the time advantage is not obvious for the specimen subjected to tensile stress, as the occurrence of high AE dominant frequency and the sharp increase of cumulative AE counts are synchronous. Cracks that develop quickly in brittle rock under tensile stress should be responsible for the difference.

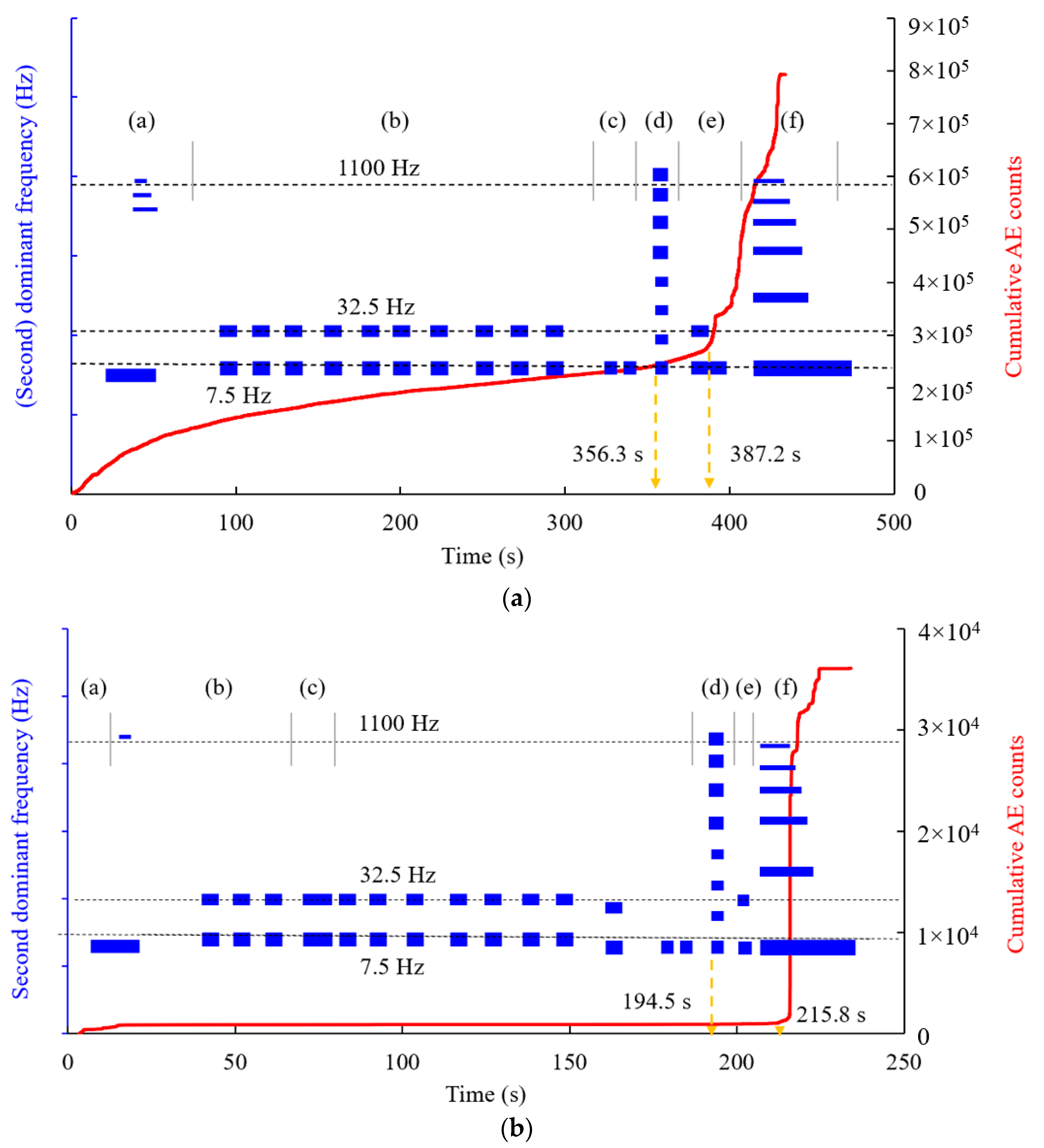
3.3. Characteristics of Vibration Signals

3.3.1. Uniaxial Compression Tests

The whole vibration waveform of the marble specimen in the uniaxial compression test is shown in Figure 4a. The waveform is divided into three stages, including elastic stage (I), plastic stage (II), and failure stage (III). Typical frequency spectra in each stage are shown in Figure 4b–f, and the detailed parameters are listed in Table 1.
In the elastic stage (I), fluctuation phase (a), stable phase (b), and fluctuation phase (c) are identified. In the fluctuation phase (a), the holes and natural fissures in marble specimens are compacted as the axial stress is relatively small. As indicated by Figure 4b, the dominant frequency is 7.5 Hz and located in the low-frequency band, and the corresponding maximum amplitude is approximately 0.13197 mm/s. The residual spectrum possesses high-frequency, low-amplitude characteristics; the high frequency reaches up to approximately 1100 Hz, while the low amplitude is approximately 0.012 Hz. In stable phase (b), as shown in Figure 4c, the bimodal low-frequency waveform is representative. The dominant frequency is 10 Hz and the second dominant frequency is 32.5 Hz, while the amplitude is relatively low, only approximately 0.004–0.008 mm/s. The typical frequency spectrum in the fluctuation phase (c) in Figure 4d possesses similar evolution properties as the fluctuation phase (a) in Figure 4b. The maximum velocity amplitude reaches up to 3.92 mm/s in the elastic stage (I).
In the plastic stage (II), the fluctuation phase (d) and stable phase (e) are identified, whose typical spectra are shown in Figure 4e,f, respectively. In the fluctuation phase (d), the frequency spectrum evenly distributes in a wide frequency band (7.5 Hz–1100 Hz). The dominant frequency is not apparent. A wide frequency band means that multi-sources lead to specimen vibration, and they possess similar intensity. The maximum velocity amplitude is 1.02 mm/s. The typical frequency spectrum in stable phase (e) is bimodal low frequency, indicating that two sources with relatively high amplitude lead to specimen vibration. The dominant frequency is 10 Hz, the corresponding amplitude is 0.019 mm/s, and the second dominant frequency is 32.5 Hz; the corresponding second maximum amplitude is 0.007 mm/s.
The typical frequency spectrum of the fluctuation phase (f) in the failure stage (III) is shown in Figure 4g. The dominant frequency is 7.5 Hz, and the corresponding maximum amplitude is 0.66 mm/s. The maximum velocity amplitude in the failure stage (III) reaches as high as 18.35 mm/s, indicating that the specimen is dramatically vibrating due to multi-crack development before rock failure.

3.3.2. Brazilian Tests

The whole waveform of marble specimens in the Brazilian test is shown in Figure 5a. Although obvious plastic deformation is not reflected from the stress-strain curve, the waveform is divided into elastic stage (I), plastic stage (II), and failure stage (III) according to the laser waveform features. Typical frequency spectra in each stage are shown in Figure 5b–f, and the detailed parameters are listed in Table 2.
In the elastic stage (I), fluctuation phase (a), stable phase (b), and fluctuation phase (c) are identified. In the fluctuation phase (a), unimodal low frequency waveforms are predominant, the dominant frequency is 27.5 Hz, and the corresponding amplitude is 0.01325 mm/s. In the stable phase (b), bimodal low frequency waveforms are detected, the dominant frequency and second dominant frequency are 10 Hz and 27.5 Hz, and the corresponding amplitudes are 0.00801 mm/s and 0.00656 mm/s. Bimodal low frequency waveforms are representative in the fluctuation phase (c). The maximum velocity amplitudes in each phase are almost the same, generally smaller than 0.2 mm/s.
In the plastic stage (II), severe fluctuation of the laser waveform is monitored in the fluctuation phase (d), wide frequency signals are representative, and then a stable phase (e) is followed. In this stage, the maximum velocity amplitude reaches up to 0.64 mm/s, more than twice the maximum velocity 0.35 mm/s in the elastic stage (I). Combined with the AE activities around 200 s in Figure 3b, it can be found that cracks are unstably developing, and thus this stage can be recognized as the plastic stage. This is an advantage of LDV signals versus stress-strain curves and AE monitoring, as it can prompt the plastic state. Furthermore, severe vibration of the specimen leads to signals overlap and wide frequency bands are formed, forecasting the oncoming specimen failure. It can be seen that there is a significant difference between laser and AE signals (Figure 5 and Figure 3b) that the laser signals can reflect more abundant information about global vibration, rather than the waveform released by local microcracks of AE signals.
In the failure stage (III), unimodal low frequency signals are predominant. Figure 5f shows the typical frequency spectra; the dominant frequency is 7.5 Hz and the corresponding amplitude is 0.04553 mm/s. The maximum velocity amplitude sours as high as 1.16 mm/s, occupying approximately 3.3 and 1.8 times the maximum velocity amplitude of the elastic stage (I) and plastic stage (II).

4. Discussion

Figure 6 is a schematic diagram of the evolution of the (second) dominant frequency of laser vibration signals and cumulative AE counts. The blue rectangle represents the laser (second) dominant frequency. Its height reflects the predominant degree of frequency. For example, in phase (a) in Figure 6a, the blue rectangles around 7.5 Hz are much higher than those around 1100 Hz, indicating that the low dominant frequency is predominant while the high dominant frequency spectra are occasional. The width reflects the amplitude of the (second) dominant frequency. The wider the rectangle, the higher the amplitude.
The distributions of the LDV (second) dominant frequency under the effect of uniaxial compression stress (Figure 6a) and tensile stress (Figure 6b) have similar characteristics. The low LDV (second) dominant frequencies concentrate around approximately 7.5 Hz and 32.5 Hz, and they are observed from initial loading to final failure. However, the high LDV (second) dominant frequencies occur around 1100 Hz, and they are only observed in phases (a), (d), and (f). The high LDV frequency spectra in (d) and (f) are quite different. The frequency spectra of phase (d) are distributed in a wide frequency band with low amplitude, while the frequency spectra of phase (f) are generally distributed in both low and high frequency bands with high amplitude. Due to the instantaneous energy release of rock final failure, the highest amplitude occurs in phase (f), occupying approximately eighteen times the maximum amplitude in phase (d) in the uniaxial compression test (18.35 mm/s and 1.02 mm/s) and approximately twice in the Brazilian test (1.16 mm/s and 0.64 mm/s).
Comparing the parameter-based and waveform-based AE evolution characteristics with LDV signals characteristics, i.e., Figure 3, Figure 4, Figure 5 and Figure 6, effective information for forecasting rock failure can be obtained. It should be noted that these physical phenomena are highly related to stress conditions, as the cracking behaviors are controlled by stress distribution. Under uniaxial compression stress, the cumulative AE count curves increased sharply at 387.2 s, the AE high dominant frequency became dense at 356.3 s, and the LDV wide frequency band frequency spectra occurred at 356.3 s. It can be found that the appearance of LDV wide frequency is synchronous with intensive AE high dominant frequency, and 30.9 s earlier than the rapid increase of the AE count. Under indirect tensile stress, the AE high dominant frequency and sharp increase of cumulative AE counts curves occurred at 215.8 s; however, the LDV wide frequency band frequency spectra occurred at 194.5 s, 21.3 s earlier than the AE recognization method.
Consequently, the appearance of wide frequency spectra could be regarded as an early warning of the failure of marble specimens. Furthermore, relatively high velocity amplitudes, i.e., 3.92 mm/s under uniaxial compression stress and 0.35 mm/s under indirect tensile stress, were observed, which could have an alarming effect for wide frequency signals. Compared with AE monitoring, it is especially important that the LDV technology is remote, non-contacting, and much earlier in warning, which is significant for forecasting geological disasters.

5. Conclusions

The laser vibration waveform characteristics of marble specimens were investigated with LDV in uniaxial compression tests and Brazilian tests. The parameter-based and waveform-based AE analysis methods were taken as comparisons. A failure criterion of the loaded marble specimen was proposed to forecast the oncoming failure of marble.
1. The unimodal low frequency, bimodal low frequency spectra, and wide frequency spectra were predominant for the laser vibration waveform. In the elastic stage, the low (second) dominant frequency was distributed around approximately 7.5 Hz and 32.5 Hz. Wide frequency spectra always occurred in the plastic stage, while the high (second) dominant frequency spectra were observed in the failure stage.
2. The LDV whole vibration waveform could reflect plastic deformation of marble specimens. It was proposed that the appearance of LDV wide frequency spectra could be regarded as an early warning for rock failure, and the high velocity amplitude in the elastic stage acted as a pioneer before the appearance of wide frequency.
3. The rock failure time indicated by the AE dominant frequency, cumulative AE counts, and laser frequency spectra characteristics were compared. It was found that the results are affected by stress conditions. Under uniaxial compression stress, forecasting with AE high dominant frequency or laser wide frequency is preferable to cumulative AE counts. Under indirect tensile stress, forecasting with laser-wide frequency is preferable to the AE high dominant frequency and cumulative AE counts.

Author Contributions

Conceptualization, Q.X. and X.F.; Data curation, Y.B.; Funding acquisition, Q.X.; Methodology, J.D.; Writing—original draft, S.L.; Writing—review & editing, Y.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the project (KJQN201902504) from Scientific and Technological Research Program of Chongqing Municipal Education Commission and the open project (LNTCCMA-20200103) from the Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Castellini, P.; Martarelli, M.; Tomasini, E.P. Laser Doppler Vibrometry: Development of advanced solutions answering to technology’s needs. Mech. Syst. Signal Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
  2. Sugimoto, T.; Uechi, I.; Sugimoto, K.; Utagawa, N.; Katakura, K. Study on the non-contact acoustic inspection method for concrete structures by using strong ultrasonic sound source. Phys. Procedia 2006, 70, 398–401. [Google Scholar] [CrossRef]
  3. Fujino, Y.; Kaito, K.; Abe, M. Detection of structural damage by ambient vibration measurement using laser Doppler vibrometer. In Proceedings of the Health Monitoring & Management of Civil Infrastructure Systems, Newport Beach, CA, USA, 6–8 March 2001. [Google Scholar]
  4. Chen, S.E.; Petro, S. Nondestructive bridge cable tension assessment using laser vibrometry. Exp. Tech. 2005, 29, 29–32. [Google Scholar] [CrossRef]
  5. Matsuoka, K.; Uehan, F.; Kusaka, H.; Tomonaga, H. Experimental validation of Non-Marker simple image displacement measurements for railway bridges. Appl. Sci. 2021, 11, 7032. [Google Scholar] [CrossRef]
  6. De Grassi, M.; Copparoni, S.; Tomasini, E.P.; Esposito, E. Quality control and programmed maintenance of ventilated wall facings: Pathologies surveying with laser vibrometry. In Proceedings of the International Workshop on Management of Durability in the Building Process, Milano, Italy, 25–26 June 2003. [Google Scholar]
  7. Sättele, M.; Krautblatter, M.; Bründl, M.; Straub, D. Forecasting rock slope failure: How reliable and effective are warning systems? Landslides 2016, 13, 737–750. [Google Scholar] [CrossRef] [Green Version]
  8. Pappalardo, G.; Mineo, S.; Imposa, S.; Grassi, S.; Leotta, A.; La Rosa, F.; Salerno, D. A quick combined approach for the characterization of a cliff during a post-rockfall emergency. Landslides 2020, 17, 1063–1081. [Google Scholar] [CrossRef]
  9. He, Z.; Xie, M.; Huang, Z.; Li, Y.; Sui, Z.L.; Lu, Y.D.; Golosov, A.M. Experimental hazardous rock block stability assessment based on vibration feature parameters. Adv. Civ. Eng. 2020, 2020, 8837459. [Google Scholar] [CrossRef]
  10. Ma, G.; Sawada, K.; Yashima, A.; Saito, H. Experimental study of the applicability of the remotely positioned laser doppler vibrometer to rock-block stability assessment. Rock Mech. Rock Eng. 2015, 48, 787–802. [Google Scholar] [CrossRef]
  11. Du, Y.; Xie, M.; Jiang, Y.; Li, B.; Chicas, S. Experimental rock stability assessment using the frozen–thawing test. Rock Mech. Rock Eng. 2017, 50, 1049–1053. [Google Scholar] [CrossRef]
  12. Jia, B.; Wu, Z.; Du, Y. Real-time stability assessment of unstable rocks based on fundamental natural frequency. Int. J. Rock Mech. Min. Sci. 2019, 124, 104134. [Google Scholar] [CrossRef]
  13. Ban, Y.; Fu, X.; Xie, Q. Revealing the laminar shale microdamage mechanism considering the relationship between fracture geometrical morphology and acoustic emission power spectrum characteristics. Bull. Eng. Geol. Environ. 2020, 79, 1083–1096. [Google Scholar] [CrossRef]
  14. Zhu, X.; Chen, X.; Dai, F. Mechanical properties and acoustic emission characteristics of the bedrock of a hydropower station under cyclic triaxial loading. Rock Mech. Rock Eng. 2020, 53, 5203–5221. [Google Scholar] [CrossRef]
  15. Verstrynge, E.; Lacidogna, G.; Accornero, F.; Tomor, A. A review on acoustic emission monitoring for damage detection in masonry structures. Constr. Build. Mater. 2021, 268, 121089. [Google Scholar] [CrossRef]
  16. Ono, K. Review on structural health evaluation with acoustic emission. Appl. Sci. 2018, 8, 958. [Google Scholar] [CrossRef] [Green Version]
  17. Zhang, R.; Liu, J.; Sa, Z.; Wang, Z.; Lu, S.; Lv, Z. Fractal characteristics of acoustic emission of gas-bearing coal subjected to true triaxial loading. Measurement 2021, 169, 108349. [Google Scholar] [CrossRef]
  18. Chen, L.; Zhao, J.; Zheng, Z. Acoustic emission characteristics of compressive deformation and failure of siltstone under different water contents. Adv. Mater. Sci. Eng. 2017, 2017, 4035487. [Google Scholar] [CrossRef] [Green Version]
  19. Sendrowicz, A.; Myhre, A.O.; Wierdak, S.W.; Vinogradov, A. Challenges and accomplishments in mechanical testing instrumented by in situ techniques: Infrared thermography, digital image correlation, and acoustic emission. Appl. Sci. 2021, 11, 6718. [Google Scholar] [CrossRef]
  20. Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Chen, Y. Acoustic emission characteristics of red sandstone specimens under uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2018, 51, 969–988. [Google Scholar] [CrossRef]
  21. Jin, P.J.; Wang, E.Y.; Song, D.Z. Study on correlation of acoustic emission and plastic strain based on coal-rock damage theory. Geomech. Eng. 2017, 12, 627–637. [Google Scholar] [CrossRef]
  22. Xu, G.; He, C.; Chen, Z.; Su, A. Transverse isotropy of phyllite under Brazilian tests: Laboratory testing and numerical simulations. Rock Mech. Rock Eng. 2018, 51, 1111–1135. [Google Scholar] [CrossRef]
  23. Li, J.; Hu, Q.; Yu, M.; Li, X.; Hu, J.; Yang, H. Acoustic emission monitoring technology for coal and gas outburst. Energy Sci. Eng. 2019, 7, 443–456. [Google Scholar] [CrossRef] [Green Version]
  24. Manthei, G.; Eisenblatter, J.; Dahmb, T. Moment tensor evaluation of acoustic emission sources in salt rock. Constr. Build. Mater. 2001, 15, 297–309. [Google Scholar] [CrossRef]
  25. Manthei, G.; Plenkers, K. Review on in situ acoustic emission monitoring in the context of structural health monitoring in mines. Appl. Sci. 2018, 8, 1595. [Google Scholar] [CrossRef] [Green Version]
  26. Ban, Y.; Fu, X.; Xie, Q.; Dyskin, A.; He, C.B.; Duan, J.; Pasternak, E. Fracturing of shales with slots under uniaxial compression parallel to bedding layers. J. Pet. Sci. Eng. 2022, 211, 110163. [Google Scholar] [CrossRef]
  27. Li, L.R.; Deng, J.H.; Zheng, L.; Liu, J.F. Dominant frequency characteristics of acoustic emissions in white marble during direct tensile tests. Rock Mech. Rock Eng. 2017, 50, 1337–1346. [Google Scholar] [CrossRef]
  28. Aggelis, D.G.; Soulioti, D.V.; Sapouridis, N.; Barkoula, N.M.; Paipetis, A.S.; Matikas, T.E. Acoustic emission characterization of the fracture process in fibre reinforced concrete. Constr. Build. Mater. 2011, 25, 4126–4131. [Google Scholar] [CrossRef]
  29. Sharafisafa, M.; Aliabadian, Z.; Shen, L. Crack initiation and failure of block-in-matrix rocks under Brazilian test using digital image correlation. Theor. Appl. Fract. Mech. 2020, 109, 102743. [Google Scholar] [CrossRef]
  30. Li, D.; Wong, L.N.Y. The Brazilian disc test for rock mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2020, 46, 269–287. [Google Scholar] [CrossRef]
Applsci 12 02223 g001 550
Figure 1. The loading-acoustical-optical testing system.
Figure 1. The loading-acoustical-optical testing system.
Applsci 12 02223 g001
Applsci 12 02223 g002 550
Figure 2. Stress-strain relationship and failure mode of marble specimens in (a) Brazilian test and (b) uniaxial compression test.
Figure 2. Stress-strain relationship and failure mode of marble specimens in (a) Brazilian test and (b) uniaxial compression test.
Applsci 12 02223 g002
Applsci 12 02223 g003 550
Figure 3. Evolution of AE and cumulative AE curves with time. (a) Uniaxial compression test; (b) Brazilian test.
Figure 3. Evolution of AE and cumulative AE curves with time. (a) Uniaxial compression test; (b) Brazilian test.
Applsci 12 02223 g003
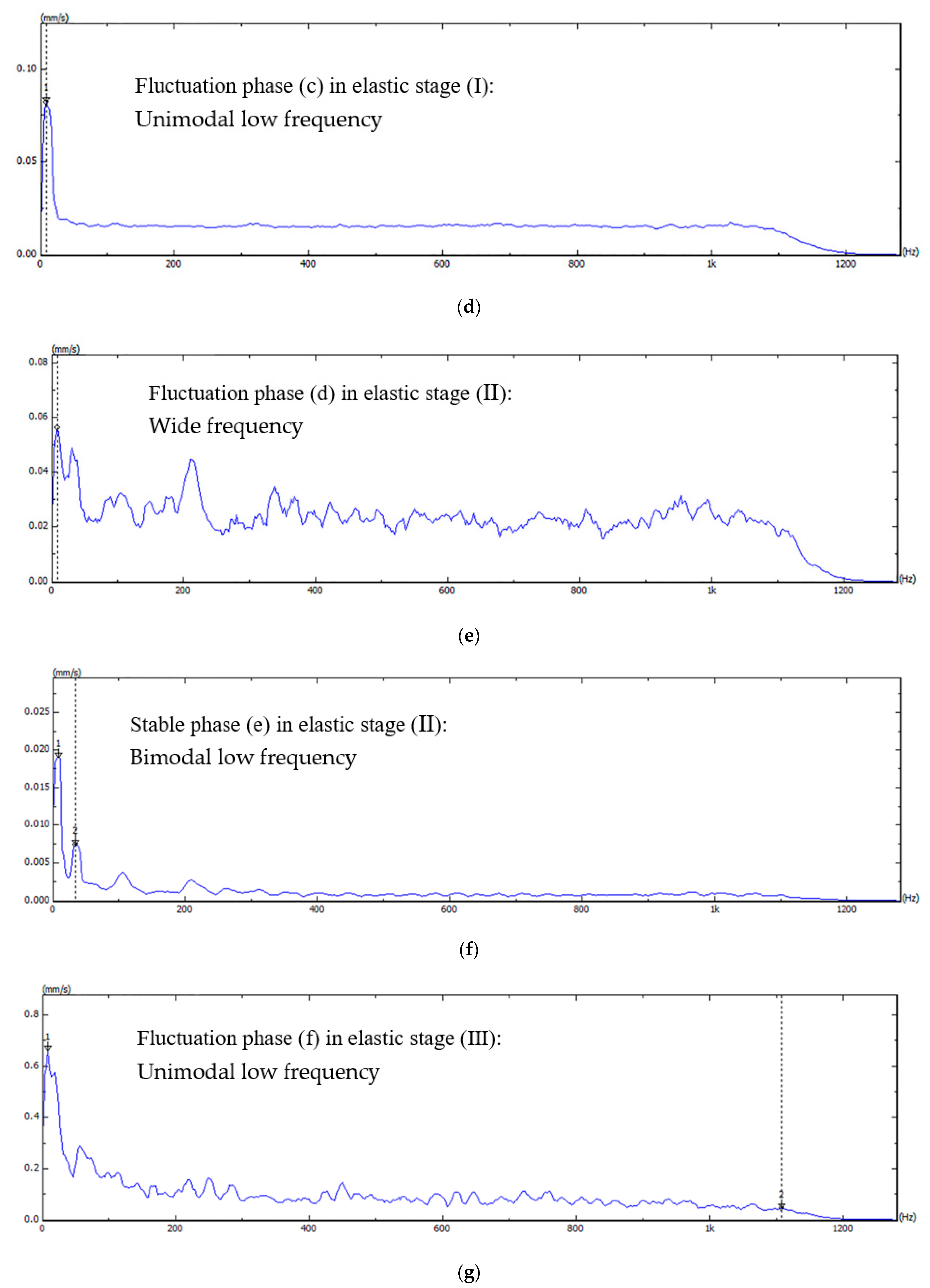
Applsci 12 02223 g004a 550Applsci 12 02223 g004b 550
Figure 4. The whole waveform during the loading process (a) and typical frequency spectra in each phase (b–g) of the marble specimen in the uniaxial compression test.
Figure 4. The whole waveform during the loading process (a) and typical frequency spectra in each phase (b–g) of the marble specimen in the uniaxial compression test.
Applsci 12 02223 g004aApplsci 12 02223 g004b
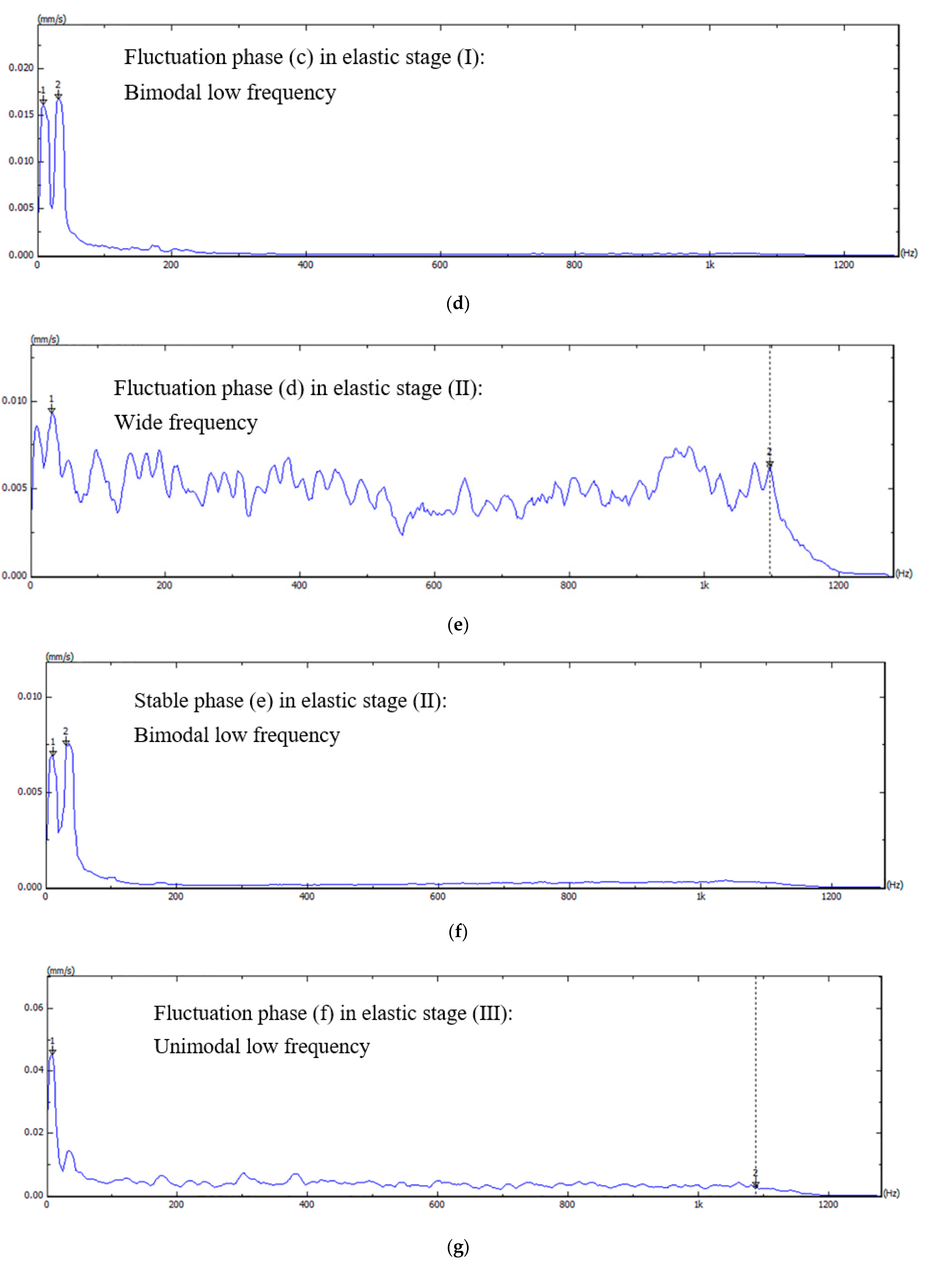
Applsci 12 02223 g005a 550Applsci 12 02223 g005b 550
Figure 5. The whole waveform during the loading process (a) and typical frequency spectra in each phase (b–g) of the marble specimen in the Brazilian test.
Figure 5. The whole waveform during the loading process (a) and typical frequency spectra in each phase (b–g) of the marble specimen in the Brazilian test.
Applsci 12 02223 g005aApplsci 12 02223 g005b
Applsci 12 02223 g006 550
Figure 6. Schematic diagram of the distribution of dominant frequency and cumulative AE counts of marble specimens in (a) uniaxial compression test and (b) Brazilian test.
Figure 6. Schematic diagram of the distribution of dominant frequency and cumulative AE counts of marble specimens in (a) uniaxial compression test and (b) Brazilian test.
Applsci 12 02223 g006
Table
Table 1. Characteristics of frequency spectra in each phase in the uniaxial compression test.
Table 1. Characteristics of frequency spectra in each phase in the uniaxial compression test.
Phase-StageProfileDominant Frequency (Hz)Maximum Amplitude (mm/s)Second Dominant Frequency (Hz)Second Maximum Amplitude (mm/s)Wide Frequency
(Hz)		Maximum Amplitude (mm/s)
(a)-(I)Unimodal low frequency7.50.13197//
(b)-(I)Bimodal low frequency100.0066132.50.00446
(c)-(I)Unimodal low frequency7.50.0824
(d)-(II)Wide frequency////7.5–11000.056
(e)-(II)Unimodal low frequency100.01932.50.007
(f)-(III)Unimodal low frequency7.50.66
Table
Table 2. Characteristics of frequency spectra in each phase in the Brazilian test.
Table 2. Characteristics of frequency spectra in each phase in the Brazilian test.
Phase-StageProfileDominant Frequency (Hz)Maximum Amplitude (mm/s)Second Dominant Frequency (Hz)Second Maximum Amplitude (mm/s)Wide Frequency
(Hz)		Maximum Amplitude (mm/s)
(a)-(I)Unimodal low frequency27.50.01325//
(b)-(I)Bimodal low frequency100.0080127.50.00656
(c)-(I)Bimodal low frequency7.50.01616300.01679
(d)-(II)Wide frequency////30–10700.00932
(e)-(II)Bimodal low frequency100.0075300.00695
(f)-(III)Unimodal low frequency7.50.04553
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Xie, Q.; Duan, J.; Ban, Y.; Fu, X.; Liu, S. Laser Vibration Characteristics of Marble Specimens and Failure Criterion. Appl. Sci. 2022, 12, 2223. https://doi.org/10.3390/app12042223

AMA Style

Xie Q, Duan J, Ban Y, Fu X, Liu S. Laser Vibration Characteristics of Marble Specimens and Failure Criterion. Applied Sciences. 2022; 12(4):2223. https://doi.org/10.3390/app12042223

Chicago/Turabian Style

Xie, Qiang, Jun Duan, Yuxin Ban, Xiang Fu, and Shilin Liu. 2022. "Laser Vibration Characteristics of Marble Specimens and Failure Criterion" Applied Sciences 12, no. 4: 2223. https://doi.org/10.3390/app12042223

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop