Prediction Model of Tunnel Boring Machine Disc Cutter Replacement Using Kernel Support Vector Machine
Abstract
:1. Introduction
2. The Proposed Prediction Framework
2.1. Evaluation Function and Related Parameters
2.2. Introduction of Support Vector Machine
3. Data Sources Description
3.1. Project Summary
3.2. Introduction to Studied TBM
3.3. TBM Data and Geological Survey Data
4. Validation and Analysis
4.1. Data Preparation
4.1.1. Extraction of TBM Thrusting Phases
4.1.2. Parameter Selection
- (1)
- (Rock type: Unlike subway tunnel construction, hard rock tunnel construction may encounter more flexible geological conditions. Generally, different types of rock have different value ranges of petrophysical parameters.
- (2)
- Uniaxial compressive strength: The measurement of the strength characteristics of rock materials, which is widely used to represent geological conditions in previous research.
- (3)
- Advance rate: The derivative of advance displacement, which is related to the TBM forward velocity.
- (4)
- Trust: The pressure of the thrust cylinders, which provides the major power of driving TBM forward.
- (5)
- Cutterhead rotational speed: The angular velocity of cutterhead rotating with TBM spindle, which is related to the relative velocity of cutter to rock.
- (6)
- Advance mileage: The displacement distance of TBM during the whole tunneling, which is related to the rolling distances of disc cutters.
- (7)
- Advance displacement: When TBM works in the gripping-thrusting-regripping procedure, the propulsion cylinders reach out and retract cyclically. Advance displacement is the stroke of propulsion cylinders.
- (8)
- Drive motor current: The electric current of the drive motor operating at constant power mode, which shows the working power of the drive motors.
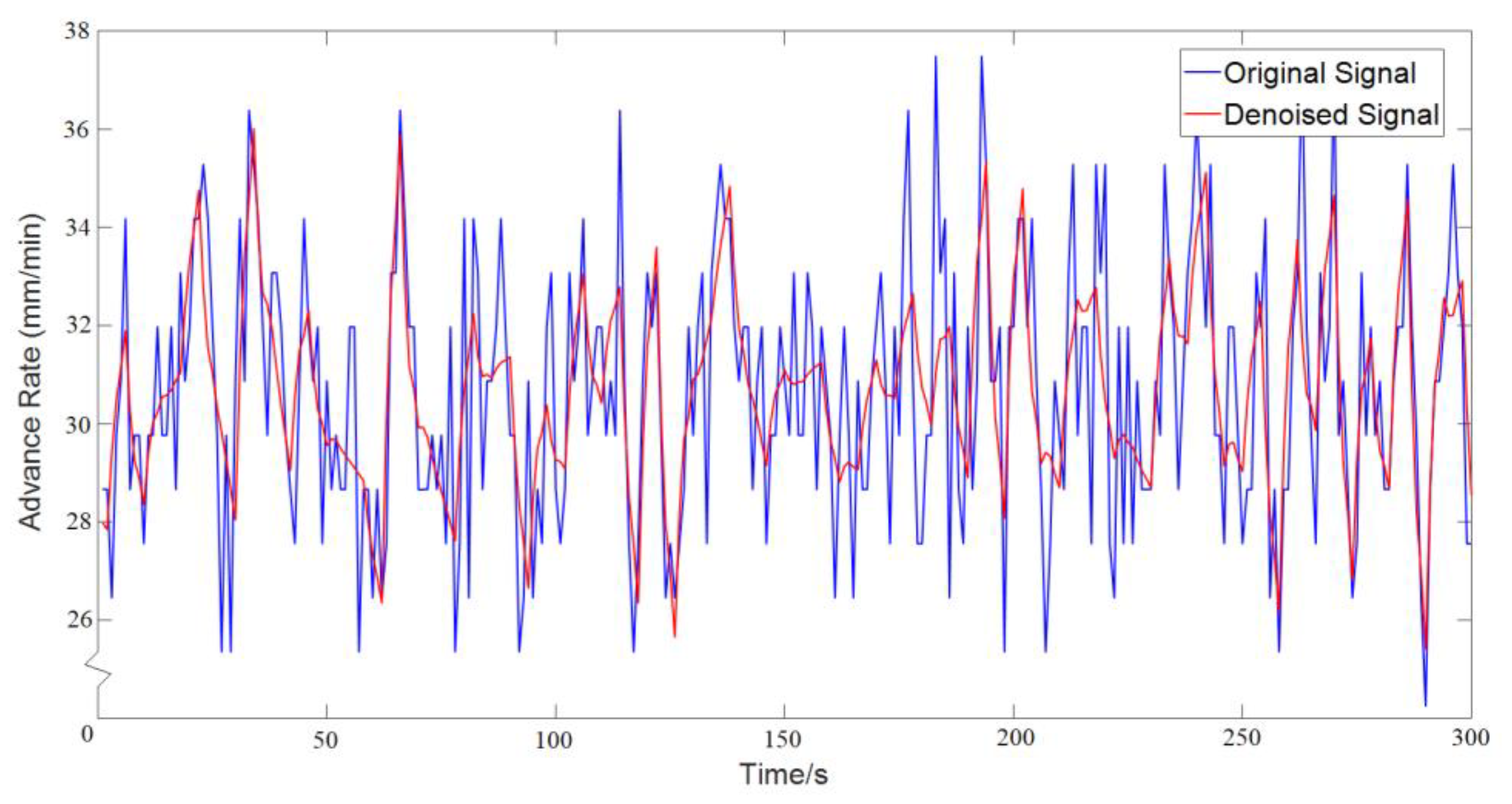
4.1.3. Denoising and Normalization
4.1.4. Time Feature Construction
4.2. Study Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.; Huang, X.; Gong, Q.; Du, L.; Pan, Y.-C.; Liu, J.-P. Application and development of hard rock TBM and its prospect in China. Tunn. Undergr. Space Technol. 2016, 57, 33–46. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, Q.; Zhao, J. Challenges and opportunities of using tunnel boring machines in mining. Tunn. Undergr. Space Technol. 2016, 57, 287–299. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Azali, S.T.; Zhao, J. Introduction of an empirical TBM cutter wear prediction model for pyroclastic and mafic igneous rocks; a case history of Karaj water conveyance tunnel, Iran. Tunn. Undergr. Space Technol. 2014, 43, 222–231. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.-P.; Pan, Y.-C.; Zhang, X.; Peng, X.; Gong, Q.; Du, L. A Wear Rule and Cutter Life Prediction Model of a 20-in. TBM Cutter for Granite: A Case Study of a Water Conveyance Tunnel in China. Rock Mech. Rock Eng. 2017, 50, 1303–1320. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Zhao, X.; Zhang, Q. Development of a prediction model for the wear evolution of disc cutters on rock TBM cutterhead. Tunn. Undergr. Space Technol. 2017, 67, 147–157. [Google Scholar] [CrossRef]
- Yang, J.-H.; Zhang, X.-P.; Ji, P.-Q.; Liu, Q.-S.; Lu, X.-J.; Wei, J.-P.; Qi, S.-H.; Fang, H.-G.; Fang, J.-N.; Geng, Y.-J. Analysis of disc cutter damage and consumption of TBM1 section on water conveyance tunnel at Lanzhou water source construction engineering. Tunn. Undergr. Space Technol. 2018, 85, 67–75. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Cheng, W.-C.; Arulrajah, A. Cutter-disc consumption during earth pressure balance tunnelling in mixed strata. Proc. Inst. Civ. Eng.-Geotech. Eng. 2018, 171, 363–376. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yin, Z.-Y.; Lyu, H.-M. Prediction of Disc Cutter Life During Shield Tunneling with AI via the Incorporation of a Genetic Algorithm into a GMDH-Type Neural Network. Engineering 2020, 7, 238–251. [Google Scholar] [CrossRef]
- Hassanpour, J. Development of an empirical model to estimate disc cutter wear for sedimentary and low to medium grade metamorphic rocks. Tunn. Undergr. Space Technol. 2018, 75, 90–99. [Google Scholar] [CrossRef]
- Schneider, E.U.P.D.-I.E.; Thuro, U.P.D.R.N.K.; Galler, U.P.D.-I.D.R. Forecasting penetration and wear for TBM drives in hard rock—Results from the ABROCK research project/Prognose von Penetration und Verschleiß für TBM-Vortriebe im Festgestein—Erkenntnisse aus dem Forschungsprojekt ABROCK. Géoméch. Tunn. 2012, 5, 537–546. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Lin, L.; Xia, Y.; Tan, Q.; Zhu, Z.; Mao, Q.; Zhou, M. Experimental study on wear of TBM disc cutter rings with different kinds of hardness. Tunn. Undergr. Space Technol. 2018, 82, 346–357. [Google Scholar] [CrossRef]
- Yu, H.; Tao, J.; Huang, S.; Qin, C.; Xiao, D.; Liu, C. A field parameters-based method for real-time wear estimation of disc cutter on TBM cutterhead. Autom. Constr. 2021, 124, 103603. [Google Scholar] [CrossRef]
- Zhao, H.L.; Sun, Z.C.; Chen, K.; Wang, H.Z.; Yang, Y.D.; Zhou, J.J.; Li, F.Y.; Zhang, B.; Song, F.L. Synthesis, Property and Wear Detection of Disc Cutter for Shield Tunneling Machine of Nanobelt Ca0.68Si9Al3(ON)16: Eu2+ Luminescence Fibers. J. Inorg. Mater. 2018, 33, 866–872. [Google Scholar] [CrossRef]
- Gharahbagh, E.A.; Mooney, M.A.; Frank, G.; Walter, B.; DiPonio, M.A. Periodic inspection of gauge cutter wear on EPB TBMs using cone penetration testing. Tunn. Undergr. Space Technol. 2013, 38, 279–286. [Google Scholar] [CrossRef]
- Gong, Q.; Wu, F.; Wang, D.; Qiu, H.; Yin, L. Development and Application of Cutterhead Working Status Monitoring System for Shield TBM Tunnelling. Rock Mech. Rock Eng. 2021, 54, 1731–1753. [Google Scholar] [CrossRef]
- Wang, F.; Men, C.; Kong, X.; Meng, L. Optimum Design and Application Research of Eddy Current Sensor for Measurement of TBM Disc Cutter Wear. Sensors 2019, 19, 4230. [Google Scholar] [CrossRef] [Green Version]
- Lan, H.; Xia, Y.; Ji, Z.; Fu, J.; Miao, B. Online monitoring device of disc cutter wear—Design and field test. Tunn. Undergr. Space Technol. 2019, 89, 284–294. [Google Scholar] [CrossRef]
- Karami, M.; Zare, S.; Rostami, J. Tracking of disc cutter wear in TBM tunneling: A case study of Kerman water conveyance tunnel. Bull. Eng. Geol. Environ. 2020, 80, 201–219. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Zhao, J.; Azali, S.T. TBM performance and disc cutter wear prediction based on ten years experience of TBM tunnelling in Iran. Géoméch. Tunn. 2015, 8, 239–247. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, Y.; Chen, K.; Li, F.; Zhou, J.; Zhang, B.; Chen, Q. Disc Cutter’s Rock Breaking Ability and Wear Resistance in Extremely Hard Rock: A Case Study in Qinling Tunnel of Han River to Wei River Water Diversion Project. Geotech. Geol. Eng. 2019, 37, 4901–4910. [Google Scholar] [CrossRef]
- Zare, S.; Bruland, A. Applications of NTNU/SINTEF Drillability Indices in Hard Rock Tunneling. Rock Mech. Rock Eng. 2012, 46, 179–187. [Google Scholar] [CrossRef]
- Gehring, K. Performance and cutter-wear prediction for tunnel boring machines. Felsbau 1995, 13, 439–448. [Google Scholar]
- Wang, L.; Kang, Y.; Zhao, X.; Zhang, Q. Disc cutter wear prediction for a hard rock TBM cutterhead based on energy analysis. Tunn. Undergr. Space Technol. 2015, 50, 324–333. [Google Scholar] [CrossRef]
- Ko, T.Y.; Lee, S.S.; Ko, T.Y. Effect of Rock Abrasiveness on Wear of Shield Tunnelling in Bukit Timah Granite. Appl. Sci. 2020, 10, 3231. [Google Scholar] [CrossRef]
- Park, B.; Lee, C.; Choi, S.-W.; Kang, T.-H.; Chang, S.-H. Discrete-Element Analysis of the Excavation Performance of an EPB Shield TBM under Different Operating Conditions. Appl. Sci. 2021, 11, 5119. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, H.; Chen, Z.; Chen, X.; Huang, L.; Liu, S. Effects of Jointed Rock Mass and Mixed Ground Conditions on the Cutting Efficiency and Cutter Wear of Tunnel Boring Machine. Rock Mech. Rock Eng. 2018, 52, 1303–1313. [Google Scholar] [CrossRef]
- Acaroglu, O.; Ozdemir, L.; Asbury, B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction. Tunn. Undergr. Space Technol. 2008, 23, 600–608. [Google Scholar] [CrossRef]
- Qiao, J.L.; Meng, Q.J.; Liu, J.Q.; Jin, J.X. Prediction of wear life of shield disc cutter in complex formations based on genetic pro-gramming. Ind. Mine Autom. 2018, 9, 51–58. [Google Scholar] [CrossRef]
- Yang, H.Y. Progress and Trend of Construction Machinery Intelligence. Constr. Mach. Technol. Manag. 2017, 12, 19–21. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H. Modelling and prediction of tool wear using LS-SVM in milling operation. Int. J. Comput. Integr. Manuf. 2015, 1–16. [Google Scholar] [CrossRef]
- Sun, S.; Hu, X.; Cai, W.; Zhong, J. Tool Breakage Detection of Milling Cutter Insert Based on SVM. IFAC-PapersOnLine 2019, 52, 1549–1554. [Google Scholar] [CrossRef]
- Kong, D.; Chen, Y.; Li, N.; Duan, C.; Lu, L.; Chen, D. Tool Wear Estimation in End Milling of Titanium Alloy Using NPE and a Novel WOA-SVM Model. IEEE Trans. Instrum. Meas. 2019, 69, 5219–5232. [Google Scholar] [CrossRef]
- Bruland, A. Hard Rock Tunnel Boring. Trondheim. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2000. [Google Scholar]
- Zhang, Q.; Liu, Z.; Tan, J. Prediction of geological conditions for a tunnel boring machine using big operational data. Autom. Constr. 2019, 100, 73–83. [Google Scholar] [CrossRef]
- Fan, J.; Lee, J.; Lee, Y. A Transfer Learning Architecture Based on a Support Vector Machine for Histopathology Image Classification. Appl. Sci. 2021, 11, 6380. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Pan, H.; Cheng, J.; Cheng, J. A novel deep stacking least squares support vector machine for rolling bearing fault diagnosis. Comput. Ind. 2019, 110, 36–47. [Google Scholar] [CrossRef]
- Di, Q.; Wu, Z.; Chen, T.; Chen, F.; Wang, W.; Qin, G.; Chen, W. Artificial intelligence method for predicting the maximum stress of an off-center casing under non-uniform ground stress with support vector machine. Sci. China Technol. Sci. 2020, 63, 2553–2561. [Google Scholar] [CrossRef]
- Tinoco, J.; Correia, A.G.; Cortez, P. Support vector machines applied to uniaxial compressive strength prediction of jet grouting columns. Comput. Geotech. 2014, 55, 132–140. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, J.; Asteris, P.G.; Armaghani, D.J.; Tahir, M.M. Supervised Machine Learning Techniques to the Prediction of Tunnel Boring Machine Penetration Rate. Appl. Sci. 2019, 9, 3715. [Google Scholar] [CrossRef] [Green Version]
- CJWRC. Standard for Engineering Classification of Rock Mass. GB/T 50218-2014. 2014. Available online: https://ebook.chinabuilding.com.cn/zbooklib/bookpdf/probation?SiteID=1&bookID=59005 (accessed on 16 February 2022).
- Yang, Z.; He, B.; Liu, Y.; Wang, D.; Zhu, G. Classification of rock fragments produced by tunnel boring machine using convolutional neural networks. Autom. Constr. 2021, 125, 103612. [Google Scholar] [CrossRef]
- Sun, Y.; Genton, M.G. Functional Boxplots. J. Comput. Graph. Stat. 2011, 20, 316–334. [Google Scholar] [CrossRef]
- Mirzargar, M.; Whitaker, R.T.; Kirby, R.M. Curve Boxplot: Generalization of Boxplot for Ensembles of Curves. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2654–2663. [Google Scholar] [CrossRef]
- Xie, W.; Chkrebtii, O.; Kurtek, S. Visualization and Outlier Detection for Multivariate Elastic Curve Data. IEEE Trans. Vis. Comput. Graph. 2019, 26, 3353–3364. [Google Scholar] [CrossRef] [PubMed]
- La, Y.S.; In, K.M.; Bumjoo, K. Prediction of replacement period of shield TBM disc cutter using SVM. J. Korean Tunn. Undergr. Space Assoc. 2019, 21, 641–656. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yin, Z.-Y.; Lyu, H.-M. Data in intelligent approach for estimation of disc cutter life using hybrid metaheuristic algorithm. Data Brief 2020, 33, 106479. [Google Scholar] [CrossRef] [PubMed]

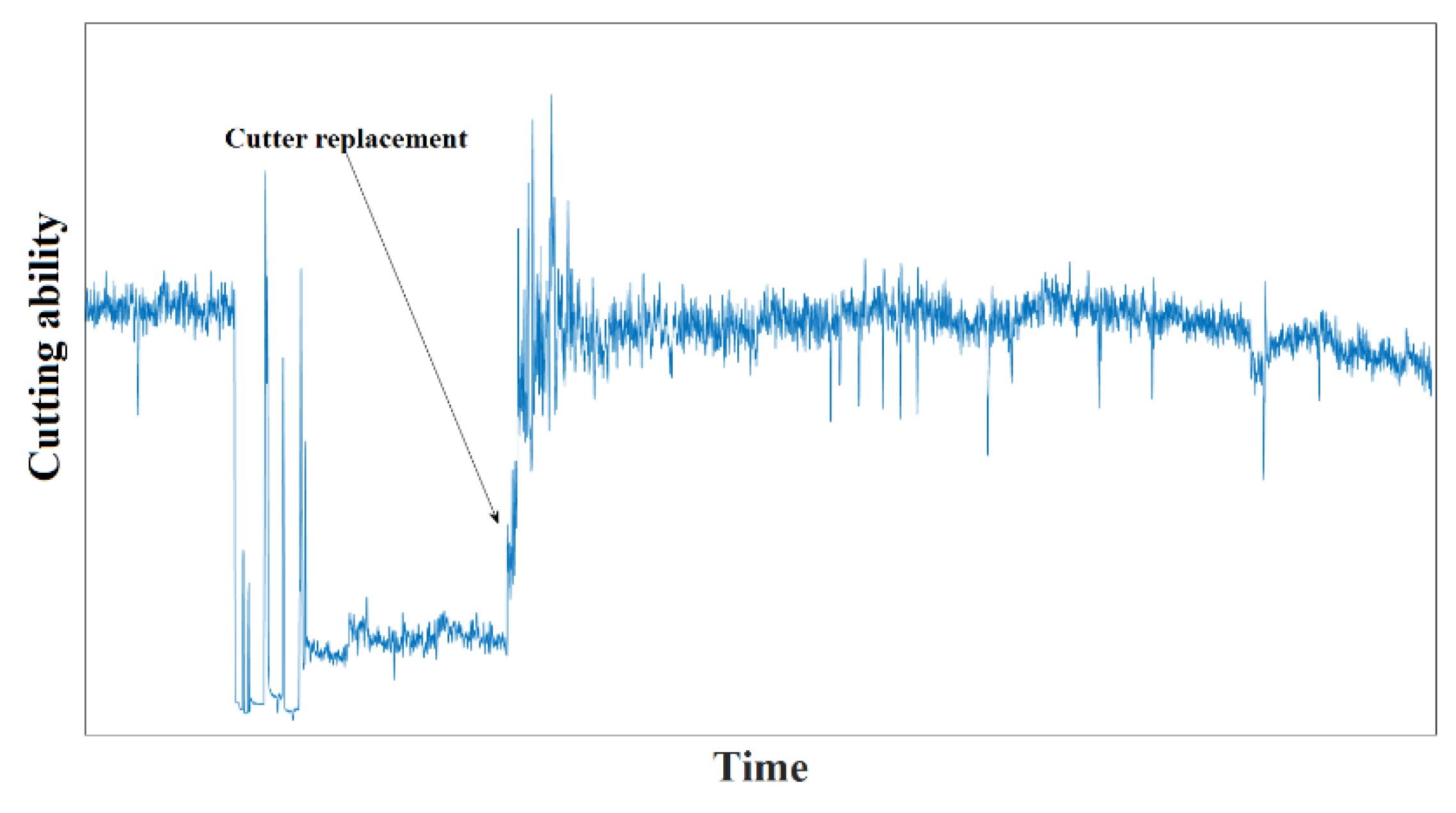

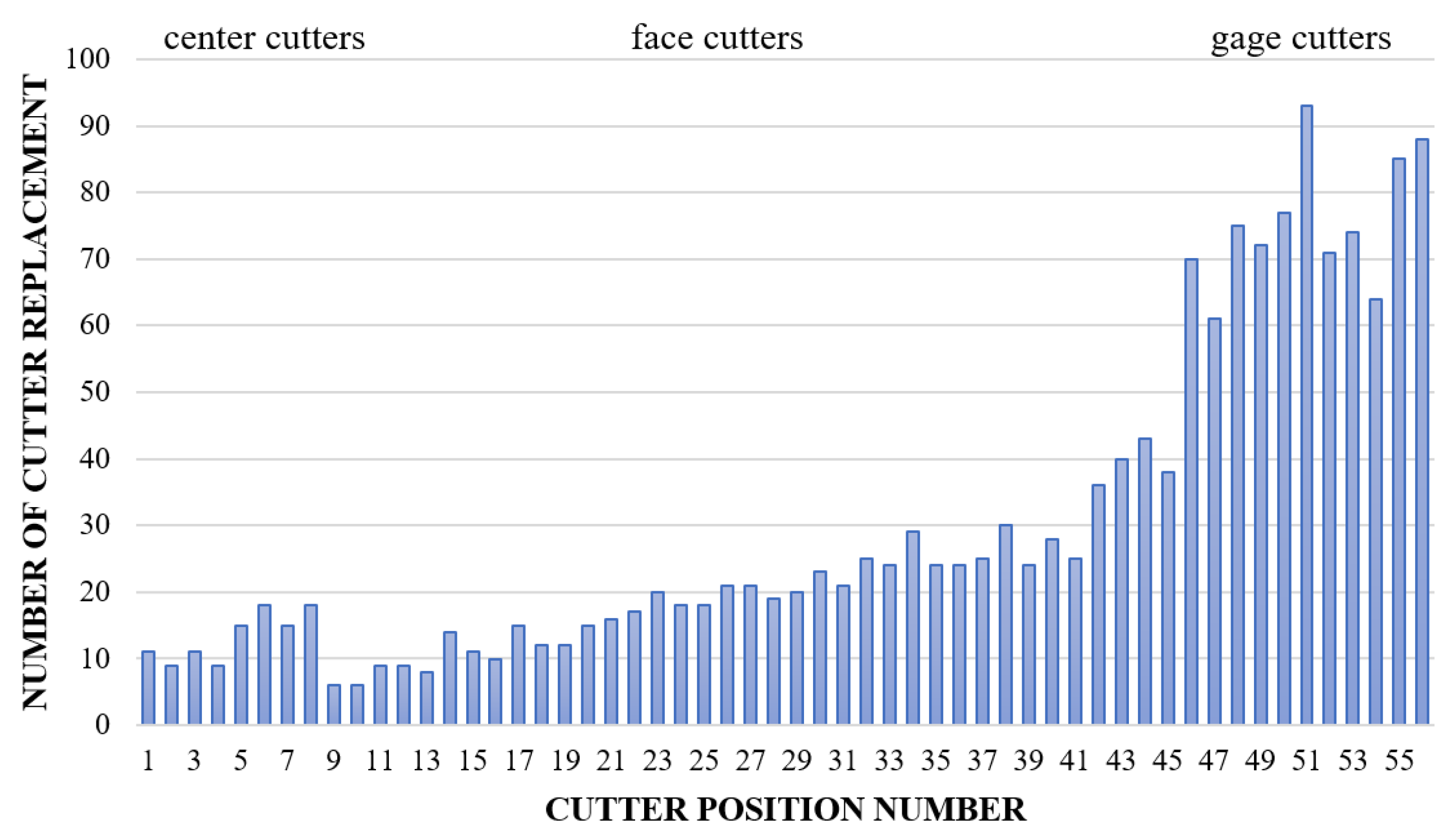
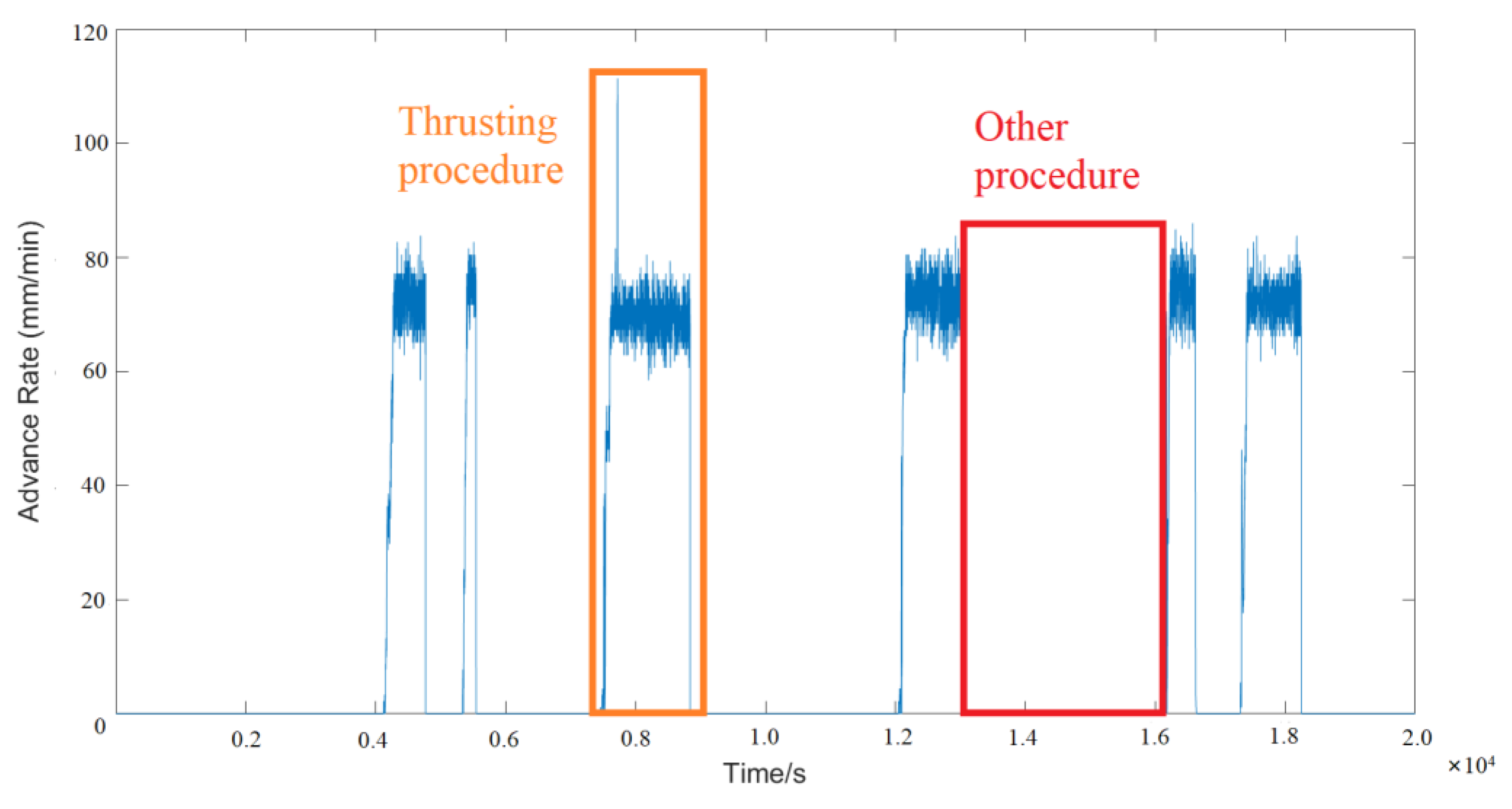

| Models | Technical Parameter | Parameter Value |
|---|---|---|
| Whole TBM | Main part length | 20 m |
| Main part quality | 615 t | |
| Regripping time | 5 min | |
| Trusting stroke | 1800 mm | |
| Cutterhead | Diameter | 7930 mm |
| Number of central disc cutters | 6 | |
| Central disc cutter diameter | 432 mm | |
| Number of face disc cutters | 38 | |
| Face disc cutter diameter | 483 mm | |
| Number of gage disc cutter | 12 | |
| Gage disc cutter diameter | 483 mm | |
| Space between disc cutters | 82 mm/80 mm |
| V | F | T | RSP | AM | AD | I | MT | MF | ||
|---|---|---|---|---|---|---|---|---|---|---|
| V | 1 | |||||||||
| F | 0.06 | 1 | ||||||||
| T | 0.11 | 0.76 | 1 | |||||||
| RSP | 0.05 | 0.51 | 0.34 | 1 | ||||||
| AM | −0.03 | 0.35 | 0 | −0.02 | 1 | |||||
| AD | 0.06 | 0.21 | 0.34 | 0.09 | −0.03 | 1 | ||||
| 0.99 | 0.04 | 0.1 | 0 | −0.03 | 0.06 | 1 | ||||
| I | 0.1 | 0.78 | 0.95 | 0.46 | 0.06 | 0.31 | 0.08 | 1 | ||
| MT | 0.11 | 0.76 | 1 | 0.34 | 0 | 0.34 | 0.1 | 0.95 | 1 | |
| MF | 0.05 | 0.5 | 0.33 | 1 | −0.02 | 0.09 | 0 | 0.45 | 0.33 | 1 |
| Parameters | Features Value |
|---|---|
| Rock type | Type index |
| UCS | Average value |
| Advance rate | Average value, Peak value, Variance |
| Trust | Average value, Peak value, Variance |
| RSP | Average value, Peak value, Variance |
| Advance mileage | Interval value from the last disc cutter replacement |
| Advance displacement | Sample range |
| Drive motor current | Maximum, Minimum, Average value, Peak of 10 motor current variance, Peak of 5 min motor current kurtosis index |
| Predicted Class | Positive | Negative | |
|---|---|---|---|
| True Class | |||
| Positive | TP (true positive) | FN (false negative) | |
| Negative | FP (false positive) | TN (true negative) | |
| Models | Best Hyper-Parameters | Test Performance | Training Time/s | |||
|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 | |||
| KSVM | Kernel function: Gaussian Kernel scale: 1.05 Box constraint level: 500 Penalty factor: 3 | 98.1% | 98.7% | 98.3% | 98.5% | 1316 |
| DT | Number of splits: 693 Split criteria: Minimized deviations | 95.6% | 97.1% | 95.9% | 96.5% | 432 |
| KNN | Number of neighbors: 3 Distance metric: Hamming Distance weight: Inverse Distance Weighting | 96.8% | 99.2% | 95.8% | 97.5% | 866 |
| NB | Distribution: Kernel Kernel type: Gaussian | 72.8% | 78.3% | 79.9% | 79.1% | 2151 |
| CNN | Number of convolutional layer: 6 Dropout rate: 0.3 | 98.9% | 99.9% | 98.3% | 99.1% | 6500 |
| SAE | Number of stacked autoencoder: 4 | 99.0% | 99.4% | 98.9% | 99.2% | 5219 |
| Models | Test Performance | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 | |
| Operational data KSVM | 94.4% | 97.0% | 94.1% | 95.6% |
| Operational and geological data KSVM | 98.1% | 98.7% | 98.3% | 98.5% |
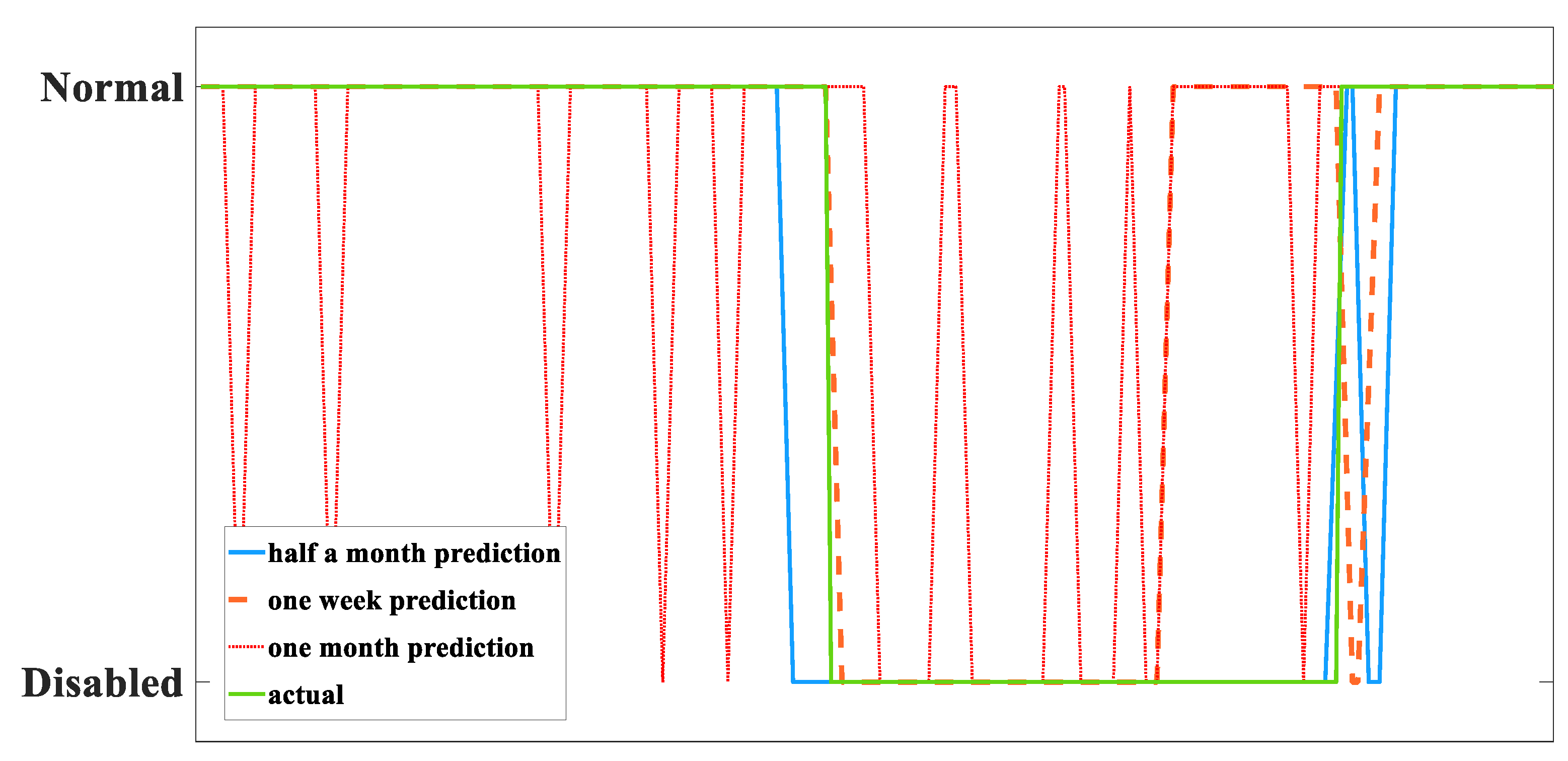
| Training Time Length | Test Performance | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 | |
| One month | 72.7% | 59.1% | 83.0% | 71.1% |
| Half a month | 90.0% | 98.7% | 73.6% | 86.2% |
| One week | 82.2% | 78.7% | 80.4% | 79.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Huang, S.; Wang, D.; Zhu, G.; Zhang, D. Prediction Model of Tunnel Boring Machine Disc Cutter Replacement Using Kernel Support Vector Machine. Appl. Sci. 2022, 12, 2267. https://doi.org/10.3390/app12052267
Liu Y, Huang S, Wang D, Zhu G, Zhang D. Prediction Model of Tunnel Boring Machine Disc Cutter Replacement Using Kernel Support Vector Machine. Applied Sciences. 2022; 12(5):2267. https://doi.org/10.3390/app12052267
Chicago/Turabian StyleLiu, Yang, Shuaiwen Huang, Di Wang, Guoli Zhu, and Dailin Zhang. 2022. "Prediction Model of Tunnel Boring Machine Disc Cutter Replacement Using Kernel Support Vector Machine" Applied Sciences 12, no. 5: 2267. https://doi.org/10.3390/app12052267
APA StyleLiu, Y., Huang, S., Wang, D., Zhu, G., & Zhang, D. (2022). Prediction Model of Tunnel Boring Machine Disc Cutter Replacement Using Kernel Support Vector Machine. Applied Sciences, 12(5), 2267. https://doi.org/10.3390/app12052267





