Leakage Effect on the Transmission Properties of a Duct Loaded with a Helmholtz Resonator
Abstract
:1. Introduction
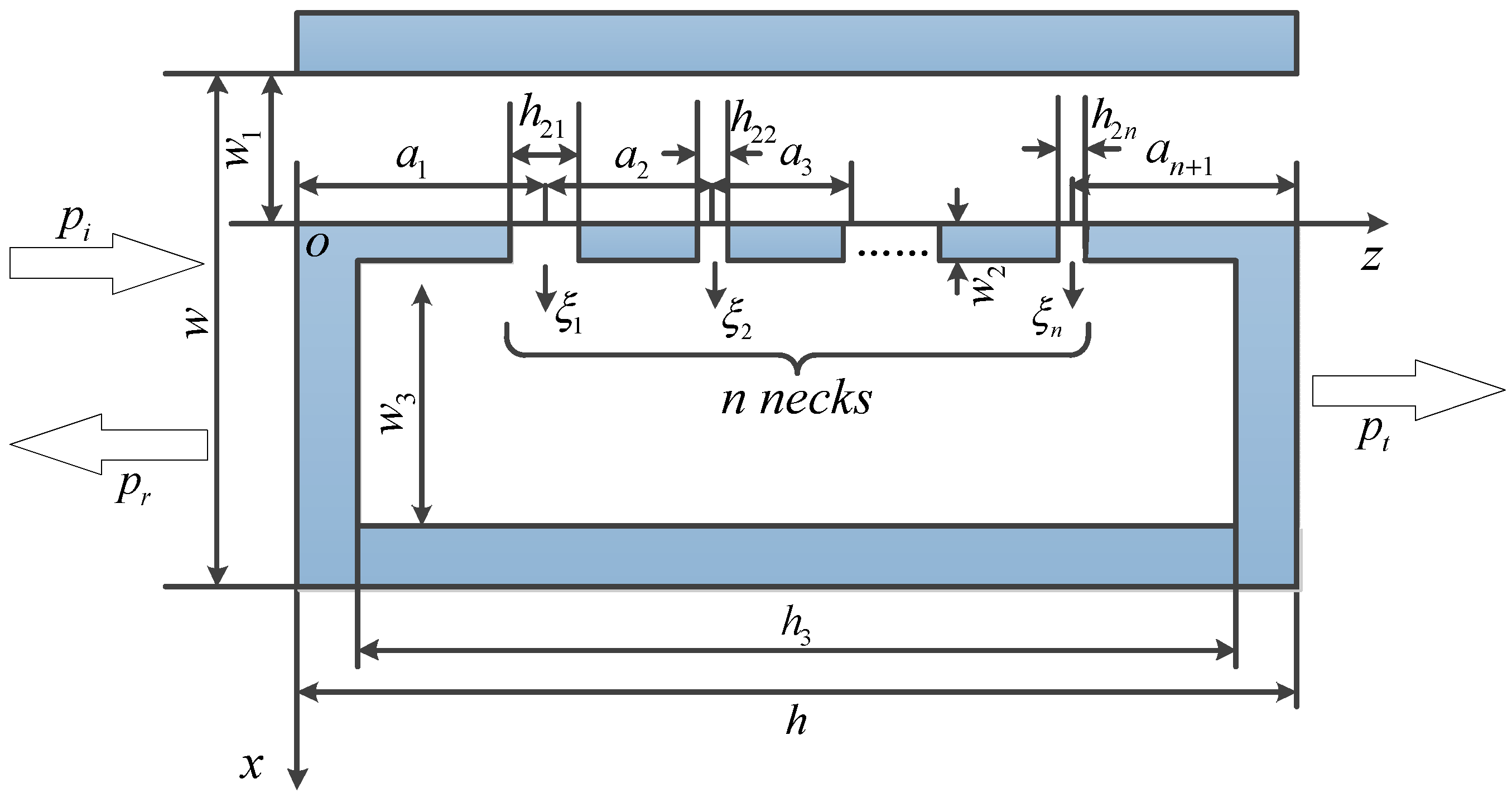
2. Acoustic Transmission of the DHR Device
2.1. Impedance Formulas
2.2. Acoustic Transfer Relations in the Duct
2.3. Reflection and Transmission Coefficients
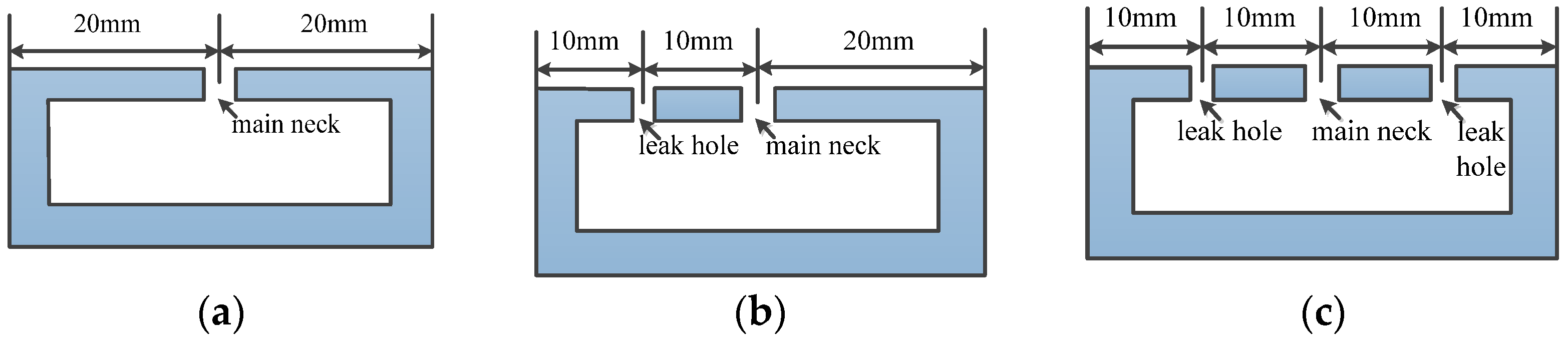
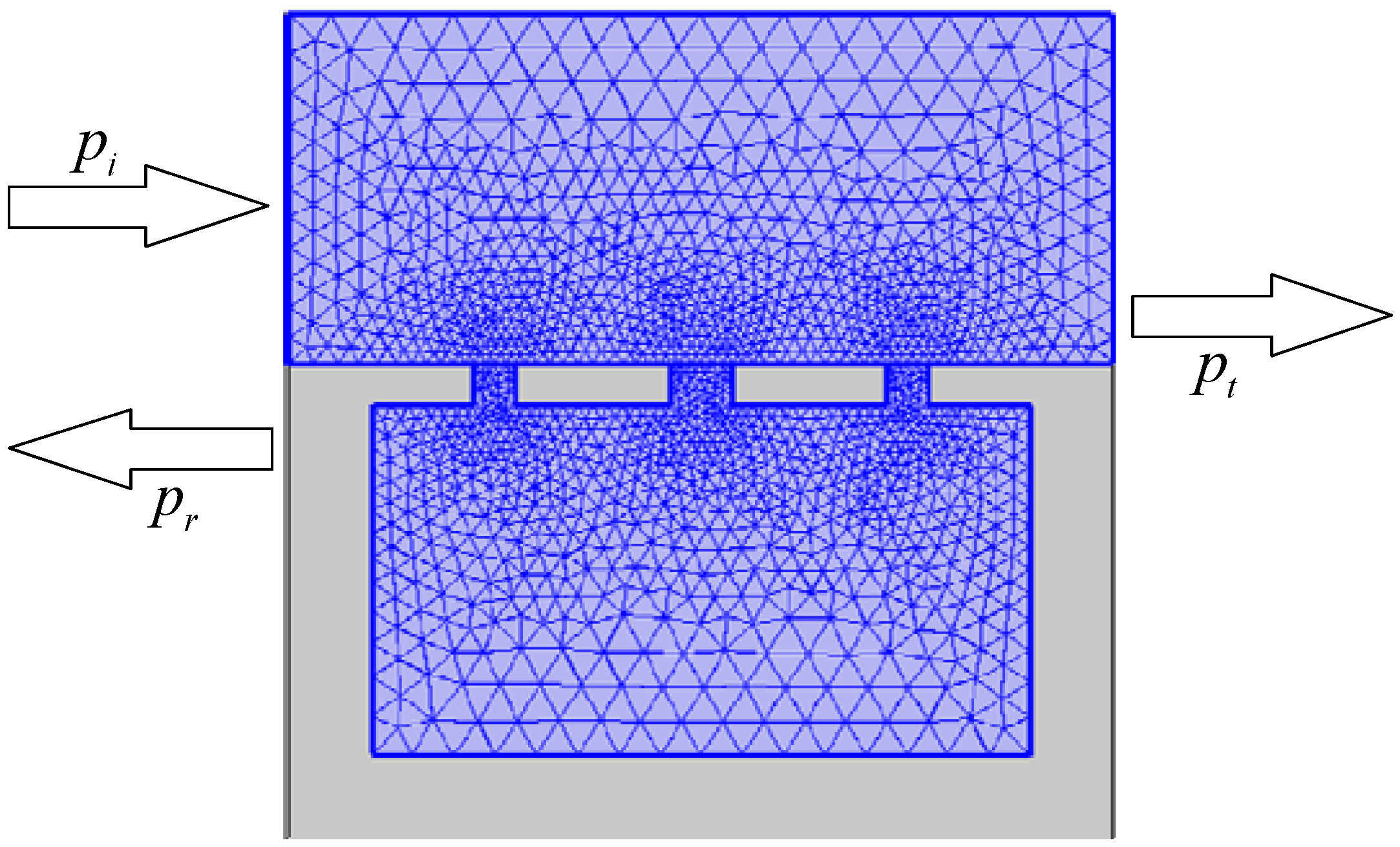
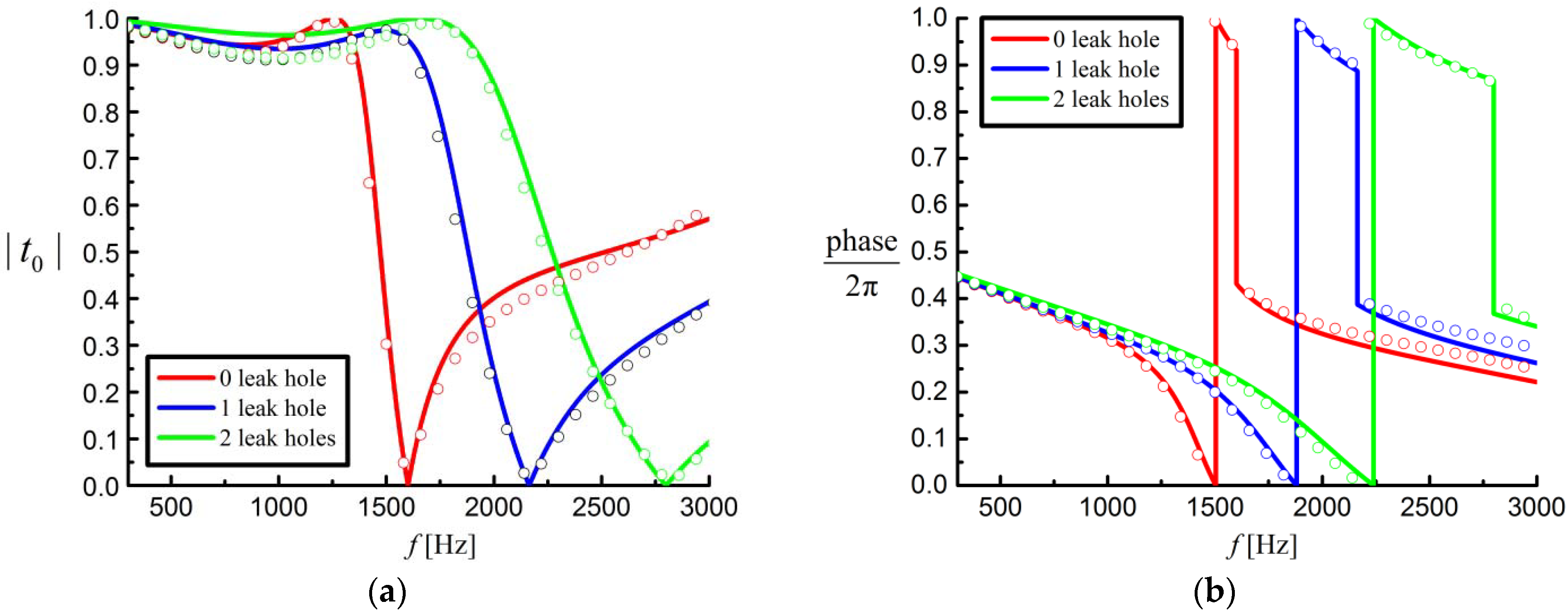
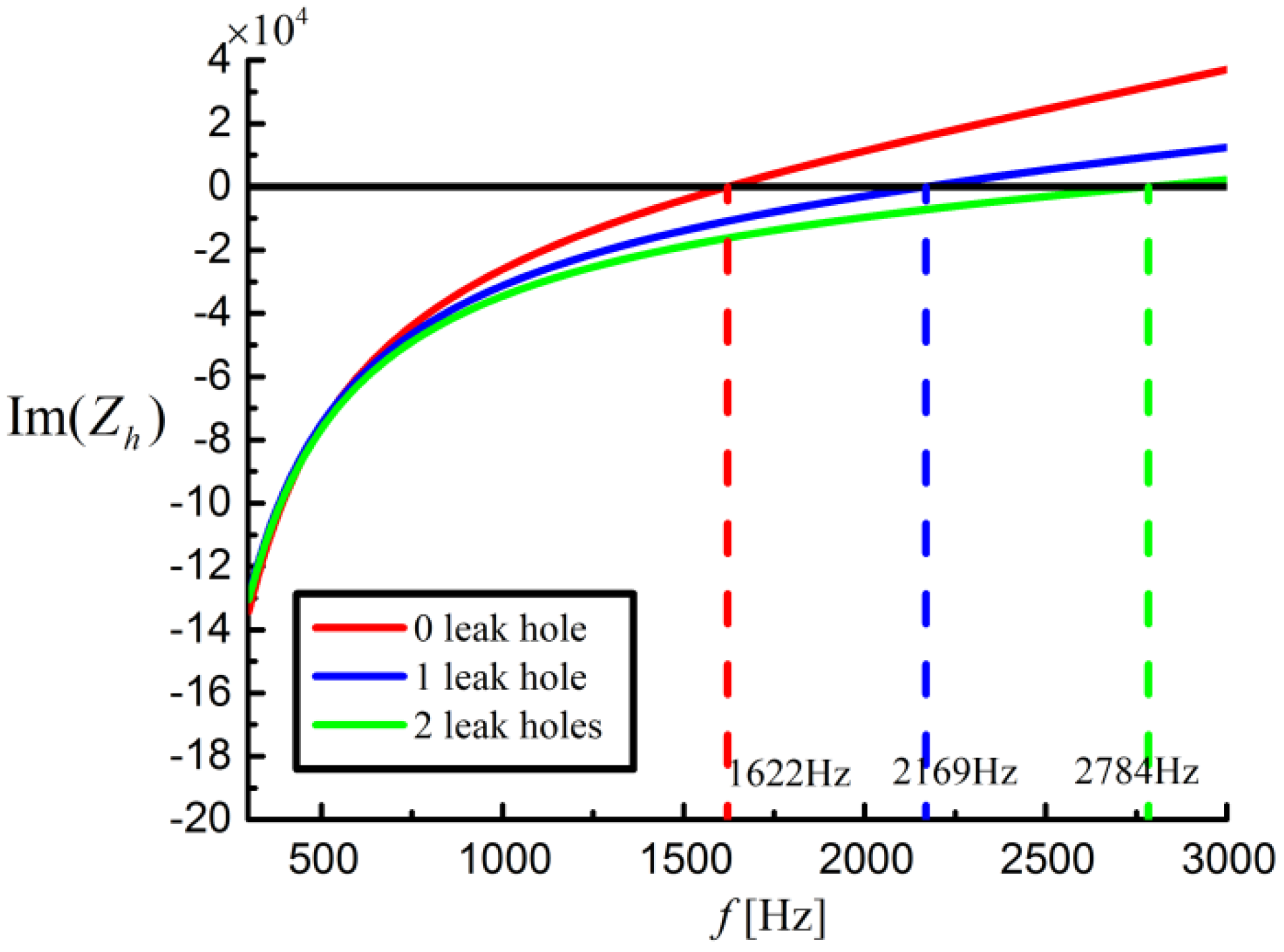
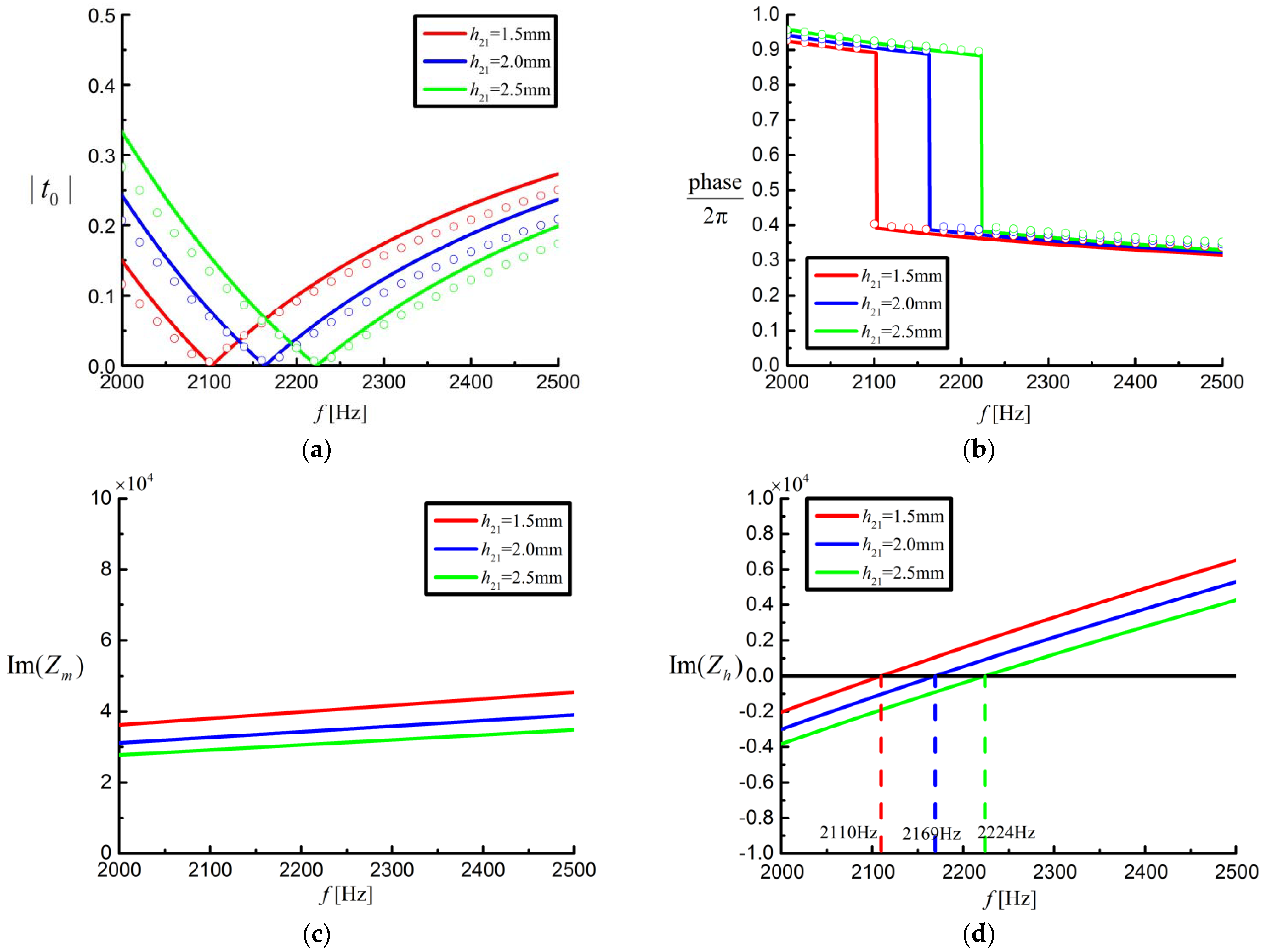
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wu, D.; Zhang, N.; Mak, C.M.; Cai, C. Hybrid noise control using multiple Helmholtz resonator arrays. Appl. Acoust. 2019, 143, 31–37. [Google Scholar] [CrossRef]
- Huang, S.B.; Fang, X.S.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. J. Acoust. Soc. Am. 2019, 145, 254–262. [Google Scholar] [CrossRef]
- Lee, T.; Nomura, T.; Iizuka, H. Damped resonance for broadband acoustic absorption in one-port and two-port systems. Sci. Rep. 2019, 9, 13077. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.P.; Zhang, X.T.; Sun, H.X.; Yuan, S.Q.; Qian, J.; Ge, Y. Broadband tunable acoustic asymmetric focusing lens from dual-layer metasurfaces. Phys. Rev. Appl. 2018, 10, 014016. [Google Scholar] [CrossRef]
- Li, J.F.; Shen, C.; Rubio, A.D.; Tretyakov, S.A.; Cummer, S.A. Systematic design and experimental demonstration of bianisotropic metasurfaces for scattering-free manipulation of acoustic wavefronts. Nat. Commun. 2018, 9, 1342. [Google Scholar] [CrossRef] [PubMed]
- Lan, J.; Zhang, X.W.; Liu, X.Z.; Li, Y.F. Wavefront manipulation based on transmissive acoustic metasurface with membrane-type hybrid structure. Sci. Rep. 2018, 8, 14171. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S.; Yin, J.; Yu, G.K.; Peng, L.H.; Wang, N. Acoustic superlens using Helmholtz-resonator-based metamaterials. Appl. Phys. Lett. 2015, 107, 193505. [Google Scholar] [CrossRef]
- Lan, J.; Li, Y.; Xu, Y.; Liu, X.Z. Manipulation of acoustic wavefront by gradient metasurface based on Helmholtz Resonators. Sci. Rep. 2017, 8, 10587. [Google Scholar] [CrossRef] [Green Version]
- Gong, K.; Wang, X.; Ouyang, H.; Mo, J. Supplementary material of tuneable gradient Helmholtz-resonator-based acoustic metasurface for acoustic focusing. J. Phys. D Appl. Phys. 2019, 52, 385303. [Google Scholar] [CrossRef]
- Park, C.M.; Lee, S.H. Propagation of acoustic waves in a metamaterial with a refractive index of near zero. Appl. Phys. Lett. 2013, 102, 241906. [Google Scholar] [CrossRef]
- Ning, L.; Wang, Y.Z.; Wang, Y.S. Active control of elastic metamaterials consisting of symmetric double helmholtz resonator cavities. Int. J. Mech. Sci. 2019, 153–154, 287–298. [Google Scholar] [CrossRef]
- Hu, X.; Ho, K.M.; Chan, C.T.; Zi, J. Homogenization of acoustic metamaterials of Helmholtz resonators in fluid. Phys. Rev. B 2008, 77, 172301. [Google Scholar] [CrossRef] [Green Version]
- Fang, N.; Xi, D.J.; Xu, J.Y.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Wright, O.B. Origin of negative density and modulus in acoustic metamaterials. Phys. Rev. B 2016, 93, 024302. [Google Scholar] [CrossRef] [Green Version]
- Edalati, K.; Rastkhah, N.; Kermani, A.; Seiedi, M.; Movafeghi, A. The use of radiography for thickness measurement and corrosion monitoring in pipes. Int. J. Press. Vessels Pip. 2006, 83, 736–741. [Google Scholar] [CrossRef]
- Vargas-Arista, B.; Hallen, J.M.; Albiter, A. Effect of artificial aging on the microstructure of weldment on API 5L X-52 steel pipe. Mater. Charact. 2007, 58, 721–729. [Google Scholar] [CrossRef]
- Selamet, A.; Kim, H.; Huff, N.T. Leakage effect in Helmholtz resonators. J. Acoust. Soc. Am. 2009, 126, 1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, I.; Jeon, K.; Park, J. The effect of leakage on the acoustic performance of reactive silencers. Appl. Acoust. 2013, 74, 479–484. [Google Scholar] [CrossRef]
- Langfeldt, F.; Hoppen, H.; Gleine, W. Resonance frequencies and sound absorption of Helmholtz resonators with multiple necks. Appl. Acoust. 2019, 145, 314–319. [Google Scholar] [CrossRef]
- Zhao, H.F.; Xiao, X.; Xu, P.; Zhao, T.C.; Song, L.G.; Pan, X.X.; Mi, J.C.; Xu, M.Y.; Wang, Z.L. Dual-tube Helmholtz resonator-based triboelectric nanogenerator for highly efficient harvesting of acoustic Energy. Adv. Energy Mater. 2019, 9, 1902824. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, L.B.; Xu, Q.Q.; Yan, C.Y. Gas pipeline leakage detection based on acoustic technology. Eng. Fail. Anal. 2013, 31, 1–7. [Google Scholar] [CrossRef]
- Mostafapour, A.; Davoudi, S. Analysis of leakage in high pressure pipe using acoustic emission method. Appl. Acoust. 2013, 74, 335–342. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, L.B.; Liang, W.; Ding, Q.K. Integrated leakage detection and localization model for gas pipelines based on the acoustic wave method. J. Loss Prev. Process Ind. 2014, 27, 74–88. [Google Scholar] [CrossRef]
- Li, Y.; Qi, S.B.; Assouar, M.B. Theory of metascreen-based acoustic passive phased array. New J. Phys. 2016, 18, 043024. [Google Scholar] [CrossRef]
- Lee, I.; Selamet, A.; Huff, N.T. Acoustic impedance of perforations in contact with fibrous material. J. Acoust. Soc. Am. 2006, 119, 2785–2797. [Google Scholar] [CrossRef]
- Qi, L.H.; Yu, G.K.; Wang, X.L.; Wang, G.B.; Wang, N. Interference-induced angle-independent acoustical transparency. J. Appl. Phys. 2014, 116, 234506. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Zhao, Y. Leakage Effect on the Transmission Properties of a Duct Loaded with a Helmholtz Resonator. Appl. Sci. 2022, 12, 2402. https://doi.org/10.3390/app12052402
Ou Y, Zhao Y. Leakage Effect on the Transmission Properties of a Duct Loaded with a Helmholtz Resonator. Applied Sciences. 2022; 12(5):2402. https://doi.org/10.3390/app12052402
Chicago/Turabian StyleOu, Yang, and Yonghui Zhao. 2022. "Leakage Effect on the Transmission Properties of a Duct Loaded with a Helmholtz Resonator" Applied Sciences 12, no. 5: 2402. https://doi.org/10.3390/app12052402
APA StyleOu, Y., & Zhao, Y. (2022). Leakage Effect on the Transmission Properties of a Duct Loaded with a Helmholtz Resonator. Applied Sciences, 12(5), 2402. https://doi.org/10.3390/app12052402




