Thickness-Stretch Vibration of an Infinite Piezoelectric Plate with Flexoelectricity
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Three-Dimensional Governing Equations
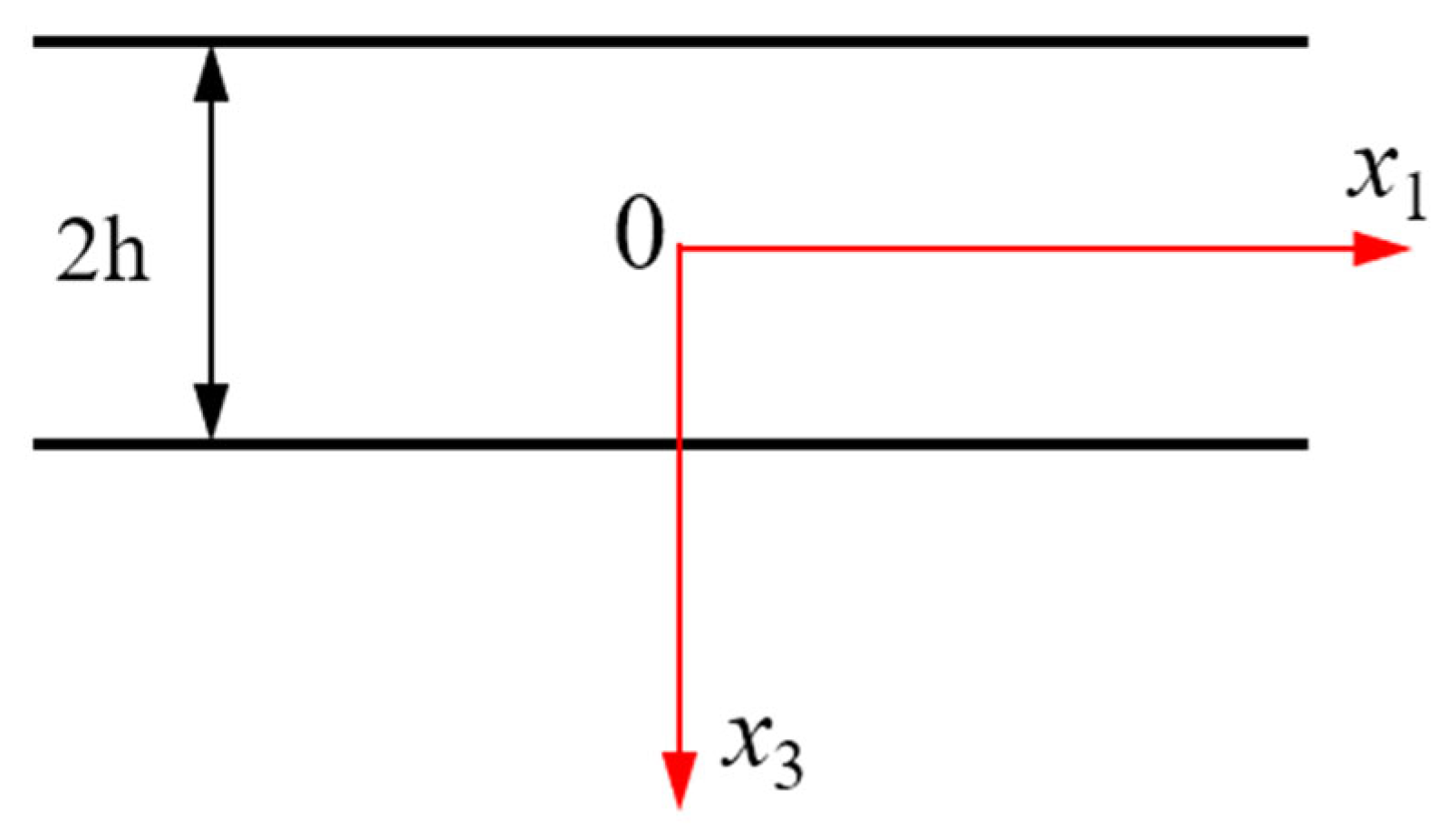
2.2. One-Dimensional Model for Thickness-Stretch Vibration
- (a)
- Open circuit condition (OP)
- (b)
- Short circuit condition (SC)
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, T.D.; Mao, S.; Yeh, Y.-W.; Purohit, P.K.; McAlpine, M.C. Nanoscale Flexoelectricity. Adv. Mater. 2013, 25, 946–974. [Google Scholar] [CrossRef] [PubMed]
- Tagantsev, A.K. Piezoelectricity and flexoelectricity in crystalline dielectrics. Phys. Rew. B 1986, 34, 5883–5889. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Hu, S. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Deng, Q.; Lv, S.; Li, Z.; Tan, K.; Liang, X.; Shen, S. The impact of flexoelectricity on materials, devices, and physics. J. Appl. Phys. 2020, 128, 080902. [Google Scholar] [CrossRef]
- Qi, L. Rayleigh wave propagation in semi-infinite flexoelectric dielectrics. Phys. Scr. 2019, 94, 065803. [Google Scholar] [CrossRef]
- Yang, W.; Deng, Q.; Liang, X.; Shen, S. Lamb wave propagation with flexoelectricity and strain gradient elasticity considered. Smart Mater. Struct. 2018, 27, 085003. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, S.; Chen, Y.; Chen, J.; Hu, P.; Wu, H.; Zhou, Y. Thickness-twist waves in the nanoplates with flexoelectricity. Mech. Adv. Mater. Struc. 2020, 28, 2343–2350. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, W. Converse flexoelectric effect in comb electrode piezoelectric microbeam. Phys. Lett. A 2012, 376, 1661–1663. [Google Scholar] [CrossRef]
- Yan, Z. Size-dependent bending and vibration behaviors of piezoelectric circular nanoplates. Smart Mater. Struct. 2016, 25, 035017. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, T.; Wang, J.; Huang, B.; Kim, H.S. Bending stress analysis of a piezoelectric nanoplate with flexoelectricity under inhomogeneous electric fields. AIP Adv. 2019, 9, 055029. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Huang, B.; Wang, J. Flexoelectric effect on thickness-shear vibration of a rectangular piezoelectric crystal plate. Mater. Res. Express 2021, 8, 115702. [Google Scholar] [CrossRef]
- Kane, T.R.; Mindlin, R.D. High-frequency extensional vibrations of plates. J. Appl. Mech. 1956, 23, 277–283. [Google Scholar] [CrossRef]
- Yang, J.S.; Krishnaswamy, S. An approximate analysis of thickness-stretch waves in an elastic plate. Wave Motion 1999, 30, 291–301. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, H.; Hu, Y.; Jiang, Q. Performance of a piezoelectric harvester in thickness-stretch mode of a plate. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1872–1876. [Google Scholar] [CrossRef]
- Huang, D.; Yang, J. On the propagation of long thickness-stretch waves in piezoelectric plates. Ultrasonics 2014, 54, 1277–1280. [Google Scholar] [CrossRef]
- Yang, Z.; Hu, Y.; Wang, J.; Yang, J. Nonlinear coupling between thickness-shear and thickness-stretch modes in a rotated Y-cut quartz resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 220–224. [Google Scholar] [CrossRef]
- Liu, N.; Yang, J.; Wang, J. Thickness-stretch vibration of a crystal plate carrying a micro-rod array. Sci. China Phys. Mech. 2012, 2152–2157. [Google Scholar] [CrossRef]
- Ji, X.; Fan, Y.; Han, T.; Cai, P. Nonlinear thickness-stretch vibration of thin-film acoustic wave resonators. Acoust. Phys. 2016, 62, 160–164. [Google Scholar] [CrossRef]
- Sun, J.B.; Du, J.K.; Wang, J.; Pan, X.B. Thickness-extension vibration of magnetoelectric plate with electrodes. In Proceedings of the 2011 SPAWDA Symposium on Piezoelectricity, Acoustic Waves, and Device Applications, Shanghai, China, 9–11 December 2012. [Google Scholar]
- Yang, J. Thickness vibration of an electroelastic plate under biasing fields. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 2195–2201. [Google Scholar] [CrossRef]
- Zhang, H.; Turner, J.A.; Yang, J.; Kosinski, J.A. Electroelastic Effect of Thickness Mode Langasite Resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 2120–2128. [Google Scholar] [CrossRef] [Green Version]
- Gong, X.; Han, M.; Shang, X.; Xiong, J.; Jie, D.; Sekimoto, H. Two-dimensional analysis of spurious modes in aluminum nitride film resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 1171–1176. [Google Scholar] [CrossRef]
- Zhang, R.; Liang, X.; Shen, S. A Timoshenko dielectric beam model with flexoelectric effect. Meccanica 2016, 51, 1181–1188. [Google Scholar] [CrossRef]
- Yang, J. Analysis of Piezoelectric Devices; World Scientific: Singapore, 2006. [Google Scholar]
- Singhal, A.; Mohammad Sedighi, H.; Ebrahimi, F.; Kuznetsova, I. Comparative study of the flexoelectricity effect with a highly/weakly interface in distinct piezoelectric materials (PZT-2, PZT-4, PZT-5H, LiNbO3, BaTiO3). Wave Random Complex 2021, 31, 1780–1798. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectric polarization of barium strontium titanate in the paraelectric state. Appl. Phys. Lett. 2002, 81, 3440–3442. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Huang, B.; Wang, J. Thickness-Stretch Vibration of an Infinite Piezoelectric Plate with Flexoelectricity. Appl. Sci. 2022, 12, 2436. https://doi.org/10.3390/app12052436
Guo Y, Huang B, Wang J. Thickness-Stretch Vibration of an Infinite Piezoelectric Plate with Flexoelectricity. Applied Sciences. 2022; 12(5):2436. https://doi.org/10.3390/app12052436
Chicago/Turabian StyleGuo, Yan, Bin Huang, and Ji Wang. 2022. "Thickness-Stretch Vibration of an Infinite Piezoelectric Plate with Flexoelectricity" Applied Sciences 12, no. 5: 2436. https://doi.org/10.3390/app12052436






