Efficient LDPC Encoder Design for IoT-Type Devices
Abstract
:1. Introduction
1.1. Relevant Research Works
1.2. This Research Contributions
- We show how the Richardson–Urbanke encoding algorithm [43] utilized for QC-LDPC codes can be decomposed into simple, repeated operations of cyclic shifts and additions.
- We present a CPU implementation of this encoding with a QC-LDPC matrix representation that can be efficiently stored in the system’s RAM.
- We provide the experimental results of the implementation in comparison with other classic block ECC schemes: the RS (Reed–Solomon) and BCH (Bose–Chaudhuri–Hocquenghem) codes. Comparisons are made in terms of memory usage, block encoding time, energy savings and error-correction performance.
2. Error Correction for IoT End-Node Devices
- The encoding time, which is connected with encoding complexity;
- The coding scheme gain, which is the possible reduction in transmission power due to the application of an effective ECC scheme.
3. LDPC Codes
3.1. Preliminaries
3.2. QC-LDPC Codes
- -
- An all-zero zero matrix;
- -
- An identity matrix;
- -
- An identity matrix with circularly shifted columns.
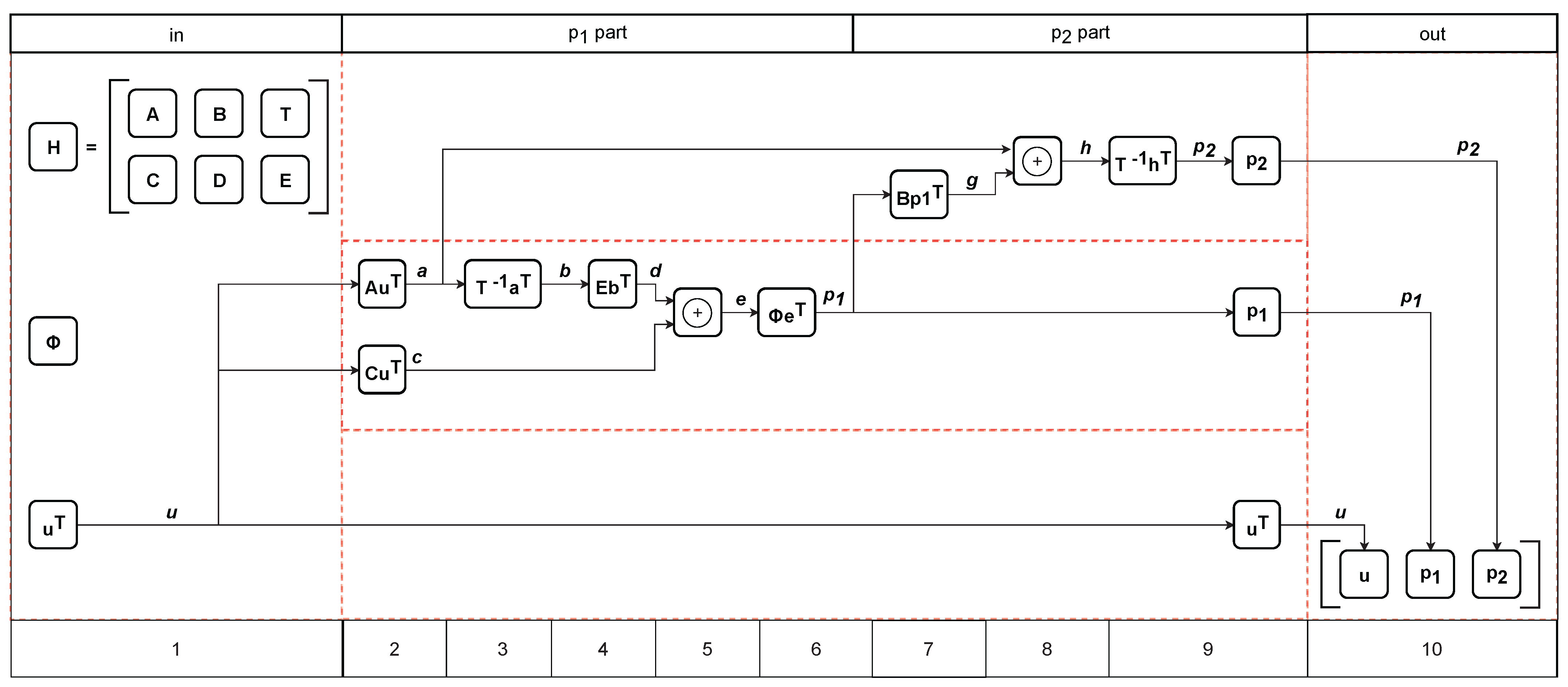
4. Richardson–Urbanke Encoding Algorithm
5. LDPC Encoder Design for a Microcontroller Implementation
5.1. Elementary Computations
- Sparsely structured matrix by vector multiplication over , e.g., ;
- Inverse of a lower-triangular sparse matrix by vector multiplication over , e.g., ;
- Addition over , e.g., .
- A zero matrix (); then, .
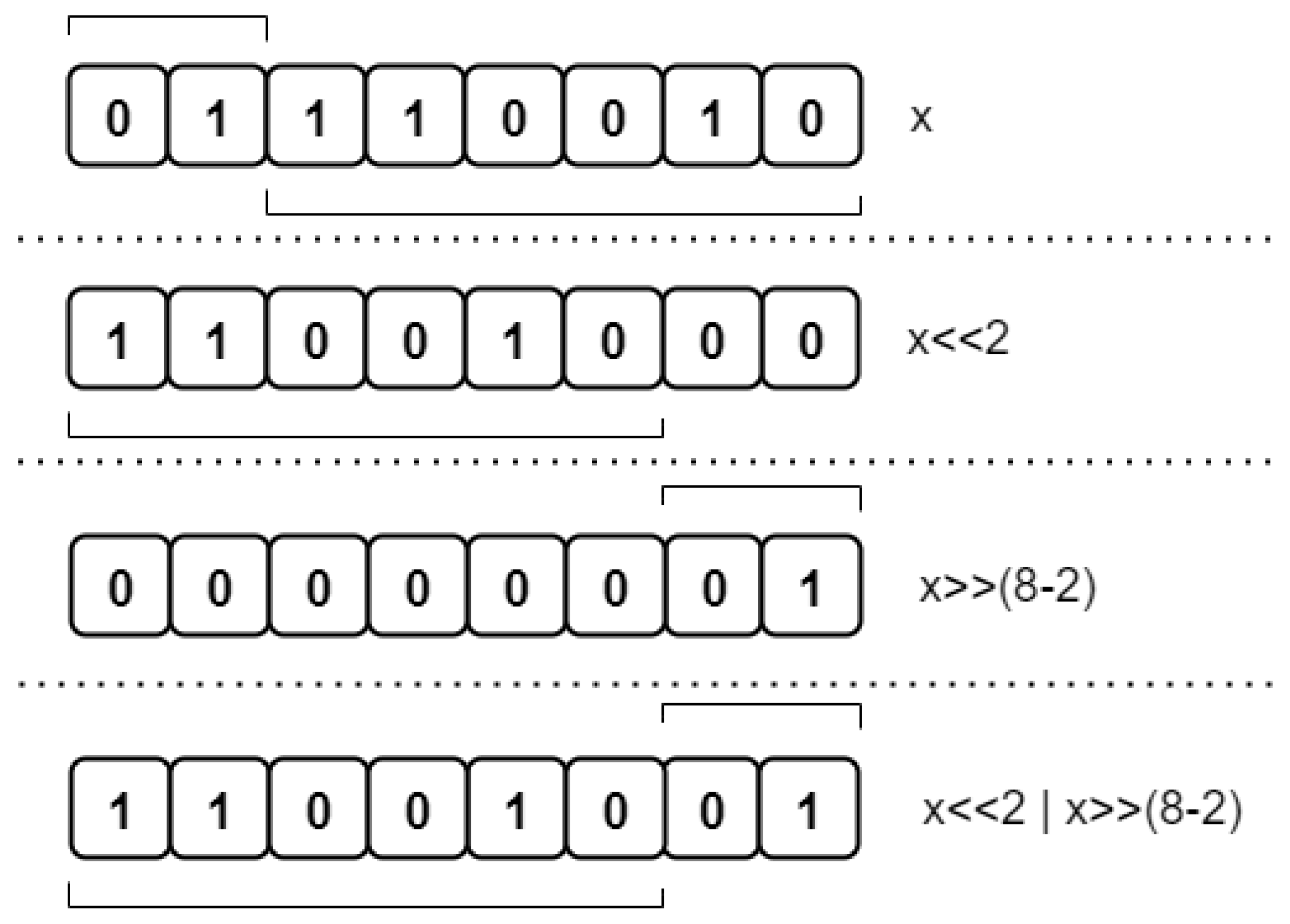
- A circular shift of an identity matrix by ; then it can easily be verified that is a circular shift of by positions.
- Circular shift operations of subvectors of length P;
- Subvector additions over realized with XOR operations.
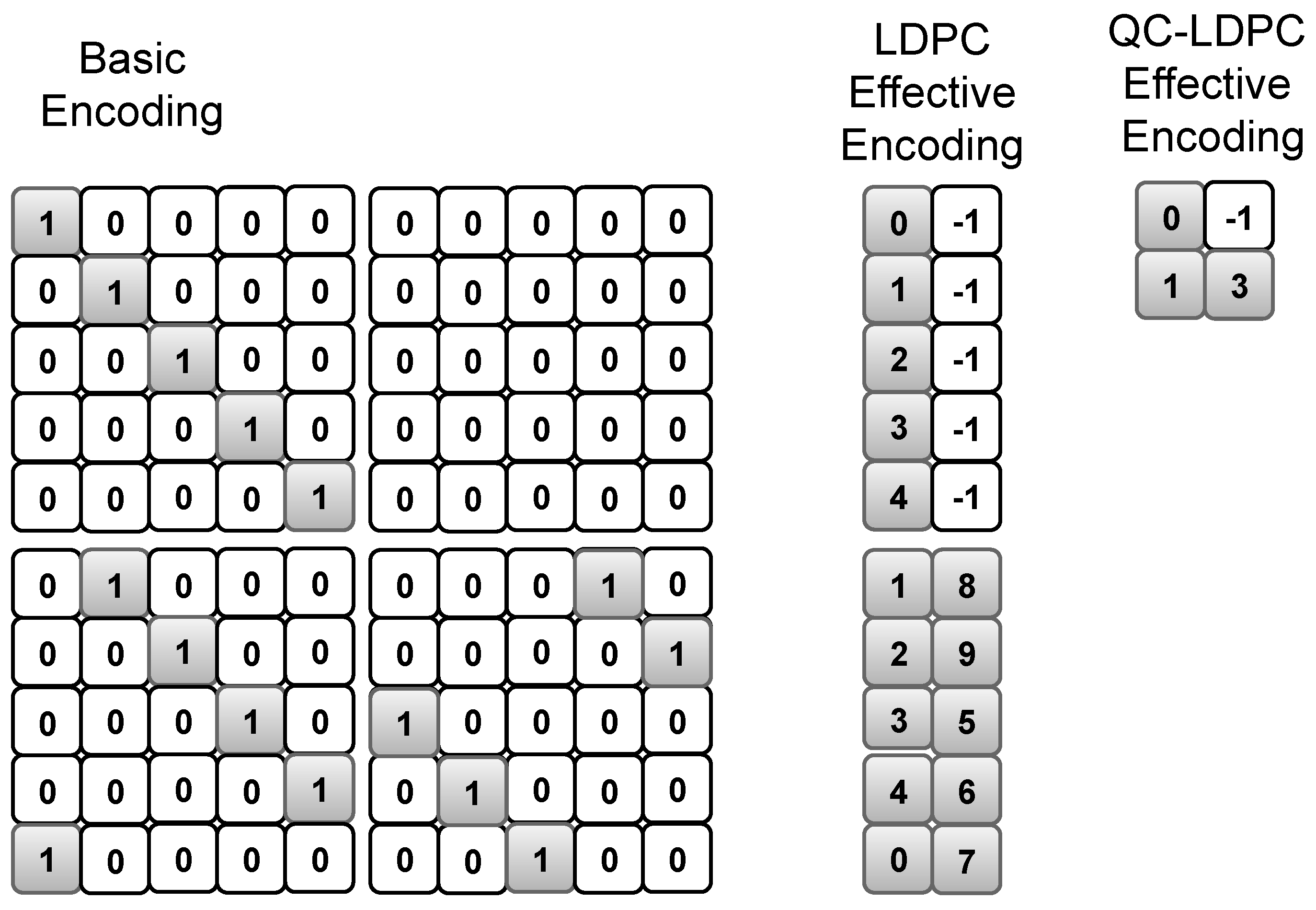
5.2. Parity-Check Matrix Representations in Memory
5.3. Implementation of Elementary Operations
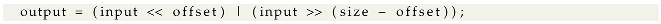
5.4. Microcontroller Implementation Issues
6. Numerical Results
| Algorithm 1. QC-LDPC parity-check matrix construction. |
|
- The encoding combines operation for a blocks of P bits because multiplication by a whole submatrix can be done in a single shift operation;
- The QC-LDPC parity-check matrix, which can be used directly for encoding, is by definition sparse; therefore, the number of multiplications by submatrices is also relatively small.
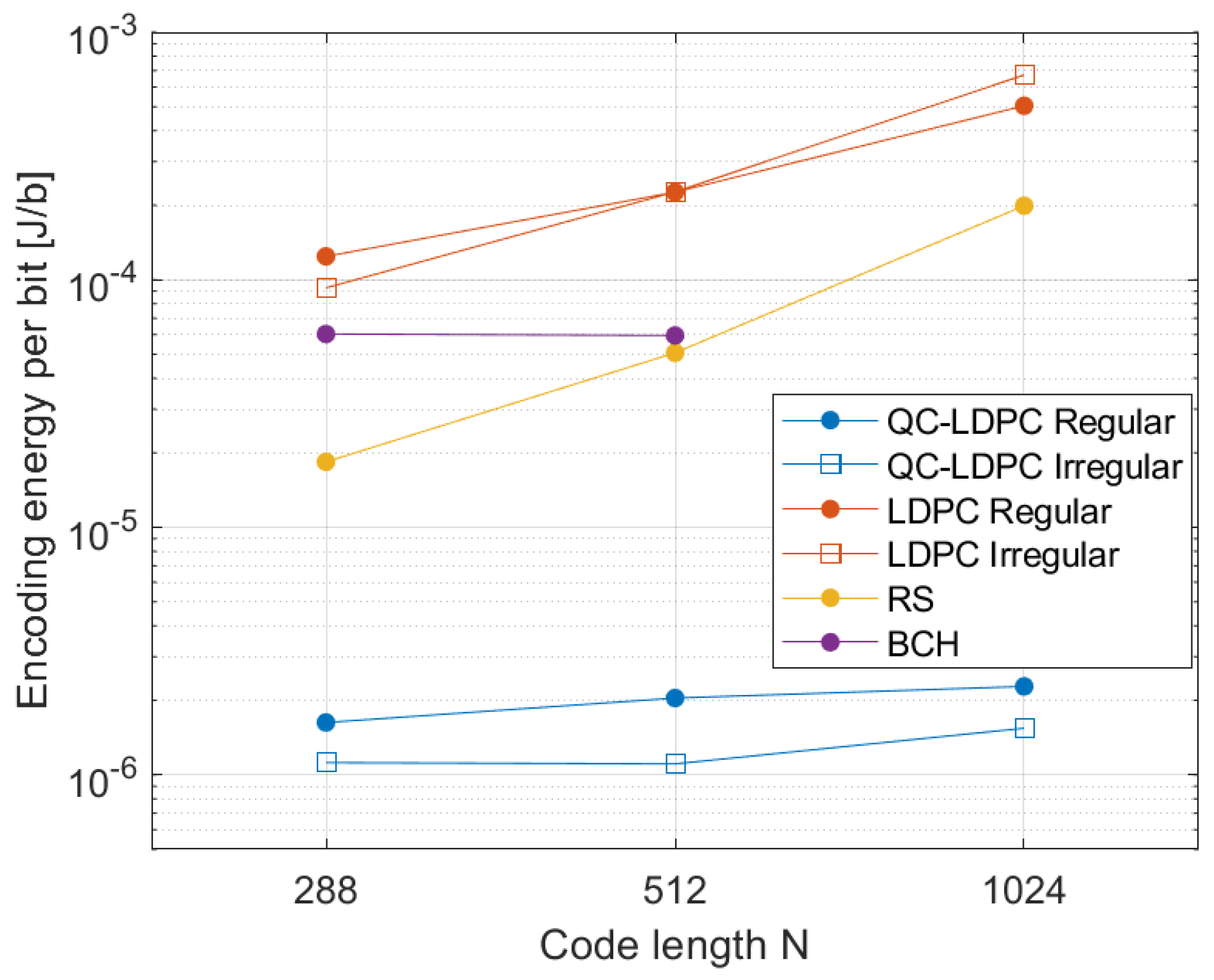
6.1. Memory Utilization
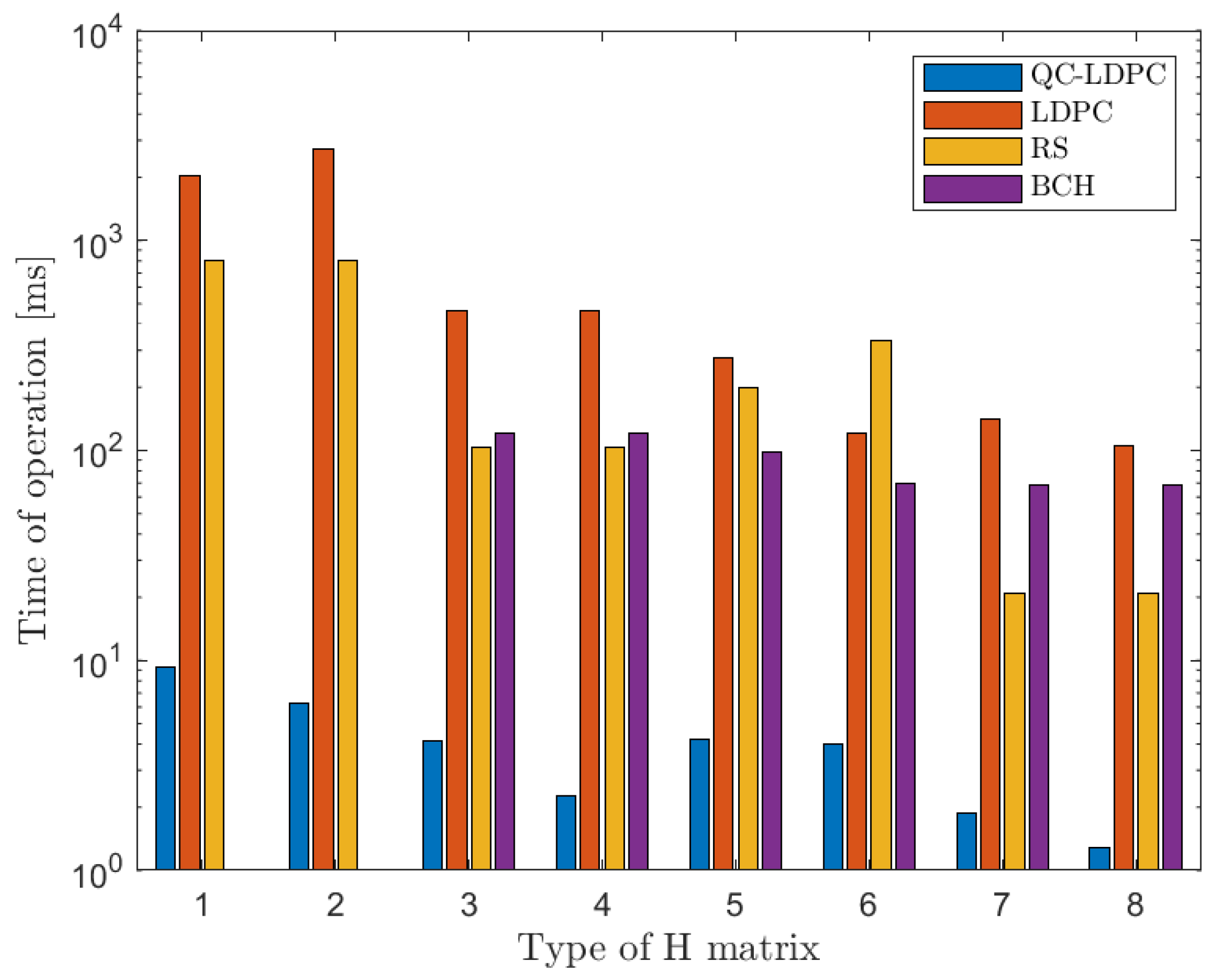
6.2. Block Encoding Time
- The voltage supplied to the circuit is 3.6 V.
- The current in the active mode with 80 MHz clock is 33.5 mA.
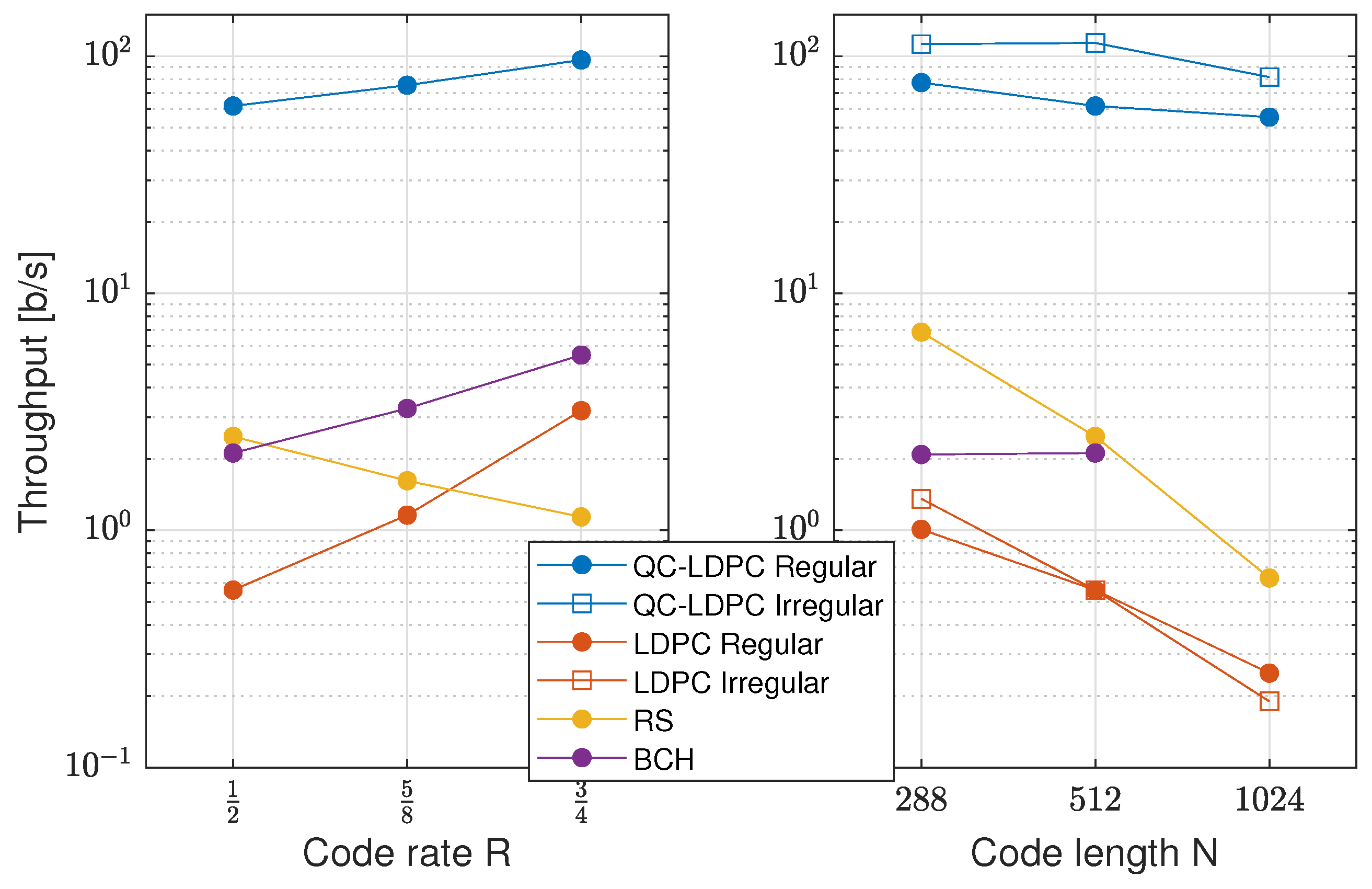
6.3. Throughput
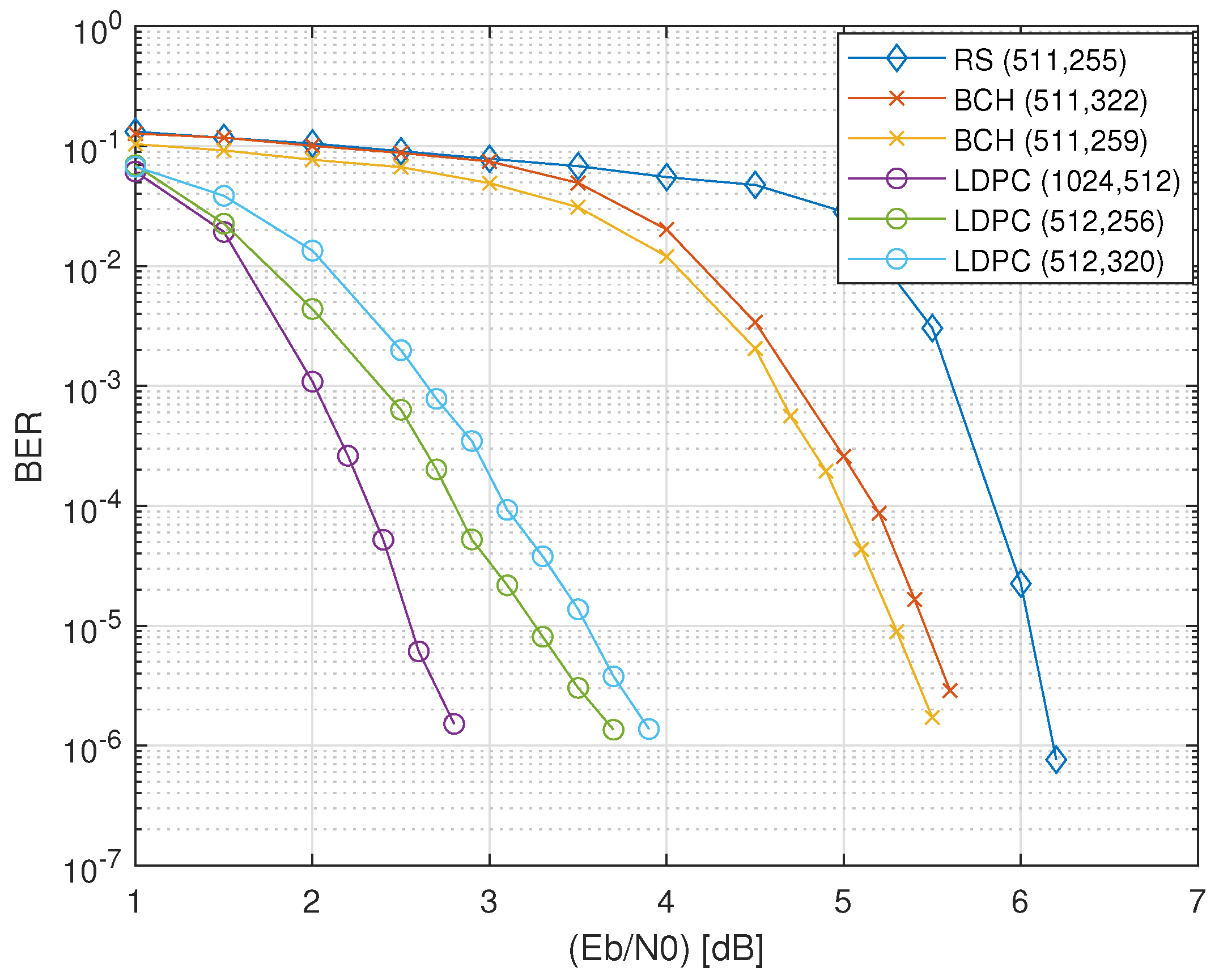
6.4. Error-Correction Performance
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Swamy, S.N.; Kota, S.R. An Empirical Study on System Level Aspects of Internet of Things (IoT). IEEE Access 2020, 8, 188082–188134. [Google Scholar] [CrossRef]
- Dubal, V.A.; Rao, Y.S. A Low-Power High-Performance Sensor Node for Internet of Things. In Proceedings of the IEEE Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; pp. 607–612. [Google Scholar]
- Rajasekaran, C.; Raguvaran, K. Microcontroller Based Reconfigurable IoT Node. In Proceedings of the IEEE 4th International Conference on Frontiers of Signal Processing, Poitiers, France, 24–27 September 2018; pp. 12–16. [Google Scholar]
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon Limit Error-Correcting Coding and Decoding: Turbo-Codes. In Proceedings of the (IEEE) International Conference on Communications, Geneva, Switzerland, 23–26 May 1993; pp. 1064–1070. [Google Scholar]
- Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Gallager, R. Low-density parity-check codes. IRE Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef] [Green Version]
- MacKay, D.J.C. Good Error-Correcting Codes Based on Very Sparse Matrices. IEEE Trans. Inf. Theory 1999, 45, 399–431. [Google Scholar] [CrossRef] [Green Version]
- Condo, C. VLSI Implementation of a Multi-ModeTurbo/LDPC Decoder Architecture. IEEE Trans. Circuits Syst. I 2013, 60, 1441–1454. [Google Scholar] [CrossRef]
- Nguyen, T.T.B.; Tan, T.N.; Lee, H. Low-Complexity High-Throughput QC-LDPC Decoder for 5G New Radio Wireless Communication. Electronics 2021, 10, 1–18. [Google Scholar]
- Zhu, Y.; Xing, Z.; Li, Z.; Zhang, Y.; Hu, Y. High Area-Efficient Parallel Encoder with Compatible Architecture for 5G LDPC Codes. Symmetry 2021, 13, 700. [Google Scholar] [CrossRef]
- Hailes, P.; Xu, L.; Maunder, R.G.; Al-Hashimi, B.M.; Hanzo, L. A Survey of FPGA-Based LDPC Decoders. IEEE Commun. Surv. Tutor. 2015, 18, 1098–1122. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Zhang, Y.; Li, W.; Huang, L.K.; Cosmas, J.; Li, D.; Maple, C. Low Latency Parallel Turbo Decoding Implementation for Future Terrestrial Broadcasting Systems. IEEE Trans. Broadcast. 2018, 64, 96–104. [Google Scholar] [CrossRef] [Green Version]
- Lazarenko, A. FPGA Design and Implementation of DVB-S2/S2X LDPC Encoder. In Proceedings of the IEEE International Conference on Electrical Engineering and Photonics, St. Petersburg, Russia, 17–18 October 2019; pp. 98–102. [Google Scholar]
- Petrović, V.L.; El Mezeni, D.M.; Radošević, A. Flexible 5G New Radio LDPC Encoder Optimized for High Hardware Usage Efficiency. Electronics 2021, 10, 1106. [Google Scholar] [CrossRef]
- Tarver, C.; Tonnemacher, M.; Chen, H.; Zhang, J.; Cavallaro, J.R. GPU-Based, LDPC Decoding for 5G and Beyond. IEEE Open J. Circuits Syst. 2021, 2, 278–290. [Google Scholar] [CrossRef]
- Liao, S.; Zhan, Y.; Shi, Z.; Yang, L. A High Throughput and Flexible Rate 5G NR LDPC Encoder on a Single GPU. In Proceedings of the IEEE International Conference on Advanced Communications Technology (ICACT), Pyeongchang-gun, Korea, 7–10 February 2021; pp. 29–34. [Google Scholar]
- Richardson, T.J.; Shokrollahi, M.A.; Urbanke, R.L. Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes. IEEE Trans. Inf. Theory 2001, 47, 619–637. [Google Scholar] [CrossRef] [Green Version]
- Kelley, C.A.; Deepak, S. Pseudocodewords of Tanner Graphs. IEEE Trans. Inf. Theory 2007, 53, 4013–4038. [Google Scholar] [CrossRef]
- Divsalar, D.; Dolinar, S.; JoJones, C.R.; Andrews, K. Capacity-Approaching Protograph Codes. IEEE J. Sel. Areas Commun. 2009, 27, 876–888. [Google Scholar] [CrossRef]
- Hu, X.Y.; Eleftheriou, E.; Arnold, D.M. Regular and Irregular Progressive Edge-Growth Tanner Graphs. IEEE Trans. Inf. Theory 2005, 51, 386–398. [Google Scholar] [CrossRef]
- Gholami, M.; Raeisi, G. Large Girth Column-Weight Two and Three LDPC Codes. IEEE Commun. Lett. 2014, 18, 1671–1674. [Google Scholar] [CrossRef]
- Bocharova, I.E.; Kudryashov, B.; Johannesson, R. Searching for Binary and Nonbinary Block and Convolutional LDPC Codes. IEEE Trans. Inf. Theory 2016, 62, 163–183. [Google Scholar] [CrossRef]
- Tasdighi, A.; Banihashemi, A.H.; Sadeghi, M.R. Symmetrical Constructions for Regular Girth-8 QC-LDPC Codes. IEEE Trans. Commun. 2017, 52, 1242–1247. [Google Scholar] [CrossRef]
- Sulek, W. Protograph Based Low-Density Parity-Check Codes Design with Mixed Integer Linear Programming. IEEE Access 2019, 7, 1424–1438. [Google Scholar] [CrossRef]
- Sulek, W.; Kucharczyk, M. Partial parallel encoding and algorithmic construction of non-binary structured IRA codes. China Commun. 2016, 13, 103–116. [Google Scholar] [CrossRef]
- Fossorier, M.P.C.; Mihaljevic, M.; Imai, H. Reduced Complexity Iterative Decoding of Low-Density Parity Check Codes Based on Belief Propagation. IEEE Trans. Commun. 1999, 47, 673–680. [Google Scholar] [CrossRef]
- Li, J.; Liu, K.; Lin, S.; Abdel-Ghaffar, K. Algebraic Quasi-Cyclic LDPC Codes: Construction, Low Error-Floor, Large Girth and a Reduced-Complexity Decoding Scheme. IEEE Trans. Commun. 2014, 62, 2626–2637. [Google Scholar] [CrossRef]
- Stark, M.; Lewandowsky, J.; Bauch, G. Information-Bottleneck Decoding of High-Rate Irregular LDPC Codes for Optical Communication Using Message Alignment. Appl. Sci. 2018, 10, 1884. [Google Scholar] [CrossRef] [Green Version]
- Marques da Silva, M.; Dinis, R.; Martins, G. On the Performance of LDPC-Coded Massive MIMO Schemes with Power-Ordered NOMA Techniques. Appl. Sci. 2021, 11, 8684. [Google Scholar] [CrossRef]
- Lin, C.F. UFMC-Based Underwater Voice Transmission Scheme with LDPC Codes. Appl. Sci. 2021, 11, 1818. [Google Scholar] [CrossRef]
- Sulek, W. Pipeline processing in low-density parity-check codes hardware decoder. Bull. Pol. Acad. Sci. Tech. Sci. 2011, 59, 149–155. [Google Scholar]
- Mahdi, A.; Paliouras, V. A Low Complexity-High Throughput QC-LDPC Encoder. IEEE Trans. Signal Process. 2014, 62, 2696–2708. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, S.; Willett, P. Nonbinary LDPC Coding for Multicarrier Underwater Acoustic Communication. IEEE J. Sel. Areas Commun. 2008, 26, 1684–1696. [Google Scholar] [CrossRef]
- Boutillon, E.; Conde-Canecia, L.; Ghouwayel, A.A. Design of a GF(64)-LDPC Decoder Based on the EMS Algorithm. IEEE Trans. Circuits Syst. I 2013, 60, 2644–2656. [Google Scholar] [CrossRef] [Green Version]
- Sulek, W. Non-binary LDPC Decoders Design for Maximizing Throughput of an FPGA Implementation. Circuits Syst. Signal Process. 2016, 35, 4060–4080. [Google Scholar] [CrossRef]
- Zhao, S.; Ma, X. Construction of High-Performance Array-Based Non-Binary LDPC Codes with Moderate Rates. IEEE Commun. Lett. 2016, 20, 13–16. [Google Scholar] [CrossRef]
- IEEE Standard: IEEE P802.16; Local and Metropolitan Area Networks Part 16: Air Interface for Fixed and Mobile Broadband Wireless Access Systems. IEEE: Piscataway, NJ, USA, 2006.
- IEEE 802.11-2016; IEEE Standard for Information Technology–Telecommunications and Information Exchange between Systems Local and Metropolitan Area Networks–Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. IEEE: Piscataway, NJ, USA, 2016.
- 3GPP TS 38.212 Version 16.2.0 Release 16. Multiplexing and Channel Coding; 5G; NR; ETSI: Sophia Antipoli, France, 2020. [Google Scholar]
- Theodoropoulos, D.; Kranitis, N.; Paschalis, A. An efficient LDPC encoder architecture for space applications. In Proceedings of the IEEE 22nd International Symposium on On-Line Testing and Robust System Design (IOLTS), Sant Feliu de Guixols, Spain, 4–6 July 2016; pp. 149–154. [Google Scholar]
- Nguyen, T.T.B.; Nguyen Tan, T.; Lee, H. Efficient QC-LDPC Encoder for 5G New Radio. Electronics 2019, 8, 668. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Wang, H. A High Throughput Implementation of QC-LDPC Codes for 5G NR. IEEE Access 2019, 7, 185373–185384. [Google Scholar] [CrossRef]
- Richardson, T.J.; Urbanke, R.L. Efficient Encoding of Low-Density Parity-Check Codes. IEEE Trans. Inf. Theory 2001, 47, 638–656. [Google Scholar] [CrossRef] [Green Version]
- Fossorier, M.P.C. Quasi-Cyclic Low-Density Parity-Check Codes from Circulant Permutation Matrices. IEEE Trans. Inf. Theory 2004, 50, 1788–1793. [Google Scholar] [CrossRef] [Green Version]
- Myung, S.; Yang, K.; Kim, J. Quasi-Cyclic LDPC Codes for Fast Encoding. IEEE Trans. Inf. Theory 2005, 51, 2894–2901. [Google Scholar] [CrossRef]
- Tanner, R.M. A Recursive Approach to Low Complexity Codes. IEEE Trans. Inf. Theory 1981, IT-27, 533–547. [Google Scholar] [CrossRef] [Green Version]
- Tasdighi, A.; Banihashemi, A.H.; Sadeghi, M.R. Efficient Search of Girth-Optimal QC-LDPC Codes. IEEE Trans. Inf. Theory 2016, 62, 1552–1564. [Google Scholar] [CrossRef]
- Xu, H.; Feng, D.; Luo, R.; Bai, B. Construction of Quasi-Cyclic LDPC Codes via Masking with Successive Cycle Elimination. IEEE Commun. Lett. 2016, 20, 2370–2373. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D.J., Jr. Error Control Coding: Fundamentals and Applications, 2nd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- RSCODE Project. Available online: http://rscode.sourceforge.net (accessed on 3 October 2021).
- Generic Binary BCH Encoding/Decoding Library. Available online: https://github.com/Parrot-Developers/bch. (accessed on 14 January 2022).


| Vector | Length | Vector | Length |
|---|---|---|---|
| Matrix | K | N | P | R | Distribution | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | 512 | 1024 | 32 | Reg., | 1023 | 511 | - | - | - | ||
| H2 | 512 | 1024 | 32 | Irreg., | 1023 | 511 | - | - | - | ||
| H3 | 256 | 512 | 32 | Reg., | 511 | 255 | 259 | 30 | |||
| H4 | 256 | 512 | 32 | Irreg., | 511 | 255 | 259 | 30 | |||
| H5 | 320 | 512 | 32 | Reg., | 511 | 321 | 322 | 22 | |||
| H6 | 384 | 512 | 32 | Reg., | 511 | 383 | 385 | 14 | |||
| H7 | 144 | 288 | 16 | Reg., | 255 | 143 | 147 | 14 | |||
| H8 | 144 | 288 | 16 | Irreg., | 255 | 143 | 147 | 14 |
| Matrix ID | Energy Saved [J/bit] | Matrix ID | Energy Saved [J/bit] |
|---|---|---|---|
| H1 | 196.81 | H2 | 197.55 |
| H3 | 48.65 | H4 | 49.59 |
| H5 | 76.29 | H6 | 108.94 |
| H7 | 16.75 | H8 | 17.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyla, J.; Sułek, W.; Izydorczyk, W.; Dziczkowski, L.; Filipowski, W. Efficient LDPC Encoder Design for IoT-Type Devices. Appl. Sci. 2022, 12, 2558. https://doi.org/10.3390/app12052558
Hyla J, Sułek W, Izydorczyk W, Dziczkowski L, Filipowski W. Efficient LDPC Encoder Design for IoT-Type Devices. Applied Sciences. 2022; 12(5):2558. https://doi.org/10.3390/app12052558
Chicago/Turabian StyleHyla, Jakub, Wojciech Sułek, Weronika Izydorczyk, Leszek Dziczkowski, and Wojciech Filipowski. 2022. "Efficient LDPC Encoder Design for IoT-Type Devices" Applied Sciences 12, no. 5: 2558. https://doi.org/10.3390/app12052558
APA StyleHyla, J., Sułek, W., Izydorczyk, W., Dziczkowski, L., & Filipowski, W. (2022). Efficient LDPC Encoder Design for IoT-Type Devices. Applied Sciences, 12(5), 2558. https://doi.org/10.3390/app12052558







