1. Introduction
Non-uniform composite beams, including functionally graded materials (FGM) beams, have important applications in engineering because they can change geometric and material properties, while most of the excitations applied on mechanical structures in nature and engineering practice are random forces. In recent years, the problems of mechanical structure damage caused by vibration have achieved more and more attention, which make the vibration reliability analysis of non-uniform composite beam structures under random load of great significance.
Before the study of non-uniform composite beams, researchers have done a lot of work on uniform composite beams dynamics. In references [
1,
2,
3,
4,
5,
6,
7,
8,
9], the free vibration of a composite beam structure is solved by the finite element method. In addition to the finite element method, there are some other methods to solve the free vibration responses of composite beams. By using a global higher order beam theory, Matsunaga analyzed natural frequencies and buckling stresses of simply supported multilayered composite beams through the method of power series expansion of displacement components [
10]. Atlihan et al. used differential quadrature method (DQM) to analyze the free vibration of laminated composite beams [
11]. The natural frequencies of longitudinal and transverse vibration modes have been obtained by using the method of power series [
12]. Except for the free vibration analysis, Raja, Prathap and Sinha developed a control scheme based on the linear quadratic regulator/independent modal space control (LQR/IMSC) method and used this to do the active vibration control of composite sandwich beams [
13]. Ramanamurthy, Chandrasekaran and Nishant used finite element method for damage detection [
14]. Xu et al. proved the feasibility of the ultrasonic non-destructive testing with the combination of a strain measurement for fatigue crack details detection of headed shear studs in composite beams [
15]. Tao et al. obtained the fitting formula for calculating the equivalent flexural stiffness of composite beams through extensive parameter analysis, and they studied and analyzed the equivalent flexural stiffness of composite frame beams to evaluate their vertical deflection [
16]. Kim et al. studied the free and forced vibration of cracked laminated composite beam through the Jacobi–Ritz method and the first-order shear deformation theory (FSDT) [
17,
18].
In addition to research and understanding of the uniform composite beam, some researchers have also used various methods to solve and analyze vibration responses of the non-uniform beams. For the geometrically non-uniform beams, the vibration responses of non-uniform beams were solved and analyzed by the amatrix transfer method in [
19,
20,
21,
22]. In addition, Wu investigated the free vibration characteristics of a non-uniform cantilever beam carrying multiple two degree-of-freedom spring–damper–mass systems by means of two finite element methods, FEM1 and FEM2 [
23]. Ho and Chen used Timoshenko beam theory, Hamilton principle and differential transformation method (DTM) to study the vibration of axially loaded non-uniform spinning twisted Timoshenko beam [
24]. Martinez Castro et al. gave the semi-analytic solution of moving load problem, which is used to analyze the stress of multi-span uniform beam and non-uniform beam under a moving load [
25]. Mazanoglu and Sabuncu studied the bending vibration of non-uniform Rayleigh beams with single-edge and double-edge cracks [
26]. Chen et al. presented the design, test and analysis of a non-uniform thickness piezoelectric beam for impact vibration energy harvesting. [
27]. Clementi et al. determined the frequency response curve of a non-uniform beam under nonlinear vibration by the multiple time scale method analytically [
28]. Based on the nonlocal elastic theory, Chakraverty and Behera studied the free vibration of non-uniform Euler–Bernoulli nanobeams by using the Rayleigh–Ritz method [
29]. Celik studied the free vibration of non-uniform Euler–Bernoulli beams under different support conditions through the Chebyshev wavelet collocation method [
30]. For beam structures with anisotropic material properties (FGM), the finite element method was used to solve and analysis the free vibration of FGM beam in references [
31,
32,
33]. Differential transformation method and transfer matrix method (TMM) were also used to study the free vibration of an FGM beam in references [
34,
35]. Abdelrahman et al. developed an analytical solution method using Navier’s procedure to study the dynamic behavior of carbon nanotube reinforced functional gradient (FG) beams on two parameter elastic foundation under a moving load [
36]. Esen et al. studied and analyzed the free vibration and dynamic response of an S-shaped FG Timoshenko beam model under a moving load based on Navier’s method [
37]. There is also some research work on the non-uniform FGM beam. Rajasekaran used the differential transformation (DT) based dynamic stiffness approach to study the free vibration of axially functionally graded non-uniform beams under different boundary conditions [
38]. Heshmati and Daneshmand described the effect of different profile variations on vibrational properties of non-uniform beams made of graded porous materials [
39]. Under the framework of nonlocal strain gradient theory, Rajasekaran and Khaniki used the Lagrange interpolation method, Gaussian quadrature method and Wilson multiplier method to study the bending, buckling and vibration behavior of depth functionally graded in depth direction non-uniform nanobeams [
40]. Adomian Decomposition Method (ADM) has been used to analyze the free and forced vibration of general non-uniform cone beams with axial functionally graded material by Keshmiri et al. [
41,
42,
43].
Based on dynamic modeling and analysis of different structures, their reliability analysis under random load excitation can be conducted. Siddiqui and Ahmad carried out nonlinear dynamic analysis of the platform for response calculation. The response history obtained has been used for the fatigue reliability analysis of Tension leg platform (TLP) tethers under long crested random sea and associated wind [
44]. Jensen et al. used a standard gradient-based algorithm with a line search to solve the reliability optimization problem of a structural system under random load [
45]. Liu and Zhang deduced the calculation expression of the mean value of structural dynamic reliability under stationary random excitation, and conveniently obtained the dynamic reliability analysis results of random structures under random excitation [
46]. Singh et al. determined the fatigue reliability of an automotive crankshaft by stochastically inducing random loads [
47]. In summary, there have been many studies on the dynamic analysis of composite structures and non-uniform beams, and the vibration and reliability analysis of uniform structures and mechanical parts with certain design under random loads is also a common and well-studied problem in engineering. However, to the best of the authors’ knowledge, there is no research on the vibration reliability analysis of a non-uniform composite beam under a random load. Considering the various mechanical properties as well as unknown response and strain/stress distribution of the non-uniform structures made from multiple composite layers, the reliability of such structures can be different from traditional uniform structures as novel research [
48,
49], especially under different random dynamic loads. There is no explicit expression for the random load whose excitation frequency and amplitude are changing, so the analytical solution of forced vibration at each time point needs to be solved by iterative method. To deal with this challenge, a model combining ADM and iteration numerical process is proposed to solve the vibration response and dynamic stress-distribution of the non-uniform composite beams for reliability analysis in this research.
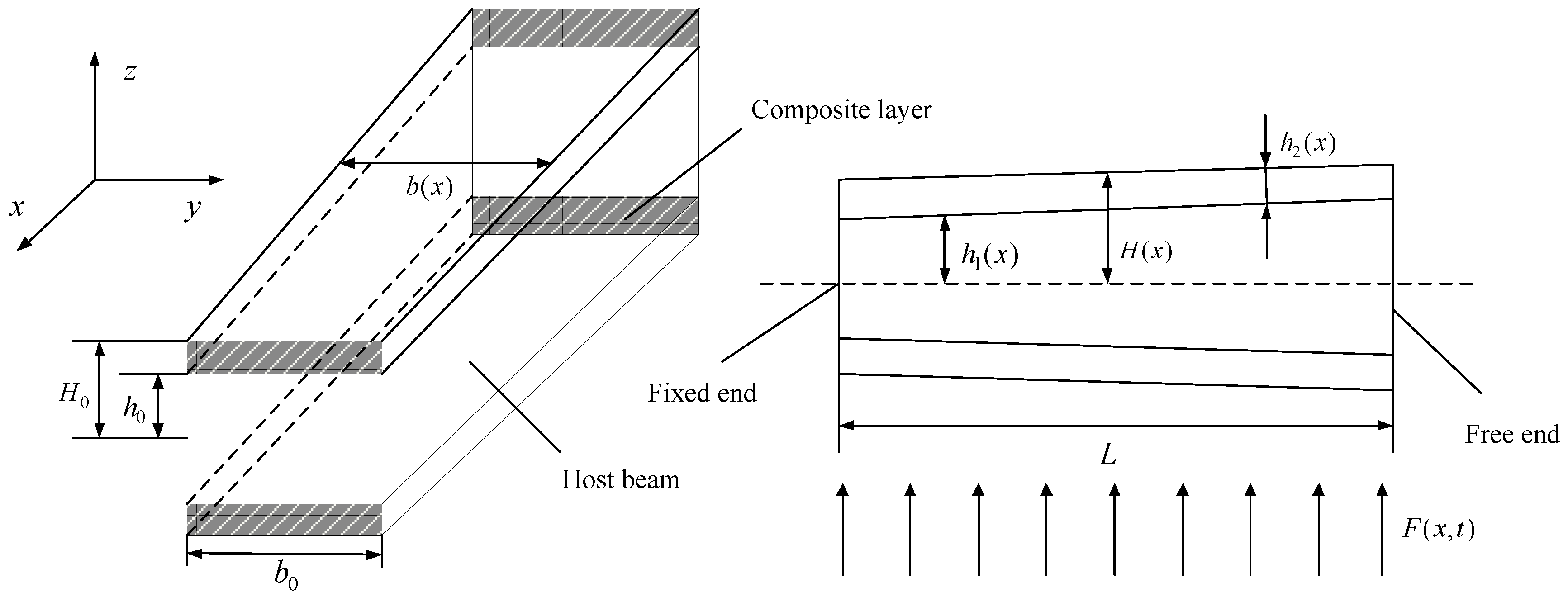
In this paper, the vibration responses and reliability of a general non-uniform beam with tapered composite layers and host beam under random load are calculated and analyzed. The cross-section rigidity and mass distribution can be adjusted by changing the volume proportion of different materials of the non-uniform laminated composite beam. The angular frequency and amplitude of random base motion acceleration accord with Gaussian distribution. The vibration mode shapes and nature frequencies are calculated, and the vibration solution under random base motion excitation is solved by the iteration numerical method. In the parameter studies, the influences of the base motion excitation frequencies variation on amplitude and strain of beam are studied. Then, the effects of base motion excitation amplitudes on vibration responses and reliability are analyzed. In addition, the vibration responses and reliability in different periods of time are calculated. Finally, the reliability of non-uniform beams with different taper ratios of composite layers and host beam is solved and analyzed.
4. Conclusions
In this paper, an iterative method is proposed to solve the forced vibration responses and reliability of non-uniform composite beam under random load. Considering the change of frequency and acceleration amplitude of base motion excitation in the iteration process, the vibration response of beam in each short time period/iteration step is calculated by ADM and Duhamel integral considering both the transient and steady response. Through numerical studies, the results reveal the following conclusions:
(1) ADM is used to be combined with iteration progress solving non-uniform composite beam structural vibration under random load. The correctness of the mathematical model is proved. Comparing solutions under random and harmonic base motion, the vibration response under random load shows the randomness and non-frequency characteristics, and its vibration amplitude is larger than the one under the same level harmonic excitation.
(2) Within the ranges of studied design parameters, the composite beam nature frequencies increase with the increment of , , and decrease with the increment of . has little effect on nature frequencies.
(3) The higher mean value and variance of base motion excitation frequency, the smaller amplitude and maximum strain of the non-uniform composite beam can be excited.
(4) The greater mean and variance of the base motion excitation amplitude, the greater vibration amplitude and strain of the non-uniform composite beam, and the lower the vibration reliability in the same time period.
(5) The vibration reliability will increase or decrease with the increment of operation time considered, but the overall trend is downward if the operation time of the system is long enough.
(6) The reliability of the non-uniform composite beam increases with the increment of and decreases with the increment of . For the multiple layered composite beam, different design parameters lead to different reliability results. Reasonable design can enhance structural reliability.
(7) However, the research results obtained within the range of parameters studied occur when the operation time is long enough. When the calculation/analysis time duration is very short, the results may change. The statement that the operation time is long enough means that the analyzed period should be enough to ensure that the excitation amplitude and frequency distribution law can be illustrated and judged from the data points of the random loads in the calculation process.