Meta-Heuristic Technique-Based Parametric Optimization for Electrochemical Machining of Monel 400 Alloys to Investigate the Material Removal Rate and the Sludge
Abstract
:1. Introduction
2. Objectives
3. Materials and Experimentation
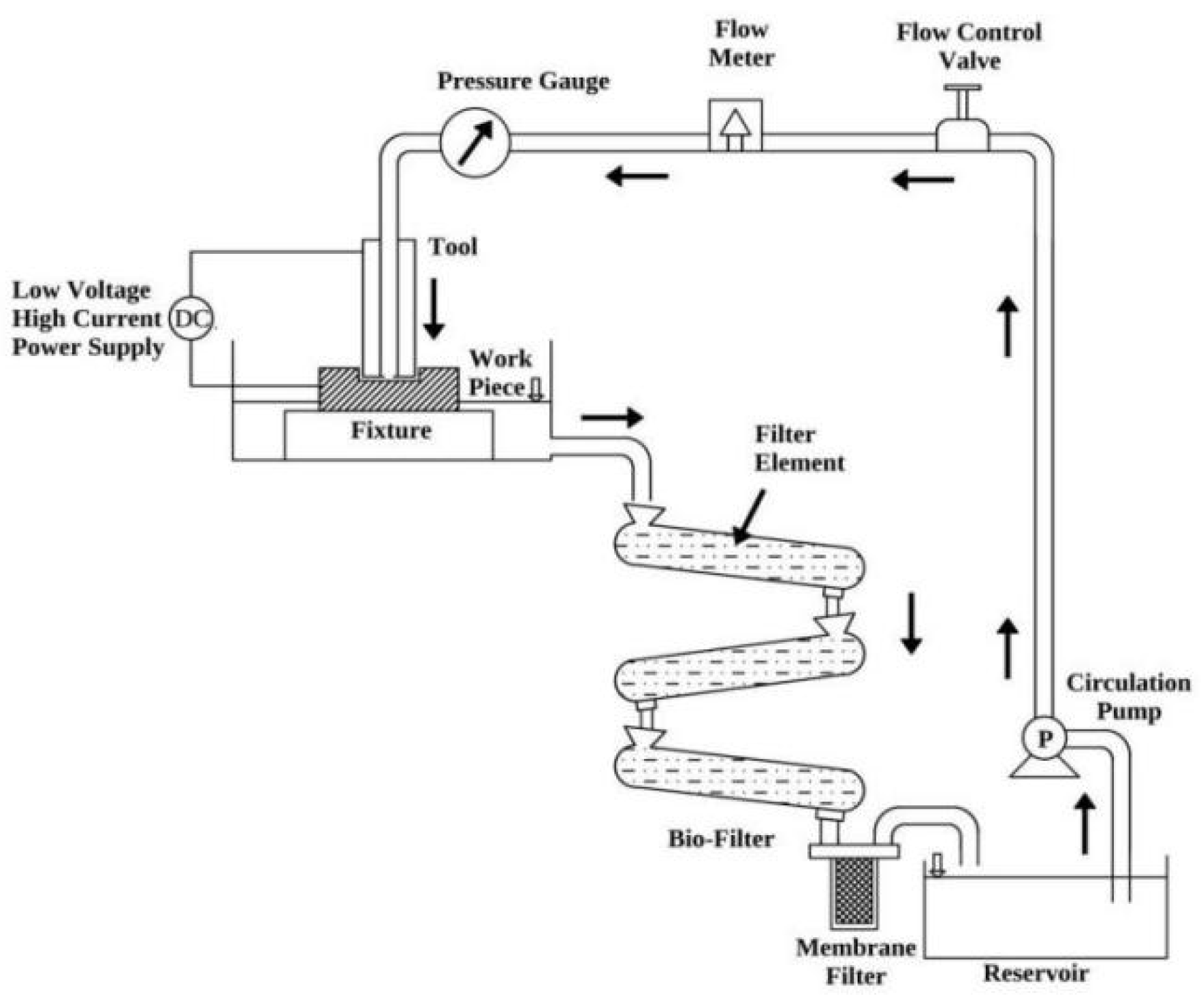
Experimental Design and Measurements
4. Optimization Techniques and Procedures
4.1. Mathematical Modeling of Experimentation
4.2. TOPSIS Method for Multi-Objective Optimization
| Algorithm 1 Pseudo-code for TOPSIS. |
| 1: Read alternate and objectives matrix— with weights () and types of objectives () |
| 2: For each alternative (i = 1, 2, 3, …, m) and objective (j = 1, 2, 3, …, n) |
| 3: Compute Normalized value of using |
| 4: Calculate Performance matrix () using |
| 5: End |
| 6: For each objective (j = 1, 2, 3, …, n) |
| 7: Determine positive ideal () and negative ideal solution () |
| 8: For minimization objective— and |
| 9: For maximization objective— and |
| 10: End |
| 11: For each alternative (i = 1, 2, 3, …, m) |
| 12: Calculated Ideal and negative ideal separation () |
| 13: Determine relative closeness ( ) |
| 14: End |
| 15: Rank alternatives w.r.t. in descending order |
4.3. Grey Wolf Optimizer
4.4. Moth-Flame Optimization Algorithm (MFO)
Mathematical Formulation of the MFO Algorithm
5. ANOVA and Parametric Influence on Performances
Parametric Influence on the Performance Measures
6. Multi-Objective Optimization of ECM Process Parameters
6.1. RSM Optimization Tool
6.2. Applications of Meta-Heuristics for Optimization of the Process Parameters
| Algorithm 2 Grey Wolf Optimization Algorithm |
| 1: Initialize no. of grey wolf (Xij—i =1,2,..nw and j = 1,2,..nd) 2: While (it < nitr) 3: Determine the fitness function Fik 4: Calculate Pareto optimal distance fi 5: Sort fi in descending order and set as sfi 6: Store the first wolf’s data as Xit. and Fit. 7: Using the sorted data, assign Xa. = X1, Xb. = X2. and Xd. = X3. 8: Compute a = 2-it*(2/nitr) 9: For each wolf, Update the position using A1 = 2*a*rand()-a 10: C1 = 2*rand() 11: Da. = abs(C1*Xa.-X i.) 12: X1. = Xa.-A1*Da. 13: A2 = 2*a*rand()-a 14: C2 = 2*rand() 15: Db. = abs(C1*Xb.-Xi.) 16: X2. = Xb.-A2*Db. 17: A3 = 2*a*rand()-a 18: C3 = 2*rand() 19: Dd. = abs(C1*Xd.-X i.) 20: X3. = Xd.-A3*Dd. 21: X i. = (X1. + X2. + X3.)/3 22: Check Xi. within bounds 23: End 24: End 25: Using TOPSIS method convert Fit. into fi 27: Sort fi in descending order and display the first wolf’s data (optimum data) 28: Print the best solution |
| Algorithm 3 Moth-Flame Optimization Algorithm |
| 1: Initialize the parameters for Moth-flame 2: Initialize Moth position Mi randomly 3: For each i = 1:n Calculate the fitness valute fi 4: End 5: While (i ≤ imax) 6: Update the position of Mi 7: Calculate the no. of flames 8: Compute the fitness value fi 9: If (i = 1) then F = sort (M) OF = sort (OM) 10: Else F = sort (Mt-1, Mt) OF = sort (Mt-1, Mt) 11: End 12: For each i = 1:n 13: For each j = 1:d Update the values of r and t 14: Calculate the value of D w.r.t. corresponding Moth 15: Update M(i,j) w.r.t. corresponding Moth 16: End 17: End 18: End 19: Print the best solution |
| Algorithm 4 Particle Swarm Optimization Algorithm |
| 1: Initialize Particle Position P 2: For i = 1 to itrmax 3: For each particle p in P 4: Evaluate fp = f(p) 5: If fp is better than f(pB); pB= p; 6: End 7: End 8: gB= best p in P 9: For each particle p in P 10: Compute v = v + c1*rand()*(pB– p) + c2 *rand()*(gB-p) 11: Update p = p + v 12: End 13: End 14: Print the best solution |
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skoczypiec, S.; Lipiec, P.; Bizoń, W.; Wyszyński, D. Selected Aspects of Electrochemical Micromachining Technology Development. Materials 2021, 14, 2248. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Zhu, Z.; Wang, D. Electrochemical Dissolution Behavior of the Nickel-Based Cast Superalloy K423A in NaNO3 Solution. Electrochim. Acta 2017, 253, 379–389. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z.; Xing, J.; Zhu, D. Effect of tube-electrode inner diameter on electrochemical discharge machining of nickel-based super alloy. Chin. J. Aeronaut. 2016, 29, 1103–1110. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Zhu, Z.; Zhu, Y. Electrochemical deep grinding of cast nickel-base superalloys. J. Manuf. Process. 2019, 47, 291–296. [Google Scholar] [CrossRef]
- Bi, X.; Zeng, Y.; Qu, N. Wire electrochemical micromachining of high-quality pure-nickel microstructures focusing on different machining indicators. Precis. Eng. 2020, 61, 14–22. [Google Scholar] [CrossRef]
- Tayal, A.; Kalsi, N.S.; Gupta, M.K.; Garcia-Collado, A.; Sarikaya, M. Reliability and economic analysis in sustainable machining of Monel 400 alloy. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 5450–5466. [Google Scholar] [CrossRef]
- Rajurkar, K.P.; Hadidi, H.; Pariti, J.; Reddy, G.C. Review of Sustainability Issues in Non-Traditional Machining Processes. Procedia Manuf. 2017, 7, 714–720. [Google Scholar] [CrossRef]
- Chakraborty, S.; Bhattacharyya, B.; Diyaley, S. Applications of optimization techniques for parametric analysis of non-traditional machining processes: A Review. Manag. Sci. Lett. 2019, 9, 467–494. [Google Scholar] [CrossRef]
- Mukherjee, R.; Chakraborty, S. Selection of the optimal electrochemical machining process parameters using biogeography-based optimization algorithm. Int. J. Adv. Manuf. Technol. 2013, 64, 781–791. [Google Scholar] [CrossRef]
- Ayyappan, S.; Sivakumar, K. Investigation of electrochemical machining characteristics of 20MnCr5 alloy steel using potassium dichromate mixed aqueous NaCl electrolyte and optimization of process parameters. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1984–1996. [Google Scholar] [CrossRef]
- Ayyappan, S.; Sivakumar, K. Enhancing the performance of electrochemical machining of 20MnCr5 alloy steel and optimization of process parameters by PSO-DF optimizer. Int. J. Adv. Manuf. Technol. 2016, 82, 2053–2064. [Google Scholar] [CrossRef]
- Sohrabpoor, H.; Khanghah, S.; Shahraki, S.; Teimouri, R. Multi-objective optimization of electrochemical machining process. Int. J. Adv. Manuf. Technol. 2016, 82, 1683–1692. [Google Scholar] [CrossRef]
- Rao, R.V.; Rai, D.P.; Balic, J. A multi-objective algorithm for optimization of modern machining processes. Eng. Appl. Artif. Intell. 2017, 61, 103–125. [Google Scholar] [CrossRef]
- Mehrvar, A.; Basti, A.; Jamali, A. Inverse modelling of electrochemical machining process using a novel combination of soft computing methods. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3436–3446. [Google Scholar] [CrossRef]
- Singh, D.; Shukla, R. Parameter optimization of electrochemical machining process using black hole algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2017, 282, 012006. [Google Scholar] [CrossRef] [Green Version]
- Kalaimathi, M.; Venkatachalam, G.; Sivakumar, M.; Ayyappan, S. Multi-response optimisation of electrochemical machining process parameters by harmony search-desirability function optimiser. Int. J. Manuf. Technol. Manag. 2020, 34, 331–348. [Google Scholar] [CrossRef]
- Diyaley, S.; Chakraborty, S. Optimization of electrochemical machining process parameters using teaching-learning-based algorithm. AIP Conf. Proc. 2020, 2273, 050010. [Google Scholar] [CrossRef]
- Kasdekar, D.K.; Parashar, V.; Arya, C. Artificial neural network models for the prediction of MRR in Electro-chemical machining. Mater. Today Proc. 2018, 5 Pt 1, 772–779. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, P.P.; Kumar, V. Application of grey-fuzzy logic technique for parametric optimization of non-traditional machining processes. Grey Syst. Theory Appl. 2018, 8, 46–68. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Lin, X.; Liu, J. An Improved Gray Wolf Optimization Algorithm to Solve Engineering Problems. Sustainability 2021, 13, 3208. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. Optimization of production time in the multi-pass milling process via a robust grey wolf optimizer. Neural Comput. Appl. 2018, 29, 1321–1336. [Google Scholar] [CrossRef]
- Kharwar, P.K.; Verma, R.K. Nature instigated Grey wolf algorithm for parametric optimization during machining (Milling) of polymer nanocomposites. J. Thermoplast. Compos. Mater. 2021, 1–23. [Google Scholar] [CrossRef]
- Kulkarni, O.; Kulkarn, S. Process Parameter Optimization in WEDM by Grey Wolf Optimizer. Mater. Today Proc. 2018, 5 Pt 1, 4402–4412. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mitra, A. Parametric optimization of abrasive water-jet machining processes using grey wolf optimizer. Mater. Manuf. Process. 2018, 33, 1471–1482. [Google Scholar] [CrossRef]
- Sekulic, M.; Pejic, V.; Brezocnik, M.; Gostimirović, M.; Hadzistevic, M. Prediction of surface roughness in the ball-end milling process using response surface methodology, genetic algorithms, and grey wolf optimizer algorithm. Adv. Prod. Eng. Manag. 2018, 13, 18–30. [Google Scholar] [CrossRef]
- Kharwar, P.K.; Verma, R.K. Exploration of nature inspired Grey wolf algorithm and Grey theory in machining of multiwall carbon nanotube/polymer nanocomposites. Eng. Comput. 2020, 1–22. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-Flame Optimization Algorithm: A Novel Nature-inspired Heuristic Paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, X.; Liu, J. An Improved Moth-Flame Optimization Algorithm for Engineering Problems. Symmetry 2020, 12, 1234. [Google Scholar] [CrossRef]
- Yıldız, B.; Yildiz, A.R. Moth-flame optimization algorithm to determine optimal machining parameters in manufacturing processes. Mater. Test. 2017, 59, 425–429. [Google Scholar] [CrossRef]
- Sivalingam, V.; Sun, J.; Mahalingam, S.K.; Nagarajan, L.; Natarajan, Y.; Salunkhe, S.; Nasr, E.A.; Davim, J.P.; Hussein, H.M.A.M. Optimization of Process Parameters for Turning Hastelloy X under Different Machining Environments Using Evolutionary Algorithms: A Comparative Study. Appl. Sci. 2021, 11, 9725. [Google Scholar] [CrossRef]
- Kamaruzaman, A.F.; Mohd Zain, A.; Alwee, R.; Md Yusof, N.; Najarian, F. Optimization of Surface Roughness in Deep Hole Drilling using Moth-Flame Optimization. ELEKTRIKA-J. Electr. Eng. 2019, 18, 62–68. [Google Scholar] [CrossRef]
- Karthick, M.; Anand, P.; Siva Kumar, M.; Meikandan, M. Exploration of MFOA in PAC parameters on machining Inconel 718. Mater. Manuf. Process. 2021, 1–13. [Google Scholar] [CrossRef]
- Lmalghan, R.; Rao, M.C.K.; Arunkumar, S.; Rao, S.S.; Herbert, M.A. Machining Parameters Optimization of AA6061 Using Response Surface Methodology and Particle Swarm Optimization. Int. J. Precis. Eng. Manuf. 2018, 19, 695–704. [Google Scholar] [CrossRef]
- Abu-Mahfouz, I.; Banerjee, A.; Rahman, E. Evolutionary Optimization of Machining Parameters Based on Surface Roughness in End Milling of Hot Rolled Steel. Materials 2021, 14, 5494. [Google Scholar] [CrossRef]
- Kalaimathi, M.; Venkatachalam, G.; Sivakumar, M.; Ayyappan, S. Experimental investigation on the suitability of ozonated electrolyte in travelling-wire electrochemical machining. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4589–4599. [Google Scholar] [CrossRef]
- Ayyappan, S.; Sivakumar, K. Experimental investigation on the performance improvement of electrochemical machining process using oxygen-enriched electrolyte. Int. J. Adv. Manuf. Technol. 2014, 75, 479–487. [Google Scholar] [CrossRef]
- Qu, N.; Fang, X.; Li, W.; Zeng, Y.; Zhu, D. Wire electrochemical machining with axial electrolyte fushing for titanium alloy. Chin. J. Aeronaut. 2013, 26, 224–229. [Google Scholar] [CrossRef] [Green Version]
- Qu, N.S.; Ji, H.J.; Zeng, Y.B. Wire electrochemical machining using reciprocated traveling wire. Int. J. Adv. Manuf. Technol. 2014, 72, 677–683. [Google Scholar] [CrossRef]
- Leese, R.; Ivanov, A. Electrochemical micromachining: Review of factors affecting the process applicability in micro-manufacturing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 195–207. [Google Scholar] [CrossRef]
- Zhang, Y. Investigation into Current Efficiency for Pulse Electrochemical Machining of Nickel Alloy. University of Nebraska–Lincoln. 2010. Available online: http://digitalcommons.unl.edu/imsediss/2 (accessed on 10 November 2021).
- Trimmer, A.L.; Hudson, J.L.; Kock, M.; Schuster, R. Single-step electrochemical machining of complex nanostructures with ultrashort voltage pulses. Appl. Phys. Lett. 2003, 82, 3327–3329. [Google Scholar] [CrossRef]
- Rathod, V.; Doloi, B.; Bhattacharyya, B. Experimental investigations into machining accuracy and surface roughness of microgrooves fabricated by electrochemical micromachining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1781–1802. [Google Scholar] [CrossRef]
- Shunmugesh, K.; Panneerselvam, K. Optimization of machining process parameters in drilling of CFRP using multi-objective Taguchi technique, TOPSIS and RSA techniques. Polym. Polym. Compos. 2017, 25, 185–192. [Google Scholar] [CrossRef]
- Balaji, K.; Siva Kumar, M.; Yuvaraj, N. Multi objective taguchi–grey relational analysis and krill herd algorithm approaches to investigate the parametric optimization in abrasive water jet drilling of stainless steel. Appl. Soft Comput. J. 2021, 102, 107075. [Google Scholar] [CrossRef]
















| Monel 400 Alloys | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Composition and weight (%) | C | Si | Mn | P | S | Cr | Mo | Fe | V |
| 0.047 | 0.172 | 1.03 | 0.012 | 0.01 | 0.1 | 0.1 | 1.66 | 0.029 | |
| W | Cu | Al | Co | Nb | Ti | Mg | Ni | ||
| 0.1 | 29.24 | 0.01 | 0.103 | 0.1 | 0.047 | 0.031 | 67.4 | ||
| Factors | Type | Condition/size |
|---|---|---|
| Work piece | Monel 400 alloys | Hardened material |
| Electrolyte | NaCl | 130–190 g/L |
| Tool | Copper | C101 |
| Voltage | DC | 11, 13, 15 V |
| Tool feed rate | Horizontal feed | 0.1 mm/min |
| IEG | 0.1 mm | |
| Current | DC | 50 A |
| Flow rate | 1–3 L/min | |
| Machining time | 5 min |
| S.No. | Process Parameters | Levels | ||||
|---|---|---|---|---|---|---|
| −2 | −1 | 0 | 1 | 2 | ||
| 1 | Voltage (V) | 11 | 12 | 13 | 14 | 15 |
| 2 | Electrolyte concentration (g/L) | 130 | 145 | 160 | 175 | 190 |
| 3 | Flow rate (L/min) | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| Exp.No. | EC (g/L) | V (V) | FR (L/min) | Experimental Value | Calculated Values | ||
|---|---|---|---|---|---|---|---|
| MRR (g/min) | NP (PPM) | MRR (g/min) | NP (PPM) | ||||
| 1 | 190 | 13 | 2.0 | 0.225 | 65.08 | 0.20327 | 64.44446 |
| 2 | 160 | 13 | 2.0 | 0.219 | 57.26 | 0.20438 | 56.57423 |
| 3 | 145 | 12 | 2.5 | 0.204 | 58.06 | 0.19676 | 56.35493 |
| 4 | 175 | 14 | 2.5 | 0.215 | 67.45 | 0.22844 | 68.97187 |
| 5 | 160 | 13 | 2.0 | 0.208 | 55.05 | 0.20438 | 56.57423 |
| 6 | 130 | 13 | 2.0 | 0.129 | 50.65 | 0.15130 | 51.46866 |
| 7 | 160 | 13 | 1.0 | 0.062 | 55.48 | 0.07344 | 55.19648 |
| 8 | 160 | 13 | 2.0 | 0.216 | 56.45 | 0.20438 | 56.57423 |
| 9 | 175 | 12 | 1.5 | 0.157 | 58.63 | 0.16119 | 58.03033 |
| 10 | 160 | 11 | 2.0 | 0.142 | 57.29 | 0.14094 | 59.88398 |
| 11 | 160 | 13 | 2.0 | 0.171 | 56.45 | 0.20438 | 56.57423 |
| 12 | 160 | 13 | 3.0 | 0.216 | 66.75 | 0.20555 | 67.22471 |
| 13 | 145 | 12 | 1.5 | 0.114 | 55.24 | 0.09985 | 53.53437 |
| 14 | 145 | 14 | 2.5 | 0.243 | 60.08 | 0.23782 | 60.49203 |
| 15 | 160 | 13 | 2.0 | 0.209 | 55.40 | 0.20438 | 56.57423 |
| 16 | 175 | 14 | 1.5 | 0.187 | 58.24 | 0.19324 | 59.76420 |
| 17 | 160 | 15 | 2.0 | 0.212 | 68.16 | 0.21405 | 65.75495 |
| 18 | 145 | 14 | 1.5 | 0.132 | 54.03 | 0.11226 | 55.20372 |
| 19 | 160 | 13 | 2.0 | 0.203 | 58.65 | 0.20438 | 56.57423 |
| 20 | 175 | 12 | 2.5 | 0.149 | 66.13 | 0.16774 | 64.77025 |
| Response | a | b | c | d | e | f | g | h | i | j |
|---|---|---|---|---|---|---|---|---|---|---|
| MRR | −2.381 | 0.0123 | 0.112 | 0.621 | 0.0003 | −0.003 | 0.0143 | 0.00003 | −0.007 | −0.065 |
| NP | 389 | −0.551 | −41.8 | −49.5 | 0.0011 | 0.131 | 1.23 | 0.00154 | 1.561 | 4.64 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MRR | NP | MRR | NP | MRR | NP | MRR | NP | MRR | NP | |
| Model | 9 | 9 | 0.037278 | 437.944 | 0.004142 | 48.660 | 10.39 | 13.29 | 0.001 | 0.000 |
| Linear | 3 | 3 | 0.025497 | 347.518 | 0.008499 | 115.839 | 21.32 | 31.64 | 0.000 | 0.000 |
| EC | 1 | 1 | 0.002700 | 168.372 | 0.002700 | 168.372 | 6.77 | 45.99 | 0.026 | 0.000 |
| V | 1 | 1 | 0.005345 | 34.468 | 0.005345 | 34.468 | 13.41 | 9.42 | 0.004 | 0.012 |
| FR | 1 | 1 | 0.017452 | 144.678 | 0.017452 | 144.678 | 43.78 | 39.52 | 0.000 | 0.000 |
| Square | 3 | 3 | 0.007095 | 79.698 | 0.002365 | 26.566 | 5.93 | 7.26 | 0.014 | 0.007 |
| EC*EC | 1 | 1 | 0.001154 | 3.003 | 0.001154 | 3.003 | 2.89 | 0.82 | 0.120 | 0.386 |
| V*V | 1 | 1 | 0.001136 | 61.290 | 0.001136 | 61.290 | 2.85 | 16.74 | 0.122 | 0.002 |
| FR*FR | 1 | 1 | 0.006615 | 33.779 | 0.006615 | 33.779 | 16.59 | 9.23 | 0.002 | 0.013 |
| 2-Way Interaction | 3 | 3 | 0.004685 | 10.728 | 0.001562 | 3.576 | 3.92 | 0.98 | 0.044 | 0.442 |
| EC*V | 1 | 1 | 0.000193 | 0.002 | 0.000193 | 0.002 | 0.48 | 0.00 | 0.502 | 0.981 |
| EC*FR | 1 | 1 | 0.004082 | 7.681 | 0.004082 | 7.681 | 10.24 | 2.10 | 0.009 | 0.178 |
| V*FR | 1 | 1 | 0.000410 | 3.045 | 0.000410 | 3.045 | 1.03 | 0.83 | 0.334 | 0.383 |
| Error | 10 | 10 | 0.003987 | 36.607 | 0.000399 | 3.661 | ||||
| Lack of Fit | 5 | 5 | 0.002498 | 28.127 | 0.000500 | 5.625 | 1.68 | 3.32 | 0.292 | 0.107 |
| Pure Error | 5 | 5 | 0.001489 | 8.480 | 0.000298 | 1.696 | ||||
| Total | 19 | 19 | 0.041264 | 474.551 | ||||||
| Model | S | R-sq | R-sq (adj) | R-sq (pred) |
|---|---|---|---|---|
| MRR | 0.01997 | 90.34% | 81.64% | 44.22% |
| NP | 1.91331 | 92.29% | 85.34% | 47.85% |
| Response | Goal | Lower | Target | Upper | Weight | Importance |
|---|---|---|---|---|---|---|
| NP | Minimum | 50.6452 | 68.1613 | 1 | 1 | |
| MRR | Maximum | 0.062 | 0.2429 | 1 | 1 |
| Solution | EC | V | FR | NP Fit | MRR Fit | Composite Desirability |
|---|---|---|---|---|---|---|
| 1 | 130 | 12.8586 | 2.57576 | 53.9394 | 0.217350 | 0.835117 |
| Optimization Problem | Grey Wolf Optimization (GWO) Algorithm |
|---|---|
| Number of solutions | Number of grey wolves (i = 1, 2, … nw) |
| Combination of parameters within their bounds | Position of grey wolf (Xij) |
| Number of parameters, factors, and independent variables | Number of dimensions involved in defining the position of a wolf (j = 1, 2, … nd) |
| Value of best parameters | Position of prey (Xbest) |
| Response value, output, and dependant variable | Fitness of grey wolf (Fik) |
| First best three solution’s parameters | Position of alpha, beta, and delta grey wolves (Xa., Xb., and Xd.) |
| First best three solution’s fitness values | Fitness of alpha, beta, and delta grey wolves (Fa., Fb., and Fd.) |
| Except for best first three solutions | Omega grey wolf |
| Optimization Problem | Moth Flame Optimization (MFO) Algorithm | Particle Swarm Optimization (GWO) Algorithm |
|---|---|---|
| Number of solutions | Number of moths (i = 1, 2, … nm) | Number of particles (i = 1, 2, … np) |
| Combination of parameters within their bounds | Position of moth (Mij) | Position of particle (Pij) |
| Number of parameters, factors, andindependent variables | Number of dimensions involved in defining the position of moth (j = 1, 2, … nd) | Number of dimensions involved in defining the position of particle (j = 1, 2, … nd) |
| Number of better solutions | Number of flames (i1 = 1, 2, … nf) | Fitness of particle (fi) |
| Combination of parameters within their bounds | Position of flames (Fi1j) | |
| Response value, output, and dependant variable | Fitness of moth (fi) | Global best (gB) |
| GWO Algorithm | MFO Algorithm | PSO Algorithm | |||
|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value |
| Maximum number of grey wolves | 100 | Maximum number of moths | 100 | Maximum number of particles | 100 |
| Constant a | 2 to 0 | Position of moth close to the flame (t) | From −1 to −2 | Learning factors (C1 and C2) | 2 and 2 |
| Coefficient vectors A | −2a to 2a | Update mechanism | Logarithmic spiral | Inertia weight (ω) | From 0.4 to 0.9 |
| Coefficient vectors C | 2*rand(0,1) | Adaptive number of flames | round((mf-(itr*(mf-1)/max_itr))) | Number of particles | 30 |
| No. of iterations (nitr) | 100 | No. of iterations (nitr) | 100 | No. of iterations (nitr) | 100 |
| Algorithms | EC | V | FR | MRR | NP |
|---|---|---|---|---|---|
| RSM | 130.000 | 12.8586 | 2.5758 | 0.217 | 53.9400 |
| PSO | 130.401 | 12.7735 | 2.0378 | 0.156 | 51.3507 |
| GWO | 132.014 | 13.2406 | 2.8455 | 0.242 | 57.7202 |
| MFO | 132.014 | 13.2406 | 2.8455 | 0.242 | 57.7202 |
| R.No. | GWO | MFO | PSO | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EC | V | FR | MRR | NP | EC | V | FR | MRR | NP | EC | V | FR | MRR | NP | |
| 1 | 134.440 | 13.850 | 2.835 | 0.251 | 60.739 | 134.440 | 13.850 | 2.835 | 0.251 | 60.739 | 131.070 | 12.188 | 1.946 | 0.135 | 51.413 |
| 2 | 135.769 | 13.942 | 2.815 | 0.251 | 61.324 | 135.769 | 13.942 | 2.815 | 0.251 | 61.324 | 130.401 | 12.774 | 2.038 | 0.156 | 51.351 |
| 3 | 130.034 | 12.754 | 2.265 | 0.185 | 52.015 | 130.034 | 12.754 | 2.265 | 0.185 | 52.015 | 130.033 | 12.709 | 1.794 | 0.114 | 51.026 |
| 4 | 130.444 | 12.755 | 2.043 | 0.156 | 51.355 | 130.444 | 12.755 | 2.043 | 0.156 | 51.355 | 130.717 | 12.427 | 1.931 | 0.136 | 51.168 |
| 5 | 132.014 | 13.241 | 2.846 | 0.242 | 57.720 | 132.014 | 13.241 | 2.846 | 0.242 | 57.720 | 130.047 | 12.363 | 1.904 | 0.129 | 51.110 |
| 6 | 131.611 | 13.909 | 2.947 | 0.256 | 61.669 | 131.611 | 13.909 | 2.947 | 0.256 | 61.669 | 130.310 | 12.588 | 1.867 | 0.126 | 51.046 |
| 7 | 135.416 | 13.038 | 2.469 | 0.217 | 54.597 | 135.416 | 13.038 | 2.469 | 0.217 | 54.597 | 130.630 | 12.623 | 1.891 | 0.132 | 51.097 |
| 8 | 131.808 | 13.122 | 2.628 | 0.227 | 55.281 | 131.808 | 13.122 | 2.628 | 0.227 | 55.281 | 130.508 | 12.809 | 1.880 | 0.132 | 51.150 |
| 9 | 133.968 | 13.719 | 2.996 | 0.255 | 61.918 | 133.968 | 13.719 | 2.996 | 0.255 | 61.918 | 130.923 | 12.609 | 1.829 | 0.122 | 51.101 |
| 10 | 132.374 | 12.824 | 2.548 | 0.217 | 54.160 | 132.374 | 12.824 | 2.548 | 0.217 | 54.160 | 130.167 | 12.553 | 1.630 | 0.082 | 51.215 |
| 11 | 130.319 | 13.339 | 2.460 | 0.214 | 54.328 | 130.319 | 13.339 | 2.460 | 0.214 | 54.328 | 130.598 | 12.673 | 1.892 | 0.132 | 51.104 |
| 12 | 132.275 | 12.697 | 2.634 | 0.220 | 54.608 | 132.275 | 12.697 | 2.634 | 0.220 | 54.608 | 130.580 | 12.182 | 1.883 | 0.124 | 51.339 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagarajan, V.; Solaiyappan, A.; Mahalingam, S.K.; Nagarajan, L.; Salunkhe, S.; Nasr, E.A.; Shanmugam, R.; Hussein, H.M.A.M. Meta-Heuristic Technique-Based Parametric Optimization for Electrochemical Machining of Monel 400 Alloys to Investigate the Material Removal Rate and the Sludge. Appl. Sci. 2022, 12, 2793. https://doi.org/10.3390/app12062793
Nagarajan V, Solaiyappan A, Mahalingam SK, Nagarajan L, Salunkhe S, Nasr EA, Shanmugam R, Hussein HMAM. Meta-Heuristic Technique-Based Parametric Optimization for Electrochemical Machining of Monel 400 Alloys to Investigate the Material Removal Rate and the Sludge. Applied Sciences. 2022; 12(6):2793. https://doi.org/10.3390/app12062793
Chicago/Turabian StyleNagarajan, Vengatajalapathi, Ayyappan Solaiyappan, Siva Kumar Mahalingam, Lenin Nagarajan, Sachin Salunkhe, Emad Abouel Nasr, Ragavanantham Shanmugam, and Hussein Mohammed Abdel Moneam Hussein. 2022. "Meta-Heuristic Technique-Based Parametric Optimization for Electrochemical Machining of Monel 400 Alloys to Investigate the Material Removal Rate and the Sludge" Applied Sciences 12, no. 6: 2793. https://doi.org/10.3390/app12062793
APA StyleNagarajan, V., Solaiyappan, A., Mahalingam, S. K., Nagarajan, L., Salunkhe, S., Nasr, E. A., Shanmugam, R., & Hussein, H. M. A. M. (2022). Meta-Heuristic Technique-Based Parametric Optimization for Electrochemical Machining of Monel 400 Alloys to Investigate the Material Removal Rate and the Sludge. Applied Sciences, 12(6), 2793. https://doi.org/10.3390/app12062793








