A Dynamic Procedure for Time and Space Domain Based on Differential Cubature Principle
Abstract
:1. Introduction
2. Basic Principles of the DCM
3. Space—Time Dynamic Analysis Method Based on DCM
3.1. Dynamic Equation and Initial and Boundary Conditions
3.2. Space–Time Discretization and Numerical Scheme of DC Dynamic Analysis
3.3. Stability Analysis of Transfer Matrix Q
- (1)
- When the spectral radius R(Q) is close to 1, the time-history displacement shows a stable form. To a certain extent, when it is less than 1, the time-history displacement of free vibration will gradually decay, and the decay rate is negatively correlated with R(Q).
- (2)
- When the spectral radius R(Q) is greater than 1 to a certain extent, it will lead to the accumulation and amplification of errors, and eventually lead to instability.
3.4. Forced Vibration Analysis of Beams
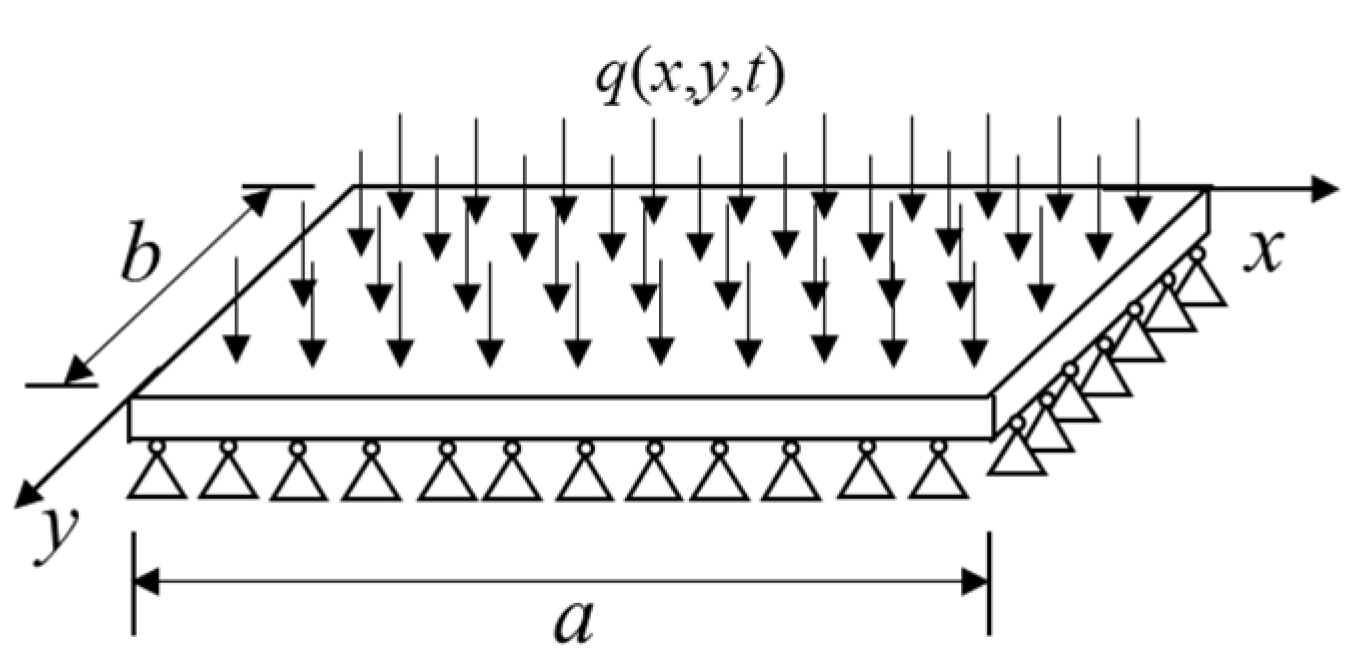
4. Space–Time Dynamic Analysis of Forced Vibration of Thin Plate
4.1. Dynamic Equation and Initial and Boundary Conditions
4.2. Discrete Form of Three-Dimension DC Grid
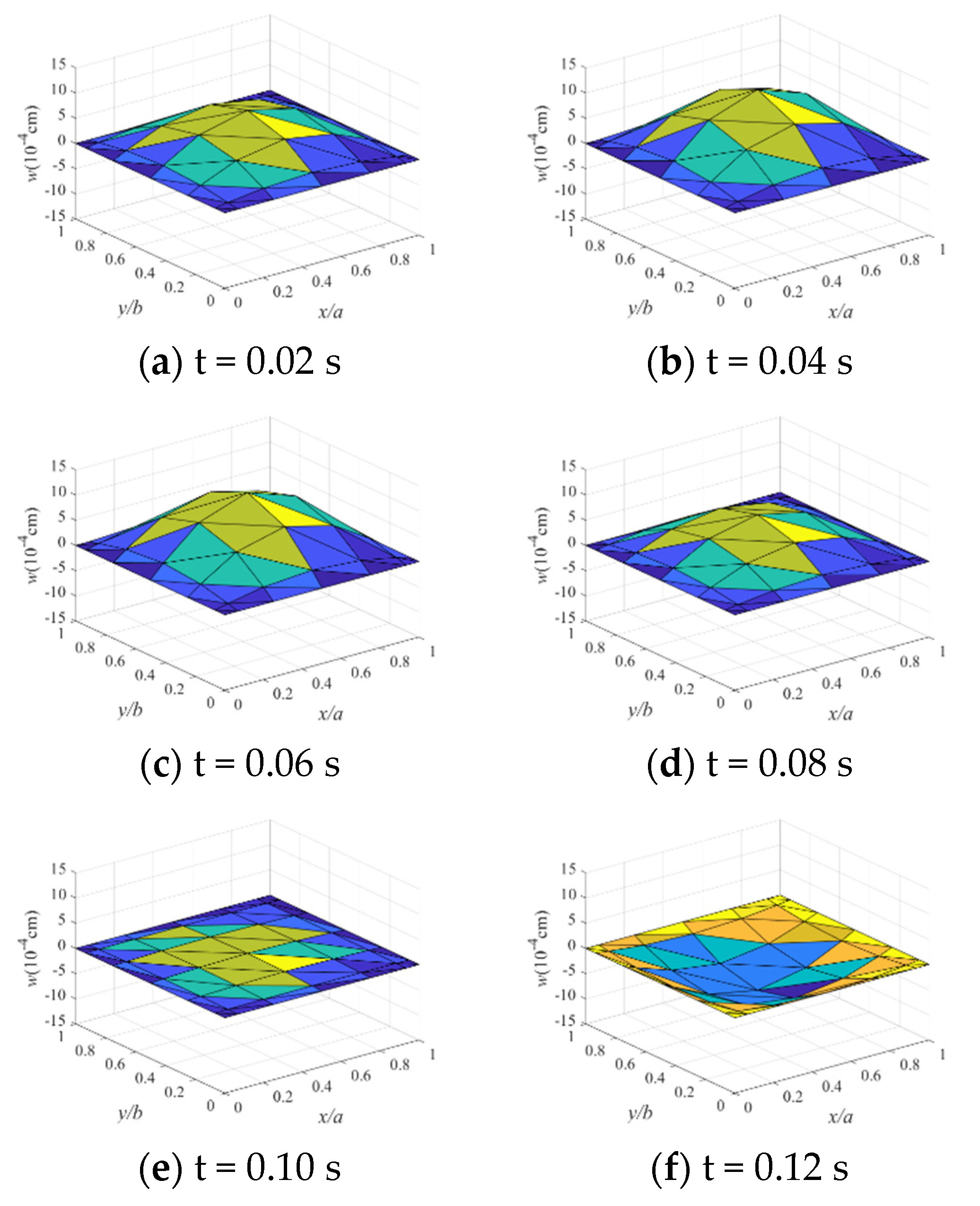
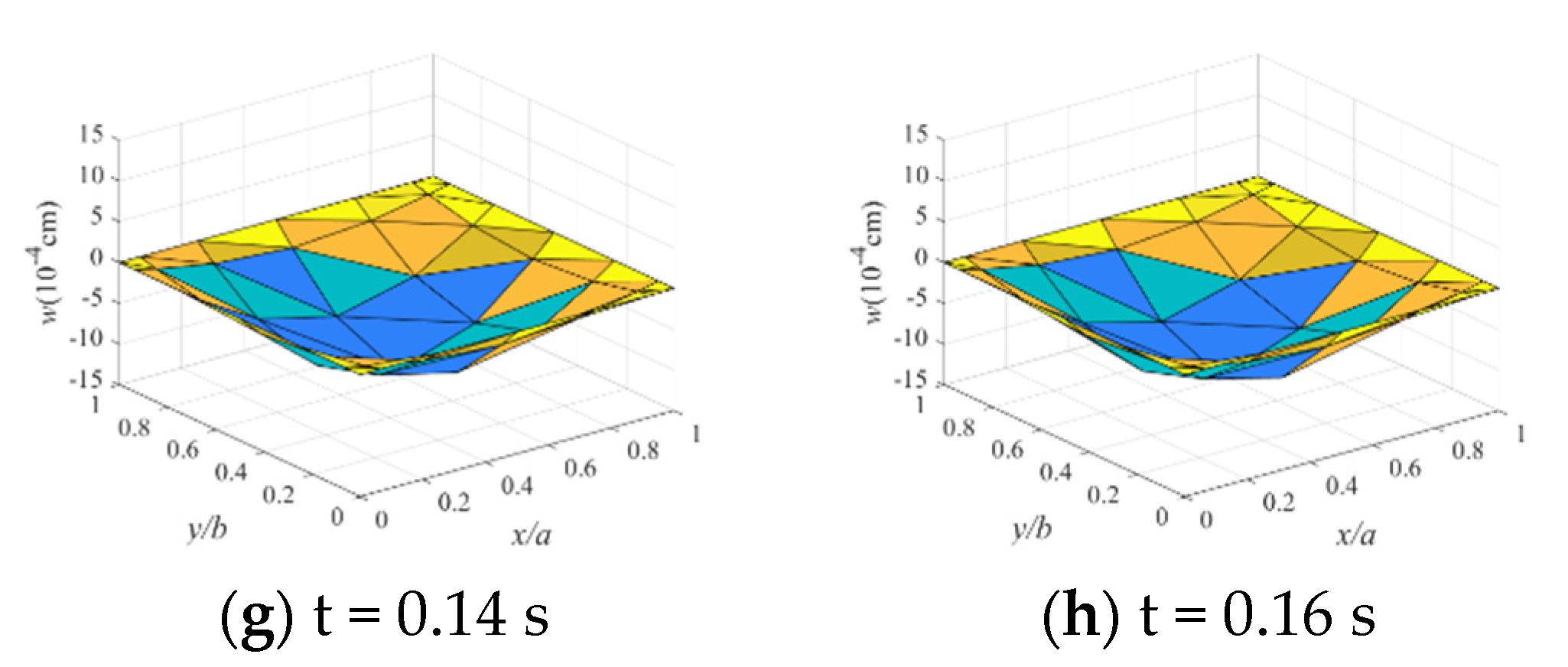
4.3. Analysis Results and Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cloughr, W.; Penzien, J. Dynamics of Structures, 2nd ed.; Revised; Computers and Structures, Inc.: New York, NY, USA, 2003; pp. 156–219. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineerin, 3rd ed.; Tsinghua University Press: Beijing, China, 2009; pp. 815–836. [Google Scholar]
- Houbolt, J.C. A recurrence matrix solution for the dynamic response of elastic aircraft. J. Aeronaut. Sci. 1950, 17, 540–550. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Wilson, E.L.; Farhoomand, I.; Bathe, K.J. Nonlinear dynamic analysis of complex structures. Earthq. Eng. Struct. Dyn. 1973, 1, 241–252. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.; Kashef, B.G.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature method in computational mechanics: A review. Appl. Mech. Rev. 1996, 49, 1–28. [Google Scholar] [CrossRef]
- Xinwei, W. Differential quadrature in the analysis of structural components. Adv. Mech. 1995, 25, 232–240. (In Chinese) [Google Scholar]
- Fung, T.C. Stability and accuracy of differential quadrature method in solving dynamic problems. Comput. Methods Appl. Eng. 2002, 191, 1311–1331. [Google Scholar] [CrossRef]
- Fung, T. Solving initial problems by differential quadrature method, Part 1: First-order equations. Int. J. Numer. Methods Eng. 2001, 50, 1411–1427. [Google Scholar] [CrossRef]
- Shu, C.; Yao, Q.; Yeo, K.S. Block-marching in time with DQ discretization: An efficient method for time-dependent problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 4587–4597. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X. An assessment of the differential quadrature time integration scheme for nonlinear dynamic equations. J. Sound Vib. 2008, 314, 246–253. [Google Scholar] [CrossRef]
- Tong, L.H.W. A time-stepping method of seismic response analysis for structures using differential quadrature rule. Chin. J. Theor. Appl. Mech. 2011, 43, 430–435. (In Chinese) [Google Scholar]
- Hongjing, L.; Xu, L.; Tong, W. Two numerical schemes of differential quadrature analysis procedure for response of the earthquake-resistant structures. J. Basic Sci. Eng. 2011, 19, 758–766. (In Chinese) [Google Scholar]
- Yuchen, M.; Hongjing, L.; Guangjun, S. Basic characteristics of differential quadrature method for dynamic response analysis of structures. J. Vib. Shock. 2020, 39, 214–221. (In Chinese) [Google Scholar]
- Civan, F. Solving multivariable mathematical models by the quadrature and cubature method. Numer. Method Partial. Differ. Equ. 1994, 10, 545–567. [Google Scholar] [CrossRef]
- Malik, M.; Civan, F. A comparative study of differential quadrature and cubature methods vis-à-vis some conventional techniques in context of convection-diffusion-reaction problems. Chem. Eng. Sci. 1995, 50, 531–547. [Google Scholar] [CrossRef]
- Leiw, K.M.; Liu, F.L. Differential cubature method for Kirchhoff plates of arbitrary shape. Comput. Methods Appl. Mech. Eng. 1997, 145, 1–10. [Google Scholar] [CrossRef]
- Liu, F.L.; Liew, K.M. Differential cubature method for static solutions of arbitrarily shaped thick plates. Int. J. Solids Struct. 1998, 35, 3655–3674. [Google Scholar] [CrossRef]
- Wu, L.; Feng, W. Differential cubature method for buckling analysis of arbitrary quadrilateral thick plates. Struct. Eng. Mech. 2003, 16, 259–274. [Google Scholar] [CrossRef]
- Pang, G.F.; Chen, W.; Sze, K.Y. Differential quadrature and cubature methods for steady-state space-fractional advection-diffusion equations. Comput. Modeling Eng. Sci. 2014, 97, 299–322. [Google Scholar]
- Wu, L.; Li, J.; Li, Y. On free vibration of thick superelliptical plates. Eng. Mech. 2002, 19, 121–125. (In Chinese) [Google Scholar]
- Wu, L.; Li, X.; Wang, L. Differential cubature method for solving axisymmetric free vibration of thick circular plates. J. Vib. Shock. 2003, 22, 75–77. (In Chinese) [Google Scholar]
- Wu, L.; Liu, J. Free vibration analysis of arbitrary shaped thick plates by differential cubature method. Int. J. Mech. Sci. 2005, 47, 63–81. [Google Scholar] [CrossRef]
- Hajmohammad, M.H.; Kolahchi, R.; Zarei, M.S.; Nouri, A.H. Dynamic response of auxetic honeycomb plates integrated with agglomerated CNT-reinforced face sheets subjected to blast load based on visco-sinusoidal theory. Int. J. Mech. Sci. 2019, 153, 391–401. [Google Scholar] [CrossRef]
- Bendarma, A.; Gourgue, H.; Jankowiak, T.; Rusinek, A.; Kardellass, S.; Klosak, M. Perforation tests of composite structure specimens at wide range of temperatures and strain rates-experimental analysis. Mater. Today: Proc. 2020, 24, 7–10. [Google Scholar] [CrossRef]
- Compean, F.I.; Olvera, D.; Campa, F.J.; De Lacalle, L.L.; Elias-Zuniga, A.; Rodriguez, C.A. Characterization and stability analysis of a multivariable milling tool by the enhanced multistage homotopy perturbation method. Int. J. Mach. Tools Manuf. 2012, 57, 27–33. [Google Scholar] [CrossRef]
- Xu, Z. Elastic Mechanics (Part 2); Higher Education Press: Beijing, China, 2006; p. 12. (In Chinese) [Google Scholar]
- Rihan, A.O. The hybrid-Trefftz Finite Element Method for Forced Vibration Analysis of Thin Plate. Master Thesis, Tianjin University, Tianjin, China, 2007. (In Chinese). [Google Scholar]
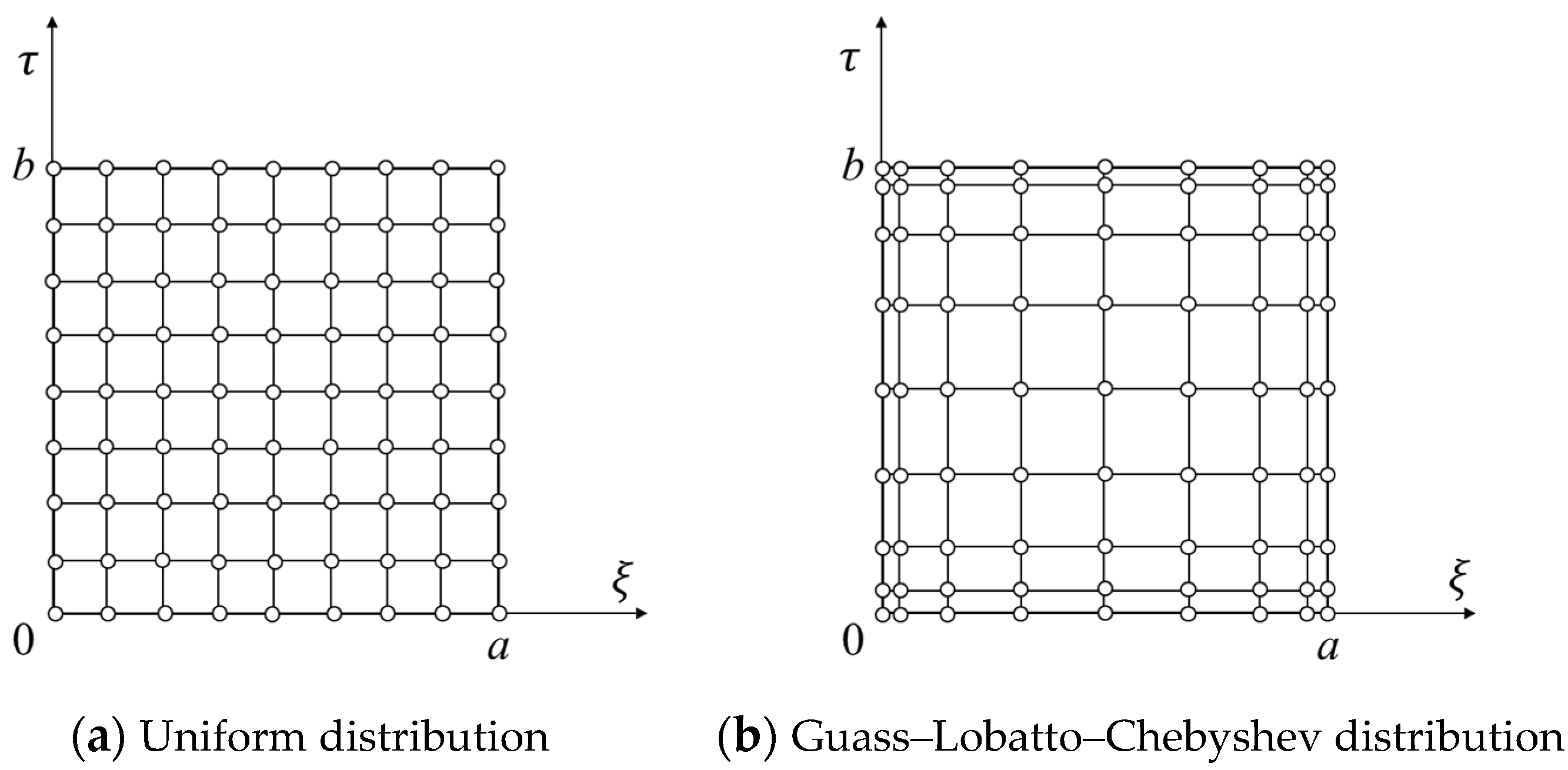
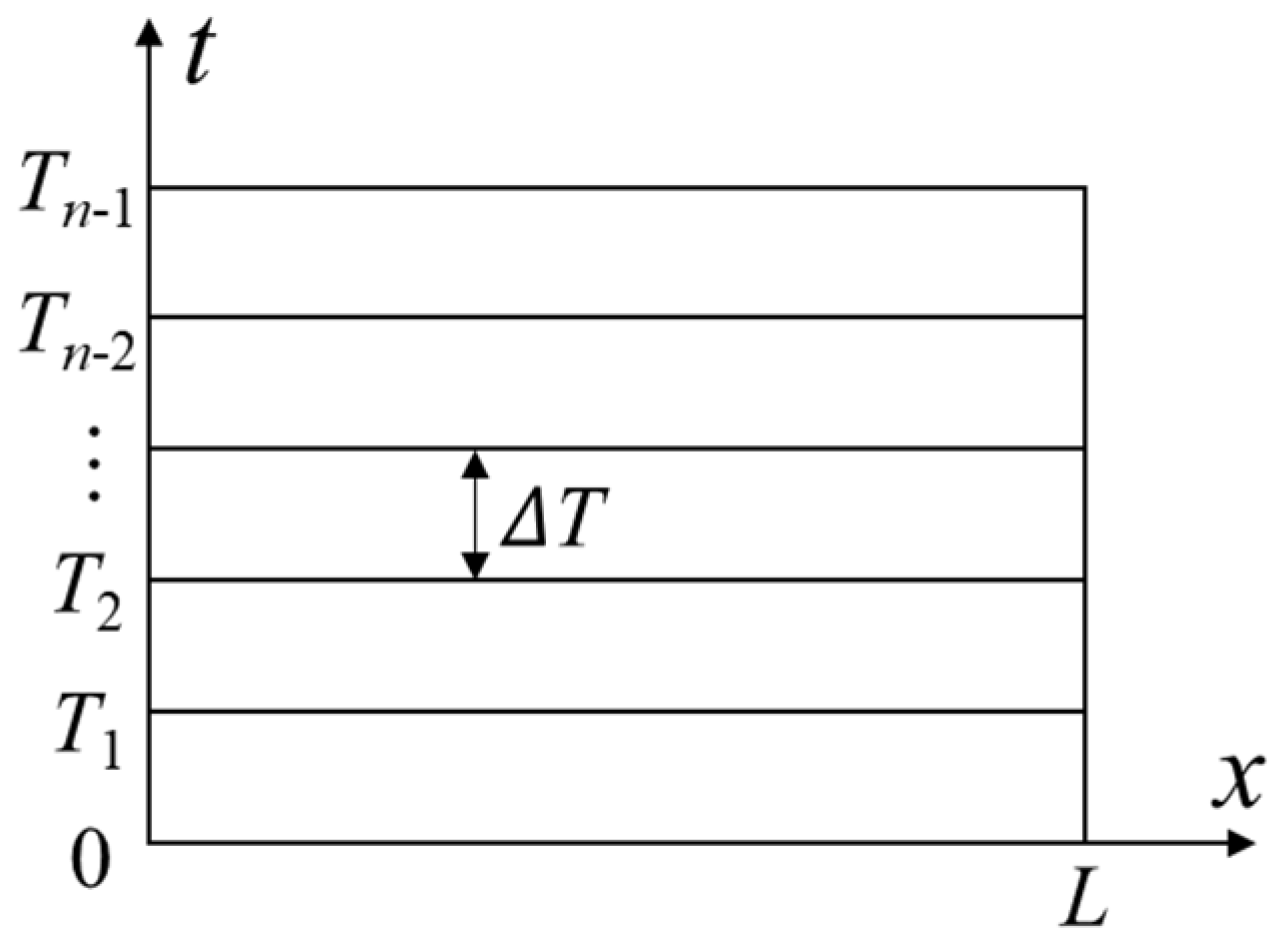
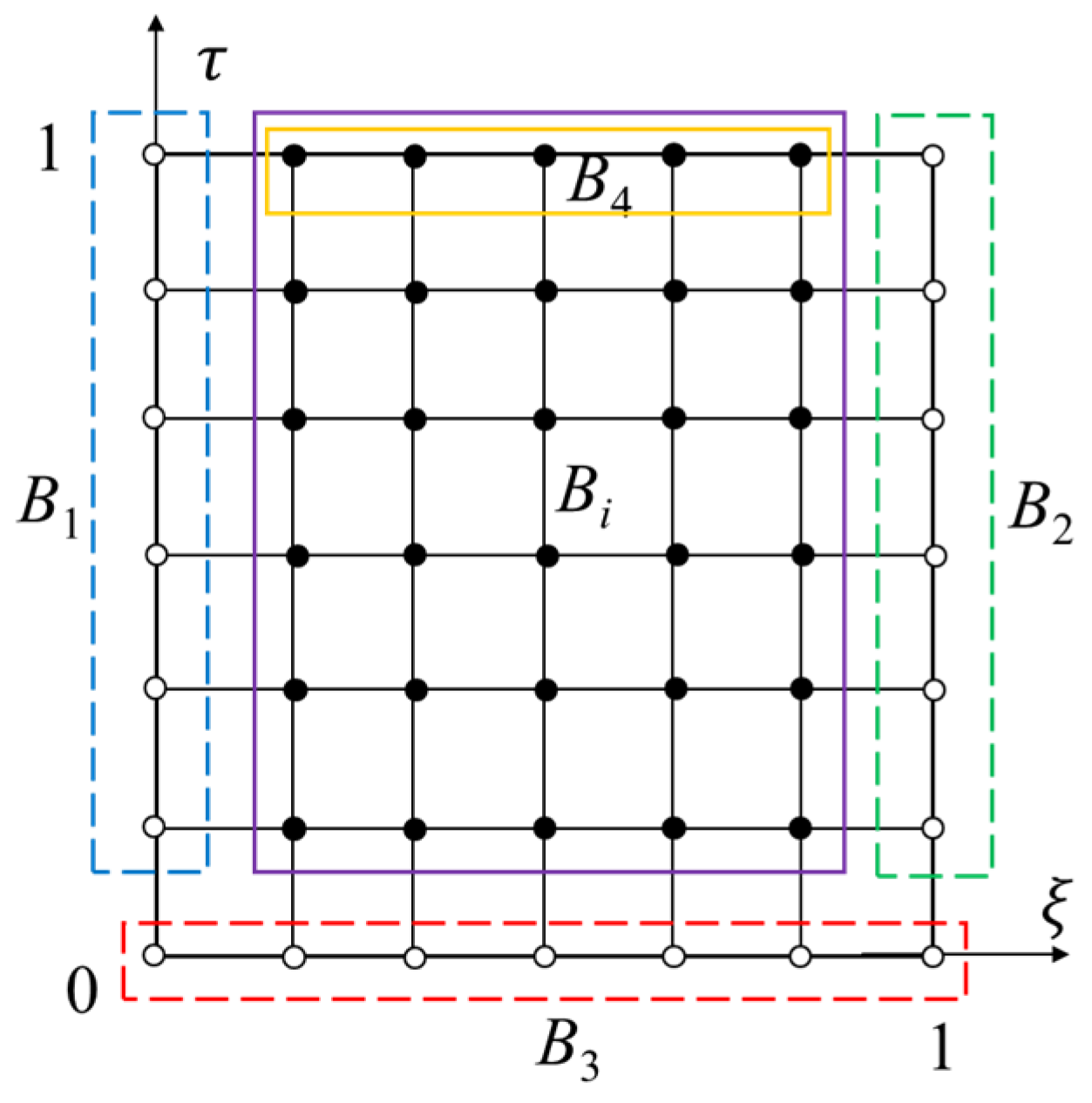

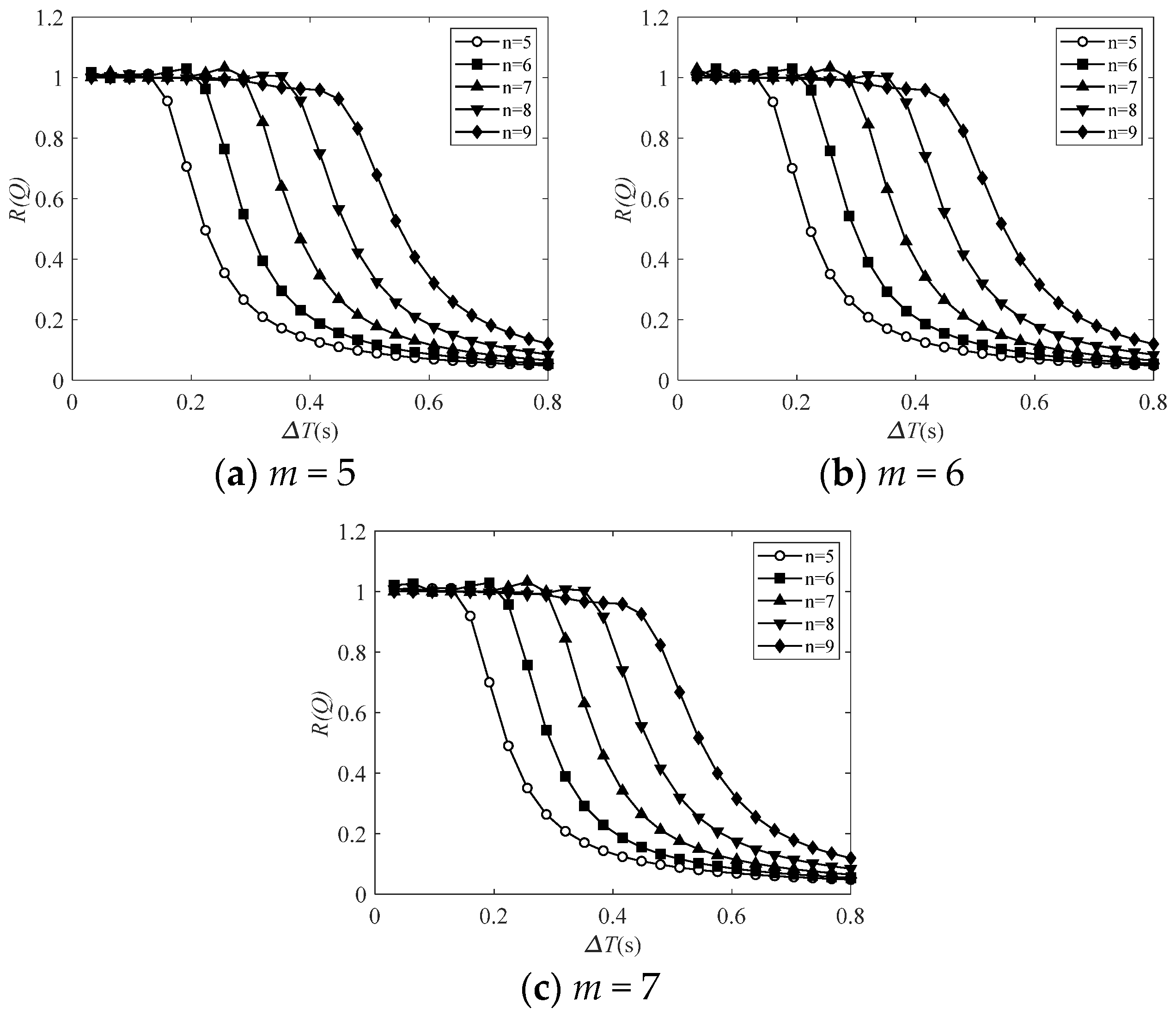

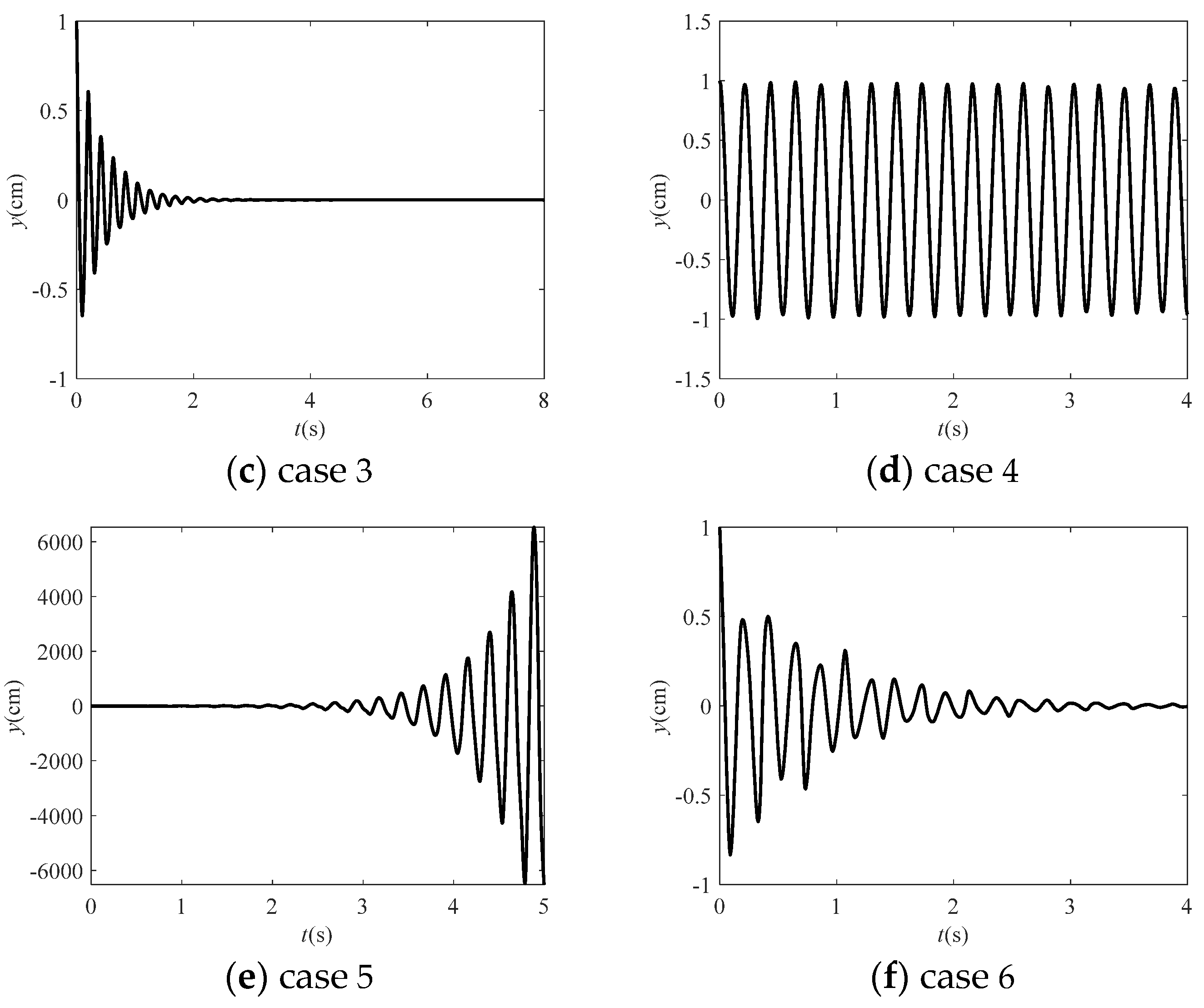





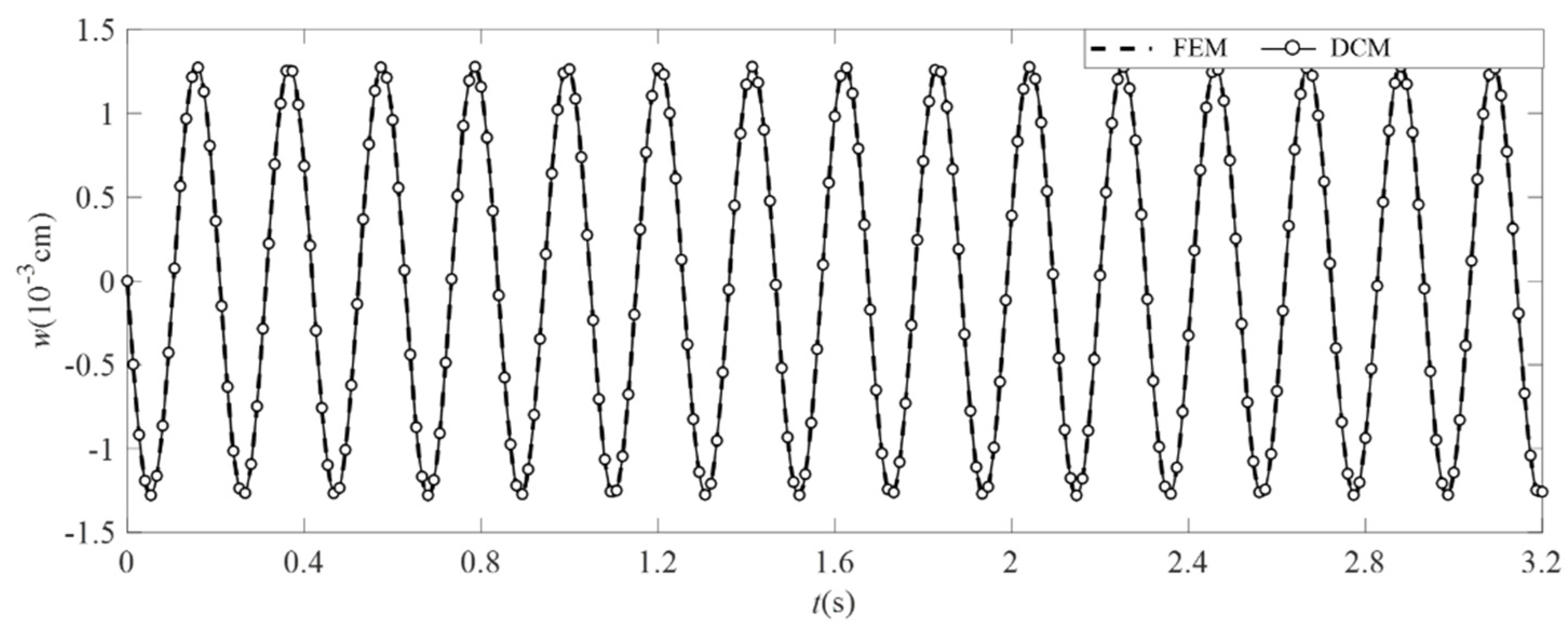
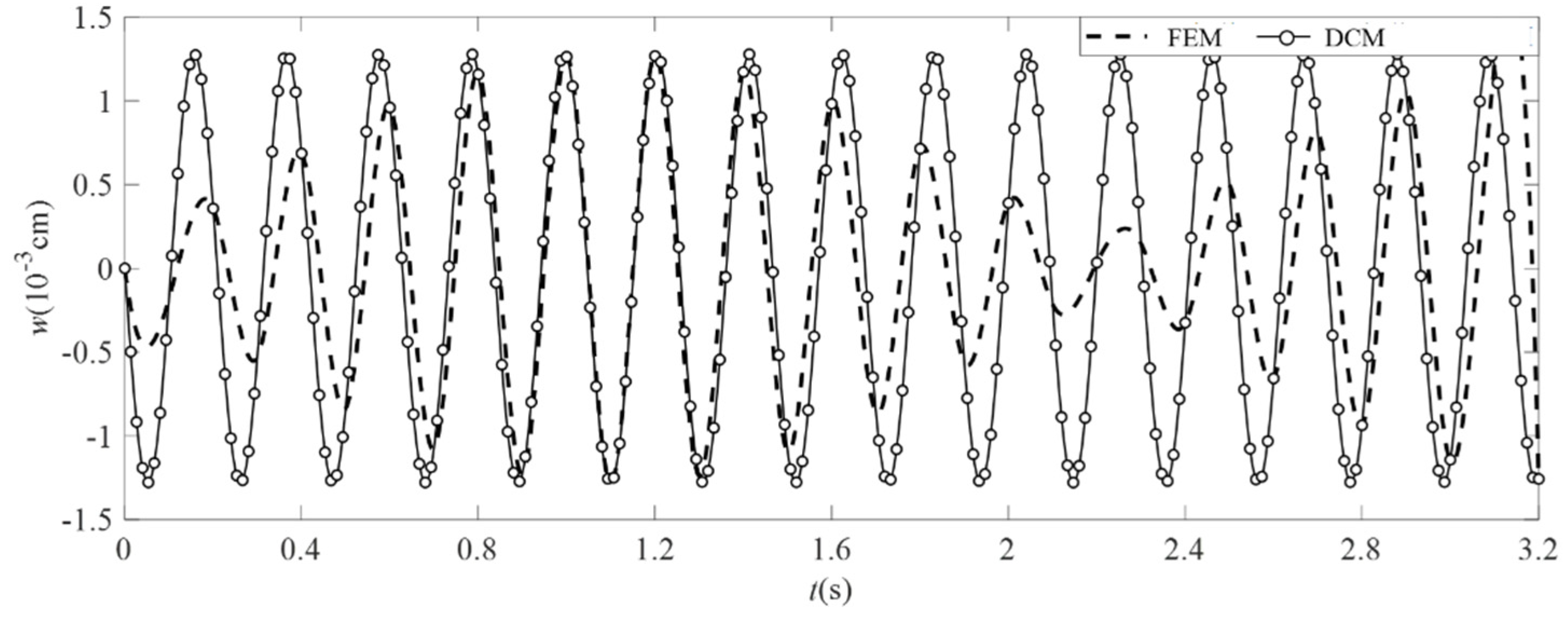
| m = 5, n = 5 | m = 5, n = 7 | |||||
|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
| distribution form | CGL | CGL | CGL | CGL | equally spaced | CGL |
| (s) | 0.064 | 0.16 | 0.2 | 0.16 | 0.25 | 0.35 |
| R(Q) | 1.0015 | 0.9229 | 0.6477 | 0.9984 | 1.5524 | 0.6521 |
| t | x/L = 0.067 | x/L = 0.25 | x/L = 0.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DC Solution | Exact | Error(%) | DC Solution | Exact | Error(%) | DC Solution | Exact | Error(%) | |
| 0.5 | −17.8585 | −17.8586 | −0.0006 | −60.4521 | −60.4507 | 0.0023 | −85.4954 | −85.4902 | 0.0061 |
| 1.0 | 4.4188 | 4.4173 | 0.0340 | 14.9579 | 14.9522 | 0.0381 | 21.1544 | 21.1457 | 0.0411 |
| 1.5 | 11.9420 | 11.9414 | 0.0050 | 40.4245 | 40.4211 | 0.0084 | 57.1711 | 57.1641 | 0.0122 |
| 2.0 | −4.0400 | −4.0345 | 0.1363 | −13.6756 | −13.6567 | 0.1384 | −19.3410 | −19.3135 | 0.1424 |
| 2.5 | −4.3708 | −4.3747 | −0.0891 | −14.7953 | −14.8083 | −0.0878 | −20.9244 | −20.9421 | −0.0845 |
| 3.0 | −2.2223 | −2.2274 | −0.2290 | −7.5225 | −7.5398 | −0.2294 | −10.6388 | −10.6629 | −0.2260 |
| 3.5 | 0.4370 | 0.4372 | −0.0457 | 1.4553 | 1.4799 | −1.6623 | 2.0940 | 2.0929 | 0.0526 |
| 4.0 | 10.8579 | 10.8553 | 0.0240 | 36.7545 | 36.7448 | 0.0264 | 51.9807 | 51.9650 | 0.0302 |
| 4.5 | −2.3860 | −2.3960 | −0.4174 | −8.0769 | −8.1104 | −0.4130 | −11.4229 | −11.4698 | −0.4089 |
| 5.0 | −16.4010 | −16.3886 | 0.0757 | −55.5183 | −55.4748 | 0.0784 | −78.5177 | −78.4532 | 0.0822 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
|---|---|---|---|---|---|---|
| EI | 7.772 104 | 4.772 105 | 4.772 106 | 2.772 107 | 4.772 108 | 4.772 109 |
| 1.1776 | 2.9180 | 9.2274 | 22.2406 | 92.2743 | 291.7971 |
| t(s) | Exact [29] (10−4 cm) | Reference [30] (10−4 cm) | Error 1 (%) | 5 × 5 × 9 DC (10−4 cm) | Error 2 (%) | 7 × 7 × 9 DC (10−4 cm) | Error 3 (%) |
|---|---|---|---|---|---|---|---|
| 0.02 | 7.22 | 7.4243 | 2.83 | 7.1684 | 0.7184 | 7.2166 | 0.0471 |
| 0.04 | 11.92 | 12.1476 | 1.91 | 11.8333 | 0.7273 | 11.9129 | 0.0596 |
| 0.06 | 12.45 | 12.6330 | 1.47 | 12.3641 | 0.6900 | 12.4472 | 0.0225 |
| 0.08 | 8.637 | 8.7165 | 0.92 | 8.5758 | 0.7086 | 8.6335 | 0.0405 |
| 0.10 | 1.804 | 1.7890 | −0.83 | 1.7917 | 0.6818 | 1.8037 | 0.0166 |
| 0.12 | −5.658 | −5.5115 | −2.59 | −5.6183 | −0.7017 | −5.6561 | −0.0336 |
| 0.14 | −11.14 | −11.4976 | 3.21 | −11.0657 | −0.6670 | −11.1401 | −0.0009 |
| 0.16 | −12.74 | −12.9477 | 1.63 | −12.6471 | −0.7292 | −12.7321 | −0.0620 |
| Numerical Method | FEM(20 × 20) | DCM | |||
|---|---|---|---|---|---|
| ΔT = 0.1 s | ΔT = 0.05 s | ΔT = 0.01 s | (5 × 5 × 9) | (7 × 7 × 9) | |
| cpu-time (s) | 17 | 23 | 47 | 0.4394 | 0.8663 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Li, H.; Mei, Y. A Dynamic Procedure for Time and Space Domain Based on Differential Cubature Principle. Appl. Sci. 2022, 12, 2832. https://doi.org/10.3390/app12062832
Xu Q, Li H, Mei Y. A Dynamic Procedure for Time and Space Domain Based on Differential Cubature Principle. Applied Sciences. 2022; 12(6):2832. https://doi.org/10.3390/app12062832
Chicago/Turabian StyleXu, Qiang, Hongjing Li, and Yuchen Mei. 2022. "A Dynamic Procedure for Time and Space Domain Based on Differential Cubature Principle" Applied Sciences 12, no. 6: 2832. https://doi.org/10.3390/app12062832
APA StyleXu, Q., Li, H., & Mei, Y. (2022). A Dynamic Procedure for Time and Space Domain Based on Differential Cubature Principle. Applied Sciences, 12(6), 2832. https://doi.org/10.3390/app12062832





