Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction
Abstract
:1. Introduction
- We construct time-evolving adjacency graphs at different time slots with self-adaptive time embeddings and node embeddings based on a tensor-composing method. This method makes full use of information shared in the time domain and is parameter-efficient compared to defining an adaptive graph in each time slot.
- To model the inter-node patterns in traffic networks, we apply a kind of mix-hop graph convolution that utilizes both the adaptive time-evolving graphs and a predefined distance-based graph. This kind of graph convolution module is verified as being effective in capturing more comprehensive inter-node dependency than those with static graphs.
- We integrate the aforementioned graph convolution module with RNN encoder–decoder structure to form a general traffic prediction framework, which allows it to learn the dynamics of inter-node dependency when modeling traffic sequential features. Experiments on two real-world traffic datasets demonstrate the superiority of the proposed model over multiple competitive baselines, especially in short-term prediction.
2. Related Work
2.1. Traffic Prediction Methods
2.2. Graph Convolutional Networks
3. Proposed Method
3.1. Problem Preliminaries
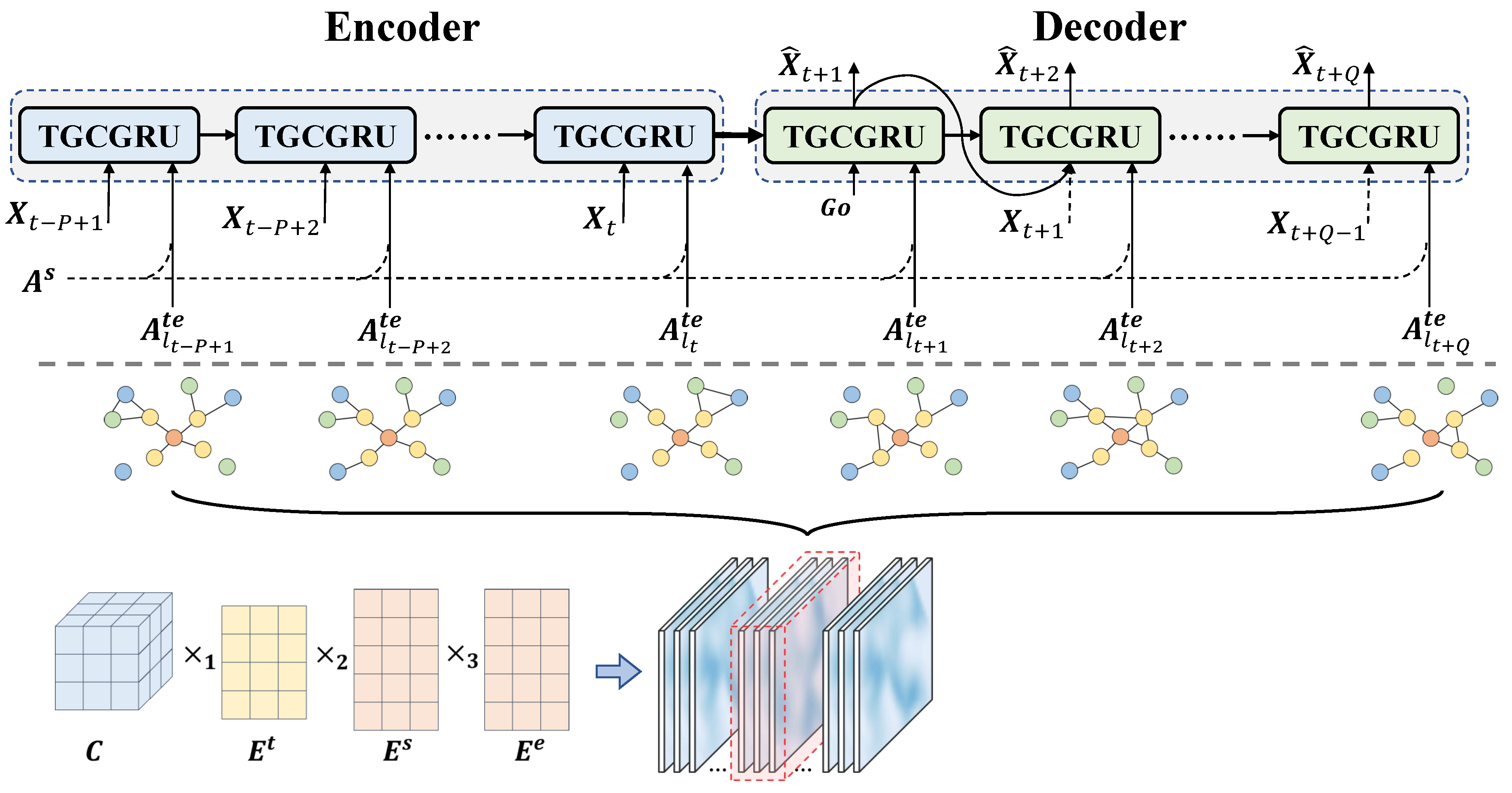
3.2. Method Overview
3.3. Generation of Time-Evolving Adaptive Graphs
3.4. Graph Convolution Module
3.5. Temporal Recurrent Module
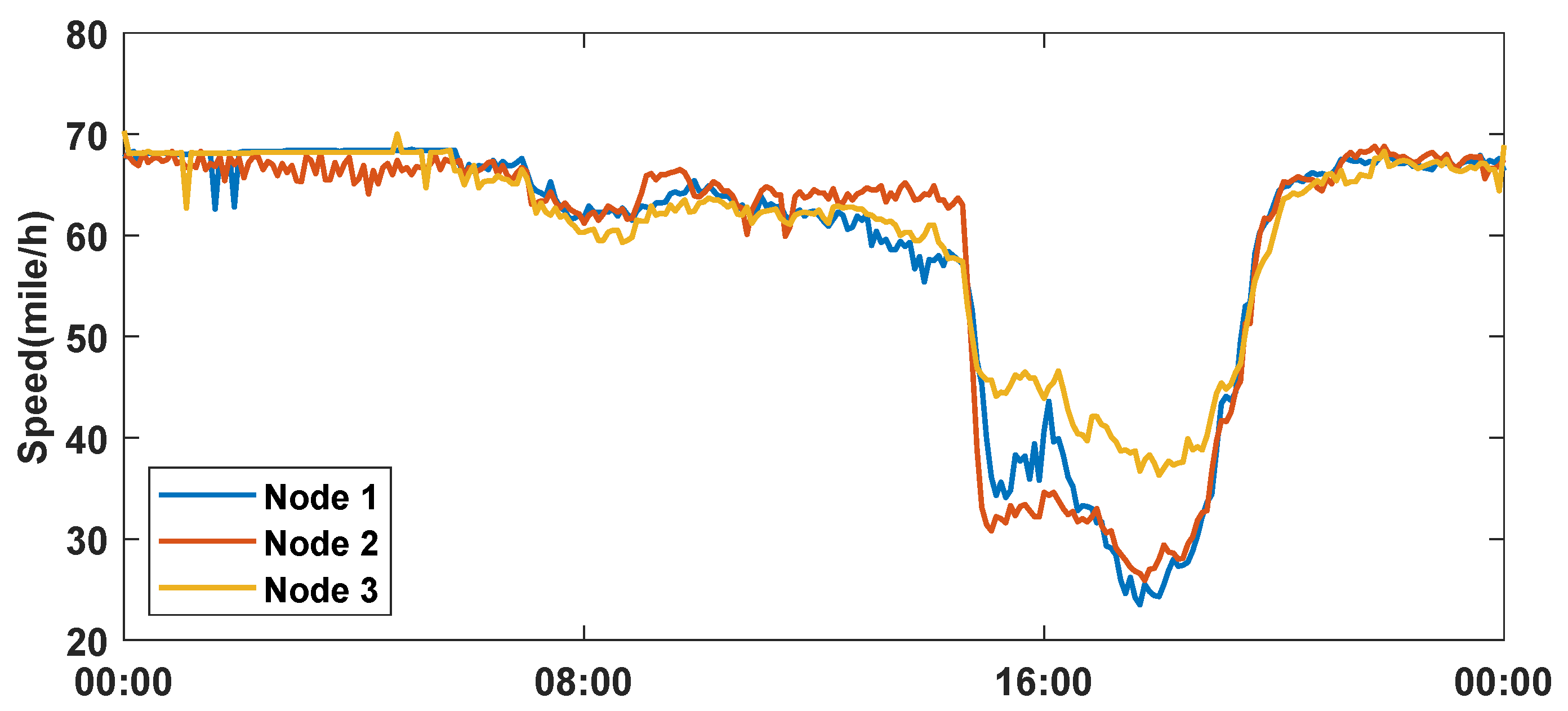
3.6. Example of the Prediction Process of TEGCRN
4. Experiments and Discussion
4.1. Datasets
4.2. Baseline Methods
- HA: Historical Average, which views the traffic flow as seasonal signals and predicts future speed with the average of the values at the same time slots of previous weeks.
- ARIMA: Auto-Regressive Integrated Moving Average model with Kalman filter, a traditional time-series predicting method.
- FC-LSTM [37]: RNN sequence-to-sequence model with LSTM units, using a fully-connected layer when calculating the inner hidden vectors.
- DCRNN [12]: Diffusion Convolutional Recurrent Neural Network, which combines the bidirectional graph convolution with GRU encoder–decoder model. Only the distance-based graph is utilized and the adjacency in different time steps remains static.
- STGCN [13]: Spatiotemporal Graph Convolutional Network, which alternately stacks temporal 1-D CNN with spectral graph convolution ChebyNet to form a predicting framework in a complete convolutional manner. Likewise, it relies only on the distance-based static graph.
- MTGNN [21]: This model introduces a uni-directional adaptive graph and mix-hop propagation into graph convolutions, and introduces dilated inception layers on the time dimension to capture features in receptive fields of multiple sizes.
4.3. Experiments Settings and Metrics
4.4. Prediction Performance
4.5. Ablation Study
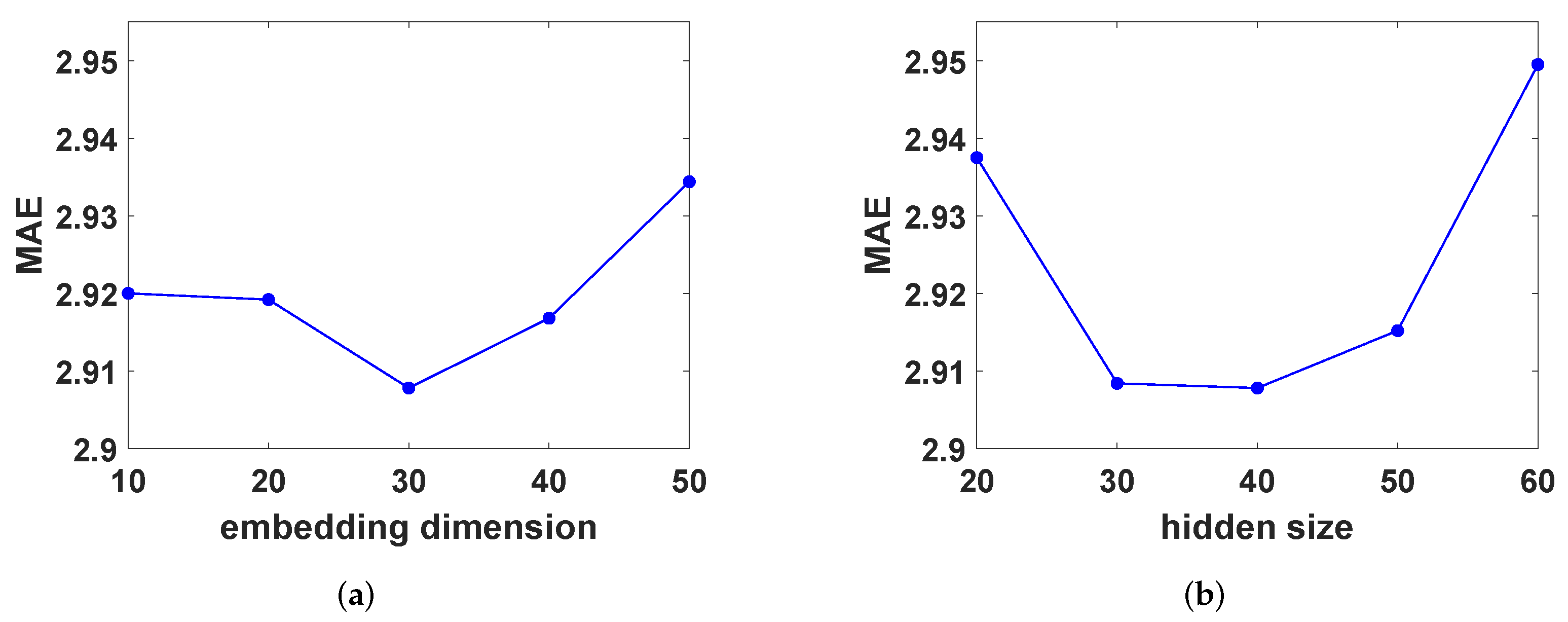
4.6. Parameters Study
4.7. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RNN | Recurrent Neural Network |
| CNN | Convolutional Neural Network |
| GCN | Graph Convolutional Network |
| POI | Point of Interest |
| TEGCRN | Time-Evolving Graph Convolution Recurrent Network |
| ARIMA | Auto-Regressive Integrated Moving Average |
| VAR | Vector Auto-Regression |
| SVR | Support Vector Regression |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
References
- Kechagias, E.P.; Gayialis, S.P.; Konstantakopoulos, G.D.; Papadopoulos, G.A. An application of an urban freight transportation system for reduced environmental emissions. Systems 2020, 8, 49. [Google Scholar] [CrossRef]
- Kechagias, E.P.; Gayialis, S.P.; Konstantakopoulos, G.D.; Papadopoulos, G.A. Traffic flow forecasting for city logistics: A literature review and evaluation. Int. J. Decis. Support Syst. 2019, 4, 159–176. [Google Scholar] [CrossRef]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Lippi, M.; Bertini, M.; Frasconi, P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning. IEEE Trans. Intell. Transp. Syst. 2013, 14, 871–882. [Google Scholar] [CrossRef]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Tan, H. Short-term traffic flow forecasting with spatial-temporal correlation in a hybrid deep learning framework. arXiv 2016, arXiv:1612.01022. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Yao, H.; Wu, F.; Ke, J.; Tang, X.; Jia, Y.; Lu, S.; Gong, P.; Ye, J.; Li, Z. Deep multi-view spatial-temporal network for taxi demand prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Lin, Z.; Feng, J.; Lu, Z.; Li, Y.; Jin, D. Deepstn+: Context-aware spatial-temporal neural network for crowd flow prediction in metropolis. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1020–1027. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1907–1913. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 922–929. [Google Scholar]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 914–921. [Google Scholar]
- Kong, X.; Xing, W.; Wei, X.; Bao, P.; Zhang, J.; Lu, W. STGAT: Spatial-temporal graph attention networks for traffic flow forecasting. IEEE Access 2020, 8, 134363–134372. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Z. Spatial-Temporal Fusion Graph Neural Networks for Traffic Flow Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 4189–4196. [Google Scholar]
- Chen, W.; Chen, L.; Xie, Y.; Cao, W.; Gao, Y.; Feng, X. Multi-range attentive bicomponent graph convolutional network for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3529–3536. [Google Scholar]
- Geng, X.; Li, Y.; Wang, L.; Zhang, L.; Yang, Q.; Ye, J.; Liu, Y. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3656–3663. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Online, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Wang, Y.; Papageorgiou, M. Real-time freeway traffic state estimation based on extended Kalman filter: A general approach. Transp. Res. Part Methodol. 2005, 39, 141–167. [Google Scholar] [CrossRef]
- Kumar, S.V. Traffic flow prediction using Kalman filtering technique. Procedia Eng. 2017, 187, 582–587. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y. A comparative study of three multivariate short-term freeway traffic flow forecasting methods with missing data. J. Intell. Transp. Syst. 2016, 20, 205–218. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.I.; Jegelka, S. Representation learning on graphs with jumping knowledge networks. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5449–5458. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Chen, D.; Lin, Y.; Li, W.; Li, P.; Zhou, J.; Sun, X. Measuring and relieving the over-smoothing problem for graph neural networks from the topological view. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3438–3445. [Google Scholar]
- Xu, B.; Shen, H.; Cao, Q.; Cen, K.; Cheng, X. Graph convolutional networks using heat kernel for semi-supervised learning. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1928–1934. [Google Scholar]
- Li, Q.; Han, Z.; Wu, X.M. Deeper insights into graph convolutional networks for semi-supervised learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Han, L.; Du, B.; Sun, L.; Fu, Y.; Lv, Y.; Xiong, H. Dynamic and Multi-faceted Spatio-temporal Deep Learning for Traffic Speed Forecasting. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 547–555. [Google Scholar]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Gao, H.; Ji, S. Towards deeper graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Online, 6–10 July 2020; pp. 338–348. [Google Scholar]
- Klicpera, J.; Bojchevski, A.; Günnemann, S. Predict then Propagate: Graph Neural Networks meet Personalized PageRank. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Bengio, S.; Vinyals, O.; Jaitly, N.; Shazeer, N. Scheduled sampling for sequence prediction with recurrent Neural networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 1, Montreal, QC, Canada, 7–12 December 2015; pp. 1171–1179. [Google Scholar]




| Models | Graph Construction for Inter-Node Dependency | Inter-Node Dependency Evolves with Time? | Spatial Modeling | Temporal Modeling |
|---|---|---|---|---|
| DCRNN [12] | road distance graph | ✕ | diffusion convolution 1 | GRU |
| STGCN [13] | road distance graph | ✕ | ChebyNet | CNN |
| ASTGCN [15] | road binary graph | ✕ | ChebyNet + attention | CNN + attention |
| Graph-WaveNet [14] | road distance graph + adaptive graph | ✕ | mix-hop GCN | dilated CNN |
| STSGCN [16] | spatio and temporal augmented graph | ✕ | JK-Net | – 2 |
| STFGNN [18] | spatio and temporal and time-series similarity augmented graph | ✕ | JK-Net | – |
| MRA-BGCN [19] | road distance graph + edge-wise line graph | ✕ | GCN + attention | GRU |
| MTGNN [21] | adaptive graph | ✕ | mix-hop GCN + residual | dilated CNN + inception |
| TEGCRN (ours) | road distance graph + adaptive graph | ✓ | mix-hop GCN + residual | GRU |
| Dataset | Nodes | Edges | Size | Sample Rate | Missing Proportion |
|---|---|---|---|---|---|
| METR-LA | 207 | 1515 | 34272 | 5 min | 8.109% |
| PEMS-BAY | 325 | 2369 | 52116 | 5 min | 0.003% |
| 15 min (3 Steps) | 30 min (6 Steps) | 60 min (12 Steps) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| HA | 4.16 | 7.80 | 13.00% | 4.16 | 7.80 | 13.00% | 4.16 | 7.80 | 13.00% |
| ARIMA | 3.99 | 8.21 | 9.60% | 5.15 | 10.45 | 12.70% | 6.90 | 13.23 | 17.40% |
| FC-LSTM | 3.44 | 6.30 | 9.60% | 3.77 | 7.23 | 10.90% | 4.37 | 8.69 | 13.20% |
| DCRNN | 2.77 | 5.38 | 7.30% | 3.15 | 6.45 | 8.80% | 3.60 | 7.60 | 10.50% |
| STGCN | 2.88 | 5.74 | 7.62% | 3.47 | 7.24 | 9.57% | 4.59 | 9.40 | 12.70% |
| Graph-WaveNet | 2.69 | 5.15 | 6.90% | 3.07 | 6.22 | 8.37% | 3.53 | 7.37 | 10.01% |
| MTGNN | 2.69 | 5.18 | 6.86% | 3.05 | 6.17 | 8.19% | 3.49 | 7.23 | 9.87% |
| TEGCRN | 2.65 | 5.10 | 6.74% | 3.04 | 6.16 | 8.22% | 3.49 | 7.32 | 10.03% |
| 15 min (3 Steps) | 30 min (6 Steps) | 60 min (12 Steps) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| HA | 2.88 | 5.59 | 6.80% | 2.88 | 5.59 | 6.80% | 2.88 | 5.59 | 6.80% |
| ARIMA | 1.62 | 3.30 | 3.50% | 2.33 | 4.76 | 5.4% | 3.38 | 6.50 | 8.30% |
| FC-LSTM | 2.05 | 4.19 | 4.80% | 2.20 | 4.55 | 5.20% | 2.37 | 4.96 | 5.70% |
| DCRNN | 1.38 | 2.95 | 2.90% | 1.74 | 3.97 | 3.90% | 2.07 | 4.74 | 4.90% |
| STGCN | 1.36 | 2.96 | 2.90% | 1.81 | 4.27 | 4.17% | 2.49 | 5.69 | 5.79% |
| Graph-WaveNet | 1.30 | 2.74 | 2.73% | 1.63 | 3.70 | 3.67% | 1.95 | 4.52 | 4.63% |
| MTGNN | 1.32 | 2.79 | 2.77% | 1.65 | 3.74 | 3.69% | 1.94 | 4.49 | 4.53% |
| TEGCRN | 1.29 | 2.72 | 2.69% | 1.60 | 3.67 | 3.59% | 1.88 | 4.39 | 4.43% |
| Method | Overall MAE | Overall RMSE | Overall MAPE |
|---|---|---|---|
| TEGCRN | 2.908 | 5.705 | 7.866% |
| Static Adpative | 2.969 | 5.792 | 8.072% |
| Static Predefined | 3.015 | 5.887 | 8.258% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mai, W.; Chen, J.; Chen, X. Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction. Appl. Sci. 2022, 12, 2842. https://doi.org/10.3390/app12062842
Mai W, Chen J, Chen X. Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction. Applied Sciences. 2022; 12(6):2842. https://doi.org/10.3390/app12062842
Chicago/Turabian StyleMai, Weimin, Junxin Chen, and Xiang Chen. 2022. "Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction" Applied Sciences 12, no. 6: 2842. https://doi.org/10.3390/app12062842
APA StyleMai, W., Chen, J., & Chen, X. (2022). Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction. Applied Sciences, 12(6), 2842. https://doi.org/10.3390/app12062842







