Dynamic Impact Factor and Resonance Analysis of Curved Intercity Railway Viaduct
Abstract
:1. Introduction
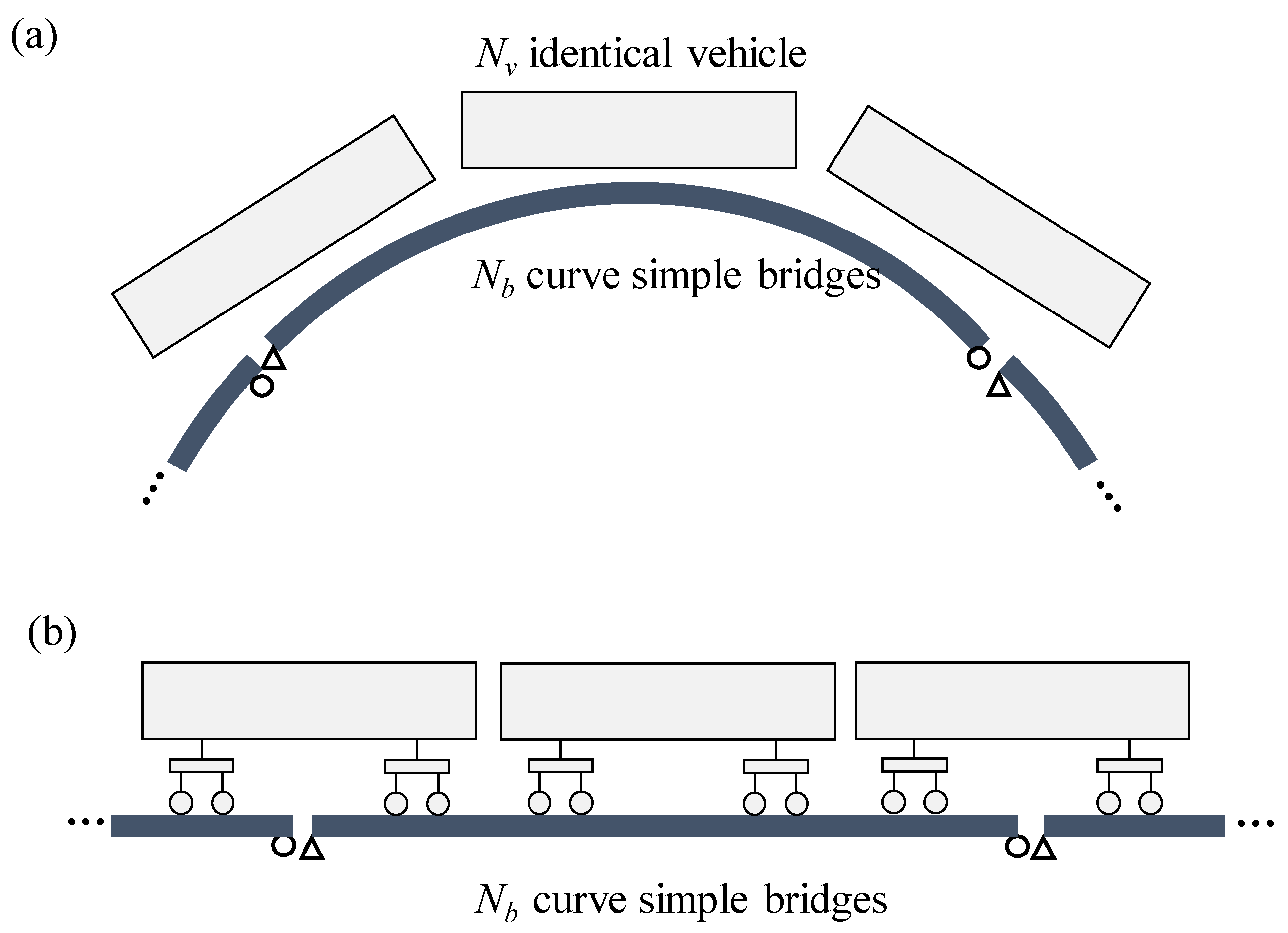
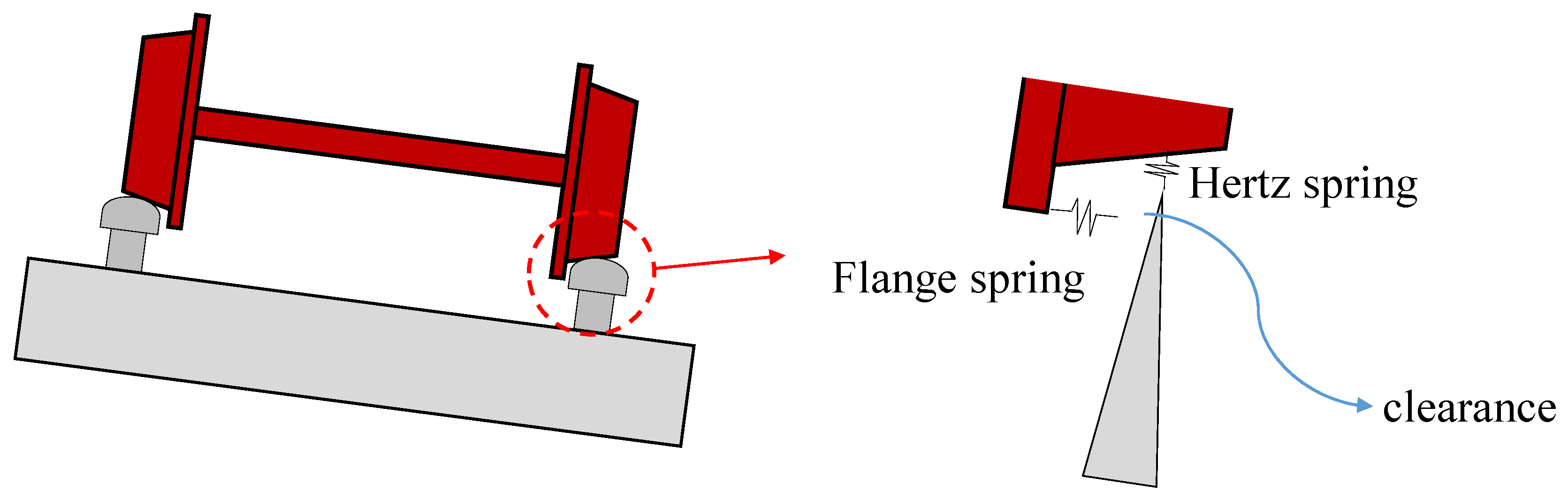
2. Intercity Vehicle-Curve Bridge System Model
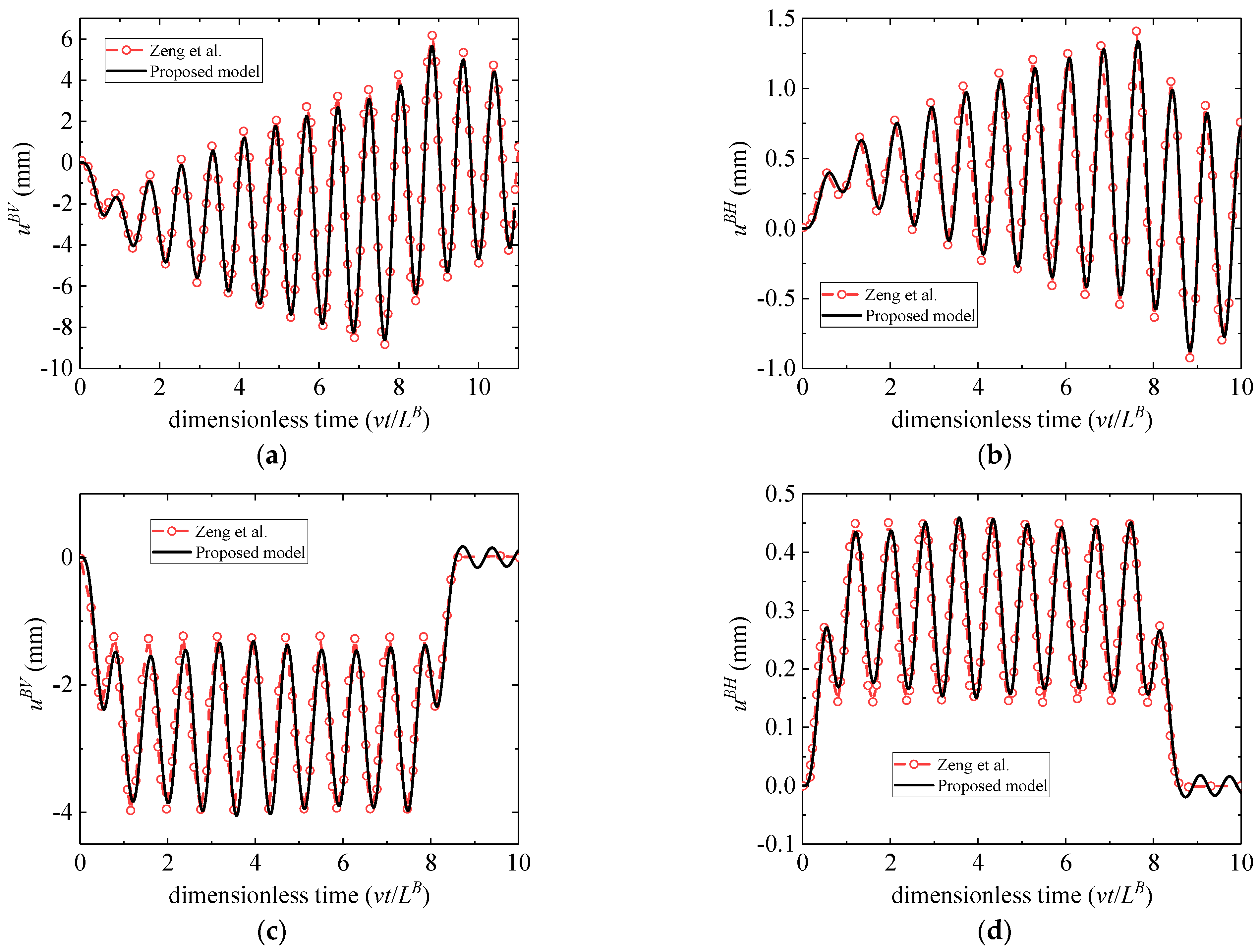
3. Model Validation
4. Numerical Analysis
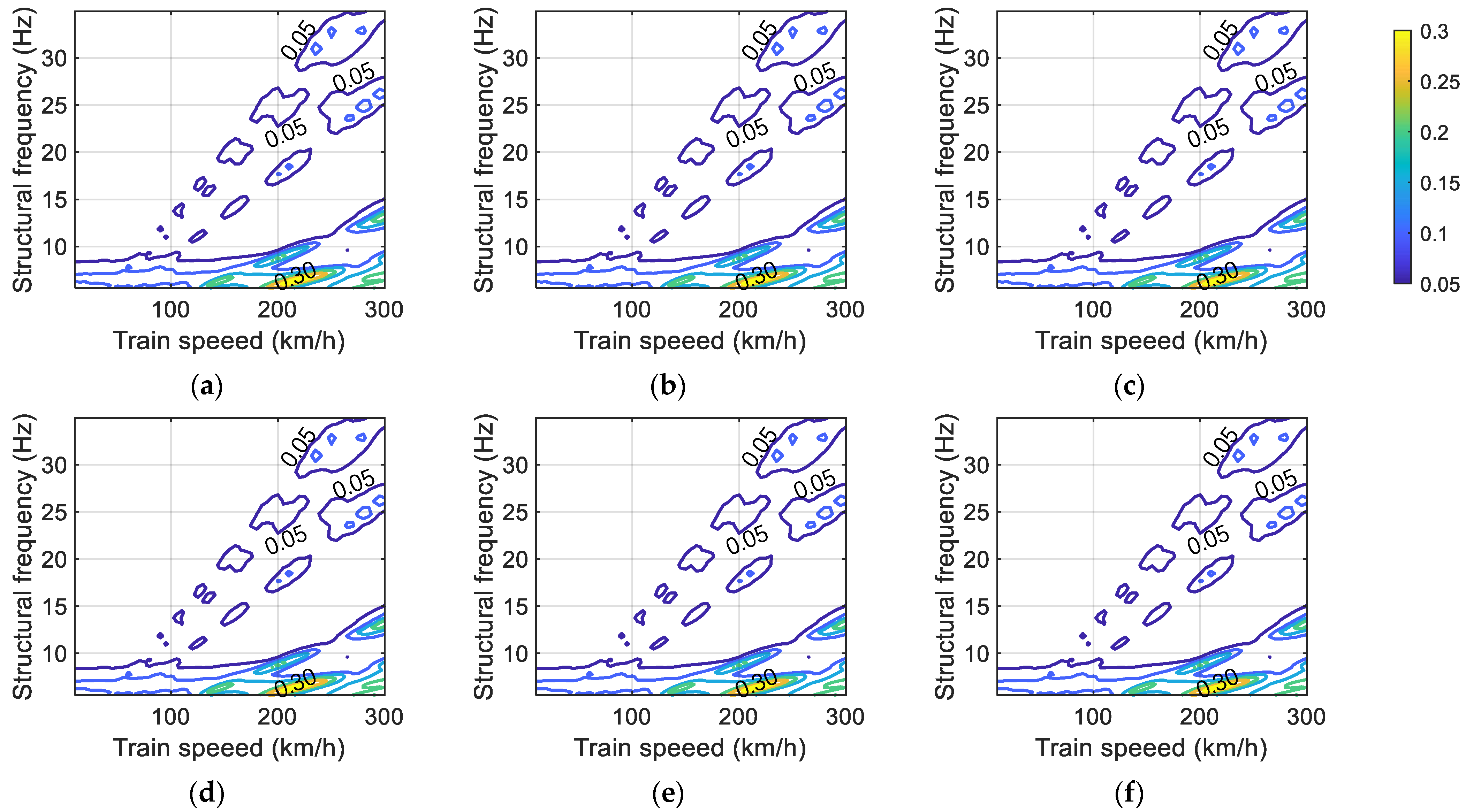
4.1. Resonance Condition
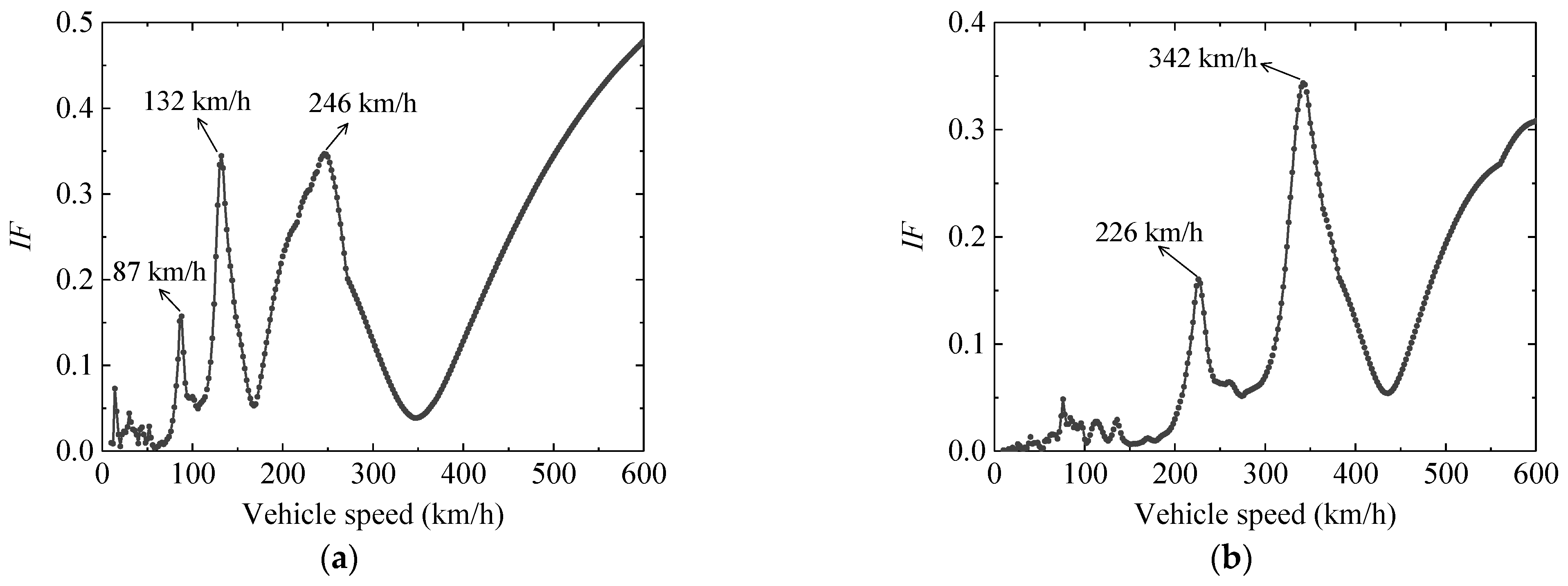
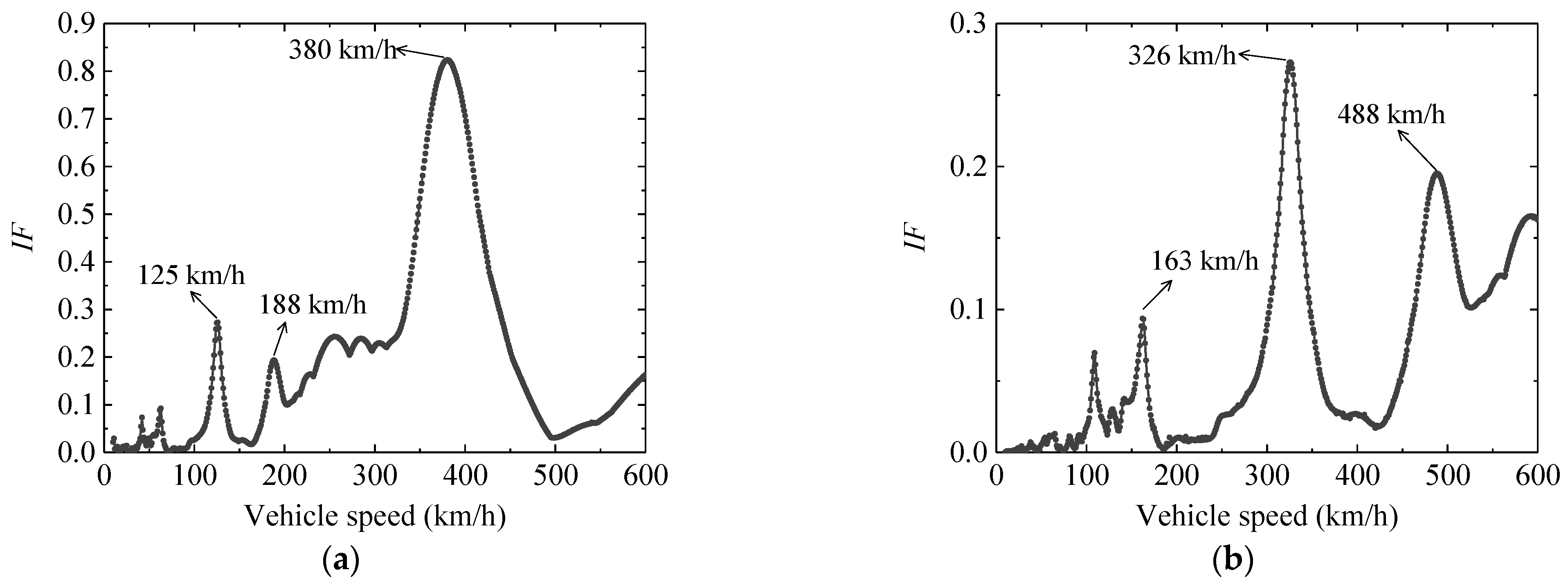
4.2. Dynamic Impact Factor Calculation
4.2.1. Dynamic Impact Factor of the Bridge with a Span of 30 m
4.2.2. Dynamic Impact Factor (IF) of the Bridge with a Span of 25 m
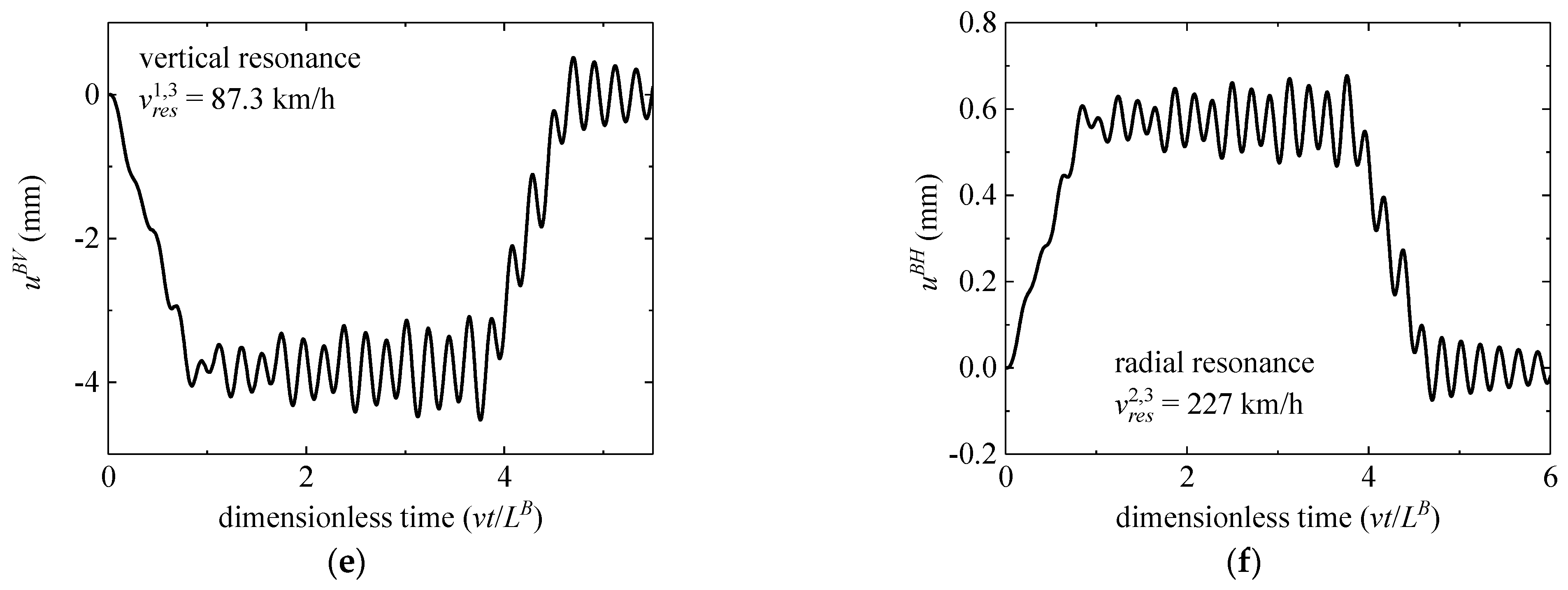
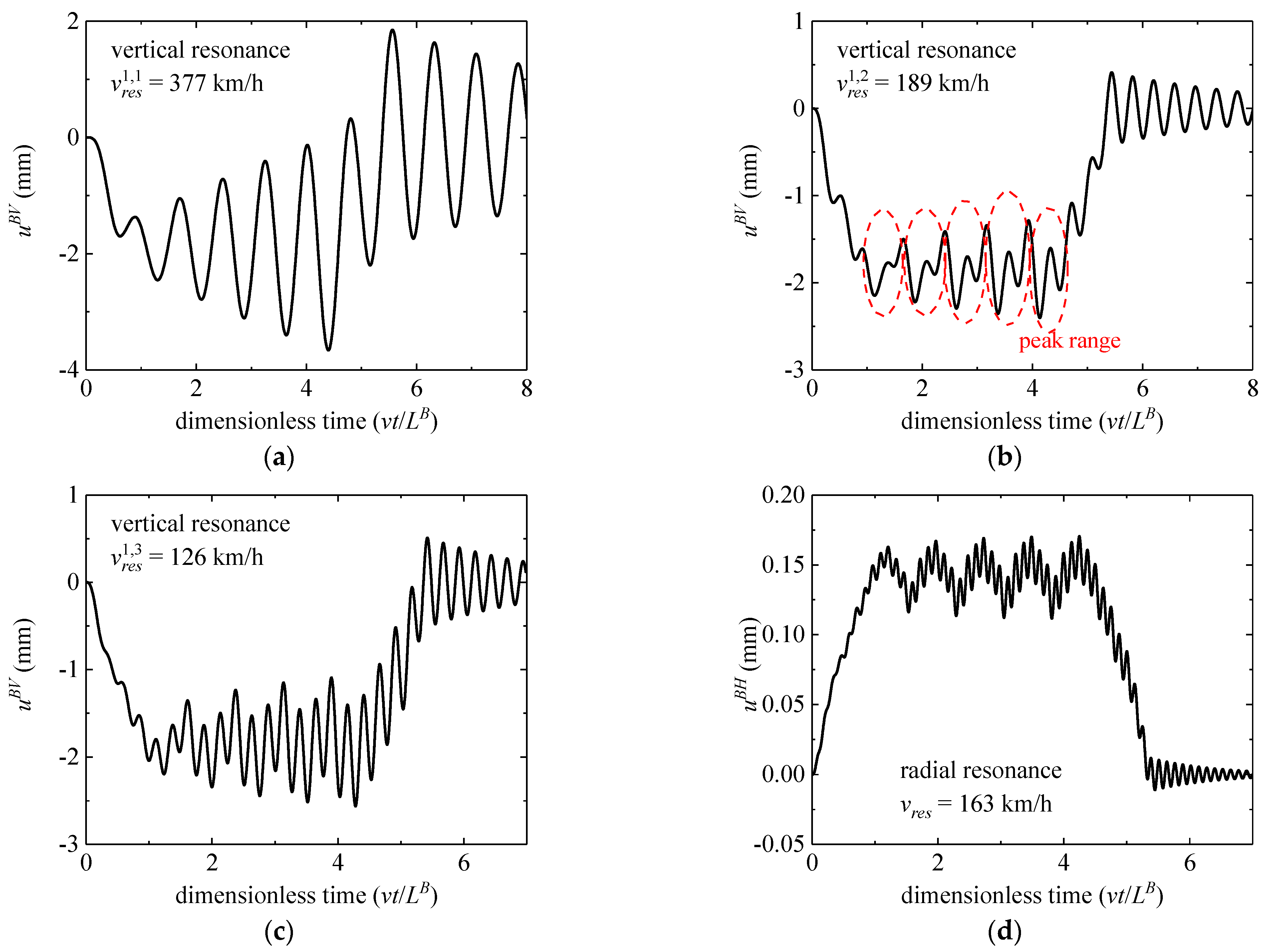
4.3. Time-History Response under Resonance
4.4. Parameter Analysis
5. Conclusions
- (1)
- It is observed that the results from the numerical calculations are consistent with the theoretically computed results. However, there are certain disparities in some instances. There may be some differences.
- (2)
- Under the different resonant speeds, the response curves of bridge mid-span moving force under vehicle load show varying trends. Under the low order resonant speed, the dynamic response trend of the bridge is regular, and the vehicle still has a large range of free vibrations after leaving the bridge. The dynamic response curve of the bridge is rough under high-order resonant velocity.
- (3)
- Both the vertical and radial IFs of the curved intercity rail bridge are not affected by the curve radius.
- (4)
- From the parameter analysis, it is concluded that the reasonable natural vibration characteristics of the bridge can be selected according to different design speeds for structural optimization, which can effectively reduce the dynamic factor of a curved bridge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Y.; Jiang, L.; Zhou, W.; Lai, Z.; Chai, X. An analytical solution to the mapping relationship between bridge structures vertical deformation and rail deformation of high-speed railway. Steel Compos. Struct. 2019, 33, 209–224. [Google Scholar] [CrossRef]
- Feng, Y.; Jiang, L.; Zhou, W.; Chen, M. Post-earthquake track irregularity spectrum of high-speed railways continuous girder bridge. Steel Compos. Struct. 2021, 40, 323–338. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Lai, Z.; Xiang, P.; Chen, Y. Sensitivity and dynamic analysis of train-bridge coupled system with multiple random factors. Eng. Struct. 2020, 221, 111083. [Google Scholar] [CrossRef]
- Liu, X.; Xiang, P.; Jiang, L.; Lai, Z.; Zhou, T.; Chen, Y. Stochastic Analysis of Train–Bridge System Using the Karhunen–Loéve Expansion and the Point Estimate Method. Int. J. Str. Stab. Dyn. 2020, 20, 2050025. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Yang, Y.-B.; Yau, J.-D. Three-Dimensional Analysis of Train-Rail-Bridge Interaction Problems. Veh. Syst. Dyn. 2001, 36, 1–35. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Yang, Y.-B. Steady-state response and riding comfort of trains moving over a series of simply supported bridges. Eng. Struct. 2003, 25, 251–265. [Google Scholar] [CrossRef]
- Zhu, Z.; Gong, W.; Wang, K.; Liu, Y.; Davidson, M.T.; Jiang, L. Dynamic effect of heavy-haul train on seismic response of railway cable-stayed bridge. J. Cent. South. Univ. 2020, 27, 1939–1955. [Google Scholar] [CrossRef]
- Dinh, V.N.; Kim, K.D.; Warnitchai, P. Dynamic analysis of three-dimensional bridge–high-speed train interactions using a wheel–rail contact model. Eng. Struct. 2009, 31, 3090–3106. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Chen, S. Investigation of axle-span ratio and moving load speed affecting bridge extreme response using a moving load amplitude spectrum method. Structures 2020, 28, 2633–2645. [Google Scholar] [CrossRef]
- Xu, L.; Liu, H.; Yu, Z. A coupled model for investigating the interfacial and fatigue damage evolution of slab tracks in vehicle-track interaction. Appl. Math. Model. 2022, 101, 772–790. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Zhao, Y.; Yu, Z.; Wang, K. Modelling of vehicle-track related dynamics: A development of multi-finite-element coupling method and multi-time-step solution method. Veh. Syst. Dyn. 2020. [Google Scholar] [CrossRef]
- Xu, L.; Liu, X. Matrix coupled model for the vehicle–track interaction analysis featured to the railway crossing. Mech. Syst. Signal. Process. 2021, 152, 107485. [Google Scholar] [CrossRef]
- Xu, L.; Yu, Z.; Shan, Z. Numerical simulation for train–track–bridge dynamic interaction considering damage constitutive relation of concrete tracks. Arch. Civ. Mech. Eng. 2021, 21, 116. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Y.; Zhu, Z.; Li, Z.; Liu, H.; Yu, Z. Vehicle-track random vibrations considering spatial frequency coherence of track irregularitives. Veh. Syst. Dyn. 2021. [Google Scholar] [CrossRef]
- Yazdani, M.; Azimi, P. Assessment of railway plain concrete arch bridges subjected to high-speed trains. Structures 2020, 27, 174–193. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Carvalho, H.; Ribeiro, D.; Calçada, R.; Tokunaga, M.; Tanabe, M.; Zhai, W.M. Assessment of train running safety on bridges: A literature review. Eng. Struct. 2021, 241, 112425. [Google Scholar] [CrossRef]
- Zakeri, J.A.; Shadfar, M.; Feizi, M.M. Sensitivity analysis of bridge-track-train system to parameters of railway. Lat. Am. J. Solids Struct. 2014, 11, 598–612. [Google Scholar] [CrossRef] [Green Version]
- Jahangiri, M.; Zakeri, J.-A. Dynamic analysis of train-bridge system under one-way and two-way high-speed train passing. Struct. Eng. Mech. 2017, 64, 33–44. [Google Scholar] [CrossRef]
- Song, L.; Cui, C.; Liu, J.; Yu, Z.; Jiang, L. Corrosion-fatigue life assessment of RC plate girder in heavy-haul railway under combined carbonation and train loads. Int. J. Fatigue 2021, 151, 106368. [Google Scholar] [CrossRef]
- Zeng, Q.; Yang, Y.B.; Dimitrakopoulos, E.G. Dynamic response of high speed vehicles and sustaining curved bridges under conditions of resonance. Eng. Struct. 2016, 114, 61–74. [Google Scholar] [CrossRef]
- Zeng, Q.; Dimitrakopoulos, E.G. Seismic response analysis of an interacting curved bridge-train system under frequent earthquakes: Seismic response analysis of an interacting curved bridge-train system under frequent earthquakes. Earthq. Eng. Struct. Dyn. 2016, 45, 1129–1148. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Yau, J.-D.; Hsu, L.-C. Vibration of simple beams due to trains moving at high speeds. Eng. Struct. 1997, 19, 936–944. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yau, J.D. Resonance of high-speed trains moving over a series of simple or continuous beams with non-ballasted tracks. Eng. Struct. 2017, 143, 295–305. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yau, J.D. Vertical and pitching resonance of train cars moving over a series of simple beams. J. Sound Vib. 2015, 337, 135–149. [Google Scholar] [CrossRef]
- Xia, H.; Li, H.L.; Guo, W.W.; De Roeck, G. Vibration Resonance and Cancellation of Simply Supported Bridges under Moving Train Loads. J. Eng. Mech. 2014, 140, 04014015. [Google Scholar] [CrossRef] [Green Version]
- Xin, L.; Li, X.; Zhang, J.; Zhu, Y.; Xiao, L. Resonance Analysis of Train–Track–Bridge Interaction Systems with Correlated Uncertainties. Int. J. Str. Stab. Dyn. 2020, 20, 2050008. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, L.; Zhou, W.; Liu, S.; Liu, X.; Wu, L.; Zhou, T.; Shao, G. Study of resonance condition of railway bridge subjected to train loads with a four-beam system. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Dimitrakopoulos, E.G.; Zeng, Q. A three-dimensional dynamic analysis scheme for the interaction between trains and curved railway bridges. Comput. Struct. 2015, 149, 43–60. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Wu, C.-M.; Yau, J.-D. Dynamic response of a horizontally curved beam subjected to vertical and horizontal moving loads. J. Sound Vib. 2001, 242, 519–537. [Google Scholar] [CrossRef]
- Wang, Z.L.; Xu, Y.L.; Li, G.Q.; Chen, S.W.; Zhang, X.L. Dynamic analysis of a coupled system of high-speed maglev train and curved viaduct. Int. J. Str. Stab. Dyn. 2018, 18, 1850143. [Google Scholar] [CrossRef]
- Yang, Y.; Mace, B.R.; Kingan, M.J. Vibroacoustic analysis of periodic structures using a wave and finite element method. J. Sound Vib. 2019, 457, 333–353. [Google Scholar] [CrossRef]
- Yang, Y.; Mace, B.R.; Kingan, M.J. Prediction of sound transmission through, and radiation from, panels using a wave and finite element method. J. Acoust. Soc. Am. 2017, 141, 2452–2460. [Google Scholar] [CrossRef] [PubMed]
- Cook, R. Concepts and Applications of Finite Element Analysis; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Liu, X.; Jiang, L.; Xiang, P.; Lai, Z.; Liu, L.; Cao, S.; Zhou, W. Probability analysis of train-bridge coupled system considering track irregularities and parameter uncertainty. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Cheng, Y.-C.; Chen, C.-H.; Hsu, C.-T. Derailment and Dynamic Analysis of Tilting Railway Vehicles Moving Over Irregular Tracks Under Environment Forces. Int. J. Str. Stab. Dyn. 2017, 17, 1750098. [Google Scholar] [CrossRef]
- Muñoz, S.; Aceituno, J.F.; Urda, P.; Escalona, J.L. Multibody model of railway vehicles with weakly coupled vertical and lateral dynamics. Mech. Syst. Signal. Process. 2019, 115, 570–592. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Xiang, P.; Lai, Z.; Feng, Y.; Cao, S. Dynamic response limit of high-speed railway bridge under earthquake considering running safety performance of train. J. Cent. South. Univ. 2021, 28, 968–980. [Google Scholar] [CrossRef]
- Lai, Z.; Jiang, L.; Zhou, W.; Yu, J.; Zhang, Y.; Liu, X.; Zhou, W. Lateral girder displacement effect on the safety and comfortability of the high-speed rail train operation. Veh. Syst. Dyn. 2021. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, L.; Li, C.; Liu, X.; Li, J. An efficent computing strategy based on the unconditionally stable explicit algorithm for the nonlinear train-track-bridge system under an earthquake. Soil Dyn. Earthq. Eng. 2021, 145, 106718. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Xiang, P.; Jiang, L.; Lai, Z. Safety and comfort assessment of a train passing over an earthquake-damaged bridge based on a probability model. Struct. Infrastruct. Eng. 2021. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Yao, Z.; Wu, Y.S. Vehicle-Bridge Interaction Dynamics: With Applications to High-Speed Railways; World Scientific: River Edge, NJ, USA, 2004; ISBN 978-981-238-847-6. [Google Scholar]




| Parameter | Value | Unit |
|---|---|---|
| Elastic modulus | 3.45 × 1010 | Pa |
| Sectional area | 3.6552 | m2 |
| Poisson’s ratio | 0.2 | - |
| Iy | 1.3514 | m4 |
| Iz | 9.1108 | m4 |
| Density | 2.65 × 103 | kg/m3 |
| Damping ratio | 2% | - |
| Span length | 30 and 25 | m |
| Curve radius | 400 | m |
| Span Length | Order of Vibration | Frequency/Hz | Mode |
|---|---|---|---|
| 30 m | First | 3.83 | Vertical bending |
| Second | 9.95 | Transverse bending | |
| Third | 15.324 | Vertical bending | |
| Fourth | 39.789 | Transverse bending | |
| 25 m | First | 5.52 | Vertical bending |
| Second | 14.32 | Transverse bending | |
| Third | 22.066 | Vertical bending | |
| Fourth | 57.297 | Transverse bending |
| Parameter | Symbol | Unit | Value | Parameter | Symbol | Unit | Value |
|---|---|---|---|---|---|---|---|
| Mass of wheel | mw | kg | 1420 | Lateral stiffness of primary suspension | kyp | N/m | 10.4 × 106 |
| Mass of bogie | mt | kg | 2550 | vertical stiffness of Secondary suspension | kzs | N/m | 1.7 × 106 |
| Mass of car body | mc | kg | 21,920 | Lateral stiffness of secondary suspension | kys | N/m | 10.4 × 106 |
| Roll mass moment of car body | Icx | kg·m2 | 14,890 | Vertical damping of primary suspension | czp | N·s/m | 1.7 × 106 |
| Pitch mass moment of car body | Icy | kg·m2 | 617,310 | Lateral damping of primary suspension | cyp | N·s/m | 10.4 × 106 |
| Yaw mass moment of car body | Icz | kg·m2 | 617,310 | Vertical damping of secondary suspension | czs | N·s/m | 1.7 × 106 |
| Roll mass moment of bogie | Itx | kg·m2 | 1050 | Lateral damping of secondary suspension | cys | N·s/m | 10.4 × 106 |
| Pitch mass moment of bogie | Ity | kg·m2 | 1750 | Length of carriage | dv | m | 19 |
| Yaw mass moment of bogie | Itz | kg·m2 | 1980 | Distance between wheelset of one bogie | L1 | m | 2.2 |
| Vertical stiffness of primary suspension | kzp | N/m | 1.7 × 106 | Distance between bogie of one carriage | L2 | m | 12.5 |
| Note | i = 1 | i = 2 | i = 3 | i = 4 | |
|---|---|---|---|---|---|
| n = 1 | First order of vertical vibration | 262 km/h | 131 km/h | 87 km/h | 65 km/h |
| n = 2 | First order of transverse vibration | 680 km/h | 340 km/h | 227 km/h | 170 km/h |
| n = 3 | Second order of vertical vibration | 1048 km/h | 524 km/h | 349 km/h | 262 km/h |
| n = 4 | Second order of transverse vibration | 2357 km/h | 1179 km/h | 786 km/h | 589 km/h |
| Note | i = 1 | i = 2 | i = 3 | i = 4 | |
|---|---|---|---|---|---|
| n = 1 | First order of vertical vibration | 377 km/h | 189 km/h | 126 km/h | 94 km/h |
| n = 2 | First order of transverse vibration | 979 km/h | 490 km/h | 326 km/h | 245 km/h |
| n = 3 | Second order of vertical vibration | 1509 km/h | 754 km/h | 503 km/h | 377 km/h |
| n = 4 | Second order of transverse vibration | 3394 km/h | 1697 km/h | 1131 km/h | 849 km/h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Cui, C.; Liu, X.; Wang, M. Dynamic Impact Factor and Resonance Analysis of Curved Intercity Railway Viaduct. Appl. Sci. 2022, 12, 2978. https://doi.org/10.3390/app12062978
Wang J, Cui C, Liu X, Wang M. Dynamic Impact Factor and Resonance Analysis of Curved Intercity Railway Viaduct. Applied Sciences. 2022; 12(6):2978. https://doi.org/10.3390/app12062978
Chicago/Turabian StyleWang, Jun, Chenxing Cui, Xiang Liu, and Mingjie Wang. 2022. "Dynamic Impact Factor and Resonance Analysis of Curved Intercity Railway Viaduct" Applied Sciences 12, no. 6: 2978. https://doi.org/10.3390/app12062978
APA StyleWang, J., Cui, C., Liu, X., & Wang, M. (2022). Dynamic Impact Factor and Resonance Analysis of Curved Intercity Railway Viaduct. Applied Sciences, 12(6), 2978. https://doi.org/10.3390/app12062978






