Development of Automatic Crack Growth Simulation Program Based on Finite Element Analysis
Abstract
:Featured Application
Abstract
1. Introduction
2. Development of AI-FEM
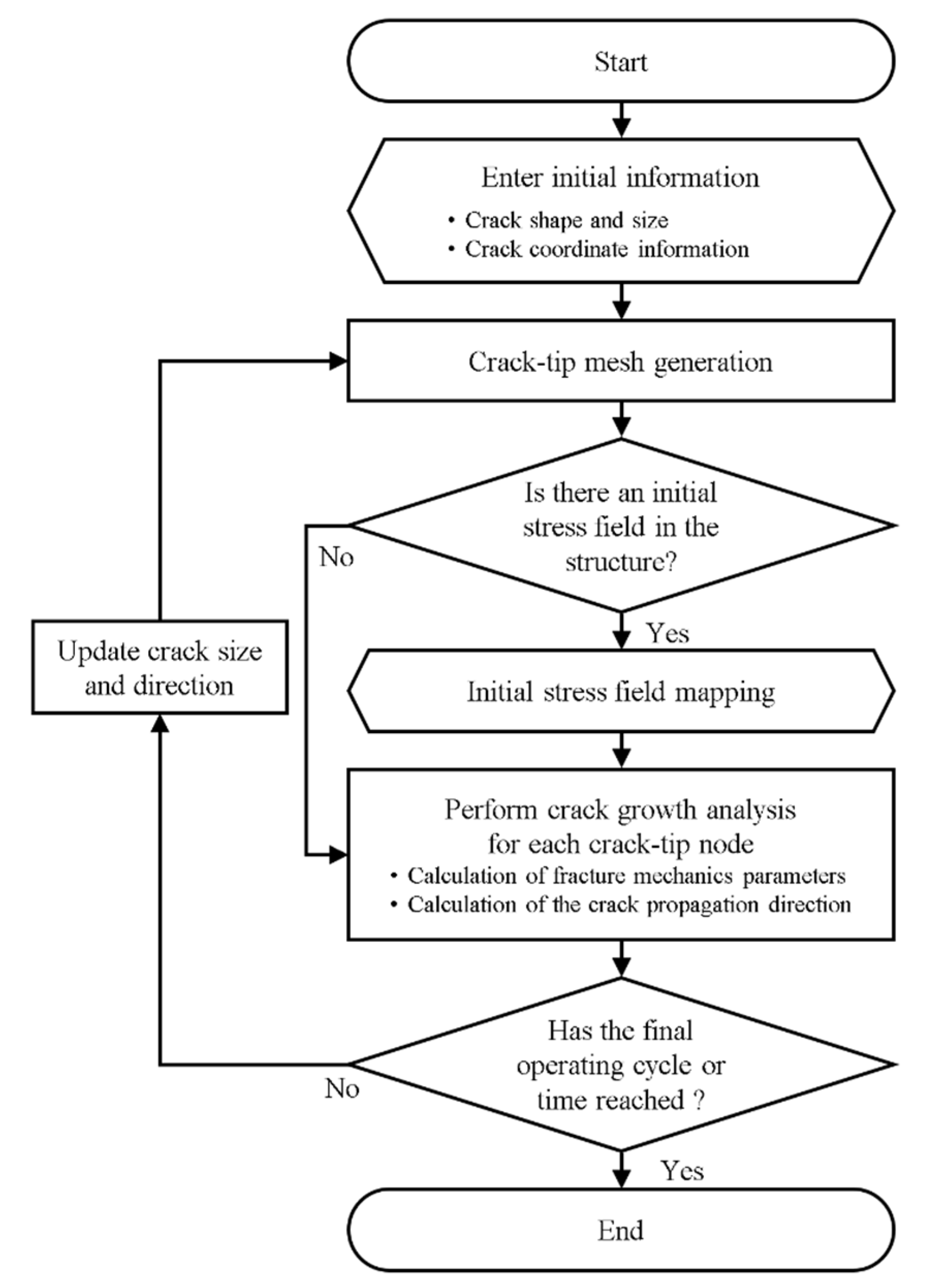
2.1. The Overall Procedures of AI-FEM
2.2. Crack Tip Meshing Criteria
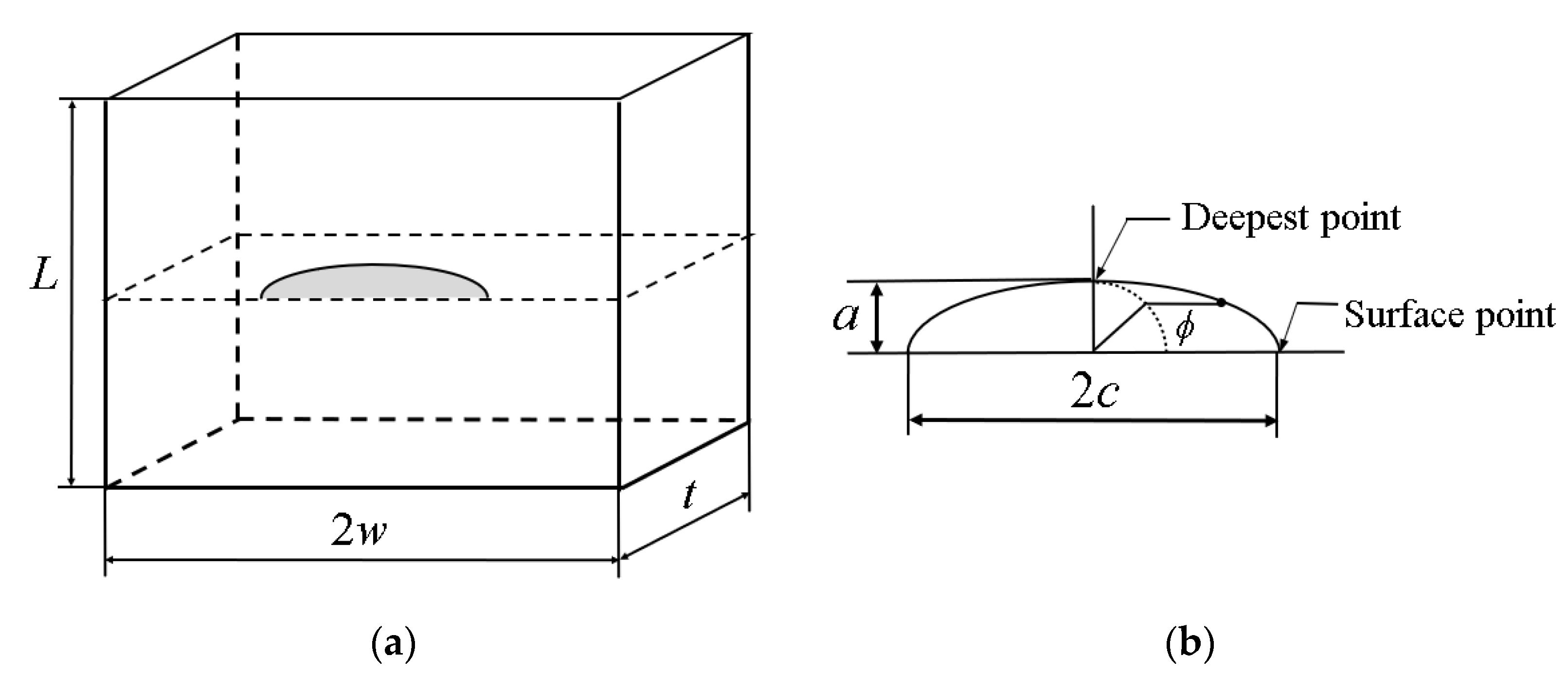
2.2.1. Geometry and Materials
2.2.2. FE Model
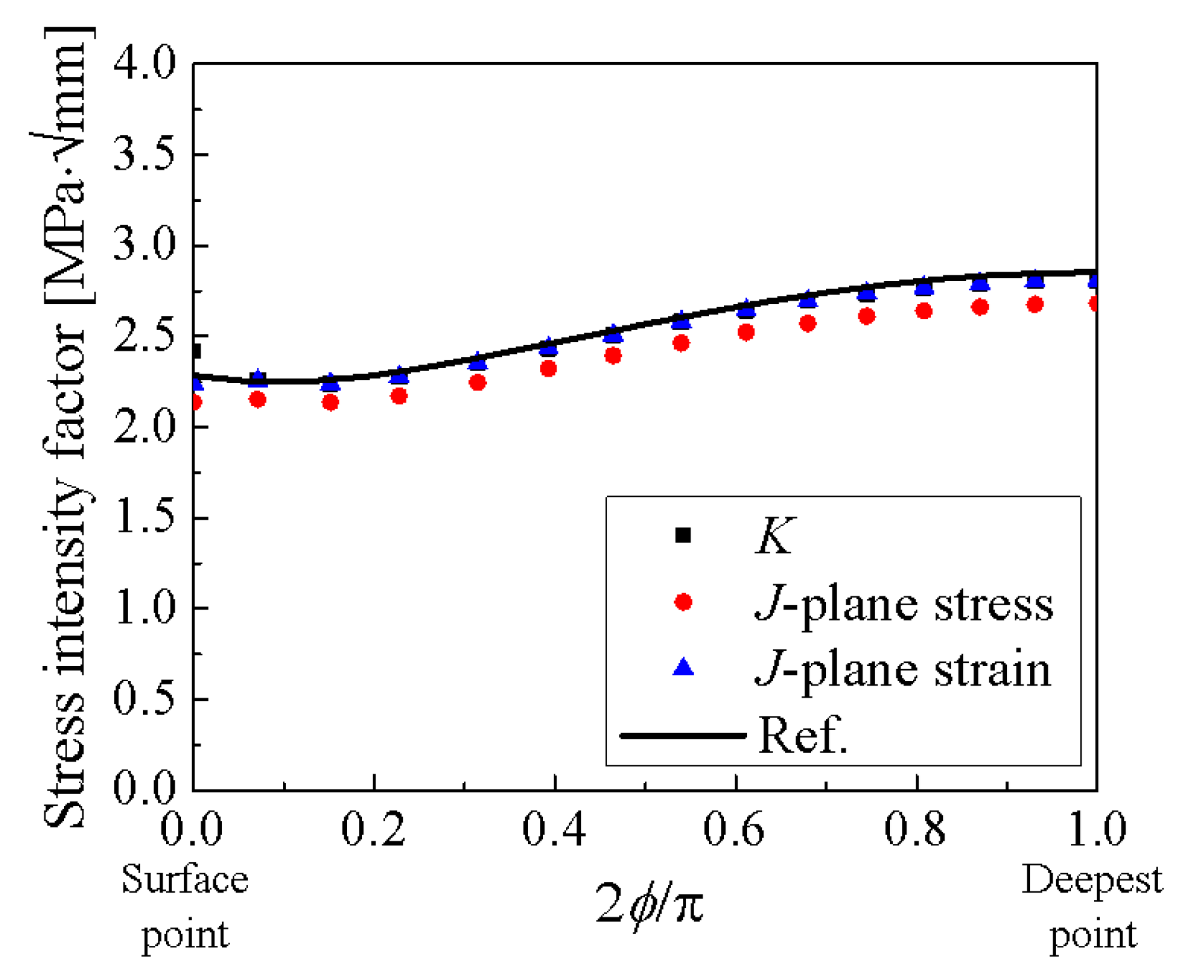
2.2.3. The Effect of the SIF Calculation Method
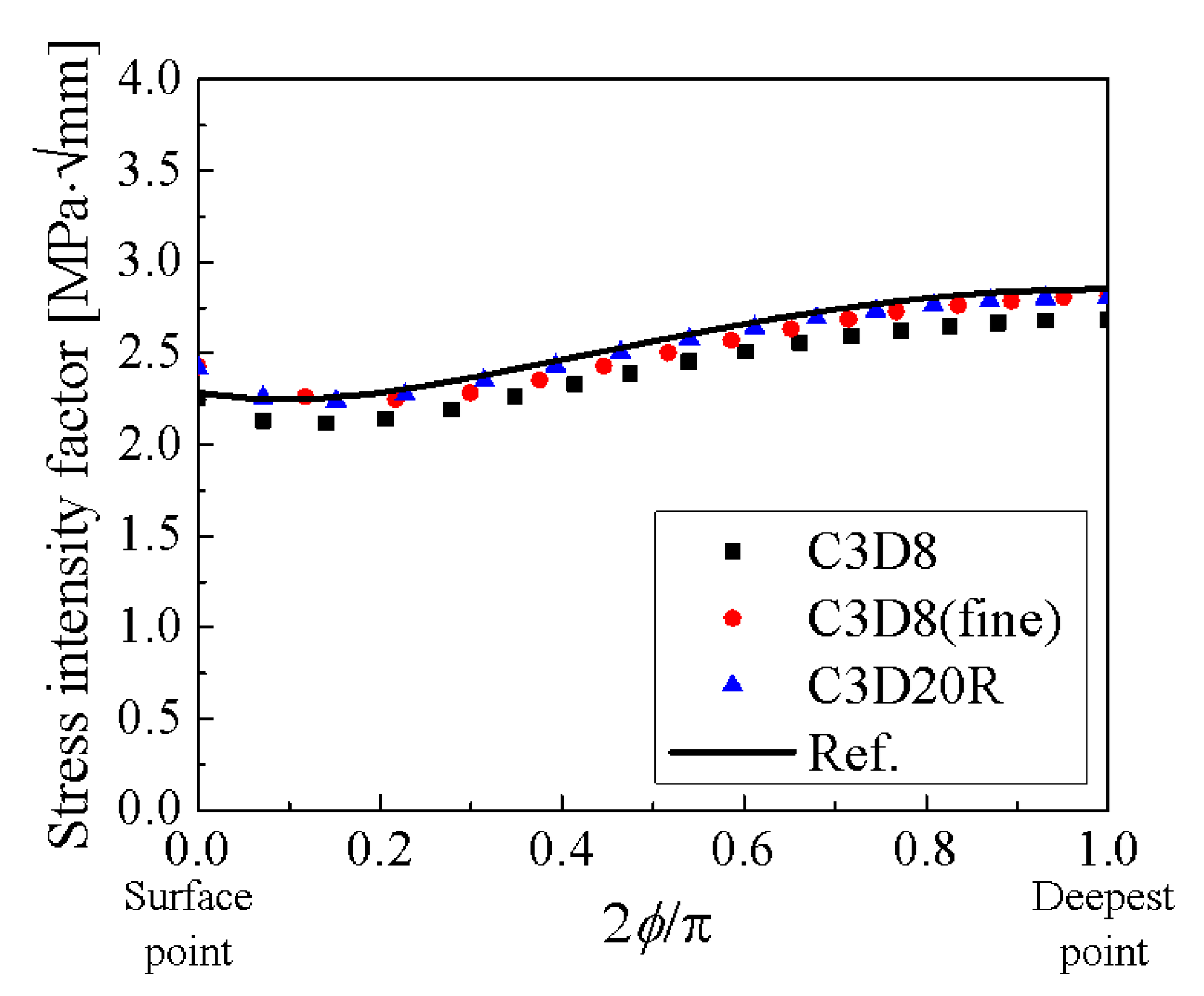
2.2.4. The Effect of Element Type
2.2.5. The Effect of Crack Tip Element Characteristic
2.2.6. The Effect of Shape Variables of Crack Tip Mesh
3. Detailed Function of AI-FEM
3.1. Overview of the Program
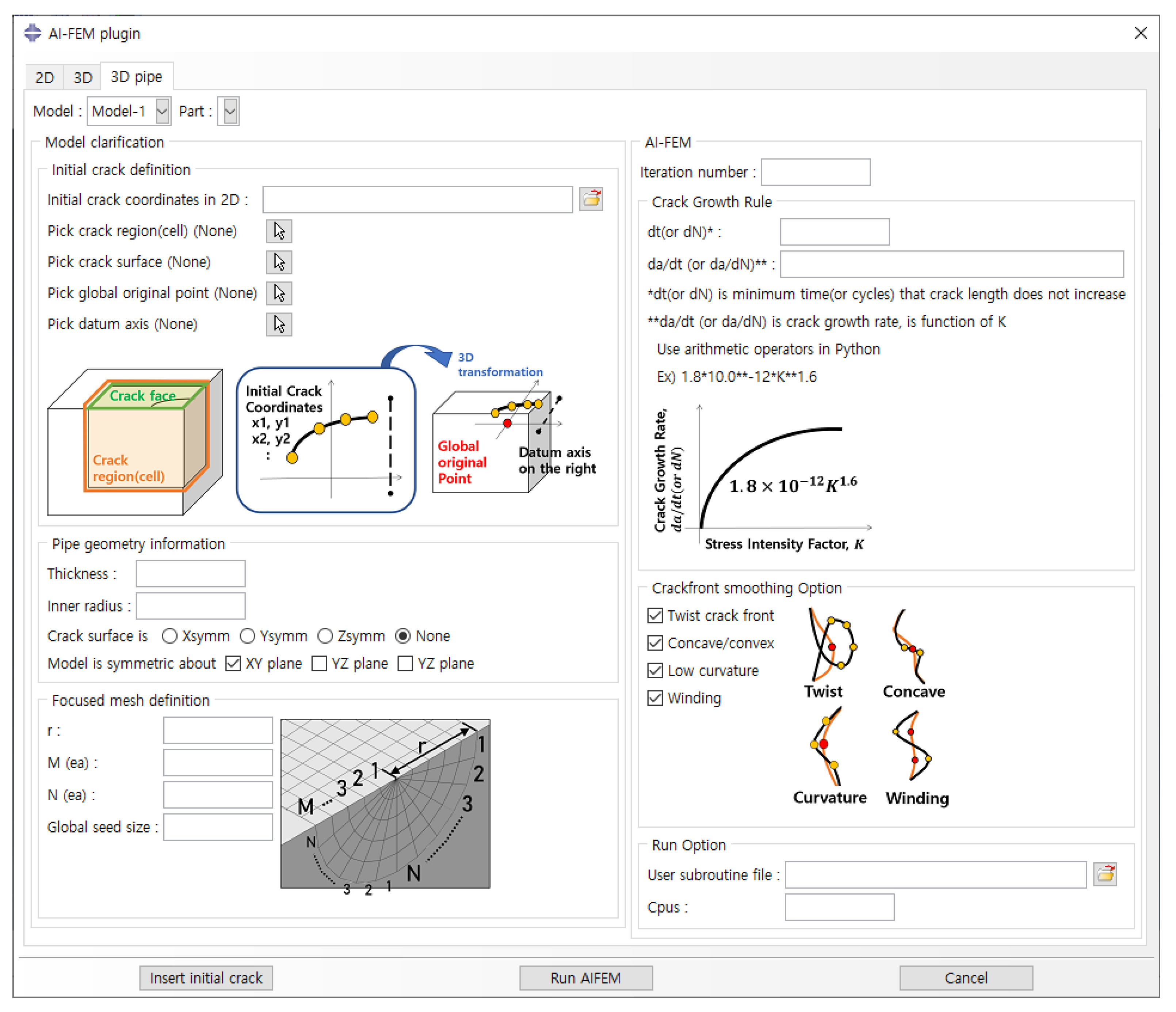
3.2. Defining the Structure and Crack Geometry
3.3. Defining the Crack Growth Characteristics
- Twist crack front: If crack propagation is large at a specific region in one cycle, normal directions at adjacent nodes may cross each other, which may cause twisting of the crack tip. This option helps to smooth the mesh of the crack tip by creating one node at the average point of the twisted node coordinates.
- Concave/convex: When the curvature between the nodes forming the crack tip is small, the two nodes are integrated to make the crack tip smooth.
- Low curvature: When nodes are concentrated in one area, the average point of the nodes within a certain distance is calculated and then combined into one node.
- Winding: If the curvature of the crack tip is repeated in an S-shape, the angle between the two points is relaxed.
4. Verification of AI-FEM
4.1. Comparison of SCC Growth with the ASME Method
4.1.1. Geometry
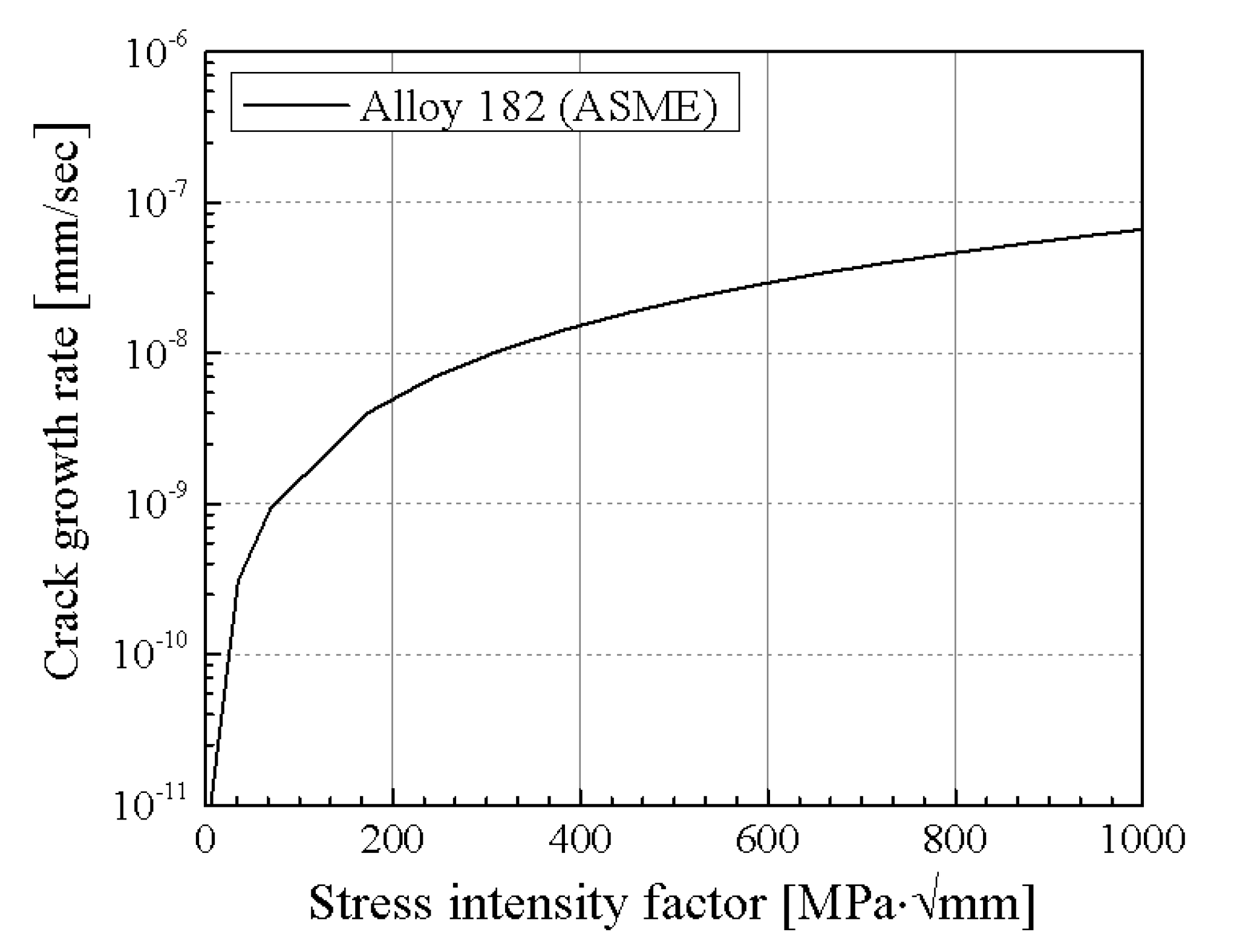
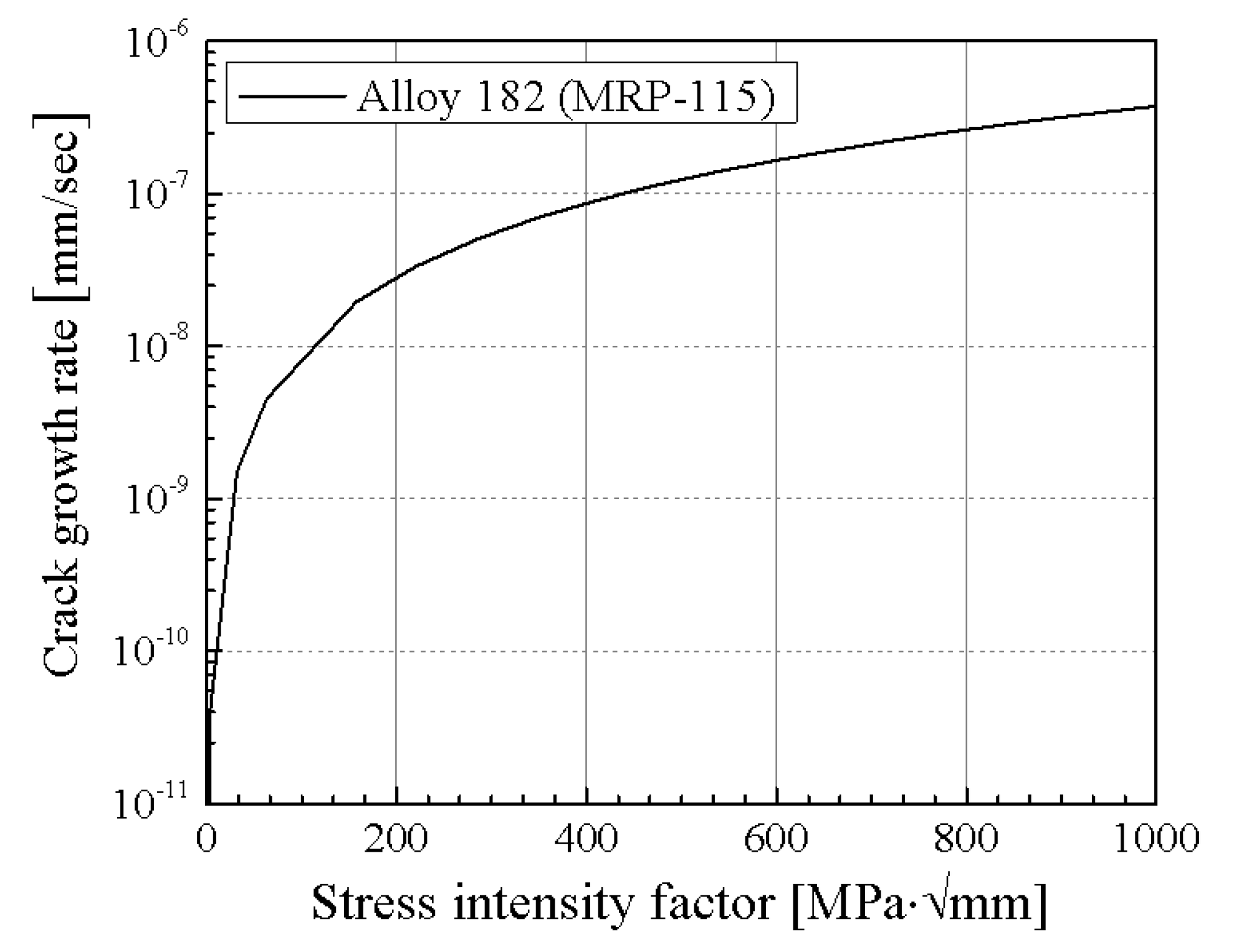
4.1.2. SCC Growth Law
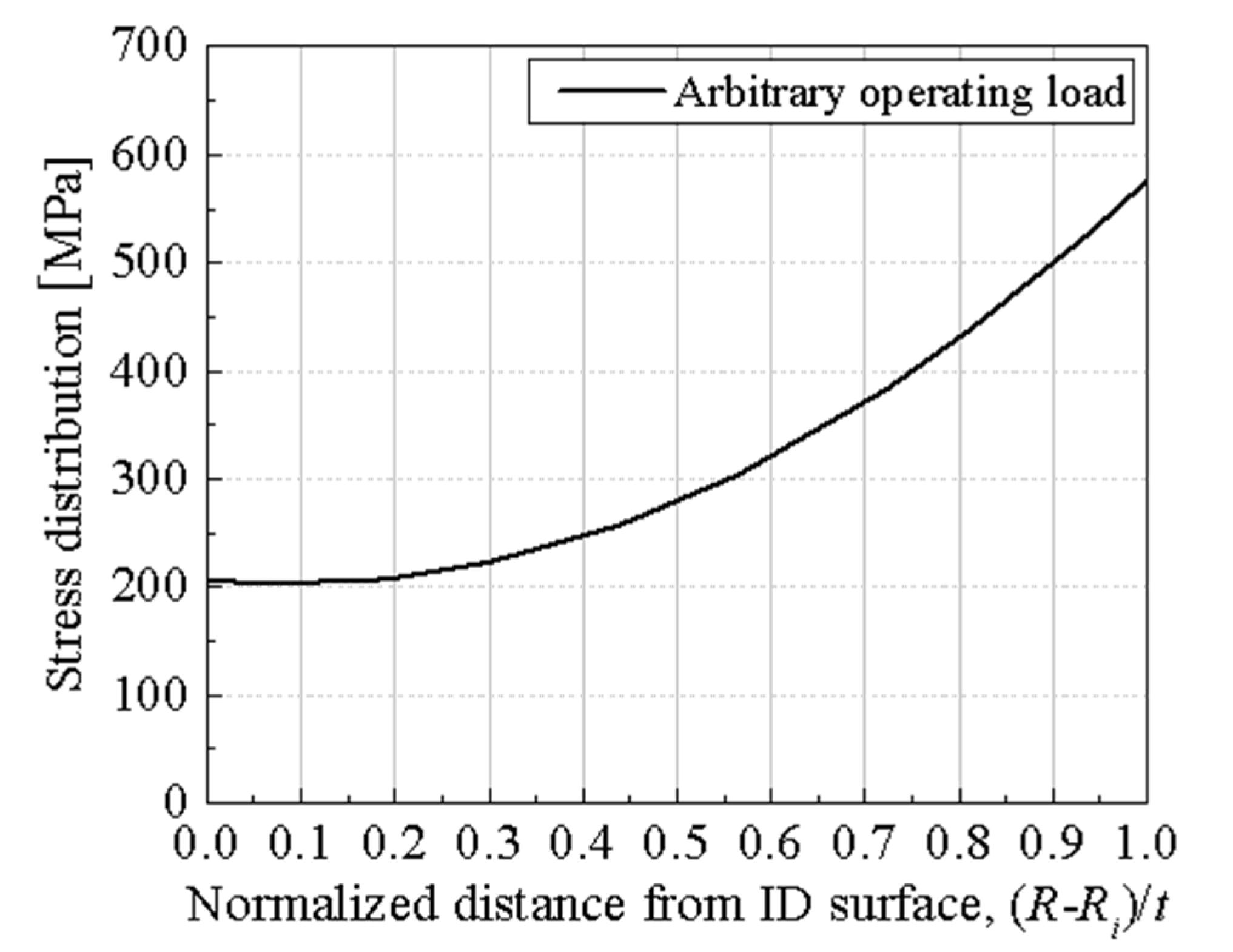
4.1.3. Loading Conditions
4.1.4. SCC Growth Calculation Using ASME Code, Sec. XI
- Obtain the stress distribution in the pipe thickness direction by performing the thermal-structural coupling analysis of cracked pipe. This stress result is curve-fitted using the stress distribution formula of Equation (3) presented in ASME code, Sec. XI, App. A, A-3000.
- Calculate the SIF using the SIF formula of Equations (4) and (5) presented in ASME code, Sec. XI, App. A, A-3411 by applying the stress distribution formula.
- Calculate the crack growth rate for the corresponding SIF using the SCC growth rate calculation formula presented in ASME code, Sec. XI, App. C. When using this formula, if the crack growth cycle is defined largely, the SIF may change rapidly, and the crack growth rate may not be calculated accurately. Therefore, the crack growth cycle should be defined short enough in consideration of accuracy. (In this study, it was set to 100 h.)
- The crack size is updated by adding the calculated crack growth amount to the crack of the previous cycle.
- By repeating the above process until the load reaches the final cycle, the final crack size can be calculated.
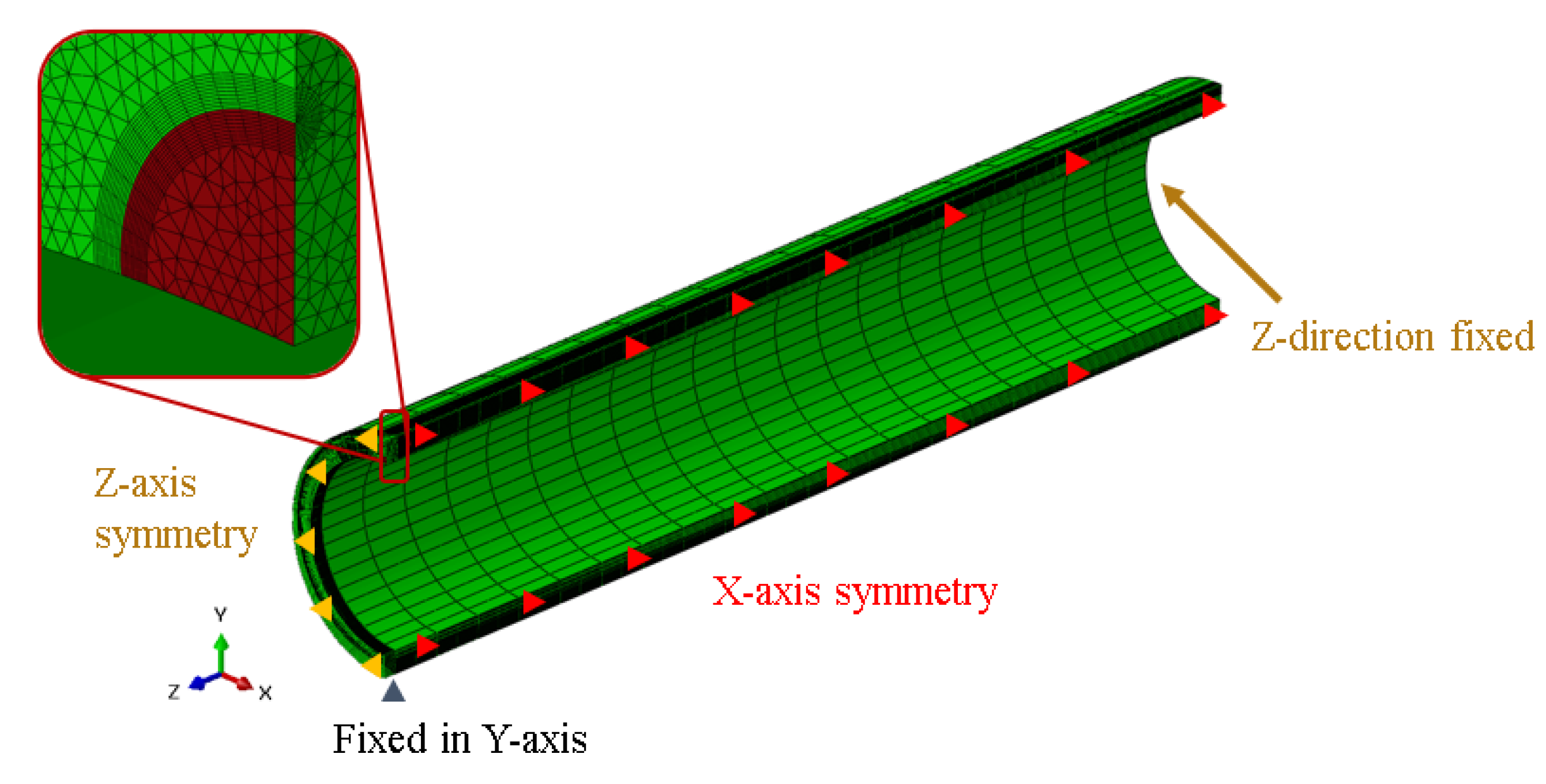
4.1.5. FE Model
4.1.6. Results
4.2. Comparison of Natural Crack Growth with AFEA Method including Cracking Transition
4.2.1. Cracking Transition Method
4.2.2. Geometry
4.2.3. SCC Growth Law
4.2.4. FE Model and Loading Conditions
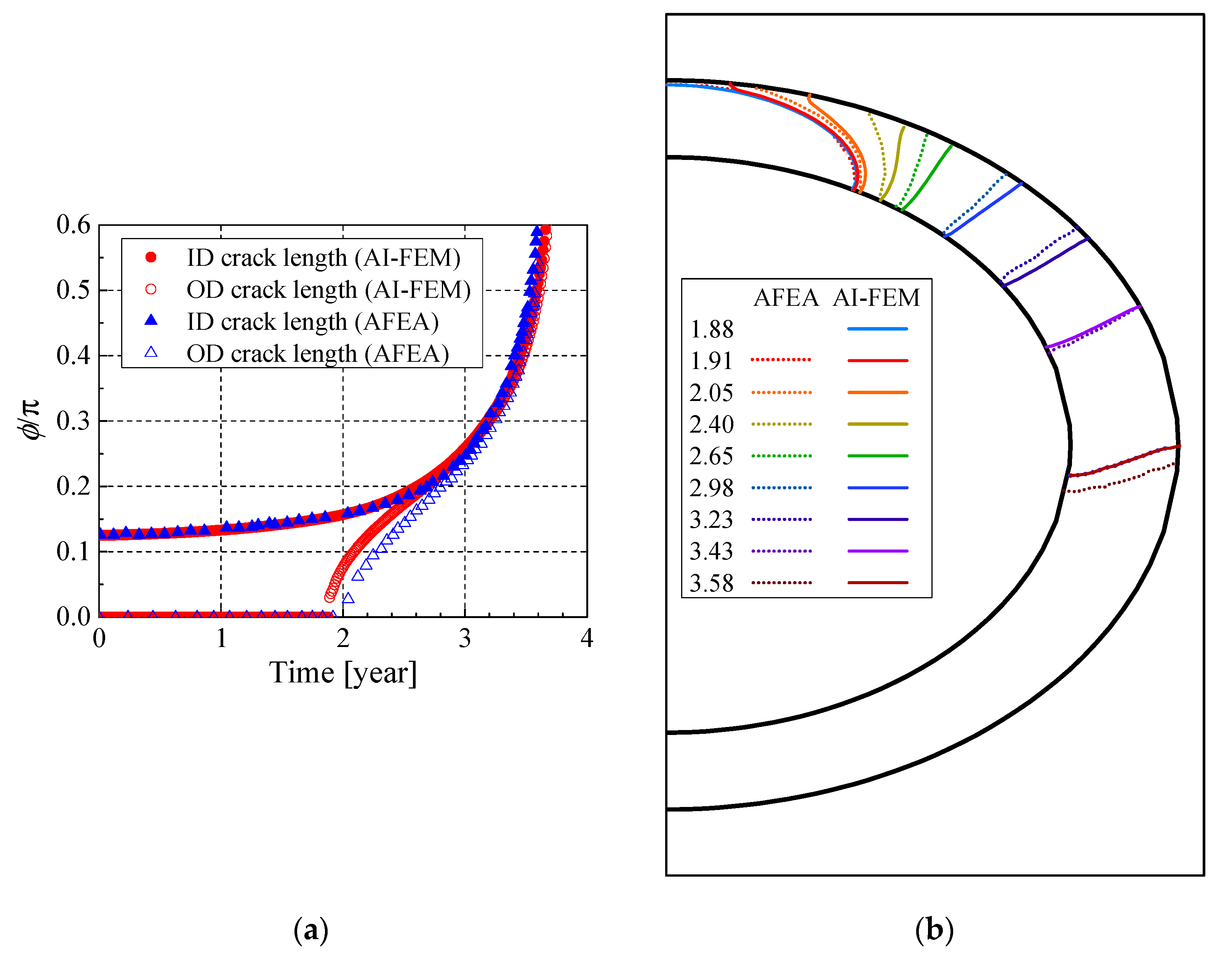
4.2.5. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Terachi, T.; Yamada, T.; Miyamoto, T.; Arioka, K. SCC growth behaviors of austenitic stainless steels in simulated PWR primary water. J. Nucl. Mater. 2012, 426, 59–70. [Google Scholar] [CrossRef]
- Sullivan, E.J.; Anderson, M.T. Assessment of Weld Overlays for Mitigating Primary Water Stress Corrosion Cracking at Nickel Alloy Butt Welds in Piping Systems Approved for Leak-before-Break; No. PNNL-21660; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2012. [Google Scholar]
- King, C.; Frederick, G. Technical Basis for Preemptive Weld Overlays for Alloy 82/182 Butt Welds in PWRs (MRP-169); EPRI Topical Report; Electric Power Research Institute: Palo Alto, CA, USA, 2005; p. 1012843. [Google Scholar]
- Kamaya, M. Growth evaluation of multiple interacting surface cracks. Part I: Experiments and simulation of coalesced crack. Eng. Fract. Mech. 2008, 75, 1336–1349. [Google Scholar] [CrossRef]
- White, G.; Broussard, J.; Collin, J.; Klug, M.; Harrington, C.; DeBoo, G. Advanced FEA modeling of PWSCC crack growth in PWR dissimilar metal piping butt welds and application to the industry inspection and mitigation program. In Proceedings of the ASME Pressure Vessels and Piping Conference, Chicago, IL, USA, 27–31 July 2008; Volume 48296. [Google Scholar]
- Chen, X.; Chen, X.; Chan, A.; Cheng, Y.; Wang, H. A FDEM parametric investigation on the impact fracture of monolithic glass. Buildings 2022, 12, 271. [Google Scholar] [CrossRef]
- Chen, X.; Luo, T.; Ooi, E.T.; Ooi, E.H.; Song, C. A quadtree-polygon-based scaled boundary finite element method for crack propagation modeling in functionally graded materials. Theor. Appl. Fract. Mech. 2018, 94, 120–133. [Google Scholar] [CrossRef]
- Chen, X.; Chan, A.H. Modelling impact fracture and fragmentation of laminated glass using the combined finite-discrete element method. Int. J. Impact Eng. 2018, 112, 15–29. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yvonnet, J.; Zhu, Q.Z.; Bornert, M.; Chateau, C. A phase-field method for computational modeling of interfacial damage interacting with crack propagation in realistic microstructures obtained by microtomography. Comput. Meth. Appl. Mech. Eng. 2016, 312, 567–595. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, S.; Mianroodi, J.R.; Brepols, T.; Reese, S. Direction-dependent fracture in solids: Atomistically calibrated phase-field and cohesive zone model. J. Mech. Phys. Solids. 2021, 147, 104253. [Google Scholar] [CrossRef]
- Rezaei, S.; Harandi, A.; Brepols, T.; Reese, S. An anisotropic cohesive fracture model: Advantages and limitations of length-scale insensitive phase-field damage models. Eng. Fract. Mech. 2022, 261, 108177. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Z.; Wang, T.; Zeng, Q.; Li, X.; Zhuang, Z. XFEM modeling for curved fracture in the anisotropic fracture toughness medium. Comput. Mech. 2019, 63, 869–883. [Google Scholar] [CrossRef]
- Hou, J.; Goldstraw, M.; Maan, S.; Knop, M. An Evaluation of 3D Crack Growth Using ZENCRACK. ACK. Defense Science and Technology Organization; Report Number: DSTO-TR-1158; Department of Defence: Melbourne, Australia, 2001. [Google Scholar]
- Rudland, D.L.; Shim, D.J.; Zhang, T.; Wilkowski, G. Implications of Wolf Creek Indications—Final Report, Program Final Report to the NRC; ADAMS File Number ML072470394; Engineering Mechanics Corporation of Columbus: Columbus, OH, USA, 2007. [Google Scholar]
- Shim, D.J.; Rudland, D.; Harris, D. Modeling of subcritical crack growth due to stress corrosion cracking: Transition from surface crack to through-wall crack. In Proceedings of the 2011 ASME Pressure Vessels and Piping Conference, Baltimore, MD, USA, 17–21 July 2011; Volume 44564. [Google Scholar]
- Nakamura, H.; Tajima, S.; Hazama, O.; Gu, W. Automated fracture mechanics and fatigue analyses based on three-dimensional finite element for welding components. In Proceedings of the ASME 2014 Pressure Vessels and Piping Conference, Anaheim, CA, USA, 20–24 July 2014; Volume 45998. [Google Scholar]
- Nakamura, H.; Matsushima, E.; Okamoto, A.; Umemoto, T. Fatigue crack growth under residual stress field in low-carbon steel. Nucl. Eng. Des. 1986, 94, 241–247. [Google Scholar] [CrossRef]
- Ogawa, T.; Itatani, M.; Hayashi, T.; Saito, T. SCC growth prediction for surface crack in welded joint using advanced FEA. In Proceedings of the 2020 ASME Pressure Vessels and Piping Conference, Virtual, 3 August 2020; Volume 83860. [Google Scholar]
- Materials Reliability Program: Advanced FEA Evaluation of Growth of Postulated Circumferential PWSCC Flaws in Pressurizer Nozzle Dissimilar Metal Welds; MRP-216, Rev. 1; EPRI: Palo Alto, CA, USA, 2007.
- Dassault Systemes Corp. ABAQUS/Standard User’s Manuals; Ver. 2020; Dassault Systèmes SE: Vélizy-Villacoublay, France, 2020. [Google Scholar]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Raju, I.S.; Newman, J.C. Stress-intensity factors for a wide lange of semi-elliptical surface cracks in finite-thickness plates. Eng. Fract. Mech. 1979, 11, 817–829. [Google Scholar] [CrossRef]
- Shim, D.J.; Kurth, R.; Rudland, D. Development of non-idealized surface to through-wall crack transition model. In Proceedings of the 2013 ASME Pressure Vessels and Piping Conference, Paris, France, 14–18 July 2013; Volume 55706. [Google Scholar]
- Materials Reliability Program: Crack Growth Rates for Evaluating Primary Water Stress Corrosion Cracking (PWSCC) of Alloy 82, 182, and 132 Welds; EPRI: Palo Alto, CA, USA, 2004.

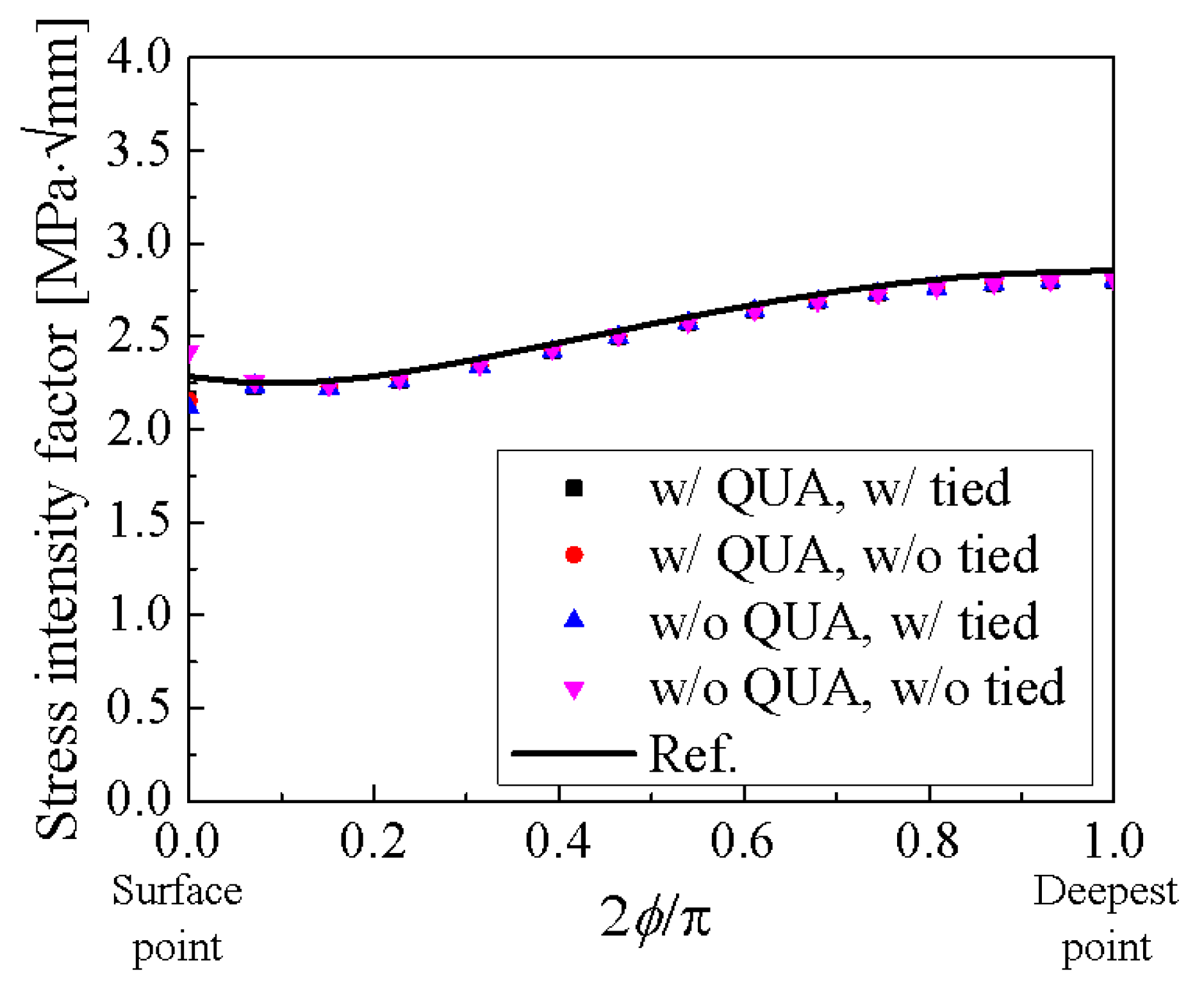
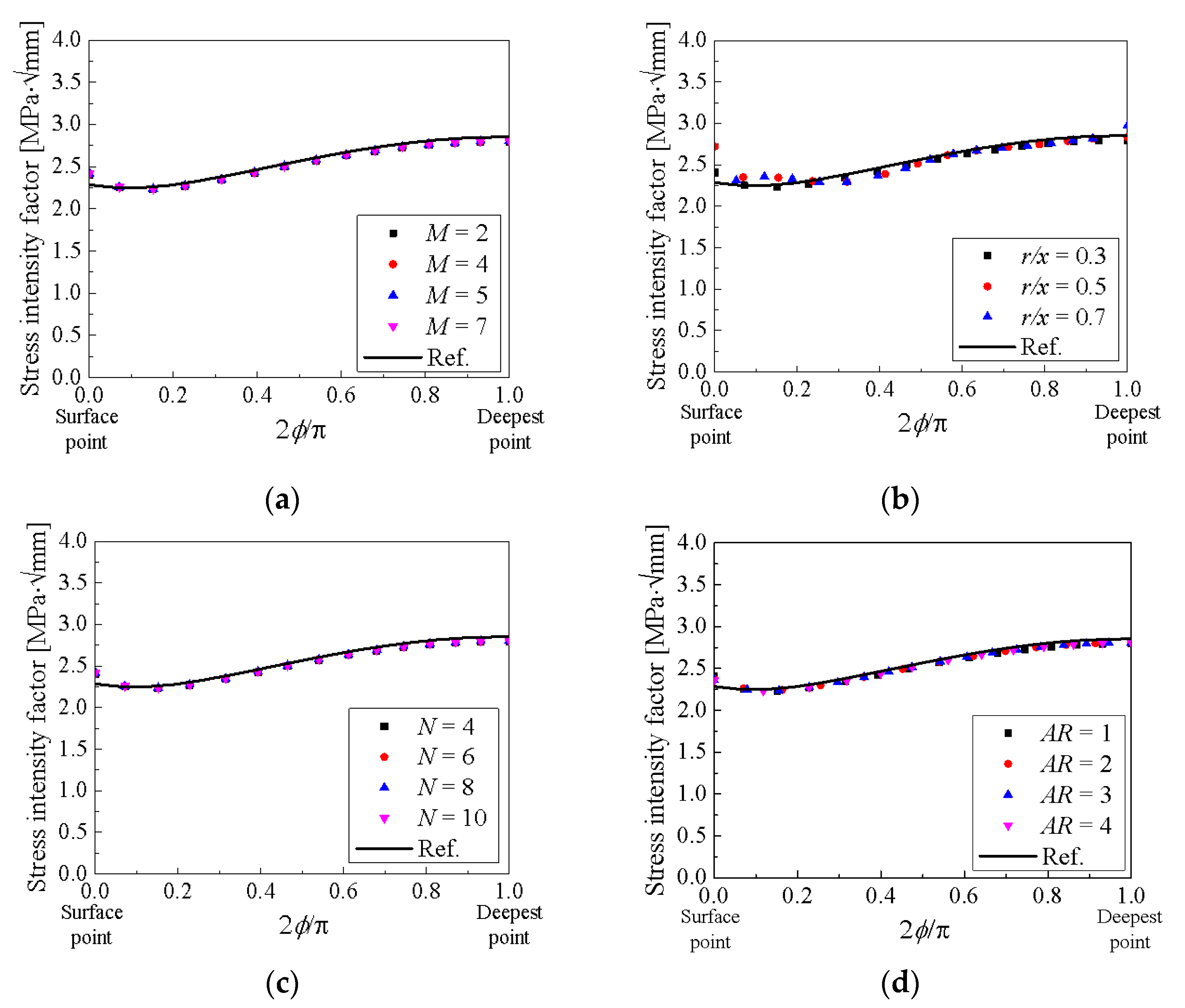


| w/t | a/t | a/c |
|---|---|---|
| 3.15 | 0.3 | 0.5 |
| M | r/x | N | AR |
|---|---|---|---|
| 2, 4, 5, 7 | 0.3, 0.5, 0.7 | 4, 6, 8, 10 | 1, 2, 3, 4 |
| M | r/x | N | AR |
|---|---|---|---|
| 5 | 0.3 | 6 | 1 |
| M | r/x | N | AR |
|---|---|---|---|
| 5 | 0.3 | 8 | 1 |
| a/t | a/c | |
|---|---|---|
| Case 1 | 0.3 | 1 |
| Case 2 | 1/2 | |
| Case 3 | 1/3 | |
| Case 4 | 0.5 | 1 |
| Case 5 | 1/2 | |
| Case 6 | 1/3 | |
| Case 7 | 0.6 | 1 |
| KIth | ø | η | ||||
|---|---|---|---|---|---|---|
| 0 | 31 | 1.103 × 10−3 | 1076.7 | 1009.67 | 0 | 1.6 |
| Initial | ASME (1.5 yr) | AI-FEM (1.5 yr) | Difference | ||
|---|---|---|---|---|---|
| Case 1 | a [mm] | 25.15 | 30.48 | 30.23 | 0.82% |
| l [mm] | 50.55 | 62.74 | 60.45 | 3.64% | |
| Case 2 | a [mm] | 25.15 | 33.78 | 33.53 | 0.74% |
| l [mm] | 101.09 | 113.28 | 112.27 | 0.89% | |
| Case 3 | a [mm] | 25.15 | 35.81 | 35.31 | 1.40% |
| l [mm] | 151.38 | 162.31 | 161.54 | 0.47% | |
| Case 4 | a [mm] | 42.16 | 53.34 | 52.58 | 1.42% |
| l [mm] | 84.07 | 105.41 | 102.87 | 2.41% | |
| Case 5 | a [mm] | 42.16 | 61.21 | 60.20 | 1.65% |
| l [mm] | 168.40 | 191.77 | 189.23 | 1.32% | |
| Case 6 | a [mm] | 42.164 | 68.33 | 66.29 | 2.99% |
| l [mm] | 252.48 | 275.08 | 271.02 | 1.48% | |
| Case 7 | a [mm] | 50.55 | 67.31 | 65.53 | 2.64% |
| l [mm] | 101.09 | 128.27 | 123.19 | 3.96% | |
| Internal Pressure [MPa] | Axial Tension [MPa] | Global Bending Moment [N mm] |
|---|---|---|
| 15.41 | 27.58 | 1.62 × 108 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.-B.; Park, S.-H.; Jang, Y.-Y.; Huh, N.-S.; Park, S.-H.; Park, N.-H.; Park, J. Development of Automatic Crack Growth Simulation Program Based on Finite Element Analysis. Appl. Sci. 2022, 12, 3075. https://doi.org/10.3390/app12063075
Lee G-B, Park S-H, Jang Y-Y, Huh N-S, Park S-H, Park N-H, Park J. Development of Automatic Crack Growth Simulation Program Based on Finite Element Analysis. Applied Sciences. 2022; 12(6):3075. https://doi.org/10.3390/app12063075
Chicago/Turabian StyleLee, Gi-Bum, Seung-Hyun Park, Youn-Young Jang, Nam-Su Huh, Sung-Hoon Park, Noh-Hwan Park, and Jun Park. 2022. "Development of Automatic Crack Growth Simulation Program Based on Finite Element Analysis" Applied Sciences 12, no. 6: 3075. https://doi.org/10.3390/app12063075
APA StyleLee, G.-B., Park, S.-H., Jang, Y.-Y., Huh, N.-S., Park, S.-H., Park, N.-H., & Park, J. (2022). Development of Automatic Crack Growth Simulation Program Based on Finite Element Analysis. Applied Sciences, 12(6), 3075. https://doi.org/10.3390/app12063075






