Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors
Abstract
:1. Introduction
- We mathematically formulate the moving object coverage problem;
- We propose four algorithms, including two greedy algorithms and two meta-heuristic algorithms (a GA and a DPSO algorithm), for the moving object coverage problem to determine the movement of each mobile sensor, with the aim of minimizing not only the total traveled distance but also the unbalanced residual energy of the sensors;
- We describe the results of the intensive experiments we conducted to evaluate the performance of the proposed algorithms and compare it with that of the greedy algorithms;
- We present a comparison between the quality of the trajectories generated by our GA and DPSO algorithms, highlighting which one is preferable for mobile sensor movement tracking in different environments.
2. Related Works
3. Preliminaries and Problem Statement
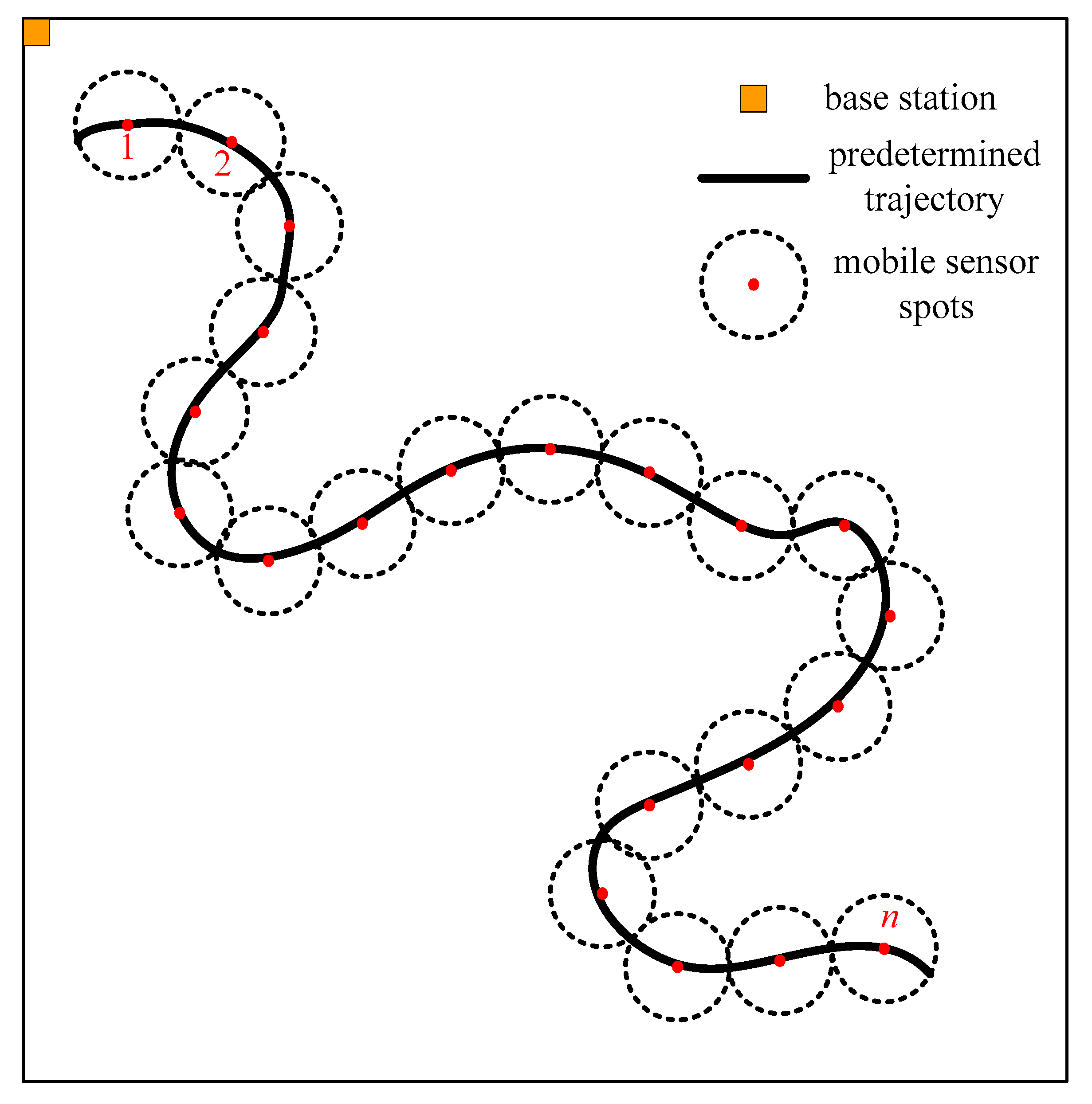
3.1. Network Model and Problem Definition
3.2. Greedy Algorithms
| Algorithm 1: Greedy_minimum_weight_matching |
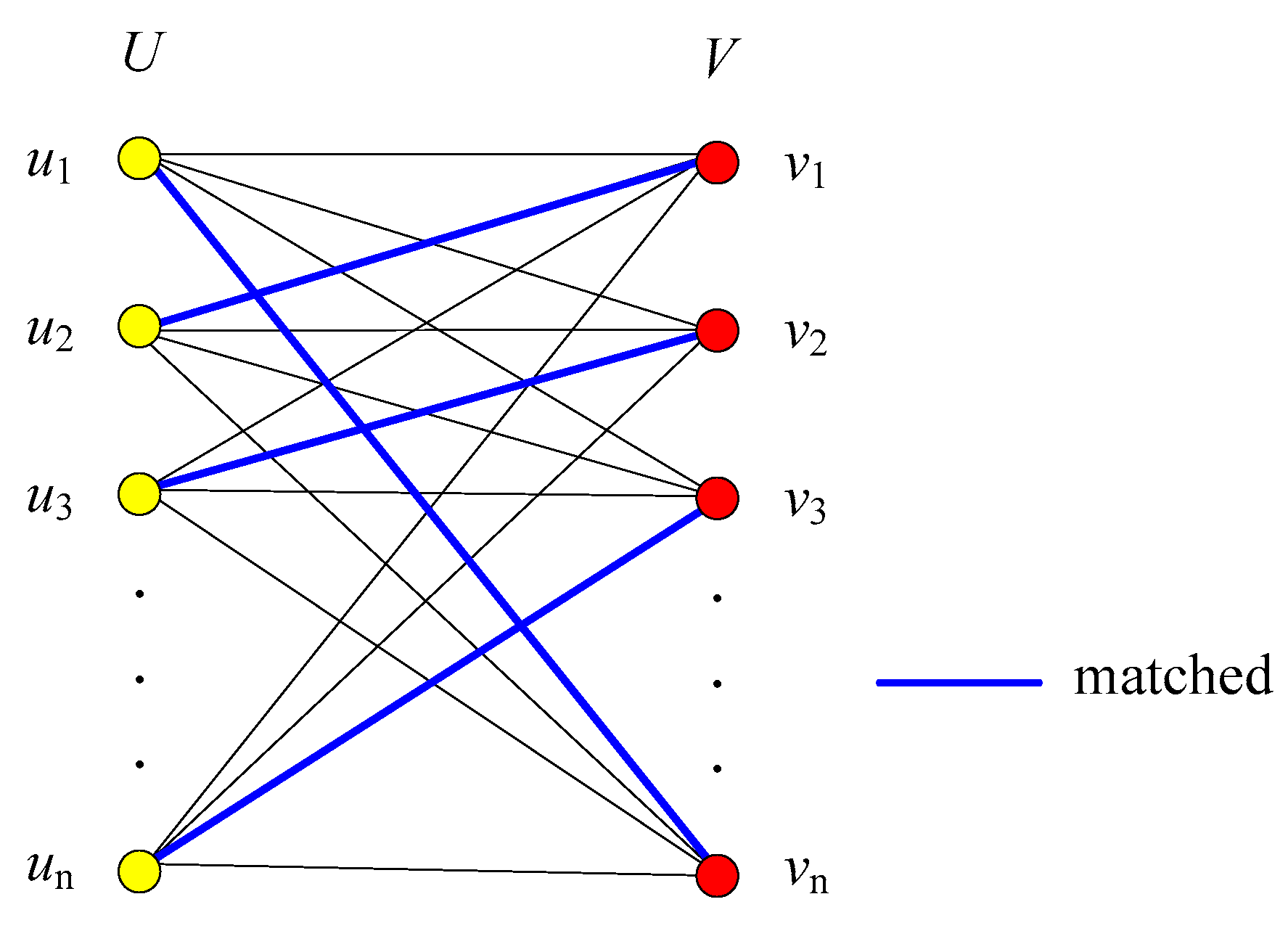
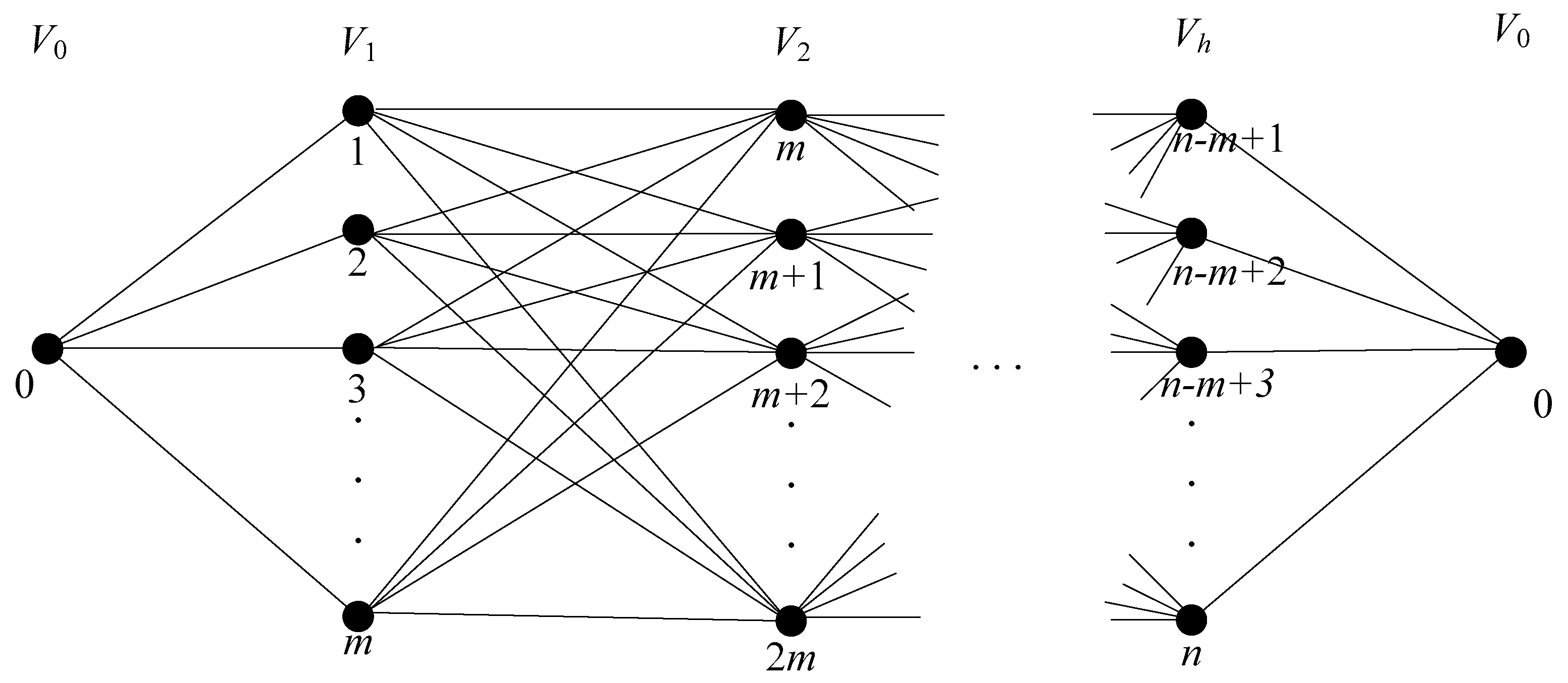
| Input: P, m, n Output: A set M of minimum weight matchings of sensor spots 1: Partition P into , , …, zones, where h = and = {(i − 1)m + 1, …, im}, 1 ≤ i ≤ h 2: M = φ 3: i = 1 4: while i < h do 5: Construct a weighted complete bipartite graph = (, , E), where E refers to the weighted edges between and . 6: Find the minimum weight matching of by using the Hungarian method 7: M = M ∪ 8: i = i + 1 9: end while 10: return M = {, , …, } |
| Algorithm 2: Greedy_bottleneck_matching |
| Input: P, m, n Output: A set M of bottleneck matchings of sensor positions 1: Partition P into , , …, zones, where h = and = {(i − 1)m + 1, …, im}, 1 ≤ i ≤ h 2: M = φ 3: i = 1 4: while i < h do 5: Construct a weighted complete bipartite graph = (, , E), where E represents the weighted edges between and . 6: Find the bottleneck matching of by using the Hopcroft–Karp algorithm 7: M = M ∪ 8: i = i + 1 9: end while 10: return M = {, , …, } |
4. Proposed GA and DPSO Solutions
4.1. GA
4.1.1. Chromosome Representation
4.1.2. Fitness Evaluation
4.1.3. Selection
4.1.4. GA Operators
Crossover
Mutation
4.1.5. Pseudocode of the GA
| Algorithm 3: GA_moving_object_coverage |
| 1: Generate the initial population 2: Evaluate the fitness of each individual in the population 3: while (number of generation < maximum generations) do 4: while (current crossover queue length < population size) do 5: Randomly select two different chromosomes C1 and C2 6: if (C1.fitness > C2.fitness) 7: Reproduce chromosome C1 to crossover queue 8: else 9: Reproduce chromosome C2 to crossover queue 10: end if 11: end while 12: while (current crossover queue is not empty) do 13: Select and remove two individuals from the queue 14: Crossover the selected two individuals under a certain probability 15: Place these two individuals into the new population 16: end while 17: for (each individual in the new population) do 18: Mutating the individual under a certain probability 19: end for 20: Evaluate the fitness of each individual in the new population 21: Set the best fitness value as partial_optimal 21: Increase number of generation by 1 22: end while 23: global_optimal = partial_optimal 24: return global_optimal |
4.2. DPSO Algorithm
4.2.1. DPSO Approach
- The first component is , which represents the velocity of the particle. denotes the mutation operator, which corresponds to a probability of In other words, a uniform random number r is generated between 0 and 1. If r is less than , the mutation operator is applied to generate a possible new particle by . Otherwise, the current particle is kept as
- The second component is the “cognitive” part of the particle; that is, it represents the individual-level thinking of the particle. represents the crossover operator, which corresponds to a probability of Depending on the choice of a uniform random number, the outcome is either or .
- The third component, is the “social” part of the particle, representing interparticle collaboration. denotes the crossover operator, which corresponds to a probability of Depending on the choice of a uniform random number, the outcome is either or .
- The mutation operator on a position is defined as the exchange of two randomly selected sensor spots in a randomly selected zone. For example, with = |1 2 3|4 5 6|7 8 9| and the mutation point being the first and second positions in zone 3, by applying the mutation operator, we obtain = |1 2 3|4 5 6|8 7 9|.
- The crossover operator is defined as taking and as the first and second parents as the crossover operator, respectively. When the crossover operator is applied, each of the different sensor spots in and , from left to right, is taken to be exchanged if a uniform random number r ∈ (0, 1) is generated and if r < . For example, with = |1 2 3|5 4 6|9 7 8| and = |1 2 3|5 4 6|9 8 7|, we obtain = |1 2 3|5 4 6|9 8 7| if both generated uniform random numbers are less than . The exchanged result must be a legal solution; therefore, some adjustments must be made. In our implementation, if = |1 2 3|5 4 6|9 8 8| after the exchange of and on the second position in zone 3, we adjust the third position in zone 3 from 8 to 7 to ensure its legality as a solution.
- The crossover operator is defined as the taking of and as the first and second parent for the crossover operator, respectively. When the crossover operator is applied, similar to the operation in , each of the sensor spots in and is taken, from left to right, to be exchanged if a uniform random number r ∈ (0, 1) is generated and if r < .
4.2.2. Pseudocode of the DPSO Algorithm
| Algorithm 4: DPSO_moving_object_coverage |
| 1: Initialize the parameters of DPSO. Set the swarm size and generate the initial particles with position and velocity, and set the generation counter to 1. 2: for (each particle in the swarm) do 3: Compute the fitness value of each particle 4: Set the particle_best value of each particle to itself 5: end for 6: Set global_best value to the best fit particle 7: while (number of generation < maximum generations) do 8: for (each particle in the swarm) do 9: Compute the new velocity and new position by using the mutation operator and crossover operators and in (17) under a certain probability 10: Update fitness of new position 11: if (new fitness < particle_best) 12: particle_best = new fitness 13: end if 14: end for 15: Find the particle with the best fitness and update global_best 16: Increase the number of generation by 1 17: end while 18: return global_best |
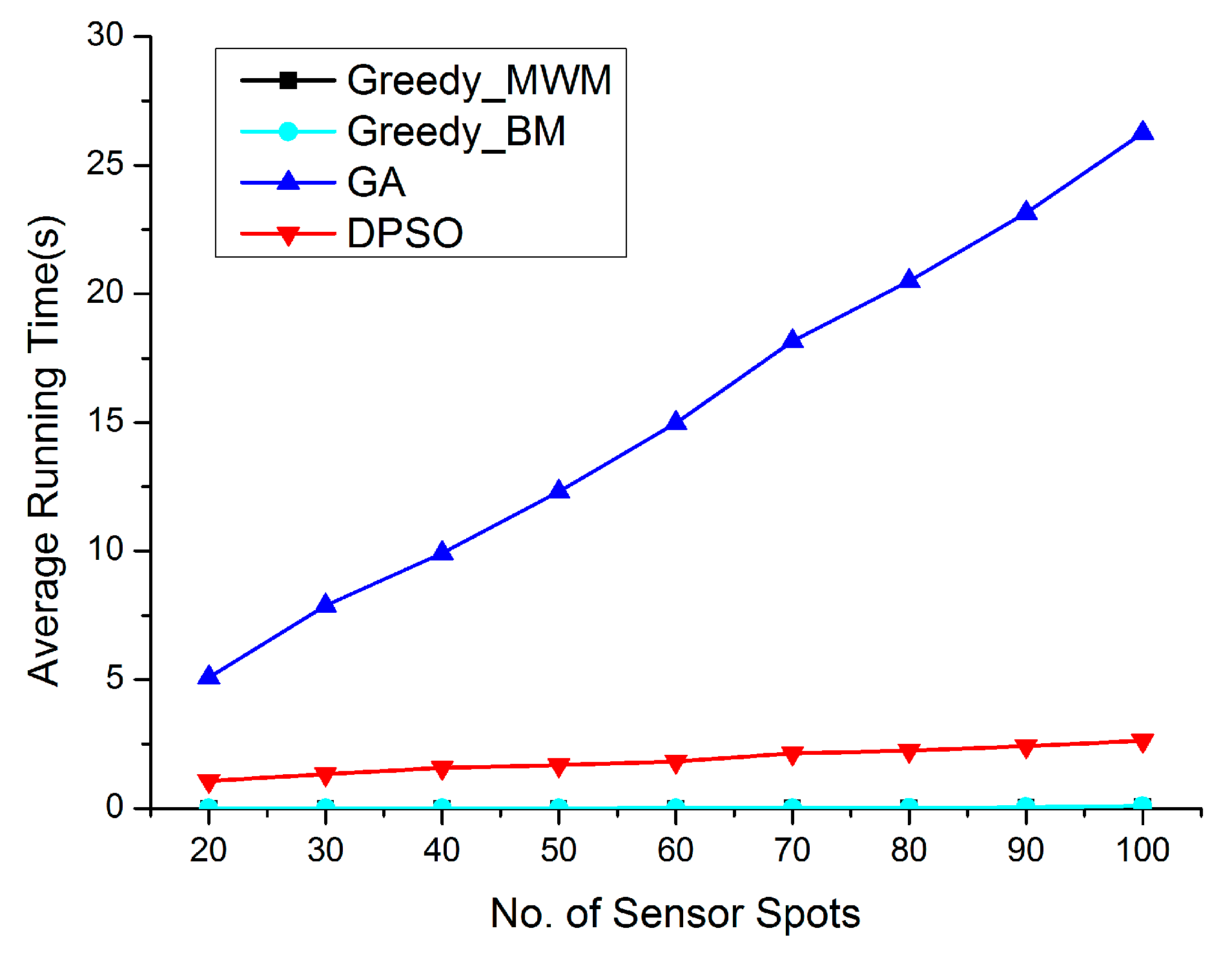
5. Performance Evaluation and Comparison
- The GA generated better trajectories than the DPSO algorithm in 7 of the 40 scenarios;
- The DPSO algorithm generated significantly better trajectories than the GA in 18 of the 40 scenarios;
- The GA and DPSO generated similarly performing trajectories in 15 of the 40 scenarios.
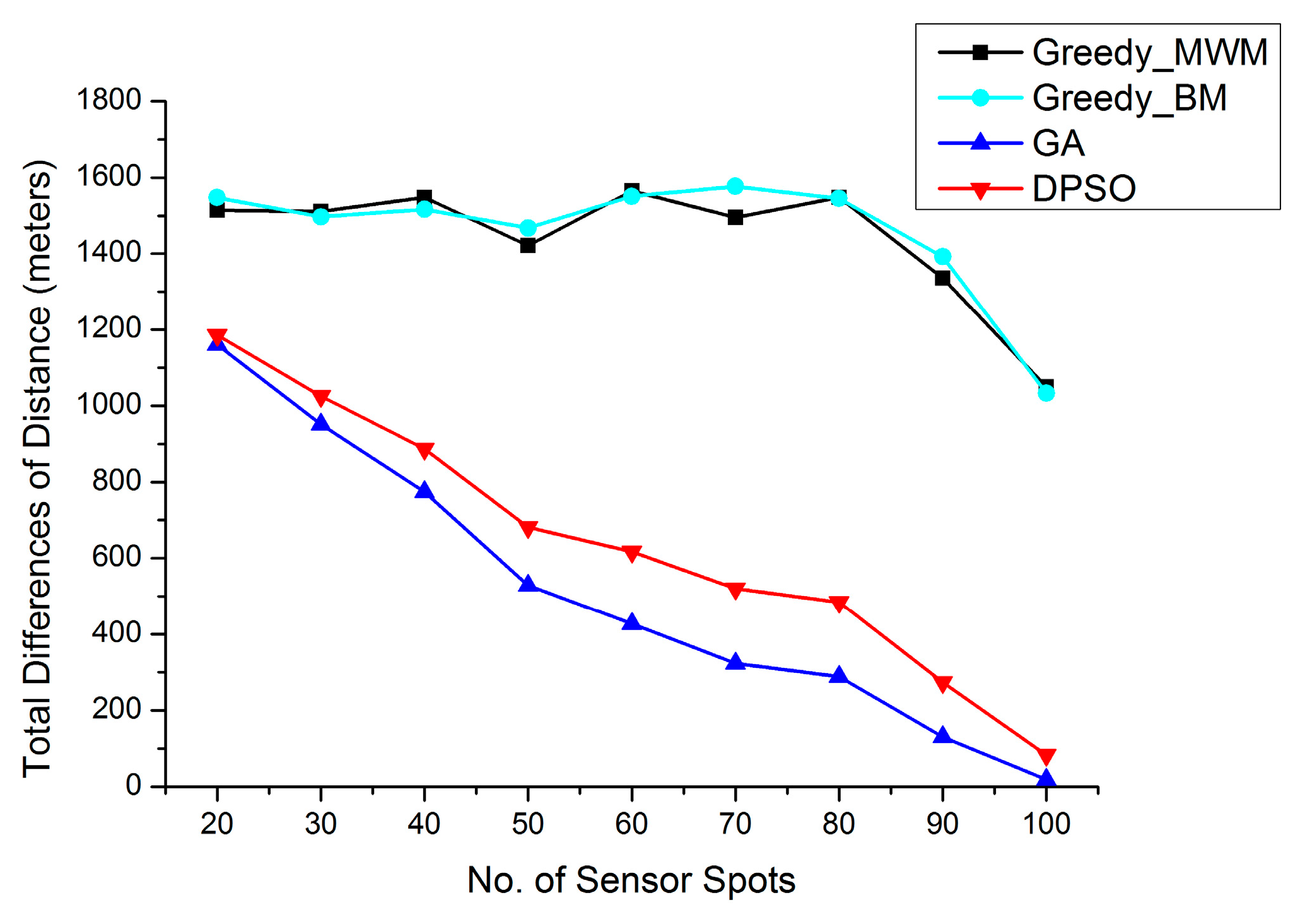
- The GA generated better trajectories than the DPSO algorithm in terms of average traveled distance as the problem scale increased;
- The GA generated significantly better trajectories than the DPSO algorithm in terms of the average difference in the distance traveled, regardless of the problem scale;
- The GA generated significantly better trajectories than the DPSO algorithm in terms of average fitness values, regardless of the problem scale.
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Kulaib, A.R.; Shubair, R.M.; Al-Qutayri, M.A.; Ng, J.W.P. An overview of localization techniques for wireless sensor networks. In Proceedings of the International Conference on Innovations in Information Technology, Abu Dhabi, United Arab Emirates, 25–27 April 2011; pp. 167–172. [Google Scholar] [CrossRef]
- Sibley, G.T.; Rahimi, M.H.; Sukhatme, G.S. Robomote: A tiny mobile robot platform for large-scale sensor networks. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 1143–1148. [Google Scholar] [CrossRef]
- Liang, C.K.; Lin, Y.H. A coverage optimization strategy for mobile wireless sensor networks based on genetic algorithm. In Proceedings of the IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 1272–1275. [Google Scholar] [CrossRef]
- Aslam, J.; Butler, Z.; Constantin, F.; Crespi, V.; Cybenko, G.; Rus, D. Tracking a moving object with a binary sensor network. In Proceedings of the International Conference on Embedded networked sensor systems, Dana Point, CA, USA, 20–21 October 2003; pp. 150–161. [Google Scholar] [CrossRef]
- Kung, H.T.; Vlah, D. Efficient location tracking using sensor networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 16–20 March 2003. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, G. DCTC: Dynamic convoy tree-based collaboration for target tracking in sensor networks. IEEE Trans. Wireless Commun. 2004, 3, 1689–1701. [Google Scholar] [CrossRef] [Green Version]
- Jin, G.Y.; Lu, X.Y.; Park, M.S. Dynamic clustering for object tracking in wireless sensor networks. In Proceedings of the International Symposium on Ubiquitous Computing Systems, Seoul, Korea, 11–13 October 2006; pp. 200–209. [Google Scholar] [CrossRef]
- Souza, E.L.; Nakamura, E.F.; Pazzi, R.W. Target tracking for sensor networks: A survey. ACM Comput. Surv. 2017, 49, 1–31. [Google Scholar] [CrossRef]
- Leela Rani, P.; Sathish Kumar, G.A. Detecting Anonymous Target and Predicting Target Trajectories in Wireless Sensor Networks. Symmetry 2021, 13, 719. [Google Scholar] [CrossRef]
- Manjeshwar, A.; Agrawal, D.P. APTEEN: A hybrid protocol for efficient routing and comprehensive information retrieval in wireless sensor networks. In Proceedings of the International Parallel and Distributed Processing Symposium, Lauderdale, FL, USA, 15–19 April 2002; pp. 195–202. [Google Scholar] [CrossRef]
- Chen, T.S.; Chen, J.J.; Wu, C.H. Distributed object tracking using moving trajectories in wireless sensor networks. Wirel. Netw. 2016, 22, 2415–2437. [Google Scholar] [CrossRef]
- Lin, K.W.; Hsieh, M.H.; Tseng, V.S. A novel prediction based strategy for object tracking in sensor networks by mining seamless temporal movement patterns. Expert Syst. Appl. 2010, 37, 2799–2807. [Google Scholar] [CrossRef]
- Yu, X.; Liang, J. Genetic fuzzy tree based node moving strategy of target tracking in multimodal wireless sensor networks. IEEE Access 2018, 6, 25764–25772. [Google Scholar] [CrossRef]
- Liu, B.; Dousse, O.; Nain, P.; Towsley, D. Dynamic Coverage of Mobile Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 301–311. [Google Scholar] [CrossRef] [Green Version]
- Burgos, U.; Amozarrain, U.; Gomez-Calzado, C.; Lafuente, A. Routing in Mobile Wireless Sensor Networks: A Leader-Based Approach. Sensors 2017, 17, 1587. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, N.T.; Liu, B.H. The mobile sensor deployment problem and the target coverage problem in mobile wireless sensor networks are NP-hard. IEEE Syst. J. 2019, 13, 1312–1315. [Google Scholar] [CrossRef]
- De Freitas, E.P.; Heimfarth, T.; Netto, I.F.; Lino, C.E.; Pereira, C.E.; Ferreira, A.M.; Wagner, F.R.; Freitas, L.T. UAV relay network to support WSN connectivity. In Proceedings of the International Congress on Ultra Modern Telecommunications and Control Systems (ICUMT), Moscow, Russia, 18–20 October 2010; pp. 309–314. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, H.A.; Barreto, R.S.; Fontao, A.L.; Loureiro, A.A.; Nakamura, E.F. A novel greedy forward algorithm for routing data toward a high speed sink in wireless sensor networks. In Proceedings of the 19th International Conference on Computer Communications and Networks (ICCCN), Zurich, Switzerland, 2–5 August 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Jawhar, I.; Mohamed, N.; Al-Jaroodi, J.; Zhang, S. A framework for using unmanned aerial vehicles for data collection in linear wireless sensor networks. J. Intell. Rob. Syst. 2014, 74, 437–453. [Google Scholar] [CrossRef]
- Ali, Z.A.; Masroor, S.; Aamir, M. UAV based data gathering in wireless sensor networks. Wireless Pers. Commun. 2019, 106, 1801–1811. [Google Scholar] [CrossRef]
- Daponte, P.; Vitto, L.D.; Mazzilli, G.; Picariello, F.; Rapuano, S.; Riccio, M. Metrology for drone and drone for metrology: Measurement systems on small civilian drones. In Proceedings of the 2015 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 4–5 June 2015; pp. 306–311. [Google Scholar] [CrossRef]
- Flammini, F.; Pragliola, C.; Smarra, G.; Naddei, R. Towards automated drone surveillance in railways: State-of-the-art and future directions. In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems (ACIVS), Lecce, Italy, 24–27 October 2016; pp. 336–348. [Google Scholar] [CrossRef]
- Hu, Z.; Gu, D.; Song, Z.; Li, H. Localization in wireless sensor networks using a mobile anchor node. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; pp. 602–607. [Google Scholar] [CrossRef]
- Huang, K.F.; Chen, P.J.; Jou, E. Grid-based localization mechanism with mobile reference node in wireless sensor networks. J. Electron. Sci. Technol. 2014, 12, 283–287. [Google Scholar] [CrossRef]
- Farmani, M.; Moradi, H.; Dehghan, S.M. The modified Hilbert path for mobile-beacon-based localization in wireless sensor networks. Trans. Inst. Meas. Control 2013, 36, 916–923. [Google Scholar] [CrossRef]
- Rezazadeh, J.; Moradi, M.; Ismail, A.S. Superior path planning mechanism for mobile beacon-assisted localization in wireless sensor networks. IEEE Sens. J. 2014, 14, 3052–3064. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, S.; Chen, J.; Ren, T. Node localization algorithm of wireless sensor networks with mobile beacon node. Peer-to-Peer Netw. Appl. 2017, 10, 795–807. [Google Scholar] [CrossRef]
- Alomari, A.; Phillips, W.; Aslam, N.; Comeau, F. Swarm intelligence optimization techniques for obstacle-avoidance mobility-assisted localization in wireless sensor networks. IEEE Access 2018, 6, 22368–22385. [Google Scholar] [CrossRef]
- Li, Z.; Lei, L. Sensor node deployment in wireless sensor networks based on improved particle swarm optimization. In Proceedings of the International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Chengdu, China, 25–27 September 2009; pp. 215–217. [Google Scholar] [CrossRef]
- Peiravi, A.; Mashhadi, H.R.; Javadi, S.H. An optimal energy-efficient clustering method in wireless sensor networks using multi-objective genetic algorithm. Int. J. Commun. Syst. 2013, 26, 114–126. [Google Scholar] [CrossRef]
- Zungeru, A.M.; Seng, K.P.; Ang, L.M.; Conge Chia, W. Energy efficiency performance improvements for anti-based routing algorithm in wireless sensor networks. J. Sens. 2013, 2013, 759654. [Google Scholar] [CrossRef]
- Norouzi, A.; Zaim, A.H. Genetic algorithm application in optimization of wireless sensor networks. Sci. World J. 2014, 2014, 286575. [Google Scholar] [CrossRef] [PubMed]
- Lanza-Gutiettez, J.M.; Gomez-Pulido, J.A. Assuming multiobjective metaheuristics to solve a three-objective optimization problem for relay node deployment in wireless sensor networks. Appl. Soft Comput. 2015, 30, 675–687. [Google Scholar] [CrossRef]
- Chang, W.L.; Zeng, D.; Chen, R.C.; Guo, D. An artificial bee colony algorithm for data collection path planning in sparse wireless sensor networks. Int. J. Mach. Learn. Cybern. 2015, 6, 375–383. [Google Scholar] [CrossRef]
- Zeng, B.; Dong, Y. An improved harmony search based energy-efficient routing algorithm for wireless sensor networks. Appl. Soft Comput. 2016, 41, 135–147. [Google Scholar] [CrossRef]
- Zhu, N.; Vasilakos, A.V. A genetic framework for energy evaluation on wireless sensor networks. Wirel. Netw. 2016, 22, 1199–1220. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Efrat, A.; Itai, A.; Katz, M.J. Geometry helps in bottleneck matching and related problems. Algorithmica 2001, 31, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D.E. Genetic algorithms; Pearson Education: New Delhi, India, 2006. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; Wiley: Toronto, ON, Canada, 2000. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Pan, Q.; Tasgetiren, M.F.; Liang, Y.C. A discrete particle swarm optimization algorithm for the permutation flowshop sequencing problem with makespan criterion. In Research and Development in Intelligent Systems XXIII, SGAI 2006; Bramer, M., Coenen, F., Tuson, A., Eds.; Springer: London, UK, 2006; pp. 19–31. [Google Scholar] [CrossRef]
- Lian, Z.; Gi, X.; Jiao, B. A novel particle swarm optimization algorithm for permutation flow-shop scheduling to minimize makespan. Chaos Solitons Fractals 2008, 35, 851–861. [Google Scholar] [CrossRef]
- Shi, X.; Liang, Y.; Lee, H.; Lu, C.; Wang, Q. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Abdel-Kader, R.F. Hybrid discrete PSO with GA operators for efficient QoS-multicast routing. Ain Shams Eng. J. 2011, 2, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inf. 2013, 9, 132–141. [Google Scholar] [CrossRef]
- Xu, S.H.; Liu, J.P.; Zhang, F.H.; Wang, L.; Sun, L.J. A combination of genetic algorithm and particle swarm optimization for vehicle routing problem with time windows. Sensors 2015, 15, 21033–21053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MATLAB Two-Sample T-Test. Available online: http://www.mathworks.com/help/stats/ttest2.html (accessed on 3 December 2021).





| Parameter | Value | Meaning |
|---|---|---|
| AM | 1000 m × 1000 m | Network monitoring area |
| r | 25 m | Sensors’ coverage radius |
| (x0, y0) | (0, 0) | Base station location |
| n | 20, 30,…, 100 | Number of sensor spots |
| m | 5 | Number of mobile sensors |
| P | 100 | Population size |
| Pc | 0.8 | Probability of crossover (GA only) |
| Pm | 0.1 | Probability of mutation (GA only) |
| 0.1 | Probability of mutation (DPSO only) | |
| 0.5 | Probability of crossover (DPSO only) | |
| 0.5 | Probability of crossover (DPSO only) | |
| Ic | 100, 1000 | Number of generations (GA) or iterations (DPSO) |
| Scenario | Average Traveled Distance and Standard Deviation of Generated Trajectories (50 Trials) | p-Value (Test-T) | Average Are Statistically Different | Winner | ||
|---|---|---|---|---|---|---|
| GA | DPSO | GA | PSO | |||
| 1 | 2992.4393 ± 1.8196 | 2992.9436 ± 3.6418 | 0.381 | no | ||
| 2 | 3128.3941 ± 2.0386 | 3129.8614 ± 2.7980 | 0.005 | yes | X | |
| 3 | 3209.4913 ± 1.0822 | 3207.5020 ± 2.0464 | 0.000 | yes | X | |
| 4 | 3220.0346 ± 0.9116 | 3219.3740 ± 2.2181 | 0.049 | yes | X | |
| 5 | 2856.9409 ± 3.8808 | 2854.5864 ± 5.4068 | 0.011 | yes | X | |
| 6 | 3014.5629 ± 3.0619 | 3011.0986 ± 4.2573 | 0.000 | yes | X | |
| 7 | 3001.8451 ± 3.4108 | 3002.7971 ± 3.7244 | 0.210 | no | ||
| 8 | 2991.8435 ± 1.5807 | 2990.9248 ± 2.5517 | 0.034 | yes | X | |
| 9 | 2902.0144 ± 2.6819 | 2899.2818 ± 3.7795 | 0.000 | yes | X | |
| 10 | 2989.3441 ± 1.7431 | 2988.9386 ± 2.7793 | 0.383 | no | ||
| 11 | 3058.3370 ± 1.3551 | 3057.3041 ± 2.9977 | 0.009 | yes | X | |
| 12 | 3030.9654 ± 0.5501 | 3027.7668 ± 3.4714 | 0.000 | yes | X | |
| 13 | 3010.7018 ± 1.2675 | 3008.8785 ± 2.7130 | 0.000 | yes | X | |
| 14 | 2812.4526 ± 2.9295 | 2807.2978 ± 4.4937 | 0.000 | yes | X | |
| 15 | 3003.6262 ± 3.5982 | 2999.7705 ± 4.8891 | 0.011 | yes | X | |
| 16 | 3053.5578 ± 1.4282 | 3054.4615 ± 2.9521 | 0.088 | no | ||
| 17 | 3008.8329 ± 1.6307 | 3005.3759 ± 3.9018 | 0.000 | yes | X | |
| 18 | 2622.5295 ± 6.0524 | 2628.4946 ± 7.1286 | 0.000 | yes | X | |
| 19 | 3081.6292 ± 2.5140 | 3085.4334 ± 4.9469 | 0.000 | yes | X | |
| 20 | 3250.4881 ± 2.2775 | 3248.7471 ± 2.5949 | 0.002 | yes | X | |
| 21 | 2972.0539 ± 3.0167 | 2972.9801 ± 3.3745 | 0.158 | no | ||
| 22 | 2973.8529 ± 2.1972 | 2973.3860 ± 2.8221 | 0.374 | no | ||
| 23 | 2874.8155 ± 2.4585 | 2870.9051 ± 4.1883 | 0.000 | yes | X | |
| 24 | 3100.4265 ± 1.6634 | 3101.8846 ± 4.0950 | 0.033 | yes | X | |
| 25 | 2977.7085 ± 3.4182 | 2978.8530 ± 4.6732 | 0.187 | no | ||
| 26 | 2900.0235 ± 1.9922 | 2901.5632 ± 3.4843 | 0.008 | yes | X | |
| 27 | 3045.3884 ± 2.1302 | 3045.2916 ± 2.9441 | 0.833 | no | ||
| 28 | 3157.2719 ± 1.1186 | 3156.7508 ± 2.8880 | 0.242 | no | ||
| 29 | 3019.8295 ± 1.7735 | 3020.7697 ± 3.2370 | 0.093 | no | ||
| 30 | 2797.1633 ± 3.3278 | 2796.4397 ± 6.5181 | 0.479 | no | ||
| 31 | 3010.7305 ± 1.7398 | 3013.0609 ± 3.4161 | 0.000 | yes | X | |
| 32 | 2995.7100 ± 2.1156 | 2993.5887 ± 4.9071 | 0.005 | yes | X | |
| 33 | 2774.9727 ± 2.1628 | 2776.1326 ± 5.0659 | 0.164 | no | ||
| 34 | 2868.4977 ± 2.5431 | 2864.9081 ± 5.0707 | 0.000 | yes | X | |
| 35 | 2917.6947 ± 4.3329 | 2919.3911 ± 5.5848 | 0.115 | no | ||
| 36 | 2974.5797 ± 2.9380 | 2971.5000 ± 4.3944 | 0.000 | yes | X | |
| 37 | 2974.2939 ± 3.3901 | 2975.9473 ± 5.2312 | 0.056 | no | ||
| 38 | 3057.1951 ± 1.6681 | 3058.3120 ± 2.6079 | 0.018 | yes | X | |
| 39 | 2856.6309 ± 2.9443 | 2852.8555 ± 3.4337 | 0.000 | yes | X | |
| 40 | 2973.7681 ± 3.8462 | 2971.8546 ± 6.2907 | 0.077 | no | ||
| Total | 15/40 | 7/40 | 18/40 | |||
| Problem Scales | Similar Quality | GA Wins | DPSO Wins |
|---|---|---|---|
| 20 | 23 | 4 | 13 |
| 30 | 15 | 5 | 20 |
| 40 | 15 | 7 | 18 |
| 50 | 13 | 11 | 16 |
| 60 | 10 | 15 | 15 |
| 70 | 10 | 29 | 1 |
| 80 | 5 | 31 | 4 |
| 90 | 0 | 40 | 0 |
| 100 | 0 | 40 | 0 |
| Problem Scales | Similar Quality | GA Wins | DPSO Wins |
|---|---|---|---|
| 20 | 0 | 40 | 0 |
| 30 | 0 | 40 | 0 |
| 40 | 0 | 40 | 0 |
| 50 | 0 | 40 | 0 |
| 60 | 0 | 40 | 0 |
| 70 | 0 | 40 | 0 |
| 80 | 0 | 40 | 0 |
| 90 | 0 | 40 | 0 |
| 100 | 0 | 40 | 0 |
| Problem Scales | Similar Quality | GA Wins | DPSO Wins |
|---|---|---|---|
| 20 | 0 | 40 | 0 |
| 30 | 0 | 40 | 0 |
| 40 | 0 | 40 | 0 |
| 50 | 0 | 40 | 0 |
| 60 | 0 | 40 | 0 |
| 70 | 0 | 40 | 0 |
| 80 | 0 | 40 | 0 |
| 90 | 0 | 40 | 0 |
| 100 | 0 | 40 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-W.; Liang, C.-K. Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors. Appl. Sci. 2022, 12, 3340. https://doi.org/10.3390/app12073340
Chen H-W, Liang C-K. Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors. Applied Sciences. 2022; 12(7):3340. https://doi.org/10.3390/app12073340
Chicago/Turabian StyleChen, Hao-Wei, and Chiu-Kuo Liang. 2022. "Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors" Applied Sciences 12, no. 7: 3340. https://doi.org/10.3390/app12073340
APA StyleChen, H. -W., & Liang, C. -K. (2022). Genetic Algorithm versus Discrete Particle Swarm Optimization Algorithm for Energy-Efficient Moving Object Coverage Using Mobile Sensors. Applied Sciences, 12(7), 3340. https://doi.org/10.3390/app12073340






